Древние храмы и гробницы, религиозные сооружения строились с учетом астрономических наблюдений. Это видно из строгой ориентации многих сооружений на небесные светила. И в наши дни, когда возникает догадка, что сооружение было направлено на какую-то конкретную звезду, это можно проверить с большой долей точности, используя знание прецессии.
В древности объектом поклонения являлись «небесные боги».
Воссоздавая картину неба в конкретную эпоху, мы можем узнать, что являлось важным для отправления определенного религиозного культа в то далекое время.
До того, как компьютеры стали общедоступными, долгое время прецессию вычисляли «вручную», на бумаге. Это было довольно сложно, поскольку приходилось, например, использовать формулы сферической геометрии. Тем более появлялась сложность в расчетах при проверке нескольких звезд или дат. В наши дни сделать вычисления проще, существуют персональные компьютеры, и прецессию можно узнать, задав необходимые данные в астрономическую программу.

Воздействие луны, солнца и планет, наряду с формой самой земли, являются причинами прецессионного движения земли. Эти факторы заставляет ось нашей планеты совершать очень медленное круговое вращение, радиусом равным наклону эклиптики.
Можно представить себе вращающуюся Землю, причем ось ее вращения сама совершает круговое движение, делая полный оборот приблизительно за 26000 лет.
Для наблюдателя прецессия представляется медленным перемещением звездного неба. То же самое звездное небо появляется через 26000 лет.
На небесной сфере ось описывает окружность так называемого малого круга небесной сферы с центром в северном полюсе эклиптики для северного полушария и в южном полюсе эклиптики — для южного полушария, с угловым радиусом примерно 23,5 градуса (угол наклона земной оси к плоскости эклиптики).
Также наблюдается сложное движение, быстрое относительно периода прецессии «покачивание полюсов», называемое нутацией. Период нутации земной оси равен 18,6 лет, её амплитуда составляет около 17″ (угловых секунд). Эти короткие колебания каждые 18,6 года влияют на размеренное движение прецессии. Однако, нутацию обычно игнорируют в расчетах прецессии, поскольку определить ее для отдаленного периода не представляется возможным.
При этом на угол наклона земной оси к плоскости эклиптики прецессия (в отличие от нутации) не влияет.
Цикл прецессии можно разделить на два полуцикла в 13000 лет, в начале которых звезды находятся в своем самом низком и самом высоком положении над горизонтом.

Ранее о прецессии в работе Поляриссимы севера.
Прецессия и нутация не свойственны движению самих звезд. Видимое изменение положения звезд на небе на самом деле является следствием вращения Земли.
Однако и сами ночные светила движутся и чем ближе к нам они находятся, тем заметнее эти перемещения. Изменение положения звезд определяется изменением их
склонения
и
прямого восхождения
.
Заметив движение Солнца «на восток» вдоль линии эклиптики со скоростью примерно 1 градус 23 минуты в столетие относительно неподвижной звезды или созвездия, древние египтяне без особого труда заключили, что полный цикл для возвращения на прежнее место должен занимать приблизительно 26000 лет. Как именно они пришли к этой идее? По всей видимости поняли, что этот процесс представляет из себя «цикл» (то есть должен был иметь начало и конец), и этот цикл повторяется:)
Расчеты не составляют труда:
01° 23′ = 1.3833° — за 100 лет.
13.833° — за 1000 лет.
180° — за 13000 лет – половина цикла.
360° — за 26000 лет – полный цикл.
Древние не только разделили зодиак на двенадцать частей, но также знали, что солнце проходит 12 областей неба, находясь при этом в каждой области 2160 лет. Если умножить 2160 лет на 12, то получается 25 920, время цикла прецессии, Великий год Платона. Это очень большой срок, но его делили на периоды в 2160 лет, а этот период, в свою очередь, делили на 30 градусов, получая маленькие периоды по 72 года, ставшие базисными в концепции «вечного возвращения».
амиды
Как менялось положение звезд (изменение небесных координат) в результате прецессии земной оси для наблюдателя с земли, находящегося в районе Великой пирамиды?
Египетских астрономов интересовало время появления из-за горизонта звезд и пересечение ими меридиана, особенно это касалось Сириуса и созвездия Ориона, и было бы просто невероятно, если бы они не заметили смещения этих звезд.

Сириус является одной из самых близких к нам звезд и находится на расстоянии 8,4 световых лет. Его склонение меняется на -1,21 секунды в год. Понятно, что за тысячи лет это смещение довольно существенно, и потому должно быть учтено. Что касается звезд пояса Ориона, то они от нас расположены очень далеко, на расстоянии 1400 световых лет, и потому их смещение зафиксировать не удалось. Вряд ли смещение, если оно и было, составило за прошедшее с эпохи пирамид время больше одной минуты.
Для Сириуса, 10500 лет до нэ. склонение составляло -58.43 в начале цикла, в самом нижнем положении на небе, высота составляла всего лишь 1.06 градуса над горизонтом . В 7500 году до нэ. звезда пересекла линию меридиана уже под 15.6 градусами, и этот угол постепенно увеличивается. В 2000 году уже 43.3 градуса.
Эффект прецессии лучше всего наблюдать на меридиональной линии.

Таблица 1
Для Альнитак пояса Ориона, наименьшее склонение (ок. -50 градусов) было в 10500 году до н.э. В эпоху пирамид, ок.2500 года до н.э., наклон составлял -15 градусов. Приблизительно через 13000 лет, в 2500 году н.э. звезда достигнет своего максимума и будет находиться под самым большим склонением (ок. -0,8 градусов), очень близко к небесному экватору.

Затем начнется движение вниз с той же скоростью, до тех пор, пока звезда не достигнет своего самого нижнего положения на линии горизонта.
Это произойдет еще через 13 тысяч лет.

Египтологи считают, что религиозные представления, нашедшие свое выражение в эпоху строительства пирамид, возникли, по крайней мере, за 500 лет до нее. За 500 лет наблюдений — между 2950 и 2450 годами до н.э. — изменение склонения Дзеты Ориона составило приблизительно 2 градуса 16 минут.
Это дает скорость изменения угла, равное примерно 27 минутам в столетие — это значение равно видимому размеру луны. Прецессия приводит к изменению угла наклона звезды примерно на полградуса в столетие. За столетие, в крайнем случае, два, это смещение однозначно должно было быть замечено египтянами.
Звезда Альнитак (Дзета Ориона). Точка наблюдения – Великая пирамида.
| Звезда, Альнитак | 2500 | 500 | 1 | 500 до | 2500 до | 2750 до нэ | 7500 до нэ | 10000 до нэ |
| Азимут, восход | 92° | 94.44° | 95.83° | 97.55° | 107.24° | 108.7° | 140.4° | 152.2° |
| Прямое восхождение | 6ч06м | 4ч25м | 4ч01м | 3ч37м | 2ч 02м | 1ч50м | 21ч48м | 18ч56м |
| Склонение | -01°52′ | -3° 59′ | -5°15 | -6° 46′ | -15° 03′ | -16°17′ | — 42° 19′ | -50° 23′ |
Таблица 2. Данные StarCalc 5.72.
Для Дзеты Ориона расчеты показали, что изменение угла, под которым видна звезда при подъеме из-за горизонта, например, между 2750 г. до н.э.: 2500 г. до н.э.(250 лет) составит 1,46 градуса. Азимут 108,8 и азимут 107,24 градуса соответственно. Это в три раза больше размера полной луны, и просто невероятно, что такая информация могла пройти мимо наблюдателей за звездами.
Таким образом, египтяне наверняка знали, что звезды медленно смещаются. Отсюда можно предположить, что строители пирамиды, ориентируя южную шахту камеры царя Великой пирамиды на Альнитак Дзету Ориона (Тайны шахт Великой Пирамиды Часть1), знали, что эта звезда изменит свое положение. И еще они знали, что ориентация шахты как бы «фиксирует» какую-то временную точку общего великого цикла.
Вполне резонно заключить, что древние архитекторы знали о скорости прецессионного изменения. Таблица ниже показывает изменения в склонении и угле подъема над горизонтом (высоте) по линии меридиана для звезды Альнитак на протяжении 13 тысяч лет.
| Год | Склонение | Высота по меридиану |
| 2500 год н.э. | — 01°52′ | 58°10′ |
| 2000 год н.э. | — 1°54′ | 58°08′ |
| 1000 год н.э. | — 2°59′ | 57°03′ |
| 1 год до н.э. | — 5°15 | 54°47′ |
| 1000 год до н.э. | — 8°28′ | 51°34′ |
| 2000 год до н.э. | — 12°38′ | 47°24′ |
| 2600 год до н.э. | — 15°32′ | 44°30′ |
| 7500 год до н.э. | — 42°19′ | 17°43′ |
| 10000 год до н.э. | — 50°23′ | 09°39′ |
| 10500 год до н.э. | — 50°34′ | 09°28′ |
Таблица 3
Звезда Альнитак в нижней точке (что отмечало собой начало цикла в 10500 году до н.э.) находилась под углом склонения -50 градусов 34 минуты; то есть угол между ней и линией горизонта в южном направлении составлял 9 градусов 28 минут. В самой высокой точке в конце цикла, который наступит приблизительно в 2500 году, звезда будет иметь склонение -1 градус 52 минуты; угол наклона над горизонтом чуть более 58 градусов.
Итак, за первую половину прецессионного периода в 13000 лет Альнитак в поясе Ориона совершает подъем над южным горизонтом на угловое расстояние равное 48 градусам 42 минутам: 58° 10′ — 09°28′ = 48°42′. На такую величину изменилось склонение звезды: 50° 34′ — 01° 52′ = 48°42′. Следовательно и место восхода и захода звезды изменяется на такой же градус за установленный период.
Получается, в среднем за каждые 100 лет Альнитак смещался на 22,5 минуты по меридиану на север.
Однако, как показывают расчеты, смещения эти происходили далеко не равномерно. Об этом ниже.
Мы видим, что склонение звезды может измениться на значение вдвое больше значения наклона эклиптики (23.5°). То есть в одно время у звезды может быть почти нулевое склонение, когда она находится близко к экватору; -01° 52′, а в другое — склонение −50° 34′.
Хотя мы видим эту громадную разницу в одной экваториальной координате (склонении), соответствующая эклиптическая координата практически не изменится, т.е. не меняется положение звезды относительно движения Земли вокруг Солнца. Это движение происходит совершенно независимо от направления оси Земли, поэтому, несмотря на эту огромную разницу в склонении, расстояние звезд от эклиптики на юг или север практически не поменяются.
Теперь, имея представление о положении звезды в 10500 году до н.э., можно сказать следующее.
Положение звезд пояса Ориона на западном «берегу» Млечного Пути с поразительной точностью соответствует расположению и ориентации трех пирамид Гизе относительно Нила!
В древности была широко распространена идентификация Нила с Океаном. Даже Диодор писал, что «египтяне считали Океаном свою реку Нил, на берегах которой были рождены их боги«.
Египтяне, жившие по берегам Нила и имевшие звездную религию, стали связывать свою реку с небесным океаном — Млечным Путем. Как Нил разделяет страну на две половины, так и Млечный Путь делит ночное небо.
«Египтяне… с самой древности… изображали небеса в виде Благословенных островов, омываемых водами Нила… другие жили на берегах воображаемого небесного Нила, где они построили города; похоже на то, что египтяне не представляли без Нила небеса… «

Приблизительно в 2600-2750 году до н.э., когда строилась Великая пирамида, соответствие было заметно во время подъема Сириуса (гелиакического), совпадавшее с восходом Солнца. Пояс Ориона тогда находился не на западном «берегу» Млечного Пути, а на восточном.
«Тексты пирамид» говорят о важном «вьющемся водном потоке» на восточном краю неба, сразу вспоминается Нил, его мощное течение, поля тростника и разливы.
«Ты можешь поднять меня [умершего короля] к вьющемуся водному потоку, ты можешь
поместить меня среди богов, недвижимых звезд…» (Тексты пирамид, 1759) «Будь тверд, о, царь, на нижней стороне неба, с Прекрасной звездой на излучине вьющегося потока…«(Тексты пирамид, 2061) «Я подошел к моим водным дорогам, которые находятся на берегу тока великой воды, к месту успокоения… которое находится на Горизонте… «(Тексты пирамид, 508) «Вьющийся водный поток течет, поля разлива наполнены водой, и я [умерший царь] направляюсь выше них к восточной стороне неба, ко дворцу, где боги примут меня, где я буду рожден снова молодым…
Часть 2 следует…

Пятьдесят восемь навигационных звёзд имеют особый статус в области астрономической навигации. Из приблизительно 6000 звёзд, видимых невооружённым глазом в оптимальных условиях, выбранные звёзды являются одними из самых ярких и охватывают 38 созвездий на небесной сфере, располагаясь в полосе от -70° до +89° склонения. Многие из навигационных звёзд получили названия в древности от вавилонян, греков, римлян и арабов.
Полярная звезда выделяется особо из-за её близости к северному полюсу мира. При навигации в Северном полушарии существуют специальные методы для определения географической широты местоположения наблюдателя и для определения величины поправки компаса по Полярной. Остальные 57 навигационных звёзд, занесённые в морские альманахи, позволяют штурману определять местоположение в любой точке Земли. Дополнительная группа из 115 «табличных звёзд» также может использоваться для астрономической навигации в условиях, когда основные труднодоступны для наблюдений.
Координаты звёзд, — склонение и прямое восхождение или звёздное дополнение, — с высокой точностью указываются в альманахах, в данной статье, для идентификации звёзд, эти величины округлены до ближайшего градуса. Помимо таблиц, используются звёздные атласы, которые помогают штурману в определении навигационных звёзд, показывают созвездия, их относительные позиции на небе и яркость.
Обзор
В оптимальных условиях около 6000 звёзд видны невооружённым глазом для наблюдателя на Земле[1]. 58 из них известны в навигационной астрономии как «навигационные звёзды», в том числе 19 звёзд первой величины, 38 звёзд второй величины и Полярная[1]. Выбор звёзд осуществляется Управлением Морского Альманаха (англ.) (рус. и Военно-морской Обсерваторией США. Обе организации выпускают ежегодный Морской Альманах (англ.) (рус., который публикуют совместно с 1958 года[2]. Критериями выбора звёзд являются их распределение по небесной сфере, яркость и лёгкость идентификации[3]. Информация о дополнительных 115 звёздах, известных как «табличные звёзды», также доступна штурману[1]. В данной статье представлена информация о названии, приблизительной позиции на небесной сфере и о видимой звёздной величине 58 навигационных звёзд в табличной форме и на звёздных картах.
Для целей навигации в России используются следующие 13 звёзд
- Полярная;
- Арктур;
- Вега;
- Капелла;
- Поллукс;
- Альтаир;
- Регул;
- Альдебаран;
- Денеб;
- Бетельгейзе;
- Процион;
- Альферац;
- Алиот;
К этим звёздам добавляются ещё 5 звезд южного полушария неба:
- Сириус, Ригель, Антарес, Спика, Фомальгаут
Чтобы безошибочно отыскать навигационную звезду, недостаточно знать, в каком созвездии она находится. В облачную погоду, например, наблюдается только часть звёзд[4].
При космических полётах существует другое ограничение: в иллюминатор виден лишь небольшой участок неба. Поэтому необходимо уметь быстро распознать нужную навигационную звезду по цвету и блеску[4].
Навигационные звёзды наблюдаются штурманом с двумя целями. В первую очередь, чтобы получить линию положения, измерив высоту звезды над горизонтом с помощью секстанта и обработав измерение методами звёздной навигации[5]. Несколько линий положения можно пересечь на карте, чтобы получить сведения о местоположении наблюдателя. Второе типичное использование навигационных звёзд заключается в определении величины поправки компаса путём вычисления азимута звезды и сравнения его с азимутом, измеренным с помощью компаса судна[6]. Существуют и другие цели наблюдения звёзд.
Штурманы обычно выбирают звёзды, используя одну из двух систем именования звёзд: по названию или по обозначению Байера[1]. Все звёзды имеют собственные имена с 1953 года[1]. Обозначения Байера используются с 1603 года и они состоят из греческой буквы, присвоенной звезде, и названия созвездия, в котором находится звезда (см. Список созвездий и их латинское название (родительный падеж))[1]. В данной статье применяются оба способа именования звёзд.
Положение каждой звезды на небесной сфере указывается с помощью экваториальной системы координат, двумя координатами: склонением и прямым восхождением (в астрономии, в навигации применяется звёздное дополнение), которые подобны широте и долготе на поверхности Земли. Чтобы определить склонение 

Важной характеристикой, представленной в таблицах и в звёздных атласах, является яркость звезды, выраженная в терминах видимой величины. Видимая величина — это логарифмическая шкала яркости, построенная таким образом, чтобы тело одной величины было примерно в 2,512 раз ярче, чем тело другой (следующей) величины[Прим. 1][7]. Таким образом, тело с яркостью 1m будет в 2.5125 или в 100 раз ярче, чем тело с яркостью в 6m[7]. Самые тусклые звёзды, которые можно увидеть через пятиметровый наземный телескоп, имеют 20-ю величину, а очень яркие объекты, такие как Солнце и полная Луна, имеют видимые величины −26m,7 и −12m,6 соответственно[7].
Таблица
| Описание полей таблицы | |
|---|---|
| Название столбца | Описание |
| № | Номер, используемый для обозначения звёзд в навигационных таблицах и на звёздных картах.[Прим. 2] |
| Название | Общепринятые названия звёзд, используемые в навигационных альманахах и на звёздных картах. |
| Обозначение по Байеру | Альтернативные обозначения звёзд, состоящие из греческой буквы, присвоенной звезде, и латинского названия созвездия в родительном падеже. |
| Этимология | Происхождение или смысл названия[8] |
Звёздное дополнение  | Угловое расстояние от точки весеннего равноденствия до круга склонения звезды, отсчитываемое к западу. |
Склонение  | Угловое расстояние от небесного экватора к северу (С) или к югу (Ю). |
| Видимая звёздная величина | Обозначение яркости звезды. |
Таблица навигационных звёзд устроена следующим образом. В первом столбце указывается идентификационный номер звезды, за которым следует общепринятое название, обозначение по Байеру и этимология. Затем даётся приблизительное положение звезды, подходящее для целей идентификации (склонение и звёздное дополнение), за которым следует видимая величина звезды. В заключительной колонке приводятся ссылки на источники данных: «Американский навигатор для практических нужд» (англ. The American Practical Navigator‘) и запись звезды в базе данных SIMBAD, проекта Центра астрономических данных в Страсбурге или CDS. Звёзды, используемые для целей навигации в России, обозначены значком
![]() .
.
| №[Прим. 2] | Название звезды (рус.)/ (англ.) | Обозначение по Байеру | Этимология | Звёздное дополнение | Склонение | Видимая звёздная величина | Примечание |
|---|---|---|---|---|---|---|---|
| 1 | Альферац / Alpheratz | α Андромеды | пуп Пегаса | 358° | С 29° | 2.06 | [8][9] |
| 2 | Анкаа / Ankaa | α Феникса | «птица Феникс» на арабском языке | 354° | Ю 42° | 2.37 | [8][10] |
| 3 | Шедар / Schedar | α Кассиопеи | грудь Кассиопеи | 350° | С 56° | 2.25 | [8][11] |
| 4 | Дифда / Diphda | β Кита | вторая лягушка (Фомальгаут был когда-то первой) | 349° | Ю 18° | 2.04 | [8][12] |
| 5 | Ахернар / Achernar | α Эридана | конец реки Эридан | 336° | Ю 57° | 0.46 | [8][13] |
| 6 | Хамаль / Hamal | α Овна | взрослый ягненок | 328° | С 23° | 2.00 | [8][14] |
| 7 | Акамар / Acamar | θ Эридана | конец реки Эридан (другая форма Ахернара) | 316° | Ю 40° | 2.9 | [8][15] |
| 8 | Менкар / Menkar | α Кита | нос (Кита) | 315° | С 04° | 2.5 | [8][16] |
| 9 | Мирфак / Mirfak | α Персея | локоть Плеяд | 309° | С 50° | 1.79 | [8][17] |
| 10 | Альдебаран / Aldebaran | α Тельца | последователь (за Плеядами) | 291° | С 16° | 0.85 перем[Прим. 3] | [8][18] |
| 11 | Ригель / Rigel | β Ориона | [левая] нога Ориона) | 282° | Ю 08° | 0.12 | [8][19] |
| 12 | Капелла / Capella | α Возничего | Козочка | 281° | С 46° | 0.08 | [8][20] |
| 13 | Беллатрикс / Bellatrix | γ Ориона | воительница | 279° | С 06° | 1.64 | [8][21] |
| 14 | Эль-Нат / Elnath | β Тельца | бодающий рог Тельца | 279° | С 29° | 1.68 | [8][22] |
| 15 | Альнилам / Alnilam | ε Ориона | нитка жемчуга | 276° | Ю 01° | 1.70 | [8][23] |
| 16 | Бетельгейзе / Betelgeuse | α Ориона | подмышка (Ориона) | 271° | С 07° | 0.50 перем[Прим. 3] | [8][24] |
| 17 | Канопус / Canopus | α Киля | город в Древнем Египте | 264° | Ю 53° | −0.72 | [8][25] |
| 18 | Сириус / Sirius | α Большого Пса | яркий, блестящий | 259° | Ю 17° | −1.46 | [8][26] |
| 19 | Адара / Adhara | ε Большого Пса | девственница | 256° | Ю 29° | 1.51 | [8][27] |
| 20 | Процион / Procyon | α Малого Пса | перед собакой (т.к. восходит перед «Собачьей звёздой», т.е. Сириусом) | 245° | С 05° | 0.38 | [8][28] |
| 21 | Поллукс / Pollux | β Близнецов | один из близнецов-Диоскуров, (второй близнец Кастор, α Близнецов) | 244° | C 28° | 1.15 | [8][29] |
| 22 | Авиор / Avior | ε Киля | придуманное в 1930-х годах имя | 234° | Ю 59° | 1.86 | [8][30] |
| 23 | Сухайль / Suhail | λ Парусов | сокращенная форма Аль- Сухайль, мужское арабское имя | 223° | Ю 43° | 2.23 | [8][31] |
| 24 | Миаплацидус / Miaplacidus | β Киля | тихие воды | 222° | Ю 70° | 1.70 | [8][32] |
| 25 | Альфард / Alphard | α Гидры | одинокая звезда | 218° | Ю 09° | 2.00 | [8][33] |
| 26 | Регул / Regulus | α Льва | принц | 208° | С 12° | 1.35 | [8][34] |
| 27 | Дубхе / Dubhe | α Большой Медведицы | спина Большой Медведицы | 194° | С 62° | 1.8 | [8][35] |
| 28 | Денебола / Denebola | β Льва | хвост Льва | 183° | С 15° | 2.14 | [8][36] |
| 29 | Гиенах / Gienah | γ Ворона | правое крыло Ворона | 176° | Ю 17° | 2.59 | [8][37] |
| 30 | Акрукс / Acrux | α Южного Креста | составлено из обозначения Байера α и латинского названия созвездия Crux | 174° | Ю 63° | 0.79 | [8][38] |
| 31 | Гакрукс / Gacrux | γ Южного Креста | составлено из обозначения Байера γ и латинского названия созвездия Crux | 172° | Ю 57° | 1.63 | [8][39] |
| 32 | Алиот / Alioth | ε Большой Медведицы | курдюк | 167° | C 56° | 1.76 | [8][40] |
| 33 | Спика / Spica | α Девы | колос пшеницы в руках Деметры | 159° | Ю 11° | 1.04 | [8][41] |
| 34 | Алькаид / Alkaid | η Большой Медведицы | от (ар.) القايد القائد «ал-каид банат наш» — «предводитель плакальщиц» | 153° | С 49° | 1.85 | [8][42] |
| 35 | Хадар / Hadar | β Центавра | нога кентавра | 149° | Ю 60° | 0.60 | [8][43] |
| 36 | Менкент / Menkent | θ Центавра | плечо Центавра | 149° | Ю 36° | 2.06 | [8][44] |
| 37 | Арктур / Arcturus | α Волопаса | Страж Медведицы | 146° | C 19° | −0.05 перем[Прим. 3] | [8][45] |
| 38 | Ригель Кентаурус / Rigil Kentaurus | α Центавра | нога Центавра | 140° | Ю 61° | −0.27 | [8][46] |
| 39 | Зубен Эльгенуби / Zubenelgenubi | α Весов | южная клешня (Скорпиона) | 138° | Ю 16° | 2.75 | [8][47] |
| 40 | Кохаб / Kochab | β Малой Медведицы | сокращённая форма от «Полярной звезды», названа так в эпоху, когда она была поляриссимой, т.е. около 1500 г. до н.э. – 300 г. н. э. | 137° | С 74° | 2.08 | [8][48][Прим. 4] |
| 41 | Альфекка / Alphecca | α Северной Короны | яркая [звезда] разорванного [ круга ] | 127° | С 27° | 2.24 | [8][49] |
| 42 | Антарес / Antares | α Скорпиона | соперник Марса (в цвете) | 113° | Ю 26° | 1.09 | [8][50] |
| 43 | Атрия / Atria | α Южного Треугольника | составлено из обозначения Байера α и латинского названия созвездия [Tri]angulum [A]ustrale | 108° | Ю 69° | 1.92 | [8][51] |
| 44 | Сабик / Sabik | η Змееносца | второй победитель или завоеватель | 103° | Ю 16° | 2.43 | [8][52] |
| 45 | Шаула / Shaula | λ Скорпиона | поднятый [хвост] Скорпиона | 097° | Ю 37° | 1.62 | [8][53] |
| 46 | Рас Альхаге / Rasalhague | α Змееносца | голова заклинателя змеи | 096° | С 13° | 2.10 | [8][54] |
| 47 | Этамин / Eltanin | γ Дракона | голова дракона | 091° | С 51° | 2.23 | [8][55] |
| 48 | Каус Аустралис / Kaus Australis | ε Стрельца | южная часть лука (Стрельца) | 084° | Ю 34° | 1.80 | [8][56] |
| 49 | Вега / Vega | α Лиры | атакующий орёл или атакующий гриф | 081° | С 39° | 0.03 | [8][57] |
| 50 | Нунки / Nunki | σ Стрельца | созвездие святого города (Эриду) | 076° | Ю 26° | 2.06 | [8][58] |
| 51 | Альтаир / Altair | α Орла | парящий орёл | 063° | С 09° | 0.77 | [8][59] |
| 52 | Пеакок / Peacock | α Павлина | транслитерация английского названия созвездия | 054° | Ю 57° | 1.91 | [8][60] |
| 53 | Денеб / Deneb | α Лебедя | хвост курицы | 050° | С 45° | 1.25 | [8][61] |
| 54 | Эниф / Enif | ε Пегаса | нос лошади | 034° | С 10° | 2.40 | [8][62] |
| 55 | Альнаир / Al Na’ir | α Журавля | яркий (хвост южной рыбы) | 028° | Ю 47° | 1.74 | [8][63] |
| 56 | Фомальгаут / Fomalhaut | α Южной Рыбы | рот южной рыбы | 016° | Ю 30° | 1.16 | [8][64] |
| 57 | Маркаб / Markab | α Пегаса | седло (Пегаса) | 014° | С 15° | 2.49 | [8][65] |
| * [Прим. 2] | Полярная звезда / Polaris[8] | α Малой Медведицы | Полярная звезда | 319° | С 89° | 2.01 перем[Прим. 3] | [8][66] |
Звёздные карты
| Объекты на звёздных картах | |
|---|---|
| Объект | Описание объекта |
| ТЕКСТ В ВЕРХНЕМ РЕГИСТРЕ | Название созвездия. |
| | Звезда величиной 1,5m и ярче. Обозначается своим именем, номером (по Флемстиду) и греческой буквой по Байеру. |
| | Звезда величиной 1,6m и тусклее. Обозначается своим именем, номером по Флемстиду и греческой буквой по Байеру. |
| | Табличная звезда величиной 2,6m и ярче. Обозначается греческой буквой по Байеру. |
| | Табличная звезда величиной 2,6m и тусклее. Обозначается греческой буквой по Байеру. |
| | Нетабличная звезда, без метки. |
| Пунктирная линия | Очертание созвездия. |
Штурманы используют звёздные карты, чтобы идентифицировать звезду по её положению относительно других звёзд. Звёздные карты, представленные в «Морском альманахе» и «Американском навигаторе…», представляют собой схемы со звёздами 5 типов, указанных в таблице справа, и охватывающие разные части небесной сферы. Две диаграммы – азимутальные проекции северной и южной полярной области. Ещё две покрывают экваториальную область небесной сферы, от склонения -30° до +30°. Экваториальные карты являются проекциями Меркатора полушарий небесной сферы. Обратите внимание, что в отличие от географических карт, восток находится слева, а запад справа. Таким образом, штурман может удерживать звёздную карту перед собой на фоне неба, и расположение звёзд на карте будет соответствовать виду небосвода[1].
На звёздных картах созвездия обозначаются прописными буквами, а их очертания обозначаются пунктирными линиями. 58 навигационных звёзд показаны синим цветом и обозначены собственными именами, номером звезды по Флемстиду и греческой буквой по Байеру. Дополнительные 115 табличных звёзд, также используемых для навигации, показаны красным цветом и помечены греческой буквой по Байеру. Некоторые дополнительные звёзды, непригодные для навигации, даны на картах для узнаваемости созвездий, они представлены небольшими безымянными красными точками.
Звёзды, видимые на экваторе
Экваториальные звёзды (часть 1)
Экваториальная область полушария небесной сферы (звёздные дополнения 
Все подписанные навигационные звёзды, изображённые на карте, являются ссылками на дополнительные сведения


Экваториальные звёзды (часть 2)
Экваториальная область полушария небесной сферы (звёздные дополнения 
Все подписанные навигационные звёзды, изображённые на карте, являются ссылками на дополнительные сведения
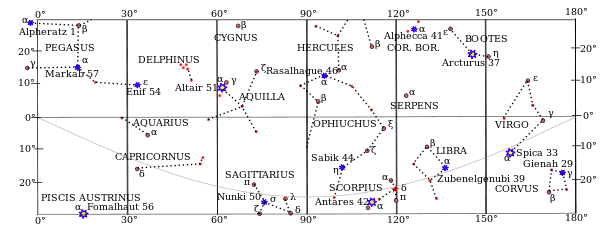

Северные звёзды


Все подписанные навигационные звёзды, изображённые на карте, являются ссылками на дополнительные сведения
11 северных звёзд, имеющих склонения от +30° до +90°, перечислены по возрастанию величины их прямого восхождения. Начиная от Шедара в созвездии Кассиопеи, список включает звёзды из созвездий Возничего, Большой и Малой Медведицы, Дракона, Лиры и Лебедя. Две самые яркие северные звезды – Вега и Капелла.
На карте склонение отложено вдоль радиуса, от +90° в центре до +30° на внешнем краю. Звёздное дополнение отложено по окружности, начиная с 0° слева на карте, увеличиваясь против часовой стрелки.
Южные звёзды


Все подписанные навигационные звёзды, изображённые на карте, являются ссылками на дополнительные сведения
18 южных звёзд, имеющих склонения от -30° до -90°, перечислены по возрастанию величины их прямого восхождения.
Начиная с Анкаа в созвездии Феникса, в список входят звёзды из созвездий Эридана, Киля, Южного Креста, Центавра, Весов, Южного Треугольника, Скорпиона, Стрельца, Павлина и Журавля. Самые яркие звёзды на южном небе – Канопус, Альфа Центавра, Ахернар и Хадар.
На карте склонение отложено вдоль радиуса, от -90° в центре до -30° на внешнем краю. Звёздное дополнение отложено по окружности, начиная с 0° справа на карте, увеличиваясь по часовой стрелке.
Примечания
- ↑ Шаг градаций яркости равен корню пятой степени из числа 100, иррациональным числом, известным как отношение Погсона.
- ↑ 1 2 3 В этом списке используются номера из навигационного альманаха, который включает только 57 звёзд. Полярная, включённая в список, указанный в «Американском навигаторе для практических нужд», дана без номера.
- ↑ 1 2 3 4 Индекс «перем» после числового значения обозначает, эта звезда переменная, чья величина изменяется со временем
- ↑ Для получения дополнительной информации см. Статью, в которой изображены полярные звёзды
- Ссылки
- ↑ 1 2 3 4 5 6 7 (англ.) Bowditch, 2002, p. 249
- ↑ (англ.) History of the Nautical Almanac. US Naval Observatory. Дата обращения: 24 ноября 2018. Архивировано 20 августа 2018 года.
- ↑ (англ.) Wright and Whitney, 1992, p. 273.
- ↑ 1 2 (рус.) Астронавигация, Проект К-16 Архивная копия от 16 ноября 2018 на Wayback Machine
- ↑ (англ.) Bowditch, 2002, pp. 301–303.
- ↑ (англ.) Bowditch, 2002, pp. 271–274.
- ↑ 1 2 3 (англ.) Bowditch, 2002, p. 219.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 (англ.) Bowditch, 2002, p. 248.
- ↑ (англ.) Database entry for Alpheratz, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Alpha Phe, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Schedar, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Beta Ceti, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Achernar, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Hamal, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Acamar, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Menkar, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Mirfak, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Aldebaran Архивная копия от 28 ноября 2018 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Rigel Архивная копия от 9 декабря 2018 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Capella Архивная копия от 12 декабря 2020 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Bellatrix, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for bet Tau, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Alnilam Архивная копия от 9 декабря 2018 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Betelgeuse Архивная копия от 19 ноября 2019 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Canopus, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Sirius Архивная копия от 27 февраля 2021 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Adhara Архивная копия от 12 мая 2022 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Procyon, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Pollux, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Eps Car, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for lam Vel, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Beta Car, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Alphard, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Regulus, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Dubhe, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Denebola, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Gienah, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Acrux Архивная копия от 24 июня 2016 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Gacrux, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Alioth, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Spica Архивная копия от 15 марта 2016 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Alkaid, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Agena, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Menkent, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Arcturus Архивная копия от 17 марта 2016 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Alpha Centauri Архивная копия от 15 октября 2017 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Alpha Librae, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Kochab, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Alphecca, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Antares Архивная копия от 27 февраля 2021 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Atria, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Sabik, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Shaula, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Rasalhague, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Eltanin, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ «> (англ.) Database entry for Kaus Australis, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Vega Архивная копия от 26 сентября 2017 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Nunki, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Altair, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Peacock, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Deneb Архивная копия от 9 декабря 2018 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Enif Архивная копия от 28 ноября 2018 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Alpha Gruis, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Fomalhaut Архивная копия от 16 марта 2016 на Wayback Machine, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Markab, SIMBAD, Центр астрономических данных в Страсбурге
- ↑ (англ.) Database entry for Polaris, SIMBAD, Центр астрономических данных в Страсбурге
Внешние ссылки
- (англ.) Bowditch, LL.D., Nathaniel. 15: Navigational Astronomy // The American Practical Navigator: An Epitome of Navigation (англ.). — Bethesda, MD: Национальное агентство геопространственной разведки, 2002. — ISBN 0-939837-54-4.
- (англ.) Strasbourg Astronomical Data Center (CDS). SIMBAD. Set of Identifications, Measurements, and Bibliography for Astronomical Data. Strasbourg: University of Strasbourg (2010).
- (англ.) United States Army Research Office. 2010 Nautical Almanac. — Arcata, CA: Paradise Cay Publications, 2009. — С. 28, leaf. — ISBN 0-939837-85-4.
- Wright, Frances; Whitney, Charles Allen. Learn to navigate by the tutorial system developed at Harvard (англ.). — Cambridge, Md: Cornell Maritime Press (англ.) (рус., 1992. — ISBN 0-87033-426-3.
![]()
Эта страница в последний раз была отредактирована 8 августа 2022 в 16:41.
Как только страница обновилась в Википедии она обновляется в Вики 2.
Обычно почти сразу, изредка в течении часа.
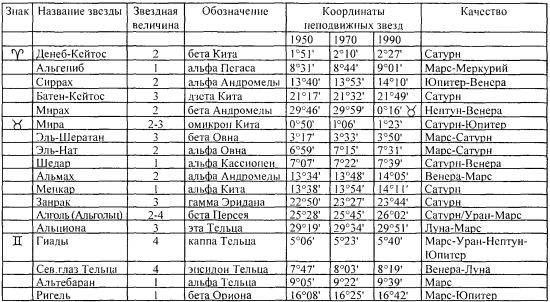
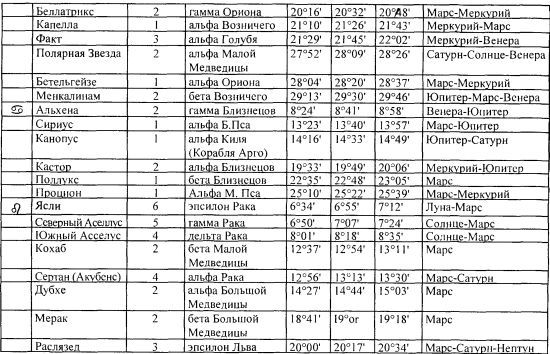
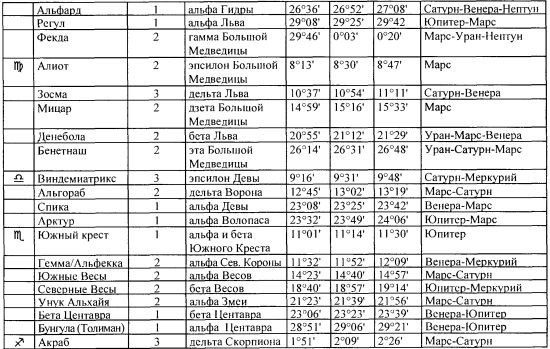
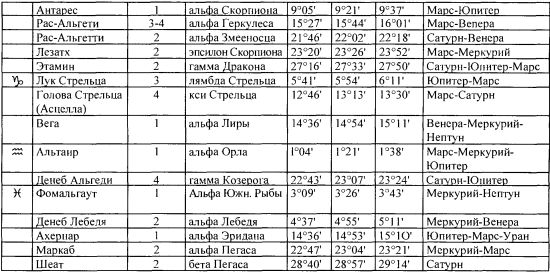
Таблица 18.
Неподвижные звёзды
Читайте также
Звезды. тайна падающей звезды
Звезды. тайна падающей звезды
В народе существует поверье, что если загадать желание на падающую звезду и сделать это до того, как она погаснет, то в будущем году желание обязательно сбудется. Для этого надо еще до боя курантов в двенадцать часов в новогоднюю ночь
Чакровая таблица
Чакровая таблица
Чакровая таблица является уникальным диагностическим инструментом, позволяющим в короткие сроки получить информацию о причинах происходящего с человеком.
Таблица имеет несколько секторов, которые дают соответствующую информацию:– Внутренний
Традиционная локализация и неподвижные звезды
Традиционная локализация и неподвижные звезды
Различные города уже давно имели связанные с ними конкретные градусы (см. «Чувствительные градусы», глава 13, где даны примеры). Они обычно считаются градусом асцендента города. Уолли[373] в комментариях к Птолемею отмечает, что
Неподвижные звезды и другие факторы в древней китайской астрологии
Неподвижные звезды и другие факторы в древней китайской астрологии
Богатая китайская традиция в мунданной астрологии, насколько нам известно, не исследована западными астрологами, хотя некоторые ученые, такие как великий д-р Джозеф Нидхэм, открыли эту область и
ПРИЛОЖЕНИЕ А. НЕПОДВИЖНЫЕ ЗВЕЗДЫ, СВЯЗАННЫЕ СО СЛЕПОТОЙ
ПРИЛОЖЕНИЕ А. НЕПОДВИЖНЫЕ ЗВЕЗДЫ, СВЯЗАННЫЕ СО СЛЕПОТОЙ
С потерей зрения ассоциируется большое количество неподвижных звёзд и подавляющее большинство туманностей, ввиду облакоподобной нечёткости и размытости последних. Указания на слепоту трактуются двояко — как
Таблица I
Таблица I
Додекабрьские датыБольшой Взрыв — 1 январяВозникновение галактики Млечного Пути — 1 маяВозникновение Солнечной системы — 9 сентябряОбразование планеты Земля — 14 сентябряПоявление жизни на Земле — 25 сентябряОбразование древнейших земных гор — 2
Таблица II
Таблица II
Космический календарьД е к а б р ьЧисла1. Образование кислородной атмосферы на Земле.5. Интенсивное извержение вулканов и образование каналов на Марсе.16. Первые черви.17. Конец докембрийского периода. Палеозойская эра и начало кембрийского периода.
Таблица III
Таблица III
31 декабряЧ а с ы, м и н у т ы, с е к у н д ыПоявление проконсула и рамапитека — возможных предков обезьян и человека — 13.30.00Первые люди — 22.30.00Широкое использование каменных орудий — 23.00.00Использование огня пекинским человеком — 23.46.00Начало последнего периода
ВТОРАЯ ТАБЛИЦА
ВТОРАЯ ТАБЛИЦА
На планету Земля цвета снега Алалу бежал; из тайны времён Начала он об этом месте узнал.К запретным сферам Алалу свой путь держал; никто прежде не бывал;Никто через Кованый браслет, пройти попыток не предпринимал.Тайна времён Начала Алалу направление
ТРЕТЬЯ ТАБЛИЦА
ТРЕТЬЯ ТАБЛИЦА
Разве Алалу не умер? друг друга спрашивали они. Он и впрямь в ином мире все это время жил? говорили они и поверить тому не могли.Неужели он не на Нибиру скрывался, и в колеснице в другой мир подался?Тех, кто колесницами управляет, для совета призвали, учёные
ДЕВЯТАЯ ТАБЛИЦА
ДЕВЯТАЯ ТАБЛИЦА
В дни Лу-Маха Мардук и Игиги на земных женщинах женились.В те дни на Земле бедствия усилились.В те дни на Лахму засуха и пыль планету охватили.Ануннаки Энлиль, Энки и Нинмах, кто судьбы других решали, друг с другом совещались.Условиям, что на Земле и на Лахму
ДЕСЯТАЯ ТАБЛИЦА
ДЕСЯТАЯ ТАБЛИЦА
Все Ануннаки собрались в Сийпаре, Дня Потопа они ожидалиВ то время, когда напряжение ожидания возрастало, Властилину Энке спящему в доме своём, видение было,В сноведении образ человека он увидел; светлого и лучистого, небесам подобного;И когда человек
ДВЕНАДЦАТАЯ ТАБЛИЦА
ДВЕНАДЦАТАЯ ТАБЛИЦА
Ану решил ещё раз Землю посетить; вместе со своей супругой Анту он хотел путешествие это совершить.К его приезду Ануннаки все подготовили, новые дома в Эдине они построили.В горной местности, где потомки Сима обитали, к старым землям черноголовые люди
ТРИНАДЦАТАЯ ТАБЛИЦА
ТРИНАДЦАТАЯ ТАБЛИЦА
Во Втором Регионе Цивилизованное Человечество не достигло полного рассвета,Тем, что дано Инанне было, она пренебрегала, другие царства, что ей не принадлежали, она получить желала.Когда тысячный год пошёл, царский титул от Унуг-ки к другому городу
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
ФГОУ ВПО МОРСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ
ИМЕНИ АДМИРАЛА Ф.Ф. УШАКОВА
Кафедра судовождения
АСТРОНОМИЧЕСКОЕ ОПРЕДЕЛЕНИЕ
ШИРОТЫ
Методические указания к выполнению лабораторных работ
по мореходной астрономии
Специальность 180402
Составил: Н.А.Мищик
Новороссийск
| Цель работы: | Подготовка по мореходной астрономии, изложенная в Кодексе ПДМНВ в разделе В-II/1, рекомендует ВПК уметь «вести расчет широт по Полярной звезде или по меридиональной высоте солнца ». |
| Пособия и инструменты: | Морской астрономический ежегодник; Калькулятор; Остро оточенный простой карандаш; Резинка. |
Рассматриваемые методы были разработаны еще в эпоху великих географических открытий, и хотя они позволяют получить только одну координату судна – широту, но являются составной частью других способов определение места судна, поэтому данные методы не утратили своей актуальности.
Определение широты по меридиональной высоте Солнца
Теория метода
Если светило находится на меридиане наблюдателя (чаще всего это происходит в момент верхней кульминации), то его высота является меридиональной H. В этом случае легко получить широту. Напоминаем, что высота h наименование не имеет. Но если светило находится на меридиане наблюдателя, то меридиональная высота H одноименно с точкой (Nили S), над которой измеряется высота. В этом же случае зенитное расстояние Z=90 – H разноименно с H. Рассмотрим на следующем рисунке несколько вариантов кульминации светила и выведем формулу для нахождения широты.

Рис. Варианты кульминации светила
Таблица различных вариантов кульминации светил
| Светило | Широта и склонение | Меридиональная высота Н | Зенитное расстояние Z = 90 — H | Широта |
| C1 | δ и φ одноименны, но δ < φ | HS | ZN | φN = ZN + δN |
| C2 | δ и φ разноименны | HS | ZN | φN = ZN — δS |
| C3 | δ и φ одноименны, но δ > φ | HN | ZS | φN = δN — ZS |
| C4 | δ и φ одноименны, но δ > 90 – φ, незаходящее | Hвк верхняя кульминация | φN = Hвк — Δ | |
| C5 | δ и φ одноименны, но δ > 90 – φ, незаходящее | Hнк нижняя кульминация | φN = Hнк + Δ |
В последних двух вариантах (C4 и C5) Δ = 90˚ – δ – это полярное расстояние, дуга меридиана от повышенного полюса до светила.
Первые три варианта кульминации светил являются наиболее распространенными для кульминации Солнца. В этих случаях широта по меридиональной высоте определяется выражением
φ = Z ± δ,
Правило знаков.
+, если Z и δ одноименны, и
–, если Z и δ разноименны, причем вычитаем из большей величины меньшую и широте приписываем наименование большей величины.
Меридиональная высота Солнца Н измеряется в момент кульминации, поэтому составной частью решения данной задачи является определение судового времени кульминации Солнца. Рассмотрим последовательно этапы этого метода на конкретной задаче.
Задача 1.12октября в полдень необходимо определить широту судна. На середину дня дана счислимая долгота λс = 100º15′W.
Планирование
Определение судового времени кульминации.
| + | Тк | 11ч46м 12.10 | ||||
| λW | 6ч41м | 2 и 3 | ||||
| – | Тгр | 18ч27м 12.10 | 5 → | δт | 7º37,2′S | Δ = +0,9 |
| Nп | 7W | Δδ | +0,4 | |||
| Тск | 11ч27м | δ | 7º37,6′S |
Комментарий.
| 1. Местное время кульминации Тк выбираем по дате из МАЕ на правой странице внизу. Как будет показано ниже, при расчете широты необходимо выбрать полудиаметр R Солнца. Его значение (R=16,0′) приведено здесь же. |  Фрагмент 1 из МАЕ |
2. Долготу переводим в часовую меру. Существует 3 способа перевода.
2.1. Табличный. При помощи Приложения 3, которое представлено в МАЕ на странице 288.

Фрагмент Приложения 3
2.2. Калькуляторный. На калькуляторе долготу делим на 15, т.к. 1ч=15º. Лучше всего эту операцию производить на двухстрочном калькуляторе.
2.3. В уме. Зная, что 15º=1ч, 1º=4м и 15′=1м, долготу представляем в следующем виде: 100º15′=90º + 10º + 15′ = 6∙15º + 10º + 1∙15′ = 6ч + 10∙4м + 1м =6ч41м
3. Какой знак придать долготе? Тк– это местное время кульминации на заданной долготе. Гринвичское и местное время связано долготой. Т.к. в этой задаче долгота западная (W-ая), то гринвичский меридиан находится от наблюдателя к востоку, а на востоке время больше, то W-ая долгота прибавляется, а восточная (Е-вая) – вычитается.
4. Чтобы определить номер пояса, надо посмотреть на долготу в часовой мере 7ч35м и округлить до целого часа.
W-ый пояс вычитается, а Е-вый – прибавляется.
| |  Фрагмент 3 из МАЕ |
Наблюдения.В судовое время 11ч27м над северной частью горизонта измерена меридиональная высота Солнца ОС мер = 67º52,2′. Высота глаза наблюдателя е = 15,2 м, i+s = +2,2′.
мер = 67º52,2′. Высота глаза наблюдателя е = 15,2 м, i+s = +2,2′.
Вычисления
| Комментарий | |||
ОС мер мер | 67º52,2′N | ||
| i+s | + 2,2 | ||
| Δhd | – 6,9 | ||
| hв | 67º47,5′ | ||
| Δhρ+p | – 0,3 | ||
| R | +16,0 | ||
| H | 68º04,2′N | ||
| + | 90-H=Z | 21º55,8′S | |
| δ | 7º37,6′S | ||
| φo | 29º33,4′S |
Комментарий.
1. Меридиональной высоте приписывается наименование той точки, над которой кульминирует Солнце. В этой задаче наименование указано – N.
Зенитное расстояние имеет наименование противоположное меридиональной высоте.
Если зенитное расстояние Z и склонение δ одноименны, то они складываются, и получается широта φ.
Если Z и δ разноименны, то из большей величины вычитается меньшая, и широте приписывается наименование большей величины.
Определение широты по высоте Полярной звезды
Теория метода
Высота полюса мира над горизонтом всегда равна широте места. К сожалению, в самих полюсах нет звезд, измеряя высоты которых, можно было практически сразу после исправления поправками получать широту. Недалеко от северного полюса РN находится достаточно яркая звезда  Малой Медведицы, называемой Полярной звездой. Координаты Полярной на 2001 г.α = 38°45′ и δ= 89°16′. Следовательно, её полярное расстояние Δ = 90° — δ < 1° = 44′. Поэтому высота Полярной звезды близка к широте и может отличаться на небольшую величину х.
Малой Медведицы, называемой Полярной звездой. Координаты Полярной на 2001 г.α = 38°45′ и δ= 89°16′. Следовательно, её полярное расстояние Δ = 90° — δ < 1° = 44′. Поэтому высота Полярной звезды близка к широте и может отличаться на небольшую величину х.

Пусть Полярная звезда находится в произвольной точке С. Из данной точки опустим сферический перпендикуляр на меридиан наблюдателя. Величина х — есть проекция полярного расстояния на меридиан наблюдателя. Так как полярное расстояние мало (44′), то прямоугольный треугольник PNCD можно считать плоским.
Из данного прямоугольного треугольника имеем x = Δcostм
Из рисунка видно, что φ = ho — x (*)
На основании основной формулы времени, имеем x = Δсos(Sм — α).
Подставляя в формулу (*) значение х, получаем φ = ho — Δсos(Sм — α)
Ведём обозначения I = — Δo сos(Sм — αo) (**)
где Δo и αo — среднегодовые значения прямого восхождения и полярного расстояния Полярной звезды.
Окончательно широта по высоте Полярной звезды определяется следующей формулой
φ = ho + I + II + III.
Так как все поправки зависят от звездного местного времени, следовательно, для определения широты по высоте Полярной звезды кроме исправления высот необходимо рассчитать звездное местное время, чтобы по этому аргументу выбрать поправки I, II и III.
Задача 2.29 мая 2001, находясь в счислимой долготе λс = 151º13,0′W, в Тс = 19ч31м измерили высоту звезды Полярной. Время измерений по хронометру Тхр = 1ч36м39с, uхр = +4м58с, ОС = 40°15,4¢, i+s = – 2,9¢, высота глаза наблюдателя е = 15,8 м.
Решение
| Комментарий | |||
| + | Тс | 03ч41м 29.05 | 1. По судовому времени и номеру пояса находим приближенное гринвичское время и гринвичскую дату. |
| Nп | 10W | ||
| прТгр | 13ч41м 29.05 | ||
| 12ч+Тхр | 13ч36м39с | ||
| uхр | + 4м58с | 2. Прибавляя поправку хронометра, находим точное гринвичское время. | |
| Тгр | 13ч41м37с | ||
| + | tтγ | 82º07,2′ | |
| Δt | 10 26,0 | ||
| – | tгр | 92º33,2′ | |
| λ | 151º13,0′W | 3. По МАЕ рассчитываем звездное местное время. | |
| tм | 301º20,2 |
| Комментарий | |||
| ОС | 40°15,4¢ | Производим исправление высот, | |
| i+s | – 2,9¢ | вводя поправки секстана, | |
| Δhd | – 7,0¢ | за наклонение горизонта, | |
| hв | 40°05,5¢ | ||
| Δhρ | – 1,1¢ | за астрономическую рефракцию. | |
| прho | 40°04,4¢ | К обсервованной высоте придаем | |
| I | + 5,4 | поправку I, | |
| II | + 0,2 | поправку II, | |
| III | – 0,3 | и поправку III. | |
| φ | 40°09,7¢N | Получаем обсервованную широту. |
Поправка I выбирается из таблицы I «Широта по высоте Полярной», которая расположена в МАЕ на страницах 277-278. Входим в эту таблицу по звездному местному времени 301º20,2 (десятки градусов сверху и градусы с минутами слева), и выполняем элементарную интерполяцию. Данная поправка учитывает суточное вращение небесной сферы. Поправка может быть как положительной, так и отрицательной. Её максимальное значение достигает величины полярного расстояния, (около 43,7΄) 
Фрагмент таблицы I «Широта по высоте Полярной».
Поправка I I выбирается из таблицы I I «Широта по высоте Полярной», которая расположена в МАЕ на странице 279. Входим в эту таблицу по звездному местному времени 301º20,2 (слева или справа) и по высоте сверху. Интерполяцию практически выполнять не надо. Поправка всегда положительная.

Фрагмент таблицы I I «Широта по высоте Полярной».
Поправка I I I выбирается из таблицы I I I, которая расположена в МАЕ на странице 280. Входим в эту таблицу по звездному местному времени 301º20,2 слева и по дате сверху. Интерполяцию выполнять не надо. Поправка учитывает годовое изменение экваториальных координат Полярной звезды. Поправка может быть как положительной, так и отрицательной.

Фрагмент таблицы I I I «Широта по высоте Полярной».
Индивидуальное задание
Номер индивидуального задания выдается преподавателем. Для первых 5-ти вариантов даются ответы. Эти варианты рекомендуются для самостоятельной отработки навыков решения этих задач
1. Определение широты по меридиональной высоте Солнца
| № | Дата | λ | ОС мер мер | i+s | е(м) |
| 1.1 | 21 декабря | 164º32,0′W | 43º24,4′к S | + 2,5 | 18,3 |
| 1.2 | 13 февраля | 90 33,0 Е | 80 05,6 к S | + 2,2 | 18,2 |
| 1.3 | 30 мая | 128 16,0 W | 74 36,5 к S | – 3,2 | 13,5 |
| 1.4 | 3 августа | 88 33,0 Е | 80 32,2 к N | – 1,6 | 14,3 |
| 1.5 | 11 октября | 35 18,0 W | 65 54,0 к N | – 2,2 | 11,6 |
| 1.6 | 21 декабря | 94 02,0 Е | 55 12,2 к S | – 3,0 | 19,9 |
| 1.7 | 13 февраля | 86 04,0 W | 58 34,0 к N | – 2,6 | 18,1 |
| 1.8 | 23 марта | 153 14,0 Е | 42 34,5 к N | – 1,8 | 17,6 |
| 1.9 | 30 мая | 161 32,0 W | 79 52,6 к N | + 1,8 | 13,5 |
| 1.10 | 3 августа | 143 43,0 Е | 62 24,5 к N | + 2,6 | 18,0 |
| 1.11 | 12 октября | 96 14,0 W | 50 50,8 к N | + 1,8 | 13,8 |
| 1.12 | 19 декабря | 85 58,0 W | 71 52,5 к S | + 1,4 | 18,1 |
| 1.13 | 23 марта | 153 14,0 Е | 63 56,3 к N | – 1,8 | 18,2 |
| 1.14 | 30 мая | 175 44,0 W | 39 02,3 к N | – 1,6 | 10,9 |
| 1.15 | 10 октября | 131 03,0 E | 46 26,4 к S | – 0,4 | 14,0 |
| 1.16 | 21 декабря | 146 12,0 W | 70 11,2 к N | – 2,6 | 11,2 |
| 1.17 | 28 мая | 49 16,0 Е | 49 37,5 к N | – 2,6 | 19,3 |
| 1.18 | 11 октября | 35 13,0 W | 65 54,0 к S | – 2,2 | 11,6 |
| 1.19 | 12 февраля | 94 02,0 Е | 61 02,6 к S | + 1,8 | 17,2 |
| 1.20 | 24 марта | 64 58,0 W | 51 03,9 к S | + 1,3 | 11,2 |
| 1.21 | 29 мая | 165 45,0 Е | 76 24,3 к N | + 3,1 | 13,5 |
| 1.22 | 2 августа | 125 14,0 W | 51 16,2 к N | – 1,4 | 20,1 |
| 1.23 | 10 октября | 158 32,0 Е | 37 23,9 к N | + 1,7 | 14,0 |
| 1.24 | 12 февраля | 168 16,0 W | 38 29,3 к S | + 3,1 | 16,9 |
| 1.25 | 4 августа | 171 16,0 Е | 50 32,9 к S | – 2,4 | 19,6 |
| 1.26 | 26 октября | 148 44,0 W | 71 25,6 к S | + 1,5 | 15,4 |
| 1.27 | 14 февраля | 149 26,0 Е | 79 50,5 к S | + 1,8 | 15,3 |
| 1.28 | 12 февраля | 179 29,0 W | 42 35,8 к N | – 2,3 | 15,5 |
| 1.29 | 11 октября | 178 16,0 Е | 46 23,0 к S | – 1,9 | 18,2 |
| 1.30 | 25 марта | 159 29,0 W | 38 49,8 к S | + 2,8 | 20,6 |
| 1.31 | 12 октября | 177 13,0 Е | 39 49,5 к N | + 2,4 | 20,6 |
| 1.32 | 30 мая | 138 28,0 W | 54 21,2 к S | + 1,6 | 14,8 |
| 1.33 | 22 декабря | 82 46,0 Е | 75 18,5 к S | – 1,2 | 18,0 |
| 1.34 | 2 августа | 162 14,0 W | 78 58,4 к N | – 2,2 | 16,3 |
| 1.35 | 23 декабря | 149 03,0 Е | 51 23,4 к N | – 2,8 | 14,5 |
| 1.36 | 3 августа | 92 31,0 W | 81 07,4 к S | – 1,6 | 15,2 |
| 1.37 | 29 мая | 71 02,0 Е | 58 47,6 к N | + 0,8 | 11,6 |
| 1.38 | 12 октября | 176 10,0 W | 58 32,2 к N | – 1,6 | 17,6 |
| 1.39 | 9 сентября | 67 33,0 Е | 61 08,4 к N | + 1,6 | 10,5 |
| 1.40 | 14 февраля | 89 41,0 W | 49 32,6 к N | + 3,3 | 18,0 |
| 1.41 | 24 марта | 132 24,0 Е | 62 21,5 к N | – 1,9 | 19,0 |
| 1.42 | 2 августа | 110 03,0 W | 42 35,9 к N | – 1,6 | 13,0 |
| 1.43 | 12 октября | 178 02,0 Е | 55 51,4 к S | + 3,2 | 18,9 |
| 1.44 | 8 сентября | 172 15,0 W | 81 16,2 к S | – 2,4 | 19,0 |
| 1.45 | 3 августа | 152 48,0 Е | 57 54,6 к S | + 3,7 | 17,8 |
| 1.46 | 8 сентября | 94 41,0 W | 71 25,6 к S | + 3,1 | 14,9 |
| 1.47 | 14 февраля | 124 45,0 Е | 55 54,3 к S | + 2,8 | 12,6 |
| 1.48 | 25 марта | 84 14,0 W | 70 32,8 к S | + 2,7 | 9,5 |
| 1.49 | 7 сентября | 165 48,0 Е | 65 23,7 к N | – 2,2 | 19,8 |
| 1.50 | 10 октября | 73 33,0 W | 48 51,3 к N | – 2,9 | 16,7 |
Ответы
| № | Тгр | δ | H | Z | φ | |
| 1.1 | 22ч56м | 21.12 | 23º26,3′S | 43º34,7′S | 46º25,3′N | 22º59,0′N |
| 1.2 | 6 12 | 13.02 | 13 19,2 S | 80 16,2 S | 9 43,8 N | 3 35,4 S |
| 1.3 | 20 30 | 30.05 | 21 52,3 N | 74 42,4 S | 15 17,6 N | 37 09,9 N |
| 1.4 | 6 12 | 3.08 | 17 28,5 N | 80 39,6 N | 9 20,4 S | 8 08,1 N |
| 1.5 | 14 07 | 11.10 | 7 11,0 S | 66 01,4 N | 23 58,6 S | 31 09,6 S |
2. Определение широты по Полярной звезде
| № | Дата | Тс | λ | Tхр | uxp | ОС | i+s | e (м) |
| 2.1 | 10 октября | 5ч26м | 95º11,0′W | 11ч22м20с | +3м59с | 45º02,6′ | +3,1 | 19,0 |
| 2.2 | 21 декабря | 6 27 | 64 36,0W | 10 26 34 | +1 20 | 38 31,6 | +2,4 | 13,9 |
| 2.3 | 11 февраля | 18 27 | 105 27,8W | 1 23 40 | +3 29 | 48 35,6 | -2,5 | 15,3 |
| 2.4 | 24 марта | 5 02 | 164 26,8Е | 5 58 28 | +3 30 | 42 36,9 | -1,8 | 15,4 |
| 2.5 | 28 мая | 20 43 | 163 16,6Е | 9 45 45 | -1 56 | 48 54,6 | + 1,8 | 17,6 |
| 2.6 | 5 августа | 4 54 | 143 15,6Е | 6 51 29 | +2 43 | 28 45,6 | +2,7 | 19,4 |
| 2.7 | 11 октября | 5 12 | 137 58,6Е | 8 12 19 | -0 10 | 37 33,4 | -1,5 | 14,5 |
| 2.8 | 21 декабря | 16 54 | 164 32,4Е | 5 55 33 | -1 27 | 51 23,6 | + 1,9 | 12,6 |
| 2.9 | 13 февраля | 5 54 | 81 15,4Е | 12 53 17 | +1 12 | 35 11,2 | + 1,9 | 17,2 |
| 2.10 | 24 марта | 18 55 | 83 48,6W | 1 02 14 | -7 17 | 24 35,6 | +2,6 | 13,8 |
| 2.11 | 27 мая | 20 17 | 131 47,5W | 5 17 50 | -0 42 | 42 26,5 | -3,2 | 20,5 |
| 2.12 | 3 августа | 19 58 | 63 42,6W | 12 01 25 | -3 12 | 41 24,6 | +3,2 | 11,7 |
| 2.13 | 9 октября | 18 13 | 145 37,6W | 4 15 32 | -2 11 | 43 21,6 | -2,4 | 13.9 |
| 2.14 | 20 декабря | 17 40 | 132 36,3w | 2 45 29 | -5 21 | 41 32,6 | -2,8 | 19,4 |
| 2.15 | 13 февраля | 18 13 | 65 06,4W | 10 12 16 | +1 38 | 45 19,5 | -2,2 | 16,5 |
| 2.16 | 25 марта | 5 40 | 147 34,6E | 7 45 53 | -5 47 | 25 48,6 | +2,5 | 15,2 |
| 2.17 | 29 мая | 20 31 | 38 14,6E | 5 34 15 | -2 28 | 42 36,4 | -0,9 | 14,4 |
| 2.18 | 1 августа | 20 03 | 57 49,8W | 11 56 12 | +5 34 | 42 36,9 | +0,7 | 13,1 |
| 2.19 | 12 октября | 5 03 | 154 32,4W | 3 0107 | +2 39 | 28 36,9 | +3,4 | 17,2 |
| 2.20 | 22 декабря | 5 31 | 173 19,5E | 5 27 14 | +4 31 | 21 32,6 | +2,3 | 13,8 |
| 2.21 | 14 февраля | 6 30 | 154 49,4E | 8 25 16 | +4 58 | 49 14,5 | + 1,8 | 12,9 |
| 2.22 | 25 марта | 19 13 | 28 32,6W | 9 15 33 | -2 45 | 51 49,6 | -1,8 | 18,8 |
| 2.23 | 29 мая | 4 26 | 141 29,6W | 1 31 48 | -5 19 | 29 32,5 | -1,1 | 13,8 |
| 2.24 | 4 августа | 4 26 | 162 25,7W | 3 29 41 | -3 30 | 33 24,8 | +2,7 | 16,5 |
| 2.25 | 12 октября | 17 55 | 164 32,9E | 6 53 55 | +0 31 | 51 23,8 | +3,1 | 16,2 |
| 2.26 | 23 декабря | 18 26 | 98 35,6W | 1 29 09 | -2 58 | 33 29,6 | -3,9 | 12,1 |
| 2.27 | 14 февраля | 5 58 | 72 16,7W | 10 54 35 | +4 14 | 32 49,4 | -2,6 | 19,5 |
| 2.28 | 23 марта | 19 12 | 153 43,6W | 5 16 47 | -4 42 | 38 17,6 | +3,4 | 20,0 |
| 2.29 | 30 мая | 4 12 | 166 48,6W | 3 15 57 | -3 52 | 34 11,6 | -1,8 | 17,4 |
| 2.30 | 2 августа | 20 02 | 163 42,7E | 8 56 54 | +4 59 | 39 35,8 | + 1,9 | 18,8 |
| 2.31 | 6 сентября | 19 27 | 123 24,5W | 3 32 02 | -4 21 | 41 18,6 | +3,3 | 16,8 |
| 2.32 | 10 октября | 5 30 | 95 14,9W | 11 34 31 | -3 44 | 46 26,2 | +3,4 | 19,5 |
| 2.33 | 20 декабря | 17 43 | 138 26,6W | 2 40 59 | +2 09 | 28 17,2 | -2,7 | 11,8 |
| 2.34 | 13 февраля | 5 55 | 157 24,5E | 8 01 12 | -5 44 | 34 26,9 | +3,4 | 13,5 |
| 2.35 | 7 сентября | 19 12 | 34 25,8E | 5 10 57 | +129 | 39 50,7 | -3,8 | 14,7 |
| 2.36 | 23 марта | 5 16 | 62 18,6W | 9 13 27 | +3 10 | 48 15,8 | +2,7 | 16,8 |
| 2.37 | 27 мая | 21 13 | 105 28,7W | 4 14 30 | -1 12 | 51 27,5 | +0,8 | 18,1 |
| 2.38 | 8 сентября | 4 26 | 162 24,4E | 5 30 55 | -4 13 | 54 18,2 | -1,3 | 19,7 |
| 2.39 | 3 августа | 19 12 | 170 36,5E | 8 18 07 | -5 43 | 22 14,6 | +2,8 | 20,6 |
| 2.40 | 11 октября | 5 17 | 28 47,2W | 7 14 52 | +1 33 | 27 52,0 | -1,2 | 18,5 |
| 2.41 | 22 декабря | 17 42 | 39 16,4W | 8 39 45 | +2 21 | 33 16,7 | +2,9 | 9,5 |
| 2.42 | 10 сентября | 4 58 | 165 28,4E | 5 54 36 | +3 33 | 39 44,5 | -1,2 | 11,8 |
| 2.43 | 13 февраля | 18 26 | 44 16,5E | 3 29 38 | -3 20 | 42 26,8 | +1,7 | 13,6 |
| 2.44 | 24 марта | 19 12 | 47 12,9W | 10 14 48 | -1 58 | 50 29,5 | -3,6 | 15,9 |
| 2.45 | 29 мая | 3 27 | 128 25,6W | 12 30 14 | -2 57 | 48 24,7 | +3,2 | 17,2 |
| 2.46 | 8 сентября | 4 42 | 160 28,5E | 5 40 27 | +2 02 | 41 16,5 | -2,4 | 19,5 |
| 2.47 | 3 августа | 19 31 | 170 25,1Е | 8 34 21 | -2 38 | 34 58,5 | +1,8 | 12,6 |
| 2.48 | 12 октября | 5 27 | 132 46,5W | 2 25 12 | +154 | 31 15,8 | -2,4 | 14,5 |
| 2.49 | 20 декабря | 17 16 | 151 12,7W | 3 10 42 | +5 40 | 47 19,5 | +2,6 | 18,5 |
| 2.50 | 9 сентября | 18 58 | 19 26,2E | 6 01 26 | -2 59 | 35 05,8 | -3,2 | 20,1 |
Ответы
| № | Тгр | Sм | ho | I | II | III | φo | |
| 3.1 | 11ч26м19с | 10.10 | 95º31,7′ | 44º57,0′ | -23,7 | +0,2 | -0,3 | 44º33,2′N |
| 3.2 | 10 27 54 | 21.12 | 182 26,0 | 38 24,9 | +35,4 | +0,1 | -0,3 | 39 00,1N |
| 3.3 | 1 27 09 | 12.02 | 58 29,5 | 48 25,4 | -41,0 | 0,0 | +0,1 | 47 44,5N |
| 3.4 | 18 01 58 | 23.03 | 256 13,6 | 42 27,1 | +34,5 | +0,1 | -0,2 | 43 01,5N |
| 3.5 | 9 43 49 | 28.05 | 195 13,6 | 48 48,1 | +40,2 | +0,1 | +0,5 | 49 28,9N |
Читайте также:
Рекомендуемые страницы:

Вам нужно быстро и легко написать вашу работу? Тогда вам сюда…
©2015-2022 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2019-04-04
Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:

Мы поможем в написании ваших работ!
В каждом месте земной поверхности высота hp полюса мира всегда равна географической широте φ этого места, т. е. hp=φ (1)
а плоскость небесного экватора и плоскости небесных параллелей наклонены к плоскости истинного горизонта под углом
 i=90°—φ (2)
i=90°—φ (2)
Высота h и зенитное расстояние z любой точки небесной сферы, в том числе и любого светила, связаны между собою зависимостью
h+z=90° (3)
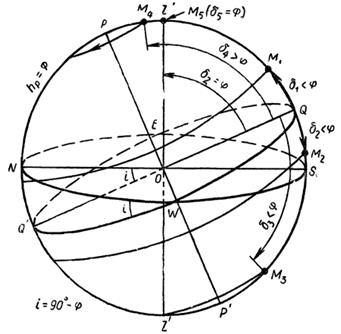
В момент верхней кульминации (рис. 1) светило со склонением δ<φ (светила M1, M2 и M3) пересекает небесный меридиан к югу от зенита z (над или под точкой юга S) и его зенитное расстояние
zв=φ-δ (4)
высота
hв= (90°—φ) +δ (5)
азимут AB=0° и часовой угол tB = 0°=0ч.
Рис. 1. Верхняя кульминация светил
При δ>φ светило (M4) в верхней кульминации пересекает небесный меридиан к северу от зенита (над точкой севера Ν), между зенитом Z и северным полюсом мира Р, и тогда зенитное расстояние светила
zв=δ—φ (6)
высота hв=(90°-δ)+φ (7)
азимут AB=180°, а часовой угол tB = 0° = 0ч.
В момент нижней кульминации (рис. 2) светило пересекает небесный меридиан под северным полюсом мира: незаходящее светило (M1)—над точкой севера N, заходящее светило (М2 и M3) и невосходящее светило (M4)—под точкой севера. В нижней кульминации высота светила
hн=δ-(90°-φ) (8)
его зенитное расстояние zн=180°—δ—φ (9)
 азимут Aн=180° и часовой угол tн=180°=12ч.
азимут Aн=180° и часовой угол tн=180°=12ч.
Рис. 2. Нижняя кульминация светил
В зависимости от φ, светила с δ<0° могут в нижней кульминации проходить под точкой юга S (светило M5) и тогда Aн=0°, а часовой угол tн=180°=12ч. В этом случае при решении задач получится zн>180° или hн< — 90°, чего быть не может, и, следовательно, реальное зенитное расстояние z=360°-zн, а высота h=-(180°+hн), но всегда h = 90°—z. Направление кульминации относительно зенита отмечается буквами: S (или ю)—кульминация к югу и N (или с) — кульминация к северу от зенита. Из формулы (8) следует, что при
δ≥+(90°-φ) (10)
высота hн≥0°, т. е. светило никогда не заходит под горизонт (незаходящее светило), а, согласно формуле (5), у невосходящего светила hв<=0° и склонение
δ≤-(90°-φ) (11)
Пример 1.Определить зенитное расстояние, высоту, азимут и часовой угол звезды Капеллы (а Возничего) в верхней и нижней кульминации на северном тропике (φ=+23°27′), на географической широте φ=+45°58′ и на северном полярном круге (φ=+66°33′). Склонение Капеллы δ=+45°58′.
Данные: Капелла (α Возничего), δ=+45°58′;
северный тропик, φ=+23°27′; место с φ = +45°58′;
северный полярный круг, φ=+66°33′.
Решение: Склонение Капеллы δ = +45°58′>φ северного тропика, и поэтому следует воспользоваться формулами (6) и (3):
zв= δ-φ = +45°58′-23°27′ = 22°31’N, hв=90°—zв=90°—22°31’=+67°29’N;
следовательно, азимут Aв=180°, а часовой угол tв=0° = 0ч.
На географической широте φ=+45°58’=δ зенитное расстояние Капеллы zв=δ-φ=0°, т. е. в верхней кульминации она находится в зените, и ее высота hв=+90°, часовой угол tв=0°=0ч, а азимут AB неопределенный.
Те же величины для северного полярного круга вычисляются по формулам (4) и (3), так как склонение звезды δ<φ=+66°33′:
zв = φ—δ =+66°33’—45°58′ = 20°35’S, hв=90°—zв= +90°—20°35’= +69°25’S, а поэтому Aв=0° и tв = 0°=0ч,
Вычисления высоты hн и зенитного расстояния zн Капеллы в нижней кульминации проводятся по формулам (8) и (3): на северном тропике (φ=+23°27′)
hн=δ— (90°—φ) = + 45°58′-(90°—23°27′) = -20°35’N,
т. е. в нижней кульминации Капелла заходит за горизонт, и ее зенитное расстояние
zн=90°—hн=90°-(-20°35′) = 110°35′ N, азимут Aн=180° и часовой угол tн=180°=12ч,
На географической широте φ=+45°58′ у звезды hн=δ-(90°-φ) = +45°58′-(90°-45°58′) = + 1°56’N,
т. е. она уже незаходящая, и ее zн=90°—hн=90°-1°56’=88°04′ N, Aн=180° и tн=180°=12ч
На северном полярном круге (φ = +66°33′)
hн = δ—(90°—φ) = +45°58’— (90°—66°33′) = +22°31′ N, и zн = 90°—hн = 90°—22°31′ = 67°29′ N,
т. е. звезда тоже не заходит за горизонт.
Пример 2.На каких географических параллелях звезда Капелла (δ=+45°58′) не заходит за горизонт, никогда не видна и в нижней кульминации проходит в надире?
Данные: Капелла, δ=+45°58′.
Решение. По условию (10)
φ≥ + (90°—δ) = + (90°—45°58′), откуда φ≥+44°02′, т. е. на географической параллели, с φ=+44°02′ и севернее ее, вплоть до северного полюса Земли (φ=+90°), Капелла является незаходящей звездой.
Из условия симметрии небесной сферы находим, что в южном полушарии Земли Капелла не восходит в местностях с географической широтой от φ=-44°02′ до южного географического полюса (φ=-90°).
Согласно формуле (9), нижняя кульминация Капеллы в надире, т. е. при zΗ=180°=180°—φ—δ, происходит в южном полушарии Земли, на географической параллели с широтой φ=-δ =-45°58′.
Задача 1.Определить высоту полюса мира и наклонение небесного экватора к истинному горизонту на земном экваторе, на северном тропике (φ=+23°27′), на северном полярном круге (φ = +66°33′) и на северном географическом полюсе.
Задача 2.Склонение звезды Мицара (ζ Большой Медведицы) равно +55°11′. На каком зенитном расстоянии и на какой высоте она бывает в верхней кульминации в Пулкове (φ=+59°46′) и Душанбе (φ=+38°33′)?
Задача 3.На каком наименьшем зенитном расстоянии и наибольшей высоте бывают в Евпатории (φ = +45°12′) и Мурманске (φ=+68°59′) звезды Алиот (ε Большой Медведицы) и Антарес (а Скорпиона), склонение которых соответственно равно +56°14′ и -26°19′? Указать азимут и часовой угол каждой звезды в эти моменты.
Задача 4.В некотором месте наблюдения звезда со склонением +32°19′ поднимается над точкой юга на высоту в 63°42′. Найти зенитное расстояние и высоту этой звезды в том же месте при азимуте, равном 180°.
Задача 5.Решить задачу для той же звезды при условии ее наименьшего зенитного расстояния 63°42′ к северу от зенита.
Задача 6.Какое склонение должны иметь звезды, чтобы в верхней кульминации проходить в зените, а в нижней кульминации — в надире, точке севера и точке юга места наблюдения? Чему равна географическая широта этих мест?
Задача 7.Вычислить зенитное расстояние, высоту, азимут и часовой угол в верхней и нижней кульминации звезды β Лебедя (имеющей склонение +27°51′) на земном экваторе, на северном и южном тропике (φ=±23°27′), на географической широте (φ=±27°51′), на северном и южном полярных кругах (φ=±66°33′) и географических полюсах. По найденным значениям высоты в верхней и нижней кульминации построить график ее зависимости от географической широты, проанализировать закономерность изменения высоты и указать, на какой географической широте понятие кульминаций отсутствует.
Задача 8.Чему равна разность зенитных расстояний двух звезд при одноименных кульминациях в одном пункте наблюдения?
Задача 9.Решить предыдущую задачу для звезд γ Андромеды и α Овна, склонение которых равно +42°05′ и +23°14′. Указать различие азимутов и часовых углов этих звезд в одноименных кульминациях в Днепропетровске (φ=+48°28′) и в Душанбе (φ=+38°33′).
Задача 10.Найти разность зенитных расстояний звезды при ее разноименных кульминациях в одном пункте наблюдения.
Задача 11.Решить предыдущую задачу для звезд, верхняя кульминация которых в Ярославле (φ = +57°38′) и Ташкенте (φ=+41°18′) происходит над точкой юга.
Задача 12.Вычислить разность наибольшей и наименьшей высоты звезды Альдебарана (а Тельца) в тех местах, где обе ее кульминации бывают к северу от зенита. В пределах каких географических параллелей возможны эти явления? Склонение Альдебарана равно +16°25′.
Задача 13.Найти разность зенитных расстояний при одноименных кульминациях одной и той же звезды на различных географических параллелях.
Задача 14.Решить предыдущую задачу для звезд Алиота (ε Большой Медведицы) и Спики (α Девы) по наблюдениям в Пулкове (φ=+59°46′) и в Ашхабаде (φ= +37°45′). Склонение этих звезд равно соответственно +56°14′ и -10°54′.
Задача 15.У звезды α Большой Медведицы, склонение +62°01′, а у звезды α Южной Рыбы —29°54′. Чему равны высота полюса мира и наклонение небесного экватора к истинному горизонту на тех географических параллелях, где эти звезды проходят в зените, кульминируют в точке юга и точке севера? Рассмотреть обе кульминации и сделать обобщающий вывод.
Задача 16.В Москве (φ = +55°45′) звезда η Большой Медведицы в нижней кульминации находится на высоте +15°19′ Круглосуточно ли пребывает она над горизонтом Горького (φ=+56°20′) и Ашхабада (φ=+37°45′)?
Задача 17.Склонение звезды Денеба (α Лебедя) равно +45°06′. Найти условия ее видимости в Кирове (φ = +58°36′) и Ла-Плате (φ = -34°54′).
Задача 18.Звезды с каким склонением проходят в зените и надире Петрозаводска (φ=+61°47′), Тбилиси (φ = =+41°42′) и Канберры (φ=-35°20′) и каковы условия их видимости в этих городах?
Задача 19.На каких географических параллелях звезды Бега (α Лиры) и β Скорпиона становятся незаходящими? Склонение этих звезд соответственно равно +38°44′ и —19°40′.
Задача 20.С каких географических параллелей северного земного полушария становятся видимы звезды Толиман (α Центавра) и Канопус (α Киля), склонение которых соответственно равно —60°38′ и —52°40′? Какие из этих звезд видны на территории СССР в Кушке (φ = = +35°15′)?
Задача 21.С каких географических параллелей звезды Алголь (β Персея, δ=+40°46′) и Антарес (α Скорпиона, δ=-26°19′) становятся невосходящими?
Задача 22.Вычислить пояса географической широты, в которых основные звезды Большой Медведицы и Южного Креста не восходят над горизонтом, полностью восходят и заходят, а также совсехм не заходят. Склонение этих звезд Большой Медведицы находится в пределах от +62°01′ (α) до +49°26′ (η), а Южного Креста — от -62°49′ (α) до -56°50′ (γ).
Ответы — Кульминация светил. Вид звездного неба

Анализируя освещенность помещений солнцем в Archicad, выписал высоты солнца в основных направлениях в дни весеннего равноденствия, летнего солнцестояния и в самый короткий день. Высота солнца в этих направления позволяет получить общую картину. Параллельно осознал для себя несколько закономерностей насчет положения солнца, над которыми раньше просто не задумывался.
На рисунке изображена траектория солнца в разные времена года.

- Азимут и время восхода солнца
- — 21 июня солнце всходит ровно на северо-востоке в 4.45
- — 21 марта и 21 сентября солнце всходит ровно на востоке в 7.30
- — 21 декабря солнце всходит ровно на юго-востоке в 10.15
- Азимут и время заход солнца
- — 21 июня заходит ровно на северо-западе в 22.10
- — 21 марта и 21 сентября солнце заходит ровно на западе в 19.40
- — 21 декабря солнце заходит ровно на юго-западе в 16.50
Самое высокое положение солнца на горизонтом в полдень (по нашему времени в 13.30), независимо от времени года. Высота солнца в 13.30 варьируется от 10 градусов зимой до 58 градусов летом.
- 21 декабря — 10 градусов
- 21 марта — 34 градуса
- 21 сентября — 34 градуса
- 21 июня — 58 градусов

Как-то я не осознавал, что 21 декабря солнце поднимается над горизонтом всего на 10 градусов. Совсем мы северная страна.
- Вот формулы для расчета вы соты солнца в полдень.
- Высота полуденного солнца зимой = наклон земной оси — широта
- Высота полуденного солнца весной и осенью = 90 — широта
- Высота полуденного солнца весной и осенью = 180 — наклон земной оси — широта
- Наклон земной оси равен примерно 66 градусов, наша широта примерно 56 градусов.
Летом солнце освещает даже северные окна домов, что происходит рано утром и поздно вечером. 21 июня солнце встает ровно на северо-востоке и садится на северо-западе. Солнце в этих направлениях видно только один день в году, его высота над горизонтом в этот день — 0 градусов.
Солнце в направлениях на восток и на запад бывает видно ровно половину года. Остальную половину года солнца в этих направлениях не видно, потому что оно еще либо не встало, либо уже село. Высота солнца над горизонтом в направлениях ровно на восток и запад варьируется в течении полугода от 0 до 29 градусов
- — 21 декабря солнца в этих направлениях вообще не видно
- — 21 марта 0 градусов (солнце ровно на горизонте)
- — 21 сентября 0 градусов (солнце ровно на горизонте)
- — 22 июня 29 градусов
- Солнце в направлении на юго-восток и юго-запад видно круглый год. При этом его высота на горизонтом варьируется от 0 градусов до 51 градуса
- — 21 декабря 0 градусов
- — 21 марта 26 градусов
- — 21 сентября 26 градусов
- — 22 июня 51,5 градус
- Параллельно с этим осознал для несколько интересных фактов
- — на экваторе день равен ночи на протяжении всего года
- — на экваторе солнце всходит ровно на востоке, а заходит на западе на протяжении всего года
- — высота солнца на экваторе в полдень варьируется в зависимости от времени года от 66 градусов с юга, 66 градусов с севера, и 90 градусов в дни весеннего равноденствия
- — в день весеннего равноденствия ночь равна дню на всех широтах
Азимут и высота солнца над горизонтом
Продолжаем тему, начатую статьей Восход и закат солнца.
На повестке дня вычисление азимута солнца и его высоты над горизонтом в любой момент времени в точке с заданными координатами. Азимут мы откладываем от севера по часовой стрелке.
Алгоритм расчета взят отсюда. Описал его какой-то хороший швед. Он старался как мог, но все равно для стороннего человека ничего не понятно.
Например, я могу еще понять, как мы переходим от одной системы координат к другой, но понять, почему долгота перигелия солнца вычисляется как
, где d — количество дней от эпохи J2000 — это уже выше моих сил.
Видимо где-то далеко, в башне из слоновой кости, сидят астрономы, и все эти цифры рассчитывают, а потом все остальные смертные их используют. Может быть какой-нибудь астроном когда-нибудь расскажет о том, как это все происходит; пока же пришлось взять на веру все эти магические цифры и воплотить расчет в жизнь. Очевидно, так делает большинство.
Есть несколько книг, которые обычно рекомендуют людям на форумах, когда не хотят отвечать развернуто, типа, «смотри вон там», и я тоже приведу их здесь:
Jean Meeus. Astronomical algorithms
Peter Duffett-Smith. Practical Astronomy with your calculator.
Как и в случае калькуляторов для расчета времени восхода и захода солнца, ниже представлены два калькулятора — первый берет информацию о координатах и часовом поясе из справочника городов, т. е.
остается только выбрать город и ввести время наблюдения; а второй позволяет задать координаты и часовой пояс «вручную».
Информацию о городах могут добавлять в справочник зарегистрированные пользователи.
Отрицательная высота над горизонтом соответствует темному времени суток — солнце «под» горизонтом. Пересечение с горизонтом утром происходит примерно на азимуте 90 градусов, из чего можно сделать смелый вывод, что солнце восходит все-таки на востоке.
Paul Schlyter (это швед) утверждает, что ошибка в расчетах не превышает одной угловой минуты для дат в диапазоне 1900 – 2100.
ДеньТочность вычисления
Знаков после запятой: 2
Высота над горизонтом (градусы)
Дата :Точность вычисления
Знаков после запятой: 2
Высота над горизонтом (градусы)
Азимут и высота солнца над горизонтом
- Следующий уникальный калькулятор служит для перевода экзотических единиц длины в…
- Следующий онлайн калькулятор о фунтах. Ранее он был очень популярен,…
- Следующий онлайн калькулятор может вычислить уровень жидкости в цилиндрической таре…
- Следующий онлайн калькулятор переводит температуры между разными шкалами.
Помните калькулятор… - Следующий калькулятор интересен тем, что он переводит древние российские денежные…
- Следующий калькулятор будет очень полезен тем, кто решил купить или…
- Следующий калькулятор работает очень просто, вам нужно ввести всего одно…
- Следующий онлайн калькулятор считает рост человека благодаря русской системе мер…
- Следующий онлайн калькулятор может вычислить габариты экрана телевизоров, компьютеров, проекторов,…
- Перед вами 2 калькулятора: один поможет вам подобрать формат снимков…
- Следующие 2 калькуляторы переводят заданное число плиток в квадратные метры…
- Перед вами 2 онлайн-калькулятора. Они переводят меры площади из метрической…
- Следующий необычный калькулятор переводит меры длины из русской системы в…
- Перед вами 2 калькулятора, которые предназначены для перевода мер длины…
- Следующий простенький калькулятор переводит введенную вами toC из кельвинов в…
- Следующий калькулятор предназначен для перевода кг в фунты. Также есть…
- Следующий онлайн калькулятор переводит калибр древних артиллерийских орудий из фунтов…
- Давайте вспомним калькулятор, который переводит градусы Цельсия в градусы Фаренгейта:…
- Как вы уже могли заметить на нашем сайте есть несколько…
- Следующий уникальный калькулятор переводит градусы Цельсия в градусы Фаренгейта. Наверное,…
- Следующий калькулятор умеет переводить значение угла, которое задано в градусах,…
- Следующий калькулятор делает перевод единиц измерения углов из градусов, минут,…
- Следующий калькулятор делает расчет объема сегмента цилиндра. Давайте посмотрим каким…
- Следующий онлайн-калькулятор считает объем жидкости в бочке, которая имеет цилиндрическую…
- Следующий калькулятор служит для детального подсчета суммарной работы аппарата.
Вам… - Перед вами отличный помощник для IT специалистов. С помощью данного…
- Следующий калькулятор переводит числа, записанные римскими цифрами в простые десятичные…
- Следующий калькулятор переводит скорость из м/с в км/час. Часто при…
- Начнем с истории. В 17 веке итальянским ученым Торричелли было…
- Следующий онлайн-калькулятор рассчитывает параметры горловины для цилиндрического бочки.
Все работает…
Азимут и высота солнца над горизонтом
Высота Солнца над горизонтом – величина непостоянная. В течение дня из-за вращения Земли она проходит путь от 0 до 90 градусов и обратно через фазы восхода, зенита и заката.
Но это если наблюдать за нашим светилом из своего города.
В масштабах планеты угол, под которым его лучи падают на поверхность Земли в разных регионах, влияют как на климатические условия, так и на продолжительность времени суток.
Демонстрация принципа азимута
Демонстрация принципа азимута
На ледяных полюсах лучи солнечного света едва касаются нашей планеты. Там очень холодно, а день и ночь длятся по полгода и называются полярными. А вот жаркому экватору достается больше всего солнечного света, который падает туда под прямым углом.
В тех краях и климат намного приятнее, и день с ночью имеют практически одинаковую продолжительность. Эти наблюдения подтверждают простой факт: чем выше Солнце, тем больше тепла и света оно дает, а его высота над горизонтом равна углу падения его лучей.
Северное сияние, Норвегия
Северное сияние, Норвегия
Еще один способ следить за перемещением нашей звезды на небе – это вычисление ее азимута. Сделать это можно с помощью онлайн-калькуляторов для любой точки Земли, например, для Москвы. Понадобятся лишь дата и время. Скажем, в полдень 15-го июня 2018-го года азимут и высота Солнца над горизонтом в Москве составляли 167,29 и 57,08 градуса соответственно.
Вычисление времени восхода и захода в цифровую эру тоже стало делом нескольких кликов. В той же Москве 22-го декабря 2018-го года Солнце встало только в 8:57, а зашло за горизонт уже в 15:58, подарив москвичам лишь семь часов светового дня.
Онлайн калькулятор для расчета положения Солнца по городам на нашем сайте в левой части страницы!
Декабрь — это вообще месяц самых длинных ночей в Северном полушарии, а 22-ое декабря — это дата зимнего солнцестояния, самого короткого дня и самой долгой ночи в году для этой части света. Всему виной опять же высота Солнца над горизонтом. Зимой и особенно в декабре ее значения самые низкие за весь год.
Уникальность статьи 100%
Solar azimuth angle — Wikipedia
Угол солнечного азимута является азимут углом в положении Солнца . Эта горизонтальная координата определяет ВС «ы относительно направления вдоль местного горизонта , в то время как солнечный зенитный угол (или ее комплементарного угол солнечного возвышения ) определяет видимые Солнца высоты .
Есть несколько соглашений об азимуте Солнца; однако он традиционно определяется как угол между линией, направленной на юг, и тенью, отбрасываемой вертикальным стержнем на Земле .
Это соглашение гласит, что угол положительный, если тень идет к востоку от юга, и отрицательный, если к западу от юга. Например, направление на восток будет на 90 °, а на запад — на -90 °.
Другое соглашение — обратное; он также имеет начало прямо на юге, но измеряет углы по часовой стрелке, так что на восток теперь отрицательно, а на западе теперь положительно.
Однако, несмотря на традицию, наиболее общепринятым соглашением для анализа солнечного излучения , например, для приложений солнечной энергии , является направление на север по часовой стрелке , поэтому восток равен 90 °, юг — 180 °, а запад — 270 °.
Это определение используется NREL в своих калькуляторах положения Солнца, а также в формулах, представленных здесь.
Однако фотографии Landsat и другие продукты USGS , хотя также определяют азимутальные углы относительно прямого севера, принимают углы против часовой стрелки как отрицательные.
Обычные тригонометрические формулы
В следующих формулах предполагается направление на север по часовой стрелке.
Угол солнечного азимута может быть рассчитан с хорошим приближением по следующей формуле, однако углы следует интерпретировать с осторожностью, потому что обратный синус , то есть x = sin −1 y или x = arcsin y , имеет несколько решений, только одно из которых будет быть правильным.
грех ϕ s знак равно — грех час потому что δ грех θ s . { displaystyle sin phi _ { mathrm {s}} = { frac {- sin h cos delta} { sin theta _ { mathrm {s}}}}.}
Следующие формулы также могут использоваться для аппроксимации азимутального угла Солнца, но в этих формулах используется косинус, поэтому азимутальный угол, показанный калькулятором, всегда будет положительным и должен интерпретироваться как угол между нулем и 180 градусов, когда часовой угол , h , является отрицательным (утро), а угол между 180 и 360 градусами, когда часовой угол, h , положительным (днем). (Эти две формулы эквивалентны, если принять формулу аппроксимации « угла возвышения Солнца »).
потому что ϕ s знак равно грех δ потому что Φ — потому что час потому что δ грех Φ грех θ s потому что ϕ s знак равно грех δ — потому что θ s грех Φ грех θ s потому что Φ . { displaystyle { begin {align} cos phi _ { mathrm {s}} & = { frac { sin delta cos Phi — cos h cos delta sin Phi} { sin theta _ { mathrm {s}}}} [5pt] cos phi _ { mathrm {s}} & = { frac { sin delta — cos theta _ { mathrm { s}} sin Phi} { sin theta _ { mathrm {s}} cos Phi}}. end {выравнивается}}}
Итак, практически говоря, азимут компаса, который является практическим значением, используемым повсюду (например, в авиакомпаниях как так называемый курс) на компасе (где север равен 0 градусов, восток — 90 градусов, юг — 180 градусов, а запад — 270 градусов). можно рассчитать как
компас ϕ s знак равно 360 — ϕ s . { displaystyle { text {compass}} phi _ { mathrm {s}} = 360- phi _ { mathrm {s}}.}
В формулах используется следующая терминология:
Кроме того, деление приведенной выше формулы синуса на первую формулу косинуса дает формулу касательной, которая используется в Морском альманахе .
Формула на основе подсолнечной точки и функции atan2 { displaystyle operatorname {atan2}}
«Венок Аналеммаса». Ежегодная экскурсия по положению Солнца, определяемая тройкой , и с шагом в 1 час, если смотреть на географический центр смежных Соединенных Штатов. Серая часть означает, что сейчас ночь. S Икс { displaystyle S_ {x}}
S y { displaystyle S_ {y}}
S z { displaystyle S_ {z}}
В публикации 2021 года представлен метод, в котором используется формула солнечного азимута, основанная на подсолнечной точке и функции atan2 , как определено в Fortran 90 , что дает однозначное решение без необходимости подробного рассмотрения. Подсолнечная точка — это точка на поверхности Земли, над которой находится Солнце.
Метод сначала вычисляет склонение Солнца и уравнение времени с использованием уравнений из астрономического альманаха, то это дает x-, y- и г-компонента единичного вектор , указывающей к Солнцу, через векторный анализ , а не сферическую тригонометрию , следующим образом:
ϕ s знак равно δ , λ s знак равно — 15 ( Т грамм M Т — 12 + E м я п / 60 ) , S Икс знак равно потому что ϕ s грех ( λ s — λ о ) , S y знак равно потому что ϕ о грех ϕ s — грех ϕ о потому что ϕ s потому что ( λ s — λ о ) , S z знак равно грех ϕ о грех ϕ s + потому что ϕ о потому что ϕ s потому что ( λ s — λ о ) . { displaystyle { begin {align} phi _ {s} & = delta, lambda _ {s} & = — 15 (T _ { mathrm {GMT}} -12 + E _ { mathrm {min }} / 60), S_ {x} & = cos phi _ {s} sin ( lambda _ {s} — lambda _ {o}), S_ {y} & = cos phi _ {o} sin phi _ {s} — sin phi _ {o} cos phi _ {s} cos ( lambda _ {s} — lambda _ {o}), S_ {z} & = sin phi _ {o} sin phi _ {s} + cos phi _ {o} cos phi _ {s} cos ( lambda _ {s} — lambda _ {o}). end {align}}}
где
- δ { displaystyle delta}
это склонение Солнца, - ϕ s { displaystyle phi _ {s}}
— широта подсолнечной точки, - λ s { displaystyle lambda _ {s}}
долгота подсолнечной точки, - Т грамм M Т { displaystyle T _ { mathrm {GMT}}}
среднее время по Гринвичу или всемирное координированное время, - E м я п { displaystyle E _ { mathrm {min}}}
это уравнение времени в минутах, - ϕ о { displaystyle phi _ {o}}
широта наблюдателя, - λ о { displaystyle lambda _ {o}}
долгота наблюдателя, - S Икс , S y , S z { Displaystyle S_ {x}, S_ {y}, S_ {z}}
представляют собой x-, y- и z-компоненты, соответственно, единичного вектора, направленного к Солнцу.
Это можно показать . С помощью приведенной выше математической схемы зенитный угол Солнца и азимутальный угол Солнца просто S Икс 2 + S y 2 + S z 2 знак равно 1 { displaystyle S_ {x} ^ {2} + S_ {y} ^ {2} + S_ {z} ^ {2} = 1}
Z знак равно а c о s ( S z ) { Displaystyle Z = mathrm {acos} (S_ {z})}
,
γ s знак равно а т а п 2 ( — S Икс , — S y ) { displaystyle gamma _ {s} = mathrm {atan2} (-S_ {x}, — S_ {y})}
. (Соглашение по часовой стрелке)
где
- Z { displaystyle Z}
— зенитный угол Солнца, - γ s { displaystyle gamma _ {s}}
— азимутальный угол Солнца в соответствии с соглашением «юг-часовой стрелке».
Если кто-то предпочитает соглашение по северу по часовой стрелке или соглашение по востоку и против часовой стрелки, формулы будут
γ s знак равно а т а п 2 ( S Икс , S y ) { displaystyle gamma _ {s} = mathrm {atan2} (S_ {x}, S_ {y})}
, (Соглашение о севере по часовой стрелке)
γ s знак равно а т а п 2 ( S y , S Икс ) { displaystyle gamma _ {s} = mathrm {atan2} (S_ {y}, S_ {x})}
. (Восточная конвенция против часовой стрелки)
Наконец, значения , и на 1-часовой операции в течение всего года может быть представлена в виде 3D сюжета «венца Аналеммы » в качестве графического изображения всех возможных положений Солнца с точки зрения солнечного зенитного угла и угла солнечного азимута для любого данного местоположения. S Икс { displaystyle S_ {x}}
S y { displaystyle S_ {y}}
S z { displaystyle S_ {z}}
Смотрите также
Рекомендации
Внешние ссылки
- Калькуляторы положения Солнца от Национальной лаборатории возобновляемых источников энергии (NREL)
- Алгоритм положения Солнца для приложений солнечного излучения (NREL)
- Рабочая тетрадь Excel с функциями VBA для определения солнечного азимута, высоты Солнца, рассвета, восхода солнца, солнечного полудня, заката и сумерек, написанная Грегом Пеллетье , переведенная из онлайн-калькуляторов NOAA для положения Солнца и восхода / захода солнца.
- Рабочая тетрадь Excel с калькулятором временных рядов положения Солнца и солнечной радиации, автор Грег Пеллетье.
- Калькулятор положения солнца Бесплатный онлайн-инструмент для оценки положения солнца с помощью трех различных алгоритмов.
- PVCDROM Azimuth Angle — онлайн-материал по фотоэлектрической технике UNSW, ASU, NSF et al.
Формула высоты солнца над горизонтом
Вычисление азимута и высоты солнца над горизонтом по заданным координатам и времени наблюдения. Возможно как задание координат вручную, так и выбор значения из справочника городов.
Продолжаем тему, начатую статьей Восход и закат солнца.
На повестке дня вычисление азимута солнца и его высоты над горизонтом в любой момент времени в точке с заданными координатами. Азимут мы откладываем от севера по часовой стрелке.
Алгоритм расчета взят отсюда. Описал его какой-то хороший швед. Он старался как мог, но все равно для стороннего человека ничего не понятно. Например, я могу еще понять, как мы переходим от одной системы координат к другой, но понять, почему долгота перигелия солнца вычисляется как , где d — количество дней от эпохи J2000 — это уже выше моих сил.
Видимо где-то далеко, в башне из слоновой кости, сидят астрономы, и все эти цифры рассчитывают, а потом все остальные смертные их используют. Может быть какой-нибудь астроном когда-нибудь расскажет о том, как это все происходит; пока же пришлось взять на веру все эти магические цифры и воплотить расчет в жизнь. Очевидно, так делает большинство.
Есть несколько книг, которые обычно рекомендуют людям на форумах, когда не хотят отвечать развернуто, типа, «смотри вон там», и я тоже приведу их здесь:
Jean Meeus. Astronomical algorithms Peter Duffett-Smith. Practical Astronomy with your calculator.
Как и в случае калькуляторов для расчета времени восхода и захода солнца, ниже представлены два калькулятора — первый берет информацию о координатах и часовом поясе из справочника городов, т. е.
остается только выбрать город и ввести время наблюдения; а второй позволяет задать координаты и часовой пояс «вручную».
Информацию о городах могут добавлять в справочник зарегистрированные пользователи.
Отрицательная высота над горизонтом соответствует темному времени суток — солнце «под» горизонтом. Пересечение с горизонтом утром происходит примерно на азимуте 90 градусов, из чего можно сделать смелый вывод, что солнце восходит все-таки на востоке.
Paul Schlyter (это швед) утверждает, что ошибка в расчетах не превышает одной угловой минуты для дат в диапазоне 1900 – 2100.
Устанавливая рекомендуемое программное обеспечение вы соглашаетесь с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .
Как определить полуденную высоту Солнца над горизонтом в дни летнего и зимнего солнцест., вес. и осеннего равноденствия ?
Bо время весеннего и осеннего равноденствий полуденная высота Солнца равна дополнению географической широты места до 90°, а во время зимнего и летнего солнцестояний она меньше или больше равноденственной на угол, равный наклонности эклиптики к экватору.
В дни равноденствий высота полуденного Солнца (φ0) над горизонтом для разных широт (φ1) определяется по формуле:
Что лучше webrip или hdrip
Координаты Донецка: 48°00′32″ с. ш. 37°48′15″ в. д.
В г. Донецке 21 марта и 23 сентября в полдень Солнце находится на высоте:
Летом , когда Солнце находится над тропиком каждого полушария, высота его в полдень увеличивается на 23° 27′, т. е.
- φ0 = 90° – φ1 + 23° 27′
- φ0 = 90°- 48° +23° 27’= 65° 27′
- В Донецке 21 июня высота Солнца равна 65°27′
Зимой , когда Солнце перемещается в противоположное полушарие, высота его соответственно уменьшается и достигает минимума в дни солнцестояния, когда ее следует уменьшить на 23°27′, т. е.
- φ0 = 90° – φ1- 23° 27′
- φ0 = 90°- 48° – 23° 27’= 18° 33′
- В Донецке 22 декабря Солнце находится на высоте 18° 33′
определить можно так: 90 минус широта данного места. например в Москве широта 56 градусов, значит высота солнца в полдень в дни равноденствий будет 90 – 56 = 34 градуса над горизонтом.
- Определение высоты полуденного солнца
- (угла падения солнечных лучей)
- Дни равноденствия: весеннего – 21 марта осеннего – 23 сентября
- 90° – широта места =
- Летнее солнцестояния – 22 июня
- Зимнее солнцестояние – 22 декабря
- 90° – широта – 23,5°=
- Определение высоты полуденного солнца
- (угла падения солнечных лучей)
- Дни равноденствия: весеннего – 21 марта осеннего – 23 сентября
- 90° – широта места =
- Летнее солнцестояния – 22 июня
- Зимнее солнцестояние – 22 декабря
- 90° – широта – 23,5°=
- Определение высоты полуденного солнца
- (угла падения солнечных лучей)
- Дни равноденствия: весеннего – 21 марта осеннего – 23 сентября
- 90° – широта места =
- Летнее солнцестояния – 22 июня
- Зимнее солнцестояние – 22 декабря
- 90° – широта – 23,5°=
- Как определить географические широты по высоте Солнца в полдень?
1.Для более точного определения необходимо знать только одну величину – склонение Солнца. Склонение – расстояние от экватора, т. е. насколько Солнце севернее или южнее экватора.Максимальная высота экватора над горизонтом равна 90 – fi.
- Поэтому широта равна fi = 90 – h + d.
- (fi – широта, h – высота Солнца, d – склонение Солнца).
- 2. Широта места в градусах, определяемая по высоте светила в полдень рассчитывается так:fi = (90-betta)+23*cos(Tet);
- Эта формула, полученная мной, является приближенной, в ней обозначены:
fi – широта места, betta – угол между плоскостью горизонта и направлением на солнце (высота Солнца) , 23.
5 – угол наклона земной оси, Tet – угловое положение Земли на эллиптической орбите относительно положения, соответствующего 22 июня.
Следует отметить, что в полдень солнце точно на юге для представителей северного полушария, для южного полушария оно на севере, это надо учитывать при расчете широты
Частное скрытая камера россия
Солнце – источник жизни. Так говорится практически во всех научных трудах, посвященных природе, и публикациях на различные физико-географические темы.
На самом деле, конечно, источник жизни еще не найден, а Солнце – это просто раскаленный шар, звезда, испускающая в мировое пространство электромагнитные волны различной длины. Солнце и не подозревает о том, какую пользу оно приносит биосфере и Земле в целом.
Поэтому наша звезда – это не источник жизни, а главное средство для ее поддержания. А точнее – одно из самых главных.
Солнечные лучи несут к поверхности Земли тепло и свет. Сама по себе солнечная радиация не имеет температуры, однако, соприкоснувшись с земным веществом, она чудесным образом превращается в привычное для нас тепло.
Нет такого места на открытой (дневной) поверхности Земли, куда бы ни разу не проникали солнечные лучи. Повсюду во всех местах – отправимся ли мы на юг или на север – нас будет сопровождать солнечный свет.
Однако, находясь в северных широтах, мы сразу заметим, что солнце хоть и светит чрезвычайно ярко, но совершенно не греет; а на черноморских или средиземноморских курортах долгое нахождение под солнцем без головного убора чревато неприятностями – можно получить солнечный удар.
Отсюда возникает вопрос: если солнечный свет есть везде, то почему же одни части Земли избалованы солнечным теплом, а другие – обделены им, а то и вовсе лишены.
Всё дело в том, что Земля имеет шарообразную форму. Из-за этого электромагнитная солнечная радиация вынуждена падать на земную поверхность под разным углом – от 0 до 90 градусов.
Угол падения 0 ° подразумевает то, что лучи Солнца слегка соприкасаются с поверхностью, идут по касательной, скользят по поверхности, естественно, не принося ей никакого тепла. Такое наблюдается между полярными кругами и полюсами. Максимум тепла поверхность получает тогда, когда лучи падают на нее отвесно – под углом 90 градусов.
При этом говорят, что солнце находится в зените. В таком положении оно бывает только в пространстве, лежащем между двумя ключевыми параллелями – Северным тропиком и Южным тропиком.
Отсюда следует вывод: чем больше угол падения лучей Солнца, тем больше нагревается земная поверхность. Этим и объясняется разница между климатом севера и юга.
Угол падения солнечных лучей равен высоте солнца над линией горизонта. Например, если солнце в тропиках в какой-либо день поднялось на высоту 90 градусов над горизонтом, то угол падения солнечных лучей на земную поверхность там также составляет 90 градусов. Высота же солнца над горизонтом зависит от географической широты местности.
Широта, на которой находится местность, определяет изменение высоты солнца над горизонтом в течение года. Изменение высоты солнечного диска в течение года называется годовым диапазоном высоты солнца. В каждой местности наблюдаются свои крайние значения годового диапазона.
1С изменить значение в табличной части документа
На полюсах, например, высота солнца в течение года меняется от -23,5 градусов (зимнее солнцестояние) до 23,5 градусов (летнее солнцестояние). «Минус» означает то, что солнце опускается ниже горизонта, т.е.
наступает полярная ночь (в дни весеннего и осеннего равноденствия солнце в этих регионах едва проглядывает из-за горизонта, то есть находится на высоте 0 градусов). В Северном полушарии на широте 45 градусов годовой диапазон составляет от 21,5 ° (зимнее солнцестояние) до 68 ,5 ° (летнее солнцестояние).
На широте 0 градусов (на экваторе) годовой диапазон высоты солнца меняется от 66,5 (минимум) до 90 градусов (максимум).
Именно крайние значения диапазона высоты солнца определяют тип климата местности, степень его сезонной контрастности, долготу дня и пр.
Циркуляция атмосферы и подстилающая поверхность – важнейшие факторы, но крайние значения диапазона высоты солнечного диска являются первичным, решающим климатообразующим фактором, который определяют годовую интенсивность инсоляции местности, а именно – какое количество суммарной солнечной радиации получает поверхность за год. Чем ближе крайние значения диапазона высоты солнца подходят к 90 ° , тем теплее климат и тем меньше разница между зимой и летом (сезонный контраст всё более и более сглаживается).
Самой высшей точки на небосводе солнечный диск достигает в полдень. В северном или южном направлении с каждым градусом широты уменьшается или увеличивается и градус полуденной высоты солнца над горизонтом.
Например, если на широте 0 ° высота полуденного солнца составляет 90 градусов, то на широте 1 ° в северном или южном полушарии в этот же момент времени солнце находится на высоте 89 градусов над горизонтом. На широте 2 ° солнце достигнет высоты 88 градусов и т.д.
Таким образом, зная положение солнца в какой-либо точке Земли, можно определить на какой высоте находится солнце в другой точке Земли в это же время. И для этого необходимо всего лишь знать широты этих точек.
Изменение высоты солнца (угла падения лучей) с широтой – главная причина зональности климата, почвенно-растительного покрова и ландшафтов в целом. Зональность – главнейшая географическая закономерность, она – альфа и омега географической науки.
- ПОЛУДЕННАЯ ВЫСОТА СОЛНЦА НАД ГОРИЗОНТОМ ДЛЯ ВСЕХ ШИРОТ СЕВЕРНОГО И ЮЖНОГО ПОЛУШАРИЯ (в градусах)
- широта весеннее летнее осеннее зимнее
- равноденствие солнцестояние равноденствие солнцестояние
- Мария Сухоруких
- Распечатать
Производство астрономических вычислений, определение азимута
Геодезические азимуты (дирекционные углы) направлений могут определяться геодезическим, астрономическим или гироскопическим методом. Геодезическим методом дирекционные углы определяются посредством угловой передачи от исходных направлений.
- Для определения дирекционных углов геодезическим методом прокладываются угловые ходы или развиваются сети треугольников.
- Дирекционные углы со средними квадратическими погрешностями 1 и 2// определяются астрономическим методом.
- Дирекционные углы со средней квадратической погрешностью 3// могут определяться из астрономических наблюдений, а также геодезическим методом от сторон ГГС 1 и 2 классов или от направлений, дирекционные углы которых получены из астрономических наблюдений со средней квадратической погрешностью 1 и 2//.
Дирекционные углы со средними квадратическими погрешностями 5, 10, 15, 30 и 60// определяются из астрономических и гироскопических наблюдений или геодезическим методом от сторон ГГС 1-4 классов и от направлений с известными дирекционными углами требуемой точности. При определении дирекционных углов со средней квадратической погрешностью 15-60// в качестве исходных могут использоваться направления с пунктов ГГС на ориентирные пункты.
Определение дирекционных углов геодезическим методом с точностью 3-60 //
Для определения дирекционных углов геодезическим методом прокладываются угловые ходы или развиваются сети треугольников.
При определении дирекционных углов со средними квадратическими погрешностями 3-10// прокладывается не менее трех угловых ходов от трех исходных пунктов (рис.) или развивается сеть треугольников, опирающихся не менее чем на три исходных пункта (рис.
), на каждом из которых наблюдаются два исходных направления.
Дирекционные углы со средними квадратическими погрешностями 15, 30 и 60// разрешается определять проложением одного разомкнутого хода между двумя исходными направлениями, не являющимися взаимообратными.
При определении дирекционных углов со средними квадратическими погрешностями 3-10// угловые ходы прокладываются по трехштативной системе. При этом, если длины сторон более 500 м, наблюдения могут выполняться на визирные цели. Для проложения ходов по трехштативной системе используется теодолит и комплект из двух визирных марок.
Определение астрономического азимута по часовому углу Полярной звезды
Азимут по часовому углу Полярной звезды можно определять днем и ночью. Дневные наблюдения следует начинать не ранее чем чрез 30 мин после восхода Солнца и прекращать за 30 мин до его захода; ночные наблюдения следует начинать не ранее чем через 30 мин после захода Солнца и прекращать за 30 мин до его восхода.
Наблюдения выполняют со столика знака, бетонного столба или с надежно укрепленного штатива. При наблюдениях со столба или штатива высота визирного луча над препятствием должна быть не менее 2 м.
В ночное время визирование производят на фонари, в дневное время – на марки или визирные цилиндры геодезических знаков.
Наблюдение ведут на постоянной нити, т.е. вращая наводящий винт алидады, наводят на земной предмет и Полярную звезду одну из нитей биссектора трубы, установленного в нульпункте. При этом необходимо иметь в виду, что если во время наблюдений при круге «лево» наводят на объект левую нить биссектора, то при круге «право» эта нить будет справа.
- Моменты наведений нити биссектора на Полярную звезду фиксируют по звездному хронометру; нить наводят на звезду под удар целых секунд хронометра.
- Каждый прием наблюдения азимута выполняют в следующем порядке:
- · наведение трубы на земной предмет, отсчеты по горизонтальному кругу;
- · наведение трубы на Полярную звезду, отсчеты Т по хронометру, накладному уровню и горизонтальному кругу;
- · перекладка уровня на 1800;
- · второе наведение трубы на Полярную звезду, отсчеты по хронометру, накладному уровню и горизонтальному кругу;
- · второе наведение трубы на земной предмет, отсчеты по горизонтальному кругу.
Указанные действия составляют один полуприем. В другом полуприеме трубу переводят через зенит и все перечисленные действия повторяют. Алидаду инструмента в первом полуприеме вращают по ходу часовой стрелки, во втором полуприеме – против хода часовой стрелки. Биссекторы микроскопов наводят на «младший» и «старший» штрихи по одному разу.
Полевой контроль каждого полуприема выполняют сразу же после его окончания. Для этого сравнивают повторное наблюдение земного предмета с первоначальным, разность между которыми не должна превышать 6//.
При определении азимута со средними квадратическими ошибками + 5// и + 10// подготовка к наблюдениям, наблюдения и обработка журнала производятся также, как и при определении азимута со средней квадратической ошибкой + 2//.
Определение астрономического азимута по часовому углу Солнца со средней квадратической ошибкой + 10//
Азимут по часовому углу Солнца можно наблюдать при высоте Солнца не более 500. наиболее выгодным временем для наблюдения азимута являются утренние и вечерние часы. Начинать наблюдения следует не ранее чем через 30 мин после восхода Солнца, и заканчивать не позднее, чем за 30 мин до его захода.
Азимут определяют теодолитом ОТ-02 шестью приемами с перестановкой лимба на угол σ = 1800 / n , где n – число приемов.
Непосредственно перед наблюдениями инструмент тщательно нивелируют.
Наблюдения Солнца ведут со светофильтром, после того как изображение Солнца попало в поле зрения трубы, вертикальную нить сетки нитей трубы подводят наводящим винтом алидады к левому или правому краю диска Солнца.
В момент соприкасания нити с краем диска Солнца наблюдатель подает команду «Есть», по которой помощник наблюдателя отсчитывает и записывает в журнал показания часов, а наблюдатель диктует ему отсчет по горизонтальному кругу.
- При круге «лево» и круге «право» вертикальную нить сетки наводят на диаметрально противоположные края диска Солнца, с тем, чтобы среднее из отсчетов по горизонтальному кругу относилось к центру Солнца.
- Прием наблюдения азимута выполняют в следующем порядке:
- Круг «лево» (КЛ):
- наведение трубы на земной предмет; запись отсчетов по горизонтальному кругу;
- наведение трубы на левый (правый) край диска Солнца; запись отсчетов по часам и горизонтальному кругу;
- Круг «право» (КП);
- наведение трубы на левый (правый) край диска Солнца; запись отсчетов по часам и горизонтальному кругу;
- наведение трубы на земной предмет; запись отсчетов по горизонтальному кругу.
Азимут по часовому углу Солнца можно определять при высоте Солнца не более 50°. Наиболее выгодным временем для наблюдения азимута являются утренние и вечерние часы. Начинать наблюдения следует не ранее чем через 30 мин после восхода Солнца и заканчивать не позднее чем за 30 мин до захода.
Для регистрации моментов наблюдений Солнца применяют палубные часы ЧП или двухстрелочный секундомер 51СД, которые устанавливают по московскому времени. Поправку часов следует определять из приема сигналов поверки времени (шесть точек) не реже чем через 2 ч.
Значения широты φ и долготы λ, пункта наблюдения, необходимые для вычисления азимута, могут быть получены через геодезические координаты, определенные по топографической карте масштаба 1: 50 000, с учетом уклонений отвесной линии, снятых со специальной карты с ошибкой не более 5″.
Перед началом каждого приема теодолит тщательно горизонтируют. Во время наблюдений отсчеты по уровню не берут, но следят, чтобы пузырек уровня не отклонялся от середины более чем на два деления.
- Наблюдения Солнца ведут со светофильтром. Каждый прием определения азимута выполняют в следующем порядке:
- — Визируют при КЛ (КП) центральной вертикальной нитью на земной предмет; берут отсчеты по горизонтальному кругу;
- — Наводят при КЛ (КП) зрительную трубу на Солнце (перед наведением надевают на окуляр зрительной трубы светофильтр); подводят вертикальную нить наводящим винтом вращения алидады к левому (правому) краю диска Солнца; регистрируют момент соприкосновения нити с краем диска Солнца по часам или двухстрелочному секундомеру, берут отсчеты по горизонтальному кругу;
- — Переводят зрительную трубу через зенит и вновь визируют сначала на Солнце (теперь уже на другой край его диска), а – затем на земной предмет.
- В журнале показывается, на какой именно край диска Солнца наводилась вертикальная нить в каждом полуприеме.
При наблюдении с палубными часами момент соприкасания нити с краем диска Солнца регистрирует помощник наблюдателя по команде наблюдателя «Есть». При наблюдении с двухстрелочным секундомером этот момент регистрирует сам наблюдатель.
- Азимут Солнца вычисляют по формулам:
- ctg ά= x- y/sin t°
- x= sin φ ctg t°
- y= cos φ tg δ°
- α= ± ά
- где t° -часовой угол Солнца в момент его наблюдения в пункте с долготой λ;
Продолжаем тему, начатую статьей Восход и закат солнца.
На повестке дня вычисление азимута солнца и его высоты над горизонтом в любой момент времени в точке с заданными координатами. Азимут мы откладываем от севера по часовой стрелке.
Алгоритм расчета взят отсюда. Описал его какой-то хороший швед. Он старался как мог, но все равно для стороннего человека ничего не понятно. Например, я могу еще понять, как мы переходим от одной системы координат к другой, но понять, почему долгота перигелия солнца вычисляется как, где d — количество дней от эпохи J2000 — это уже выше моих сил.
Видимо где-то далеко, в башне из слоновой кости, сидят астрономы, и все эти цифры рассчитывают, а потом все остальные смертные их используют. Может быть какой-нибудь астроном когда-нибудь расскажет о том, как это все происходит; пока же пришлось взять на веру все эти магические цифры и воплотить расчет в жизнь. Очевидно, так делает большинство.
Есть несколько книг, которые обычно рекомендуют людям на форумах, когда не хотят отвечать развернуто, типа, «смотри вон там», и я тоже приведу их здесь:
Jean Meeus. Astronomical algorithms
Peter Duffett-Smith. Practical Astronomy with your calculator.
Как и в случае калькуляторов для расчета времени восхода и захода солнца, ниже представлены два калькулятора — первый берет информацию о координатах и часовом поясе из справочника городов, т. е. остается только выбрать город и ввести время наблюдения; а второй позволяет задать координаты и часовой пояс «вручную». Информацию о городах могут добавлять в справочник зарегистрированные пользователи.
Отрицательная высота над горизонтом соответствует темному времени суток — солнце «под» горизонтом. Пересечение с горизонтом утром происходит примерно на азимуте 90 градусов, из чего можно сделать смелый вывод, что солнце восходит все-таки на востоке.
Paul Schlyter (это швед) утверждает, что ошибка в расчетах не превышает одной угловой минуты для дат в диапазоне 1900 – 2100.
![]()
Положение солнца по городам
Точность вычисления
Знаков после запятой: 2
Высота над горизонтом (градусы)
![]()
Положение Солнца
Точность вычисления
Знаков после запятой: 2
Высота над горизонтом (градусы)
Анализируя освещенность помещений солнцем в Archicad, выписал высоты солнца в основных направлениях в дни весеннего равноденствия, летнего солнцестояния и в самый короткий день. Высота солнца в этих направления позволяет получить общую картину. Параллельно осознал для себя несколько закономерностей насчет положения солнца, над которыми раньше просто не задумывался.
На рисунке изображена траектория солнца в разные времена года.

Азимут и время восхода солнца
— 21 июня солнце всходит ровно на северо-востоке в 4.45
— 21 марта и 21 сентября солнце всходит ровно на востоке в 7.30
— 21 декабря солнце всходит ровно на юго-востоке в 10.15
Азимут и время заход солнца
— 21 июня заходит ровно на северо-западе в 22.10
— 21 марта и 21 сентября солнце заходит ровно на западе в 19.40
— 21 декабря солнце заходит ровно на юго-западе в 16.50
Самое высокое положение солнца на горизонтом в полдень (по нашему времени в 13.30), независимо от времени года. Высота солнца в 13.30 варьируется от 10 градусов зимой до 58 градусов летом.
21 декабря — 10 градусов
21 марта — 34 градуса
21 сентября — 34 градуса
21 июня — 58 градусов

Как-то я не осознавал, что 21 декабря солнце поднимается над горизонтом всего на 10 градусов. Совсем мы северная страна.
Вот формулы для расчета вы соты солнца в полдень.
Высота полуденного солнца зимой = наклон земной оси — широта
Высота полуденного солнца весной и осенью = 90 — широта
Высота полуденного солнца весной и осенью = 180 — наклон земной оси — широта
Наклон земной оси равен примерно 66 градусов, наша широта примерно 56 градусов.
Летом солнце освещает даже северные окна домов, что происходит рано утром и поздно вечером. 21 июня солнце встает ровно на северо-востоке и садится на северо-западе. Солнце в этих направлениях видно только один день в году, его высота над горизонтом в этот день — 0 градусов.
Солнце в направлениях на восток и на запад бывает видно ровно половину года. Остальную половину года солнца в этих направлениях не видно, потому что оно еще либо не встало, либо уже село. Высота солнца над горизонтом в направлениях ровно на восток и запад варьируется в течении полугода от 0 до 29 градусов
— 21 декабря солнца в этих направлениях вообще не видно
— 21 марта 0 градусов (солнце ровно на горизонте)
— 21 сентября 0 градусов (солнце ровно на горизонте)
— 22 июня 29 градусов
Солнце в направлении на юго-восток и юго-запад видно круглый год. При этом его высота на горизонтом варьируется от 0 градусов до 51 градуса
— 21 декабря 0 градусов
— 21 марта 26 градусов
— 21 сентября 26 градусов
— 22 июня 51,5 градус
Параллельно с этим осознал для несколько интересных фактов
— на экваторе день равен ночи на протяжении всего года
— на экваторе солнце всходит ровно на востоке, а заходит на западе на протяжении всего года
— высота солнца на экваторе в полдень варьируется в зависимости от времени года от 66 градусов с юга, 66 градусов с севера, и 90 градусов в дни весеннего равноденствия
— в день весеннего равноденствия ночь равна дню на всех широтах

<span style=»font: 0.9em sans-serif;»>60°</span>
<span style=»font: 0.9em sans-serif;»>60°</span>
<span style=»font: 0.9em sans-serif;»>120°</span>
<span style=»font: 1em/1em sans-serif;»>150°</span>
<span style=»font: 0.9em sans-serif;»>5°</span>
<span style=»font: 0.9em sans-serif;»>15°</span>
<span style=»font: 0.9em sans-serif;»>25°</span>
<span style=»font: 0.9em sans-serif;»>35°</span>
<span style=»font: 0.9em sans-serif;»>45°</span>
<span style=»font: 0.9em sans-serif;»>55°</span>
<span style=»font: 0.9em sans-serif;»>65°</span>
<span style=»font: 0.9em sans-serif;»>75°</span>
<span style=»font: 0.9em sans-serif;»>15°</span>
<span style=»font: 0.9em sans-serif;»>25°</span>
<span style=»font: 0.9em sans-serif;»>45°</span>
<span style=»font: 0.9em sans-serif;»>55°</span>
<span style=»font: 0.9em sans-serif;»>65°</span>
<span style=»font: 0.9em sans-serif;»>75°</span>
<span style=»font: 0.9em sans-serif;»>85°</span>
<span style=»font: 0.9em sans-serif;»>95°</span>
<span style=»font: 0.9em sans-serif;»>105°</span>
<span style=»font: 0.9em sans-serif;»>115°</span>
<span style=»font: 0.9em sans-serif;»>125°</span>
<span style=»font: 0.9em sans-serif;»>145°</span>
<span style=»font: 0.9em sans-serif;»>155°</span>
<span style=»font: 0.9em sans-serif;»>165°</span>
<span style=»font: 0.9em sans-serif;»>10°</span>
<span style=»font: 0.9em sans-serif;»>20°</span>
<span style=»font: 0.9em sans-serif;»>40°</span>
<span style=»font: 0.9em sans-serif;»>50°</span>
<span style=»font: 0.9em sans-serif;»>70°</span>
<span style=»font: 0.9em sans-serif;»>80°</span>
<span style=»font: 0.9em sans-serif;»>20°</span>
<span style=»font: 0.9em sans-serif;»>50°</span>
<span style=»font: 0.9em sans-serif;»>70°</span>
<span style=»font: 0.9em sans-serif;»>80°</span>
<span style=»font: 0.9em sans-serif;»>130°</span>
<span style=»font: 0.9em sans-serif;»>140°</span>
<span style=»font: 0.9em sans-serif;»>160°</span>
<span style=»font: 0.9em sans-serif;»>20°</span>
<span style=»font: 0.9em sans-serif;»>30°</span>
<span style=»font: 0.9em sans-serif;»>40°</span>
<span style=»font: 0.9em sans-serif;»>20°</span>
<span style=»font: 0.9em sans-serif;»>30°</span>
<span style=»font: 0.9em sans-serif;»>70°</span>
<span style=»font: 0.9em sans-serif;»>80°</span>
<span style=»font: 0.9em sans-serif;»>5°</span> N
<span style=»font: 0.9em sans-serif;»>15°</span>
<span style=»font: 0.9em sans-serif;»>25°</span>
<span style=»font: 0.9em sans-serif;»>35°</span>
<span style=»font: 0.9em sans-serif;»>75°</span>
<span style=»font: 0.9em sans-serif;»>5°</span> S
<span style=»font: 0.9em sans-serif;»>15°</span>
<span style=»font: 0.9em sans-serif;»>25°</span>
<span style=»font: 0.9em sans-serif;»>35°</span>
<span style=»font: 0.9em sans-serif;»><b>45°</b></span>
<span style=»font: 0.9em sans-serif;»>65°</span>
<span style=»font: 0.9em sans-serif;»>75°</span>
1.
Кульминацией светила называют явление прохождения светла через небесный меридиан в процессе его суточного движения.
Различие между верхней и нижней кульминациями состоит в том, что в момент верхней кульминации светило поднимается на максимальную высоту над горизонтом, а в момент нижнего — на минимальную высоту.
2.
а) звезда $M_1$ кульминирует между зенитом и точкой юга;
б) звезда $M_2$ кульминирует между зенитом и полюсом мира.
3.
4.
5.
- а) звезда Вега проходит через зенит;
- б) звезда Сириус в верхней кульминации находится на высоте $h = 64°13’$ к югу от зенита;
- в) высота звезды Денеб в верхней кульминации $h = 83°47’$ к северу от зенита;
- г) звезда Альтаир проходит через зенит.
Решения и ответы.
6.
Присоединяйтесь к Telegram-группе @superresheba_11,
делитесь своими решениями и пользуйтесь материалами, которые присылают другие участники группы!
Что такое кульминация звёзд
Как оказалось, не все знают, что такое кульминация звёзд. По определению, кульминация означает наиболее высокий момент чего-либо. Собственно говоря, в астрономии под этим подразумевают наивысший момент движения космического объекта.
Итак, кульминация звезды — это момент её прохождения сквозь небесный меридиан во время суточного движения светила.
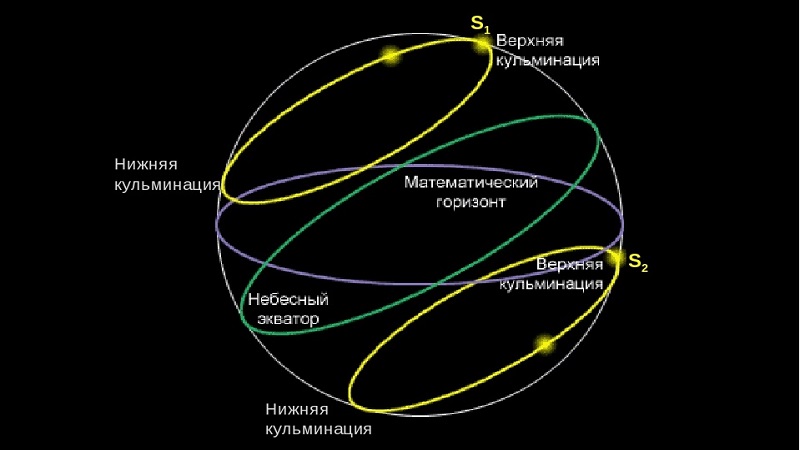
Стоит напомнить, что небесный меридиан является кругом сферы неба, который проходить сквозь зенит, полюс мира, а также южный полюс мира и надир.
Полюс мира представляет собой, можно сказать, отправную точку. Она лежит на небесной сфере, и как раз вокруг неё происходит видимое суточное движение звёзд. Причем перемещаются они по кругу параллельно экватору.
На Земле, как и в космосе — всегда есть на что посмотреть. Например сериалы Нетфликс, которые не оставят вас равнодушными.
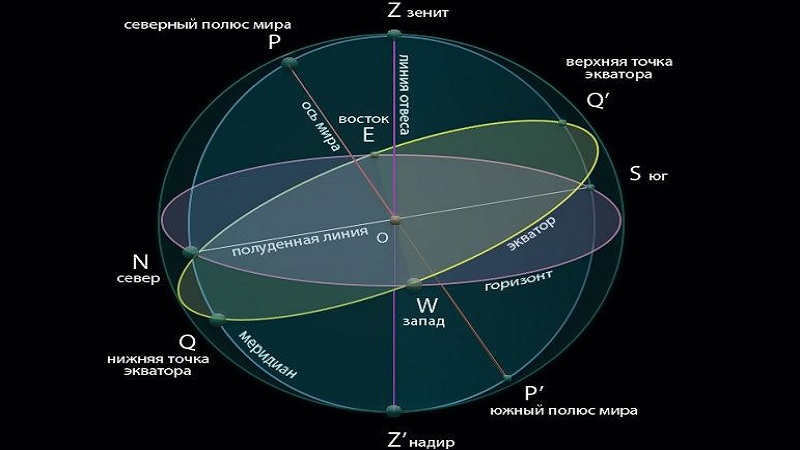
Какая бывает кульминация звезд
Любое светило в течение суток пересекает меридиан неба в двух точках. Другими словами, вот этот момент и называется кульминацией.
Период между описываемым пересечением звёздных тел составляет половину суток, то есть 12 часов.
Так как кульминация звёзд происходит два раза за сутки, то она бывает двух видов:
- верхняя, когда высота светила достигает максимального значения;
- нижняя, наоборот, наступает в то время, когда высота звезды минимальна.
Как рассчитывается кульминация звёзд
Поскольку высота полюса мира над горизонтом равна географической широте местности, то определить значения момента пересечений звёздного тела и небесного меридиана не так уж сложно.
В действительности, верхняя и нижняя кульминация звезды рассчитывается по формуле:

где h — высота, ф — географическая широта и δ — склонение.
Получается, что если известно склонение и высота звезды в момент кульминации, то можно рассчитать географическую широту местности, откуда проводятся наблюдения.
Что интересно, незаходящая звезда для определённой географической широты наблюдается и в верхней, и в нижней кульминации. А вот если светило находится далеко от небесного экватора в сторону юга, то его пересечение с меридианом может быть незаметно.

Для понимания, как и когда происходит кульминация звёзд можно обратиться к нашему главному светилу. Правда, самый простой пример, это Солнце. Оно, как и другие звёзды, два раза в сутки пересекает небесный меридиан. И все мы хорошо знаем это время. Во-первых, верхняя солнечная кульминация-это полдень. Во-вторых, спустя половину суток (12 часов), наступает полночь или нижняя кульминация.
Как видно, люди долгое время наблюдали за движением небесных тел. Они выделили определённые особенности и научились применять их в своей жизни. В целом, само наблюдение за загадочными и светящимися звёздными точками, небесной сферой и космосом безумно увлекательное и красивое зрелище.
Оценка статьи:
![]() Загрузка…
Загрузка…
