Новый октябрьский тренировочный вариант (тренировочная работа) №37812197 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
скачать вариант
скачать ответы
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812197:
Ответы и решения:
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом.
Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Задание 2 № 366653 Гравий продаётся в больших мешках по 2м 3 . Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между полями?
Правильный ответ: 3
Задание 3 № 366654 Найдите площадь территории, которая не занята постройками и полями. Ответ дайте в квадратных метрах.
Правильный ответ: 248
Задание 4 № 366655 Найдите расстояние между противоположными углами (диагональ) участка в метрах.
Правильный ответ: 40
Задание 5 № 366656 Владимир планирует купить трактор для обслуживания полей. Он рассматривает два варианта: трактор с бензиновым двигателем и трактор с дизельным двигателем. Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице. Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?
Правильный ответ: 800
Задание 10 № 325580 В магазине канцтоваров продаётся 100 ручек, из них 37 – красные, 8 – зелёные, 17 – фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что Алиса наугад вытащит красную или чёрную ручку.
Правильный ответ: 0,56
Задание 14 № 394406 Три конькобежца, скорости которых в некотором порядке образуют геометрическую прогрессию, одновременно стартуют (из одного места) по кругу. Через некоторое время второй конькобежец обгоняет первого, пробежав на 400 метров больше его. Третий конькобежец пробегает то расстояние, который пробежал первый к моменту обгона его вторым, за время на мин больше, чем первый. Найдите скорость первого конькобежца в м/мин.
Правильный ответ: 600
Задание 15 № 324839 В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
Правильный ответ: 12
Задание 16 № 311354 Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера центрального ∠AOC равна 96°.
Правильный ответ: 42
Задание 17 № 324364 Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Правильный ответ: 27556
Задание 18 № 311762 На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
Правильный ответ: 2
Задание 19 № 340590 Укажите номера верных утверждений. 1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. 2) Треугольник со сторонами 1, 2, 4 существует. 3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат. 4) В любом параллелограмме диагонали равны.
Правильный ответ: 13
Задание 21 № 311653 Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?
Правильный ответ: 2 кг
Задание 24 № 311969 Окружность касается стороны AB треугольника ABC, у которого ∠ C = 90°, и продолжений его сторон AC и BC за точки A и B соответственно. Докажите, что периметр треугольника ABC равен диаметру этой окружности.
Задание 25 № 339675 Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Правильный ответ: корень из 427
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:
Вариант Ларина №295 ОГЭ 2022 по математике 9 класс с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Прототипы заданий 19 ОГЭ по математике. Материал для подготовки к ОГЭ.
Для выполнения задания 19 необходимо уметь проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения.
Подробнее узнать виды заданий на данной позиции в КИМах можно по кодификатору
| Карточки для отработки задания 19 с ответамиИсточник: math100.ru → скачать |
| Тренинг задания 19 ОГЭ по математике → Скачать вариант 1 → Скачать ответы 1 → Скачать вариант 2 → Скачать ответы 2 |
| Материалы для отработки задания 19 Автор: Е. А. Ширяева → задания ФИПИ |
| Задания 19 — презентация Автор: Токпаева Л.С. → Скачать |
| → 60 билетов с ответами по заданию 19 Автор: Ведерникова Н. В. |
| → прототипы заданий с ответами Автор: Логинова Т.Н. |
| → Задания по геометрии в ОГЭ по математике |
| Автор: Горячева Е. В. |
| → задачи из банка ФИПИ с ответами |
Связанные страницы:
Задание 15 ОГЭ по математике — треугольники, четырёхугольники, многоугольники и их элементы
Задание 17 ОГЭ по математике — площади фигур
Задание 16 ОГЭ по математике — окружность, круг и их элементы
Тренировочные варианты ОГЭ 2021 по математике с ответами
Задание 18 ОГЭ по математике — фигуры на квадратной решетке
Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.
Сегодня 20.01.2022 15:03 свежие новости час назад
Прогноз на сегодня : Решу огэ математика задание 19 340590 . Развитие событий.
Актуально сегодня (20.01.2022 15:03): Решу огэ математика задание 19 340590
..
1. Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
9041462618282665b80f0416d63c2cfc aab710dd7a954c09bdd1a7746a453fb5
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
Решу огэ математика задание 19 340590
firmware phone samsung champ | spuiten en slikken перевод на русский | firmware for radio priority 2 staff | программа листомер скачать | интернет магазины отделочных материалов в красноярске | скачать драйвера на realtek rtl8168 8111 для windows 7 | where to get the firmware ue40d6100sw | индивидуалки липецка | игра престолов 1 сезон 3 серия вк | кино в сша презентация |
Invision Community © 2022 IPS, Inc.
Карта сайт Rss
s
p
Углы
1. Задание 19 № 40
Найдите тангенс угла AOB, изображенного на рисунке.
2. Задание 19 № 311485
На квадратной сетке изображён угол 
. Найдите 
.
3. Задание 19 № 316348
Найдите тангенс угла, изображённого на рисунке.
4. Задание 19 № 316374
Найдите тангенс угла, изображённого на рисунке.
5. Задание 19 № 323618
Найдите тангенс угла AOB, изображённого на рисунке.
6. Задание 19 № 340184
Найдите угол ABC. Ответ дайте в градусах.
7. Задание 19 № 341331
Найдите тангенс угла AOB.
8. Задание 19 № 348484
Найдите тангенс угла 
. Размер клетки 1 × 1.
9. Задание 19 № 348529
Найдите угол 
. Ответ дайте в градусах.
10. Задание 19 № 348622
Найдите тангенс угла , изображённого на рисунке.
11. Задание 19 № 348734
Найдите тангенс угла , изображённого на рисунке.
12. Задание 19 № 349019
Найдите угол ABC. Ответ дайте в градусах.
13. Задание 19 № 349174
Найдите тангенс угла
14. Задание 19 № 349261
Найдите угол . Ответ дайте в градусах.
15. Задание 19 № 349373
Найдите угол ABC. Ответ дайте в градусах.
16. Задание 19 № 349404
Найдите угол . Ответ дайте в градусах.
17. Задание 19 № 349410
Найдите тангенс угла , изображённого на рисунке.
18. Задание 19 № 349506
Найдите тангенс угла , изображённого на рисунке.
19. Задание 19 № 349517
Найдите тангенс угла , изображённого на рисунке.
20. Задание 19 № 349574
Найдите тангенс угла , изображённого на рисунке.
21. Задание 19 № 349593
Найдите тангенс угла , изображённого на рисунке.
22. Задание 19 № 350327
Найдите угол
23. Задание 19 № 350657
Найдите угол . Ответ дайте в градусах.
24. Задание 19 № 350842
Найдите угол
25. Задание 19 № 350906
Найдите угол . Ответ дайте в градусах.
26. Задание 19 № 350958
Найдите тангенс угла
27. Задание 19 № 351332
Найдите угол . Ответ дайте в градусах.
28. Задание 19 № 351373
Найдите тангенс угла
29. Задание 19 № 351414
Найдите угол ABC. Ответ дайте в градусах.
30. Задание 19 № 351667
Найдите угол . Ответ дайте в градусах.
31. Задание 19 № 352060
Найдите тангенс угла
32. Задание 19 № 352485
Найдите тангенс угла
33. Задание 19 № 352892
Найдите угол . Ответ дайте в градусах.
34. Задание 19 № 353222
Найдите угол . Ответ дайте в градусах.
35. Задание 19 № 353296
Найдите угол . Ответ дайте в градусах.
36. Задание 19 № 353345
Найдите угол . Ответ дайте в градусах
37. Задание 19 № 353533
Найдите угол . Ответ дайте в градусах.
38. Задание 19 № 353584
Найдите тангенс угла
В данном задании необходимо решить уравнение степени больше двух — это может быть биквадратное или кубическое уравнение. Ниже мы приводим алгоритмы решения типовых заданий.
Задание OM2101o
Решите уравнение и запишите в ответ наибольший из корней:
x4 = (4x — 5)2
Алгоритм решения:
- Определить тип уравнения.
- Перенести правую часть уравнения в левую.
- Привести уравнение к виду, при котором можно его многочлен слева разложить на множители.
- Разложить на множители.
- Приравнять каждый множитель к нулю
- Решить полученные уравнения.
- Записать ответ.
Решение:
1. Уравнение четвертой степени.
2. Перенесем правую часть уравнения в левую:
x4 — (4x — 5)2 = 0
3. Уравнение уже приведено к виду, при котором можно его левую часть разложить на множители.
4. Данное уравнение разложим на множители по формуле разности квадратов. Получим:
(х2 – (4х-5))( х2 + (4х-5)) = 0, или (х2 – 4х+5)(х2 + 4х-5) = 0.
5. Приравняем каждый множитель к нулю:
х2 – 4х+5 = 0 и х2 + 4х-5 = 0
6. Решим каждое из уравнений по формулам дискриминанта и корней:
Для первого уравнения:
D = b2-4ac = 16-20 = — 4, это означает, что первое уравнение х2 – 4х+5 = 0 не имеет корней.
Для второго уравнения:
Определим корни второго уравнения:
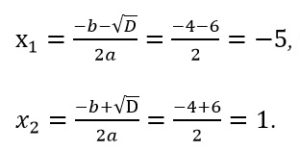Получили два корня: -5; 1.
Ответ: 1
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2102o
Решите уравнение и запишите в ответ наибольший из корней: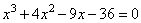
5. После деления получаем квадратный трехчлен:
Ответ: 3
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2103o
Решите уравнение и запишите в ответ наименьший из корней: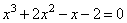
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами кубическое уравнение общего вида.
2. Найдем делители свободного члена уравнения. Это числа: 1; -1 и 2; -2.
3. Определим один из корней кубического уравнения среди делителей свободного члена .Для этого подставим каждый из этих делителей вместо x и проверим, какой их них является корнем:
— для x=1: 
— подходит это и есть один из корней.
4. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
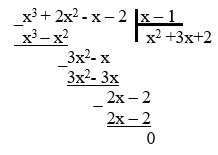
5. Получаем квадратный трехчлен
x2 +3x+2
6. Составим и решим квадратное уравнение для вычисления оставшихся двух корней. Для этого воспользуемся формулами корней квадратного уравнения и дискриминантом.
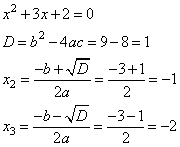
7. Получили три корня -2; -1; 1.
Ответ: -2
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2104o
Решите уравнение и запишите в ответ натуральное число, встречающееся в обоих корнях:
(х–2)4+3(х–2)2–10=0
Алгоритм решения:
- Выполняем замену выражения с х на альтернативную переменную. Это позволит упростить уравнение и привести его к форме обычного квадратного.
- Решаем полученное квадратное уравнения.
- Переходим обратно к выражению с х, для которого была выполнена замена.
- Находим искомые корни уравнения.
Решение:
(х–2)4+3(х–2)2–10=0
Выполняем замену: (х–2)2=а.
Получаем:
а2+3а–10=0
Это уравнение можно решить с помощью т.Виета. Согласно теореме, имеем:
а1+а2=–b, a1·a2=c.
Здесь а1, а2 – корни этого уравнения, b=3, c=–10.
Отсюда получаем: а1=2, а2=–5.
Возвращаемся к переменной х. Поскольку (х–2)2=а, то получим:
1) (х–2)2=2
2) (х–2)2=–5
это уравнение корней не имеет, т.к. нельзя извлечь корень из отрицательного числа
Корни уравнения: 
Ответ: 2
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2105o
Решите неравенство. Пример записи ответа: [–5; 3].
(3х–7)2≥(7х–3)2
Алгоритм решения:
- Используя формулу сокращенного умножения для квадрата разности, раскрываем скобки в левой и правой части неравенства.
- Группируем элементы (слагаемые) неравенства: слагаемые с «х» должны оказаться в левой части, свободные члены – в правой. Приводим подобные.
- Решаем полученное неравенство.
Решение:
9х2–42х+49≥49х2–42х+9
9х2–42х–49х2+42х≥9–49
–40х2≥–40
х2≤1
х≤|1| → –1≤x≤1 → xϵ[–1; 1]
Ответ: [–1; 1]
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2106o
Решите систему уравнений. В ответ запишите пару чисел сумма которых наибольшая в порядке возрастания. Например, 47, если один из корней равен 4, а другой 7.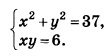
Алгоритм решения:
- Из 2-го уравнения выражаем у через х.
- Подставляем полученное выражение для у в 1-е уравнение.
- В полученном уравнении с одной переменной (х) выполняем тождественные преобразования. Приводим его к квадратичному виду.
- Выполняем замену х2 на а. Решаем полученное квадратное уравнение.
- Возвращаемся от а к х. Находим все значения (корни) для х.
- Определяем соответствующие им значения для у.
- Фиксируем в ответе пары соответствующих корней.
Решение:
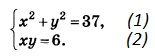
Из (2) выражаем у через х:
Полученное выражение для у подставляем в (1):
Выполним преобразования:
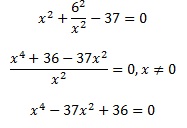
Выполним замену: х2= , а≠0 .
Получим:
а2–37а+36=0
По теореме Виета а1=1, а2=36
Отсюда имеем:
х2=1 → х=±1 → х1=–1, х2=1
х2=36 → х=±6 → х3=–6, х4=6
Теперь возвращаемся к уравнению, в котором у выражено через х. И вычисляем соответствующие значения для у:
Корни системы: (–1; –6), (1; 6), (–6; –1), (6; 1)Ответ: 16
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание 20OM21R
Решите уравнение х3 + 6х2=4х + 24. В ответе запишите только число без знаков, например «5».
Нам дано уравнение третьей степени: х3 + 6х2=4х + 24
В данном уравнении перенесем все слагаемые в одну сторону ( в левую), изменяя при этом знаки: х3 + 6х2 – 4х – 24=0
Теперь сгруппируем слагаемые: (х3 + 6х2) – (4х + 24)=0
Вынесем общий множитель за скобки из каждой группы: х2(х + 6) – 4(х + 6)=0
Вынесем за скобки выражение (х + 6): (х + 6)(х2– 4)=0
Приравняем каждый множитель к нулю и решим полученные уравнения:
х + 6=0 и х2– 4=0
х=6 х2=4, отсюда х1,2=±2
Ответ: 2
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2001
Найти значение выражения 41a – 11b + 15, если 4a−9b+39a−4b+3=5
Для начала преобразуем нашу дробь, которая дана по условию. Применим правило пропорции, умножив на 5 знаменатель данной дроби:
4a−9b+39a−4b+3=5
5(9а – 4b + 3)=4a – 9b+3
Раскроем скобки и перенесем слагаемые с буквами а и b влево, а свободные члены вправо (не забывая изменять при переносе знаки на противоположные):
45a – 20b +15 =4a – 9b+3
45a – 20b – 4a + 9b=3 – 15
Приведем подобные слагаемые:
41a – 11b = — 12
Выпишем выражение, значение которого надо найти: 41a – 11b + 15 и заменим в нем 41a – 11b на число -12, полученное при упрощении нашей дроби:
41a – 11b + 15= — 12 + 15=3. Видим, что значение нашего выражения получилось равным 3.Ответ: 3
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2002
Решить уравнение: х2−2х+√5−х=√5−х+24
Данное уравнение является квадратным. Но в его условии присутствует квадратный корень, что усложняет нам задачу для нахождения его корней, в том плане, что необходимо увидеть, какие же ограничения на переменную х здесь будут.
Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного корня): ограничение на х: 5−х≥0
Решаем полученное неравенство: −х≥−5, отсюда х≤5. Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.
Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):
х2−2х+√5−х − √5−х− 24=0
Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:
х2−2х− 24=0
Итак, корнями уравнения х2−2х− 24=0 будут числа -4 и 6.
Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 не≤5, а число минус 4 записываем в ответ нашего уравнения, так как −4≤5 .
Ответ: -4
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2003
Решить неравенство −11(х−2)2−3≥0
Имеем дробное неравенство, где решать надо будет только знаменатель. Но для этого посмотрим, что решением неравенства являются числа, которые больше или равны нулю. Для этого наш знаменатель должен быть отрицательным числом, так как числитель – число тоже отрицательное, а при делении двух отрицательных чисел получим число положительное. Далее, знаменатель не должен быть равен нулю, так как на нуль делить нельзя. Следовательно, начнем решение с того, что выпишем знаменатель, который должен быть отрицательным числом:
(х – 2)2 – 3<0
У нас получилось квадратное неравенство, которое мы и должны решать. Начнем с раскрытия скобок по формуле сокращенного умножения и приведения подобных слагаемых:
х2 – 4х+4 – 3 <0
х2 – 4х+1 <0
Получим квадратное неравенство, для которого надо найти интервал отрицательных чисел (<0)
Для этого найдем нули функции, решая с помощью дискриминанта:
Д=(-4)2 — 4∙1∙1=16-4=12
х1=4− √122=2(2−√3)2=2−√3
Знаем, что х2 будет отличаться только знаком, получим, что х2=2+√3
Теперь отмечаем числа на числовом луче и показываем интервалы справа налево путем чередования знаков. Видим, что наш интервал отрицательных чисел – от точки (2−√3) до точки (2+√3).
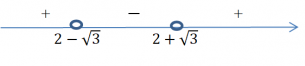
Ответ: (2−√3 ; 2+√3)
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2004
Сократите дробь 36n4n−2∙32n−1
Чтобы решить данное задание, необходимо понимать, что выполнять действия умножение и деление степеней мы можем в том случае, если они имеют одинаковые основания. Поэтому разложим на множители основание 36 нашего числителя так, чтобы вместо 36 были числа 4 и 3, которые есть в знаменателе.
(3∙3∙4)n4n−2∙32n−1
Теперь представим каждый множитель в виде степени:
3n∙3n∙4n4n−2∙32n−1
Разложим знаменатель дроби на множители по свойству степеней
3n∙3n∙4n4n∙4−2∙32n∙3−1
Теперь можно сократить числитель и знаменатель на 3n и в 4n степени
Получим дробь, которую преобразуем по свойству степеней:
14−2∙3−1 = 42∙311=16∙3=48
Ответ: 48
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2005
Решить неравенство(х−5)2<√7(х−5)
Для того чтобы начать решать неравенство, мы должны понимать, интервал каких чисел будем находить – положительных или отрицательных. Для этого перенесем выражение из правой части в левую, изменяя знак на противоположный, и справа от знака «меньше» образуется нуль:
(х−5)2−√7(х−5)<0
Теперь вынесем за скобки общий множитель (х-5), получим:
(х−5)(х−5−√7)<0
Найдем нули функции, приравнивая каждый множитель к нулю:
х−5=0, откуда х=5
х−5−√7=0,
откуда:
х=5+√7
Отметим эти числа на числовом луче и найдем интервал отрицательных чисел:
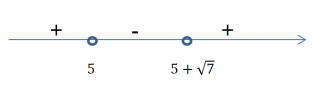
Итак, видно, что необходимый интервал от 5 до (5+√7)
Ответ: (5;5+√7)Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
- ОГЭ по математике
Материалы для отработки задания №6 ОГЭ по математике — числа и вычисления.
Типы заданий:
→ Действия с обыкновенными дробями.
→ Действия с десятичными дробями.
→ Степени.
→ Сравнение чисел.
| Теория для задания 6 Автор: Е. А. Ширяева → скачать |
| Практика для задания 6 Автор: Е. А. Ширяева → скачать |
| Варианты заданий 6 с ответами Источник: https://math100.ru → скачать |
| Карточки для отработки задания №6 с ответами → скачать
|
Решение типовых задач №6 на ОГЭ по математике
Связанные страницы:
На плане изображено домохозяйство. При входе на участок справа от ворот находится баня, а слева – гараж, отмеченный цифрой 7. Площадь, занятая гаражом, равна 32 м2. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки. Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м × 1 м. Между баней и гаражом имеется площадка площадью 64 м2, вымощенная такой же плиткой. К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
1. Найдите, на сколько метров периметр участка земли, занятого под жилой дом, больше периметра участка земли, занятого под сарай.
2. Тротуарная плитка продаётся в упаковках по 8 штук. Сколько упаковок понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
3. Найдите общую площадь (в м2) участка, которую занимают сарай и баня.
4. Найдите расстояние от теплицы до бани (расстояние между двумя ближайшими точками по прямой) в метрах. В ответе укажите квадрат полученного значения.
5. Хозяин дома планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котёл), руб. | Прочее оборудование и монтаж, руб. | Средняя потребляемая мощность, кВт | Средний расход газа, м 3/час | Тариф | |
| Газовое отопление | 30 000 | 19 706 | 1,2 | – | 5,7 руб./м3 |
| Электрическое отопление | 20 000 | 15 000 | – | 5,7 | 5,5 руб./(кВт∙ч) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического оборудования?
Разбираем решение заданий перспективной модели измерительных материалов ОГЭ по математике 2020 года. Модель опубликована на сайте ФИПИ 12 апреля для обсуждения.
Задание № 1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане.
| Объекты | жилой дом | сарай | баня | теплица |
| Цифры | 3 | 4 | 6 | 1 |
Ответ: 3461.
Задание № 2
Тротуарная плитка продается в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
Решение:
Определяем по рисунку общую площадь площадки перед гаражом и всех дорожек. Сначала считаем количество клеток размером 1м на 1м.
Всего клеток 90 = 64 + 26.
Площадь каждой клетки (плитки) 1 м2.
Площадь дорожек и площадки вместе составляет 90 м2.
В одной упаковке 4 плитки.
90 : 4 = 22 (остаток 2).
Нужно приобрести 23 упаковки плитки.
Ответ: 23.
Задание № 3
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
Решение:
Нужно разделить фигуру на две части, которые являются прямоугольниками.
Площадь, занимаемая жилым домом, равна сумме площадей прямоугольников 1 и 2.
Подсчитаем клетки.
1 фигура — 8, вторая — 9. Всего 17 клеток. Площадь каждой клетки равна площади квадрата со стороной
2 м, то есть 4 м2.
17 * 4 = 68 ( м2) — площадь, которую занимает жилой дом.
Ответ: 68.
Задание №4
Найдите расстояние от жилого дома до гаража ( расстояние между двумя ближайшими точками по прямой) в метрах.
Решение:
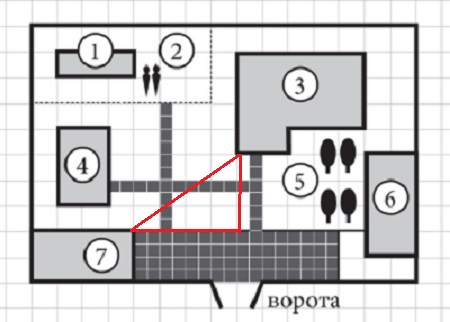
Расстоянием от жилого дома до гаража является является длина гипотенузы прямоугольного треугольника. Найдем гипотенузу по теореме Пифагора.
Длина катетов равна 6 м и 8 м.
Квадрат гипотенузы равен сумме квадратов катетов, то есть 36 + 64 = 100 (м2).
Гипотенуза равна 10 м.
Перспективная модель ОГЭ по математике 2020: задание №5
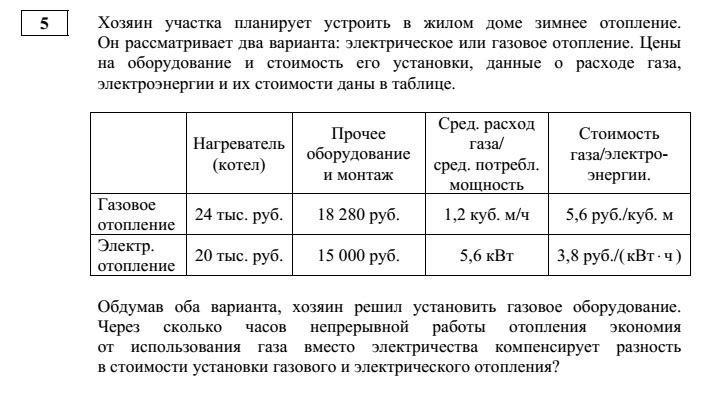
Решение:
Сначала рассмотрим на сколько рублей дороже обошлась установка газового оборудования по сравнению с электрическим отоплением.
24000 + 18280 — (20000 + 15000) = 7280 (рублей) — разность в стоимости.
Рассчитаем стоимость часа работы газового оборудования: 1,2 * 5,6 = 6,72 (руб/ч).
Найдем стоимость часа работы электрического котла: 5,6 * 3,8 = 21,28 (руб/ч).
Экономия от использования газа в час: 21,28 — 6,72 = 14,56 (руб/ч).
7280 : 14,56 = 500 (часов) — непрерывной работы нужно для компенсации разности в стоимости установки газового и электрического оборудования.
Ответ: 500.
1. Задание 1 № 366577
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | жилой дом | сарай | баня | теплица |
| Цифры |
Прочитайте внимательно текст и выполните задание.
На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м.
Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м × 1 м. Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
2. Задание 2 № 366578
Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
3. Задание 3 № 366579
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
4. Задание 4 № 366581
Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Задание 5 № 366582
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель | Прочее | Сред. расход | Стоимость газа / | |
| Газовое отопление | 24 тыс. руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 тыс. руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт · ч ) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости покупки и установки газового и электрического отопления?
6. Задание 6 № 333006
Найдите значение выражения .
7. Задание 7 № 316336
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.
Какое из следующих неравенств верно?
1)
2)
3)
4)
8. Задание 8 № 401223
Сколько целых чисел расположено между и ?
9. Задание 9 № 333007
Решите уравнение .
10. Задание 10 № 325560
В таблице представлены результаты четырёх стрелков, показанные ими на тренировке.
| Номер стрелка | Число выстрелов | Число попаданий |
| 1 | 42 | 28 |
| 2 | 70 | 20 |
| 3 | 54 | 45 |
| 4 | 46 | 42 |
Тренер решил послать на соревнования того стрелка, у которого относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите в ответе его номер.
11. Задание 11 № 34
Установите соответствие между графиками функций и формулами, которые их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
12. Задание 12 № 311337
Длину окружности l можно вычислить по формуле , где R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать ).
13. Задание 13 № 185
Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
14. Задание 14 № 394427
Мощности пяти различных электромоторов составляют возрастающую геометрическую прогрессию. Мощность самого слабого электромотора — 5 кВт, а третьего по мощности — 20 кВт. Найдите мощность самого мощного электромотора, ответ дайте в кВт.
15. Задание 15 № 339495
В треугольнике ABC AB = BC, а высота AH делит сторону BC на отрезки BH = 64 и CH = 16. Найдите cosB.
16. Задание 16 № 356339
Площадь круга равна 90. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
17. Задание 17 № 169878
Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен . Найдите площадь параллелограмма.
18. Задание 18 № 311958
На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённой из вершины прямого угла.
19. Задание 19 № 340590
Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) В любом параллелограмме диагонали равны.
20. Задание 20 № 311588
Найдите значение выражения: при
21. Задание 21 № 338992
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 60 км. Отдохнув, он отправился обратно в А, увеличив скорость на 10 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
22. Задание 22 № 311576
Известно, что парабола проходит через точку и её вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую
23. Задание 23 № 311548
Найдите величину угла AOE, если OE — биссектриса угла AOC, OD — биссектриса угла COB.
24. Задание 24 № 340387
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке E стороны BC. Докажите, что E — середина BC.
25. Задание 25 № 339366
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 10 и MB = 18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
Прочитайте внимательно текст и выполните задание.
На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м.
Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м × 1 м. Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | жилой дом | сарай | баня | теплица |
|---|---|---|---|---|
| Цифры |
Источник: Демонстрационная версия ОГЭ—2020 по математике., Демонстрационная версия ОГЭ—2021 по математике.
2
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
Источник: Демонстрационная версия ОГЭ—2020 по математике., Демонстрационная версия ОГЭ—2021 по математике.
3
Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.
Источник: Демонстрационная версия ОГЭ—2020 по математике., Демонстрационная версия ОГЭ—2021 по математике.
4
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котел) | Прочее оборудование и монтаж | Сред. расход газа / сред. потребл. мощность | Стоимость газа / электро-энергии | |
|---|---|---|---|---|
| Газовое отопление | 24 тыс. руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 тыс. руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт · ч ) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости покупки и установки газового и электрического отопления?
Источник: Демонстрационная версия ОГЭ—2020 по математике., Демонстрационная версия ОГЭ—2021 по математике.
Спрятать решение
Решение.
Заметим, что, поскольку одна плитка имеет площадь 1 м2, для площадки перед гаражом понадобится 16 · 4 = 64 плитки. Для того чтобы выложить все дорожки, понадобится ещё 26 плиток. Значит, всего необходимо 90 плиток. Теперь найдём, сколько упаковок плитки понадобилось: 
Следовательно, чтобы выложить все дорожки и площадку перед гаражом понадобится 23 упаковки плитки.
Ответ: 23.
Источник: Демонстрационная версия ОГЭ—2020 по математике., Демонстрационная версия ОГЭ—2021 по математике.
1. Задание 1 № 366577
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | жилой дом | сарай | баня | теплица |
| Цифры |
Прочитайте внимательно текст и выполните задание.
На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м.
Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м × 1 м. Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
2. Задание 2 № 366578
Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
3. Задание 3 № 366579
Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
4. Задание 4 № 366581
Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Задание 5 № 366582
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель | Прочее | Сред. расход | Стоимость газа / | |
| Газовое отопление | 24 тыс. руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 тыс. руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт · ч ) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости покупки и установки газового и электрического отопления?
6. Задание 6 № 333006
Найдите значение выражения .
7. Задание 7 № 316336
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.
Какое из следующих неравенств верно?
1)
2)
3)
4)
8. Задание 8 № 401223
Сколько целых чисел расположено между и ?
9. Задание 9 № 333007
Решите уравнение .
10. Задание 10 № 325560
В таблице представлены результаты четырёх стрелков, показанные ими на тренировке.
| Номер стрелка | Число выстрелов | Число попаданий |
| 1 | 42 | 28 |
| 2 | 70 | 20 |
| 3 | 54 | 45 |
| 4 | 46 | 42 |
Тренер решил послать на соревнования того стрелка, у которого относительная частота попаданий выше. Кого из стрелков выберет тренер? Укажите в ответе его номер.
11. Задание 11 № 34
Установите соответствие между графиками функций и формулами, которые их задают.
| А) | Б) | В) |
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
| А | Б | В |
12. Задание 12 № 311337
Длину окружности l можно вычислить по формуле , где R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать ).
13. Задание 13 № 185
Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
14. Задание 14 № 394427
Мощности пяти различных электромоторов составляют возрастающую геометрическую прогрессию. Мощность самого слабого электромотора — 5 кВт, а третьего по мощности — 20 кВт. Найдите мощность самого мощного электромотора, ответ дайте в кВт.
15. Задание 15 № 339495
В треугольнике ABC AB = BC, а высота AH делит сторону BC на отрезки BH = 64 и CH = 16. Найдите cosB.
16. Задание 16 № 356339
Площадь круга равна 90. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
17. Задание 17 № 169878
Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен . Найдите площадь параллелограмма.
18. Задание 18 № 311958
На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённой из вершины прямого угла.
19. Задание 19 № 340590
Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) В любом параллелограмме диагонали равны.
20. Задание 20 № 311588
Найдите значение выражения: при
21. Задание 21 № 338992
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 60 км. Отдохнув, он отправился обратно в А, увеличив скорость на 10 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
22. Задание 22 № 311576
Известно, что парабола проходит через точку и её вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую
23. Задание 23 № 311548
Найдите величину угла AOE, если OE — биссектриса угла AOC, OD — биссектриса угла COB.
24. Задание 24 № 340387
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке E стороны BC. Докажите, что E — середина BC.
25. Задание 25 № 339366
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 10 и MB = 18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Огэ математика 340590
Задание 19 № 340590
Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) В любом параллелограмме диагонали равны.
1) «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой» — Верно, это аксиома планиметрии.
2) Треугольник со сторонами 1, 2, 4 существует» — Неверно: для того, чтобы существовал треугольник, сумма длин любых его двух сторон должна быть больше длины третьей стороны.
3) «Если в ромбе один из углов равен 90°, то такой ромб — квадрат» — Верно, в этом случае противоположный угол тоже будет равен 90°, а значит и два других (равных) угла будут равны по 90°.
4) «В любом параллелограмме диагонали равны» — Не верно, диагонали в произвольном параллелограмме не равны.
Задание 19 № 340590
Задание 19 340590.
Oge. sdamgia. ru
25.07.2017 16:21:37
2017-07-25 16:21:37
Источники:
Https://oge. sdamgia. ru/problem? id=340590
Решу огэ математика 366653 — Подготовка к ГИА » /> » /> .keyword { color: red; } Огэ математика 340590
Решу огэ математика 366653
Решу огэ математика 366653
Гравий продаётся в больших мешках по 2 м 3 . Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между полями?
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Задание 1 № 366652
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Прямо перед воротами предполагается построить жилой дом. Значит, дом отмечен цифрой 5. Капустой планируется засеять поле, ближайшее к гаражу, значит, поле с капустой отмечено цифрой 2. На поле рядом с картофелем планируется посеять кукурузу, следовательно, поле с кукурузой отмечено цифрой 6. Оставшееся поле с репой отмечено цифрой 4.
Задание 3 № 366654
Найдите площадь территории, которая не занята постройками и полями. Ответ дайте в квадратных метрах.
Площадь всего участка равна
Площадь гаража равна
Площадь жилого дома равна
Площадь полей, засеянных капустой, морковью и репой, равна
Площадь полей, засеянных кукурузой и картофелем, равна
Таким образом, площадь территории, которая не занята постройками или полями, равна
Задание 4 № 366655
Найдите расстояние между противоположными углами (диагональ) участка в метрах.
Найдём расстояние между противоположными углами участка по теореме Пифагора:
Задание 5 № 366656
Владимир планирует купить трактор для обслуживания полей. Он рассматривает два варианта: трактор с бензиновым двигателем и трактор с дизельным двигателем. Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице.
Цена
| Дизельный двигатель | 990 000 | 5,5 л/ч | 47 |
| Бензиновый двигатель | 900 000 | 7 л/ч | 53 |
ТрактораСредний расход
ТопливаСтоимость топлива
Руб. за л
Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?
Разность в стоимости тракторов равна 990 000 − 900 000 = 90 000 руб. Стоимость топлива за час работы трактора с дизельным двигателем равна 47 · 5,5 = 258,5 руб. Стоимость топлива за час работы трактора с бензиновым двигателем равна 53 · 7 = 371 руб. Следовательно, за час работы трактора Владимир экономит 371 − 258,5 = 112,5 руб. Таким образом, Владимир компенсирует разницу в стоимости между тракторами с разными двигателями через
Задание 2 № 366653
Задание 5 № 366656
Задание 2 366653.
Источники:
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу огэ математика 366653
Решу огэ математика 366653
Решу огэ математика 366653
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Гравий продаётся в больших мешках по 2 м 3 . Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между полями?
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Найдите площадь территории, которая не занята постройками и полями. Ответ дайте в квадратных метрах.
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Найдите расстояние между противоположными углами (диагональ) участка в метрах.
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Владимир планирует купить трактор для обслуживания полей. Он рассматривает два варианта: трактор с бензиновым двигателем и трактор с дизельным двигателем. Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице.
Цена
| Дизельный двигатель | 990 000 | 5,5 л/ч | 47 |
| Бензиновый двигатель | 900 000 | 7 л/ч | 53 |
ТрактораСредний расход
ТопливаСтоимость топлива
Руб. за л
Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице.
Источники:
Решу ОГЭ 2022 тренировочный вариант №37812197 по математике 9 класс с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword < color: red; >Решу огэ математика 366653
Решу ОГЭ 2022 тренировочный вариант №37812197 по математике 9 класс с ответами
Решу ОГЭ 2022 тренировочный вариант №37812197 по математике 9 класс с ответами
Новый октябрьский тренировочный вариант (тренировочная работа) №37812197 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812197:
Ответы и решения:
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом.
Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Задание 2 № 366653 Гравий продаётся в больших мешках по 2м 3 . Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между полями?
Правильный ответ: 3
Задание 3 № 366654 Найдите площадь территории, которая не занята постройками и полями. Ответ дайте в квадратных метрах.
Правильный ответ: 248
Задание 4 № 366655 Найдите расстояние между противоположными углами (диагональ) участка в метрах.
Правильный ответ: 40
Задание 5 № 366656 Владимир планирует купить трактор для обслуживания полей. Он рассматривает два варианта: трактор с бензиновым двигателем и трактор с дизельным двигателем. Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице. Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?
Правильный ответ: 800
Задание 10 № 325580 В магазине канцтоваров продаётся 100 ручек, из них 37 – красные, 8 – зелёные, 17 – фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что Алиса наугад вытащит красную или чёрную ручку.
Правильный ответ: 0,56
Задание 14 № 394406 Три конькобежца, скорости которых в некотором порядке образуют геометрическую прогрессию, одновременно стартуют (из одного места) по кругу. Через некоторое время второй конькобежец обгоняет первого, пробежав на 400 метров больше его. Третий конькобежец пробегает то расстояние, который пробежал первый к моменту обгона его вторым, за время на мин больше, чем первый. Найдите скорость первого конькобежца в м/мин.
Правильный ответ: 600
Задание 15 № 324839 В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
Правильный ответ: 12
Задание 16 № 311354 Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера центрального ∠AOC равна 96°.
Правильный ответ: 42
Задание 17 № 324364 Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Правильный ответ: 27556
Задание 18 № 311762 На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
Правильный ответ: 2
Задание 19 № 340590 Укажите номера верных утверждений. 1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. 2) Треугольник со сторонами 1, 2, 4 существует. 3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат. 4) В любом параллелограмме диагонали равны.
Правильный ответ: 13
Задание 21 № 311653 Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?
Правильный ответ: 2 кг
Задание 24 № 311969 Окружность касается стороны AB треугольника ABC, у которого ∠ C = 90°, и продолжений его сторон AC и BC за точки A и B соответственно. Докажите, что периметр треугольника ABC равен диаметру этой окружности.
Задание 25 № 339675 Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Решу ОГЭ 2022 тренировочный вариант №37812197 по математике 9 класс с ответами
Новый октябрьский тренировочный вариант (тренировочная работа) №37812197 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом.
Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Задание 2 № 366653 Гравий продаётся в больших мешках по 2м 3 . Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между полями?
Правильный ответ: 3
Задание 3 № 366654 Найдите площадь территории, которая не занята постройками и полями. Ответ дайте в квадратных метрах.
Правильный ответ: 248
Задание 4 № 366655 Найдите расстояние между противоположными углами (диагональ) участка в метрах.
Правильный ответ: 40
Задание 5 № 366656 Владимир планирует купить трактор для обслуживания полей. Он рассматривает два варианта: трактор с бензиновым двигателем и трактор с дизельным двигателем. Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице. Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?
Правильный ответ: 800
Задание 10 № 325580 В магазине канцтоваров продаётся 100 ручек, из них 37 – красные, 8 – зелёные, 17 – фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что Алиса наугад вытащит красную или чёрную ручку.
Правильный ответ: 0,56
Задание 14 № 394406 Три конькобежца, скорости которых в некотором порядке образуют геометрическую прогрессию, одновременно стартуют (из одного места) по кругу. Через некоторое время второй конькобежец обгоняет первого, пробежав на 400 метров больше его. Третий конькобежец пробегает то расстояние, который пробежал первый к моменту обгона его вторым, за время на мин больше, чем первый. Найдите скорость первого конькобежца в м/мин.
Правильный ответ: 600
Задание 15 № 324839 В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
Правильный ответ: 12
Задание 16 № 311354 Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера центрального ∠AOC равна 96°.
Правильный ответ: 42
Задание 17 № 324364 Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Правильный ответ: 27556
Задание 18 № 311762 На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.
Правильный ответ: 2
Задание 19 № 340590 Укажите номера верных утверждений. 1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. 2) Треугольник со сторонами 1, 2, 4 существует. 3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат. 4) В любом параллелограмме диагонали равны.
Правильный ответ: 13
Задание 21 № 311653 Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?
Правильный ответ: 2 кг
Задание 24 № 311969 Окружность касается стороны AB треугольника ABC, у которого ∠ C = 90°, и продолжений его сторон AC и BC за точки A и B соответственно. Докажите, что периметр треугольника ABC равен диаметру этой окружности.
Задание 25 № 339675 Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Задание 3 366654 Найдите площадь территории, которая не занята постройками и полями.
Источники:
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу огэ математика 366653
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Гравий продаётся в больших мешках по 2 м 3 . Сколько мешков с гравием понадобится для того, чтобы засыпать пространство между полями?
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Найдите площадь территории, которая не занята постройками и полями. Ответ дайте в квадратных метрах.
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Найдите расстояние между противоположными углами (диагональ) участка в метрах.
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Владимир планирует купить трактор для обслуживания полей. Он рассматривает два варианта: трактор с бензиновым двигателем и трактор с дизельным двигателем. Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице.
Цена
| Дизельный двигатель | 990 000 | 5,5 л/ч | 47 |
| Бензиновый двигатель | 900 000 | 7 л/ч | 53 |
ТрактораСредний расход
ТопливаСтоимость топлива
Руб. за л
Обдумав оба варианта, Владимир решил купить трактор с дизельным двигателем. Через сколько часов непрерывной работы экономия от использования трактора с дизельным двигателем вместо трактора с бензиновым двигателем компенсирует разность в стоимости этих тракторов?
Владимир купил участок, чтобы заняться фермерством. План его фермы изображен на рисунке, сторона каждой клетки равна 2 м. Ферму планируется обнести забором. Вход будет осуществляться через единственные ворота. Прямо перед воротами предполагается построить жилой дом. За ним будет построен гараж с отдельным въездом. Наибольшее поле будет отведено под посев картофеля. На поле рядом с ним планируется посадить кукурузу. Поле, обозначенное на плане цифрой 3, планируется засеять морковью. Поле, ближайшее к гаражу, планируется отвести под капусту. Оставшееся поле будет засеяно репой. Пустое пространство между полями планируется засыпать гравием. Чтобы засыпать 4 м 2 гравием, требуется 0,2 м 3 материала. Также Владимир планирует купить трактор для хозяйственных нужд.
Цены за покупку трактора и стоимость топлива, данные о расходе топлива даны в таблице.
OГЭ 2022, математика задания, ответы, решения.
Dankonoy. com
20.04.2020 18:10:35
2020-04-20 18:10:35
Источники:
Https://dankonoy. com/gia/gia2/archives/8071
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Огэ математика 340590
Огэ математика 340590
Огэ математика 340590
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Объекты
| Туалет | Детская | Гостиная | Кухня |
Цифры
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1. Напротив входа расположена туалетная комната, а справа от нее — ванная комната.
Гостиная занимает наибольшую площадь в квартире, а справа от неё находится кухня. Прямо перед гостиной находится детская. Из детской можно попасть на балкон, отмеченный цифрой 6.
Потолок в гостиной планируется покрасить в красный цвет. Для покраски одного 1 м 2 потолка требуется 0,25 л краски.
В квартире планируется установить счётчик электроэнергии. Имеется возможность установить однотарифный или двухтарифный счётчик.
Краска продаётся в банках по 3 л. Сколько банок краски требуется купить, чтобы покрасить потолок в гостиной?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1. Напротив входа расположена туалетная комната, а справа от нее — ванная комната.
Гостиная занимает наибольшую площадь в квартире, а справа от неё находится кухня. Прямо перед гостиной находится детская. Из детской можно попасть на балкон, отмеченный цифрой 6.
Потолок в гостиной планируется покрасить в красный цвет. Для покраски одного 1 м 2 потолка требуется 0,25 л краски.
В квартире планируется установить счётчик электроэнергии. Имеется возможность установить однотарифный или двухтарифный счётчик.
Найдите площадь, которую занимают детская и балкон. Ответ дайте в квадратных метрах.
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1. Напротив входа расположена туалетная комната, а справа от нее — ванная комната.
Гостиная занимает наибольшую площадь в квартире, а справа от неё находится кухня. Прямо перед гостиной находится детская. Из детской можно попасть на балкон, отмеченный цифрой 6.
Потолок в гостиной планируется покрасить в красный цвет. Для покраски одного 1 м 2 потолка требуется 0,25 л краски.
В квартире планируется установить счётчик электроэнергии. Имеется возможность установить однотарифный или двухтарифный счётчик.
Найдите расстояние между противоположными углами детской комнаты в метрах. Ответ запишите в виде
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1. Напротив входа расположена туалетная комната, а справа от нее — ванная комната.
Гостиная занимает наибольшую площадь в квартире, а справа от неё находится кухня. Прямо перед гостиной находится детская. Из детской можно попасть на балкон, отмеченный цифрой 6.
Потолок в гостиной планируется покрасить в красный цвет. Для покраски одного 1 м 2 потолка требуется 0,25 л краски.
В квартире планируется установить счётчик электроэнергии. Имеется возможность установить однотарифный или двухтарифный счётчик.
Хозяин квартиры планирует установить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о потребляемой мощности, и тарифах оплаты даны в таблице.
Однотарифный
5000 руб.
3,5 кВт
3 руб./(кВт · ч )
Двухтарифный
8 675 руб.
3,5 кВт
3 руб./(кВт · ч) днём
Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1. Напротив входа расположена туалетная комната, а справа от нее — ванная комната.
Гостиная занимает наибольшую площадь в квартире, а справа от неё находится кухня. Прямо перед гостиной находится детская. Из детской можно попасть на балкон, отмеченный цифрой 6.
Потолок в гостиной планируется покрасить в красный цвет. Для покраски одного 1 м 2 потолка требуется 0,25 л краски.
В квартире планируется установить счётчик электроэнергии. Имеется возможность установить однотарифный или двухтарифный счётчик.
Вход и выход осуществляются через единственную дверь.
Oge. sdamgia. ru
07.12.2020 22:28:21
2018-05-28 07:59:49
Источники:
Https://oge. sdamgia. ru/test? id=40955846