Задание 8 номер 341704

сайты — меню — вход — новости

1. Задание 1 № 406563

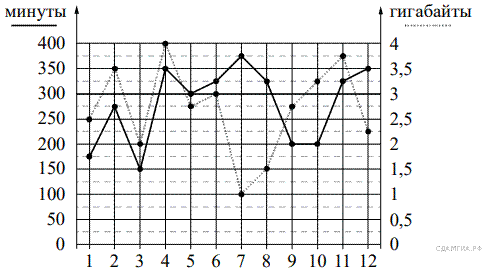
Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета.

Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответе нужно записать

число 51118).

Мобильный интернет	2,5 Гб	3 Гб	3,25 Гб	1 Гб
Номер месяца

На рисунке точками показано количество минут исходящих вызовов и трафик мобильного интернета в гигабайтах, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2019 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.

В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляла 350 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:

• пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ;

• пакет интернета, включающий 3 гигабайта мобильного интернета;

• пакет СМС, включающий 120 СМС в месяц;

• безлимитные бесплатные входящие вызовы.

Стоимость минут, интернета и СМС сверх пакета тарифа указана в таблице.

Исходящие вызовы	3 руб./мин.
Мобильный интернет (пакет)	90 руб. за 0,5 Гб
СМС	2 руб./шт.

Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 110 СМС.

Решение.

Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года.

Из рисунка видно, что 2,5 Гб было потрачено в первый месяц, 3 Гб — потрачено в шестой, 3,25 Гб — в десятый, 1 Гб — в седьмой.

Ответ: 16107.

2. Задание 2 № 406675

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику израсходованных минут и гигабайтов.

ПЕРИОДЫ		ХАРАКТЕРИСТИКИ
А) январь−февраль Б) февраль−март В) август–сентябрь Г) ноябрь–декабрь		1) Расход минут увеличился, а расход гигабайтов уменьшился. 2) Расход гигабайтов увеличился, а расход минут уменьшился. 3) Расход минут увеличился, и расход гигабайтов увеличился. 4) Расход минут уменьшился, и расход гигабайтов уменьшился.

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Решение.

Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года, а сплошной линей — количество минут исходящих вызовов.

За период январь−февраль расход минут увеличился, и расход гигабайтов увеличился.

За период февраль−март расход минут уменьшился, и расход гигабайтов уменьшился.

За период август–сентябрь расход гигабайтов увеличился, а расход минут уменьшился.

За период ноябрь–декабрь расход минут увеличился, а расход гигабайтов уменьшился.

Таким образом, получается соответствие: А — 3, Б — 4, В — 2, Г — 1.

Ответ: 3421.

3. Задание 3 № 406564

Сколько рублей потратил абонент на услуги связи в июне?

Решение.

По рисунку видно, что за июнь абонент потратил 3 Гб интернета, 325 минут исходящих вызовов, и в условии сказано, что за год отправил 110 СМС.

Количество потраченного интернета и СМС не превысило это количество в пакете тарифа, а исходящих вызовов сверх пакета было потрачено 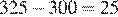минут.

Вычислим стоимость услуг связи, потраченных абонентом в июне:

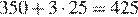рублей.

Ответ: 425.

4. Задание 4 № 406565

Какое наименьшее количество минут исходящих вызовов за месяц было в 2019 году?

Решение.

Сплошной линей на графике показано количество минут исходящих вызовов, израсходованных за каждый месяц года.

Из рисунка видно, что в третьем месяце было потрачено 150 минут, что является наименьшим количеством за 2019 год.

Ответ: 150.

5. Задание 5 № 367694

Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м² площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.

Место	Цена земли (млн руб.)	Цена строительства (млн руб.)	Длина коммуникаций (м)	Стоимость аренды за 1 м2 (руб./месяц)
Центр	64,4
Окраина	11,2

Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.

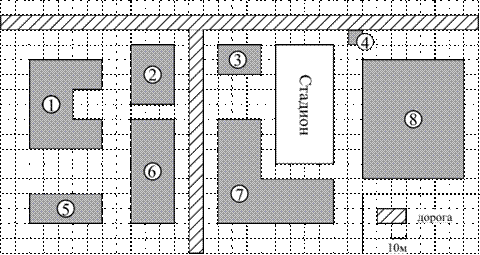
На плане (см. рисунок) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.

Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м². А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.

Решение.

Стоимость постройки ТРК в центре города равна

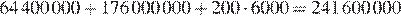рублей.

Стоимость постройки ТРК на окраине города равна

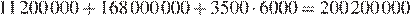рублей.

Разница в стоимости составляет

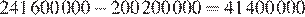рублей.

Разница в стоимости аренды составляет

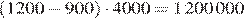рублей.

Значит, более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций через 34,5 месяцев. Округляя, получаем ответ — 35 месяцев.

Ответ: 35.

6. Задание 6 № 203743

Запишите в ответе номера выражений, значения которых положительны.

Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.

Решение.

Найдём значения выражений:

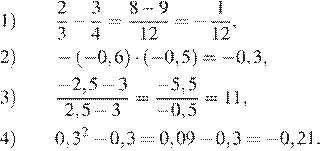
Таким образом, искомое выражение указано под номером 3.

7. Задание 7 № 314800

На координатной прямой отмечены числа а и b. Какое из следующих утверждений неверно?

В ответе укажите номер правильного варианта.

1)

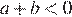
2)

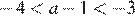
3)

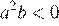
4)

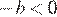
Решение.

Заметим, что 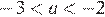и 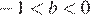, и проверим все варианты ответа:

1) 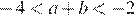, значит, 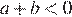— верно.

2) 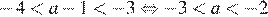— верно.

3) 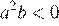— верно, поскольку 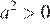, а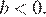

4) 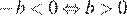— неверно.

Неверным является утверждение 4.

Примечание.

Нетрудно заметить, что справедливо неравенство: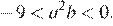

8. Задание 8 № 341704

Найдите значение выражения 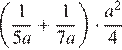при a = 7,7.

Решение.

Упростим выражение:

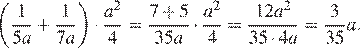
Подставим в полученное выражение значение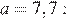

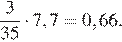
Ответ: 0,66.

9. Задание 9 № 338610

Решите уравнение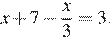

Решение.

Последовательно получаем:

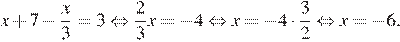
Ответ: −6.

10. Задание 10 № 325541

Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся.

Решение.

Вероятность того, что стрелок промахнётся равна 1 − 0,8 = 0,2. Вероятность того, что стрелок первые два раза попал по мишеням равна 0,8² = 0,64. Откуда, вероятность события, при котором стрелок сначала два раза попадает в мишени, а третий раз промахивается равна 0,64 · 0,2 = 0,128.

Ответ: 0,128.

11. Задание 11 № 193089

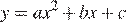Найдите значение по графику функции , изображенному на рисунке.

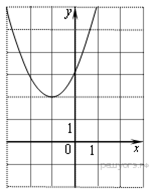
Решение.

Абсцисса вершины параболы равна −1, поэтому 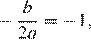откуда 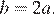Парабола пересекает ось ординат в точке с ординатой 3, поэтому 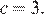Тем самым, уравнение параболы принимает вид 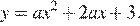Поскольку парабола проходит через точку (−1; 2), имеем:

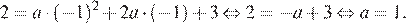
Верный ответ указан под номером 2.

Ответ: 2.

12. Задание 12 № 338396

Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.

Решение.

Найдем расстояние, на котором находится наблюдатель от места удара молнии:

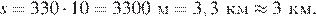
Ответ: 3.

13. Задание 13 № 311312

Решите неравенство .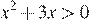

В ответе укажите номер правильного варианта.

1)

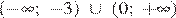
2)

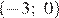
3)

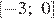
4)

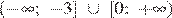
Решение.

Решим данное неравенство:

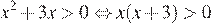. Произведение двух сомножителей будет больше нуля, если его сомножители имеют одинаковый знак.

В данном случае это выполняется при следующих значениях :

1) ;

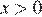2) ;

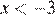Решением неравенства будет являться объединение этих промежутков: 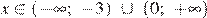, что соответствует первому варианту ответа.

Ответ: 1

14. Задание 14 № 394426

Давление воздуха под колоколом равно 625 мм ртутного столба. Каждую минуту насос откачивает из-под колокола 20% находящегося там воздуха. Определите давление (в мм рт. ст.) через 5 минут после начала работы насоса.

Решение.

Через минуту давление воздуха (в мм рт. ст.) под колоколом станет 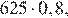через две минуты — 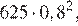…, через 5 минут давление станет 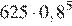или

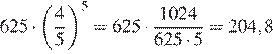мм рт. ст.

Ответ: 204,8.

15. Задание 15 № 348371

Высота BH ромба ABCD делит его сторону AD на отрезки AH = 44 и HD = 11. Найдите площадь ромба.

Решение.

Заметим, что сторона ромба AB = AD = AH + HD = 44 + 11 = 55.

Из прямоугольного треугольника ABH найдем BH по теореме Пифагора:

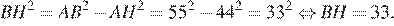
Площадь ромба можно найти как произведение основания на высоту:

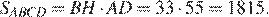
Ответ: 1815.

16. Задание 16 № 339975

Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Решение.

Радиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника 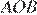по теореме Пифагора найдём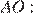

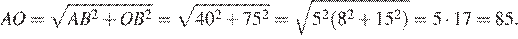
Найдём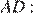

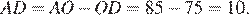
Ответ: 10.

17. Задание 17 № 324017

Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.

Решение.

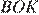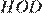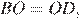
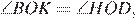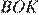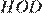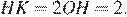Проведём построение и введём обозначения, как показано на рисунке. Учитывая, что и получаем Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники и , они прямоугольные, следовательно, треугольники и равны, откуда то есть высота Найдём площадь ромба как произведение стороны на высоту:

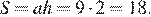
Ответ: 18.

18. Задание 18 № 311485

На квадратной сетке изображён угол 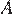. Найдите .

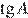Решение.

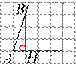
Опустим перпендикуляр BH. Треугольник ABH — прямоугольный. Таким образом,

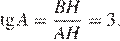
Ответ: 3.

19. Задание 19 № 341676

Какие из следующих утверждений верны?

1) Треугольника со сторонами 1, 2, 4 не существует.

2) Смежные углы равны.

3) Все диаметры окружности равны между собой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

1) «Треугольника со сторонами 1, 2, 4 не существует» — верно, большая сторона треугольника должна быть меньше суммы двух других.

2) «Смежные углы равны» — неверно, смежные углы 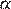и 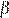связаны соотношением: .

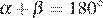3) «Все диаметры окружности равны между собой» — верно.

Ответ: 13.

20. Задание 20 № 311591

Решите уравнение: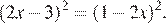

Решение.

Перенесем все члены влево и применим формулу разности квадратов:

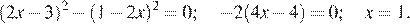
Другой способ. Раскроем скобки, пользуясь формулой квадрата разности:

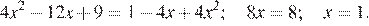
Ответ: 1.

21. Задание 21 № 314507

Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.

Решение.

Пусть скорость пешехода — x км/ч, 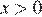, тогда скорость велосипедиста равна (x + 11) км/ч.

Составим таблицу по данным задачи:

	Скорость, км/ч	Время, ч	Расстояние, км
Пешеход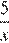
Велосипедист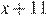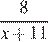

Так как по пути велосипедист сделал остановку на ч., составим уравнение:

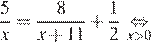
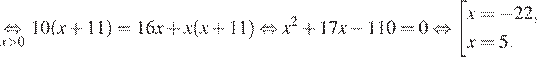
Корень −22 не подходит нам по условию задачи. Скорость пешехода равна 5 км/ч.

Ответ: 5 км/ч.

22. Задание 22 № 353274

Постройте график функции 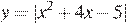. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

Решение.

График данной функции — это график параболы 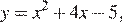отрицательная часть которого отражена относительно оси Этот график изображён на рисунке:

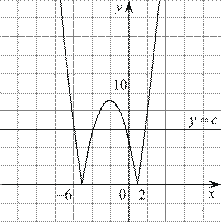
Прямая, параллельная оси абсцисс задаётся формулой 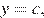где — постоянная. Из графика видно, что прямая может иметь с графиком функции не более четырёх общих точек.

Ответ: 4.

23. Задание 23 № 333321

Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56 .

Решение.

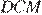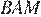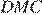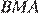Углы и равны как накрест лежащие, углы и равны как вертикальные, следовательно, треугольник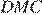и и 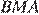подобны по двум углам.

Значит, 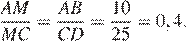Следовательно,

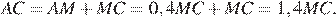
Откуда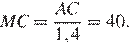

Ответ: 40.

24. Задание 24 № 349626

Окружности с центрами в точках и не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.

Решение.

Проведём построения и введём обозначения, как показано на рисунке. Пусть 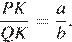Рассмотрим треугольник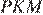и и 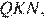они прямоугольные, углы 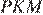и 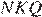равны как вертикальные, следовательно, треугольники подобны, откуда 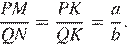Отношение радиусов равно отношению диаметров.

25. Задание 25 № 311708

В прямоугольном треугольнике ABC с прямым углом B, проведена биссектриса угла A. Известно, что она пересекает серединный перпендикуляр, проведённый к стороне BC в точке K. Найдите угол BCK, если известно, что угол ACB равен 40°.

Решение.

Так как биссектриса острого угла A прямоугольного треугольника ABC не может быть перпендикулярна BC, то биссектриса угла A и серединный перпендикуляр к BC имеют ровно одну общую точку.

Пусть N — середина BC. Рассмотрим окружность, описанную около треугольника ABC. Пусть серединный перпендикуляр к BC пересекает меньшую дугу BC в точке L (см. рисунок), тогда точка L является серединой этой дуги, ⌣BL = ⌣LC. Но тогда 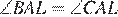как вписанные углы, опирающиеся на равные дуги, а отсюда AL — биссектриса 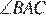. Но это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой 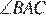. Заметим, что 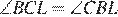как вписанные углы, опирающиеся на равные дуги.

Пусть 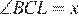. Четырехугольник ACLB — вписанный, поэтому 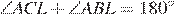, то есть 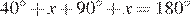, откуда 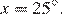Так как точки K и L совпадают,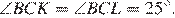

Ответ: 25°.

Задание №7

Рациональные выражения

№ 140 1. Упростите выражение , найдите
его значение при ; . В ответ запишите
полученное число.

№ 311329 2. Упростите выражение и найдите его
значение при . В ответ запишите
полученное число.

№ 311352 3. Упростите выражение и найдите его
значение при . В ответ запишите
полученное число.

№ 311372 4. Упростите выражение и найдите
его значение при . В ответ запишите
полученное число.

№ 311451 5. Упростите выражение и найдите
его значение при . В ответе запишите
найденное значение.

№ 311463 6. Представьте в виде дроби выражение
и
найдите его значение при . В ответ запишите
полученное число.

Целые выражения

№ 36 1. Упростите выражение , найдите
его значение при . В ответ запишите
полученное число.

Задание №7

Рациональные выражения

№ 311467 7. Упростите выражение и найдите его
значение при . В ответе запишите
полученное число.

№ 311471 8. Упростите выражение и найдите
его значение при

№ 311758 9. Найдите значение выражения при

№ 311814 10. Найдите значение выражения
при

№ 311846 11. Найдите значение выражения
при

№ 311954 12. Найдите значение выражения
при

Целые выражения

№ 311383 2. Найдите значение выражения
при

Задание №7

Рациональные выражения

№ 314312 13. Упростите выражение и найдите
его значение при В ответе запишите
найденное значение.

№ 314315 14. Упростите выражение и найдите
его значение при и В ответе запишите
найденное значение.

№ 316344 15. Сократите дробь

№ 318572 16. Упростите выражение и найдите
его значение при В ответе запишите
найденное значение.

№ 319060 17. Найдите значение выражения
при

Целые выражения

№ 311910 3. Найдите значение выражения
при

Задание №7

Рациональные выражения

№ 319072 18. Найдите значение выражения
при

№ 338076 19. Найдите значение выражения
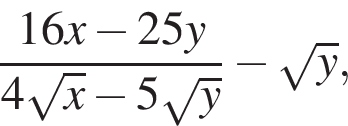если

№ 338095 20. Найдите значение выражения
при

№ 338131 21. Найдите значение выражения
при

№ 338163 22. Найдите значение выражения
при

Задание 7

Целые выражения

№ 338067 4. Найдите значение выражения при

Задание №7

Рациональные выражения

№ 338181 23. Найдите значение выражения
при

№ 338274 24. Найдите значение выражения
при

№ 338448 25. Найдите значение выражения
при

№ 341353 26. Найдите значение выражения
при a
= 78, c = 21.

№ 341704 27. Найдите значение выражения
при a
= 7,7.

Целые выражения

№ 338092 5. Найдите если

Целые выражения

№ 338423 6. Найдите значение выражения при

Прав

ответ

№

п/п

Номер

Тип

Прав

ответ

1

140

7

1,5

1

36

7

0

2

311329

7

-1

2

311383

7

16

3

311352

7

0,4

3

311910

7

27

4

311372

7

0,25

4

338067

7

-230,4

5

311451

7

1,5

5

338092

7

4

6

311463

7

-5

6

338423

7

452

7

311467

7

16

8

311471

7

1,7

9

311758

7

1

10

311814

7

0,8

11

311846

7

0,5

12

311954

7

5,6

13

314312

7

4

14

314315

7

1,5

15

316344

7

84

16

318572

7

-10,5

17

319060

7

-2

18

319072

7

-2

19

338076

7

12

20

338095

7

0,25

21

338131

7

390

22

338163

7

0,75

23

338181

7

-2,5

24

338274

7

31

25

338448

7

-2,6

26

341353

7

-8

27

341704

7

0,66

Задание 13.

Рациональные выражения

1. Упростите вы­ра­же­ние ,

най­ди­те его зна­че­ние при ; . В ответ за­пи­ши­те полученное число.

Решение.

Упростим выражение:

Найдём зна­че­ние выражения при ,  :

Ответ: 1,5.

Ответ: 1,5

140

1,5

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1313.

2. Упростите вы­ра­же­ние

и най­ди­те его зна­че­ние при . В ответ за­пи­ши­те по­лу­чен­ное число.

Решение.

Упростим выражение:

При a = −2, зна­че­ние по­лу­чен­но­го вы­ра­же­ния равно −2:2 = −1.

Ответ: -1

311329

-1

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 2)

3. Упростите вы­ра­же­ние    

и най­ди­те его зна­че­ние при   . В ответ за­пи­ши­те по­лу­чен­ное число.

Решение.

Упростим выражение:

При , зна­че­ние выражения равно 2:5 = 0,4.

Ответ: 0,4.

Ответ: 0,4

311352

0,4

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)

4. Упростите вы­ра­же­ние    

и най­ди­те его зна­че­ние при   . В ответ за­пи­ши­те полученное число.

Решение.

Упростим выражение:

При , зна­че­ние полученного вы­ра­же­ния равно 0, 25.

Ответ: 0,25.

Ответ: 0,25

311372

0,25

Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.6)

5. Упростите вы­ра­же­ние    

и най­ди­те его зна­че­ние при   . В от­ве­те запишите най­ден­ное значение.

Решение.

Упростим выражение:

При , зна­че­ние полученного вы­ра­же­ния равно 7,5 : 5 = 1,5.

Ответ: 1,5.

Ответ: 1,5

311451

1,5

Источник: ГИА-2013. Математика. Экзамен. Вариант 5

6. Представьте в виде дроби вы­ра­же­ние    

и най­ди­те его зна­че­ние при   . В ответ за­пи­ши­те по­лу­чен­ное число.

Решение.

Упростим выражение:

Найдем зна­че­ние вы­ра­же­ния при :

Ответ: −5.

Ответ: -5

311463

-5

Источник: ГИА-2013. Математика. Тренировочная работа № 1(2 вар)

7. Упростите вы­ра­же­ние    

и най­ди­те его зна­че­ние при   . В от­ве­те запишите по­лу­чен­ное число.

Решение.

Упростим выражение:

При , зна­че­ние полученного вы­ра­же­ния равно 16.

Ответ: 16.

Ответ: 16

311467

16

Источник: ГИА-2013. Математика. Тренировочная работа № 4.(1 вар.)

8. Упростите вы­ра­же­ние    

и най­ди­те его зна­че­ние при  

Решение.

Упростим выражение:

Найдем зна­че­ние выражения при :

Ответ: 1,7.

Ответ: 1,7

311471

1,7

Источник: ГИА-2012. Математика. Диагностическая работа № 1 (1 вар)

9. Найдите зна­че­ние вы­ра­же­ния

при

Решение.

Упростим выражение:

Подставим в по­лу­чен­ное вы­ра­же­ние зна­че­ние

Ответ: 1.

Ответ: 1

311758

1

10. Найдите зна­че­ние вы­ра­же­ния

при

Решение.

Упростим выражение:

Подставим в по­лу­чен­ное вы­ра­же­ние зна­че­ние

Ответ: 0,8.

Ответ: 0,8

311814

0,8

11. Найдите зна­че­ние вы­ра­же­ния

при

Решение.

Упростим выражение:

Подставим в по­лу­чен­ное вы­ра­же­ние зна­че­ние

Ответ: 0,5.

Ответ: 0,5

311846

0,5

12. Найдите зна­че­ние вы­ра­же­ния

при

Решение.

Раскроем скоб­ки и приведём к об­ще­му знаменателю:

Тем самым, ис­ко­мое зна­че­ние не за­ви­сит от Зна­че­ние вы­ра­же­ния при равно

Ответ: 5,6.

Ответ: 5,6

311954

5,6

13. Упро­сти­те вы­ра­же­ние

и най­ди­те его зна­че­ние при В от­ве­те за­пи­ши­те най­ден­ное зна­че­ние.

Решение.

Упростим выражение:

Найдём зна­че­ние вы­ра­же­ния при :

Ответ: 4.

Ответ: 4

314312

4

Источник: Банк заданий ФИПИ

14. Упро­сти­те вы­ра­же­ние

и най­ди­те его зна­че­ние при и В от­ве­те за­пи­ши­те най­ден­ное зна­че­ние.

Решение.

Упростим выражение:

  (при  и 

Найдём зна­че­ние вы­ра­же­ния при :

Ответ: 1,5.

Ответ: 1,5

314315

1,5

Источник: Банк заданий ФИПИ

15. Найдите зна­че­ние вы­ра­же­ния

при а = 6.

Решение.

Упростим выражение:

  (при ).

Найдём зна­че­ние по­лу­чен­но­го вы­ра­же­ния при

Ответ: 0,5.

Ответ: 0,5

316255

0,5

Источник: Ди­а­гно­сти­че­ская работа 01.10.2013 Ва­ри­ант МА90106

16. Сократите дробь

Решение.

Сократим дробь:

Ответ: 84.

Ответ: 84

316344

84

17. Упро­сти­те вы­ра­же­ние

и най­ди­те его зна­че­ние при В от­ве­те за­пи­ши­те най­ден­ное зна­че­ние.

Решение.

Упростим выражение:

Найдём зна­че­ние выражения при

Ответ: −10,5.

Ответ: -10,5

318572

-10,5

18. Найдите зна­че­ние выражения

при

Решение.

Упростим выражение:

Найдём зна­че­ние выражения при

Ответ: −2.

Ответ: -2

319060

-2

19. Найдите зна­че­ние выражения

при

Решение.

Упростим выражение:

Зна­че­ние вы­ра­же­ния при равно

Ответ: −2.

Ответ: -2

319072

-2

20. Найдите зна­че­ние выражения

если

Решение.

Разложим чис­ли­тель на мно­жи­те­ли по фор­му­ле разности квадратов:

Ответ: 12.

Ответ: 12

338076

12

21. Найдите зна­че­ние выражения

при

Решение.

Преобразуем выражение:

Подставим зна­че­ние

Ответ: 0,25.

Ответ: 0,25

338095

0,25

22. Найдите зна­че­ние вы­ра­же­ния

при

Решение.

Приведём в скоб­ках к об­ще­му знаменателю:

Подставим зна­че­ние

Ответ: 390.

Ответ: 390

338131

390

23. Найдите зна­че­ние выражения

при

Решение.

Преобразуем выражение:

Подставим зна­че­ние

Ответ: 0,75.

Ответ: 0,75

338163

0,75

24. Найдите зна­че­ние выражения

при

Решение.

Преобразуем выражение:

Подставим зна­че­ния

Ответ: −2,5.

Ответ: -2,5

338181

-2,5

25. Найдите зна­че­ние вы­ра­же­ния

при

Решение.

Преобразуем выражение:

Подставим зна­че­ния

Ответ: 31.

Ответ: 31

338274

31

26. Найдите зна­че­ние выражения

при

Решение.

Преобразуем выражение:

Подставим

Ответ: −2,6.

Ответ: -2,6

338448

-2,6

27. Найдите зна­че­ние вы­ра­же­ния

при a = 78, c = 21.

Решение.

Пре­об­ра­зу­ем вы­ра­же­ние:

Ответ: −8.

Ответ: -8

341353

-8

28. Найдите зна­че­ние вы­ра­же­ния

при a = 7,7.

Решение.

Упростим выражение:

Подставим в по­лу­чен­ное вы­ра­же­ние зна­че­ние

Ответ: 0,66.

Ответ: 0,66

341704

0,66

29. Найдите значение выражения: ,

если

Целые выражения

1. Упростите вы­ра­же­ние ,

най­ди­те его зна­че­ние при . В ответ за­пи­ши­те полученное число.

Решение.

Упростим выражение:

Найдём зна­че­ние полученного вы­ра­же­ния при :

Ответ: 0.

Ответ: 0

36

0

Источник: Демонстрационная вер­сия ГИА—2013 по математике.

2. Найдите зна­че­ние выражения    

при  

Решение.

Упростим выражение:

При , зна­че­ние полученного вы­ра­же­ния равно 16.

Ответ: 16.

Ответ: 16

311383

16

Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)

3. Найдите зна­че­ние вы­ра­же­ния

при

Решение.

Упростим выражение:

При получаем:

Ответ: 27.

Ответ: 27

311910

27

4. Найдите зна­че­ние выражения

при

Решение.

Преобразуем выражение:

Подставим зна­че­ние

Ответ: −230,4.

Ответ: -230,4

338067

-230,4

5. Найдите если

Решение.

Имеем:

Ответ: 4.

Ответ: 4

338092

4

6. Найдите зна­че­ние вы­ра­же­ния

при

Восемь
и
триста сорок одна тысяча семьсот четыре

Сумма	341712
Разность	-341696
Частное	0.000023412075948774378
Остаток от деления	8
Произведение	2733632
Наибольший общий делитель (НОД)	8
Наименьшее общее кратное (НОК)	341704
Среднее арифметическое	170856
Среднее геометрическое	1653.3698920689224
Гипотенуза	341704.0000936483
Простые числа-близнецы?	Нет
Расстояние Левенштейна	6
Общие делители	1, 2, 4, 8
Взаимнопростые числа?	Нет
Общие цифры	Нет

Описание

Числа 8 и 341704 имеют сумму 341712 и имеют разность -341696.

При делении 8 на 341704 получается число 0.000023. Остаток от деления 8 на 341704 – 8. При умножении 8 на 341704 получается число 2733632.

Наибольший общий делитель: 8 . Для этой пары наименьшим общим кратным (НОК) является число 341704.

Общиe делители это 1, 2, 4, 8.

Среднее арифметическое для 8 и 341704 это 170856 . Среднее геометрическое для этой пары — 1653.369892.

Эти два числ не имеют общих цифр.

Восьмое задание в модуле алгебре проверяет знания в области обращения со степенями и подкоренными выражениями.

При выполнении задания №4 ОГЭ по математике проверяются не только навыки выполнения вычисления и преобразований числовых выражений, но и умение преобразовывать алгебраические выражения. Возможно, потребуется выполнить действия со степенями с целым показателем, с многочленами, тождественные преобразования рациональных выражений.

В соответствии с материалами проведения основного экзамена могут быть задания, в которых потребуется выполнение тождественных преобразований рациональных выражений, разложение многочленов на множители, использование процентов и пропорций, признаков делимости.

Ответом в задании №8 является одна из цифр 1; 2; 3; 4 соответствующая номеру предложенного варианта ответа к заданию.

---

Теория к заданию №4

---

Из теоретического материала нам пригодятся правила обращения со степенями:

Правила работы с подкоренными выражениями:

В моих разобранных вариантах представлены данные правила — в разборе первого варианта третьего задания представлены правила обращения со степенями, а во втором и третьем варианте разобраны примеры работы подкоренными выражениями.

---

Разбор типовых вариантов задания №4 ОГЭ по математике

---

Первый вариант задания

Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11ⁿ ?

1. 121ⁿ
2. 11ⁿ⁺²
3. 11²ⁿ
4. 11ⁿ⁺³

Решение:

Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:

• при умножении степени складываются
• приделении степени вычитаются
• при возведении степени в степень степени перемножаются
• при извлечении корня степени делятся

Кроме того, для решения необходимо представить 121 как степень 11, а именно это 11².

121 • 11ⁿ = 11² • 11ⁿ

С учетом правила умножения, складываем степени:

  11² • 11ⁿ = 11ⁿ⁺²

Следовательно, нам подходит второй ответ.

Ответ: 2

---

Второй вариант задания

Значение какого из данных ниже выражений является наибольшим?

1. 3√5
2. 2√11
3. 2√10
4. 6,5

Решение:

Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:

• 3√5

Переносим 3 под корень:

3√5 =  √(3² •5) = √(9•5) =  √45

• 2√11

Переносим 2 под корень:

2√11 = √(2² • 11) = √(4 • 11) =√44

• 2√10

Переносим 2 под корень:

2√10 = √(2² • 10) = √(4 • 10) =√40

• 6,5

Возводим 6,5 в квадрат:

6,5 = √(6,5²) = √42,25

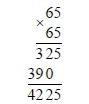
Посмотрим на все получившиеся варианты:

1. 3√5 =  √45
2. 2√11 = √44
3. 2√10 = √40
4. 6,5 = √42,25

Следовательно, правильный ответ первый

Ответ: 1

---

Третий вариант задания

Какое из данных чисел является рациональным?

1. √810
2. √8,1
3. √0,81
4. все эти числа иррациональны

Решение:

Для решения этой задачи нужно действовать следующим образом:

Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:

0,9

90

Рассмотри каждое из них:

0,9 = √(0,9)² = √0,81

90 = √(90²) = √8100

Следовательно, число √0,81 является рациональным, остальные же числа

• √810
• √8,1

хотя и похожи на форму 9 в квадрате, не являются рациональными.

Таким образом, правильный ответ третий.

Ответ: 3

---

Четвертый вариант задания

По просьбе подписчика моего сообщества Спадило Дианы, привожу разбор следующего задания №4:

Какое из данных ниже чисел является значением выражения?

Решение:

Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:

16 — 14 = 2

Суммарно наши действия выглядят так:

Ответ: 4

Хотите, чтобы ваше задание я разобрал и представил здесь? Подписывайтесь на мою группу Спадило и присылайте задание в личные сообщения группы!

---

Пятый вариант задания (демонстрационный вариант ОГЭ 2017)

Значение какого из выражений является рациональным числом?

1. √6-3
2. √3•√5
3. (√5)²
4. (√6-3)²

Решение:

В данном задании у нас проверяют навыки операций с иррациональными числами.

Разберем каждый вариант ответа в решении:

1) √6-3

√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…

При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.

2) √3•√5

При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:

√3•√5 = √(3•5) = √15

Но √15 является иррациональным, поэтому данный вариант ответа не подходит.

3) (√5)²

При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:

(√5)² = 5

Данный вариант ответа нам подходит.

4) (√6-3)²

Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.

Ответ: 3

---

Шестой вариант задания

Найдите значение выражения:

Решение:

В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=7² и 100=10². И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:

По аналогии извлекаем и 2-й корень:

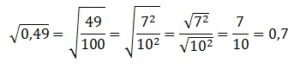
В итоге получаем:

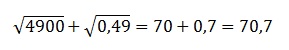
Ответ: 70,7

---

Седьмой вариант задания

Найдите значение выражения:

Решение:

Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:

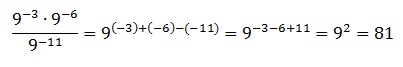
Ответ: 81