
СДАМ ГИА: РЕШУ ОГЭ
Образовательный портал для подготовки к экзаменам
Математика
математика
Математика
Информатика
≡ Русский язык
Письменный экзамен
Устное собеседование
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
сайты — меню — вход — новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
НАШИ БОТЫ
 |  |
На сайте что-то не так? Отключите адблок
Новости
9 января
7 секретов эффективной подготовки к ЕГЭ и ОГЭ
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
30 октября
Телефон, whatsapp и другие запреты в школе
21 марта
Новый сервис: рисование
9 февраля
Об ошибках в математике: проверьте браузер
31 января
Внедрили тёмную тему!
17 января
Разместили утвержденное расписание ОГЭ 2022
9 октября
Как восстановить доступ к Решу ЕГЭ, если у вас Windows XP
ЧУЖОЕ НЕ БРАТЬ!
Зайчиков и Поваляев стащили наши тесты
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 8 № 338131 
i
Найдите значение выражения при
Спрятать решение
Решение.
Приведём в скобках к общему знаменателю:
Подставим значение
Ответ: 390.
Аналоги к заданию № 338131: 353153 338154 338337 352236 353036 Все
Раздел кодификатора ФИПИ: 2.4 Преобразование рациональных выражений.
Спрятать решение
·
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023

СДАМ ГИА: РЕШУ ОГЭ
Образовательный портал для подготовки к экзаменам
Математика
математика
Математика
Информатика
≡ Русский язык
Письменный экзамен
Устное собеседование
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
сайты — меню — вход — новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
НАШИ БОТЫ
 |  |
На сайте что-то не так? Отключите адблок
Новости
9 января
7 секретов эффективной подготовки к ЕГЭ и ОГЭ
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
30 октября
Телефон, whatsapp и другие запреты в школе
21 марта
Новый сервис: рисование
9 февраля
Об ошибках в математике: проверьте браузер
31 января
Внедрили тёмную тему!
17 января
Разместили утвержденное расписание ОГЭ 2022
9 октября
Как восстановить доступ к Решу ЕГЭ, если у вас Windows XP
ЧУЖОЕ НЕ БРАТЬ!
Зайчиков и Поваляев стащили наши тесты
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 8 № 338131 
i
Найдите значение выражения при
Спрятать решение
Решение.
Приведём в скобках к общему знаменателю:
Подставим значение
Ответ: 390.
Аналоги к заданию № 338131: 353153 338154 338337 352236 353036 Все
Раздел кодификатора ФИПИ: 2.4 Преобразование рациональных выражений.
Спрятать решение
·
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Рациональные уравнения
1. Задание 4 № 311381. Решите уравнение: 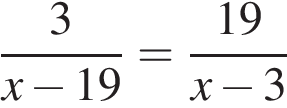 .
.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
2. Задание 4 № 311393. Решите уравнение 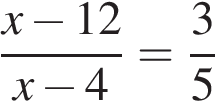 .
.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
3. Задание 4 № 311755. Решите уравнение 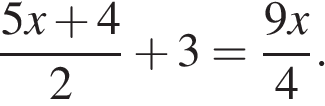
4. Задание 4 № 316225. Решите уравнение: 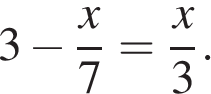
5. Задание 4 № 316341. Решите уравнение: 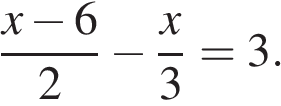
6. Задание 4 № 338483. Решите уравнение 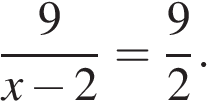
7. Задание 4 № 338503. Решите уравнение 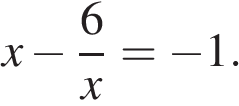
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
8. Задание 4 № 338583. Решите уравнение 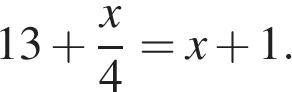
9. Задание 4 № 338723. Решите уравнение 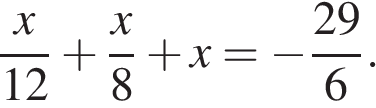
10. Задание 4 № 338805. Решите уравнение 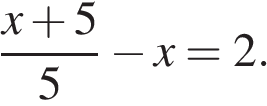
11. Задание 4 № 338937. Решите уравнение 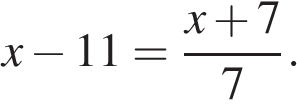
Рациональные выражения
1. Задание 7 № 140. Упростите выражение 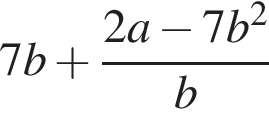 , найдите его значение при
, найдите его значение при  ;
; 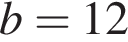 . В ответ запишите полученное число.
. В ответ запишите полученное число.
2. Задание 7 № 311329. Упростите выражение 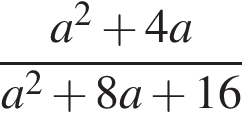 и найдите его значение при
и найдите его значение при 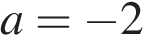 . В ответ запишите полученное число.
. В ответ запишите полученное число.
3. Задание 7 № 311352. Упростите выражение 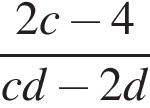 и найдите его значение при
и найдите его значение при 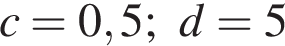 . В ответ запишите полученное число.
. В ответ запишите полученное число.
4. Задание 7 № 311372. Упростите выражение 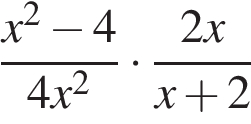 и найдите его значение при
и найдите его значение при  . В ответ запишите полученное число.
. В ответ запишите полученное число.
5. Задание 7 № 311451. Упростите выражение 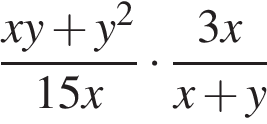 и найдите его значение при
и найдите его значение при 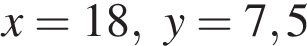 . В ответе запишите найденное значение.
. В ответе запишите найденное значение.
6. Задание 7 № 311463. Представьте в виде дроби выражение 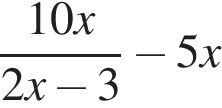 и найдите его значение при
и найдите его значение при 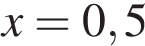 . В ответ запишите полученное число.
. В ответ запишите полученное число.
7. Задание 7 № 311467. Упростите выражение 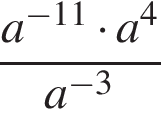 и найдите его значение при
и найдите его значение при 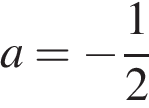 . В ответе запишите полученное число.
. В ответе запишите полученное число.
8. Задание 7 № 311471. Упростите выражение 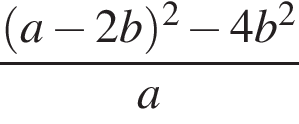 и найдите его значение при
и найдите его значение при 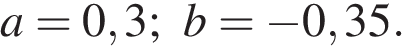
9. Задание 7 № 311758. Найдите значение выражения 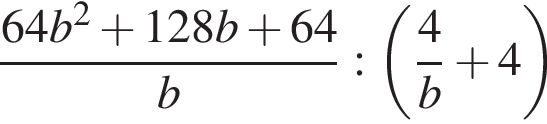 при
при 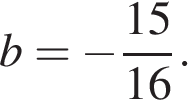
10. Задание 7 № 311814. Найдите значение выражения 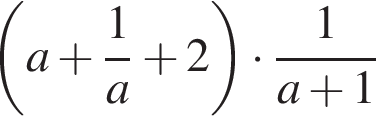 при
при 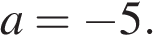
11. Задание 7 № 311846. Найдите значение выражения 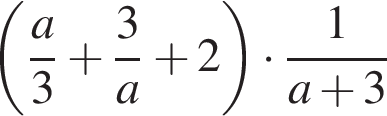 при
при 
12. Задание 7 № 311954. Найдите значение выражения 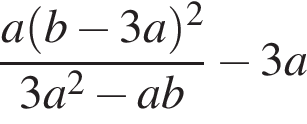 при
при 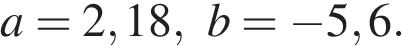
13. Задание 7 № 314312. Упростите выражение 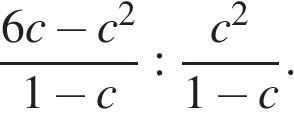 и найдите его значение при
и найдите его значение при 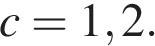 В ответе запишите найденное значение.
В ответе запишите найденное значение.
14. Задание 7 № 314315. Упростите выражение 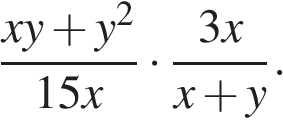 и найдите его значение при
и найдите его значение при 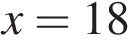 и
и  В ответе запишите найденное значение.
В ответе запишите найденное значение.
15. Задание 7 № 316344. Сократите дробь 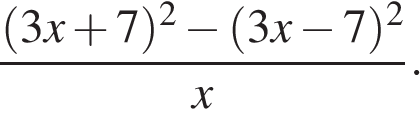
16. Задание 7 № 318572. Упростите выражение 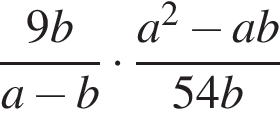 и найдите его значение при
и найдите его значение при 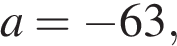
 В ответе запишите найденное значение.
В ответе запишите найденное значение.
17. Задание 7 № 319060. Найдите значение выражения 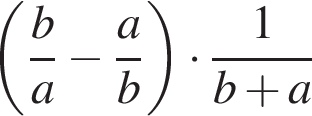 при
при 
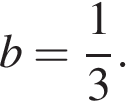
18. Задание 7 № 319072. Найдите значение выражения 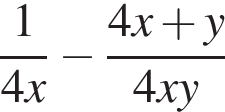 при
при 
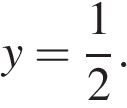
19. Задание 7 № 338076. Найдите значение выражения 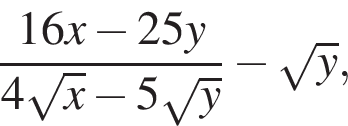 если
если 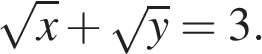
20. Задание 7 № 338095. Найдите значение выражения 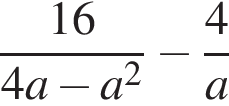 при
при 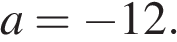
21. Задание 7 № 338131. Найдите значение выражения 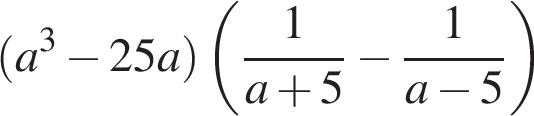 при
при 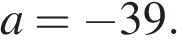
22. Задание 7 № 338163. Найдите значение выражения 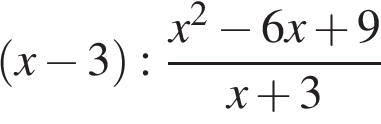 при
при 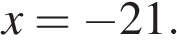
23. Задание 7 № 338181. Найдите значение выражения 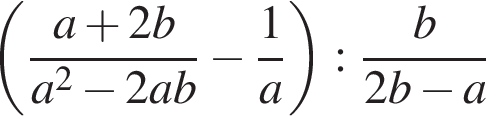 при
при 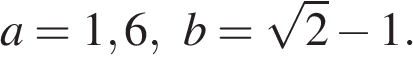
24. Задание 7 № 338274. Найдите значение выражения 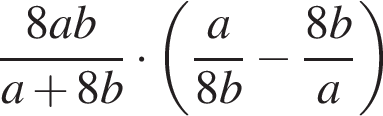 при
при 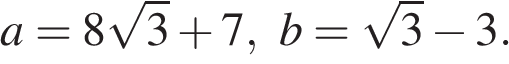
25. Задание 7 № 338448. Найдите значение выражения 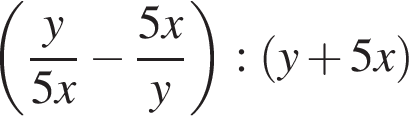 при
при 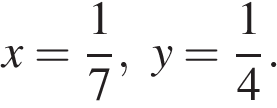
Задание №7
Рациональные выражения
№ 140 1. Упростите выражение ![]() , найдите
, найдите
его значение при ![]() ;
; ![]() . В ответ запишите
. В ответ запишите
полученное число.
№ 311329 2. Упростите выражение ![]() и найдите его
и найдите его
значение при ![]() . В ответ запишите
. В ответ запишите
полученное число.
№ 311352 3. Упростите выражение ![]() и найдите его
и найдите его
значение при ![]() . В ответ запишите
. В ответ запишите
полученное число.
№ 311372 4. Упростите выражение ![]() и найдите
и найдите
его значение при ![]() . В ответ запишите
. В ответ запишите
полученное число.
№ 311451 5. Упростите выражение ![]() и найдите
и найдите
его значение при ![]() . В ответе запишите
. В ответе запишите
найденное значение.
№ 311463 6. Представьте в виде дроби выражение
![]() и
и
найдите его значение при ![]() . В ответ запишите
. В ответ запишите
полученное число.
Целые выражения
№ 36 1. Упростите выражение ![]() , найдите
, найдите
его значение при ![]() . В ответ запишите
. В ответ запишите
полученное число.
Задание №7
Рациональные выражения
№ 311467 7. Упростите выражение ![]() и найдите его
и найдите его
значение при ![]() . В ответе запишите
. В ответе запишите
полученное число.
№ 311471 8. Упростите выражение ![]() и найдите
и найдите
его значение при ![]()
№ 311758 9. Найдите значение выражения ![]() при
при
![]()
№ 311814 10. Найдите значение выражения
![]() при
при
![]()
№ 311846 11. Найдите значение выражения
![]() при
при
![]()
№ 311954 12. Найдите значение выражения
![]() при
при
![]()
Целые выражения
№ 311383 2. Найдите значение выражения
![]() при
при
![]()
Задание №7
Рациональные выражения
№ 314312 13. Упростите выражение ![]() и найдите
и найдите
его значение при ![]() В ответе запишите
В ответе запишите
найденное значение.
№ 314315 14. Упростите выражение ![]() и найдите
и найдите
его значение при ![]() и
и ![]() В ответе запишите
В ответе запишите
найденное значение.
№ 316344 15. Сократите дробь ![]()
№ 318572 16. Упростите выражение ![]() и найдите
и найдите
его значение при ![]()
![]() В ответе запишите
В ответе запишите
найденное значение.
№ 319060 17. Найдите значение выражения
![]() при
при
![]()
![]()
Целые выражения
№ 311910 3. Найдите значение выражения
![]() при
при
![]()
Задание №7
Рациональные выражения
№ 319072 18. Найдите значение выражения
![]() при
при
![]()
![]()
№ 338076 19. Найдите значение выражения
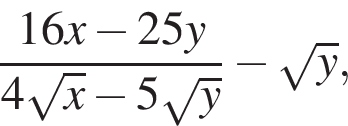 если
если
![]()
№ 338095 20. Найдите значение выражения
![]() при
при
![]()
№ 338131 21. Найдите значение выражения
![]() при
при
![]()
№ 338163 22. Найдите значение выражения
![]() при
при
![]()
Задание 7
Целые выражения
№ 338067 4. Найдите значение выражения ![]() при
при
![]()
Задание №7
Рациональные выражения
№ 338181 23. Найдите значение выражения
![]() при
при
![]()
№ 338274 24. Найдите значение выражения
![]() при
при
![]()
№ 338448 25. Найдите значение выражения
![]() при
при
![]()
№ 341353 26. Найдите значение выражения
![]() при a
при a
= 78, c = 21.
№ 341704 27. Найдите значение выражения
![]() при a
при a
= 7,7.
Целые выражения
№ 338092 5. Найдите ![]() если
если ![]()
Целые выражения
№ 338423 6. Найдите значение выражения ![]() при
при
![]()
Прав
ответ
№
п/п
Номер
Тип
Прав
ответ
1
140
7
1,5
1
36
7
0
2
311329
7
-1
2
311383
7
16
3
311352
7
0,4
3
311910
7
27
4
311372
7
0,25
4
338067
7
-230,4
5
311451
7
1,5
5
338092
7
4
6
311463
7
-5
6
338423
7
452
7
311467
7
16
8
311471
7
1,7
9
311758
7
1
10
311814
7
0,8
11
311846
7
0,5
12
311954
7
5,6
13
314312
7
4
14
314315
7
1,5
15
316344
7
84
16
318572
7
-10,5
17
319060
7
-2
18
319072
7
-2
19
338076
7
12
20
338095
7
0,25
21
338131
7
390
22
338163
7
0,75
23
338181
7
-2,5
24
338274
7
31
25
338448
7
-2,6
26
341353
7
-8
27
341704
7
0,66
Восьмое задание в модуле алгебре проверяет знания в области обращения со степенями и подкоренными выражениями. При выполнении задания №8 ОГЭ по математике проверяются не только навыки выполнения вычисления и преобразований числовых выражений, но и умение преобразовывать алгебраические выражения. Возможно, потребуется выполнить действия со степенями с целым показателем, с многочленами, тождественные преобразования рациональных выражений. В соответствии с материалами проведения основного экзамена могут быть задания, в которых потребуется выполнение тождественных преобразований рациональных выражений, разложение многочленов на множители, использование процентов и пропорций, признаков делимости. Ответом в задании №8 является одна из цифр 1; 2; 3; 4 соответствующая номеру предложенного варианта ответа к заданию.
Теория к заданию №8
Из теоретического материала нам пригодятся правила обращения со степенями:

Правила работы с подкоренными выражениями:
Кроме этого, нам понадобятся формулы сокращенного умножения:
Квадрат суммы
(a + b)2 = a2 + 2ab + b2
Квадрат разности
(a – b)2 = a2 – 2ab + b2
Разность квадратов
a2 – b2 = (a + b)(a – b)
Куб суммы
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Куб разности
(a – b)3 = a3 – 3a2b + 3ab2 – b3
Сумма кубов
a3 + b3 = (a + b)( a2 – ab + b2)
Разность кубов
a3 – b3 = (a – b)( a2 + ab + b2)
Правила операций с дробями:

Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11n ?
- 121n
- 11n+2
- 112n
- 11n+3
Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:
- при умножении степени складываются
- приделении степени вычитаются
- при возведении степени в степень степени перемножаются
- при извлечении корня степени делятся
Кроме того, для решения необходимо представить 121 как степень 11, а именно это 112.
121 • 11n = 112 • 11n
С учетом правила умножения, складываем степени:
112 • 11n = 11n+2
Следовательно, нам подходит второй ответ.
Ответ: 2
pазбирался: Даниил Романович | обсудить разбор | оценить
Значение какого из данных ниже выражений является наибольшим?
- 3√5
- 2√11
- 2√10
- 6,5
Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:
- 3√5
Переносим 3 под корень:
3√5 = √(3² •5) = √(9•5) = √45
- 2√11
Переносим 2 под корень:
2√11 = √(2² • 11) = √(4 • 11) =√44
- 2√10
Переносим 2 под корень:
2√10 = √(2² • 10) = √(4 • 10) =√40
- 6,5
Возводим 6,5 в квадрат:
6,5 = √(6,5²) = √42,25
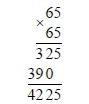
Посмотрим на все получившиеся варианты:
- 3√5 = √45
- 2√11 = √44
- 2√10 = √40
- 6,5 = √42,25
Следовательно, правильный ответ первый.
Ответ: 3√5
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из данных чисел является рациональным?
- √810
- √8,1
- √0,81
- все эти числа иррациональны
Для решения этой задачи нужно действовать следующим образом:
Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:
0,9
90
Рассмотри каждое из них:
0,9 = √(0,9)² = √0,81
90 = √(90²) = √8100
Следовательно, число √0,81 является рациональным, остальные же числа
- √810
- √8,1
хотя и похожи на форму 9 в квадрате, не являются рациональными.
Таким образом, правильный ответ третий.
Ответ: √0,81
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из данных ниже чисел является значением выражения?


Заметим, что в знаменателе присутствует разность (4 – √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² – (√14)². После этого знаменатель легко вычисляется:
16 – 14 = 2
Суммарно наши действия выглядят так:

Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
Значение какого из выражений является рациональным числом?
- √6-3
- √3•√5
- (√5)²
- (√6-3)²
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
1) √6-3
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
2) √3•√5
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
√3•√5 = √(3•5) = √15
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
3) (√5)²
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
(√5)² = 5
Данный вариант ответа нам подходит.
4) (√6-3)²
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
Ответ: 3
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
![]()
В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=72 и 100=102. И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:
![]()
По аналогии извлекаем и 2-й корень:
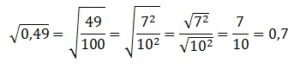
В итоге получаем:
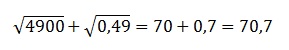
Ответ: 70,7
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
![]()
Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:
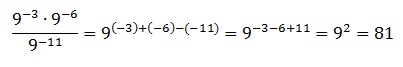
Ответ: 81
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения: (x + 5)2 — x (x- 10) при x = — 1/20
В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:
(x + 5)2 – x (x – 10) = x2 + 2 • 5 • x + 25 – x2 + 10x
Затем приведем подобные слагаемые:
x2 + 2 • 5 • x + 25 – x2 + 10x = 20 x + 25
Далее подставим x из условия:
20 x + 25 = 20 • (-1/20) + 25 = – 1 + 25 = 24
Ответ: 24
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:

при a = 13, b = 6,8
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй – в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:

Далее выносим из числителя второй дроби a:

Сокращаем (a-b):

И получаем:
a/2
Подставляем значение a = 13:
13 / 2 = 6,5
Ответ: 6,5
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:

при x = √45 , y = 0,5
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель – это 15 x y, для этого необходимо первую дробь домножить на 5 y – и числитель и знаменатель, естественно:

Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y – (3 x + 5 y) = 5 y – 3 x – 5 y = – 3 x
Тогда дробь примет вид:
![]()
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: – 1/5 y
Подставим значение y = 0,5: – 1 / (5 • 0,5) = – 1 / 2,5 = – 0,4
Ответ: -0,4
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения

где a = 9, b = 36
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю – это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
9b² + 5a – 9b²
Приведем подобные слагаемые – это 9b² и – 9b², в числителе остается 5a. Запишем конечную дробь:
5a/b
Вычислим её значение, подставив числа из условия:
5•9/36 = 1,25
Ответ: 1,25
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения при x = 12:
![]()
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
![]()
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
![]()
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
![]()
Подставляем числовое значение для х в полученное выражение и находим результат:
![]() Ответ: 0,6
Ответ: 0,6
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
![]()
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:

теперь переходим от деления дробей к их умножению:

затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
![]()
сокращаем выражение на (a–5b):

Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений):

Подставим полученные значения в выражение и найдем конечный результат:
![]() Ответ: 39
Ответ: 39
pазбирался: Даниил Романович | обсудить разбор | оценить
Найти значение выражения
(3∙8)737∙85
В числителе дроби возведем в степень каждый множитель:
(3∙8)737 ∙85=37∙8737∙85
Теперь сократим (выполним деление степеней), сократятся 37 полностью, а при сокращении на 85 по свойству степеней останется 82, возведем 8 во вторую степень, получим 64, т.е.
(3∙8)737 ∙85=37∙8737∙85=82=64
Ответ: 64
pазбирался: Даниил Романович | обсудить разбор | оценить
Материалы для отработки задания №8 ОГЭ по математике.
Для выполнения задания 8 необходимо уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений.
| Практика для задания 8 с ответами Тренинг действия с корнями → вариант 1 ответы → вариант 2 ответы |
| Карточки для отработки задания 8 Источник: math100.ru → скачать |
| Материалы для отработки задания 8 Автор: Е. А. Ширяева → теория → задания |
| Теория для задания 8 Источник: synergy.ru → скачать |
Решение типовых задач №8 на ОГЭ по математике
Связанные страницы:
Решение заданий 1 — 5 ОГЭ по математике
Ключевые задания по геометрии для подготовки к ОГЭ
Тренировочные задания по теме «Вероятность» ОГЭ Математика
Тренировочные варианты ОГЭ 2022 по математике с ответами
Теория и практика по заданию 11 (ОГЭ по математике)

СДАМ ГИА: РЕШУ ОГЭ
Образовательный портал для подготовки к экзаменам
Математика
сайты — меню — вход — новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
НАШИ БОТЫ
На сайте что-то не так? Отключите адблок
Новости
30 марта
Подготовься к ЕГЭ или ОГЭ за 1,5 месяца на курсе Флеш
21 марта
Новый сервис: рисование
9 февраля
Об ошибках в математике: проверьте браузер
31 января
Внедрили тёмную тему!
17 января
Разместили утвержденное расписание ОГЭ 2022
9 октября
Как восстановить доступ к Решу ЕГЭ, если у вас Windows XP
ЧУЖОЕ НЕ БРАТЬ!
Зайчиков и Поваляев стащили наши тесты
Наша группа
Задания
Версия для печати и копирования в MS Word
Задание 8 № 338131
Найдите значение выражения при
Спрятать решение
Решение.
Приведём в скобках к общему знаменателю:
Подставим значение
Ответ: 390.
Аналоги к заданию № 338131: 353153 338154 338337 352236 353036 Все
Раздел кодификатора ФИПИ: 2.4 Преобразование рациональных выражений.
Спрятать решение
·
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2022

СДАМ ГИА: РЕШУ ОГЭ
Образовательный портал для подготовки к экзаменам
Математика
сайты — меню — вход — новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
НАШИ БОТЫ
На сайте что-то не так? Отключите адблок
Новости
30 марта
Подготовься к ЕГЭ или ОГЭ за 1,5 месяца на курсе Флеш
21 марта
Новый сервис: рисование
9 февраля
Об ошибках в математике: проверьте браузер
31 января
Внедрили тёмную тему!
17 января
Разместили утвержденное расписание ОГЭ 2022
9 октября
Как восстановить доступ к Решу ЕГЭ, если у вас Windows XP
ЧУЖОЕ НЕ БРАТЬ!
Зайчиков и Поваляев стащили наши тесты
Наша группа
Задания
Версия для печати и копирования в MS Word
Задание 8 № 338131
Найдите значение выражения при
Спрятать решение
Решение.
Приведём в скобках к общему знаменателю:
Подставим значение
Ответ: 390.
Аналоги к заданию № 338131: 353153 338154 338337 352236 353036 Все
Раздел кодификатора ФИПИ: 2.4 Преобразование рациональных выражений.
Спрятать решение
·
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2022
Задание 13.
Рациональные выражения
1. Упростите выражение ![]() ,
,
найдите его значение при ![]() ;
; ![]() . В ответ запишите полученное число.
. В ответ запишите полученное число.
Решение.
Упростим выражение:
![]()
Найдём значение выражения при ![]() ,
, ![]() :
:
![]()
Ответ: 1,5.
Ответ: 1,5
140
1,5
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1313.
2. Упростите выражение ![]()
и найдите его значение при ![]() . В ответ запишите полученное число.
. В ответ запишите полученное число.
Решение.
Упростим выражение:
![]()
При a = −2, значение полученного выражения равно −2:2 = −1.
Ответ: -1
311329
-1
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 2)
3. Упростите выражение ![]()
и найдите его значение при ![]() . В ответ запишите полученное число.
. В ответ запишите полученное число.
Решение.
Упростим выражение:
![]()
При ![]() , значение выражения равно 2:5 = 0,4.
, значение выражения равно 2:5 = 0,4.
Ответ: 0,4.
Ответ: 0,4
311352
0,4
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)
4. Упростите выражение ![]()
и найдите его значение при ![]() . В ответ запишите полученное число.
. В ответ запишите полученное число.
Решение.
Упростим выражение:
![]()
При ![]() , значение полученного выражения равно 0, 25.
, значение полученного выражения равно 0, 25.
Ответ: 0,25.
Ответ: 0,25
311372
0,25
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.6)
5. Упростите выражение ![]()
и найдите его значение при ![]() . В ответе запишите найденное значение.
. В ответе запишите найденное значение.
Решение.
Упростим выражение:
![]()
При ![]() , значение полученного выражения равно 7,5 : 5 = 1,5.
, значение полученного выражения равно 7,5 : 5 = 1,5.
Ответ: 1,5.
Ответ: 1,5
311451
1,5
Источник: ГИА-2013. Математика. Экзамен. Вариант 5
6. Представьте в виде дроби выражение ![]()
и найдите его значение при ![]() . В ответ запишите полученное число.
. В ответ запишите полученное число.
Решение.
Упростим выражение:
![]()
Найдем значение выражения при ![]() :
:
Ответ: −5.
Ответ: -5
311463
-5
Источник: ГИА-2013. Математика. Тренировочная работа № 1(2 вар)
7. Упростите выражение
и найдите его значение при . В ответе запишите полученное число.
Решение.
Упростим выражение:
При , значение полученного выражения равно 16.
Ответ: 16.
Ответ: 16
311467
16
Источник: ГИА-2013. Математика. Тренировочная работа № 4.(1 вар.)
8. Упростите выражение
и найдите его значение при
Решение.
Упростим выражение:
Найдем значение выражения при :
Ответ: 1,7.
Ответ: 1,7
311471
1,7
Источник: ГИА-2012. Математика. Диагностическая работа № 1 (1 вар)
9. Найдите значение выражения
при
Решение.
Упростим выражение:
Подставим в полученное выражение значение
Ответ: 1.
Ответ: 1
311758
1
10. Найдите значение выражения
при
Решение.
Упростим выражение:
Подставим в полученное выражение значение
Ответ: 0,8.
Ответ: 0,8
311814
0,8
11. Найдите значение выражения
при
Решение.
Упростим выражение:
Подставим в полученное выражение значение
Ответ: 0,5.
Ответ: 0,5
311846
0,5
12. Найдите значение выражения
при
Решение.
Раскроем скобки и приведём к общему знаменателю:
Тем самым, искомое значение не зависит от Значение выражения при равно
Ответ: 5,6.
Ответ: 5,6
311954
5,6
13. Упростите выражение
и найдите его значение при В ответе запишите найденное значение.
Решение.
Упростим выражение:
Найдём значение выражения при :
Ответ: 4.
Ответ: 4
314312
4
Источник: Банк заданий ФИПИ
14. Упростите выражение
и найдите его значение при и В ответе запишите найденное значение.
Решение.
Упростим выражение:
![]() (при
(при и
Найдём значение выражения при ![]() :
:
Ответ: 1,5.
Ответ: 1,5
314315
1,5
Источник: Банк заданий ФИПИ
15. Найдите значение выражения
при а = 6.
Решение.
Упростим выражение:
(при ).
Найдём значение полученного выражения при
Ответ: 0,5.
Ответ: 0,5
316255
0,5
Источник: Диагностическая работа 01.10.2013 Вариант МА90106
16. Сократите дробь
Решение.
Сократим дробь:
Ответ: 84.
Ответ: 84
316344
84
17. Упростите выражение
и найдите его значение при В ответе запишите найденное значение.
Решение.
Упростим выражение:
Найдём значение выражения при
Ответ: −10,5.
Ответ: -10,5
318572
-10,5
18. Найдите значение выражения
при
Решение.
Упростим выражение:
Найдём значение выражения при
Ответ: −2.
Ответ: -2
319060
-2
19. Найдите значение выражения
при
Решение.
Упростим выражение:
Значение выражения при равно
Ответ: −2.
Ответ: -2
319072
-2
20. Найдите значение выражения
если
Решение.
Разложим числитель на множители по формуле разности квадратов:
Ответ: 12.
Ответ: 12
338076
12
21. Найдите значение выражения
при
Решение.
Преобразуем выражение:
Подставим значение
Ответ: 0,25.
Ответ: 0,25
338095
0,25
22. Найдите значение выражения
при
Решение.
Приведём в скобках к общему знаменателю:
Подставим значение
Ответ: 390.
Ответ: 390
338131
390
23. Найдите значение выражения
при
Решение.
Преобразуем выражение:
Подставим значение
Ответ: 0,75.
Ответ: 0,75
338163
0,75
24. Найдите значение выражения
при
Решение.
Преобразуем выражение:
Подставим значения
Ответ: −2,5.
Ответ: -2,5
338181
-2,5
25. Найдите значение выражения
при
Решение.
Преобразуем выражение:
Подставим значения
Ответ: 31.
Ответ: 31
338274
31
26. Найдите значение выражения
при
Решение.
Преобразуем выражение:
Подставим
Ответ: −2,6.
Ответ: -2,6
338448
-2,6
27. Найдите значение выражения
при a = 78, c = 21.
Решение.
Преобразуем выражение:
Ответ: −8.
Ответ: -8
341353
-8
28. Найдите значение выражения
при a = 7,7.
Решение.
Упростим выражение:
Подставим в полученное выражение значение
Ответ: 0,66.
Ответ: 0,66
341704
0,66
29. Найдите значение выражения: ,
если
Целые выражения
1. Упростите выражение ,
найдите его значение при . В ответ запишите полученное число.
Решение.
Упростим выражение:
Найдём значение полученного выражения при :
Ответ: 0.
Ответ: 0
36
0
Источник: Демонстрационная версия ГИА—2013 по математике.
2. Найдите значение выражения
при
Решение.
Упростим выражение:
При , значение полученного выражения равно 16.
Ответ: 16.
Ответ: 16
311383
16
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)
3. Найдите значение выражения
при
Решение.
Упростим выражение:
При получаем:
Ответ: 27.
Ответ: 27
311910
27
4. Найдите значение выражения
при
Решение.
Преобразуем выражение:
Подставим значение
Ответ: −230,4.
Ответ: -230,4
338067
-230,4
5. Найдите если
Решение.
Имеем:
Ответ: 4.
Ответ: 4
338092
4
6. Найдите значение выражения
при
Восьмое задание в модуле алгебре проверяет знания в области обращения со степенями и подкоренными выражениями.
При выполнении задания №4 ОГЭ по математике проверяются не только навыки выполнения вычисления и преобразований числовых выражений, но и умение преобразовывать алгебраические выражения. Возможно, потребуется выполнить действия со степенями с целым показателем, с многочленами, тождественные преобразования рациональных выражений.
В соответствии с материалами проведения основного экзамена могут быть задания, в которых потребуется выполнение тождественных преобразований рациональных выражений, разложение многочленов на множители, использование процентов и пропорций, признаков делимости.
Ответом в задании №8 является одна из цифр 1; 2; 3; 4 соответствующая номеру предложенного варианта ответа к заданию.
Теория к заданию №4
Из теоретического материала нам пригодятся правила обращения со степенями:

Правила работы с подкоренными выражениями:
В моих разобранных вариантах представлены данные правила — в разборе первого варианта третьего задания представлены правила обращения со степенями, а во втором и третьем варианте разобраны примеры работы подкоренными выражениями.
Разбор типовых вариантов задания №4 ОГЭ по математике
Первый вариант задания
Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11n ?
- 121n
- 11n+2
- 112n
- 11n+3
Решение:
Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:
- при умножении степени складываются
- приделении степени вычитаются
- при возведении степени в степень степени перемножаются
- при извлечении корня степени делятся
Кроме того, для решения необходимо представить 121 как степень 11, а именно это 112.
121 • 11n = 112 • 11n
С учетом правила умножения, складываем степени:
112 • 11n = 11n+2
Следовательно, нам подходит второй ответ.
Ответ: 2
Второй вариант задания
Значение какого из данных ниже выражений является наибольшим?
- 3√5
- 2√11
- 2√10
- 6,5
Решение:
Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:
- 3√5
Переносим 3 под корень:
3√5 = √(3² •5) = √(9•5) = √45
- 2√11
Переносим 2 под корень:
2√11 = √(2² • 11) = √(4 • 11) =√44
- 2√10
Переносим 2 под корень:
2√10 = √(2² • 10) = √(4 • 10) =√40
- 6,5
Возводим 6,5 в квадрат:
6,5 = √(6,5²) = √42,25
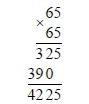
Посмотрим на все получившиеся варианты:
- 3√5 = √45
- 2√11 = √44
- 2√10 = √40
- 6,5 = √42,25
Следовательно, правильный ответ первый
Ответ: 1
Третий вариант задания
Какое из данных чисел является рациональным?
- √810
- √8,1
- √0,81
- все эти числа иррациональны
Решение:
Для решения этой задачи нужно действовать следующим образом:
Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:
0,9
90
Рассмотри каждое из них:
0,9 = √(0,9)² = √0,81
90 = √(90²) = √8100
Следовательно, число √0,81 является рациональным, остальные же числа
- √810
- √8,1
хотя и похожи на форму 9 в квадрате, не являются рациональными.
Таким образом, правильный ответ третий.
Ответ: 3
Четвертый вариант задания
По просьбе подписчика моего сообщества Спадило Дианы, привожу разбор следующего задания №4:
Какое из данных ниже чисел является значением выражения?


Решение:
Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:
16 — 14 = 2
Суммарно наши действия выглядят так:

Ответ: 4
Хотите, чтобы ваше задание я разобрал и представил здесь? Подписывайтесь на мою группу Спадило и присылайте задание в личные сообщения группы!
Пятый вариант задания (демонстрационный вариант ОГЭ 2017)
Значение какого из выражений является рациональным числом?
- √6-3
- √3•√5
- (√5)²
- (√6-3)²
Решение:
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
1) √6-3
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
2) √3•√5
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
√3•√5 = √(3•5) = √15
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
3) (√5)²
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
(√5)² = 5
Данный вариант ответа нам подходит.
4) (√6-3)²
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
Ответ: 3
Шестой вариант задания
Найдите значение выражения:
![]()
Решение:
В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=72 и 100=102. И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:
![]()
По аналогии извлекаем и 2-й корень:
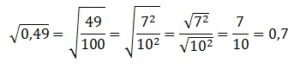
В итоге получаем:
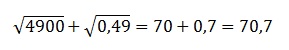
Ответ: 70,7
Седьмой вариант задания
Найдите значение выражения:
![]()
Решение:
Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:
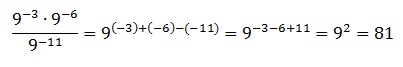
Ответ: 81
Задание 1 № 366805
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Город Гранюк | Деревня Астрелка | Хутор Южный | Город Гусевск |
| Цифры |
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.
Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.
Ответ: 1465.
2. Задание 2 № 366806
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Решение.
Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится
 пачек чая.
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
3. Задание 3 № 366807
Найдите площадь (в км2), которую занимает заказник.
Решение.

Площадь заказника равна:

Ответ: 351.
4. Задание 4 № 366808
Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Решение.
Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
 км.
км.
Ответ: 30.
5. Задание 5 № 366809
Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | |||
| Шина вида «А» | |||
| Шина вида «Б» | |||
| Спица | |||
| Педаль вида «А» | |||
| Педаль вида «Б» | |||
| Тормоз вида «А» | нет | ||
| Тормоз вида «Б» | нет | ||
| Набор крепёжных изделий |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Решение.
На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:
 руб.
руб.
Ответ: 5300.
6. Задание 6 № 316314
Найдите значение выражения: 
Решение.
Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.
7. Задание 7 № 317575
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?
1) 
2) 
3) 
4) 
Решение.
Заметим, что  и
и  Проверим все варианты ответа:
Проверим все варианты ответа:
1)  — неверно;
— неверно;
2)  — верно;
— верно;
3)  — верно;
— верно;
4)  — верно.
— верно.
Ответ указан под номером 1.
8. Задание 8 № 353586
Какое из данных ниже чисел является значением выражения 
1) 
2) 
3) 
4) 
Решение.
Последовательно получим:


Ответ: 1
9. Задание 9 № 338500
При каком значении  значения выражений
значения выражений  и
и  равны?
равны?
Решение.
Для ответа на вопрос задачи нужно решить уравнение  Решим его:
Решим его:

Ответ: 2.
10. Задание 10 № 325450
В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
Решение.
Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна 
Ответ: 0,3.
11. Задание 11 № 311406
На рисунке изображён график функции  . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке 
2) 
3) 
4) прямая  пересекает график в точках
пересекает график в точках  и
и 
Решение.
Проверим каждое из утверждений.
1) Функция возрастает на промежутке  — неверно, функция убывает на промежутке
— неверно, функция убывает на промежутке  и затем возрастает на
и затем возрастает на  .
.
2)  — неверно,
— неверно, 

3)  — верно, видно из графика.
— верно, видно из графика.
4) Прямая  пересекает график в точках
пересекает график в точках  и
и  — верно, видно из графика.
— верно, видно из графика.
Таким образом, неверные утверждения находятся под номерами 1 и 2.
Ответ: 12.
12. Задание 12 № 311543
Площадь любого выпуклого четырехугольника можно вычислять по формуле  , где
, где  — длины его диагоналей, а
— длины его диагоналей, а  угол между ними. Вычислите
угол между ними. Вычислите  , если
, если  .
.
Решение.
Выразим  :
:

Подставляя, получаем:

Ответ: 0,4.
13. Задание 13 № 338497
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.

1) 1
2) 2
3) 3
4) 4
Решение.
Решим неравенство методом интервалов:


Правильный ответ указан под номером: 4.
14. Задание 14 № 406645
В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Решение.
Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.
Найдем сумму этой прогрессии:

Ответ: 377 мест.
15. Задание 15 № 340000

В прямоугольном треугольнике  катет
катет  , а высота
, а высота  , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна  Найдите
Найдите 
Решение.
Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Углы  и
и  равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.
16. Задание 16 № 351463
 На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что  Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Решение.
Пусть длина большей дуги  равна
равна  Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.
17. Задание 17 № 169876
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на  .
.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.
———-
В открытом банке иррациональный ответ.
18. Задание 18 № 350842

Найдите угол 
Решение.

Искомый угол  опирается на
опирается на  часть окружности:
часть окружности:  . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.
. Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е. 
Ответ: 22,5
19. Задание 19 № 401617
Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.
Ответ: 13.
20. Задание 20 № 338505
Решите неравенство 
Решение.
Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение 


Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).
Таким образом, ответ 
Ответ: 
Примечание.
Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно, 
21. Задание 21 № 353527
Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли  г 21-процентного раствора, тогда взяли и
г 21-процентного раствора, тогда взяли и  г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится
г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится  г, а во втором —
г, а во втором —  г Концентрация получившегося раствора равна
г Концентрация получившегося раствора равна  или 58%.
или 58%.
Ответ: 58.
22. Задание 22 № 338288
Постройте график функции  И определите, при каких значениях
И определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение.
Упростим выражение:
По теореме, обратной теореме Виета, корни уравнения  равны -1 и -2 соответственно, тогда по формуле
равны -1 и -2 соответственно, тогда по формуле  , получаем:
, получаем:  . Имеем:
. Имеем:

График функции сводится к графику параболы  с выколотой точкой
с выколотой точкой 
Выделим полный квадрат:

Следовательно, график функции получается из графика функции  сдвигом на
сдвигом на  . (см. рис.)
. (см. рис.)

Из графика видно, что прямая  имеет с графиком функции ровно одну общую точку при
имеет с графиком функции ровно одну общую точку при  и
и 
Ответ: −1; 3.
23. Задание 23 № 339395
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.
Решение.
 Угол
Угол  — вписанный, он равен 90° и опирается на дугу
— вписанный, он равен 90° и опирается на дугу  следовательно, дуга
следовательно, дуга  равна 180°, значит, хорда
равна 180°, значит, хорда  — диаметр окружности и
— диаметр окружности и 
Ответ: 16.
24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Решение.
Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.
25. Задание 25 № 311926
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
Решение.

По свойству равнобедренной трапеции  следовательно, треугольники
следовательно, треугольники  и
и  равны. Так как
равны. Так как  =
=  треугольники
треугольники  и
и  равнобедренные, следовательно,
равнобедренные, следовательно,  и
и  — соответствующие медианы этих треугольников. Значит,
— соответствующие медианы этих треугольников. Значит,  Отрезок
Отрезок  соединяет середины диагоналей трапеции, следовательно,
соединяет середины диагоналей трапеции, следовательно,  и прямые
и прямые 
 и
и  параллельны, поэтому,
параллельны, поэтому,  — трапеция. Проведём
— трапеция. Проведём  — высоту трапеции
— высоту трапеции  и
и  — высоту трапеции
— высоту трапеции  . Прямоугольные треугольники
. Прямоугольные треугольники  и
и  подобны, значит,
подобны, значит, 
Площадь трапеции  :
: 
Площадь трапеции 


Ответ: 9.
При выполнении задания 8 ОГЭ по математике необходимо: знать свойства степеней и корней, уметь сравнивать рациональные и иррациональные числа, применять формулы сокращённого умножения.
Пример 1. Найдите значение выражения . В ответе укажите номер правильного варианта.
1) 84 2) 2352 3) 4) 252
Решение. Произведение корней равно корню из произведения, т. е. . Тогда
Ответ: 1.
Пример 2. Найдите значение выражения . В ответе укажите номер правильного варианта.
1) 2)
3)
4)
Ответ: 3.
Пример 3. На рулоне обоев имеется надпись, гарантирующая, что длина полотна обоев находится в пределах 10 ± 0,05 м. Какую длину не может иметь полотно при этом условии?
В ответе укажите номер правильного варианта.
1) 10,03 2) 10,05 3) 9,96 4) 10,08
Решение. Длина рулона находится в интервале от 10 — 0,05 = 9,95 м до 10 + 0,05 = 10,05 м. Таким образом, только число 10,08 не попадает в этот диапазон.
Ответ: 4.
Пример 4. Сравните числа и 14. В ответе укажите номер правильного варианта.
1) 2)
3)
Решение. Очевидно, что равенство между заданными числами невозможно. Предположим, что справедливо неравенство Возведём обе части неравенства в квадрат и проведём соответствующие преобразования:
Полученное неравенство неверно, а это значит, что предположение неверно. Тогда верно неравенство .
Ответ: 1.
Пример 5. Укажите наименьшее из чисел. В ответе укажите номер правильного варианта.
1) 2)
3)
4)
Решение. Сравним сначала первые три числа, представив их в виде корней:
1) 2)
3)
Из этих чисел наименьшим является . Осталось сравнить его с четвёртым значением.
Результат очевиден. Наименьшим оказалось число под номером 4.
Ответ: 4.
Пример 6. Представьте выражение в виде степени с основанием m. В ответе укажите номер правильного варианта.
1) 2)
3)
4)
Решение. Используем свойства степеней:
Ответ: 2.
Пример 7. Вычислите . В ответе укажите номер правильного варианта.
1) 2)
3)
4)
Решение. Используем свойства степеней:
Ответ: 3.
Пример 8. Какое из чисел является иррациональным? В ответе укажите номер правильного варианта.
1) 2)
3)
4) все числа иррациональны
Решение. Если в результате вычислений или преобразований всё равно остаётся корень, то число является иррациональным:
1) (рациональное число)
2) (иррациональное число)
3) (рациональное число)
Ответ: 2.
Пример 9. Какое из числовых выражений является рациональным? В ответе укажите номер правильного варианта.
1) 2)
3)
4)
Решение. Если в результате вычислений корень «исчезнет», то число является рациональным:
1) (иррациональное число)
2) (иррациональное число)
3) (иррациональное число)
4) (рациональное число)
Ответ: 4.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 8 ОГЭ по математике. Числа, вычисления и алгебраические выражения.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.01.2023

