Задание 8 номер 337700 - Большой телефонный справочник предприятий

Простой способ вычислить проценты от X

Сколько будет %

от ?

8% от 337700 это: 27016

Процент от	Разница
1% от 337700 это 3377	334323
2% от 337700 это 6754	330946
3% от 337700 это 10131	327569
4% от 337700 это 13508	324192
5% от 337700 это 16885	320815
6% от 337700 это 20262	317438
7% от 337700 это 23639	314061
8% от 337700 это 27016	310684
9% от 337700 это 30393	307307
10% от 337700 это 33770	303930
11% от 337700 это 37147	300553
12% от 337700 это 40524	297176
13% от 337700 это 43901	293799
14% от 337700 это 47278	290422
15% от 337700 это 50655	287045
16% от 337700 это 54032	283668
17% от 337700 это 57409	280291
18% от 337700 это 60786	276914
19% от 337700 это 64163	273537
20% от 337700 это 67540	270160
21% от 337700 это 70917	266783
22% от 337700 это 74294	263406
23% от 337700 это 77671	260029
24% от 337700 это 81048	256652
25% от 337700 это 84425	253275
26% от 337700 это 87802	249898
27% от 337700 это 91179	246521
28% от 337700 это 94556	243144
29% от 337700 это 97933	239767
30% от 337700 это 101310	236390
31% от 337700 это 104687	233013
32% от 337700 это 108064	229636
33% от 337700 это 111441	226259
34% от 337700 это 114818	222882
35% от 337700 это 118195	219505
36% от 337700 это 121572	216128
37% от 337700 это 124949	212751
38% от 337700 это 128326	209374
39% от 337700 это 131703	205997
40% от 337700 это 135080	202620
41% от 337700 это 138457	199243
42% от 337700 это 141834	195866
43% от 337700 это 145211	192489
44% от 337700 это 148588	189112
45% от 337700 это 151965	185735
46% от 337700 это 155342	182358
47% от 337700 это 158719	178981
48% от 337700 это 162096	175604
49% от 337700 это 165473	172227
50% от 337700 это 168850	168850
51% от 337700 это 172227	165473
52% от 337700 это 175604	162096
53% от 337700 это 178981	158719
54% от 337700 это 182358	155342
55% от 337700 это 185735	151965
56% от 337700 это 189112	148588
57% от 337700 это 192489	145211
58% от 337700 это 195866	141834
59% от 337700 это 199243	138457
60% от 337700 это 202620	135080
61% от 337700 это 205997	131703
62% от 337700 это 209374	128326
63% от 337700 это 212751	124949
64% от 337700 это 216128	121572
65% от 337700 это 219505	118195
66% от 337700 это 222882	114818
67% от 337700 это 226259	111441
68% от 337700 это 229636	108064
69% от 337700 это 233013	104687
70% от 337700 это 236390	101310
71% от 337700 это 239767	97933
72% от 337700 это 243144	94556
73% от 337700 это 246521	91179
74% от 337700 это 249898	87802
75% от 337700 это 253275	84425
76% от 337700 это 256652	81048
77% от 337700 это 260029	77671
78% от 337700 это 263406	74294
79% от 337700 это 266783	70917
80% от 337700 это 270160	67540
81% от 337700 это 273537	64163
82% от 337700 это 276914	60786
83% от 337700 это 280291	57409
84% от 337700 это 283668	54032
85% от 337700 это 287045	50655
86% от 337700 это 290422	47278
87% от 337700 это 293799	43901
88% от 337700 это 297176	40524
89% от 337700 это 300553	37147
90% от 337700 это 303930	33770
91% от 337700 это 307307	30393
92% от 337700 это 310684	27016
93% от 337700 это 314061	23639
94% от 337700 это 317438	20262
95% от 337700 это 320815	16885
96% от 337700 это 324192	13508
97% от 337700 это 327569	10131
98% от 337700 это 330946	6754
99% от 337700 это 334323	3377
100% от 337700 это 337700	0

Как можно рассчитать 8% от 337700

В магазине товар стоит 337700₽, вам дали скидку 8% и вы хотите понять сколько вы сэкономили.

Решение:

Сэкономленная сумма = Цена товара * Скидка в процентах/ 100

Сэкономленная сумма = (8 * 337700) / 100

Сэкономленная сумма = 27016₽

Проще говоря, при покупке товара за 337700₽ и скидке в 8%, вы заплатите 310684₽ и при этом сэкономите 27016₽.

Для рассчета НДС от 337700₽, вы можете использовать Калькулятор НДС онлайн

Расчеты процентов: примеры

62% от 278239
8% от 155746
92% от 78709
31% от 283269
43% от 236983
13% от 36276
65% от 331708
11% от 351044
55% от 108247
41% от 334647
35% от 111832
89% от 375065

Помогите с задачами номер 7 и 8

1 ответ:

Задание 8 номер 337700

0

0

Просмотр

ответы 1 4 220 1 3 1 4 4 4 3 2 2 2 1951,1 1

Решения

Решения к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

Все права защищены. Copyright © 2012. Учебные материалы, взяты из открытых источников. Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с нами по e-mail: [email protected]

При выполнении задания 8 ОГЭ по математике необходимо: знать свойства степеней и корней, уметь сравнивать рациональные и иррациональные числа, применять формулы сокращённого умножения.

Пример 1. Найдите значение выражения $sqrt{3cdot 7^2}cdot sqrt{3cdot 2^4}$ . В ответе укажите номер правильного варианта.

1) 84 2) 2352 3) $28sqrt{3}$ 4) 252

Решение. Произведение корней равно корню из произведения, т. е. $sqrt{a}cdot sqrt{b}=sqrt{acdot b}$ . Тогда

$sqrt{3cdot 7^2}cdot sqrt{3cdot 2^4}=sqrt{3cdot 7^2cdot 3cdot 2^4}=sqrt{3^2cdot 7^2cdot 4^2}=3cdot 7cdot 4=84 .$

Ответ: 1.

Пример 2. Найдите значение выражения ${(sqrt{40}+4)}^2$ . В ответе укажите номер правильного варианта.

1) $56+4sqrt{40}$ 2) $24$ 3) $56+8sqrt{40}$ 4) $24+8sqrt{40}$

Ответ: 3.

Пример 3. На рулоне обоев имеется надпись, гарантирующая, что длина полотна обоев находится в пределах 10 ± 0,05 м. Какую длину не может иметь полотно при этом условии?

В ответе укажите номер правильного варианта.

1) 10,03 2) 10,05 3) 9,96 4) 10,08

Решение. Длина рулона находится в интервале от 10 — 0,05 = 9,95 м до 10 + 0,05 = 10,05 м. Таким образом, только число 10,08 не попадает в этот диапазон.

Ответ: 4.

Пример 4. Сравните числа $sqrt{52}+sqrt{46}$ и 14. В ответе укажите номер правильного варианта.

1) $sqrt{52}+sqrt{46} textless 14$ 2) $sqrt{52}+sqrt{46}=14$ 3) $sqrt{52}+sqrt{46} textgreater 14$

Решение. Очевидно, что равенство между заданными числами невозможно. Предположим, что справедливо неравенство $sqrt{52}+sqrt{46} textgreater 14 .$ Возведём обе части неравенства в квадрат и проведём соответствующие преобразования:

${(sqrt{52}+sqrt{46})}^2 textgreater {14}^2 = textgreater {sqrt{52}}^2+2cdot sqrt{52}cdot sqrt{46}+{sqrt{46}}^2 textgreater 196 = textgreater 52+2cdot sqrt{52cdot 46}+46 textgreater 196$
$= textgreater 2cdot sqrt{2392} textgreater 98 = textgreater sqrt{2392} textgreater 49 = textgreater {sqrt{2392}}^2 textgreater {49}^2 = textgreater 2392 textgreater 2401.$

Полученное неравенство неверно, а это значит, что предположение неверно. Тогда верно неравенство $sqrt{52}+sqrt{46} textless 14$ .

Ответ: 1.

Пример 5. Укажите наименьшее из чисел. В ответе укажите номер правильного варианта.

1) $sqrt{35}$ 2) $2sqrt{7}$ 3) $6$ 4) $sqrt{6}+sqrt{7}$

Решение. Сравним сначала первые три числа, представив их в виде корней:

1) $sqrt{35}$ 2) $2sqrt{7}=sqrt{4}cdot sqrt{7}=sqrt{28}$ 3) $6=sqrt{36}$

Из этих чисел наименьшим является $sqrt{28}=2sqrt{7}$ . Осталось сравнить его с четвёртым значением.

$2sqrt{7}=sqrt{7}+sqrt{7} textgreater sqrt{6}+sqrt{7} .$

Результат очевиден. Наименьшим оказалось число под номером 4.

Ответ: 4.

Пример 6. Представьте выражение $frac{m^{-9}cdot m^3}{m^{-2}}$ в виде степени с основанием m. В ответе укажите номер правильного варианта.

1) $m^{-3}$ 2) $m^{-4}$ 3) $m^{-8}$ 4) $m^{-5}$

Решение. Используем свойства степеней:

$frac{m^{-9}cdot m^3}{m^{-2}}=frac{m^{-9+3}}{m^{-2}}=frac{m^{-6}}{m^{-2}}=m^{-6-(-2)}=m^{-6+2}=m^{-4} .$

Ответ: 2.

Пример 7. Вычислите $frac{7^6cdot {(7^{-9})}^2}{7^{-10}}$ . В ответе укажите номер правильного варианта.

1) $49$ 2) $-49$ 3) $frac{1}{49}$ 4) $-frac{1}{49}$

Решение. Используем свойства степеней:

$frac{7^6cdot {(7^{-9})}^2}{7^{-10}}=frac{7^6cdot 7^{-9cdot 2}}{7^{-10}}=frac{7^6cdot 7^{-18}}{7^{-10}}=frac{7^{6+(-18)}}{7^{-10}}=frac{7^{-12}}{7^{-10}}=7^{-12-(-10)}=7^{-12+10}=7^{-2}=frac{1}{7^2}=frac{1}{49} .$

Ответ: 3.

Пример 8. Какое из чисел $sqrt{0,25} , sqrt{2,5} , sqrt{2500}$ является иррациональным? В ответе укажите номер правильного варианта.

1) $sqrt{0,25}$ 2) $sqrt{2,5}$ 3) $sqrt{2500}$ 4) все числа иррациональны

Решение. Если в результате вычислений или преобразований всё равно остаётся корень, то число является иррациональным:

1) $sqrt{0,25}=sqrt{frac{25}{100}}=frac{sqrt{25}}{sqrt{100}}=frac{5}{10}=0,5$ (рациональное число)

2) $sqrt{2,5}=sqrt{2frac{5}{10}}=sqrt{frac{25}{10}}=frac{sqrt{25}}{sqrt{10}}=frac{5}{sqrt{10}}$ (иррациональное число)

3) $sqrt{2500}=50$ (рациональное число)

Ответ: 2.

Пример 9. Какое из числовых выражений является рациональным? В ответе укажите номер правильного варианта.

1) $sqrt{13}cdot sqrt{20}$ 2) $sqrt{18}-2sqrt{2}$ 3) $frac{sqrt{24}}{sqrt{8}}$ 4) $(sqrt{16}-sqrt{5})cdot (sqrt{16}+sqrt{5})$

Решение. Если в результате вычислений корень «исчезнет», то число является рациональным:

1) $sqrt{13}cdot sqrt{20}=sqrt{13}cdot sqrt{4cdot 5}=sqrt{13}cdot sqrt{4}cdot sqrt{5}=2sqrt{13cdot 5}=2sqrt{65}$ (иррациональное число)

2) $sqrt{18}-2sqrt{2}=sqrt{9cdot 2}-2sqrt{2}=3sqrt{2}-2sqrt{2}=sqrt{2}$ (иррациональное число)

3) $frac{sqrt{24}}{sqrt{8}}=sqrt{frac{24}{8}}=sqrt{3}$ (иррациональное число)

4) $left(sqrt{16}-sqrt{5}right)cdot left(sqrt{16}+sqrt{5}right)={sqrt{16}}^2-{sqrt{5}}^2=16-5=11$ (рациональное число)

Ответ: 4.

Сегодня 22.01.2022 02:36 свежие новости час назад
Прогноз на сегодня : Решу огэ математика задание 8 номер 337700 . Развитие событий.

Актуально сегодня (22.01.2022 02:36): Решу огэ математика задание 8 номер 337700

1. Решу огэ математика задание 8 номер 337700

Решу огэ математика задание 8 номер 337700

Решу огэ математика задание 8 номер 337700

Решу огэ математика задание 8 номер 337700

Решу огэ математика задание 8 номер 337700
Решу огэ математика задание 8 номер 337700
Решу огэ математика задание 8 номер 337700
Решу огэ математика задание 8 номер 337700
Решу огэ математика задание 8 номер 337700

Решу огэ математика задание 8 номер 337700

9041462618282665b80f0416d63c2cfc 5a1b3a8e46bc331f4cd961d570a3c18b
Решу огэ математика задание 8 номер 337700
Решу огэ математика задание 8 номер 337700
Решу огэ математика задание 8 номер 337700

Invision Community © 2022 IPS, Inc.
Карта сайт Rss
s
p

Источник

На какие числа делится число онлайн калькулятор. Посчитать делители числа.

Какие числа делятся на 337700?

На число 337700 без остатка (нацело) делятся следующие числа: 337700, 675400, 1013100, 1350800, 1688500, 2026200, 2363900, 2701600, 3039300, 3377000, 3714700, 4052400 и многие другие.

Какие четные числа делятся на 337700?

На число 337700 делятся следующие четные числа: 337700, 675400, 1013100, 1350800, 1688500, 2026200, 2363900, 2701600, 3039300, 3377000, 3714700, 4052400 и многие други.

Какие нечетные числа делятся на 337700?

Таких чисел нет

На какое наибольшее число делится число 337700 без остатка?

Наибольшее число на которое делится число 337700 есть само число 337700. т.е делиться на само себя без остатка.

На какое наибольшее число делится число 337700 без остатка, не считая числа 337700 и 1?

Наибольшим делителем числа 337700 не считая самого числа 337700 является число 168850.

Какое наименьшее натуральное число делится на 337700?

Наименьшее натуральное число которое делиться на число 337700 является само число 337700.

На какое наименьшее натуральное число делится число 337700?

Наименьшее натуральное число на которое можно разделить число 337700 — это число 1.

Делители числа 337700.

(что бы не забыть запишите все делители числа 337700 в блокнот.)На какие целые и(или) натуральные числа делится число 337700?

Число 337700 делится на следующие целые, натуральные числа (все делители числа 337700): 1, 2, 4, 5, 10, 11, 20, 22, 25, 44, 50, 55, 100, 110, 220, 275, 307, 550, 614, 1100, 1228, 1535, 3070, 3377, 6140, 6754, 7675, 13508, 15350, 16885, 30700, 33770, 67540, 84425, 168850, 337700

На какие четные числа делится число 337700?

Число 337700 делится на следующие четные числа (четные делители числа): 2, 4, 10, 20, 22, 44, 50, 100, 110, 220, 550, 614, 1100, 1228, 3070, 6140, 6754, 13508, 15350, 30700, 33770, 67540, 168850, 337700

На какие нечетные числа делится число 337700?

Число 337700 делится на следующие нечетные числа (нечетные делители числа): 1, 5, 11, 25, 55, 275, 307, 1535, 3377, 7675, 16885, 84425

Сколько делителей имеет число 337700?

Число 337700 имеет 36 делителей

Сколько четных делителей имеет число 337700?

Число 337700 имеет 24 четных делителя

Сколько нечетных делителей имеет число 337700?

Число 337700 имеет 12 нечетных делителей

Число 337700 прописью, словами.

— триста тридцать семь тысяч семьсот

(что бы не забыть запишите число 337700 прописью в блокнот.)

Числа кратные 337700.

— кратные числа, числу 337700 : 675400, 1013100, 1350800, 1688500, 2026200, 2363900, 2701600, 3039300, 3377000, 3714700, 4052400 и многие другие.

Простые множители числа 337700.

У числа 337700 нет простых множителей кроме 1.

Сумма цифр числа 337700.

Сумма цифр числа 337700 равна 20

Произведение цифр числа 337700.

Произведение цифр числа 337700 равна 0

Квадрат числа 337700.

Квадрат числа 337700 равен 114041290000

Куб числа 337700.

Куб числа 337700 равен 38511743633000000

Квадратный корень числа 337700.

Квадратный корень числа 337700 равен 581.1196.

Число 337700 в двоичной системе счисления.

Запись числа 337700 в двоичной системе счисления выглядит так: 1010010011100100100

Количество значащих нулей в двоичной записи числа 337700 = 11

Количество едениц в двоичной записи числа 337700 = 8

(что бы не забыть запишите число 337700 в двоичной системе счисления в блокнот.)Число 337700 в шестнадцатеричной системе счисления.

Запись числа 337700 в шестнадцатеричной системе счисления выглядит так: 52724

(что бы не забыть запишите число 337700 в шестнадцатеричной системе счисления в блокнот.)Число 337700 в восьмеричной системе счисления.

Запись числа 337700 в восьмеричной системе счисления выглядит так: 1223444

(что бы не забыть запишите число 337700 в восьмеричной системе счисления в блокнот.)Число 337700 не является простым!

Корни числа 337700.

Корень 3 степени из 337700.

Корень 3 (третьей) степени из 337700 равен 69.637582644275

Корень 4 степени из 337700.

Корень 4 (четвертой) степени из 337700 равен 24.106422568077

Корень 5 степени из 337700.

Корень 5 (пятой) степени из 337700 равен 12.7557562623

Корень 6 степени из 337700.

Корень 6 (шестой) степени из 337700 равен 8.3449135791975

Корень 7 степени из 337700.

Корень 7 (седьмой) степени из 337700 равен 6.1629713883503

Корень 8 степени из 337700.

Корень 8 (восьмой) степени из 337700 равен 4.9098291791138

Корень 9 степени из 337700.

Корень 9 (девятой) степени из 337700 равен 4.1141604881204

Корень 10 степени из 337700.

Корень 10 (десятой) степени из 337700 равен 3.5715201612618

Корень 11 степени из 337700.

Корень 11 (одиннадцатой) степени из 337700 равен 3.1812202097259

Корень 12 степени из 337700.

Корень 12 (двенадцатой) степени из 337700 равен 2.888756407037

Корень 13 степени из 337700.

Корень 13 (тринадцатой) степени из 337700 равен 2.6623896729784

Корень 14 степени из 337700.

Корень 14 (четырнадцатой) степени из 337700 равен 2.4825332602707

Корень 15 степени из 337700.

Корень 15 (пятнадцатой) степени из 337700 равен 2.3365158818673

Степени числа 337700.

337700 в 3 степени.

337700 в 3 степени равно 38511743633000000.

337700 в 4 степени.

337700 в 4 степени равно 1.3005415824864E+22.

337700 в 5 степени.

337700 в 5 степени равно 4.3919289240566E+27.

337700 в 6 степени.

337700 в 6 степени равно 1.4831543976539E+33.

337700 в 7 степени.

337700 в 7 степени равно 5.0086124008773E+38.

337700 в 8 степени.

337700 в 8 степени равно 1.6914084077763E+44.

337700 в 9 степени.

337700 в 9 степени равно 5.7118861930604E+49.

337700 в 10 степени.

337700 в 10 степени равно 1.9289039673965E+55.

337700 в 11 степени.

337700 в 11 степени равно 6.513908697898E+60.

337700 в 12 степени.

337700 в 12 степени равно 2.1997469672802E+66.

337700 в 13 степени.

337700 в 13 степени равно 7.4285455085051E+71.

337700 в 14 степени.

337700 в 14 степени равно 2.5086198182222E+77.

337700 в 15 степени.

337700 в 15 степени равно 8.4716091261362E+82.

Какое число имеет такую же сумму цифр как и число 337700?Математика. Найти сумму цифр числа 337700.

Число 337700 состоит из следующих цифр — 3, 3, 7, 7, 0, 0.

Определить сумму цифр числа 337700 не так уж и сложно.

Сумма цифр шестизначного числа 337700 равна 3 + 3 + 7 + 7 + 0 + 0 = 20.

Числа сумма цифр которых равна 20.

Следующие числа имеют такую же сумму цифр как и число 337700 — 299, 389, 398, 479, 488, 497, 569, 578, 587, 596, 659, 668, 677, 686, 695, 749, 758, 767, 776, 785.

Трехзначные числа сумма цифр которых равна 20 — 299, 389, 398, 479, 488, 497, 569, 578, 587, 596.

Четырехзначные числа сумма цифр которых равна 20 — 1199, 1289, 1298, 1379, 1388, 1397, 1469, 1478, 1487, 1496.

Пятизначные числа сумма цифр которых равна 20 — 10199, 10289, 10298, 10379, 10388, 10397, 10469, 10478, 10487, 10496.

Шестизначные числа сумма цифр которых равна 20 — 100199, 100289, 100298, 100379, 100388, 100397, 100469, 100478, 100487, 100496.

Квадрат суммы цифр числа 337700.

Квадрат суммы цифр шестизначного числа 337700 равен 3 + 3 + 7 + 7 + 0 + 0 = 20² = 400.

Сумма квадратов цифр шестизначного числа 337700.

Сумма квадратов цифр числа 337700 равна 3² + 3² + 7² + 7² + 0² + 0² = 9 + 9 + 49 + 49 + 0 + 0 = 116.

Сумма нечетных цифр числа 337700.

Сумма нечетных цифр шестизначного числа 337700 равна 3 + 3 + 7 + 7 = 20.

Квадрат суммы нечетных цифр шестизначного числа 337700.

Квадрат суммы нечетных цифр числа 337700 равна 3 + 3 + 7 + 7 = 20² = 400.

Сумма квадратов нечетных цифр шестизначного числа 337700.

Сумма квадратов нечетных цифр числа 337700 равна 3² + 3² + 7² + 7² = 9 + 9 + 49 + 49 = 116.

Произведение цифр числа 337700.

Какое число имеет такое же произведение цифр как и число 337700?Математика. Найти произведение цифр числа 337700.

Число 337700 состоит из следующих цифр — 3, 3, 7, 7, 0, 0.

Найти сумму цифр числа 337700 просто.

Решение:

Произведение цифр числа 337700 равно 3 * 3 * 7 * 7 * 0 * 0 = 0.

Числа произведение цифр которых равно 0.

Следующие числа имеют такое же произведение цифр как и число 337700 — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110.

Двухзначные числа произведение цифр которых равно 0 — 10, 20, 30, 40, 50, 60, 70, 80, 90.

Трехзначные числа произведение цифр которых равно 0 — 100, 101, 102, 103, 104, 105, 106, 107, 108, 109.

Четырехзначные числа произведение цифр которых равно 0 — 1000, 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009.

Пятизначные числа произведение цифр которых равно 0 — 10000, 10001, 10002, 10003, 10004, 10005, 10006, 10007, 10008, 10009.

Шестизначные числа произведение цифр которых равно 0 — 100000, 100001, 100002, 100003, 100004, 100005, 100006, 100007, 100008, 100009.

Квадрат произведения цифр числа 337700.

Квадрат произведения цифр шестизначного числа 337700 равен 3 * 3 * 7 * 7 * 0 * 0 = 0² = 0.

Произведение квадратов цифр шестизначного числа 337700.

Произведение квадратов цифр числа 337700 равна 3² * 3² * 7² * 7² * 0² * 0² = 9 * 9 * 49 * 49 * 0 * 0 = 0.

Запишите числа которые в сумме дают число 337700.

Задача: Данно число 337700.Какие 2(два) числа дают в сумме число 337700?Решение:

1) 90391 + 247309 = 337700

2) 67487 + 270213 = 337700

3) 59198 + 278502 = 337700

4) 59857 + 277843 = 337700

5) 120212 + 217488 = 337700

Какие 3(три) числа дают в сумме число 337700?Решение:

1) 107153 + 67685 + 162862 = 337700

2) 57092 + 55551 + 225057 = 337700

3) 28480 + 47354 + 261866 = 337700

4) 65712 + 130094 + 141894 = 337700

5) 57801 + 21138 + 258761 = 337700

Какие 4(четыре) числа дают в сумме число 337700?Решение:

1) 19781 + 76513 + 4952 + 236454 = 337700

2) 4278 + 69076 + 43052 + 221294 = 337700

3) 11628 + 91949 + 35141 + 198982 = 337700

4) 41467 + 63824 + 66437 + 165972 = 337700

5) 66388 + 47498 + 49146 + 174668 = 337700

Какие 5(пять) чисел дают в сумме число 337700?Решение:

1) 40127 + 55156 + 7299 + 61184 + 173934 = 337700

2) 20921 + 70012 + 77917 + 34972 + 133878 = 337700

3) 54900 + 11198 + 69399 + 77498 + 124705 = 337700

4) 59708 + 42661 + 32431 + 75007 + 127893 = 337700

5) 33952 + 11276 + 92586 + 91558 + 108328 = 337700

Источник

Восьмое задание в модуле алгебре проверяет знания в области обращения со степенями и подкоренными выражениями.

При выполнении задания №4 ОГЭ по математике проверяются не только навыки выполнения вычисления и преобразований числовых выражений, но и умение преобразовывать алгебраические выражения. Возможно, потребуется выполнить действия со степенями с целым показателем, с многочленами, тождественные преобразования рациональных выражений.

В соответствии с материалами проведения основного экзамена могут быть задания, в которых потребуется выполнение тождественных преобразований рациональных выражений, разложение многочленов на множители, использование процентов и пропорций, признаков делимости.

Ответом в задании №8 является одна из цифр 1; 2; 3; 4 соответствующая номеру предложенного варианта ответа к заданию.

Теория к заданию №4

Из теоретического материала нам пригодятся правила обращения со степенями:

степени

Правила работы с подкоренными выражениями:

В моих разобранных вариантах представлены данные правила — в разборе первого варианта третьего задания представлены правила обращения со степенями, а во втором и третьем варианте разобраны примеры работы подкоренными выражениями.

Разбор типовых вариантов задания №4 ОГЭ по математике

Первый вариант задания

Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11ⁿ?

121ⁿ
11ⁿ⁺²
11²ⁿ
11ⁿ⁺³

Решение:

Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:

при умножении степени складываются
приделении степени вычитаются
при возведении степени в степень степени перемножаются
при извлечении корня степени делятся

Кроме того, для решения необходимо представить 121 как степень 11, а именно это 11².

121 • 11ⁿ= 11² • 11ⁿ

С учетом правила умножения, складываем степени:

11² • 11ⁿ= 11ⁿ⁺²

Следовательно, нам подходит второй ответ.

Ответ: 2

Второй вариант задания

Значение какого из данных ниже выражений является наибольшим?

3√5
2√11
2√10
6,5

Решение:

Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:

3√5

Переносим 3 под корень:

3√5 = √(3² •5) = √(9•5) = √45

2√11

Переносим 2 под корень:

2√11 = √(2² • 11) = √(4 • 11) =√44

2√10

Переносим 2 под корень:

2√10 = √(2² • 10) = √(4 • 10) =√40

Возводим 6,5 в квадрат:

6,5 = √(6,5²) = √42,25

3-2

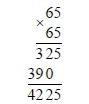
Посмотрим на все получившиеся варианты:

3√5 = √45
2√11 = √44
2√10 = √40
6,5 = √42,25

Следовательно, правильный ответ первый

Ответ: 1

Третий вариант задания

Какое из данных чисел является рациональным?

√810
√8,1
√0,81
все эти числа иррациональны

Решение:

Для решения этой задачи нужно действовать следующим образом:

Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:

0,9

Рассмотри каждое из них:

0,9 = √(0,9)² = √0,81

90 = √(90²) = √8100

Следовательно, число √0,81 является рациональным, остальные же числа

√810
√8,1

хотя и похожи на форму 9 в квадрате, не являются рациональными.

Таким образом, правильный ответ третий.

Ответ: 3

Четвертый вариант задания

По просьбе подписчика моего сообщества Спадило Дианы, привожу разбор следующего задания №4:

Какое из данных ниже чисел является значением выражения?

Разбор и решение задания №3 ОГЭ по математике

Решение:

Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:

16 — 14 = 2

Суммарно наши действия выглядят так:

Разбор и решение задания №3 ОГЭ по математике

Ответ: 4

Хотите, чтобы ваше задание я разобрал и представил здесь? Подписывайтесь на мою группу Спадило и присылайте задание в личные сообщения группы!

Пятый вариант задания (демонстрационный вариант ОГЭ 2017)

Значение какого из выражений является рациональным числом?

√6-3
√3•√5
(√5)²
(√6-3)²

Решение:

В данном задании у нас проверяют навыки операций с иррациональными числами.

Разберем каждый вариант ответа в решении:

1) √6-3

√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…

При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.

2) √3•√5

При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:

√3•√5 = √(3•5) = √15

Но √15 является иррациональным, поэтому данный вариант ответа не подходит.

3) (√5)²

При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:

(√5)² = 5

Данный вариант ответа нам подходит.

4) (√6-3)²

Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.

Ответ: 3

Шестой вариант задания

Найдите значение выражения:

Решение:

В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=7² и 100=10². И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:

По аналогии извлекаем и 2-й корень:

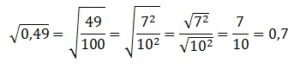
Задание №8 ОГЭ по математике

В итоге получаем:

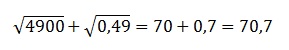
Задание №8 ОГЭ по математике

Ответ: 70,7

Седьмой вариант задания

Найдите значение выражения:

Решение:

Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:

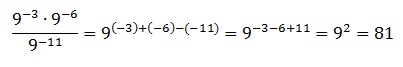
Задание №8 ОГЭ по математике

Ответ: 81

Источник