Задание 8 номер 337339 - Большой телефонный справочник предприятий

Не могу найти по номеру выполняемое многоразовое задание. Да и любые другие по номеру не найти). Пробовал произвольно выбранные задания вызвать по номеру — и ничего!)

Обсуждение

Задание 8 номер 337339

gimmegun

12 Окт 2017 г, в 09:01
редактир. 12 Окт 2017 г, в 09:06

Одной из причин может быть выбор фильтров

По спискам

По типу

при поиске.
Если это (эти) задание у Вас в Избранном, то должны быть выбраны фильтры

Избранное

Все.

Если выбраны

Все

, то задание не покажут.
Если задание не в Избранном, то соответственно наоборот — должны быть выбраны фильтры

Все

.
Другой причиной может быть то, что задание выключено или забанено.

Задание 8 номер 337339

Не годится…(( Принцип, который вы описали, до меня добрел)), я им воспользовался, результат=0. Сейчас вот еще на всякий случай попробовал. Взял номер первого попавшегося задания (оно у меня никак не отмечено), выбрал «Все», ввел номер, и тишина…

Для обсуждения вопроса/идеи необходима регистрация.

Привести подобные слагаемые 1) 8x-17x-19x+21x 2) — 9y+12y+41y-17y 3) 2,6a-5,4b-a+2b 4) — 5,6c+4,8+8,2c-9,1 5) 4,6m+8,3n-5,1-8,3m-6,4n 6) — 2/3a + 5/6b — 1/8a — 7/12b («/» дробь, а не делить)

Ответы (1)

Задание 8 номер 337339

На рисунке изображён орнамент. Он получается повторением одного и того же базового элемента. 1) Мысленно выделите базовый элемен

Nick2010

Базовый элемент и пять раз его повторения на рисунке в приложении.

Задание 8 номер 337339

Найдите сумму длин всех ребер куба,если длина его ребра равна 8 см

PELAR

В кубе всего 12 рёбер, поэтому
12*8=96 — сумма всех длин ребер куба

Задание 8 номер 337339

Помогите пожалуйста там 2 примера

Сандрулька [184]

17×
5
85

26×
3
78
короче я сделала все что тебе нужно

Задание 8 номер 337339

Из чисел -3,-2,-1, 0 , 1,2,3. выберите все те при которых значение выражения (10х-1) больше значения выражения (8х-2)

Виталий1972

Ответ:

0,1,2,3.

Пошаговое объяснение:

т.к если вместо х подставить эти числа то (10х-1) будет больше чем (8х-2).

(10*0-1)>(8*0-2)

(10*1-1)>(8*1-2)

(10*2-1)>(8*2-2)

(10*3-1)>(8*3-2)

Задание 8 номер 337339

Дополните массы до 1 кг. 650 г 125 г 280 г 450 г 950 г 830 г

Дима91 [7]

1.1000-650=350г.
2.1000-125=875г.
3.1000-280=720г.
4.1000-450=550г.
5.1000-830=170г.

Целеполагание

Диагностика

дата

Коррекция

В 1.1: знать определение квадратного корня из числа, арифметического квадратного корня из числа, обозначение корня, приближенное значение корня, возможности нахождения значения арифметического квадратного корня с любой степенью точности, уметь извлекать квадратный корень из числа

Д 1

1. Задание 3 № 205776 Какое из чисел отмечено на координатной прямой точкой A?

В ответе укажите номер правильного варианта.

1) 2) 3) 4)

9. Задание 3 № 340578 На координатной прямой отмечена точка А.

Известно, что она соответствует одному из четырех указанных ниже чисел. Какому из чисел соответствует точка А?

1) 2) 3) 0,6 4) 4

11. Задание 4 № 348386 Какое из данных чисел является иррациональным?

1) 2) 3) 4) все эти числа рациональны

16.11

6. Задание 7 № 338423. Найдите значение выражения при

7 № 311910. Найдите значение выражения при

В 1.2: знать свойства арифметического корня, уметь использовать эти свойства при решении задач

Д2

1. Задание 4 № 137272

Найдите значение выражения

В ответе укажите номер правильного варианта. 1) 2) 3) 4) 4

2. Задание 4 № 137268

Расположите в порядке возрастания числа: ; ; 5,5.

В ответе укажите номер правильного варианта.

1) 2) 3) 4)

3. Задание 4 № 137285

Найдите значение выражения .

5. Задание 4 № 317389

Найдите значение выражения

В ответе укажите номер правильного варианта. 1) 5 2) 3) 4) 40

8. Задание 4 № 337339

Найдите значение выражения

В ответе укажите номер правильного варианта. 1) 198 2) 3) 3564 4) 2178

25. Задание 4 № 318729

Значение какого выражения является рациональным числом?

В ответе укажите номер правильного варианта.

1) 2) 3) 4)

23.11

1. Задание 4 № 28

Значение какого из выражений является числом рациональным?

В ответе укажите номер правильного варианта.

1) 2) 3) 4)

12. Задание 4 № 348417 Какое из данных ниже чисел является значением выражения ?

14. Задание 4 № 316557

Значение какого из выражений является числом иррациональным?

В ответе укажите номер правильного варианта.

1) 2) 3) 4)

4. Задание 21 № 311255

Упростите выражение

8. Задание 4 № 314246

Сравните числа и 16.

В ответе укажите номер правильного варианта.

1) 2) 3)

Решение.

Возведем в квадрат положительные числа и сравним:

1)()2 = 67 +2 +61 = 128 + 2;

2) 162 = 256 = 128 + 128 = 128 + 2 · 64 = 128 + = ;

3) Так как4087 ;

4) Так как , то ()2 2 .
Учитывая, что и 16 — положительные числа, получаем, что

.Ответ: 1

12. Задание 21 № 311599

Какое из чисел больше: или ?

Дозирование домашнего задания

Удовлетворительно

Хорошо

Отлично

Домашняя работа 1

П.12, №№ 298 б, 299 а, в,300 б, г, е, 302 а, 304 а, в, д, 305 б, г

П. 12, № №307 а; 311 б, е

П.12, № №308 б, 314 в

П. 13, №№ 319 б, г, 320 а, б, г, 322 в, г, 327, 329 г, д. 323 а, б

П. 13, №№ 321 а, 330 а, в, 332 а, в

П. 13 № № 324 б, г, 331 б, г

П. 14, №№ 336 в, е, 339 б, в, 349 б, г

П. 14, №№ 337

П. 14, №№ 340 а

П. 15, №№ 352 б, 356, 363 б, д, е, 365 б

П. 15, №№ 358 в, г, 365 г

П. 15, № 367 в, г

Домашняя работа 2

П. 16, №№ 369 б, д, 370 а, д, е, 383 б, г, е, з, 385 а, в, д, ж, 386 б, г

П. 16, №№ 372 б, г, 373 а, в, 376 д, е, 387 б, в, д

П. 16, № 382 б, г

П. 17, №№ 393 г-е, 401 в, г, е, з, 402 б, г, е

П. 17, №№ 396 а, б, е, ж, 397 б, 399 а

П. 17, №№ 400 в, г, 403 в, г

Тема

Квадратный корень. Приближенное значение квадратного корня. Арифметический квадратный корень

К п. 12 есть К № 7,

п. 13 – прочитать, записать в тетрадь, корни уравнения – 3 случая

п. 14 – прочитать

П.12, № 298 а, в, 299 б, г,300 а, в, д, 302 б ; 304 б, г, е, 305 а, д

П. 12, № № 307 б; 311 а, г

П.12, № №308 а, 314 а, б

П. 13, №№ 319 а, в, 320 в, д, е, 322 а, д, 328, 329 в, е , 323 в – е, 326

П. 13, №№ 321 б, 325, 330 б, г

П. 13 №№ 324 а, в, 331 а, в

П. 14, №№ 336 а, г, 339 а, 349 а, в

П. 14, №№ 341

П. 14, № 340 б

Функция у = и ее график п. 15 – прочитать

П. 15, №№ 352 а, 355, 363 а, в, г, 365 а

П. 15, №№ 358 а, б, 365 в

П. 15, № 367а, б

Свойства арифметического квадратного корня

П. 16, №№ 369 а, г, 370 в, г, 383 а, в, д, ж, 385 б, г, е, з, 386 а, в, д

П. 16, №№ 372 а, в, 373 б, г, 376 в, г, 387 а, г, е

П. 16, № 382 а, в

П. 17, №№ 393 а — в, 401 а, д, ж, 402 а, в, д

П. 17, №№ 396 г, д, з, 397 а, 399 б

П. 17, №№ 400 а, б, 403 а, б

Главная
/
Геометрия
/
задание номер…

Геометрия, 17.03.2021 23:49, Bibi123456

Всего ответов: 3

Посмотреть ответы

Другие вопросы по: Геометрия

Вравнобедренной трапеций abcd угол a=30, меньшее основание равно боковой стороне, а высота, опущенная из вершины тупого угла b, равна 4 см. найдите векторы |cd-cb-ba|….

1) могут ли углы треугольника относиться как числа 1,2,3? 2) найдите cos и tg, если sinα= 3в корне/2 люди надеюсь есть такие на белом свете?…

Втреугольник со сторонами 20, 34, 42 вписан прямоугольник с периметром 40 так ,что его сторона лежит на большей стороне треугольника. найдите стороны прямоугольника. огромная прось…

Площадь трапеции равна 36 см^2. найдите расстояние между основаниями трапеции, если ее средняя линия равна 12 см….

Найти радиус окр если ее длина равна 88 пи см…

На отрезке ав длиной 36 см выбрана точка к. найдите длины отрезков ак и вк, если ак: вк=4: 5….

Знаешь правильный ответ?

задание номер…

Теория к заданию №4

Из теоретического материала нам пригодятся правила обращения со степенями:

степени

Правила работы с подкоренными выражениями:

В моих разобранных вариантах представлены данные правила — в разборе первого варианта третьего задания представлены правила обращения со степенями, а во втором и третьем варианте разобраны примеры работы подкоренными выражениями.

Разбор типовых вариантов задания №4 ОГЭ по математике

Первый вариант задания

Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11ⁿ?

121ⁿ
11ⁿ⁺²
11²ⁿ
11ⁿ⁺³

Решение:

Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:

при умножении степени складываются
приделении степени вычитаются
при возведении степени в степень степени перемножаются
при извлечении корня степени делятся

Кроме того, для решения необходимо представить 121 как степень 11, а именно это 11².

121 • 11ⁿ= 11² • 11ⁿ

С учетом правила умножения, складываем степени:

11² • 11ⁿ= 11ⁿ⁺²

Следовательно, нам подходит второй ответ.

Ответ: 2

Второй вариант задания

Значение какого из данных ниже выражений является наибольшим?

3√5
2√11
2√10
6,5

Решение:

Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:

3√5

Переносим 3 под корень:

3√5 = √(3² •5) = √(9•5) = √45

2√11

Переносим 2 под корень:

2√11 = √(2² • 11) = √(4 • 11) =√44

2√10

Переносим 2 под корень:

2√10 = √(2² • 10) = √(4 • 10) =√40

Возводим 6,5 в квадрат:

6,5 = √(6,5²) = √42,25

3-2

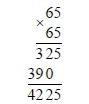
Посмотрим на все получившиеся варианты:

3√5 = √45
2√11 = √44
2√10 = √40
6,5 = √42,25

Следовательно, правильный ответ первый

Ответ: 1

Третий вариант задания

Какое из данных чисел является рациональным?

√810
√8,1
√0,81
все эти числа иррациональны

Решение:

Для решения этой задачи нужно действовать следующим образом:

Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:

0,9

Рассмотри каждое из них:

0,9 = √(0,9)² = √0,81

90 = √(90²) = √8100

Следовательно, число √0,81 является рациональным, остальные же числа

√810
√8,1

хотя и похожи на форму 9 в квадрате, не являются рациональными.

Таким образом, правильный ответ третий.

Ответ: 3

Четвертый вариант задания

По просьбе подписчика моего сообщества Спадило Дианы, привожу разбор следующего задания №4:

Какое из данных ниже чисел является значением выражения?

Разбор и решение задания №3 ОГЭ по математике

Решение:

Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:

16 — 14 = 2

Суммарно наши действия выглядят так:

Разбор и решение задания №3 ОГЭ по математике

Ответ: 4

Хотите, чтобы ваше задание я разобрал и представил здесь? Подписывайтесь на мою группу Спадило и присылайте задание в личные сообщения группы!

Пятый вариант задания (демонстрационный вариант ОГЭ 2017)

Значение какого из выражений является рациональным числом?

√6-3
√3•√5
(√5)²
(√6-3)²

Решение:

В данном задании у нас проверяют навыки операций с иррациональными числами.

Разберем каждый вариант ответа в решении:

1) √6-3

√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…

При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.

2) √3•√5

При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:

√3•√5 = √(3•5) = √15

Но √15 является иррациональным, поэтому данный вариант ответа не подходит.

3) (√5)²

При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:

(√5)² = 5

Данный вариант ответа нам подходит.

4) (√6-3)²

Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.

Ответ: 3

Шестой вариант задания

Найдите значение выражения:

Решение:

В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=7² и 100=10². И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:

По аналогии извлекаем и 2-й корень:

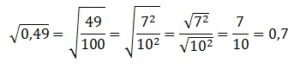
Задание №8 ОГЭ по математике

В итоге получаем:

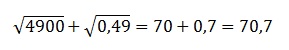
Задание №8 ОГЭ по математике

Ответ: 70,7

Седьмой вариант задания

Найдите значение выражения:

Решение:

Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:

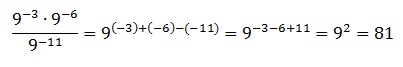
Задание №8 ОГЭ по математике

Ответ: 81

Источник

При выполнении задания 8 ОГЭ по математике необходимо: знать свойства степеней и корней, уметь сравнивать рациональные и иррациональные числа, применять формулы сокращённого умножения.

Пример 1. Найдите значение выражения $sqrt{3cdot 7^2}cdot sqrt{3cdot 2^4}$ . В ответе укажите номер правильного варианта.

1) 84 2) 2352 3) $28sqrt{3}$ 4) 252

Решение. Произведение корней равно корню из произведения, т. е. $sqrt{a}cdot sqrt{b}=sqrt{acdot b}$ . Тогда

$sqrt{3cdot 7^2}cdot sqrt{3cdot 2^4}=sqrt{3cdot 7^2cdot 3cdot 2^4}=sqrt{3^2cdot 7^2cdot 4^2}=3cdot 7cdot 4=84 .$

Ответ: 1.

Пример 2. Найдите значение выражения ${(sqrt{40}+4)}^2$ . В ответе укажите номер правильного варианта.

1) $56+4sqrt{40}$ 2) $24$ 3) $56+8sqrt{40}$ 4) $24+8sqrt{40}$

Ответ: 3.

Пример 3. На рулоне обоев имеется надпись, гарантирующая, что длина полотна обоев находится в пределах 10 ± 0,05 м. Какую длину не может иметь полотно при этом условии?

В ответе укажите номер правильного варианта.

1) 10,03 2) 10,05 3) 9,96 4) 10,08

Решение. Длина рулона находится в интервале от 10 — 0,05 = 9,95 м до 10 + 0,05 = 10,05 м. Таким образом, только число 10,08 не попадает в этот диапазон.

Ответ: 4.

Пример 4. Сравните числа $sqrt{52}+sqrt{46}$ и 14. В ответе укажите номер правильного варианта.

1) $sqrt{52}+sqrt{46} textless 14$ 2) $sqrt{52}+sqrt{46}=14$ 3) $sqrt{52}+sqrt{46} textgreater 14$

Решение. Очевидно, что равенство между заданными числами невозможно. Предположим, что справедливо неравенство $sqrt{52}+sqrt{46} textgreater 14 .$ Возведём обе части неравенства в квадрат и проведём соответствующие преобразования:

${(sqrt{52}+sqrt{46})}^2 textgreater {14}^2 = textgreater {sqrt{52}}^2+2cdot sqrt{52}cdot sqrt{46}+{sqrt{46}}^2 textgreater 196 = textgreater 52+2cdot sqrt{52cdot 46}+46 textgreater 196$
$= textgreater 2cdot sqrt{2392} textgreater 98 = textgreater sqrt{2392} textgreater 49 = textgreater {sqrt{2392}}^2 textgreater {49}^2 = textgreater 2392 textgreater 2401.$

Полученное неравенство неверно, а это значит, что предположение неверно. Тогда верно неравенство $sqrt{52}+sqrt{46} textless 14$ .

Ответ: 1.

Пример 5. Укажите наименьшее из чисел. В ответе укажите номер правильного варианта.

1) $sqrt{35}$ 2) $2sqrt{7}$ 3) $6$ 4) $sqrt{6}+sqrt{7}$

Решение. Сравним сначала первые три числа, представив их в виде корней:

1) $sqrt{35}$ 2) $2sqrt{7}=sqrt{4}cdot sqrt{7}=sqrt{28}$ 3) $6=sqrt{36}$

Из этих чисел наименьшим является $sqrt{28}=2sqrt{7}$ . Осталось сравнить его с четвёртым значением.

$2sqrt{7}=sqrt{7}+sqrt{7} textgreater sqrt{6}+sqrt{7} .$

Результат очевиден. Наименьшим оказалось число под номером 4.

Ответ: 4.

Пример 6. Представьте выражение $frac{m^{-9}cdot m^3}{m^{-2}}$ в виде степени с основанием m. В ответе укажите номер правильного варианта.

1) $m^{-3}$ 2) $m^{-4}$ 3) $m^{-8}$ 4) $m^{-5}$

Решение. Используем свойства степеней:

$frac{m^{-9}cdot m^3}{m^{-2}}=frac{m^{-9+3}}{m^{-2}}=frac{m^{-6}}{m^{-2}}=m^{-6-(-2)}=m^{-6+2}=m^{-4} .$

Ответ: 2.

Пример 7. Вычислите $frac{7^6cdot {(7^{-9})}^2}{7^{-10}}$ . В ответе укажите номер правильного варианта.

1) $49$ 2) $-49$ 3) $frac{1}{49}$ 4) $-frac{1}{49}$

Решение. Используем свойства степеней:

$frac{7^6cdot {(7^{-9})}^2}{7^{-10}}=frac{7^6cdot 7^{-9cdot 2}}{7^{-10}}=frac{7^6cdot 7^{-18}}{7^{-10}}=frac{7^{6+(-18)}}{7^{-10}}=frac{7^{-12}}{7^{-10}}=7^{-12-(-10)}=7^{-12+10}=7^{-2}=frac{1}{7^2}=frac{1}{49} .$

Ответ: 3.

Пример 8. Какое из чисел $sqrt{0,25} , sqrt{2,5} , sqrt{2500}$ является иррациональным? В ответе укажите номер правильного варианта.

1) $sqrt{0,25}$ 2) $sqrt{2,5}$ 3) $sqrt{2500}$ 4) все числа иррациональны

Решение. Если в результате вычислений или преобразований всё равно остаётся корень, то число является иррациональным:

1) $sqrt{0,25}=sqrt{frac{25}{100}}=frac{sqrt{25}}{sqrt{100}}=frac{5}{10}=0,5$ (рациональное число)

2) $sqrt{2,5}=sqrt{2frac{5}{10}}=sqrt{frac{25}{10}}=frac{sqrt{25}}{sqrt{10}}=frac{5}{sqrt{10}}$ (иррациональное число)

3) $sqrt{2500}=50$ (рациональное число)

Ответ: 2.

Пример 9. Какое из числовых выражений является рациональным? В ответе укажите номер правильного варианта.

1) $sqrt{13}cdot sqrt{20}$ 2) $sqrt{18}-2sqrt{2}$ 3) $frac{sqrt{24}}{sqrt{8}}$ 4) $(sqrt{16}-sqrt{5})cdot (sqrt{16}+sqrt{5})$

Решение. Если в результате вычислений корень «исчезнет», то число является рациональным:

1) $sqrt{13}cdot sqrt{20}=sqrt{13}cdot sqrt{4cdot 5}=sqrt{13}cdot sqrt{4}cdot sqrt{5}=2sqrt{13cdot 5}=2sqrt{65}$ (иррациональное число)

2) $sqrt{18}-2sqrt{2}=sqrt{9cdot 2}-2sqrt{2}=3sqrt{2}-2sqrt{2}=sqrt{2}$ (иррациональное число)

3) $frac{sqrt{24}}{sqrt{8}}=sqrt{frac{24}{8}}=sqrt{3}$ (иррациональное число)

4) $left(sqrt{16}-sqrt{5}right)cdot left(sqrt{16}+sqrt{5}right)={sqrt{16}}^2-{sqrt{5}}^2=16-5=11$ (рациональное число)

Ответ: 4.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 8 ОГЭ по математике. Числа, вычисления и алгебраические выражения.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.01.2023

Источник

Другие вопросы по: Геометрия

Популярные вопросы

Теория к заданию №4

Разбор типовых вариантов задания №4 ОГЭ по математике

Первый вариант задания

Решение:

Второй вариант задания

Решение:

Третий вариант задания

Решение:

Четвертый вариант задания

Решение:

Пятый вариант задания (демонстрационный вариант ОГЭ 2017)

Решение:

Шестой вариант задания

Решение:

Седьмой вариант задания

Решение: