339306 * 1 = 339306
(триста тридцать девять тысяч триста шесть)
339306 * 2 = 678612
(шестьсот семьдесят восемь тысяч шестьсот двенадцать)
339306 * 3 = 1017918
(один миллион семнадцать тысяч девятьсот восемнадцать)
339306 * 4 = 1357224
(один миллион триста пятьдесят семь тысяч двести двадцать четыре)
339306 * 5 = 1696530
(один миллион шестьсот девяносто шесть тысяч пятьсот тридцать)
339306 * 6 = 2035836
(два миллиона тридцать пять тысяч восемьсот тридцать шесть)
339306 * 7 = 2375142
(два миллиона триста семьдесят пять тысяч сто сорок два)
339306 * 8 = 2714448
(два миллиона семьсот четырнадцать тысяч четыреста сорок восемь)
339306 * 9 = 3053754
(три миллиона пятьдесят три тысячи семьсот пятьдесят четыре)
339306 * 10 = 3393060
(три миллиона триста девяносто три тысячи шестьдесят)
339306 * 11 = 3732366
(три миллиона семьсот тридцать две тысячи триста шестьдесят шесть)
339306 * 12 = 4071672
(четыре миллиона семьдесят одна тысяча шестьсот семьдесят два)
339306 * 13 = 4410978
(четыре миллиона четыреста десять тысяч девятьсот семьдесят восемь)
339306 * 14 = 4750284
(четыре миллиона семьсот пятьдесят тысяч двести восемьдесят четыре)
339306 * 15 = 5089590
(пять миллионов восемьдесят девять тысяч пятьсот девяносто)
339306 * 16 = 5428896
(пять миллионов четыреста двадцать восемь тысяч восемьсот девяносто шесть)
339306 * 17 = 5768202
(пять миллионов семьсот шестьдесят восемь тысяч двести два)
339306 * 18 = 6107508
(шесть миллионов сто семь тысяч пятьсот восемь)
339306 * 19 = 6446814
(шесть миллионов четыреста сорок шесть тысяч восемьсот четырнадцать)
339306 * 20 = 6786120
(шесть миллионов семьсот восемьдесят шесть тысяч сто двадцать)
339306 * 21 = 7125426
(семь миллионов сто двадцать пять тысяч четыреста двадцать шесть)
339306 * 22 = 7464732
(семь миллионов четыреста шестьдесят четыре тысячи семьсот тридцать два)
339306 * 23 = 7804038
(семь миллионов восемьсот четыре тысячи тридцать восемь)
339306 * 24 = 8143344
(восемь миллионов сто сорок три тысячи триста сорок четыре)
339306 * 25 = 8482650
(восемь миллионов четыреста восемьдесят две тысячи шестьсот пятьдесят)
339306 * 26 = 8821956
(восемь миллионов восемьсот двадцать одна тысяча девятьсот пятьдесят шесть)
339306 * 27 = 9161262
(девять миллионов сто шестьдесят одна тысяча двести шестьдесят два)
339306 * 28 = 9500568
(девять миллионов пятьсот тысяч пятьсот шестьдесят восемь)
339306 * 29 = 9839874
(девять миллионов восемьсот тридцать девять тысяч восемьсот семьдесят четыре)
339306 * 30 = 10179180
(десять миллионов сто семьдесят девять тысяч сто восемьдесят)
339306 * 31 = 10518486
(десять миллионов пятьсот восемнадцать тысяч четыреста восемьдесят шесть)
339306 * 32 = 10857792
(десять миллионов восемьсот пятьдесят семь тысяч семьсот девяносто два)
339306 * 33 = 11197098
(одиннадцать миллионов сто девяносто семь тысяч девяносто восемь)
339306 * 34 = 11536404
(одиннадцать миллионов пятьсот тридцать шесть тысяч четыреста четыре)
339306 * 35 = 11875710
(одиннадцать миллионов восемьсот семьдесят пять тысяч семьсот десять)
339306 * 36 = 12215016
(двенадцать миллионов двести пятнадцать тысяч шестнадцать)
339306 * 37 = 12554322
(двенадцать миллионов пятьсот пятьдесят четыре тысячи триста двадцать два)
339306 * 38 = 12893628
(двенадцать миллионов восемьсот девяносто три тысячи шестьсот двадцать восемь)
339306 * 39 = 13232934
(тринадцать миллионов двести тридцать две тысячи девятьсот тридцать четыре)
339306 * 40 = 13572240
(тринадцать миллионов пятьсот семьдесят две тысячи двести сорок)
339306 * 41 = 13911546
(тринадцать миллионов девятьсот одиннадцать тысяч пятьсот сорок шесть)
339306 * 42 = 14250852
(четырнадцать миллионов двести пятьдесят тысяч восемьсот пятьдесят два)
339306 * 43 = 14590158
(четырнадцать миллионов пятьсот девяносто тысяч сто пятьдесят восемь)
339306 * 44 = 14929464
(четырнадцать миллионов девятьсот двадцать девять тысяч четыреста шестьдесят четыре)
339306 * 45 = 15268770
(пятнадцать миллионов двести шестьдесят восемь тысяч семьсот семьдесят)
339306 * 46 = 15608076
(пятнадцать миллионов шестьсот восемь тысяч семьдесят шесть)
339306 * 47 = 15947382
(пятнадцать миллионов девятьсот сорок семь тысяч триста восемьдесят два)
339306 * 48 = 16286688
(шестнадцать миллионов двести восемьдесят шесть тысяч шестьсот восемьдесят восемь)
339306 * 49 = 16625994
(шестнадцать миллионов шестьсот двадцать пять тысяч девятьсот девяносто четыре)
339306 * 50 = 16965300
(шестнадцать миллионов девятьсот шестьдесят пять тысяч триста)
339306 * 51 = 17304606
(семнадцать миллионов триста четыре тысячи шестьсот шесть)
339306 * 52 = 17643912
(семнадцать миллионов шестьсот сорок три тысячи девятьсот двенадцать)
339306 * 53 = 17983218
(семнадцать миллионов девятьсот восемьдесят три тысячи двести восемнадцать)
339306 * 54 = 18322524
(восемнадцать миллионов триста двадцать две тысячи пятьсот двадцать четыре)
339306 * 55 = 18661830
(восемнадцать миллионов шестьсот шестьдесят одна тысяча восемьсот тридцать)
339306 * 56 = 19001136
(девятнадцать миллионов одна тысяча сто тридцать шесть)
339306 * 57 = 19340442
(девятнадцать миллионов триста сорок тысяч четыреста сорок два)
339306 * 58 = 19679748
(девятнадцать миллионов шестьсот семьдесят девять тысяч семьсот сорок восемь)
339306 * 59 = 20019054
(двадцать миллионов девятнадцать тысяч пятьдесят четыре)
339306 * 60 = 20358360
(двадцать миллионов триста пятьдесят восемь тысяч триста шестьдесят)
339306 * 61 = 20697666
(двадцать миллионов шестьсот девяносто семь тысяч шестьсот шестьдесят шесть)
339306 * 62 = 21036972
(двадцать один миллион тридцать шесть тысяч девятьсот семьдесят два)
339306 * 63 = 21376278
(двадцать один миллион триста семьдесят шесть тысяч двести семьдесят восемь)
339306 * 64 = 21715584
(двадцать один миллион семьсот пятнадцать тысяч пятьсот восемьдесят четыре)
339306 * 65 = 22054890
(двадцать два миллиона пятьдесят четыре тысячи восемьсот девяносто)
339306 * 66 = 22394196
(двадцать два миллиона триста девяносто четыре тысячи сто девяносто шесть)
339306 * 67 = 22733502
(двадцать два миллиона семьсот тридцать три тысячи пятьсот два)
339306 * 68 = 23072808
(двадцать три миллиона семьдесят две тысячи восемьсот восемь)
339306 * 69 = 23412114
(двадцать три миллиона четыреста двенадцать тысяч сто четырнадцать)
339306 * 70 = 23751420
(двадцать три миллиона семьсот пятьдесят одна тысяча четыреста двадцать)
339306 * 71 = 24090726
(двадцать четыре миллиона девяносто тысяч семьсот двадцать шесть)
339306 * 72 = 24430032
(двадцать четыре миллиона четыреста тридцать тысяч тридцать два)
339306 * 73 = 24769338
(двадцать четыре миллиона семьсот шестьдесят девять тысяч триста тридцать восемь)
339306 * 74 = 25108644
(двадцать пять миллионов сто восемь тысяч шестьсот сорок четыре)
339306 * 75 = 25447950
(двадцать пять миллионов четыреста сорок семь тысяч девятьсот пятьдесят)
339306 * 76 = 25787256
(двадцать пять миллионов семьсот восемьдесят семь тысяч двести пятьдесят шесть)
339306 * 77 = 26126562
(двадцать шесть миллионов сто двадцать шесть тысяч пятьсот шестьдесят два)
339306 * 78 = 26465868
(двадцать шесть миллионов четыреста шестьдесят пять тысяч восемьсот шестьдесят восемь)
339306 * 79 = 26805174
(двадцать шесть миллионов восемьсот пять тысяч сто семьдесят четыре)
339306 * 80 = 27144480
(двадцать семь миллионов сто сорок четыре тысячи четыреста восемьдесят)
339306 * 81 = 27483786
(двадцать семь миллионов четыреста восемьдесят три тысячи семьсот восемьдесят шесть)
339306 * 82 = 27823092
(двадцать семь миллионов восемьсот двадцать три тысячи девяносто два)
339306 * 83 = 28162398
(двадцать восемь миллионов сто шестьдесят две тысячи триста девяносто восемь)
339306 * 84 = 28501704
(двадцать восемь миллионов пятьсот одна тысяча семьсот четыре)
339306 * 85 = 28841010
(двадцать восемь миллионов восемьсот сорок одна тысяча десять)
339306 * 86 = 29180316
(двадцать девять миллионов сто восемьдесят тысяч триста шестнадцать)
339306 * 87 = 29519622
(двадцать девять миллионов пятьсот девятнадцать тысяч шестьсот двадцать два)
339306 * 88 = 29858928
(двадцать девять миллионов восемьсот пятьдесят восемь тысяч девятьсот двадцать восемь)
339306 * 89 = 30198234
(тридцать миллионов сто девяносто восемь тысяч двести тридцать четыре)
339306 * 90 = 30537540
(тридцать миллионов пятьсот тридцать семь тысяч пятьсот сорок)
339306 * 91 = 30876846
(тридцать миллионов восемьсот семьдесят шесть тысяч восемьсот сорок шесть)
339306 * 92 = 31216152
(тридцать один миллион двести шестнадцать тысяч сто пятьдесят два)
339306 * 93 = 31555458
(тридцать один миллион пятьсот пятьдесят пять тысяч четыреста пятьдесят восемь)
339306 * 94 = 31894764
(тридцать один миллион восемьсот девяносто четыре тысячи семьсот шестьдесят четыре)
339306 * 95 = 32234070
(тридцать два миллиона двести тридцать четыре тысячи семьдесят)
339306 * 96 = 32573376
(тридцать два миллиона пятьсот семьдесят три тысячи триста семьдесят шесть)
339306 * 97 = 32912682
(тридцать два миллиона девятьсот двенадцать тысяч шестьсот восемьдесят два)
339306 * 98 = 33251988
(тридцать три миллиона двести пятьдесят одна тысяча девятьсот восемьдесят восемь)
339306 * 99 = 33591294
(тридцать три миллиона пятьсот девяносто одна тысяча двести девяносто четыре)
339306 * 100 = 33930600
(тридцать три миллиона девятьсот тридцать тысяч шестьсот)
Номер варианта сайта alexlarin.net:
Условие:
23 февраля в магазине «Все для мужчин» действует 20% скидка на одежду, 30% – на обувь и 40% – на аксессуары. При этом купить со скидкой можно не более двух товаров. Иван Иванович хочет приобрести рубашку по цене 1800 руб., туфли за 3600 руб. и запонки за 1000 руб. В каком случае Иван Иванович заплатит за свою покупку меньше всего:
1) если купит со скидкой рубашку и запонки, а туфли – без скидки;
2) если купит со скидкой рубашку и туфли, а запонки – без скидки;
3) если купит со скидкой туфли и запонки, а рубашку – без скидки?
В ответ запишите, сколько рублей заплатит Иван Иванович за покупку в этом случае.
Решение:
Разберем все три варианта и сравним в итоге полученную общую стоимость покупок:
1) Если купит со скидкой рубашку и запонки, а туфли — без скидки, общая стоимость будет вычисляться таким образом : (1800*0,8+1000*0,6+3600=5640) рублей .
2) Если купит со скидкой рубашку и туфли, а запонки – без скидки, общая стоимость будет вычисляться таким образом: (1800*0,8+3600*0,7+1000=4960) рублей.
3) Если купит со скидкой туфли и запонки, а рубашку – без скидки, общая стоимость будет вычисляться таким образом: (3600*0,7+1000*0,6+1800=4920) рублей.
Сравнив итоговую стоимость покупок во всех трех вариантах, видим, что меньше всего Иван Иванович заплатит в третьем случае.
Ответ: 4920
13*2=26 км- проехал первый за 2 часа
48-26=22 км — проехал второй
22/2=11 км/час — скорость второго
С этим файлом связано 5 файл(ов). Среди них: 6_klass._instrumentalnyy_kontsert.docx, konspekt_uroka_dlya_konkursa.docx, 00071db7-da699630.ppt, pdd._klassnyy_chas_dlya_uch-sya_5-8_kl.doc, urok_muzyki_v_6_klasse_simfonicheskoe_razvitie_muzykalnyh_obrazo.
Показать все связанные файлы
Подборка по базе: Практическое задание 5 Введение в специальность Закирова.docx, Макроэкономика Практическое задание 4-5_Голосова И.С..docx, Домашнее задание на 26.docx, Практическое задание 2. Кисенкова К.А.docx, Практическое задание № 1_ПМ_магистры 2.doc, Теоретические и методические основы физического воспитания и раз, титул практическое задание.docx, ГОТОВО Задание к лекции 2 психология.docx, Практическое задание 1.docx, практическое задание 4.docx
1. Задание 1 № 407953
Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
| Ширина шины (мм) | Диаметр диска (дюймы) | ||
| 13 | 14 | 15 | |
| 165 | 165/70 | 165/65 | — |
| 175 | 175/65 | 175/65; 175/60 | — |
| 185 | 185/65; 185/60 | 185/60 | 185/55 |
| 195 | 195/60 | 195/55 | 195/55; 195/50 |
Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 15 дюймам? Ответ дайте в миллиметрах.
 |  |
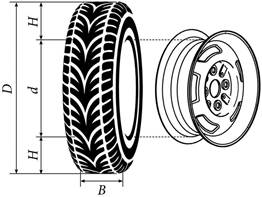| Рис. 1 | Рис. 2 |
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке 2). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр на рисунке 2) к ширине шины, то есть 
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 165/70 R13.
2. Задание 2 №
407955
На сколько миллиметров радиус колеса с шиной маркировки 205/55 R14 больше, чем радиус колеса с шиной маркировки 165/65 R14?
3. Задание 3 №
408171
На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 195/50 R15?
4. Задание 4 №
408172
Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
5. Задание 5 №
408173
На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 175/60 R14? Результат округлите до десятых.
6. Задание 6 №
348647
Найдите значение выражения 
.
7. Задание 7 №
339306
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.
Какое из следующих утверждений относительно этих чисел является верным?
1) a3>0
2) a − b > 0
3) ab < 1
4) a + b > 1
8. Задание 8 №
311383
Найдите значение выражения 
при 
9. Задание 9 №
311755
Решите уравнение 
10. Задание 10 №
132730
Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет.
11. Задание 11 №
193093
На одном из рисунков изображен график функции 
. Укажите номер этого рисунка.
| 1) | 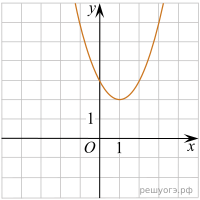 | 2) |  |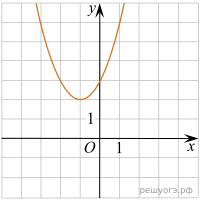
| 3) | 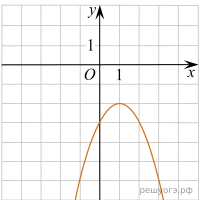 | 4) |  |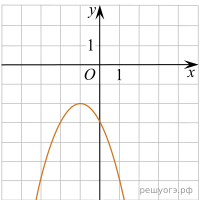
12. Задание 12 № 46
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле 
, где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
13. Задание 13 №
351881
Решите неравенство 
1) [-8;8]
2)
3) нет решений
4)
14. Задание 14 №
393958
Компания «Альфа» начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10 000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?
15. Задание 15 №
322819
Катеты прямоугольного треугольника равны 35 и 120. Найдите высоту, проведенную к гипотенузе.
16. Задание 16 №
356359
Радиус вписанной в квадрат окружности равен 
Найдите радиус окружности, описанной около этого квадрата.
17. Задание 17 №
169863
Периметр квадрата равен 40. Найдите площадь квадрата.
18. Задание 18 №
340589
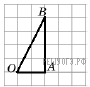Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
19. Задание 19 №
67
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Задание 20 №
311582
Упростите выражение: 
.
21. Задание 21 №
338961
Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую — со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
22. Задание 22 №
338253
Постройте график функции 
и определите, при каких значениях m прямая 
имеет с графиком ровно три общие точки.
23. Задание 23 №
311706
Высота треугольника разбивает его основание на два отрезка с длинами 8 и 9. Найдите длину этой высоты, если известно, что другая высота треугольника делит ее пополам.
24. Задание 24 №
333026
Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции.
25. Задание 25 №
311252
Стороны AC, AB, BC треугольника ABC равны 
соответственно. Точка K расположена вне треугольника ABC, причем отрезок KC пересекает отрезок AB в точке, отличной от 
Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если 
Ключ
| № п/п | № задания | Ответ |
| 1 | 407953 | 185 |
| 2 | 407955 | 5,5 |
| 3 | 408171 | 14,8 |
| 4 | 408172 | 561,2 |
| 5 | 408173 | 0,8 |
| 6 | 348647 | 6 |
| 7 | 339306 | 3 |
| 8 | 311383 | 16 |
| 9 | 311755 | -20 |
| 10 | 132730 | 0,85 |
| 11 | 193093 | 1 |
| 12 | 46 | 2,25 |
| 13 | 351881 | 2 |
| 14 | 393958 | 35000 |
| 15 | 322819 | 33,6 |
| 16 | 356359 | 4 |
| 17 | 169863 | 100 |
| 18 | 340589 | 2 |
| 19 | 67 | 12 |
| 20 | 311582 | −3. |
| 21 | 338961 | 61,6. |
| 22 | 338253 | −1; 0,5625. |
| 23 | 311706 | 12. |
| 24 | 311252 |  |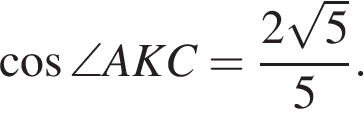
ОГЭ математика 2023. Разбор варианта Алекса Ларина № 332.
Задания 1-5
В горных районах, особенно в южных широтах с влажным климатом, земледельцы на склонах гор устраивают террасы (см. рис. выше). Земледельческие террасы — это горизонтальные площадки, напоминающие ступени. Во время дождя вода стекает с верхних террас вниз по специальным каналам. Поэтому почва на террасах не размывается и урожай не страдает. Медленный сток воды с вершины склона вниз с террасы на террасу позволяет выращивать даже влаголюбивые культуры. В Юго-Восточной Азии террасное земледелие широко применяется для производства риса, а в Средиземноморье — для выращивания винограда и оливковых деревьев. Возделывание культур на террасах повышает урожайность, но требует тяжёлого ручного труда.
Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка равна 40 м, а верхняя точка находится на высоте 12 м от подножия.
1. Земледелец на расчищенном склоне холма (ещё не террасированном) выращивал мускатный орех. Какова была площадь (в м2), отведённая под посевы?
2. Затем земледелец решил устроить террасы на своём участке (см. рисунок ниже), чтобы выращивать рис, пшено или кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла наклона, умноженный на 100%). Сколько процентов составляет уклон? Ответ округлите до десятых.
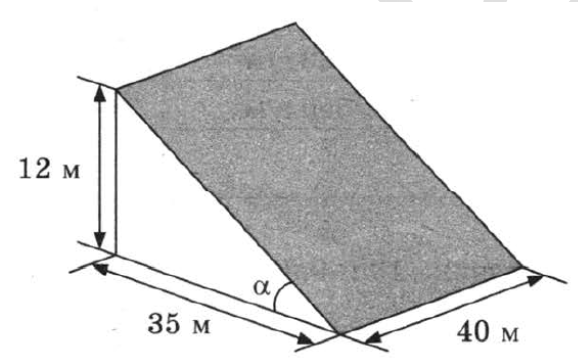
3. На сколько процентов сократилась посевная площадь после того, как земледелец устроил террасы? Ответ округлите до десятых.
4. Земледелец получает 650 г бурого риса с одного квадратного метра засеянной площади. При шлифовке из бурого риса получается белый рис, но при этом теряется 16% массы. Сколько килограммов белого риса получит земледелец со всего своего участка?
5. В таблице дана урожайность культур, которые может засеять земледелец на своём террасированном участке. За год обычно собирается два урожая: летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.
| Урожай | Урожайность риса (г/м2) | Урожайность кукурузы (г/м2) | Урожайность пшена (г/м2) |
|---|---|---|---|
| Первый (июнь) | |||
| Второй (сентябрь) |
Ответ: 1) 1480; 2) 34,3; 3) 5,4; 4) 764,4; 5) 1960
Скрыть
1.
$$S_{посевов}=АВcdot AD$$
$$Delta ABC$$ прямоугольный
по т. Пифагора $$АВ² = АС² + ВС²$$
$$АВ² = 12² + 35²$$
$$АВ² = 144 + 1225$$
$$АВ² = 1369$$
$$АВ = 37$$
$$S_{посевов}=АВcdot AD=37cdot40=1480$$
2.
Тангенс угла = отношение противолежащего катета к прилежащему
Тангенс угла склона $$= frac{12}{35}approx0,343$$
Угол склона = Тангенс угла склона $$cdot$$ 100% $$= 0,343cdot100 = 34,3$$
3.
$$S_{посевов}=АВcdot AD$$
$$Delta ABC$$ прямоугольный
по т. Пифагора $$АВ² = АС² + ВС²$$
$$АВ² = 12² + 35²$$
$$АВ² = 144 + 1225$$
$$АВ² = 1369$$
$$АВ = 37$$
$$S_{посевов}=АВcdot AD=37cdot40=1480$$
Если земледелец устроил террасы, $$S_{посевов}=АСcdot AD=35cdot40=1400$$
1480 — 100%
1400 — x%
$$x=1400cdotfrac{100}{1480}$$
$$xapprox94,6$$
100% — 94,6% = 5,4%
4.
Если земледелец устроил террасы, $$S_{посевов}=АСcdot AD=35cdot40=1400$$
Получит бурого риса $$1400cdot650$$ гр $$=910000$$ гр $$=910$$ кг
Теряется при шлифовке 16%, значит останется (100%-16%=84%) риса
910 — 100%
х — 84%
$$х=910cdotfrac{84}{100}$$
$$х=764,4$$
5.
Если земледелец устроил террасы, $$S_{посевов}=АСcdot AD=35cdot40=1400$$
Возможны варианты:
Рис + Рис $$1400cdot(650+550)$$
Рис + Пшено $$1400cdot(650+600)$$
Кукуруза + Рис $$1400cdot(800+550)$$
Кукуруза + Пшено $$1400cdot(800+600)$$
Суммируем числа в скобках. Наибольшее получается Кукуруза + Рис
Кукуруза + Рис $$1400cdot(800+600)=1960000$$ гр $$=1960$$ кг
Подписаться
В данном разделе представлены все необходимые материалы для подготовки к ОГЭ по математике 2022. Мы предоставляем как разобранные варианты с теорией по заданиям, так и тестовые варианты для самоподготовки. Пройдя курс подготовки к ОГЭ на нашем сайте, вы уверенно напишете экзамен в 9 классе в 2022 году!
Описание презентации по отдельным слайдам:
-
1 слайд
Решение задач ОГЭ и ЕГЭ по математике Булгак Ирина Викторовна
-
2 слайд
О А В С К Проведём диаметр АВ. <А – вписанный опирается на дугу СВ. <К – вписанный и опирается на ту же дугу, следовательно <K=<A. Рассмотрим треугольник АВС <C=90 ⁰. Sin<A = СВ/АВ. АВ=2R, значит 2R=CB/sin<K или R=CB/2(sin<K). Scbk=1/2 * CK*KB * sin<K, отсюда sin<K = 2S/(CK*KB), подставим в формулу для вычисления радиуса описанной окружности и получим abc R=4S , где a,b,c – стороны треугольника вписанного в окружность, а S – его площадь
-
3 слайд
Четырехугольник ABCD со сторонами АВ=19, и CD=22, вписан в окружность. Диагонали AC и BD пересекаются в точке К, причем угол АКВ = 60 . Найдите радиус окружности описанной около этого четырехугольника. А В С D М К 1 3 2 4
-
-
5 слайд
В треугольнике АВС биссектриса угла А делит высоту, проведённую из вершины В в отношении 5:4, считая от точки В. Найдите радиус окружности, описанной около треугольника АВС, если ВС = 6.
-
-
7 слайд
С В А Н М Ф Е Д Р
Краткое описание документа:
Решение 26 заданий ОГЭ по математике
- Сейчас обучается 694 человека из 75 регионов
- Сейчас обучается 864 человека из 78 регионов
- Сейчас обучается 46 человек из 22 регионов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 837 874 материала в базе
Другие материалы
Рейтинг:
5 из 5
- 29.03.2015
- 9065
- 8
Рейтинг:
4 из 5
- 29.03.2015
- 2312
- 46
Рейтинг:
2 из 5
- 29.03.2015
- 5440
- 21
-
Настоящий материал опубликован пользователем Булгак Ирина Викторовна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Пожаловаться на материал
-
Автор материала
- На сайте: 7 лет и 1 месяц
- Подписчики: 0
- Всего просмотров: 17199
- Всего материалов:
2
- ОГЭ по математике
Материалы для отработки задания №6 ОГЭ по математике — числа и вычисления.
Типы заданий:
→ Действия с обыкновенными дробями.
→ Действия с десятичными дробями.
→ Степени.
→ Сравнение чисел.
| Теория для задания 6 Автор: Е. А. Ширяева → скачать |
| Практика для задания 6 Автор: Е. А. Ширяева → скачать |
| Варианты заданий 6 с ответами Источник: https://math100.ru → скачать |
| Карточки для отработки задания №6 с ответами → скачать
|
Решение типовых задач №6 на ОГЭ по математике
Связанные страницы:
Тест «Виды потребления»
Проверочная работа по обществознанию.
Календарь диктантов 2022
Общие материалы | Вчера, 20:46
Расписание Всероссийских диктантов на 2022 год.
Задание 7 № 339306
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.
Какое из следующих утверждений относительно этих чисел является верным?
1) a3>0
2) a − b > 0
3) ab 4) a + b > 1
Спрятать решение
Решение.
Заметим, что 
откуда 
Таким образом, верным является утверждение 
Правильный ответ указан под номером: 3.
Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел., 1.4 Точки на координатной прямой.