Не могу найти по номеру выполняемое многоразовое задание. Да и любые другие по номеру не найти). Пробовал произвольно выбранные задания вызвать по номеру — и ничего!)
Обсуждение
gimmegun
12 Окт 2017 г, в 09:01
редактир. 12 Окт 2017 г, в 09:06
Одной из причин может быть выбор фильтров
По спискам
и
По типу
при поиске.
Если это (эти) задание у Вас в Избранном, то должны быть выбраны фильтры
Избранное
и
Все.
Если выбраны
Все
и
Все
, то задание не покажут.
Если задание не в Избранном, то соответственно наоборот — должны быть выбраны фильтры
Все
и
Все
.
Другой причиной может быть то, что задание выключено или забанено.
Не годится…(( Принцип, который вы описали, до меня добрел)), я им воспользовался, результат=0. Сейчас вот еще на всякий случай попробовал. Взял номер первого попавшегося задания (оно у меня никак не отмечено), выбрал «Все», ввел номер, и тишина…
Для обсуждения вопроса/идеи необходима регистрация.
Сложность: 
Среднее время решения: 40 сек.
ОГЭ по математике 2022 задание 7: номер 18 | Между какими целыми числами з…
25
Между какими целыми числами заключено число $√ {117}$? $1$) $116$ и $118$ $2$) $10$ и $11$ $3$) $11$ и $17$ $4$) $9$ и $10$
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
На координатной прямой отмечена точка $A$ (см. рис.). Известно, что она соответствует одному из четырёх указанных ниже чисел. Какому из чисел соответствует точка $A$?
- $√ {2}$
- $√ {6}$
- $√ {14}$
…
Какое из следующих неравенств не следует из неравенства $-y>x+z$?
- $x+y+z
- $x-y+z
- $x
- $x+y
На координатной прямой отмечены числа $p$ и $n$ (см. рис.). Какое из приведённых утверждений неверно?
- $n+p
- $p-n>0$
- $pn>0$
- $p^2n
Какое из приведённых ниже неравенств является верным при любых значениях $a$ и $b$, удовлетворяющих условию $b
Зло — нормативно-оценочная категория нравственного сознания, противоположная понятию добра, обобщённо обозначает нравственно-отрицательное и предосудительное в поступках и мотивах людей и в явлениях действительности. Используется для характеристики, понимания и оценки вреда, ущерба, страданий и так далее
Вставить прилагательное?
Огнем пылает золотая листва осени.
1. <u>Пусть </u>светит(сказуемое, пусть входит в повелит. накл) месяй — ночь темна.(А.Блок)
Никак . новые ботинки старые туфли комнатные тапочки шумные дети знакомые люди
Комната — это словарное слово, надо запомнить или смотреть в словарь.
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
2X^2-3X-X^2-5+2X-X^2+10=-X+5Значение многочлена равно 1, если-Х +5=1Х=4Ответ Х=4 0,3Х ^3-X^2+X+3X^2+0,7X^3=X+0,07X+0,07=1X=0,93Ответ 243Пусть берется Х кг оловаТогда цинка берется 2Х кгмеди 17Х кгт.к. получается 400 кг бронзы сост уравнениеХ +2Х +17=400Х=20Олова -20 кгЦинка- 20 х 2=40 кгМеди 17 х 20=340 кг 2) Периметр участка=60 м=6000 смПериметр треугольника равен 3+4+5=12 см Следовательно масштаб равен 12:6000=1:500 Разделили на 12Если что пиши
Автор:
Баранов М.Т., Ладыженская Т.А., Тростенцова Л.А.
С этим файлом связано 2 файл(ов). Среди них: Решу_ВПР_5_klass.docx, 1.02 Алгебра.pdf.
Показать все связанные файлы
Подборка по базе: Раздел 1. Уравнения и неравенства (с верными ответами).doc, Раздел 1. Уравнения и неравенства (с верными ответами).doc, Проблема общественного неравенства в глобальных и российский изм, 5кл.Появление неравенства. Практика.docx, Задание 2 Неравенства Григорьева.docx, простые неравенства.docx, СР_Равносильные уравнения и неравенства.doc, 21Равенства и неравенства.docx, УМК Понятие социального неравенства. Его виды.pdf, УМК Понятие социального неравенства. Его виды.docx
Решение.
Переведём обыкновенные дроби в десятичные с точностью до второго знака после запятой и сравним с числами 0,5 и 0,6:
Тк искомая точка лежит между числами 0,5 и 0,6, ближе к числу 0,6, получаем, что это число 1323
6. Задание 7 №
317102
На координатной прямой точками A, B, C и D отмечены числа 0,098; −0,02; 0,09; 0,11. Какой точкой изображается число 0,09?
В ответе укажите номер правильного варианта.
1) A 2) B 3) C 4) D
Решение. Заметим, что 
Следовательно, числу 0,09 соответствует вторая слева точка то есть точка B.
Правильный ответ указан под номером: 2.
7. Задание 7 №
322293
На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу 
Какая это точка 
В ответе укажите номер правильного варианта.
1) точка A 2) точка B 3) точка C 4) точка D
Решение. Возведём в квадрат числа 
7, 8, 9:
Число 53 лежит между числами 49 и 64 и находится ближе к числу 49, поэтому 
соответствует точке A.
8. Задание 7 №
337346
Известно, что число m отрицательное. На каком из рисунков точки с координатами 
расположены на координатной прямой в правильном порядке?
1) | 2) |
3) | 4) |
В ответе укажите номер правильного варианта.
1) 1 2) 2 3) 3 4) 4
Решение. Поскольку 
, имеем: 
Поскольку 
имеем: 
Правильный ответ указан под номером: 1.
9. Задание 7 №
340578
На координатной прямой отмечена точка А.
Известно, что она соответствует одному из четырех указанных ниже чисел. Какому из чисел соответствует точка А?
1) 
2) 
3) 0,6 4) 4
Решение. Заметим, что 
Сравним каждое из приведённых чисел с пятёью и десятью:
1) 
2)В силу цепочки неравенств: 
Таким образом, 
3) 
4) 
Правильный ответ указан под номером: 2.
10. Задание 7 №
341398
На координатной прямой отмечено число a.
Какое из утверждений относительно этого числа является верным?
1) a − 8 > 0 2) 7 − a < 0 3) a − 3 > 0 4) 2 − a > 0
Решение. Заметим, что 
, тогда:
1) 
Неверно.
2) 
Неверно.
3) 
Верно.
4) 
Неверно.
Ответ: 3.
11. Задание 7 №
384400
На координатной прямой отмечены точки A, B, C и D. Одна из них соответствует числу 
. Какая это точка?
| 1) А | 2) B | 3) C | 4) D |
Решение. Возведем все числа в квадрат:
.
92 = 81. 102 = 100. 112 = 121.
Число 85 ближе всего к числу 81, таким образом, искомому числу соответствует точка А. Ответ: 1.
Выбор верного или неверного утверждения
1. Задание 7 №
311305
Известно, что a>b>c Какое из следующих чисел отрицательно?
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4) 
Решение. 1) 
, так как по условию 
2) 
, тк по условию 
3) 
, так как по условию 
4) 
, так как . Таким образом, c-b — отрицательное число.
Правильный ответ указан под номером 4.
2. Задание 7 №
311420
Какое из следующих чисел заключено между числами 16 и 14&
В ответе укажите номер правильного варианта.
1) 0,1 2) 0,2 3) 0,3 4) 0,4
Решение. Заметим, что 
а 
Из предположенных вариантов ответа только число 0,2 лежит между ними.
Правильный указан под номером 2.
3. Задание 7 №
314802
На координатной прямой отмечены числа a и b. Какое из следующих утверждений неверно? 
1) 
2) 
3) 
4) 
Решение. Заметим, что 
и 
, и проверим все варианты ответа:
1) 
— верно, поскольку каждое слагаемое отрицательно.
2) 
— верно.
3) 
— верно, поскольку 
, а 
4) 
— неверно.
Неверным является утверждение 4.
4. Задание 7 №
316987
Какое из приведенных ниже неравенств является верным при любых значениях a и b, удовлетворяющих условию a > b?
В ответе укажите номер правильного варианта.
1) b − a < −2 2) a − b > −1 3) a − b < 3 4) b − a > −3
Решение 
Правильный ответ указан под номером: 2.
5. Задание 7 №
317041
На координатной прямой отмечено число a.
Из следующих утверждений выберите верное:
В ответе укажите номер правильного варианта.
1) (a − 6)2 > 1 2) (a − 7)2 > 1 3) a2 > 36 4) a2 > 49
Решение. Рассмотрим все варианты ответа:
1) 
2) 
3) 
4) 
Поскольку число число a лежит между числами 6 и 7, верным является только неравенство 
Правильный ответ указан под номером 3.
6. Задание 7 №
317179
На координатной прямой отмечены числа x и y. Какое из следующих утверждений об этих числах верно?
В ответе укажите номер правильного варианта.
1) 
и 
2) 
и 
3) и 4) и
Решение. Заметим, что 
Число x располагается ближе к нулю, чем число y, следовательно, 
Правильный ответ указан под номером: 1.
7. Задание 7 №
317223
Какому промежутку принадлежит число 
В ответе укажите номер правильного варианта.
1) [4; 5] 2) [5; 6] 3) [6; 7] 4) [7; 8]
Решение.
Правильный ответ указан под номером 4.
8. Задание 7 №
322419
На координатной прямой отмечены числа p, q и r.
Какая из разностей p − r, p − q, r − q отрицательна?
В ответе укажите номер правильного варианта.
1) p − r 2) p − q 3) r − q 4) ни одна из них
Решение. Заметим, что r < q < p. Разность отрицательна только в том случае, когда вычитаемое больше уменьшаемого. Это верно только для разности r − q.
Правильный ответ указан под номером: 3.
9. Задание 7 №
322422
На координатной прямой отмечены числа a, b и c. 
Какая из разностей a − b, a − c, c − b положительна?
В ответе укажите номер правильного варианта.
1) a − b 2) a − c 3) c − b 4) ни одна из них
Решение. Заметим, что a < b < c. Разность положительная только в том случае, когда уменьшаемое больше вычитаемого. Это верно только для разности c − b.
Правильный ответ указан под номером: 3.
10. Задание 7 №
337484
Значение какого из данных выражений положительно, если известно, что x > 0, y < 0?
В ответе укажите номер правильного варианта.
1) xy 2) (x − y)y 3) (y − x)y 4) (y − x)x
Решение. Заметим, что 
Имеем: 1) 
2) 
3) 
4) 
.
Правильный ответ указан под номером: 3.
1. Задание 1 № 406563
Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета.
Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответе нужно записать
число 51118).
| Мобильный интернет | 2,5 Гб | 3 Гб | 3,25 Гб | 1 Гб |
| Номер месяца |
На рисунке точками показано количество минут исходящих вызовов и трафик мобильного интернета в гигабайтах, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2019 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.
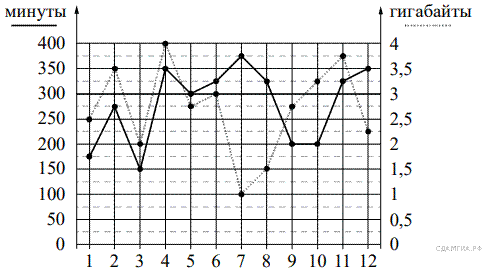
В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляла 350 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:
• пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
• пакет интернета, включающий 3 гигабайта мобильного интернета;
• пакет СМС, включающий 120 СМС в месяц;
• безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и СМС сверх пакета тарифа указана в таблице.
| Исходящие вызовы | 3 руб./мин. |
| Мобильный интернет (пакет) | 90 руб. за 0,5 Гб |
| СМС | 2 руб./шт. |
Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 110 СМС.
Решение.
Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года.
Из рисунка видно, что 2,5 Гб было потрачено в первый месяц, 3 Гб — потрачено в шестой, 3,25 Гб — в десятый, 1 Гб — в седьмой.
Ответ: 16107.
2. Задание 2 № 406675
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику израсходованных минут и гигабайтов.
| ПЕРИОДЫ | ХАРАКТЕРИСТИКИ | |
| А) январь−февраль Б) февраль−март В) август–сентябрь Г) ноябрь–декабрь | 1) Расход минут увеличился, а расход гигабайтов уменьшился. 2) Расход гигабайтов увеличился, а расход минут уменьшился. 3) Расход минут увеличился, и расход гигабайтов увеличился. 4) Расход минут уменьшился, и расход гигабайтов уменьшился. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Решение.
Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года, а сплошной линей — количество минут исходящих вызовов.
За период январь−февраль расход минут увеличился, и расход гигабайтов увеличился.
За период февраль−март расход минут уменьшился, и расход гигабайтов уменьшился.
За период август–сентябрь расход гигабайтов увеличился, а расход минут уменьшился.
За период ноябрь–декабрь расход минут увеличился, а расход гигабайтов уменьшился.
Таким образом, получается соответствие: А — 3, Б — 4, В — 2, Г — 1.
Ответ: 3421.
3. Задание 3 № 406564
Сколько рублей потратил абонент на услуги связи в июне?
Решение.
По рисунку видно, что за июнь абонент потратил 3 Гб интернета, 325 минут исходящих вызовов, и в условии сказано, что за год отправил 110 СМС.
Количество потраченного интернета и СМС не превысило это количество в пакете тарифа, а исходящих вызовов сверх пакета было потрачено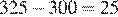 
минут.
Вычислим стоимость услуг связи, потраченных абонентом в июне:
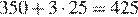рублей.
Ответ: 425.
4. Задание 4 № 406565
Какое наименьшее количество минут исходящих вызовов за месяц было в 2019 году?
Решение.
Сплошной линей на графике показано количество минут исходящих вызовов, израсходованных за каждый месяц года.
Из рисунка видно, что в третьем месяце было потрачено 150 минут, что является наименьшим количеством за 2019 год.
Ответ: 150.
5. Задание 5 № 367694
Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
| Место | Цена земли (млн руб.) | Цена строительства (млн руб.) | Длина коммуникаций (м) | Стоимость аренды за 1 м2 (руб./месяц) |
| Центр | 64,4 | |||
| Окраина | 11,2 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
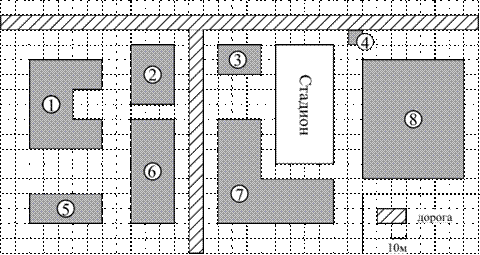
На плане (см. рисунок) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.
Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м2. А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.
Решение.
Стоимость постройки ТРК в центре города равна
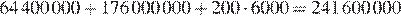рублей.
Стоимость постройки ТРК на окраине города равна
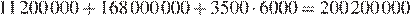рублей.
Разница в стоимости составляет
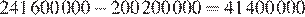рублей.
Разница в стоимости аренды составляет
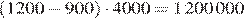рублей.
Значит, более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций через 34,5 месяцев. Округляя, получаем ответ — 35 месяцев.
Ответ: 35.
6. Задание 6 № 203743
Запишите в ответе номера выражений, значения которых положительны.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
Решение.
Найдём значения выражений:
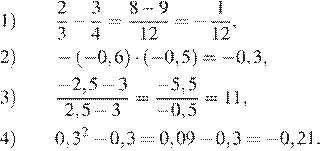
Таким образом, искомое выражение указано под номером 3.
7. Задание 7 № 314800
На координатной прямой отмечены числа а и b. Какое из следующих утверждений неверно?
В ответе укажите номер правильного варианта.
1) 
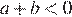
2) 
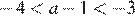
3) 
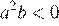
4) 
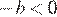
Решение.
Заметим, что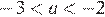 
и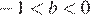 
, и проверим все варианты ответа:
1) 
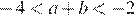, значит, 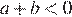— верно.
2) 
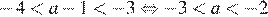— верно.
3) 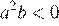— верно, поскольку 
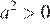, а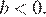 
4) 
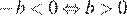— неверно.
Неверным является утверждение 4.
Примечание.
Нетрудно заметить, что справедливо неравенство: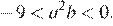 
8. Задание 8 № 341704
Найдите значение выражения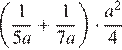 
при a = 7,7.
Решение.
Упростим выражение:
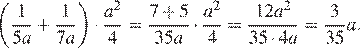
Подставим в полученное выражение значение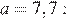 
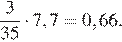
Ответ: 0,66.
9. Задание 9 № 338610
Решите уравнение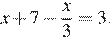 
Решение.
Последовательно получаем:
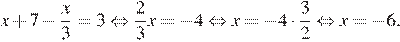
Ответ: −6.
10. Задание 10 № 325541
Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся.
Решение.
Вероятность того, что стрелок промахнётся равна 1 − 0,8 = 0,2. Вероятность того, что стрелок первые два раза попал по мишеням равна 0,82 = 0,64. Откуда, вероятность события, при котором стрелок сначала два раза попадает в мишени, а третий раз промахивается равна 0,64 · 0,2 = 0,128.
Ответ: 0,128.
11. Задание 11 № 193089
Найдите значение 
по графику функции 
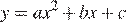, изображенному на рисунке.
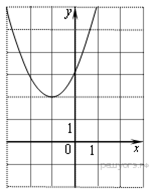
Решение.
Абсцисса вершины параболы равна −1, поэтому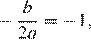 
откуда 
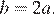Парабола пересекает ось ординат в точке с ординатой 3, поэтому 
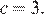Тем самым, уравнение параболы принимает вид 
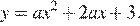Поскольку парабола проходит через точку (−1; 2), имеем:
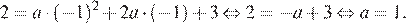
Верный ответ указан под номером 2.
Ответ: 2.
12. Задание 12 № 338396
Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.
Решение.
Найдем расстояние, на котором находится наблюдатель от места удара молнии:
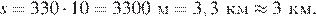
Ответ: 3.
13. Задание 13 № 311312
Решите неравенство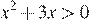 
.
В ответе укажите номер правильного варианта.
1) 
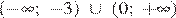
2) 
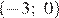
3) 
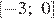
4) 
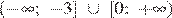
Решение.
Решим данное неравенство:
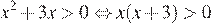. Произведение двух сомножителей будет больше нуля, если его сомножители имеют одинаковый знак.
В данном случае это выполняется при следующих значениях 
:
1) 
;
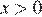2) 
;
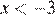Решением неравенства будет являться объединение этих промежутков: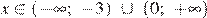 
, что соответствует первому варианту ответа.
Ответ: 1
14. Задание 14 № 394426
Давление воздуха под колоколом равно 625 мм ртутного столба. Каждую минуту насос откачивает из-под колокола 20% находящегося там воздуха. Определите давление (в мм рт. ст.) через 5 минут после начала работы насоса.
Решение.
Через минуту давление воздуха (в мм рт. ст.) под колоколом станет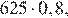 
через две минуты — 
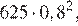…, через 5 минут давление станет 
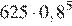или
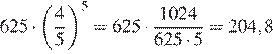мм рт. ст.
Ответ: 204,8.
15. Задание 15 № 348371
Высота BH ромба ABCD делит его сторону AD на отрезки AH = 44 и HD = 11. Найдите площадь ромба.
Решение.
Заметим, что сторона ромба AB = AD = AH + HD = 44 + 11 = 55.
Из прямоугольного треугольника ABH найдем BH по теореме Пифагора:
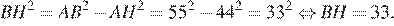
Площадь ромба можно найти как произведение основания на высоту:
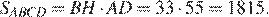
Ответ: 1815.
16. Задание 16 № 339975
Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Решение.
Радиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника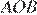 
по теореме Пифагора найдём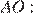 
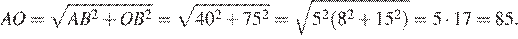
Найдём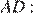 
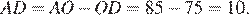
Ответ: 10.
17. Задание 17 № 324017
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Решение.
Проведём построение и введём обозначения, как показано на рисунке. Учитывая, что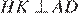 
и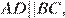 
получаем 
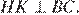Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольник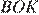и 
и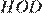 
, они прямоугольные,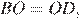 
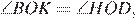следовательно, треугольник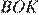и 
и 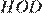равны, откуда 
то есть высота 
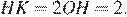Найдём площадь ромба как произведение стороны на высоту:
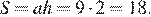
Ответ: 18.
18. Задание 18 № 311485
На квадратной сетке изображён угол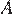 
. Найдите 
.
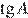Решение.
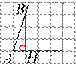
Опустим перпендикуляр BH. Треугольник ABH — прямоугольный. Таким образом,
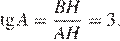
Ответ: 3.
19. Задание 19 № 341676
Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
1) «Треугольника со сторонами 1, 2, 4 не существует» — верно, большая сторона треугольника должна быть меньше суммы двух других.
2) «Смежные углы равны» — неверно, смежные углы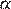 
и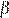 
связаны соотношением: 
.
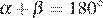3) «Все диаметры окружности равны между собой» — верно.
Ответ: 13.
20. Задание 20 № 311591
Решите уравнение: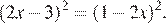 
Решение.
Перенесем все члены влево и применим формулу разности квадратов:
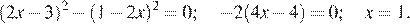
Другой способ. Раскроем скобки, пользуясь формулой квадрата разности:
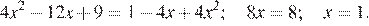
Ответ: 1.
21. Задание 21 № 314507
Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.
Решение.
Пусть скорость пешехода — x км/ч, 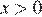, тогда скорость велосипедиста равна (x + 11) км/ч.
Составим таблицу по данным задачи:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| Пешеход | |  | |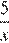
| Велосипедист |  |  |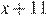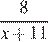
Так как по пути велосипедист сделал остановку на 
ч., составим уравнение:
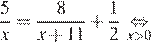
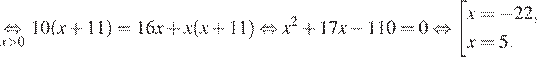
Корень −22 не подходит нам по условию задачи. Скорость пешехода равна 5 км/ч.
Ответ: 5 км/ч.
22. Задание 22 № 353274
Постройте график функции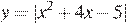 
. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Решение.
График данной функции — это график параболы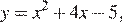 
отрицательная часть которого отражена относительно оси 
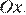Этот график изображён на рисунке:
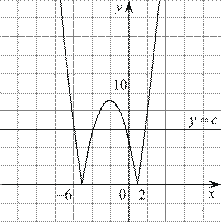
Прямая, параллельная оси абсцисс задаётся формулой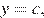 
где 
— постоянная. Из графика видно, что прямая 
может иметь с графиком функции не более четырёх общих точек.
Ответ: 4.
23. Задание 23 № 333321
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56 .
Решение.
Углы 
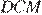и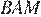 
равны как накрест лежащие, углы 
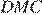и 
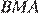равны как вертикальные, следовательно, треугольник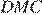и и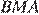 
подобны по двум углам.
Значит,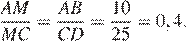 
Следовательно,
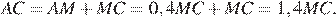
Откуда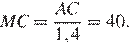 
Ответ: 40.
24. Задание 24 № 349626
Окружности с центрами в точках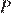 
и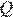 
не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.
Решение.
Проведём построения и введём обозначения, как показано на рисунке. Пусть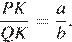 
Рассмотрим треугольник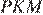и 
и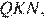 
они прямоугольные, углы 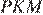и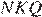 
равны как вертикальные, следовательно, треугольники подобны, откуда 
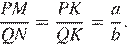Отношение радиусов равно отношению диаметров.
25. Задание 25 № 311708
В прямоугольном треугольнике ABC с прямым углом B, проведена биссектриса угла A. Известно, что она пересекает серединный перпендикуляр, проведённый к стороне BC в точке K. Найдите угол BCK, если известно, что угол ACB равен 40°.
Решение.
Так как биссектриса острого угла A прямоугольного треугольника ABC не может быть перпендикулярна BC, то биссектриса угла A и серединный перпендикуляр к BC имеют ровно одну общую точку.
Пусть N — середина BC. Рассмотрим окружность, описанную около треугольника ABC. Пусть серединный перпендикуляр к BC пересекает меньшую дугу BC в точке L (см. рисунок), тогда точка L является серединой этой дуги, ⌣BL = ⌣LC. Но тогда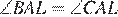 
как вписанные углы, опирающиеся на равные дуги, а отсюда AL — биссектриса 
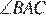. Но это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой 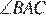. Заметим, что 
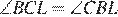как вписанные углы, опирающиеся на равные дуги.
Пусть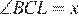 
. Четырехугольник ACLB — вписанный, поэтому 
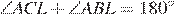, то есть 
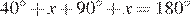, откуда 
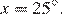Так как точки K и L совпадают,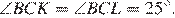 
Ответ: 25°.
Задания 1-5
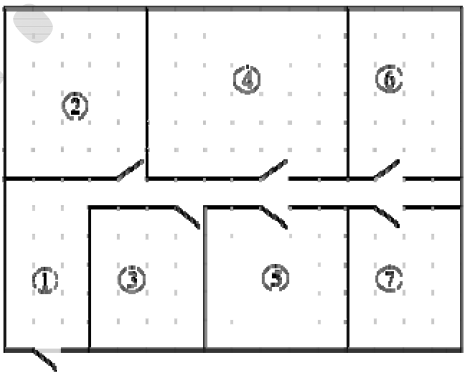
На плане (см. рис. выше) изображена схема квартиры. Сторона каждой клетки на плане соответствует 1 м. Квартира имеет прямоугольную форму. Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1, а справа находится кладовая комната, которая занимает площадь в 20 кв. м.
Гостиная занимает наибольшую площадь в квартире, а слева от неё находится кухня. Прямо перед гостиной находится детская.
В верхнем правом углу схемы находится санузел, отмеченный цифрой 6. Прямо напротив него располагается ванная комната.
В санузле и ванной комнате пол выложен плиткой, которая имеет размер 0,5 м х 0,5 м.
В квартире стоит однотарифный счётчик электроэнергии. Имеется возможность установить двухтарифный счётчик.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов, запятых и других разделительных символов.
| Объекты | гостиная | кухня | ванная комната | кладовая комната |
|---|---|---|---|---|
| Цифры |
2. Плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол в ванной комнате и санузле?
3. Найдите площадь, которую занимает гостиная. Ответ дайте в квадратных метрах.
4. Найдите расстояние от верхнего левого угла квартиры до нижнего правого угла квартиры (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Хозяин квартиры планирует установить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о потребляемой мощности, и тарифах оплаты даны в таблице (см. ниже).
Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?
| Счётчик | Однотарифный | Двухтарифный |
|---|---|---|
| Стоимость оборудования и монтажа (тыс. руб.) | 5,1 | 10 |
| Средняя потребляемая мощность (кВт) | 3,5 | 3,5 |
| Стоимость оплаты днём (06:00‐23:00) (руб./(кВт∙ч)) | 2 | 2 |
| Стоимость оплаты ночью (23:00‐06:00) (руб./(кВт∙ч)) | 2 | 1 |
Ответ: 1) 4273 2) 36 3) 42 4) 20 5) 200
Скрыть
Поскольку гостиная занимает наибольшую площадь в квартире, можно заключить, что она обозначена на схеме цифрой 4.
Слева от гостиной находится кухня, следовательно, она обозначена цифрой 2.
Ванная комната находится напротив санузла, значит, ванная обозначена на схеме цифрой 7.
Кладовая комната расположена справа от коридора, следовательно, она обозначена цифрой 3.
Скрыть
Заметим, что, поскольку одна плитка имеет площадь 0,25 м2, чтобы выложить 1 м2 пола плиткой, понадобится 4 плитки.
Площадь санузла равна 6 · 4 = 24 м2. Площадь ванной равна 4 · 5 = 20 м2.
Теперь найдём, сколько упаковок плитки понадобилось: $$frac{(24+20)cdot4}{5}=35,2$$.
Следовательно, чтобы выложить пол в ванной комнате и санузле понадобится 36 упаковок плитки.
Скрыть
Сторона одной клетки равна 1 м. Значит, площадь гостиной равна: $$7cdot6=42$$ м2.
Скрыть
Найдём расстояние между двумя ближайшими точками по прямой верхнего левого угла квартиры и нижнего правого угла квартиры по теореме Пифагора:
$$sqrt{12^2+16^2}=sqrt{144+256}=sqrt{400}=20$$.
Скрыть
Разница в стоимости установки двухтарифного и однотарифного счётчиков равна $$10 − 5,1 = 4,9$$ тыс. руб.
День использования электроэнергии с однотарифным счётчиком стоит $$2 · 3,5 · 24 = 168$$ руб.
День использования электроэнергии с двухтарифным счётчиком стоит $$3,5 · 2 · 17 + 3,5 · 1 · 7 = 143,5$$ руб.
Разница в стоимости составляет $$168 − 143,5 = 24,5$$ руб.
Значит, экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного и однотарифного счётчиков через $$frac{4900}{24,5}=200$$ дней.