Задание 6 номер 333111 - Большой телефонный справочник предприятий

СДАМ ГИА: РЕШУ ОГЭ

Образовательный портал для подготовки к экзаменам

Математика

математика

Математика

Информатика

≡ Русский язык

Письменный экзамен

Устное собеседование

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

сайты — меню — вход — новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Справочник

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

НАШИ БОТЫ

На сайте что-то не так? Отключите адблок

Новости

9 января

7 секретов эффективной подготовки к ЕГЭ и ОГЭ

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

30 октября

Телефон, whatsapp и другие запреты в школе

21 марта

Новый сервис: рисование

9 февраля

Об ошибках в математике: проверьте браузер

31 января

Внедрили тёмную тему!

17 января

Разместили утвержденное расписание ОГЭ 2022

9 октября

Как восстановить доступ к Решу ЕГЭ, если у вас Windows XP

ЧУЖОЕ НЕ БРАТЬ!

Зайчиков и Поваляев стащили наши тесты

Наша группа

Задания

Версия для печати и копирования в MS Word

Тип 6 № 333111 Добавить в вариант

Найдите значение выражения левая круглая скобка дробь: числитель: 14, знаменатель: 11 конец дроби плюс дробь: числитель: 17, знаменатель: 10 конец дроби правая круглая скобка умножить на дробь: числитель: 11, знаменатель: 15 конец дроби .

Спрятать решение

Решение.

Приведём к общему знаменателю:

дробь: числитель: 14 умножить на 10 плюс 17 умножить на 11, знаменатель: 11 умножить на 10 конец дроби умножить на дробь: числитель: 11, знаменатель: 15 конец дроби = дробь: числитель: 327, знаменатель: 10 умножить на 15 конец дроби = дробь: числитель: 109, знаменатель: 10 умножить на 5 конец дроби =2,18.

Ответ: 2,18.

Аналоги к заданию № 314282: 314288 333111 314283 314284 314285 314286 314287 314289 314290 314291 … Все

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Спрятать решение

Прототип задания

Сообщить об ошибке · Помощь

О проекте · Редакция · Правовая информация · О рекламе

Источник

Задача 6 ОГЭ по математике называется «Числа и вычисления». Это действия с обыкновенными и с десятичными дробями. Действия со степенями. Сравнение чисел.

Приступим к решению задач.

Пример 1. Найдите значение выражения $frac{0,8}{1-frac{1}{9}}.$

Решение. Вспоминаем, что при вычитании дробей нужно их привести к общему знаменателю, а при делении дробей первую из них умножаем на перевёрнутую вторую.

Посчитаем, чему равен знаменатель.

$1-frac{1}{9}= frac{9}{9}-frac{1}{9}=frac{8}{9}$

Получим:
$frac{0,8}{1-frac{1}{9}}=frac{8}{10}:frac{8}{9}=frac{8}{10}cdot frac{9}{8}=frac{9}{10}=0,9 .$

Ответ: 0,9.

Пример 2. Соотнесите обыкновенные дроби с равными им десятичными дробями.

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Решение. Каждую из данных обыкновенных дробей можно представить в виде десятичной, например, используя деление в столбик.

Задание 6 номер 333111

Итак, деление выполнено. Сопоставим полученные результаты:

Ответ: 4312.

Замечание 1. Преобразование обыкновенных дробей в десятичные можно произвести и без деления в столбик. Т. к. любая десятичная дробь записывается как обыкновенная со знаменателем 10, 100, 1000 и т. д., то данные обыкновенные дроби можно «доделать» до десятичных. Для этого используем основное свойство дроби: дробь не изменится, если её числитель и знаменатель домножить на одно и тоже число.

Задание 6 номер 333111

Замечание 2. В этой задаче можно было, наоборот, преобразовывать заданные десятичные дроби в обыкновенные путём упрощения, т. е. сокращения числителя и знаменателя.

Задание 6 номер 333111

Выбирайте любой способ. Здесь важен правильный результат!

Для выполнения следующих заданий нам потребуются свойства степеней. Напомним основные из них.

Степенью называется выражение вида $boldsymbol{a^c.}$

Здесь a — основание степени, c — показатель степени.
По определению, $a^1=a.$

Возвести число в квадрат — значит умножить его само на себя: $a^2=acdot a.$

Возвести число в куб — значит умножить его само на себя три раза: $a^3=acdot acdot a.$

Возвести число в натуральную степень n — значит умножить его само на себя n раз:

$a^n=underbrace{acdot acdot acdot acdot dots cdot a}_{n}$

По определению, ${ a}^0=1.$

Это верно для $ane 0.$ Выражение $0^0$ не определено.

Определим, что такое степень с целым отрицательным показателем.

$a^{-1}=frac{1}{a}$

$a^{-2}=frac{1}{a^2}$

$a^{-n}=frac{1}{a^n}$

Конечно, все это верно для $ane 0,$ поскольку на ноль делить нельзя.

Соберем свойства степеней и основные формулы в одной таблице.

$a^0=1$
$a^ncdot a^m=a^{n+m}$	При перемножении степеней с одинаковыми основаниями показатели степеней складываются.
$frac{a^n}{a^m}=a^{n-m}$	При делении степеней с одинаковыми основаниями показатели степеней вычитаются.
$(a^n)^m=a^{ncdot m}$	При возведении степени в степень показатели степеней перемножаются.
$a^{-n}=frac{1}{a^n}$	При возведении в отрицательную степень получаем дробь, где единица делится на степень с положительным показателем.
$(acdot b)^n=a^n cdot b^n$	При возведении произведения двух множителей в степень каждый из этих множителей возводится в заданную степень.
$(frac{a}{b})^n=frac{a^n}{b^n}$	При возведении дроби в степень получается дробь, числитель и знаменатель которой возведены в заданную степень.
$(frac{a}{b})^{-n}=(frac{b}{a})^n$	При возведении дроби в отрицательную степень дробь переворачивается, а показатель степени становится положительным.

Пример 3. Найдите значение выражения ${{(16cdot 10}^{-2})}^2cdot {(13cdot 10}^4).$

Решение. Вычислим, используя свойства степеней:

${{(16cdot 10}^{-2})}^2cdot {(13cdot 10}^4)={16}^2cdot {left({10}^{-2}right)}^2cdot {13cdot 10}^4=256cdot 13cdot ({10}^{-4}cdot {10}^4)=3 328cdot {10}^0=3328.$

Ответ: 3328.

Пример 4. Найдите значение выражения ${5cdot 10}^{-1}+{6cdot 10}^{-2}+{4cdot 10}^{-4}.$

Решение. Вычислим, используя свойства степеней:

${5cdot 10}^{-1}+{6cdot 10}^{-2}+{4cdot 10}^{-4}=5cdot frac{1}{{10}^1}+6cdot frac{1}{{10}^2}+4cdot frac{1}{{10}^4}=$
$=5cdot 0,1+6cdot 0,01+4cdot 0,0001=0,5+0,06+0,0004=0,5604.$

Ответ: 0,5604.

Пример 5. Найдите значение выражения $frac{3^8cdot 3^5}{3^9}.$

Решение. Вычислим, используя свойства степеней:

$frac{3^8cdot 3^5}{3^9}=frac{3^{8+5}}{3^9}=frac{3^{13}}{3^9}=3^{13-9}=3^4=81.$

Ответ: 81.

Источник

Действия с обыкновенными дробями

1. Задание 6 № 314127 Найдите
значение выражения

2. Задание 6 № 314264 Вычислите:

3. Задание 6 № 314265 Вычислите:

4. Задание 6 № 314288 Найдите
значение выражения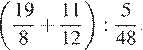

5. Задание 6 № 333006 Найдите
значение выражения .

6. Задание 6 № 333111 Найдите
значение выражения .

7. Задание 6 № 337273 Найдите
значение выражения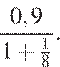

8. Задание 6 № 337375 Найдите
значение выражения

9. Задание 6 № 337385 Найдите
значение выражения

10. Задание 6 № 337509 Найдите
значение выражения

11. Задание 6 № 337528 Найдите
значение выражения

12. Задание 6 № 340581 Найдите
значение выражения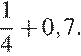

13. Задание 6 № 341664 Найдите
значение выражения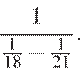

14. Задание 6 № 383596 Найдите
значение выражения

Действия с десятичными дробями

1. Задание 6 № 188 Найдите
значение выражения

2. Задание 6 № 314203 Найдите
значение выражения

3. Задание 6 № 337331 Найдите
значение выражения

4. Задание 6 № 337309 Найдите
значение выражения

5. Задание 6 № 314236 Найдите
значение выражения

6. Задание 6 № 287946 Найдите
значение выражения .

7. Задание 6 № 314233 Найдите
значение выражения

8. Задание 6 № 316314 Найдите
значение выражения:

9. Задание 6 № 316340 Найдите
значение выражения:

10. Задание 6 № 337334 Найдите
значение выражения 0,007 · 7 · 700.

11. Задание 6 № 203748 Для
каждой десятичной дроби укажите ее разложение в сумму разрядных слагаемых.

Номера запишите без пробелов, запятых и других дополнительных символов.

А. 0,7041

Б. 0,7401

В. 7,401

12. Задание 6 № 369727 Найдите
значение выражения 5,7−7,6.

13. Задание 6 № 384399 Найдите
значение выражения 4,9 − 9,4.

Степени

1. Задание Найдите значение выражения

2. Задание Найдите значение выражения

3. Задание Запишите в ответе номера тех выражений,
значение которых равно 0.

Номера запишите в порядке возрастания без пробелов, запятых и других
дополнительных символов.

4. Задание Запишите в ответе номера тех выражений,
значение которых равно −5.

Номера запишите в порядке возрастания без пробелов, запятых и других
дополнительных символов.

5. Задание Запишите десятичную дробь, равную сумме .

6. Задание Найдите значение выражения .

7. Задание Найдите значение выражения

8. Задание Найдите значение выражения

9. Задание Найдите значение выражения

10. Задание Найдите значение выражения

11. Задание Найдите значение выражения

12. Задание Найдите значение выражения

13. Задание Найдите значение выражения

14. Задание Найдите значение выражения

15. Задание Найдите значение выражения

16. Задание Найдите значение выражения

17. Задание Найдите значение выражения

18. Задание Найдите значение выражения

19. Задание Найдите значение выражения

20. Задание Найдите значение выражения

21. Задание Найдите значение выражения

22. Задание Найдите значение выражения
(4,9 · 10^− 3)(4 · 10^− 2).

23. Задание Найдите значение выражения

Сравнение чисел

1. Задание Укажите выражение, значение которого
является наименьшим.

2. Задание Запишите в ответе номера верных равенств.

Номера запишите в порядке возрастания без пробелов, запятых и других
дополнительных символов.

3. Задание Каждому выражению поставьте в соответствие
его значение:

А.	Б.	В.
1) 3,2	2) 1,75	3) 0,45

Запишите в ответ цифры,
расположив их в порядке, соответствующем буквам:

4. Задание Запишите в ответе номера выражений,
значения которых положительны.

Номера запишите в порядке возрастания без пробелов, запятых и других
дополнительных символов.

5. Задание Соотнесите обыкновенные дроби с равными им
десятичными.

А.	Б.	В.	Г.
1) 0,5	2) 0,02	3) 0,12	4) 0,625

Запишите в ответ цифры, расположив их в
порядке, соответствующем буквам:

6. Задание Расположите в порядке возрастания числа
0,1439; 1,3; 0,14.

1) 0,1439; 0,14; 1,3

2) 1,3; 0,14; 0,1439

3) 0,1439; 1,3; 0,14

4) 0,14; 0,1439; 1,3

7. Задание Расположите в порядке убывания числа
0,1327; 0,014; 0,13.

1) 0,1327; 0,014; 0,13

2) 0,014; 0,13; 0,1327

3) 0,1327; 0,13; 0,014

4) 0,13; 0,014; 0,1327

8. Задание Расположите в порядке возрастания:

9. Задание Расположите в порядке убывания:

10. Задание Укажите наибольшее из следующих чисел:

11. Задание Укажите наименьшее из следующих чисел:

12. Задание Укажите выражения, значения которых равны
0,25.

Номера запишите в порядке возрастания без пробелов, запятых и других
дополнительных символов.

13. Задание Какому из данных промежутков принадлежит
число ?

1) [0,4; 0,5]

2) [0,5; 0,6]

3) [0,6; 0,7]

4) [0,7; 0,8]

Скачано с www.znanio.ru

Источник

Тесты для отработки задания №6 ОГЭ-2020 по математике (числа и вычисления) с ответами.

→ Скачать — oge2020-ma-zadanie6

В разработку включены задания по темам:

→ действия с обыкновенными дробями;

→ действия с десятичными дробями;

→ степени

Связанные страницы:

Демоверсия ОГЭ 2020 по математике

ОГЭ 2020 по математике — 6 тренировочных вариантов с ответами

Карточки для отработки задания № 7 ОГЭ-2020 по математике

Диагностическая контрольная работа по материалам ОГЭ. Модуль «Геометрия»

Тренировочные варианты для подготовки к еГЭ по математике

Магазин видеолекций

Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим.

2016-01-29

29
Янв 2016

ОГЭ (ГИА) Задание 25ПЛАНИМЕТРИЯ

Решение всех прототипов Задания 26 ОГЭ по математике.

Инна |
Отзывов (15)

Задание 6. Числа и вычисления. Примеры с решениями.

→ Действия с обыкновенными дробями.
→ Действия с десятичными дробями.
→ Степени.
→ Сравнение чисел.

z6ogem.pdf

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задание 2 № 7

Валя шифрует русские слова (последовательности букв), записывая вместо каждой буквы её код:

Некоторые цепочки можно расшифровать не одним способом. Например, 00010101 может означать не только СКА, но и СНК. Даны три кодовые цепочки:

10111101

1010110

10111000

Найдите среди них ту, которая имеет только одну расшифровку, и запишите в ответе расшифрованное слово.

Источник: ГИА по информатике 31.05.2013. Основная волна. Центр, Урал. Вариант 1301.

Задание 2 № 27

Валя шифрует русские слова (последовательности букв), записывая вместо каждой буквы её код:

100101000

101111100

100111101

Найдите среди них ту, которая имеет только одну расшифровку, и запишите в ответе расшифрованное слово.

Источник: ГИА по информатике 31.05.2013. Основная волна. Центр, Урал. Вариант 1302.

Задание 2 № 47

Валя шифрует русские слова (последовательности букв), записывая вместо каждой буквы её код:

1010110

100000101

00011110001

Найдите среди них ту, которая имеет только одну расшифровку, и запишите в ответе расшифрованное слово.

Источник: ГИА по информатике 31.05.2013. Основная волна. Центр, Урал. Вариант 1303.

Задание 2 № 67

Валя шифрует русские слова (последовательности букв), записывая вместо каждой буквы её код:

10111101

00011110

100111101

Найдите среди них ту, которая имеет только одну расшифровку, и запишите в ответе расшифрованное слово.

Источник: ГИА по информатике 31.05.2013. Основная волна. Центр, Урал. Вариант 1304.

Задание 2 № 87

Валя шифрует русские слова (последовательности букв), записывая вместо каждой буквы её код:

100101000

100000101

0110001

Найдите среди них ту, которая имеет только одну расшифровку, и запишите в ответе расшифрованное слово.

Источник: ГИА по информатике 31.05.2013. Основная волна. Сибирь, Дальний Восток. Вариант 1305.

Пройти тестирование по этим заданиям

Каталог заданий.
Действия с обыкновенными дробями

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задание 6 № 314127

Найдите значение выражения 18 умножить на левая круглая скобка дробь: числитель: 1, знаменатель: 9 конец дроби правая круглая скобка в степени 2 минус 20 умножить на дробь: числитель: 1, знаменатель: 9 конец дроби .

Аналоги к заданию № 311234: 314127 32 311235 314128 314173 314175 314176 314177 314184 314186 … Все

Источник: Банк заданий ФИПИ

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Решение

Сообщить об ошибке · Помощь

Задание 6 № 314264

Вычислите:  дробь: числитель: 4, знаменатель: 25 конец дроби плюс дробь: числитель: 15, знаменатель: 4 конец дроби .

Аналоги к заданию № 314262: 314264 314265 383596 314263 314266 314267 314268 314269 314270 314271 … Все

Источник: Банк заданий ФИПИ

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Решение

Сообщить об ошибке · Помощь

Задание 6 № 314265

Вычислите:  дробь: числитель: 3, знаменатель: 2 конец дроби минус дробь: числитель: 9, знаменатель: 5 конец дроби .

Аналоги к заданию № 314262: 314264 314265 383596 314263 314266 314267 314268 314269 314270 314271 … Все

Источник: Банк заданий ФИПИ

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Решение

Сообщить об ошибке · Помощь

Задание 6 № 314288

Найдите значение выражения

левая круглая скобка дробь: числитель: 19, знаменатель: 8 конец дроби плюс дробь: числитель: 11, знаменатель: 12 конец дроби правая круглая скобка : дробь: числитель: 5, знаменатель: 48 конец дроби .

Аналоги к заданию № 314282: 314288 333111 314283 314284 314285 314286 314287 314289 314290 314291 … Все

Источник: Банк заданий ФИПИ

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Решение

Сообщить об ошибке · Помощь

Задание 6 № 333006

Найдите значение выражения дробь: числитель: 12, знаменатель: 20 умножить на 3 конец дроби .

Аналоги к заданию № 333006: 337375 353450 Все

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Решение

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

- Предмет:
  
  Математика
- Автор:
  
  atticusvega555
- Создано:
  
  3 года назад
Ответы

Знаешь ответ? Добавь его сюда!

Геометрия

1 минута назад

Помогите пожалуйста решить задачу по геометрии, умоляю
Математика

6 минут назад

У скольких трехзначных чисел сумма цифр равна произведению цифр? Помогите пожалуйста!!!
Физика

11 минут назад

Помогите решить задачу
Литература

16 минут назад

ПОМОГИТЕ ПОЖАЛУЙСТА. ПЕЧОРИН, ГЕРОЙ НАШЕГО ВРЕМЕНИ (княжна Мери)
Химия

21 минут назад

Предмет: Химия. Тема: Классификация неорганических соединений

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Вы не можете общаться в чате, вы забанены.

Чтобы общаться в чате подтвердите вашу почту
Отправить письмо повторно

Вопросы без ответа

Математика

2 часа назад

ПРЯМОУГОЛЬНИК ДЛИНОЙ 8 СМ И ШИРИНОЙ 4 СМ. КАК ПРОВЕСТИ В ЭТОМ ПРЯМОУГОЛЬНИКЕ ОТРЕЗОК,ЧТОБЫ ПОЛУЧИЛОСЬ ДВА ТРЕУГОЛЬНИКА.
Английский язык

4 часа назад

перестройте предложения текста употребив страдательный залог.

In January the Fernwood Company hired Martha as a secretary, In March the company sent her to school to study statistics and programming. In April the boss gave her the first raise. Just two months later, he promoted Martha to the position of supervisor of her department. In November they invited her to take a position in the company’s office in England. And in December the company gave her the new job in London.

Топ пользователей

Fedoseewa27

20959
Sofka

7417
vov4ik329

5113
DobriyChelovek

4631
olpopovich

3461
zlatikaziatik

3125
manbenzopila

2540
Udachnick

1867
Zowe

1683
NikitaAVGN

1210

Войти через Google

или

Запомнить меня

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

Выберите язык и регион

Русский

Россия

English

United States

zoom

How much to ban the user?

1 hour
1 day

Источник

Задание 1 № 366805

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	Город Гранюк	Деревня Астрелка	Хутор Южный	Город Гусевск
Цифры

Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.

Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.

Ответ: 1465.

2. Задание 2 № 366806

Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.

Решение.

Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится

пачек чая.

Таким образом, ребята должны купить 14 пачек чая.

Ответ: 14.

3. Задание 3 № 366807

Найдите площадь (в км²), которую занимает заказник.

Решение.

Площадь заказника равна:

Ответ: 351.

4. Задание 4 № 366808

Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.

Решение.

Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:

км.

Ответ: 30.

5. Задание 5 № 366809

Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.

Продукция	Цена в магазине «Вело» (руб.)	Цена в магазине «ОК» (руб.)	Срок доставки из магазина «ОК» (дни)
Подсветка для спиц
Шина вида «А»
Шина вида «Б»
Спица
Педаль вида «А»
Педаль вида «Б»
Тормоз вида «А»		нет
Тормоз вида «Б»	нет
Набор крепёжных изделий

Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?

Решение.

На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:

руб.

Ответ: 5300.

6. Задание 6 № 316314

Найдите значение выражения:

Решение.

Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.

7. Задание 7 № 317575

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?

Решение.

Заметим, что и Проверим все варианты ответа:

1) — неверно;

2) — верно;

3) — верно;

4) — верно.

Ответ указан под номером 1.

8. Задание 8 № 353586

Какое из данных ниже чисел является значением выражения

Решение.

Последовательно получим:

Ответ: 1

9. Задание 9 № 338500

При каком значении значения выражений и равны?

Решение.

Для ответа на вопрос задачи нужно решить уравнение Решим его:

Ответ: 2.

10. Задание 10 № 325450

В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.

Решение.

Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна

Ответ: 0,3.

11. Задание 11 № 311406

На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке

4) прямая пересекает график в точках и

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .

2) — неверно,

3) — верно, видно из графика.

4) Прямая пересекает график в точках и — верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

Ответ: 12.

12. Задание 12 № 311543

Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .

Решение.

Выразим :

Подставляя, получаем:

Ответ: 0,4.

13. Задание 13 № 338497

На каком из рисунков изображено решение неравенства

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

Решение.

Решим неравенство методом интервалов:

Правильный ответ указан под номером: 4.

14. Задание 14 № 406645

В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение.

Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.

Найдем сумму этой прогрессии:

Ответ: 377 мест.

15. Задание 15 № 340000

В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите

Решение.

Из прямоугольного треугольника по теореме Пифагора найдём

Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.

16. Задание 16 № 351463

На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.

Решение.

Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.

17. Задание 17 № 169876

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.

———-

В открытом банке иррациональный ответ.

18. Задание 18 № 350842

Найдите угол

Решение.

Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.

Ответ: 22,5

19. Задание 19 № 401617

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Ответ: 13.

20. Задание 20 № 338505

Решите неравенство

Решение.

Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение

Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).

Таким образом, ответ

Ответ:

Примечание.

Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,

21. Задание 21 № 353527

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.

Ответ: 58.

22. Задание 22 № 338288

Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.

Решение.

Упростим выражение:

По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:

График функции сводится к графику параболы с выколотой точкой

Выделим полный квадрат:

Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)

Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и

Ответ: −1; 3.

23. Задание 23 № 339395

Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.

Решение.

Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и

Ответ: 16.

24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.

Решение.

Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.

25. Задание 25 № 311926

В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .

Решение.

По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,

Площадь трапеции :

Площадь трапеции

Ответ: 9.

Источник