Шестое задание проверяет наши умения проведения вычислений. Это самое простое задание из всего модуля и требует от нас только знания арифметики. В первом задании арифметические действия будут самыми простыми. В демонстрационном варианте ОГЭ предлагается сложить две дроби: обыкновенную и десятичную. Тем не менее, в соответствии с документами о проведении ОГЭ, учащиеся должны быть готовы и к выполнению некоторых других несложных заданий. Ответом в первом задании является целое число или конечная десятичная дробь.
Итак, для успешного выполнения необходимо помнить:
- порядок проведения арифметических операций – сначала производятся действия в скобках, затем возведение в степень или извлечение корня, затем умножения и деления, а затем вычитания и сложения.
- правила умножения и деления в столбик
- правила вычисления обыкновенных дробей
Напоминаем правила операций с обыкновенными дробями:

Рекомендуем вычислить отдельно числитель и знаменатель, а затем разделить числитель на знаменатель. Остальные рекомендации смотрите ниже при разборе типовых вариантов первого задания ОГЭ по математике. 🙂
Найдите значение выражения:![]()
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
4,5 • 2,5
Можно произвести вычисления в столбик, тогда получим:
4,5 • 2,5 = 11,25
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
Ответ: 0,8
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:![]()
Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.
1/3 • (6 • (1/3) — 17 )
Проведя вычисления в скобках, получим:
1/3 • ( 6 • (1/3) — 17 ) = 1/3 • (6 /3 — 17 ) = 1/3 • ( 2 — 17 ) = 1/3 • ( -15 )
Теперь умножим полученное значение -15 на 1/3:
1/3 • ( -15 ) = -5
Ответ: -5
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения: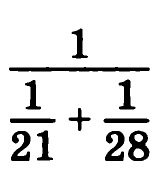
Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:
1/21 + 1/28 = 4/84 + 3/84
Затем складываем:
4/84 + 3/84 = 7/84
Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:
1 / ( 7 / 84 ) = 1 •84/7 = 84/7
Далее остается поделить 84 на 7:
84 / 7 = 12
Ответ: 12
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения: ¼ + 0,07
К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной.
Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем:
0,25 + 0,07 = 0,32
Ответ: 0,32
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
–13•(–9,3)–7,8
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
–13·(–9,3)–7,8 =
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
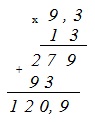
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
= 120,9–7,8 =
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
= 113,1
Ответ: 113,1
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
–0,3·(–10)4+4·(–10)2–59
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
–0,3·(–10)4+4·(–10)2–59 =
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
= –0,3·10000+4·100–59 =
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
= –3000+400–59 =
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
= –2600–59 =
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
= –(2600+59) = –2659
Ответ: -2659
pазбирался: Даниил Романович | обсудить разбор | оценить
Найти значение выражения 4,9 – 9,4.
Выполним вычитание десятичных дробей, где 9,4 больше по модулю, значит, ответ будет отрицательным. Итак, – (9,4 – 4,9)= – 4,5
Ответ: -4,5
pазбирался: Даниил Романович | обсудить разбор | оценить
Тесты для отработки задания №6 ОГЭ-2020 по математике (числа и вычисления) с ответами.
→ Скачать — oge2020-ma-zadanie6
В разработку включены задания по темам:
→ действия с обыкновенными дробями;
→ действия с десятичными дробями;
→ степени
Связанные страницы:
Демоверсия ОГЭ 2020 по математике
ОГЭ 2020 по математике — 6 тренировочных вариантов с ответами
Карточки для отработки задания № 7 ОГЭ-2020 по математике
Диагностическая контрольная работа по материалам ОГЭ. Модуль «Геометрия»
- ОГЭ по математике
Материалы для отработки задания №6 ОГЭ по математике — числа и вычисления.
Типы заданий:
→ Действия с обыкновенными дробями.
→ Действия с десятичными дробями.
→ Степени.
→ Сравнение чисел.
| Теория для задания 6 Автор: Е. А. Ширяева → скачать |
| Практика для задания 6 Автор: Е. А. Ширяева → скачать |
| Варианты заданий 6 с ответами Источник: https://math100.ru → скачать |
| Карточки для отработки задания №6 с ответами → скачать
|
Решение типовых задач №6 на ОГЭ по математике
Связанные страницы:

СДАМ ГИА: РЕШУ ОГЭ
Образовательный портал для подготовки к экзаменам
Математика
сайты — меню — вход — новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
НАШИ БОТЫ
На сайте что-то не так? Отключите адблок
Новости
30 марта
Подготовься к ЕГЭ или ОГЭ за 1,5 месяца на курсе Флеш
21 марта
Новый сервис: рисование
9 февраля
Об ошибках в математике: проверьте браузер
31 января
Внедрили тёмную тему!
17 января
Разместили утвержденное расписание ОГЭ 2022
9 октября
Как восстановить доступ к Решу ЕГЭ, если у вас Windows XP
ЧУЖОЕ НЕ БРАТЬ!
Зайчиков и Поваляев стащили наши тесты
Наша группа
Каталог заданий
Версия для печати и копирования в MS Word
1
Задание 6 № 316560
Найдите значение выражения
Аналоги к заданию № 316560: 341664 316709 316598 316708 348817 348852 349194 349444 350590 350681 … Все
Решение
·
·
Сообщить об ошибке · Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2022
Тест «Виды потребления»
Проверочная работа по обществознанию.
Календарь диктантов 2022
Общие материалы | Вчера, 20:46
Расписание Всероссийских диктантов на 2022 год.
Восьмое задание в модуле алгебре проверяет знания в области обращения со степенями и подкоренными выражениями.
При выполнении задания №4 ОГЭ по математике проверяются не только навыки выполнения вычисления и преобразований числовых выражений, но и умение преобразовывать алгебраические выражения. Возможно, потребуется выполнить действия со степенями с целым показателем, с многочленами, тождественные преобразования рациональных выражений.
В соответствии с материалами проведения основного экзамена могут быть задания, в которых потребуется выполнение тождественных преобразований рациональных выражений, разложение многочленов на множители, использование процентов и пропорций, признаков делимости.
Ответом в задании №8 является одна из цифр 1; 2; 3; 4 соответствующая номеру предложенного варианта ответа к заданию.
Теория к заданию №4
Из теоретического материала нам пригодятся правила обращения со степенями:

Правила работы с подкоренными выражениями:
В моих разобранных вариантах представлены данные правила — в разборе первого варианта третьего задания представлены правила обращения со степенями, а во втором и третьем варианте разобраны примеры работы подкоренными выражениями.
Разбор типовых вариантов задания №4 ОГЭ по математике
Первый вариант задания
Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11n ?
- 121n
- 11n+2
- 112n
- 11n+3
Решение:
Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:
- при умножении степени складываются
- приделении степени вычитаются
- при возведении степени в степень степени перемножаются
- при извлечении корня степени делятся
Кроме того, для решения необходимо представить 121 как степень 11, а именно это 112.
121 • 11n = 112 • 11n
С учетом правила умножения, складываем степени:
112 • 11n = 11n+2
Следовательно, нам подходит второй ответ.
Ответ: 2
Второй вариант задания
Значение какого из данных ниже выражений является наибольшим?
- 3√5
- 2√11
- 2√10
- 6,5
Решение:
Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:
- 3√5
Переносим 3 под корень:
3√5 = √(3² •5) = √(9•5) = √45
- 2√11
Переносим 2 под корень:
2√11 = √(2² • 11) = √(4 • 11) =√44
- 2√10
Переносим 2 под корень:
2√10 = √(2² • 10) = √(4 • 10) =√40
- 6,5
Возводим 6,5 в квадрат:
6,5 = √(6,5²) = √42,25
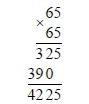
Посмотрим на все получившиеся варианты:
- 3√5 = √45
- 2√11 = √44
- 2√10 = √40
- 6,5 = √42,25
Следовательно, правильный ответ первый
Ответ: 1
Третий вариант задания
Какое из данных чисел является рациональным?
- √810
- √8,1
- √0,81
- все эти числа иррациональны
Решение:
Для решения этой задачи нужно действовать следующим образом:
Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:
0,9
90
Рассмотри каждое из них:
0,9 = √(0,9)² = √0,81
90 = √(90²) = √8100
Следовательно, число √0,81 является рациональным, остальные же числа
- √810
- √8,1
хотя и похожи на форму 9 в квадрате, не являются рациональными.
Таким образом, правильный ответ третий.
Ответ: 3
Четвертый вариант задания
По просьбе подписчика моего сообщества Спадило Дианы, привожу разбор следующего задания №4:
Какое из данных ниже чисел является значением выражения?


Решение:
Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:
16 — 14 = 2
Суммарно наши действия выглядят так:

Ответ: 4
Хотите, чтобы ваше задание я разобрал и представил здесь? Подписывайтесь на мою группу Спадило и присылайте задание в личные сообщения группы!
Пятый вариант задания (демонстрационный вариант ОГЭ 2017)
Значение какого из выражений является рациональным числом?
- √6-3
- √3•√5
- (√5)²
- (√6-3)²
Решение:
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
1) √6-3
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
2) √3•√5
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
√3•√5 = √(3•5) = √15
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
3) (√5)²
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
(√5)² = 5
Данный вариант ответа нам подходит.
4) (√6-3)²
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
Ответ: 3
Шестой вариант задания
Найдите значение выражения:
![]()
Решение:
В 1-м корне представляем 4900 в виде произведения 49·100. Оба эти числа являются точными квадратами: 49=72 и 100=102. И, значит, число под корнем можно полностью вынести из-под него, применив правила работы с подкоренными выражениями. В целом получаем:
![]()
По аналогии извлекаем и 2-й корень:
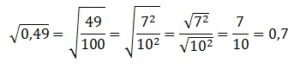
В итоге получаем:
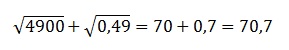
Ответ: 70,7
Седьмой вариант задания
Найдите значение выражения:
![]()
Решение:
Используем правило умножения и деления степеней с одинаковым основанием. Заключается оно в том, что при их умножении показатели степеней суммируются, а при делении вычитаются (от показателя в числителе вычитается показатель, стоящий в знаменателе). Тогда получаем:
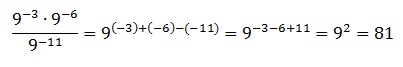
Ответ: 81
Задача 6 ОГЭ по математике называется «Числа и вычисления». Это действия с обыкновенными и с десятичными дробями. Действия со степенями. Сравнение чисел.
Приступим к решению задач.
Пример 1. Найдите значение выражения
Решение. Вспоминаем, что при вычитании дробей нужно их привести к общему знаменателю, а при делении дробей первую из них умножаем на перевёрнутую вторую.
Посчитаем, чему равен знаменатель.
Получим:
Ответ: 0,9.
Пример 2. Соотнесите обыкновенные дроби с равными им десятичными дробями.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Решение. Каждую из данных обыкновенных дробей можно представить в виде десятичной, например, используя деление в столбик.

Итак, деление выполнено. Сопоставим полученные результаты:
Ответ: 4312.
Замечание 1. Преобразование обыкновенных дробей в десятичные можно произвести и без деления в столбик. Т. к. любая десятичная дробь записывается как обыкновенная со знаменателем 10, 100, 1000 и т. д., то данные обыкновенные дроби можно «доделать» до десятичных. Для этого используем основное свойство дроби: дробь не изменится, если её числитель и знаменатель домножить на одно и тоже число.

Замечание 2. В этой задаче можно было, наоборот, преобразовывать заданные десятичные дроби в обыкновенные путём упрощения, т. е. сокращения числителя и знаменателя.

Выбирайте любой способ. Здесь важен правильный результат!
Для выполнения следующих заданий нам потребуются свойства степеней. Напомним основные из них.
Степенью называется выражение вида
Здесь a — основание степени, c — показатель степени.
По определению,
Возвести число в квадрат — значит умножить его само на себя:
Возвести число в куб — значит умножить его само на себя три раза:
Возвести число в натуральную степень n — значит умножить его само на себя n раз:
По определению,
Это верно для Выражение
не определено.
Определим, что такое степень с целым отрицательным показателем.
Конечно, все это верно для поскольку на ноль делить нельзя.
Соберем свойства степеней и основные формулы в одной таблице.
| При перемножении степеней с одинаковыми основаниями показатели степеней складываются. | |
| | При делении степеней с одинаковыми основаниями показатели степеней вычитаются. |
| | При возведении степени в степень показатели степеней перемножаются. |
| | При возведении в отрицательную степень получаем дробь, где единица делится на степень с положительным показателем. |
| При возведении произведения двух множителей в степень каждый из этих множителей возводится в заданную степень. | |
| При возведении дроби в степень получается дробь, числитель и знаменатель которой возведены в заданную степень. | |
| | При возведении дроби в отрицательную степень дробь переворачивается, а показатель степени становится положительным. |
Пример 3. Найдите значение выражения
Решение. Вычислим, используя свойства степеней:
Ответ: 3328.
Пример 4. Найдите значение выражения
Решение. Вычислим, используя свойства степеней:
Ответ: 0,5604.
Пример 5. Найдите значение выражения
Решение. Вычислим, используя свойства степеней:
Ответ: 81.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 6 ОГЭ по математике. Числа и вычисления.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.01.2023
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора – дверь в кладовую.
Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение – гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.
Задание 1: Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
Задание 2: Найдите ширину окна в спальне. Ответ дайте в сантиметрах.
Задание 3: Найдите площадь гостиной. Ответ дайте в квадратных метрах.
Задание 6 про план квартиры: Плитка для пола размером 20 см на 40 см продаётся в упаковках по 8 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол санузла?
Задание 7 про квартиру: Паркетная доска размером 20 см на 80 см продаётся в упаковках по 16 штук. Сколько упаковок паркетной доски понадобилось, чтобы выложить пол в спальне?
Задание 8: В квартире планируется подключить интернет. Предполагается, что трафик составит 850 Мб в месяц, и исходя из этого выбирается наиболее дешёвый вариант. Провайдер предлагает три тарифных плана.
Сколько рублей нужно будет заплатить за интернет за месяц, если трафик действительно будет равен 850 Мб?
Задание 9 про план квартиры: В квартире планируется заменить электрическую плиту. Характеристики электроплит, условия подключения и доставки приведены в таблице. Планируется купить электрическую плиту глубиной 60 см с духовкой объёмом не менее 54 л.
Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?
Задание 10: В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с вертикальной загрузкой вместимостью не менее 6 кг.
Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?
Решения задач про квартиру.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Решение.
Поскольку гостиная занимает наибольшую площадь в квартире, можно заключить, что она обозначена на схеме цифрой 4. Слева от гостиной находится кухня, следовательно, она обозначена цифрой 2. Ванная комната находится напротив санузла, значит, ванная обозначена на схеме цифрой 7. Кладовая комната расположена справа от коридора, следовательно, она обозначена цифрой 3.
Ответ: 4273.
Плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол в ванной комнате и санузле?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Квартира имеет прямоугольную форму. Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1, а справа находится кладовая комната, которая занимает площадь в 20 кв. м.
Гостиная занимает наибольшую площадь в квартире, а слева от неё находится кухня. Прямо перед гостиной находится детская.
В верхнем правом углу схемы находится санузел, отмеченный цифрой 6. Прямо напротив него располагается ванная комната.
В санузле и ванной комнате пол выложен плиткой, которая имеет размер 0,5 м × 0,5 м.
В квартире стоит однотарифный счётчик электроэнергии. Имеется возможность установить двухтарифный счётчик.
Решение.
Заметим, что, поскольку одна плитка имеет площадь 0,25 м2, чтобы выложить 1 м2 пола плиткой, понадобится 4 плитки. Площадь санузла равна 6 4 = 24 м2. Площадь ванной равна 4 5 = 20 м2. Теперь найдём, сколько упаковок плитки понадобилось: Следовательно, чтобы выложить пол в ванной комнате и санузле понадобится 36 упаковок плитки.
Ответ: 36.
Найдите площадь, которую занимает гостиная. Ответ дайте в квадратных метрах.
Решение.
Сторона одной клетки равна 1 м. Значит, площадь гостиной равна:
Ответ: 42.
Найдите расстояние от верхнего левого угла квартиры до нижнего правого угла квартиры (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение.
Найдём расстояние между двумя ближайшими точками по прямой верхнего левого угла квартиры и нижнего правого угла квартиры по теореме Пифагора:
Ответ: 20.
Хозяин квартиры планирует заменить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о тарифах оплаты, и их стоимости даны в таблице.
Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?
Решение.
Заметим, что, поскольку одна плитка имеет площадь 0,25 м2, чтобы выложить 1 м2 пола плиткой, понадобится 4 плитки. Площадь санузла равна 6 4 = 24 м2. Площадь ванной равна 4 5 = 20 м2. Теперь найдём, сколько упаковок плитки понадобилось: Следовательно, чтобы выложить пол в ванной комнате и санузле понадобится 36 упаковок плитки.
Ответ: 36.
Плитка для пола продаётся в упаковках по 5 штук. Сколько упаковок плитки нужно купить, чтобы покрыть пол кухни?
Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки равна 0,3 м. Кухня имеет квадратную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно. Справа от двери будут поставлены полки для посуды, слева от двери будет смонтирована раковина для мытья посуды. В углу слева от окна предполагается разместить газовую плиту. Между раковиной и плитой будет собран буфет, отмеченный цифрой 3. Площадь, занятая буфетом, по плану будет равна 0,72 м2. В центре кухни планируется поставить обеденный стол. Кроме того, в угол кухни будет поставлен холодильник, занимающий 0,36 м2 пола. Пол кухни (в том числе там, где будет стоять мебель и бытовая техника) планируется покрыть плиткой размером 30 см × 30 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,18 м2 между буфетом и плитой.
Решение.
Заметим, что, поскольку одна плитка имеет площадь 0,09 м2, чтобы выложить пол в кухне понадобится столько плитки, сколько площади занимает кухня. Сторона одной клетки равна 0,3 м, значит, площадь кухни равна 9 0,3 9 0,3 = 7,29 м2. Теперь найдём, сколько плитки понадобится: Следовательно, чтобы выложить пол в кухне, понадобится
упаковок плитки. Значит, необходимо купить 17 упаковок плитки.
Ответ: 17.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Решение.
Стол планируется поставить в центре кухни, значит, стол отмечен на плане цифрой 4. Раковина будет смонтирована слева от двери, значит, раковина отмечена цифрой 5. В углу слева от окна планируется поставить плиту, она отмечена на плане цифрой 1. Известно, что холодильник планируется поставить в угол кухни. В углах левой части кухни будут стоять плита и раковина, в угле справа от двери будут стоять полки для посуды. Значит, холодильник отмечен на плане цифрой 2.
Ответ: 4215.
Найдите площадь той части кухни, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м2.
Решение.
Сторона одной клетки равна 0,3 м. Значит, площадь кухни равна:
Владелец не станет подводить обогрев под холодильник, плиту, буфет, раковину и полки для посуды, а также на участок между буфетом и плитой, который имеет площадь 0,18 м2. Холодильник занимает площадь 0,36 м2. На плане видно, что раковина и плита также занимают 0,36 м2. Буфет занимает 0,72 м2. Полки для посуды занимают участок площадью м2. Значит, площадь той части кухни, на которой будет смонтирован электрический подогрев пола, равна
Ответ: 5,13.
Приведем другое решение.
Владелец не станет подводить подогрев под раковину, плиту и буфет, а также на участок между буфетом и плитой. По рисунку видно, что все эти участки расположены вдоль левой стены кухни и занимают общую площадь 2 0,3 9 0,3 = 1,62 м2. Кроме того, владелец не будет подводить подогрев под холодильник площадью 0,36 м2 и полки для посуды площадью 0,18 м2. Значит, площадь той части кухни, на которой будет смонтирован электрический подогрев пола, равна 7,29 − 1,62 − 0,36 − 0,18 = 5,13 м2.
Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах.
Решение.
Найдём расстояние между противоположными углами обеденного стола по теореме Пифагора:
Ответ: 1,5.
Задание 10
Владелец квартиры выбирает холодильник из двух моделей А и Б. Цена холодильников и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 4 рубля за кВт ч.
| Модель | Цена холодильника (руб) | Среднее потребление электроэнергии в сутки, кВт ч |
|---|---|---|
| А | 30 000 | 0,7 |
| Б | 28 000 | 0,9 |
Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих холодильников? Ответ округлите до целого числа.
Решение.
Заметим, что, поскольку одна плитка имеет площадь 0,09 м2, чтобы выложить пол в кухне понадобится столько плитки, сколько площади занимает кухня. Сторона одной клетки равна 0,3 м, значит, площадь кухни равна 9 0,3 9 0,3 = 7,29 м2. Теперь найдём, сколько плитки понадобится: Следовательно, чтобы выложить пол в кухне, понадобится
упаковок плитки. Значит, необходимо купить 17 упаковок плитки.
Ответ: 17.
* * * * *
Задание 11
Краска продаётся в банках по 3 л. Сколько банок краски требуется купить, чтобы покрасить потолок в гостиной?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1. Напротив входа расположена туалетная комната, а справа от нее — ванная комната.
Гостиная занимает наибольшую площадь в квартире, а справа от неё находится кухня. Прямо перед гостиной находится детская. Из детской можно попасть на балкон, отмеченный цифрой 6.
Потолок в гостиной планируется покрасить в красный цвет. Для покраски одного 1 м2 потолка требуется 0,25 л краски.
В квартире планируется установить счётчик электроэнергии. Имеется возможность установить однотарифный или двухтарифный счётчик.
Решение.
Площадь гостиной равна 5 9 = 45 м2. Для покраски одного 1 м2 потолка требуется 0,25 л краски. Значит, чтобы покрасить потолок в гостиной понадобится
0,25 45 = 11,25 л
краски. Таким образом, требуется купить 4 банки краски.
Ответ: 4.
Задание 12
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Туалет | Детская | Гостиная | Кухня |
|---|---|---|---|---|
| Цифры |
Решение.
Туалет расположен напротив входа в квартиру, следовательно, он отмечен цифрой 2. Из детской можно попасть на балкон, отмеченный цифрой 6, значит, детская отмечена на схеме цифрой 4. Гостиная занимает наибольшую площадь в квартире, поэтому гостиная отмечена цифрой 5. Кухня находится справа от гостиной, следовательно, кухня отмечена цифрой 7.
Ответ: 2457.
Задание 13
Найдите площадь, которую занимают детская и балкон. Ответ дайте в квадратных метрах.
Решение.
Сторона одной клетки равна 1 м. Значит, площадь детской и балкона равна:
м2.
Ответ: 48.
Задание 14
Найдите расстояние между противоположными углами детской комнаты в метрах. Ответ запишите в виде
Решение.
Найдём расстояние между противоположными углами детской комнаты по теореме Пифагора:
Таким образом, получаем ответ:
Ответ: 6.
Задание 15
Хозяин квартиры планирует установить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о потребляемой мощности, и тарифах оплаты даны в таблице.
| Оборудование и монтаж | Сред. потребл. мощность в час | Стоимость оплаты | |
|---|---|---|---|
| Двухтарифный | 8 675 руб. | 3,5 кВт | 3 руб./(кВт ч) днём |
| 1,5 руб./(кВт ч ) ночью (с 23:00 до 6:00) |
Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?
Решение.
Разница в стоимости установки двухтарифного и однотарифного счётчиков равна 8 675 − 5 000 = 3 675 руб. День использования электроэнергии с однотарифным счётчиком стоит 3 3,5 24 = 252 руб./(кВт ч). День использования электроэнергии с двухтарифным счётчиком стоит 3,5 3 17 + 3,5 1,5 7 = 215,25 руб./(кВт ч). Разница в стоимости составляет 252 − 215,25 = 36,75 руб./(кВт ч). Значит, экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного и однотарифного счётчиков через дней.
Ответ: 100.
* * * * *
Задание 16
Краска продаётся в банках по 2 л. Сколько банок краски требуется купить, чтобы покрасить потолок в ванной комнате и санузле?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1. Перед входом в квартиру располагается ванная комната, а справа от неё — санузел.
Гостиная занимает наибольшую площадь в квартире, из гостиной можно попасть в детскую комнату. Также в квартире есть кухня, из которой можно попасть на балкон, отмеченный цифрой 6. В конце коридора находится кладовая комната, имеющая площадь 10 м2.
Потолок в ванной комнате и санузле планируется покрасить в белый цвет. Для покраски одного 1 м2 потолка требуется 0,2 л краски.
В квартире стоит однотарифный счётчик электроэнергии. Имеется возможность установить двухтарифный счётчик.
Решение.
Площадь ванной комнаты и санузла равна
м2.
Для покраски одного 1 м2 потолка требуется 0,2 л краски. Значит, чтобы покрасить потолок в ванной комнате и санузле понадобится
0,2 24 = 4,8 л
краски. Таким образом, требуется купить 3 банки краски.
Ответ: 3.
Задание 17
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Ванная комната | Детская комната | Кухня | Кладовая комната |
|---|---|---|---|---|
| Цифры |
Решение.
Перед входом в квартиру располагается ванная комната, следовательно, ванная комната отмечена цифрой 2. Гостиная занимает наибольшую площадь в квартире, из гостиной можно попасть в детскую комнату, поэтому детская комната отмечена цифрой 7. Также в квартире есть кухня, из которой можно попасть на балкон, отмеченный цифрой 6, значит, кухня отмечена на схеме цифрой 4. В конце коридора находится кладовая комната, имеющая площадь 10 м2, следовательно, кладовая комната отмечена цифрой 8.
Ответ: 2748.
Задание 18
Найдите площадь, которую занимают кухня и балкон. Ответ дайте в квадратных метрах.
Решение.
Сторона одной клетки равна 1 м. Значит, площадь кухни и балкона равна:
м2.
Ответ: 28.
Задание 19
Найдите расстояние между противоположными углами (диагональ) ванной комнаты в метрах.
Решение.
Найдём расстояние между противоположными углами ванной комнаты по теореме Пифагора:
Ответ: 5.
Задание 20
Хозяин квартиры планирует установить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о потребляемой мощности, и тарифах оплаты даны в таблице.
| Оборудование и монтаж | Сред. потребл. мощность (в час) | Стоимость оплаты | |
|---|---|---|---|
| Двухтарифный | 8 200 руб. | 6 кВт | 5 руб./(кВт ч) днём |
| 3 руб./(кВт ч ) ночью (с 23:00 до 6:00) |
Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?
Решение.
Разница в стоимости установки двухтарифного и однотарифного счётчиков равна 8 200 − 4 000 = 4 200 руб. День использования электроэнергии с однотарифным счётчиком стоит 5 6 24 = 720 руб./(кВт ч). День использования электроэнергии с двухтарифным счётчиком стоит 6 5 17 + 6 3 7 = 636 руб./(кВт ч). Разница в стоимости составляет 720 − 636 = 84 руб./(кВт ч). Значит, экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного и однотарифного счётчиков через дней.
Ответ: 50.
* * * * *
Задание 21
Паркетная доска продаётся в упаковках по 8 шт. Сколько упаковок с паркетной доской требуется купить, чтобы покрыть пол в гостиной?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 2. Слева от него расположен балкон. Перед входом в квартиру располагается совмещённый санузел, а справа от него — детская комната.
Гостиная занимает наибольшую площадь в квартире, из гостиной можно попасть в кабинет. В конце коридора находится кухня площадью 20 м2.
Пол в гостиной планируется покрыть паркетной доской длиной 1 м и шириной 0,25 м.
В квартире проведены газопровод и электричество.
Решение.
Заметим, что чтобы покрыть паркетной доской 1 м2 пола, требуется 4 доски. Найдём площадь гостиной:
м2.
Значит, требуется 35 4 = 140 досок. Следовательно, требуется упаковок с паркетной доской. Таким образом, необходимо купить 18 упаковок.
Ответ: 18.
Задание 22
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Балкон | Детская комната | Кабинет | Кухня |
|---|---|---|---|---|
| Цифры |
Решение.
При входе в квартиру расположен коридор, отмеченный цифрой 2. Слева от него расположен балкон. Значит, балкон отмечен цифрой 1. Перед входом в квартиру располагается совмещённый санузел, а справа от него — детская комната, следовательно, детская комната отмечена на схеме цифрой 4. Гостиная занимает наибольшую площадь в квартире, из гостиной можно попасть в кабинет, поэтому кабинет отмечен цифрой 7. В конце коридора находится кухня площадью 20 м2, значит, кухня отмечена цифрой 5.
Ответ: 1475.
Задание 23
Найдите площадь коридора (коридором считается площадь квартиры, незанятая комнатами или балконом). Ответ дайте в квадратных метрах.
Решение.
Сторона одной клетки равна 1 м. Значит, площадь коридора равна:
м2.
Ответ: 25.
Задание 24
Найдите расстояние между противоположными углами детской комнаты в метрах. Ответ запишите в виде
Решение.
Найдём расстояние между противоположными углами детской комнаты по теореме Пифагора:
Таким образом, получаем ответ:
Ответ: 4.
Задание 25
Хозяин квартиры планирует установить в квартире плиту для готовки. Он рассматривает два варианта: газовая плита или электроплитка. Цены на плиты, данные о потреблении и тарифах оплаты даны в таблице.
| Цена | Сред. расход газа / сред. потребл. мощность | Стоимость газа / электро-энергии | |
|---|---|---|---|
| Газовая плита | 44 680 руб. | 1,4 куб. м/ч | 6 руб./куб. м |
| Электроплитка | 21 000 руб. | 5,8 кВт | 4 руб./(кВт ч ) |
Обдумав оба варианта, хозяин решил установить газовую плиту. Через сколько часов непрерывного использования экономия от использования газовой плиты вместо электрической компенсирует разность в стоимости установки газовой плиты и электроплитки?
Решение.
Разница в стоимости покупки газовой плиты и электроплитки равна 44 680 − 21 000 = 23 680 руб. Час использования газовой плиты стоит 1,4 6 = 8,4 руб. Час использования электроплитки стоит 5,8 4 = 23,2 руб. Разница в стоимости составляет 23,2 − 8,4 = 14,8 руб. Значит, экономия от использования газовой плиты вместо электроплитки компенсирует разность в стоимости установки газовой и электрической плит через часов.
Ответ: 1600.
* * * * *
Задание 26
Паркетная доска продаётся в упаковках по 16 шт. Сколько упаковок с паркетной доской требуется купить, чтобы покрыть пол в гостиной?
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположена прихожая, отмеченная цифрой 6. Из прихожей можно попасть в гостиную, расположенную справа от неё. В квартире есть балкон, занимающий наименьшую площадь. Перед входом в прихожую располагается спальня, а справа от неё — детская комната, в которую можно попасть только из спальни. Рядом со спальней расположен совмещенный санузел площадью 12 м2. Кроме того, в квартире есть кухня.
Пол в гостиной планируется покрыть паркетной доской длиной 1 м и шириной 0,25 м.
В квартире проведены газопровод и электричество.
Решение.
Заметим, что чтобы покрыть паркетной доской 1 м2 пола, требуется 4 доски. Найдём площадь гостиной:
м2.
Значит, требуется 30 4 = 120 досок. Следовательно, требуется упаковок с паркетной доской. Таким образом, необходимо купить 8 упаковок.
Ответ: 8.
Задание 27
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Балкон | Детская комната | Гостиная | Кухня |
|---|---|---|---|---|
| Цифры |
Решение.
В квартире есть балкон, занимающий наименьшую площадь, следовательно, балкон отмечен на схеме цифрой 1. Перед входом в прихожую располагается спальня, а справа от неё — детская комната, в которую можно попасть только из спальни, значит, детская комната отмечена цифрой 5. Из прихожей можно попасть в гостиную, расположенную справа от неё, поэтому гостиная отмечена цифрой 7. Рядом со спальней расположен совмещенный санузел площадью 12 м2, он отмечен цифрой 3. Значит, кухня отмечена цифрой 2.
Ответ: 1572.
Задание 28
Найдите площадь, которую занимают спальная комната и детская. Ответ дайте в квадратных метрах.
Решение.
Сторона одной клетки равна 1 м. Значит, площадь спальной комнаты и детской равна:
м2.
Ответ: 36.
Задание 29
Найдите расстояние d между противоположными углами кухни в метрах. В ответ запишите
Решение.
Найдём расстояние между противоположными углами кухни по теореме Пифагора:
Таким образом, получаем ответ:
Ответ: 5.
Задание 30
Хозяин квартиры планирует установить в квартире плиту для готовки. Он рассматривает два варианта: газовая плита или электроплитка. Цены на плиты, данные о потреблении и тарифах оплаты даны в таблице.
| Цена | Сред. расход газа / сред. потребл. мощность | Стоимость газа / электро-энергии | |
|---|---|---|---|
| Газовая плита | 43 730 руб. | 1,2 куб. м/ч | 5,3 руб./куб. м |
| Электроплитка | 17 000 руб. | 6,2 кВт | 3,9 руб./(кВт ч ) |
Обдумав оба варианта, хозяин решил установить газовую плиту. Через сколько часов непрерывного использования экономия от использования газовой плиты вместо электрической компенсирует разность в стоимости установки газовой плиты и электроплитки?
Решение.
Разница в стоимости покупки газовой плиты и электроплитки равна 43 730 − 17 000 = 26 730 руб. Час использования газовой плиты стоит 1,2 5,3 = 6,36 руб. Час использования электроплитки стоит 6,2 3,9 = 24,18 руб. Разница в стоимости составляет 24,18 − 6,36 = 17,82 руб. Значит, экономия от использования газовой плиты вместо электроплитки компенсирует разность в стоимости установки газовой и электрической плит через часов.
Ответ: 1500.
* * * * *
Задание 31
Паркетная доска продаётся в упаковках по 15 штук. Сколько упаковок с паркетной доской нужно купить, чтобы покрыть пол гостиной?
Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели в гостиной после ремонта. Сторона каждой клетки равна 0,4 м. Гостиная имеет прямоугольную форму. Единственная дверь гостиной деревянная, в стене напротив двери расположено окно. Справа от двери будет поставлен комод, слева от двери у стены будет собран книжный шкаф. В глубине комнаты у стены планируется поставить диван. Перед книжным шкафом будет поставлено кресло. Справа от дивана будет стоять торшер. Площадь, занятая диваном, по плану будет равна 1,28 м2. У стены справа от двери планируется поставить письменный стол, а перед ним поставить стул. Пол гостиной (в том числе там, где будет стоять мебель) планируется покрыть паркетной доской размером 40 см × 20 см. Кроме того, владелец квартиры планирует смонтировать в гостиной электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под книжный шкаф, кресло, диван и комод, а также на участок площадью 0,16 м2 между диваном и торшером.
Решение.
Заметим, что чтобы покрыть паркетной доской 0,16 м2 пола, требуется 2 доски. Найдём площадь гостиной:
м2.
Значит, требуется доски. Следовательно, требуется
упаковок с паркетной доской. Таким образом, необходимо купить 13 упаковок.
Ответ: 13.
Задание 32
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Книжный шкаф | Диван | Торшер | Стул |
|---|---|---|---|---|
| Цифры |
Решение.
Слева от двери у стены будет собран книжный шкаф, значит, книжный шкаф отмечен цифрой 1. В глубине комнаты у стены планируется поставить диван, поэтому диван отмечен на плане цифрой 3. Справа от дивана будет стоять торшер, следовательно, торшер отмечен цифрой 7. У стены справа от двери планируется поставить письменный стол, а перед ним поставить стул, значит, стул отмечен цифрой 5.
Ответ: 1375.
Задание 33
Найдите площадь той части гостиной, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м2.
Решение.
Сторона одной клетки равна 0,4 м. Значит, площадь гостиной равна:
м2.
Владелец не станет подводить обогрев под книжный шкаф, кресло, диван и комод, а также на участок площадью 0,16 м2 между диваном и торшером. Книжный шкаф занимает площадь м2. Диван занимает 1,28 м2. Кресло занимает участок площадью
м2. Комод занимает участок площадью
м2. Значит, площадь той части гостиной, на которой будет смонтирован электрический подогрев пола, равна
м2.
Ответ: 12.
Задание 34
Найдите расстояние d между противоположными углами кресла (диагональ). Ответ дайте в метрах в формате
Решение.
Найдём расстояние между противоположными углами кресла по теореме Пифагора:
Таким образом, получаем ответ:
Ответ: 0,8.
Задание 35
Владелец квартиры выбирает торшер из двух моделей А и Б. Цена торшеров и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 4 рубля за кВт ч.
| Модель | Цена торшера (руб) | Среднее потребление электроэнергии в сутки, кВт ч |
|---|---|---|
| А | 2 000 | 0,2 |
| Б | 1 200 | 0,3 |
Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих торшеров? Ответ округлите до целого числа в большую сторону.
Решение.
Разница в стоимости торшеров равна руб. Стоимость электроэнергии за сутки работы первого торшера равна
руб. Стоимость электроэнергии за сутки работы второго торшера равна
руб. Значит, при установке первого торшера владелец квартиры за сутки экономит
руб. Следовательно, в год владелец квартиры экономит
руб. Таким образом, экономия от меньшего расхода электроэнергии окупит разницу в цене этих торшеров через
лет. Округлив, получаем ответ: через 6 лет.
Ответ: 6.
* * * * *
Задание 36
Паркетная доска продаётся в упаковках по 25 штук. Сколько упаковок с паркетной доской нужно купить, чтобы покрыть пол гостиной?
Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели в гостиной после ремонта. Сторона каждой клетки равна 0,4 м. Гостиная имеет прямоугольную форму. Единственная дверь гостиной деревянная, в стене напротив двери расположено окно. Справа от двери будет поставлен письменный стол, а к нему приставлен стул, слева от двери у стены будет собран книжный шкаф. В глубине комнаты у стены планируется поставить диван, а перед ним — журнальный столик. Слева от дивана будет стоять торшер. Площадь, занятая диваном, по плану будет равна 1,6 м2. В оставшемся свободным углу планируется поставить кресло. Пол гостиной (в том числе там, где будет стоять мебель) планируется покрыть паркетной доской размером 40 см × 10 см. Кроме того, владелец квартиры планирует смонтировать в гостиной электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под книжный шкаф, кресло и диван.
Решение.
Заметим, что чтобы покрыть паркетной доской 0,16 м2 пола, требуется 4 доски. Найдём площадь гостиной:
м2.
Значит, требуется доски. Следовательно, требуется
упаковок с паркетной доской. Таким образом, необходимо купить 18 упаковок.
Ответ: 18.
Задание 37
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Стул | Диван | Журнальный столик | Кресло |
|---|---|---|---|---|
| Цифры |
Решение.
Справа от двери будет поставлен письменный стол, а к нему приставлен стул, значит, стул отмечен цифрой 6. В глубине комнаты у стены планируется поставить диван, а перед ним — журнальный столик, следовательно, диван отмечен цифрой 2, а журнальный столик отмечен цифрой 4. В оставшемся свободным углу планируется поставить кресло, поэтому кресло отмечено цифрой 3.
Ответ: 6243.
Задание 38
Найдите площадь той части гостиной, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м2.
Решение.
Сторона одной клетки равна 0,4 м. Значит, площадь гостиной равна:
м2.
Владелец не станет подводить обогрев под книжный шкаф, кресло и диван. Книжный шкаф занимает площадь м2. Диван занимает 1,6 м2. Кресло занимает участок площадью
м2. Значит, площадь той части гостиной, на которой будет смонтирован электрический подогрев пола, равна
м2.
Ответ: 14,56.
Задание 39
Найдите расстояние от дивана до письменного стола (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение.
Найдём расстояние между двумя ближайшими точками по прямой дивана и письменного стола по теореме Пифагора:
Ответ: 2.
Задание 40
Владелец квартиры выбирает торшер из двух моделей А и Б. Цена торшеров и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 5 рублей за кВт ч.
| Модель | Цена торшера (руб) | Среднее потребление электроэнергии в сутки, кВт ч |
|---|---|---|
| А | 2 100 | 0,3 |
| Б | 1 370 | 0,4 |
Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих торшеров? Ответ округлите до целого числа.
Решение.
Разница в стоимости торшеров равна руб. Стоимость электроэнергии за сутки работы первого торшера равна
руб. Стоимость электроэнергии за сутки работы второго торшера равна
руб. Значит, при установке первого торшера владелец квартиры за сутки экономит
руб. Следовательно, в год владелец квартиры экономит
руб. Таким образом, экономия от меньшего расхода электроэнергии окупит разницу в цене этих торшеров через
года.
Ответ: 4.
* * * * *
Задание 41
Паркетная доска продаётся в упаковках по 32 штуки. Сколько упаковок с паркетной доской нужно купить, чтобы покрыть пол в гостиной?
Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели в гостиной после ремонта. Сторона каждой клетки равна 0,4 м. Гостиная имеет прямоугольную форму. Единственная дверь гостиной деревянная, в стене напротив двери расположено окно. Справа от двери будет поставлен письменный стол, а к нему приставлен стул, слева от двери у стены будет собран книжный шкаф. В глубине комнаты у стены планируется поставить диван, а перед ним — журнальный столик. Площадь, занятая диваном, по плану будет равна 1,6 м2. В оставшемся свободным углу планируется поставить кресло. Слева от кресла будет стоять торшер. Пол гостиной (в том числе там, где будет стоять мебель) планируется покрыть паркетной доской размером 40 см × 5 см. Кроме того, владелец квартиры планирует смонтировать в гостиной электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под книжный шкаф, кресло и диван.
Решение.
Заметим, что чтобы покрыть паркетной доской 0,16 м2 пола, требуется 8 досок. Найдём площадь гостиной:
м2.
Значит, требуется доски. Следовательно, требуется
упаковок с паркетной доской.
Приведем другое решение.
Найдем площадь гостиной: м2.
Найдем площадь одной паркетной доски: м2.
Значит, требуется доски, или
упаковок с паркетной доской.
Ответ: 27.
Задание 42
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр без пробелов и других дополнительных символов.
| Объекты | Письменный стол | Диван | Журнальный столик | Торшер |
|---|---|---|---|---|
| Цифры |
Решение.
Справа от двери будет поставлен письменный стол, значит, письменный стол отмечен цифрой 7. В глубине комнаты у стены планируется поставить диван, а перед ним — журнальный столик, следовательно, диван отмечен цифрой 2, а журнальный столик отмечен цифрой 4. В оставшемся свободным углу планируется поставить кресло. Слева от кресла будет стоять торшер, поэтому торшер отмечен цифрой 1.
Ответ: 7241.
Задание 43
Найдите площадь той части гостиной, на которой не будет смонтирован электрический подогрев пола. Ответ дайте в м2.
Решение.
Сторона одной клетки равна 0,4 м. Владелец не станет подводить обогрев под книжный шкаф, кресло и диван. Книжный шкаф занимает площадь м2. Диван занимает 1,6 м2. Кресло занимает участок площадью
м2. Значит, площадь той части гостиной, на которой не будет смонтирован электрический подогрев пола, равна
м2.
Ответ: 3,36.
Задание 44
Найдите расстояние от журнального столика до стула (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение.
Найдём расстояние между двумя ближайшими точками по прямой журнального столика и стула по теореме Пифагора:
Ответ: 2.
Задание 45
В гостиной предполагалось класть ламинат, но решили не экономить и покрыть пол паркетной доской. Ламинат и паркетная доска продаются только в упаковках. Каждая упаковка содержит одинаковое количество м2материала. Сколько рублей можно было бы сэкономить, если бы владелец решил покрыть пол ламинатом?
| Тип покрытия | Стоимость 0,16 м2 материала (руб.) | Стоимость укладки 0,16 м2 материала (руб.) | Количество материала в упаковке (м2) |
|---|---|---|---|
| Паркетная доска | 1400 | 500 | 0,64 |
| Ламинат | 440 | 160 | 0,48 |
Решение.
Найдём площадь гостиной:
м2.
Для того, чтобы покрыть пол в гостиной паркетной доской, требуется купить 27 упаковок материала. Стоимость 27 упаковок паркетной доски равна
рублей.
Стоимость укладки паркетной доски равна
рублей.
Всего на укладку пола в гостиной паркетной доской требуется
рублей.
Для того, чтобы покрыть пол в гостиной ламинатом, требуется купить 36 упаковок материала. Стоимость 36 упаковок ламината равна
рублей.
Стоимость укладки ламината равна
рублей.
Всего на укладку пола в гостиной ламинатом требуется
рублей.
Таким образом, удалось сэкономить
рублей.
Ответ: 140400.
