Задание 5 номер 4236

Тест проверяет умение правильно употреблять слова с учётом их лексического значения и норм лексической сочетаемости.

Инструкция к тесту

В одном из приведённых ниже предложений НЕВЕРНО употреблено выделенное слово. Исправьте ошибку и запишите слово правильно.
Слово записывайте в той же форме, в какой оно стоит в предложении!


Количество вопросов в тесте:
10

Орфографический анализ — задание 5 ОГЭ 2021 по русскому языку.

Презентация для для подготовки к ОГЭ на уроках в 9 классах.

→ скачать презентацию

→ скачать pdf

Презентация содержит материалы:

→ Правописание корней

→ Правописание приставок

→ Буквы И — Ы после приставок

→ Правописание разделительных Ъ и Ь

→ Ь после шипящих укажите верное объяснение написания

→ О, Е, Ё после шипящих под ударением

Автор: Федосеева О. И.

Связанные страницы:

«Сложноподчинённое предложение» — проверочная работа 9 класс

Пунктуационный анализ Задание №3 ОГЭ по русскому языку

Тренировочные варианты ОГЭ-2020 по русскому языку

Анализ средств выразительности — задание 7 ОГЭ по русскому языку

Тренировочный вариант ОГЭ 2020 по русскому языку

Напишем

Теория: «Употребление паронимов»

Словарь паронимов от ФИПИ со значением слов.

Паронимы — это слова, частично схожие в написании и произношении, но разные или частично схожие по значению.

Пример:

  • лесной – лесистый;
  • адресат – адресант;
  • одеть – надеть;
  • водный — водяной и т. д.

Все паронимы можно условно разделить на:

1. Корневые

  • Абонемент — абонент
  • Диктант — диктат
  • Дипломант — дипломат
  • Невежа — невежда
  • Бывший — былой
  • Зачинатель — зачинщик
  • Жестокий — жесткий
  • Отборный — отборочный
  • Добротный — добрый
  • Словарный — словесный
  • Жилищный — жилой

2. Приставочные

(в, вз, вы, из, от, за, на, по, с, раз, о, у, об, пере, пре, предо, пред)

  • Вдох — вздох
  • Выбирая — избирая
  • Выдача — отдача — передача — раздача
  • Выплата — оплата — плата — уплата
  • Выплатить — заплатить — оплатить — отплатить — уплатить
  • Вырастить — нарастить — отрастить
  • Выращивание — наращивание — отращивание
  • Загородить — огородить — оградить — отгородить — перегородить
  • Занизить — понизить — снизить
  • Заплатить — оплатить
  • Заполнить — наполнить — переполнить
  • Заполнен — наполнен — переполнен
  • Надеть — одеть
  • Напоминание — упоминание
  • Обрывок — отрывок
  • Обхватить — охватить
  • Ограничить — отграничить — разграничить
  • Оклик — отклик Отклонение — уклонение
  • Отклоняться — уклоняться
  • Отличать(-ся) — различать(-ся)
  • Отличие — различие
  • Перетерпеть — претерпеть
  • Предоставить — представить

3. Суффиксальные

(смотрим на буквенные сочетания)

Н-ВЕНН

  • Бедный — бедственный
  • Безответны безответственный
  • Благодарный — благодарственный
  • Великий — величественный
  • Единичный — единственный
  • Искусный — искусственный

ЧЕСК-ЧН

  • Артистический — артистичный
  • Гармонический — гармоничный
  • Демократический — Демократичный
  • Дипломатичный — дипломатический
  • Драматический -драматичный
  • Иронический — ироничный
  • Микроскопический — микроскопичный
  • Органический — органичный
  • Практический — практичный
  • Публицистический — публицистичный
  • Романтический — романтичный
  • Сценический — сценичный
  • Технический — техничный
  • Фактический — фактичный
  • Хищнический — хищный
  • Экономический — экономичный — экономный
  • Эстетический — эстетичный
  • Этический — этичный

НН — СК

  • Враждебный — вражеский
  • Звериный — зверский
  • Жизненный — житейский
  • Зрительный — зрительский
  • Изобретательный — изобретательский
  • Популярный — популистский
  • Просвещенный — просветительский
  • Ритмичный — ритмический
  • Соседний — соседский
  • Конный — конский

ИСТ-Н

  • Болотистый — болотный
  • Глинистый — глиняный
  • Каменистый — каменный
  • Лесистый — лесной

Прил. на ТЕЛЬ

  • Благотворительный — благотворный
  • Сравнительный — сравнимый
  • Унизительный — униженный
  • Желательный — желанный
  • Длительный — длинный
  • Обвинительный — обвиненный
  • Представительный — представительский
  • Признательный — признанный

ТН

  • Высокий — высотный
  • Скрытый — скрытный

ОВОЙ — ЧН

  • Вековой — вечный
  • Звуковой — звучный

ОВАНН

  • Гарантированный — гарантийный
  • Лакированный — лаковый

ОСТН — Н

  • Личностный — личный
  • Целостный — цельный (целый)

Материал на — ЯН

  • Костный — костяной
  • Ледовый — ледяной

Существительные на — ОСТЬ

  • Выгода — выгодность
  • Наличие — наличность
  • Гордыня — гордость
  • Гуманизм — гуманность
  • Раздражение — раздражительность
  • Эффективность — эффектность
  • Сопротивление — сопротивляемость

ЧИВ, ЛИВ, ТИВ (прилагательные)

  • Дождливый — дождевой
  • Доверчивый — доверительный
  • Неудачливый — неудачный
  • Памятливый — памятный
  • Удачливый — удачный
  • Продуктивный — продуктовый
  • Эффективный — эффектный
  • Пугливый — пуганый

4. Смешанные

  • Восполнить — дополнить — заполнить — наполнить — переполнить — пополнить
  • Годичный — годовалый — годовой
  • Гуманистический — гуманитарный — гуманный
  • Деловитый — деловой — дельный — деляческий
  • Действительный — действенный — действующий
  • Двоичный — двойной — двойственный — двоякий — сдвоенный — удвоенный
  • Дружный — дружественный — дружеский
  • Информативный — информационный — информация — информированность
  • Исходный — исходящий
  • Красочный — крашеный — красящий
  • Коренастый — коренной — корневой
  • Комфортабельный — комфортный
  • Нетерпеливый – нестерпимый — нетерпимый
  • Мороженый — морозильный — морозный
  • Покупательный — покупательский — покупной
  • Производительный — производственный — производительность
  • Почтенный — почтительный — почетный
  • Царский — царственный – царствующий

Практика ЕГЭ по русскому языку: 

  • решай 5 задание 
  • тренировочные варианты

Соскучились по новым материалам по русскому языку? Мы — да. Не будем растекаться мыслью по древу, а приступим к разбору 5 задания ЕГЭ.

Чтобы правильно ответить на этот вопрос, нужно вспомнить о лексике и группах слов, которые она в себя включает.

Просмотрев рисунок, остановимся на паронимах.

Это слова, близкие по звучанию, однако они частично или полностью различны по значению. В речи они используются для выразительности и акцентировании чего-либо.

Согласитесь, если не знать значения слов — в них легко запутаться.

А сейчас перейдём к заданию 5 № 3846 (https://rus-ege.sdamgia.ru/)

В одном из приведённых ниже предложений НЕВЕРНО употреблено выделенное слово. Исправьте лексическую ошибку, подобрав к выделенному слову пароним. Запишите подобранное слово.

  1. На прилавках магазинов города лежат ОТБОРНЫЕ овощи и фрукты.
  2. Художественная гимнастика — один из самых ЭФФЕКТНЫХ и красивых видов спорта.
  3. Надо вырабатывать навыки ДИПЛОМАТИЧНОГО поведения.
  4. После просмотра фильма у меня сложилось ДВОЯКОЕ впечатление.
  5. ПРОДУКТИВНЫМ было творчество юных мастеров, которые работали под руководством известного художника-оформителя.

Итак, приступим. К слову «отборные» из предложения №1 можно найти пароним «отборочные». Раз речь идет об овощах и фруктах, прилагательное в значении «лучшие», употребленное в примере, весьма подходит к этим существительным.

С тем, что художественная гимнастика — эффектный (красивый, впечатляющий) вид спорта, вряд ли кто-то будет спорить. Слово «эффективный» можно употребить, но смысл предложения значительно изменится.

«Дипломатичное поведение» в предложении №3 нам подходит. Давайте подберём синонимы, чтобы убедиться в этом. Ловкий, тонко и умело действующий — эти слова доказывают, что исправлять ничего не нужно.

Что может быть «двойственным», а что «двояким»? Двойственный — это противоречивый, двуличный, касающийся обеих сторон, двух участников. Двойственное впечатление от фильма получилось от того, что он и понравился, и не понравился, где-то приятно удивил, а где-то испугал.

Двоякий — проявляющий себя в двух смыслах и видах, например, двоякая выгода от путешествий — можно увидеть мир и попрактиковать иностранный язык. Теперь поняли разницу?

И да, «творчество юных мастеров явно было продуктивным», а не продуктовым.

Верный ответ: двойственное.

Если возникают вопросы при нахождении лексического значения слова, можно:

  • подобрать синонимы,
  • вспомнить, как выглядит описываемый предмет,
  • пополнять словарный запас.

Больше о паронимах можно узнать в печатных и онлайн-словарях и на специализированных сайтах.

Интересной вам подготовки к экзаменам вместе с Tutoronline!

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

ВАЖНО! Никаких реальных вариантов ни до экзамена, ни во время его проведения на сайте нет, не было и не будет.

ЗАПРЕЩЕНО копирование материалов без указания активные ссылки на источник

В случае нарушения авторских прав, правообладателям обращаться по адресу:

Контакты: tolkoexamen@gmail.com

Информация по каждому номеру
России, перенесённые номера, жалобы.

Какой оператор и регион у телефонных номеров
+7 (4236) xx-xx-xx

Телефонные номера с кодом города 4236 обслуживаются у 12 операторов связи и используются в Приморском крае (административный центр края — город Владивосток).

Код 4236 иногда называют местным кодом.
Шестизначный номер телефона XX-XX-XX,
который следует за этим кодом, называется местным или городским номером.
При открытом плане нумерации, который действует в подавляющем большинстве
регионов России, местные звонки могут осуществляться с помощью этого
короткого номера, что значительно упрощает набор вручную.
Формат записи номера
с выделением скобками кода города
+7 (4236) xx-xx-xx
наиболее распространён, т.к.
очень часто используется в справочниках, визитках, блоках с контактной информацией и т.д.

Код 423 называется ABC-кодом (кодом зоны нумерации), который присваивается телефонным номерам по географическому признаку. Номера с таким кодом встречаются в одном регионе России и находятся на обслуживании у 30 операторов связи. Данные операторы могут выделить до 1 858 331 телефонных номеров с кодом 423. Такой формат записи +7 (423) 6xx-xx-xx, как правило, можно увидеть на экранах мобильных телефонов.

Используйте универсальную

форму поиска
для точного
определения оператора и региона любого телефонного номера
(учитывается перенос номеров к другому оператору),
а также просмотра жалоб, которые оставляют посетители
сайта на номера мошенников.

Как узнать, кто звонил с неизвестного номера?

Оператор Диапазон номеров Регион Ёмкость


Ростелеком

ЗАО «АКОС»

+7
(4236) 12-00-00


+7
(4236) 12-99-99

г. Арсеньев

Приморский край
10 000


Ростелеком

ПАО «Ростелеком»

+7
(4236) 13-00-00


+7
(4236) 14-99-99

г. Арсеньев

Приморский край
20 000


Билайн

ПАО «Вымпел-Коммуникации»

+7
(4236) 15-00-00


+7
(4236) 15-01-99

г. Арсеньев

Приморский край
200


Билайн

ПАО «Вымпел-Коммуникации»

+7
(4236) 15-20-00


+7
(4236) 15-69-99

г. Арсеньев

Приморский край
5 000


Ростелеком

ПАО «Ростелеком»

+7
(4236) 29-10-00


+7
(4236) 29-19-99

м.о. Анучинский

Приморский край
1 000


Ростелеком

ПАО «Ростелеком»

+7
(4236) 29-21-00


+7
(4236) 29-23-99

м.о. Анучинский

Приморский край
300


Ростелеком

ПАО «Ростелеком»

+7
(4236) 29-31-00


+7
(4236) 29-31-99

м.о. Анучинский

Приморский край
100

Приморский край обслуживают 36 операторов связи. Ёмкость всех номеров региона — 9 700 031.

Край расположен на юге Дальнего Востока, в юго-восточной части Российской Федерации. Входит в состав Дальневосточного федерального округа и Дальневосточного экономического района.

Ниже в таблице перечислены все телефонные коды Приморского края с указанием суммарной ёмкости номеров по каждой группе кодов. Дополнительно данный регион отмечен на карте России.

Можно ли определить точное местоположение человека по номеру телефона?

  • — Территория РФ
  • — Действующие регионы

Операторы номеров

Все телефонные номера
+7 (4236) xx-xx-xx
выделены

12 операторам связи.

Всего в России
действуют
1 799 операторов
стационарной и мобильной связи.

  • Ростелеком


    177 930 номеров

  • Билайн


    52 200 номеров

  • МТС


    17 500 номеров

  • ООО «Неоком»


    10 000 номеров

  • ОАО «Телекоммуникации СЭЗ «Находка»


    10 000 номеров

  • NETBYNET


    4 512 номеров

  • МегаФон


    3 000 номеров

  • Теле2


    2 000 номеров

  • Российские железные дороги


    2 000 номеров

  • ЭР-Телеком Холдинг


    500 номеров

  • ООО «Телеком-ВИСТ»


    100 номеров

  • ООО «ОктопусНет»


    35 номеров

Другие коды городов Приморского края

Все телефонные коды городов, которые начинаются на
423,
принадлежат
Приморскому краю:

Жалобы на номера, сообщения о мошенничестве, комментарии

Если Вам звонят подозрительные люди,
Вы пострадали от телефонных мошенников, часто получаете спам
по SMS или терпите рекламные звонки на номер своего телефона,
у Вас есть жалобы или претензии на работу мобильных операторов
— сообщите, пожалуйста, об этом ниже.

Кому-то такая информация может быть очень полезной и нужной.

Истоники данных:
Реестр Российской системы и плана нумерации, сформированный Федеральным агентством связи
(Россвязь),
утверждённый приказом Министерства цифрового развития,
связи и массовых коммуникаций Российской Федерации
(Минкомсвязь России),
а так же база данных перенесенных абонентских номеров
Центрального научно-исследовательского института связи
(ФГУП ЦНИИС).

Задание 5 учит вас различать слова, похожие и по значению, и по написанию. Это паронимы. Значения паронимов становятся понятны в контексте – словосочетаниях и предложениях. Запоминайте их именно так. А мы дадим вам несколько подсказок.

Задание 5 ЕГЭ по русскому языку

Формулировка задания:

В одном из приведенных ниже предложений НЕВЕРНО употреблено выделенное слово. Исправьте лексическую ошибку, подобрав к выделенному слову пароним. Запишите выделенное слово.

Радость охватила душу путешественника.

Её постигло нестерпимое горе.

Его считали человеком замкнутым и скрытым.

Это происшествие оказалось единичным.

Как видите, надо не просто найти ошибку, а подобрать нужное слово-пароним.

Паронимы – это однокоренные слова, которые различаются приставками  или суффиксами. Но при внешнем сходстве они имеют разные лексические значения и сочетаются с разными словами.

Выполним задание, обратившись к словарю паронимов:

  1. Обхватить – обнять, заключить между распростертыми руками, пальцами, лапами: обхватить ствол; обхватить пальцами запястье.

    2.  Охватить – 1) воспринять целиком что-нибудь большое: охватить взглядом; 2) включить, ввести в круг чего-либо: охватить заботой; 3) заключить в свои пределы: пламя охватило дом.

  2. Нестерпимый – с трудом переносимый, очень сильный по степени проявления: нестерпимая жара.

    3. Нетерпеливый – испытывающий или выражающий нетерпение: нетерпеливый ребенок.

    Нетерпимый – 1) такой, с которым нельзя мириться, недопустимый: нетерпимая выходка; 2) тот, кто отличается нетерпимостью: человек ограниченный и нетерпимый.

  3. Скрытный – скрывающий свои чувства, мысли, намерения, не обнаруживающий себя или скрываемый: скрытный человек, скрытная жизнь.

    4. Скрытый – скрываемый, тайный, внешне незаметный или еще не проявившийся: скрытая угроза, скрытая камера.

  4. Единичный – отдельный, обособленный, индивидуальный: единичный случай.

    5. Единственный – только один: единственная радость.

Словарь паронимов для подготовки к ЕГЭ вы вполне можете осилить, тем более что значение большинства слов вам известно. Останавливайтесь на том, что показалось трудным. Главное: запоминайте весь «куст» паронимов, а значение каждого паронима запоминайте через пример (пароним «живет» именно в контексте).

На что следует обратить внимание? Суффикс Н в прилагательном подсказывает, что прилагательное называет качество, от него можно образовать краткую форму. Другой суффикс делает прилагательное относительным, называющим признак по отношению к чему-либо.

Например: артистичный человек – артистическое кафе, благотворное влияние – благотворительное мероприятие, этичное поведение – этические нормы поведения.

Суффикс ИСТ придает прилагательному значение «с большим содержанием чего-либо»: глинистая почва, каменистая дорога, костистая рыба. Сравните эти прилагательные с их паронимами со значением «сделанный из»: глиняный, каменный, костяной.

Есть паронимы с очень узкой сочетаемостью: преходящая слава (минутная, временная, быстро проходящая), высотные дома (многоэтажные).

Порой каждый из паронимов обладает не одним, а несколькими значениями: представить  сотрудника; 2) представить отчёт; 3) представить себе картину – 1) предоставить отпуск; 2) предоставить кредит; 3) предоставить возможность оправдаться.

Есть паронимы, указывающие на разное отношение к явлению, которое они называют: зачинатель – основоположник чего-то хорошего, положительного, а зачинщик – отрицательного.

Паронимы — это результат сложившейся языковой практики, они трудно поддаются классификации. Мы говорим: ледовая арена, ледовый завал, но ледяная вершина, ледяная глыба. Здесь поможет только практическое знакомство и опыт.

Напомним знаменитую пару: надеть на себя – одеть кого-то другого.

Словарь паронимов ЕГЭ-2017 можно найти на сайте fipi

Смотрите наши видео

Источник

Автомобильное колесо, как правило, представляет из себя металлический диск, с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65R15 (см. рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 2). 

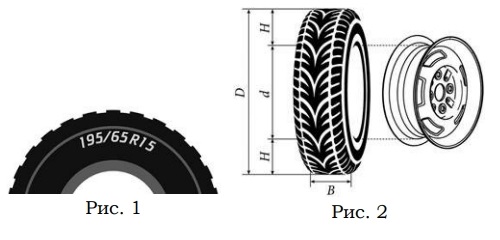Для маркировки автомобильных шин применяется единая система обозначений (см. рис. 1). Второе число (число 65 в приведённом примере) – процентное отношение высоты боковины (параметр Н на рисунке 9) к ширине шины, то есть 100cdot frac{H}{B}.
Последующая буква обозначает тип конструкции шины. В данном примере буква R обозначает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяется шины радиальной конструкции. 
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 235/65 R17.

Источник: ОГЭ Ященко 2023 (36 вар)

Задание 1

Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин. 

Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин. Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 19 дюймам? Ответ дайте в миллиметрах.

Решение

По таблице видим, что наименьшая ширина для диска 19 дюймов равна 245 мм:

Решение №3236 Автомобильное колесо, как правило, представляет из себя металлический диск, с установленной на него резиновой шиной.

Ответ: 245.

Задание 2

Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.

Решение

Найдите диаметр колеса автомобиля, выходящего с завода.

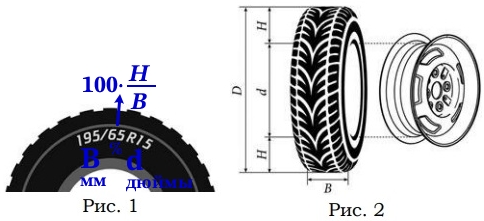
    С завода выходит вот такое колесо 235/65 R17.
    D состоит из d диска и 2-х Н. Найдём Н:

100cdot frac{H}{B}=65\frac{H}{B}=frac{65}{100}\frac{H}{235}=0,65\H=235cdot 0,65=152,75 мм

    Найдём d диска. 17 дюймов. 1 дюйм = 25,4 мм.

17·25,4 = 431,8 мм

    Найдём диаметр колеса:

D = d + 2·H = 431,8 + 2·152,75 = 737,3 мм

Ответ: 737,3.

Задание 3

На сколько миллиметров радиус колеса с шиной маркировки 220/60 R16 меньше, чем радиус колеса с шиной маркировки 245/55 R16?

Решение

На сколько миллиметров радиус колеса с шиной маркировки 22060 R16 меньше, чем радиус колеса с шиной маркировки 24555 R16

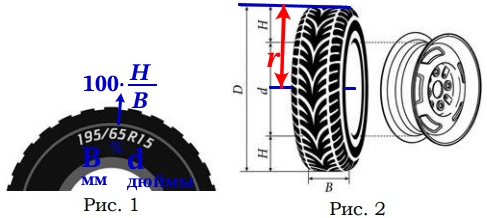
    Видим, что у наших колёс один и тот же диаметр диска 16 дюймов, значит их радиус будет отличатся только в Н. Найдём Н для 220/60 R16:

100cdot frac{H}{B}=60\frac{H}{B}=frac{60}{100}\frac{H}{220}=0,6\H=220cdot 0,6=132 мм

    Найдём Н для 245/55 R16:

100cdot frac{H}{B}=55\frac{H}{B}=frac{55}{100}\frac{H}{245}=0,55\H=245cdot 0,55=134,75 мм

    Найдём разницу:

134,75 – 132 = 2,75 мм

Ответ: 2,75.

Задание 4

На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 245/65 R17? Округлите результат до десятых.

Решение:

    Пробег при одном обороте это длина окружности шины, находится по формуле:

l = 2πR = πD

    π величина постоянная, поэтому всё будет зависеть от изменения D. На заводских шинах D = 737,3 мм (знаем из задания 2).
     Найдём D шины с маркировкой 245/65 R17.
     Найдём Н:

100cdot frac{H}{B}=65\frac{H}{B}=frac{65}{100}\frac{H}{245}=0,65\H=245cdot 0,65=159,25 мм

     Найдём d диска. 17 дюймов. 1 дюйм = 25,4 мм.

17·25,4 = 431,8 мм

     Найдём диаметр колеса:

D = d + 2·H = 431,8 + 2·159,25 = 750,3 мм

     Найдём разницу D колёс:

750,3 – 737,3 = 13 мм

     Найдём сколько это составляет процентов от заводских колёс, округлив до десятых:

frac{13}{737,3}cdot 100%≈0,0176..cdot 100% ≈1,8%

Ответ: 1,8.

Задание 5

Сергей планирует заменить зимнюю резину на летнюю на своём автомобиле. Для каждого из четырёх колёс последовательно выполняются четыре операции: снятие колеса, замена шины, балансировка колеса и установка колеса. Он выбирает между автосервисами А и Б. Затраты на дорогу и стоимость операций даны в таблице. 

Сергей планирует заменить зимнюю резину на летнюю на своём автомобиле.

Сколько рублей заплатит Сергей за замену резины на своём автомобиле, если выберет самый дешёвый вариант?

Решение:

    Затраты в автосервисе А:

110 + 4·(40 + 170 + 180 + 40) = 1830 рублей

    Затраты в автосервисе Б:

70 + 4·(50 + 175 + 170 + 50) = 1850 рублей

    Самый дешёвый вариант стоит 1830 рублей.

Ответ: 1830.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.8 / 5. Количество оценок: 52

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Задание 1 № 366805

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты Город Гранюк Деревня Астрелка Хутор Южный Город Гусевск
Цифры        

Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.

Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.

Ответ: 1465.

2. Задание 2 № 366806

Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.

Решение.

Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится

пачек чая.

Таким образом, ребята должны купить 14 пачек чая.

Ответ: 14.

3. Задание 3 № 366807

Найдите площадь (в км2), которую занимает заказник.

Решение.

Площадь заказника равна:

Ответ: 351.

4. Задание 4 № 366808

Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.

Решение.

Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:

км.

Ответ: 30.

5. Задание 5 № 366809

Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.

Продукция Цена в магазине «Вело» (руб.) Цена в магазине «ОК» (руб.) Срок доставки из магазина «ОК» (дни)
Подсветка для спиц
Шина вида «А»
Шина вида «Б»
Спица
Педаль вида «А»
Педаль вида «Б»
Тормоз вида «А» нет
Тормоз вида «Б» нет
Набор крепёжных изделий

Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?

Решение.

На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:

руб.

Ответ: 5300.

6. Задание 6 № 316314

Найдите значение выражения:

Решение.

Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.

7. Задание 7 № 317575

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?

1)

2)

3)

4)

Решение.

Заметим, что и Проверим все варианты ответа:

1) — неверно;

2) — верно;

3) — верно;

4) — верно.

Ответ указан под номером 1.

8. Задание 8 № 353586

Какое из данных ниже чисел является значением выражения

1)

2)

3)

4)

Решение.

Последовательно получим:


Ответ: 1

9. Задание 9 № 338500

При каком значении значения выражений и равны?

Решение.

Для ответа на вопрос задачи нужно решить уравнение Решим его:

Ответ: 2.

10. Задание 10 № 325450

В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.

Решение.

Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна

Ответ: 0,3.

11. Задание 11 № 311406

На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке

2)

3)

4) прямая пересекает график в точках и

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .

2) — неверно,

3) — верно, видно из графика.

4) Прямая пересекает график в точках и — верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

Ответ: 12.

12. Задание 12 № 311543

Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .

Решение.

Выразим :

Подставляя, получаем:

Ответ: 0,4.

13. Задание 13 № 338497

На каком из рисунков изображено решение неравенства

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

Решение.

Решим неравенство методом интервалов:

Правильный ответ указан под номером: 4.

14. Задание 14 № 406645

В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение.

Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.

Найдем сумму этой прогрессии:

Ответ: 377 мест.

15. Задание 15 № 340000

В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите

Решение.

Из прямоугольного треугольника по теореме Пифагора найдём

Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.

16. Задание 16 № 351463

На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.

Решение.

Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.

17. Задание 17 № 169876

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.

———-

В открытом банке иррациональный ответ.

18. Задание 18 № 350842

Найдите угол

Решение.

Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.

Ответ: 22,5

19. Задание 19 № 401617

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Ответ: 13.

20. Задание 20 № 338505

Решите неравенство

Решение.

Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение

Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).

Таким образом, ответ

Ответ:

Примечание.

Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,

21. Задание 21 № 353527

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.

Ответ: 58.

22. Задание 22 № 338288

Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.

Решение.

Упростим выражение:

По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:

График функции сводится к графику параболы с выколотой точкой

Выделим полный квадрат:

Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)

Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и

Ответ: −1; 3.

23. Задание 23 № 339395

Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.

Решение.

Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и

Ответ: 16.

24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.

Решение.

Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.

25. Задание 25 № 311926

В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .

Решение.

По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,

Площадь трапеции :

Площадь трапеции


Ответ: 9.

Источник

Страница 3 из 7

Практические задачи №1-5 к ОГЭ по математике

Прочитайте внимательно текст и выполните задания 1–5.

Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.
И так далее.

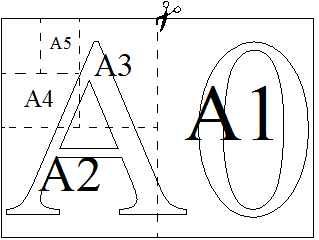
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.

Номер листа

Длина (мм)

Ширина (мм)

1

297

210

2

420

297

3

1189

841

4

841

594

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
Ответ: 3421

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А3, А5 и А6.

Номер листа

Длина (мм)

Ширина (мм)

1

210

148

2

594

420

3

148

105

4

420

297

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 2413

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А2, А3 и А4.

Номер листа

Длина (мм)

Ширина (мм)

1

841

594

2

420

297

3

594

420

4

297

210

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
Ответ: 1324

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А3, А4, А5 и А6.

Номер листа

Длина (мм)

Ширина (мм)

1

148

105

2

210

148

3

420

297

4

297

210

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3421

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А2, А5 и А6.

Номер листа

Длина (мм)

Ширина (мм)

1

594

420

2

148

105

3

210

148

4

841

594

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 4132

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А3, А4 и А6.

Номер листа

Длина (мм)

Ширина (мм)

1

594

420

2

420

297

3

148

105

4

297

210

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 1243

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А2 и А4.

Номер листа

Длина (мм)

Ширина (мм)

1

841

594

2

1189

841

3

297

210

4

594

420

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
Ответ: 2143

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А3, А4 и А5.

Номер листа

Длина (мм)

Ширина (мм)

1

420

297

2

297

210

3

841

594

4

210

148

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3124

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А4, А5 и А6.

Номер листа

Длина (мм)

Ширина (мм)

1

297

210

2

148

105

3

594

420

4

210

148

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3142

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А3, А4 и А6.

Номер листа

Длина (мм)

Ширина (мм)

1

148

105

2

420

297

3

297

210

4

841

594

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 4231

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А2, А3 и А5.

Номер листа

Длина (мм)

Ширина (мм)

1

594

420

2

420

297

3

1189

841

4

210

148

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3124

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А3, А5 и А6.

Номер листа

Длина (мм)

Ширина (мм)

1

210

148

2

841

594

3

420

297

4

148

105

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 2314

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А2, А3 и А5.

Номер листа

Длина (мм)

Ширина (мм)

1

210

148

2

594

420

3

420

297

4

841

594

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 4231

Задание 2.
Сколько листов формата А3 получится из одного листа формата А2?

Решение:

А2 594*420
А3 420*297

Ответ: 2

Задание 2.
Сколько листов формата А3 получится из одного листа формата А1?

Решение:

А1 841*594
А2 594*420 — 2 шт
А3 420*297 — 4 шт.

Ответ: 4

Задание 2.
Сколько листов формата А3 получится из одного листа формата А0?

Решение:

А0 1189*841
А1 841*594 — 2 шт.
А2 594*420 — 2*2= 4 шт
А3 420*297 — 4*2 = 8 шт.

Ответ: 8

Задание 2.
Сколько листов формата А5 получится из одного листа формата А0?

Решение:

А0 1189*841
А1 841*594 — 2 шт
А2 594*420 — 4 шт.
А3 420*297 — 8 шт.
А4 297*210 — 16 шт.
А5 210*148 — 32 шт.
Ответ: 32

Задание 2.
Сколько листов формата А5 получится из одного листа формата А1?

Решение:

А1 841*594 
А2 594*420 — 2 шт.
А3 420*297 — 4 шт.
А4 297*210 — 8 шт.
А5 210*148 — 16 шт.
Ответ: 16

Задание 2.
Сколько листов формата А5 получится из одного листа формата А3?

Решение:

А3 420*297
А4 297*210 — 2 шт.
А5 210*148 — 4 шт.
Ответ: 4

Задание 2.
Сколько листов формата А6 получится из одного листа формата А2?

Решение:

А2 594*420
А3 420*297 — 2 шт.
А4 297*210 — 4 шт.
А5 210*148 — 8 шт.
А6 148*105 — 16 шт.
Ответ: 16

Задание 2.
Сколько листов формата А6 получится из одного листа формата А0?

Решение:

А0 1189*841
А1 841*594 — 2
А2 594*420 — 4
А3 420*297 — 8
А4 297*210 — 16
А5 210*148 — 32
А6 148*105 — 64
Ответ: 64

Задание 2.
Сколько листов формата А6 получится из одного листа формата А3?

Решение:

А3 420*297
А4 297*210 — 2
А5 210*148 — 4
А6 148*105 — 8
Ответ: 8

Задание 2.
Сколько листов формата А6 получится из одного листа формата А1?

Решение:

А1 841*594
А2 594*420 — 2
А3 420*297 — 4
А4 297*210 — 8 
А5 210*148 — 16
А6 148*105 — 32
Ответ: 32

Задание 2.
Сколько листов формата А4 получится из одного листа формата А2?

Решение:

А2 594*420
А3 420*297 — 2 
А4 297*210 — 4
Ответ: 4

Задание 2.
Сколько листов формата А4 получится из одного листа формата А1?

Решение:

А1 841*594 
А2 594*420 — 2
А3 420*297 — 4
А4 297*210 — 8
Ответ: 8

Задание 2.
Сколько листов формата А4 получится из одного листа формата А0?

Решение:

А0 1189*841
А1 841*594 — 2
А2 594*420 — 4
А3 420*297 — 8
А4 297*210 — 16
Ответ: 16

Задание 3.
Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5000 см2

Ответ: 5000

Задание 3.
Найдите площадь листа формата А2. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5000 см2
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см2/2=2500 см2
Ответ: 2500

Задание 3.
Найдите площадь листа формата А3. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5 000 см2
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см2/2=2 500 см2
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см2/2=1 250 см2
Ответ: 1250

Задание 3.
Найдите площадь листа формата А6. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5 000 см2
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см2/2=2 500 см2
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см2/2=1 250 см2
Лист формата А4 имеет форму прямоугольника, площадь которого равна 1250 см2/2=625 см2
Лист формата А5 имеет форму прямоугольника, площадь которого равна 625 см2/2=312,5 см2
Лист формата А6 имеет форму прямоугольника, площадь которого равна 312,5 см2/2=156,25 см2

Ответ: 156,25

Задание 3.
Найдите площадь листа формата А5. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5 000 см2
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см2/2=2 500 см2
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см2/2=1 250 см2
Лист формата А4 имеет форму прямоугольника, площадь которого равна 1250 см2/2=625 см2
Лист формата А5 имеет форму прямоугольника, площадь которого равна 625 см2/2=312,5 см2

Ответ: 312,5

Задание 3.
Найдите площадь листа формата А4. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см2/2=5 000 см2
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см2/2=2 500 см2
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см2/2=1 250 см2
Лист формата А4 имеет форму прямоугольника, площадь которого равна 1250 см2/2=625 см2

Ответ: 625

Задание 3.
Найдите ширину листа бумаги формата А0. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А0 1189*841, то есть ширина кратная 10 будет 840

Ответ: 840

Задание 3.
Найдите ширину листа бумаги формата А1. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А1 841*594 , то есть ширина кратная 10 будет 590

Ответ: 590

Задание 3.
Найдите ширину листа бумаги формата А2. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А2 594*420 , то есть ширина кратная 10 будет 420

Ответ: 420

Задание 3.
Найдите ширину листа бумаги формата А3. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А3 420*297 , то есть ширина кратная 10 будет 300

Ответ: 300

Задание 3.
Найдите ширину листа бумаги формата А4. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А4 297*210 , то есть ширина кратная 10 будет 210
Ответ: 210

Задание 3.
Найдите ширину листа бумаги формата А5. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А5 210*148, то есть ширина кратная 10 будет 150
Ответ: 150

Задание 3.
Найдите ширину листа бумаги формата А6. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 5.

Решение:

А6 148*105, то есть ширина кратная 10 будет 110
Ответ: 110

Задание 4.
Найдите длину листа бумаги формата А1. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А1 841*594, то есть длина кратная 10 будет 840

Ответ: 840

Задание 4.
Найдите длину листа бумаги формата А2. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А2 594*420, то есть длина кратная 10 будет 600

Ответ: 600

Задание 4.
Найдите длину листа бумаги формата А3. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А3 420*297, то есть длина кратная 10 будет 420

Ответ: 420

Задание 4.
Найдите длину листа бумаги формата А4. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А4 297*210, то есть длина кратная 10 будет 300
Ответ: 300

Задание 4.
Найдите длину листа бумаги формата А5. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А5 210*148, то есть длина кратная 10 будет 210

Ответ: 210

Задание 4.
Найдите длину листа бумаги формата А6. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А6 148*105, то есть длина кратная 10 будет 150
Ответ: 150

Задание 4.
Найдите длину листа бумаги формата А7. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 5.

Решение:

А7 105*74, то есть длина кратная 10 будет 110
Ответ: …

Задание 4.
Найдите отношение длины меньшей стороны листа формата А3 к большей. Ответ округлите до десятых.

Решение:

А3 420*297 
420/297=1,41

Ответ: 1,4

Задание 4.
Найдите отношение длины меньшей стороны листа формата А4 к большей. Ответ округлите до десятых.

Решение:

А4 297*210
297/210=1,41
Ответ: 1,4

Задание 4.
Найдите отношение длины меньшей стороны листа формата А5 к большей. Ответ округлите до десятых.

Решение:

А5 210*148
210/148=1,41
Ответ: 1,4

Задание 4.
Найдите отношение длины большей стороны листа формата А2 к меньшей. Ответ округлите до десятых.

Решение:

А2 594*420
594/420=1,41
Ответ: 1,4

Задание 4.
Найдите отношение длины большей стороны листа формата А6 к меньшей. Ответ округлите до десятых.

Решение:

А6 148*105
148/105=1,409
Ответ: 1,4

Задание 4.
Найдите отношение длины большей стороны листа формата А1 к меньшей. Ответ округлите до десятых.

Решение:

А1 841*594
841/594=1,41
Ответ: 1,4

Задание 4.
Найдите отношение длины диагонали листа формата А2 к его меньшей стороне. Ответ округлите до десятых.

Решение:

А2 594*420
Меньшая сторона формата А2 равна 420 мм, большую сторона формата А2 594 мм. Диагональ является гипотенузой треугольника с катетами 420 мм и 594 мм, по теореме Пифагора имеем:
$sqrt{594*594+420*420}≈727$ мм
Найдем отношения длины диагонали к меньшей стороне:
727/420 ≈ 1,7.

Ответ: 1,7.

Задание 4.
Найдите отношение длины диагонали листа формата А0 к его меньшей стороне. Ответ округлите до десятых.

Решение:

А0 1189*841
Меньшая сторона формата А0 равна 841 мм, большую сторона формата А0 1189 мм. Диагональ является гипотенузой треугольника с катетами 841 мм и 1189 мм, по теореме Пифагора имеем:
$sqrt{841*841+1189*1189}≈1456$ мм
Найдем отношения длины диагонали к меньшей стороне:
1456/841 ≈ 1,7.

Ответ: 1,7

Задание 4.
Найдите отношение длины диагонали листа формата А7 к его меньшей стороне. Ответ округлите до десятых.

Решение:

А7 105*74
Меньшая сторона формата А7 равна 74 мм, большую сторона формата А7 105 мм. Диагональ является гипотенузой треугольника с катетами 74 мм и 105 мм, по теореме Пифагора имеем:
$sqrt{74*74+105*105}≈129$ мм
Найдем отношения длины диагонали к меньшей стороне:
129/74 ≈ 1,7.
Ответ: 1,7

Задание 5.
Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 32 листа формата А5, поэтому площадь листа формата А5 в 32 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А5 равен  дробь:
80/32, а вес пачки равен  80/32 * 500=1250  граммов.
Ответ: 1250

Задание 5.
Бумагу формата А4 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г? Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 16 листа формата А4, поэтому площадь листа формата А4 в 16 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А5 равен дробь:
80/16, а вес пачки равен  80/16 * 500=2500  граммов.
Ответ: 2500

Задание 5.
Бумагу формата А3 упаковали в пачки по 200 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 8 листов формата А3, поэтому площадь листа формата А3 в 8 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
80/8, а вес пачки равен  80/8 * 500=5000  граммов.
Ответ: 5000

Задание 5.
Бумагу формата А3 упаковали в пачки по 250 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 120 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 8 листов формата А3, поэтому площадь листа формата А3 в 8 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
120/8, а вес пачки равен  120/8 * 250=3750  граммов.
Ответ: 3750

Задание 5.
Бумагу формата А2 упаковали в пачки по 100 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 96 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 4 листа формата А2, поэтому площадь листа формата 2 в 4 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А2 равен дробь:
96/4, а вес пачки равен  96/4 * 100=2400  граммов.
Ответ: 2400

Задание 5.
Бумагу формата А1 упаковали в пачки по 80 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 120 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 2 листов формата А1, поэтому площадь листа формата А1 в 2 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А1 равен дробь:
120/2, а вес пачки равен  120/2 * 80=4800  граммов.
Ответ: 4800

Задание 5.
Бумагу формата А3 упаковали в пачки по 120 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 96 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 8 листов формата А3, поэтому площадь листа формата А3 в 8 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
96/8, а вес пачки равен  96/8 * 120=1440  граммов.
Ответ: 1440

Задание 5.
Бумагу формата А4 упаковали в пачки по 800 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 16 листов формата А4, поэтому площадь листа формата А4 в 16 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
80/16, а вес пачки равен  80/16 * 800=4000  граммов.
Ответ: 4000

Задание 5.
Бумагу формата А5 упаковали в пачки по 1000 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 144 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 32 листов формата А5, поэтому площадь листа формата А5 в 32 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А5 равен дробь:
144/32, а вес пачки равен  144/32 * 1000=4500  граммов.
Ответ: 4500

Задание 5.
Бумагу формата А6 упаковали в пачки по 320 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 108 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 64 листа формата А6, поэтому площадь листа формата А6 в 64 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А6 равен дробь:
108/64, а вес пачки равен  108/64 * 320=540  граммов.
Ответ: 540

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 15 пунктов на листе формата А4? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

15*1,41=21,15 мм ≈21 

Ответ: 21

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А5 так же, как этот же текст, напечатанный шрифтом высотой 16 пунктов на листе формата А4? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

16/1,41=11,34 мм ≈11

Ответ: 11

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
8 пунктов на листе формата А5. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А4 таким же образом? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

8*1,41=11,28 мм ≈11 

Ответ: 11

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
12 пунктов на листе формата А4. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 таким же образом? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

13*1,41=16,92 мм ≈17 

Ответ: 17

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 12 пунктов на листе формата А5? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

12*1,41=16,92 мм ≈17 

Ответ: 17

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
22 пункта на листе формата А3. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А2 таким же образом? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

22*1,41=31,02 мм ≈31

Ответ: 31

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
20 пунктов на листе формата А4. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 таким же образом? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

20*1,41=28,2 мм ≈28 

Ответ: 28

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 17 пунктов на листе формата А3? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

17/1,41=12,06 мм ≈12 

Ответ: 12

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 21 пункт на листе формата А3? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

21/1,41=14,89 мм ≈15 

Ответ: 15

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А5 так же, как этот же текст, напечатанный шрифтом высотой 20 пунктов на листе формата А4? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

20/1,41=14,84 мм ≈15 мм

Ответ: 15

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 10 пунктов на листе формата А4? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

10*1,41=14,1 мм ≈14 мм

Ответ: 14

B9A7F7

Источник

  • Задание 5 номер 368432
  • Задание 6 номер 337402
  • Задание 5 номер 367003
  • Задание 6 номер 337385
  • Задание 5 номер 366900