Задание 3 номер 12970 - Большой телефонный справочник предприятий

Задания 2, 3, 4 ОГЭ по русскому языку с пояснениями с сайта Решу ОГЭ

1. Задание 2 № 12951

Синтаксический анализ.

Прочитайте текст.

(1)Наклонились вниз на длинном стебельке белоснежные фарфоровые кольца с резными краями. (2)Кажется, что неизвестный мастер придал такую необычную форму речному жемчугу. (3)К концу лета они превратятся в оранжево-красные бусинки. (4)Словно из далеких стран попали в лес драгоценные камни.

(5)Ландыш представляется мне символом леса.

Укажите варианты ответов, в которых верно выделена грамматическая основа в одном из предложений или в одной из частей сложного предложения текста. Запишите номера ответов.

1) Кольца наклонились вниз (предложение 1)

2) Мастер придал (предложение 2)

3) Превратятся в бусики (предложение 3)

4) Камни попали (предложение 4)

5) Ландыш представляется символом (предложение 5)

2. Задание 2 № 12952

Синтаксический анализ.

Прочитайте текст.

(1)Закат тяжело пылает на кронах деревьев, золотит их старинной позолотой. (2)Последний луч солнца ещё касается их верхушек, а у подножия сосен уже темно и глухо. (3)Бесшумно летают и словно заглядывают в лицо летучие мыши. (4)На западе ещё тлеет зорька, в зарослях волчьих ягод кричит выпь. (5)Вот и озеро.

1) Закат пылает, золотит (предложение 1)

2) Луч солнца касается (предложение 2)

3) Мыши заглядывают (предложение 3)

4) Тлеет, кричит (предложение 4)

5) Озеро (предложение 5)

3. Задание 2 № 12953

Синтаксический анализ.

Прочитайте текст.

(1)В охотничью пору на Урале мы уходили в горы и бродили там, как настоящие дикари. (2)Солнечный закат в горах удивительно хорош. (3)Тени нарастают, и на нас начинает надвигаться ночная мгла. (4)Затихший воздух чутко держит каждый шорох. (5)Переживаешь тревожное настроение, которое будит воображение.

1) Мы бродили (предложение 1)

2) Закат хорош (предложение 2)

3) Мгла начинает двигаться (предложение 3)

4) Держит шорох (предложение 4)

5) Будит воображение (предложение 5)

4. Задание 2 № 12954

Синтаксический анализ.

Прочитайте текст.

(1)Часами он бродил после бури по берегу и спасал, кого ещё можно спасти. (2)Он радовался, видя, как рыба, брошенная в воду, уплывала, весело махнув хвостом. (3)Он радовался каждый раз, когда полууснувшие рыбы, плававшие в воде боком или брюшком, в конце концов оживали. (4)Подбирая на берегу большую рыбу, Ихтиандр нёс её к воде. (5)Рыба трепетала в его руках, а он смеялся и уговаривал её не биться и потерпеть ещё немного.

1) Он бродил (предложение 1)

2) Рыба уплывала (предложение 2)

3) Он радовался (предложение 3)

4) Ихтиандр нес её (предложение 4)

5) Он уговаривал не биться и потерпеть (предложение 5)

5. Задание 2 № 12955

Синтаксический анализ.

Прочитайте текст.

(1) Вот зазвенел сушняк, захрустел снег. (2)Это через сугробы по лунной дорожке пробираются дымчато-серые лоси. (3)В поисках пищи приходится шагать им по глубокому снегу в юго-восточном направлении. (4)Трудно искать пищу зимой!

(5)Скоро весна, но золотисто-красное солнышко придет в тайгу только в апреле.

1) Снег захрустел (предложение 1)

2) Это пробираются (предложение 2)

3) Им приходится (предложение 3)

4) Трудно (предложение 4)

5) Весна (предложение 5)

1. Задание 4 № 12971

Синтаксический анализ.

Замените словосочетание «солдатские могилы», построенное на основе согласования, синонимичным словосочетанием со связью управление. Напишите получившееся словосочетание.

2. Задание 4 № 12972

Синтаксический анализ.

Замените словосочетание «душевное превосходство», построенное на основе связи согласование, синонимичным словосочетанием со связью управление. Напишите получившееся словосочетание.

3. Задание 4 № 12973

Синтаксический анализ.

Замените словосочетание «приняли неохотно», построенное на основе примыкания, синонимичным словосочетанием со связью управление. Напишите получившееся словосочетание.

4. Задание 4 № 12974

Синтаксический анализ.

Замените словосочетание «друг отца», построенное на основе управления, синонимичным словосочетанием со связью согласование. Напишите получившееся словосочетание.

5. Задание 4 № 12975

Синтаксический анализ.

Замените словосочетание «надрывно ревела», построенное на основе примыкания, синонимичным словосочетанием со связью управление. Напишите получившееся словосочетание.

6. Задание 4 № 12976

Синтаксический анализ.

Замените словосочетание «дорожный набор», построенное на основе согласования, синонимичным словосочетанием со связью управление. Напишите получившееся словосочетание.

7. Задание 4 № 12977

Синтаксический анализ.

Замените словосочетание «медный самовар», построенное на основе согласования, синонимичным словосочетанием со связью управление. Напишите получившееся словосочетание.

8. Задание 4 № 12978

Синтаксический анализ.

Замените словосочетание «ветка ели», построенное на основе управления, синонимичным словосочетанием со связью согласование. Напишите получившееся словосочетание.

9. Задание 4 № 12979

Синтаксический анализ.

Замените словосочетание «солнечные лучи», построенное на основе согласования, синонимичным словосочетанием со связью управление. Напишите получившееся словосочетание.

10. Задание 4 № 12980

Синтаксический анализ.

Замените словосочетание «котлеты из хвои», построенное на основе управления, синонимичным словосочетанием со связью согласование. Напишите получившееся словосочетание.

1. Задание 3 № 12961

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Казалось(1) что кто-то тихо вздыхал среди глубокой(2) холодной ночи(3) и клубы пара(4) вылетавшие из гигантской груди(5) бесшумно проносились по небу от края (6) и затем тихо угасали в глубокой синеве.

2. Задание 3 № 12962

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

И если тебе(1) мой читатель(2) посчастливится побывать когда-нибудь в Кавказском заповеднике(3) и пройти по тропе(4) у которой(5) стоит такой обелиск(6) низко поклонись памяти защитников нашей Родины (7) отдавших свои жизни за то (8) чтобы сегодня мы жили в мире.

3. Задание 3 № 12963

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

За 75 лет(1) прошедших после гибели парохода «Челюскин»(2) и спасения всех (3)оказавшихся на льду людей(4) в печати появились десятки статей(5) легенд(6) фантастических и псевдонаучных публикаций(7) посвященных подготовке и ходу выполнения этого необычного (8)по тем временам рейса.

4. Задание 3 № 12964

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Впереди еще долгие жаркие(1) знойные (2)и просто теплые приятные деньки(3) когда солнце просыпается рано(4) а заходит очень не скоро(5) давая вволю нагуляться(6) прежде чем (7)погрузиться в сумерки.

5. Задание 3 № 12965

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

В раскопках под Новгородом(1) которые велись в продолжение десяти лет(2) были найдены сверхинтересные(3) берестяные грамоты(4) свидетельствующие о том(5) что восточные славяне обладали сравнительно высоким уровнем письма(6) подтверждая тем самым факт(7) что Русь была страной(8) высокой и прекрасной письменной культуры.

6. Задание 3 № 12966

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Некоторые уже улеглись на влажную(1) устланную осыпающейся хвоей(2) землю(3) жевали жёсткие солдатские сухари(4) копчёную колбасу(5) а кое-кто(6) открыв перочинным ножом жестяную банку(7) ел свиную тушёнку(8) намазывая её на тонко нарезанные(9) ломтики чёрствого хлеба.

7. Задание 3 № 12967

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Когда пригрело солнце(1) и коровы легли на траву отдыхать(2) пастух(3) расстегнув ворот синей рубашки(4) сняв старую шляпу(5) сел на ствол(6) поваленной берёзы(7) и занялся лещом.

8. Задание 3 № 12968

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Однажды(1) возвращаясь из Петровского(2) я заблудился в лесных оврагах(3) где под корнями дубов(4) вязов(5) и клёнов бормотали неугомонные ручьи(6) а на дне самых больших оврагов(7) можно было угодить (8)и в маленькие озёрца.

9. Задание 3 № 12969

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Продолжая держаться лапой за ушибленное место(1) медвежонок стремительно кинулся через речку(2) схватил маленького братишку за шиворот(3) и(4) всё ещё вскрикивая(5) переволок его(6) через глубокое место.

10. Задание 3 № 12970

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Рублевский ангел — возвышенная мечта об идеальном человеке(1) позволяющая глубоко заглянуть в народную душу(2) понять мироощущение(3) духовное богатство(4) наших далеких соотечественников(5) ведь ненависти и отчаянию(6) Андрей Рублев противопоставлял любовь(7) добро(8) дружеское согласие.

1. Задание 2 № 12951

Синтаксический анализ.

Прочитайте текст.

(5)Ландыш представляется мне символом леса.

1) Кольца наклонились вниз (предложение 1)

2) Мастер придал (предложение 2)

3) Превратятся в бусики (предложение 3)

4) Камни попали (предложение 4)

5) Ландыш представляется символом (предложение 5)

Ответ: 45|54

2. Задание 2 № 12952

Синтаксический анализ.

Прочитайте текст.

1) Закат пылает, золотит (предложение 1)

2) Луч солнца касается (предложение 2)

3) Мыши заглядывают (предложение 3)

4) Тлеет, кричит (предложение 4)

5) Озеро (предложение 5)

Ответ: 15|51

3. Задание 2 № 12953

Синтаксический анализ.

Прочитайте текст.

1) Мы бродили (предложение 1)

2) Закат хорош (предложение 2)

3) Мгла начинает двигаться (предложение 3)

4) Держит шорох (предложение 4)

5) Будит воображение (предложение 5)

Ответ: 23|32

4. Задание 2 № 12954

Синтаксический анализ.

Прочитайте текст.

1) Он бродил (предложение 1)

2) Рыба уплывала (предложение 2)

3) Он радовался (предложение 3)

4) Ихтиандр нес её (предложение 4)

5) Он уговаривал не биться и потерпеть (предложение 5)

Ответ: 23|32

5. Задание 2 № 12955

Синтаксический анализ.

Прочитайте текст.

(5)Скоро весна, но золотисто-красное солнышко придет в тайгу только в апреле.

1) Снег захрустел (предложение 1)

2) Это пробираются (предложение 2)

3) Им приходится (предложение 3)

4) Трудно (предложение 4)

5) Весна (предложение 5)

Ответ: 15|51

1. Задание 4 № 12971

Синтаксический анализ.

Ответ: могилысолдат

2. Задание 4 № 12972

Синтаксический анализ.

Ответ: превосходстводуши

3. Задание 4 № 12973

Синтаксический анализ.

Ответ: принялиснеохотой

4. Задание 4 № 12974

Синтаксический анализ.

Ответ: отцовдруг

5. Задание 4 № 12975

Синтаксический анализ.

Ответ: ревеласнадрывом

6. Задание 4 № 12976

Синтаксический анализ.

Ответ: набордлядороги|наборвдорогу

7. Задание 4 № 12977

Синтаксический анализ.

Ответ: самоваризмеди

8. Задание 4 № 12978

Синтаксический анализ.

Ответ: еловаяветка

9. Задание 4 № 12979

Синтаксический анализ.

Ответ: лучисолнца

10. Задание 4 № 12980

Синтаксический анализ.

Ответ: хвойныекотлеты

1. Задание 3 № 12961

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Пояснение.

Расставим знаки препинания:

Казалось,(1) что кто-то тихо вздыхал среди глубокой холодной ночи и клубы пара,(3) вылетавшие из гигантской груди,(5) бесшумно проносились по небу от края и затем тихо угасали в глубокой синеве.

1) запятая при вводном слове.

4) и 5) запятые выделяют причастный оборот.

Ответ: 145.

2. Задание 3 № 12962

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Пояснение.

Расставим знаки препинания:

И если тебе,(1) мой читатель,(2) посчастливится побывать когда-нибудь в Кавказском заповеднике и пройти по тропе,(4) у которой стоит такой обелиск,(6) низко поклонись памяти защитников нашей Родины,(7) отдавших свои жизни за то,(8) чтобы сегодня мы жили в мире.

1) и 2) запятые при обращении.

4) и 6) запятые выделяют придаточное предложение.

7) запятая открывает причастный оборот.

запятая выделяет придаточное предложение.

Ответ: 124678.

3. Задание 3 № 12963

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Пояснение.

Расставим знаки препинания:

За 75 лет,(1) прошедших после гибели парохода «Челюскин» и спасения всех оказавшихся на льду людей,(4) в печати появились десятки статей,(5) легенд,(6) фантастических и псевдонаучных публикаций,(7) посвященных подготовке и ходу выполнения этого необычного по тем временам рейса.

1) и 4) запятые выделяют причастный оборот.

5) и 6) запятые при однородных подлежащих.

7) запятая выделяет причастный оборот.

Ответ: 14567.

4. Задание 3 № 12964

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Пояснение.

Расставим знаки препинания:

Впереди еще долгие жаркие,(1) знойные и просто теплые приятные деньки,(3) когда солнцепросыпается рано,(4) а заходит очень не скоро,(5) давая вволю нагуляться, прежде чем погрузиться в сумерки.

1) запятая при однородных определениях.

3) запятая выделяет придаточное предложение.

5) запятая при однородных сказуемых.

6) запятая выделяет деепричастный оборот.

Ответ: 13456.

5. Задание 3 № 12965

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Пояснение.

Расставим знаки препинания:

В раскопках под Новгородом,(1) которые велись в продолжение десяти лет,(2) были найденысверхинтересные берестяные грамоты,(4) свидетельствующие о том,(5) что восточные славянеобладали сравнительно высоким уровнем письма,(6) подтверждая тем самым факт,(7) что Русь была страной высокой и прекрасной письменной культуры.

1) и 2) запятые выделяют придаточное предложение.

4) и 5) запятые выделяют причастный оборот.

5) запятая одновременно выделяет придаточное предложение.

6) запятая открывает деепричастный оборот.

7) запятая выделяет придаточное предложение.

Ответ: 124567.

6. Задание 3 № 12966

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Пояснение.

Расставим знаки препинания:

Некоторые уже улеглись на влажную,(1) устланную осыпающейся хвоей землю,(3) жевалижёсткие солдатские сухари, (4) копчёную колбасу,(5) а кое-кто, (6) открыв перочинным ножом жестяную банку,(7) ел свиную тушёнку,(8) намазывая её на тонко нарезанные ломтики чёрствого хлеба.

1) запятая между однородными определениями.

3) запятая между однородными сказуемыми.

4) запятая между однородными дополнениями.

5) запятая между основами, связанными сочинительным союзом А.

6) и 7) запятые выделяют деепричастный оборот.

запятая выделяет деепричастный оборот.

Ответ: 1345678.

7. Задание 3 № 12967

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Пояснение.

Расставим знаки препинания:

Когда пригрело солнце и коровы легли на траву отдыхать,(2) пастух,(3) расстегнув ворот синей рубашки,(4) сняв старую шляпу,(5) сел на ствол поваленной берёзы и занялся лещом.

2) запятая между основами в сложноподчинённом предложении.

3) запятая выделяет деепричастный оборот.

4) и 5) запятые выделяют деепричастный оборот.

4) запятая одновременно разделяет однородные обстоятельства, выраженные деепричастными оборотами.

1) запятая не нужна, потому что мы имеем дело с однородными соподчинением придаточных.

Ответ: 2345.

8. Задание 3 № 12968

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Пояснение.

Расставим знаки препинания:

Однажды,(1) возвращаясь из Петровского,(2) я заблудился в лесных оврагах,(3) где под корнями дубов,(4) вязов и клёнов бормотали неугомонные ручьи,(6) а на дне самых больших оврагов можно было угодить и в маленькие озёрца.

1) и 2) запятые выделяют деепричастный оборот.

3) запятая на границе частей в сложноподчинённом предложении.

4) запятая между однородными дополнениями (возможно: определениями).

6) запятая между основами, связанными сочинительным союзом А.

Ответ: 12346.

9. Задание 3 № 12969

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Пояснение.

Расставим знаки препинания:

Продолжая держаться лапой за ушибленное место,(1) медвежонок стремительно кинулся через речку,(2) схватил маленького братишку за шиворот и,(4) всё ещё вскрикивая,(5) переволок его через глубокое место.

1) запятая выделяет деепричастный оборот.

2) и 5) запятая при однородных сказуемых.

4) и 5) запятые выделяют деепричастный оборот.

Ответ: 1245.

10. Задание 3 № 12970

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Пояснение.

Расставим знаки препинания:

Рублевский ангел — возвышенная мечта об идеальном человеке,(1) позволяющая глубоко заглянуть в народную душу,(2) понять мироощущение,(3) духовное богатство наших далеких соотечественников,(5) ведь ненависти и отчаянию Андрей Рублев противопоставлял любовь,(7) добро,(8) дружеское согласие.

1) и 5) запятые выделяют причастный оборот.

2) и 3) внутри причастного оборота запятые между однородными.

7) и запятые между однородными дополнениями.

Ответ: 123578.

Источник

В каком числе 12сотен 1297,12970,12.,129.

Задания 3. Пунктуационный анализ

1. Задание 3 № 12961

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

2. Задание 3 № 12962

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

3. Задание 3 № 12963

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

4. Задание 3 № 12964

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

5. Задание 3 № 12965

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

6. Задание 3 № 12966

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

7. Задание 3 № 12967

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

8. Задание 3 № 12968

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

9. Задание 3 № 12969

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

10. Задание 3 № 12970

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

11. Задание 3 № 13028

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Когда я гляжу на трубящего ангела(1) написанного на западной арке продольной части храма(2) когда думаю об этом прекрасном образе(3) рожденном чувством гармонии(4) ясностью духа(5) плавной чистотой линий(6) и красок(7) то невольно воспринимаю встречу с чудом искусства(8) как встречу с самим творцом художественного совершенства.

12. Задание 3 № 13029

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Когда всматриваешься в группу «праведных жен»(1) идущих в рай(2) нарисованную на южном столпе(3) то особенно глубоко ощущаешь(4) замысел художника(5) верившего в то(6) что зло исчезнет(7) уступив в мире (8)место добру.

13. Задание 3 № 13030

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Вьюжными ночами(1) когда даже лесные гиганты стонут(2) трещат(3) и охают(4) когда небо сливается с землей(5) и неистово бухают подземные колокола(6) все живое старается укрыться в затишье: в домах(7) под раскидистой елью(8) между ее нижними лапами и землей(9) еще пахнущей занесенными сюда осенью листьями.

14. Задание 3 № 13031

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Слышалось иногда(1) как густым басом(2) гудит(3) пролетая где-то очень близко(4) невидимый жук(5) и как он(6) сухо шлепнувшись(7) о какое-то препятствие(8) сразу замолкает.

15. Задание 3 № 13032

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

К счастью(1) окраины ледяных полей были сильно поломаны(2) айсберги отсутствовали(3) и только иногда(4) гряды мелкого льда(5) нагроможденные местами(6) на полях(7) представляли серьезную опасность.

16. Задание 3 № 13033

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Глубокая тишина(1) нарушаемая всплесками рыбы(2) да криками какой-то еще (3)не уснувшей птицы(4) возившейся неподалеку(5) казалось(6) лишь подчеркивала(7) неодолимое наступление ночного покоя.

17. Задание 3 № 13034

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Невероятной кажется способность человека(1) который всю жизнь считал(2) что он aбсолютно неспособен к иностранным языкaм(3) но попaв в чужую страну(4) в экстремальную ситуaцию(5) он быстро и легко выучивaет чужой язык(6) представлявшийся до этого(7) совершенно невозможным для запоминания.

18. Задание 3 № 13035

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Он часто возвращался к матери(1) прижимался к ней(2) и(3) когда барин спрашивал его(4) хорошо ли ему на даче(5) улыбаясь(6) отвечал: «Хорошо!»

19. Задание 3 № 13036

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Звенящей(1) острой(2) как отчаянье(3) нотой(4) ворвался вой в монотонный шум дождя(5) прорезая тьму(6) и (7) замирая(8) понесся(9) над обнаженными полями.

20. Задание 3 № 13037

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

В такие летние сумерки(1) хорошо войти в сухие сени(2) в низкие комнаты (3)с только что вымытыми полами(4) где уже горят лампы(5) и за открытыми окнами шумит от падающих капель(6) и дико пахнет заброшенный сад.

21. Задание 3 № 13038

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

По-моему(1) надо идти (2) в глубь леса(3) но мои подружки(4) врассыпную разбежавшиеся по поляне(5) уже сыплют в корзинки(6) кроваво-красные ягоды.

22. Задание 3 № 13039

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

В четком строю(1) то выныривая(2) то пропадая(3) дельфины промелькнули по левому борту(4) и мне показалось(5) что они бегут(6) будто спасаясь(7) от чего-то.

23. Задание 3 № 13040

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Тихо было на небе(1) и на земле(2) только изредка набегал прохладный ветер(3) с востока(4) приподнимая гриву лошадей(5) покрытую инеем.

24. Задание 3 № 13041

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Может быть(1) нам предстоит узнать именно сегодня(2) когда(3) человеку важно связать(4) в своем сознании новейшие данные об элементарных частицах(5) о «белых карликах» и «черных дырах» Вселенной(6) с белоснежностью ромашек на лесных полянах(7) с роскошными(8) пульсирующими созвездиями над головой.

25. Задание 3 № 13042

Пунктуационный анализ.

Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые.

Сжатая рожь(1) бурьян(2) молочай(3) дикая конопля — всё(4) побуревшее от зноя(5) рыжее(6) полумёртвое(7) теперь омытое росою(8) и обласканное солнцем(9) оживало…

Источник

Новый тренировочный вариант (тренировочная работа) №7954726 решу ОГЭ 2022 года по русскому языку 9 класс с ответами, сжатым изложением (что объединяет людей) и сочинением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.

скачать тренировочный вариант

скачать ответы для варианта

прослушать аудио изложения

Решу ОГЭ 2022 по русскому языку 9 класс тренировочный вариант №7954726:

Тест изложения

Что объединяет людей? Целые этажи заботы. Человек рождается, и первая забота о нём – матери; постепенно (уже через несколько дней) о ребёнке начинает заботиться и отец. Забота скрепляет семью, скрепляет дружбу, односельчан, жителей одного города, одной страны.

Чувство заботы о другом появляется очень рано. Девочка ещё не говорит, но уже пытается заботиться о кукле, нянчит её. Мальчики, совсем маленькие, любят собирать грибы, ловить рыбу для всей семьи. Затем дети начинают заботиться о школе, в которой учатся, о селе или городе, в котором живут, о своих престарелых родителях, о своей стране. Так со временем забота увеличивается и растёт.

Если забота направлена только на себя, это уже эгоизм. Вот почему важно дарить заботу окружающим, посылая её в виде конкретных проявлений чувств любви, дружбы, патриотизма и направляя её в будущее. Только тогда забота будет объединять людей, укреплять память о прошлом.

Ответы для варианта

Задание 1 №7655 Прослушайте текст и напишите сжатое изложение. Учтите, что Вы должны передать главное содержание как каждой микротемы, так и всего текста в целом. Объём изложения — не менее 70 слов. Пишите изложение аккуратно, разборчивым почерком.

Задание 2 №13925 Синтаксический анализ. Прочитайте текст. (1)Единственными очагами древнерусской письменной культуры среди океана тьмы и невежества считались монастыри, где переписывали священные тексты и вели летописи на пергаменте— недублёной коже животных. (2)Кроме того, археологами найдено уже большое количество древнерусских грамот, написанных на берёзовой коре— бересте. (3)После тщательного изучения этих берестяных писем и записок учёные смогли предположить, что население Новгорода было грамотным по крайней мере начиная с XI века. (4)«В то время как наши предки высекали слова на камнях, славяне уже писали друг другу письма». (5)Это сообщение было опубликовано в одной из шведских газет, когда берестяные грамоты выставлялись в Швеции. Укажите верные варианты ответов. Запишите их номера.

1) Вторая часть сложного предложения 1 осложнена обособленным приложением.
2) Предложение 2 является односоставным безличным.
3) Грамматическая основа в первой части сложного предложения 3 — учёные смогли.
4) Предложение 4 сложноподчинённое с придаточным времени.
5) Сказуемое в первой части предложения 5 составное глагольное.

Ответ: 14

Задание 3 №12970 Пунктуационный анализ. Расставьте знаки препинания. Укажите цифры, на месте которых должны стоять запятые. Рублевский ангел— возвышенная мечта об идеальном человеке(1) позволяющая глубоко заглянуть в народную душу(2) понять мироощущение(3) духовное богатство(4) наших далеких соотечественников(5) ведь ненависти и отчаянию(6) Андрей Рублев противопоставлял любовь(7) добро(8) дружеское согласие.

Ответ: 123578

Задание 4 №13912 Синтаксический анализ. Замените словосочетание «доказывать с упрямством», построенное на основе управления, синонимичным словосочетанием со связью примыкание. Напишите получившееся словосочетание.

Ответ: доказывать упрямо

Задание 5 №14734 Орфографический анализ. Укажите варианты ответов, в которых дано верное объяснение написания выделенного слова. 1) ВЫЧИТАНИЕ— правописание чередующейся гласной в корне не определяется правилом (является исключением). 2) НИЗКИЙ (забор)— в качественном имени прилагательном, которое может иметь краткую форму, пишется суффикс -К-. 3) ВКЛЮЧЁННЫЙ— в суффиксе страдательного причастия прошедшего времени, образованного от глагола совершенного вида, пишется НН. 4) (отнюдь НЕ) ЗАБОТЛИВЫЙ — причастие с зависимым словом пишется с НЕ раздельно. 5 ) РАЗЪЯСНИТЬ— буква Ъ пишется в корне слова для обозначения твёрдости предшествующего согласного звука.

Ответ: 23

Задание 6 №13067 Анализ содержания текста. Какие из высказываний соответствуют содержанию текста? Укажите номера ответов. 1) В детстве рассказчица стеснялась отца, потому что считала его несуразным и смешным. 2) Когда девочка была в третьем классе, она сильно заболела. 3) Когда скорая помощь застряла в снегу, мама начала плакать, понимая, что быстро выбраться не удастся. 4) После ночи, когда машина застряла в снегу, рассказчица поняла, что была несправедлива к отцу и за внешней несуразностью не видела его огромной любви к ней. 5) Став взрослой, героиня, наряжая ёлку, плачет, потому что вспоминает, как над её отцом смеялись дети на утренниках в детском саду.

Ответ: 124

Задание 7 №13068 Анализ средств выразительности. Укажите варианты ответов, в которых средством выразительности речи является фразеологизм. 1) Он садился на стул возле ёлки, долго пиликал на своём баяне, пытаясь подобрать нужную мелодию, а наша воспитательница строго говорила ему: «Валерий Петрович, повыше!» 2) Я готова была провалиться сквозь землю от стыда и вела себя подчёркнуто холодно, показывая своим видом, что этот нелепый человек с красным носом не имеет ко мне никакого отношения. 3) По дороге попали в страшную метель, машина застряла, и водитель визгливо, как женщина, стал кричать, что теперь все мы замёрзнем. 4) Не знаю, сколько прошло времени, но внезапно ночь озарилась ярким светом фар, и длинная тень какого-то великана легла на моё лицо. 5) И я сначала в садике, а потом в школе несла тяжкий крест отцовской несуразности.

Ответ: 25

Задание 8 №13069 Лексический анализ. Найдите в тексте синоним к слову НЕЛЕПЫЙ (предложение 10). Напишите этот синоним.

Ответ: смешной

Задание 9 №8173 1. Напишите сочинение-рассуждение, раскрывая смысл высказывания современного лингвиста Л.Ю. Максимова: «При помощи абзацного отступа выделяются наиболее важные в композиции целого текста группы предложений или отдельные предложения». Аргументируя свой ответ, приведите 2 (два) примера из прочитанного текста. Приводя примеры, указывайте номера нужных предложений или применяйте цитирование. Вы можете писать работу в научном или публицистическом стиле, раскрывая тему на лингвистическом материале. Начать сочинение Вы можете словами Л.Ю. Максимова. Объём сочинения должен составлять не менее 70 слов. Работа, написанная без опоры на прочитанный текст (не по данному тексту), не оценивается. Если сочинение представляет собой пересказанный или полностью переписанный исходный текст без каких бы то ни было комментариев, то такая работа оценивается нулём баллов. Сочинение пишите аккуратно, разборчивым почерком.

Другие тренировочные варианты ОГЭ 2022 по русскому языку:

Тренировочная работа №1 статград ОГЭ 2022 по русскому языку 9 класс с ответами

Тренировочные варианты ОГЭ по русскому языку 9 класс задания с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Задание 1 № 366805

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	Город Гранюк	Деревня Астрелка	Хутор Южный	Город Гусевск
Цифры

Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.

Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.

Ответ: 1465.

2. Задание 2 № 366806

Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.

Решение.

Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится

пачек чая.

Таким образом, ребята должны купить 14 пачек чая.

Ответ: 14.

3. Задание 3 № 366807

Найдите площадь (в км²), которую занимает заказник.

Решение.

Площадь заказника равна:

Ответ: 351.

4. Задание 4 № 366808

Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.

Решение.

Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:

км.

Ответ: 30.

5. Задание 5 № 366809

Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.

Продукция	Цена в магазине «Вело» (руб.)	Цена в магазине «ОК» (руб.)	Срок доставки из магазина «ОК» (дни)
Подсветка для спиц
Шина вида «А»
Шина вида «Б»
Спица
Педаль вида «А»
Педаль вида «Б»
Тормоз вида «А»		нет
Тормоз вида «Б»	нет
Набор крепёжных изделий

Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?

Решение.

На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:

руб.

Ответ: 5300.

6. Задание 6 № 316314

Найдите значение выражения:

Решение.

Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.

7. Задание 7 № 317575

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?

Решение.

Заметим, что и Проверим все варианты ответа:

1) — неверно;

2) — верно;

3) — верно;

4) — верно.

Ответ указан под номером 1.

8. Задание 8 № 353586

Какое из данных ниже чисел является значением выражения

Решение.

Последовательно получим:

Ответ: 1

9. Задание 9 № 338500

При каком значении значения выражений и равны?

Решение.

Для ответа на вопрос задачи нужно решить уравнение Решим его:

Ответ: 2.

10. Задание 10 № 325450

В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.

Решение.

Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна

Ответ: 0,3.

11. Задание 11 № 311406

На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке

4) прямая пересекает график в точках и

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .

2) — неверно,

3) — верно, видно из графика.

4) Прямая пересекает график в точках и — верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

Ответ: 12.

12. Задание 12 № 311543

Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .

Решение.

Выразим :

Подставляя, получаем:

Ответ: 0,4.

13. Задание 13 № 338497

На каком из рисунков изображено решение неравенства

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

Решение.

Решим неравенство методом интервалов:

Правильный ответ указан под номером: 4.

14. Задание 14 № 406645

В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение.

Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.

Найдем сумму этой прогрессии:

Ответ: 377 мест.

15. Задание 15 № 340000

В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите

Решение.

Из прямоугольного треугольника по теореме Пифагора найдём

Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.

16. Задание 16 № 351463

На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.

Решение.

Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.

17. Задание 17 № 169876

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.

———-

В открытом банке иррациональный ответ.

18. Задание 18 № 350842

Найдите угол

Решение.

Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.

Ответ: 22,5

19. Задание 19 № 401617

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Ответ: 13.

20. Задание 20 № 338505

Решите неравенство

Решение.

Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение

Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).

Таким образом, ответ

Ответ:

Примечание.

Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,

21. Задание 21 № 353527

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.

Ответ: 58.

22. Задание 22 № 338288

Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.

Решение.

Упростим выражение:

По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:

График функции сводится к графику параболы с выколотой точкой

Выделим полный квадрат:

Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)

Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и

Ответ: −1; 3.

23. Задание 23 № 339395

Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.

Решение.

Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и

Ответ: 16.

24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.

Решение.

Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.

25. Задание 25 № 311926

В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .

Решение.

По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,

Площадь трапеции :

Площадь трапеции

Ответ: 9.

Источник

Страница 3 из 7

Практические задачи №1-5 к ОГЭ по математике

Прочитайте внимательно текст и выполните задания 1–5.

Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.
И так далее.

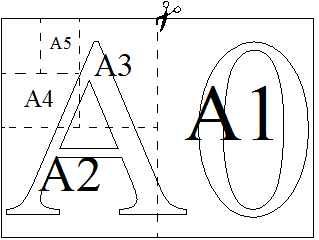
Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.

Номер листа	Длина (мм)	Ширина (мм)
1	297	210
2	420	297
3	1189	841
4	841	594

Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
Ответ: 3421

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А3, А5 и А6.

Номер листа	Длина (мм)	Ширина (мм)
1	210	148
2	594	420
3	148	105
4	420	297

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 2413

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А2, А3 и А4.

Номер листа	Длина (мм)	Ширина (мм)
1	841	594
2	420	297
3	594	420
4	297	210

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
Ответ: 1324

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А3, А4, А5 и А6.

Номер листа	Длина (мм)	Ширина (мм)
1	148	105
2	210	148
3	420	297
4	297	210

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3421

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А2, А5 и А6.

Номер листа	Длина (мм)	Ширина (мм)
1	594	420
2	148	105
3	210	148
4	841	594

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 4132

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А3, А4 и А6.

Номер листа	Длина (мм)	Ширина (мм)
1	594	420
2	420	297
3	148	105
4	297	210

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 1243

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А2 и А4.

Номер листа	Длина (мм)	Ширина (мм)
1	841	594
2	1189	841
3	297	210
4	594	420

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
Ответ: 2143

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А3, А4 и А5.

Номер листа	Длина (мм)	Ширина (мм)
1	420	297
2	297	210
3	841	594
4	210	148

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3124

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А4, А5 и А6.

Номер листа	Длина (мм)	Ширина (мм)
1	297	210
2	148	105
3	594	420
4	210	148

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3142

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А3, А4 и А6.

Номер листа	Длина (мм)	Ширина (мм)
1	148	105
2	420	297
3	297	210
4	841	594

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 4231

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А2, А3 и А5.

Номер листа	Длина (мм)	Ширина (мм)
1	594	420
2	420	297
3	1189	841
4	210	148

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 3124

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А3, А5 и А6.

Номер листа	Длина (мм)	Ширина (мм)
1	210	148
2	841	594
3	420	297
4	148	105

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 2314

Задание 1.
В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А2, А3 и А5.

Номер листа	Длина (мм)	Ширина (мм)
1	210	148
2	594	420
3	420	297
4	841	594

Решение:

А0 1189*841
А1 841*594
А2 594*420
А3 420*297
А4 297*210
А5 210*148
А6 148*105
Ответ: 4231

Задание 2.
Сколько листов формата А3 получится из одного листа формата А2?

Решение:

А2 594*420
А3 420*297

Ответ: 2

Задание 2.
Сколько листов формата А3 получится из одного листа формата А1?

Решение:

А1 841*594
А2 594*420 — 2 шт
А3 420*297 — 4 шт.

Ответ: 4

Задание 2.
Сколько листов формата А3 получится из одного листа формата А0?

Решение:

А0 1189*841
А1 841*594 — 2 шт.
А2 594*420 — 2*2= 4 шт
А3 420*297 — 4*2 = 8 шт.

Ответ: 8

Задание 2.
Сколько листов формата А5 получится из одного листа формата А0?

Решение:

А0 1189*841
А1 841*594 — 2 шт
А2 594*420 — 4 шт.
А3 420*297 — 8 шт.
А4 297*210 — 16 шт.
А5 210*148 — 32 шт.
Ответ: 32

Задание 2.
Сколько листов формата А5 получится из одного листа формата А1?

Решение:

А1 841*594
А2 594*420 — 2 шт.
А3 420*297 — 4 шт.
А4 297*210 — 8 шт.
А5 210*148 — 16 шт.
Ответ: 16

Задание 2.
Сколько листов формата А5 получится из одного листа формата А3?

Решение:

А3 420*297
А4 297*210 — 2 шт.
А5 210*148 — 4 шт.
Ответ: 4

Задание 2.
Сколько листов формата А6 получится из одного листа формата А2?

Решение:

А2 594*420
А3 420*297 — 2 шт.
А4 297*210 — 4 шт.
А5 210*148 — 8 шт.
А6 148*105 — 16 шт.
Ответ: 16

Задание 2.
Сколько листов формата А6 получится из одного листа формата А0?

Решение:

А0 1189*841
А1 841*594 — 2
А2 594*420 — 4
А3 420*297 — 8
А4 297*210 — 16
А5 210*148 — 32
А6 148*105 — 64
Ответ: 64

Задание 2.
Сколько листов формата А6 получится из одного листа формата А3?

Решение:

А3 420*297
А4 297*210 — 2
А5 210*148 — 4
А6 148*105 — 8
Ответ: 8

Задание 2.
Сколько листов формата А6 получится из одного листа формата А1?

Решение:

А1 841*594
А2 594*420 — 2
А3 420*297 — 4
А4 297*210 — 8
А5 210*148 — 16
А6 148*105 — 32
Ответ: 32

Задание 2.
Сколько листов формата А4 получится из одного листа формата А2?

Решение:

А2 594*420
А3 420*297 — 2
А4 297*210 — 4
Ответ: 4

Задание 2.
Сколько листов формата А4 получится из одного листа формата А1?

Решение:

А1 841*594
А2 594*420 — 2
А3 420*297 — 4
А4 297*210 — 8
Ответ: 8

Задание 2.
Сколько листов формата А4 получится из одного листа формата А0?

Решение:

А0 1189*841
А1 841*594 — 2
А2 594*420 — 4
А3 420*297 — 8
А4 297*210 — 16
Ответ: 16

Задание 3.
Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см²/2=5000 см²

Ответ: 5000

Задание 3.
Найдите площадь листа формата А2. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см²/2=5000 см²
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см²/2=2500 см²
Ответ: 2500

Задание 3.
Найдите площадь листа формата А3. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см²/2=5 000 см²
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см²/2=2 500 см²
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см²/2=1 250 см²
Ответ: 1250

Задание 3.
Найдите площадь листа формата А6. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см²/2=5 000 см²
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см²/2=2 500 см²
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см²/2=1 250 см²
Лист формата А4 имеет форму прямоугольника, площадь которого равна 1250 см²/2=625 см²
Лист формата А5 имеет форму прямоугольника, площадь которого равна 625 см²/2=312,5 см²
Лист формата А6 имеет форму прямоугольника, площадь которого равна 312,5 см²/2=156,25 см²

Ответ: 156,25

Задание 3.
Найдите площадь листа формата А5. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см²/2=5 000 см²
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см²/2=2 500 см²
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см²/2=1 250 см²
Лист формата А4 имеет форму прямоугольника, площадь которого равна 1250 см²/2=625 см²
Лист формата А5 имеет форму прямоугольника, площадь которого равна 625 см²/2=312,5 см²

Ответ: 312,5

Задание 3.
Найдите площадь листа формата А4. Ответ дайте в квадратных сантиметрах.

Решение:

Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м.
Лист формата А1 имеет форму прямоугольника, площадь которого равна 10 000 см²/2=5 000 см²
Лист формата А2 имеет форму прямоугольника, площадь которого равна 5 000 см²/2=2 500 см²
Лист формата А3 имеет форму прямоугольника, площадь которого равна 2 500 см²/2=1 250 см²
Лист формата А4 имеет форму прямоугольника, площадь которого равна 1250 см²/2=625 см²

Ответ: 625

Задание 3.
Найдите ширину листа бумаги формата А0. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А0 1189*841, то есть ширина кратная 10 будет 840

Ответ: 840

Задание 3.
Найдите ширину листа бумаги формата А1. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А1 841*594 , то есть ширина кратная 10 будет 590

Ответ: 590

Задание 3.
Найдите ширину листа бумаги формата А2. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А2 594*420 , то есть ширина кратная 10 будет 420

Ответ: 420

Задание 3.
Найдите ширину листа бумаги формата А3. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А3 420*297 , то есть ширина кратная 10 будет 300

Ответ: 300

Задание 3.
Найдите ширину листа бумаги формата А4. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А4 297*210 , то есть ширина кратная 10 будет 210
Ответ: 210

Задание 3.
Найдите ширину листа бумаги формата А5. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А5 210*148, то есть ширина кратная 10 будет 150
Ответ: 150

Задание 3.
Найдите ширину листа бумаги формата А6. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 5.

Решение:

А6 148*105, то есть ширина кратная 10 будет 110
Ответ: 110

Задание 4.
Найдите длину листа бумаги формата А1. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А1 841*594, то есть длина кратная 10 будет 840

Ответ: 840

Задание 4.
Найдите длину листа бумаги формата А2. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А2 594*420, то есть длина кратная 10 будет 600

Ответ: 600

Задание 4.
Найдите длину листа бумаги формата А3. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А3 420*297, то есть длина кратная 10 будет 420

Ответ: 420

Задание 4.
Найдите длину листа бумаги формата А4. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А4 297*210, то есть длина кратная 10 будет 300
Ответ: 300

Задание 4.
Найдите длину листа бумаги формата А5. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А5 210*148, то есть длина кратная 10 будет 210

Ответ: 210

Задание 4.
Найдите длину листа бумаги формата А6. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Решение:

А6 148*105, то есть длина кратная 10 будет 150
Ответ: 150

Задание 4.
Найдите длину листа бумаги формата А7. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 5.

Решение:

А7 105*74, то есть длина кратная 10 будет 110
Ответ: …

Задание 4.
Найдите отношение длины меньшей стороны листа формата А3 к большей. Ответ округлите до десятых.

Решение:

А3 420*297
420/297=1,41

Ответ: 1,4

Задание 4.
Найдите отношение длины меньшей стороны листа формата А4 к большей. Ответ округлите до десятых.

Решение:

А4 297*210
297/210=1,41
Ответ: 1,4

Задание 4.
Найдите отношение длины меньшей стороны листа формата А5 к большей. Ответ округлите до десятых.

Решение:

А5 210*148
210/148=1,41
Ответ: 1,4

Задание 4.
Найдите отношение длины большей стороны листа формата А2 к меньшей. Ответ округлите до десятых.

Решение:

А2 594*420
594/420=1,41
Ответ: 1,4

Задание 4.
Найдите отношение длины большей стороны листа формата А6 к меньшей. Ответ округлите до десятых.

Решение:

А6 148*105
148/105=1,409
Ответ: 1,4

Задание 4.
Найдите отношение длины большей стороны листа формата А1 к меньшей. Ответ округлите до десятых.

Решение:

А1 841*594
841/594=1,41
Ответ: 1,4

Задание 4.
Найдите отношение длины диагонали листа формата А2 к его меньшей стороне. Ответ округлите до десятых.

Решение:

А2 594*420
Меньшая сторона формата А2 равна 420 мм, большую сторона формата А2 594 мм. Диагональ является гипотенузой треугольника с катетами 420 мм и 594 мм, по теореме Пифагора имеем:
$sqrt{594*594+420*420}≈727$ мм
Найдем отношения длины диагонали к меньшей стороне:
727/420 ≈ 1,7.

Ответ: 1,7.

Задание 4.
Найдите отношение длины диагонали листа формата А0 к его меньшей стороне. Ответ округлите до десятых.

Решение:

А0 1189*841
Меньшая сторона формата А0 равна 841 мм, большую сторона формата А0 1189 мм. Диагональ является гипотенузой треугольника с катетами 841 мм и 1189 мм, по теореме Пифагора имеем:
$sqrt{841*841+1189*1189}≈1456$ мм
Найдем отношения длины диагонали к меньшей стороне:
1456/841 ≈ 1,7.

Ответ: 1,7

Задание 4.
Найдите отношение длины диагонали листа формата А7 к его меньшей стороне. Ответ округлите до десятых.

Решение:

А7 105*74
Меньшая сторона формата А7 равна 74 мм, большую сторона формата А7 105 мм. Диагональ является гипотенузой треугольника с катетами 74 мм и 105 мм, по теореме Пифагора имеем:
$sqrt{74*74+105*105}≈129$ мм
Найдем отношения длины диагонали к меньшей стороне:
129/74 ≈ 1,7.
Ответ: 1,7

Задание 5.
Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 32 листа формата А5, поэтому площадь листа формата А5 в 32 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А5 равен дробь:
80/32, а вес пачки равен ⁸⁰/₃₂ * 500=1250 граммов.
Ответ: 1250

Задание 5.
Бумагу формата А4 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г? Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 16 листа формата А4, поэтому площадь листа формата А4 в 16 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А5 равен дробь:
80/16, а вес пачки равен ⁸⁰/₁₆ * 500=2500 граммов.
Ответ: 2500

Задание 5.
Бумагу формата А3 упаковали в пачки по 200 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 8 листов формата А3, поэтому площадь листа формата А3 в 8 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
80/8, а вес пачки равен ⁸⁰/₈ * 500=5000 граммов.
Ответ: 5000

Задание 5.
Бумагу формата А3 упаковали в пачки по 250 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 120 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 8 листов формата А3, поэтому площадь листа формата А3 в 8 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
120/8, а вес пачки равен ¹²⁰/₈ * 250=3750 граммов.
Ответ: 3750

Задание 5.
Бумагу формата А2 упаковали в пачки по 100 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 96 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 4 листа формата А2, поэтому площадь листа формата 2 в 4 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А2 равен дробь:
96/4, а вес пачки равен 96/4 * 100=2400 граммов.
Ответ: 2400

Задание 5.
Бумагу формата А1 упаковали в пачки по 80 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 120 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 2 листов формата А1, поэтому площадь листа формата А1 в 2 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А1 равен дробь:
120/2, а вес пачки равен ¹²⁰/₂ * 80=4800 граммов.
Ответ: 4800

Задание 5.
Бумагу формата А3 упаковали в пачки по 120 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 96 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 8 листов формата А3, поэтому площадь листа формата А3 в 8 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
96/8, а вес пачки равен ⁹⁶/₈ * 120=1440 граммов.
Ответ: 1440

Задание 5.
Бумагу формата А4 упаковали в пачки по 800 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 16 листов формата А4, поэтому площадь листа формата А4 в 16 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А3 равен дробь:
80/16, а вес пачки равен ⁸⁰/16 * 800=4000 граммов.
Ответ: 4000

Задание 5.
Бумагу формата А5 упаковали в пачки по 1000 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 144 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 32 листов формата А5, поэтому площадь листа формата А5 в 32 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А5 равен дробь:
144/32, а вес пачки равен ¹⁴⁴/₃₂ * 1000=4500 граммов.
Ответ: 4500

Задание 5.
Бумагу формата А6 упаковали в пачки по 320 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 108 г. Ответ дайте в граммах.

Решение:

На листе формата А0 помещается 64 листа формата А6, поэтому площадь листа формата А6 в 64 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А6 равен дробь:
108/64, а вес пачки равен ¹⁰⁸/₆₄ * 320=540 граммов.
Ответ: 540

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 15 пунктов на листе формата А4? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

15*1,41=21,15 мм ≈21

Ответ: 21

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А5 так же, как этот же текст, напечатанный шрифтом высотой 16 пунктов на листе формата А4? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

16/1,41=11,34 мм ≈11

Ответ: 11

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
8 пунктов на листе формата А5. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А4 таким же образом? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

8*1,41=11,28 мм ≈11

Ответ: 11

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
12 пунктов на листе формата А4. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 таким же образом? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

13*1,41=16,92 мм ≈17

Ответ: 17

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 12 пунктов на листе формата А5? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

12*1,41=16,92 мм ≈17

Ответ: 17

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
22 пункта на листе формата А3. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А2 таким же образом? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

22*1,41=31,02 мм ≈31

Ответ: 31

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой
20 пунктов на листе формата А4. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 таким же образом? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

20*1,41=28,2 мм ≈28

Ответ: 28

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 17 пунктов на листе формата А3? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

17/1,41=12,06 мм ≈12

Ответ: 12

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А4 так же, как этот же текст, напечатанный шрифтом высотой 21 пункт на листе формата А3? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

21/1,41=14,89 мм ≈15

Ответ: 15

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А5 так же, как этот же текст, напечатанный шрифтом высотой 20 пунктов на листе формата А4? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

20/1,41=14,84 мм ≈15 мм

Ответ: 15

Задание 5.
Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт
(в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 10 пунктов на листе формата А4? Размер шрифта округляется до целого.

Решение:

Скажем большая сторона листа А4 равна 297 мм, а такая же сторона листа А3 – 420 мм, то есть, сторона листа А3 больше листа А4 в 420/297 раз=1,41. На самом деле не важно какие близлежащие форматы мы берем, скажем А0 или А1, А2 или А3 и т.д., так как это соотношение будет у всех близлежащих форматов одинаковое. Следовательно, размер шрифта на любых близлежащих форматах соотносится также и его нужно взять с поправочным коэффициентом К=1,41. В итоге, мы должны применить этот К либо для уменьшения, либо для увеличения, в зависимости от какого к какому формату переходим.

10*1,41=14,1 мм ≈14 мм

Ответ: 14

B9A7F7

Источник

В ОГЭ по математике с 2020 года добавили новую линейку задач (1—5). Часть учеников пребывает в шоке от того, с чем им предстоит столкнуться на экзамене. Давайте разберёмся, так ли страшен чёрт, как его малюют.

Первое что пугает – это большое количество текста в условии. Факт. Но текст этот без формул и читается почти так же легко, как художественная литература. Давайте разберём на примере.

Задание 1.

Сергей Васильевич – крупный учёный, его исследования востребованы в промышленности. На рисунке изображён план двухэтажного дома (сторона клетки соответствует 1 м), в котором он проживает с женой Валентиной Петровной и двумя детьми: Костей и Викой. На первом этаже гостиная – самая большая по площади комната. Кухня имеет вытянутую форму, её длина в два раза больше ширины, она тоже находится на первом этаже. Рядом с гостиной расположена столовая. Комната Кости расположена на втором этаже над кухней, его комната – соседняя с комнатой сестры Вики. Комната родителей расположена над столовой, рядом с ней просторный кабинет Сергея Васильевича.

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

Гостиная

Комната Кости

Кабинет

Кухня

Цифры

Решение. Сначала идёт вводная часть, по сути, первое значимое предложение:

«На первом этаже гостиная – самая большая по площади комната». Смотрим на рисунок, сразу видно, что самая большая комната на первом этаже – (3). Значит, (3) – гостиная. Подпишем её на рисунке. Кухня – тоже на первом этаже, вытянутая, длина в 2 раза больше ширины – это (1). Подпишем на рисунке: (1) – кухня.

Рядом с гостиной (3) находится столовая – это (2). Укажем её на рисунке. С первым этажом разобрались, «поднимаемся» на второй!

Комната Кости – над кухней. Значит, комната Кости – (7). Она соседняя с комнатой Вики – следовательно, комната Вики обозначена (6).

Комната родителей над столовой. Столовая – это (2). Над (2) находится (4). Она и есть комната родителей. Рядом с ней кабинет. Значит, кабинет – (5) .

Теперь на рисунке подписаны все комнаты. Заполняем таблицу. Переносим в бланк ответов по порядку цифры: 3751. Это ответ к заданию 1.

Задание 2.

На втором этаже расположен открытый балкон. На его бортике закреплены деревянные поручни. Определите их общую протяжённость (в метрах).

Решение. Бортик балкона находится по его периметру, кроме той части, которая примыкает к зданию. Его длина 11 м (считаем по сторонам клеток).

Задание 3.

Найдите площадь комнаты Вики. Ответ дайте в квадратных метрах.

Решение. Комната Вики уже подписана – это (6). Она состоит из 18 клеточек. Одна клетка соответствует квадрату 1 м на 1 м, то есть площадь одной клетки – 1 м². Площадь комнаты Вики – 18 м². Ответ: 18.

Задание 4.

В каждой из пронумерованных комнат, кроме Костиной, два окна, а в Костиной – всего одно. Других окон нет. Площадь стекла для каждого окна составляет 3 м². Стоимость окон при установке складывалась из стоимости стекла (3000 рублей за квадратный метр окна) и стоимости монтажа и фурнитуры (7000 рублей за каждое окно). Определите общую стоимость всех окон и их установки. Ответ дайте в рублях.

Решение. Пронумерованных комнат 7, в 6 из них по два окна (это уже 12 окон), в одной комнате – 1 окно. Всего 12 + 1 = 13 окон. Посчитаем стоимость одного окна. 3 м² стекла стоят 3*3000=9000 рублей, монтаж и фурнитура – 7000 рублей. Общая стоимость одного окна равна 9000+7000 = 16000 рублей. Стоимость всех окон равна 13*16 000 = 208000 рублей. Ответ: 208000.

Задание 5.

После постройки дома денег на внутреннюю отделку осталось меньше, чем планировалось первоначально, поэтому пришлось экономить.

В гостиной и столовой предполагалось класть паркетную доску, но обошлись ламинатом, а на сэкономленные деньги приобрели туристические путёвки в Крым. Ламинат и паркетная доска продаются только в упаковках. Каждая упаковка содержит одинаковое число квадратных метров материала.

Тип покрытия

Стоимость 1 м² материала (в руб.)

Стоимость укладки 1 м² (в рублях)

Количество квадратных метров

в упаковке

Паркетная доска

3200

1100

Ламинат

520

180

Сколько рублей удалось сэкономить на путёвки?

Тут ситуация чуть-чуть сложнее, чем в предыдущих заданиях. Читаем условие: гостиная и столовая – это (2) и (3). Находим их общую площадь как площадь прямоугольника длиной 9 м и шириной 5 м. Общая площадь – 45 м².

Посчитаем отдельно стоимость паркетной доски и стоимость ламината (с установкой).

а) Паркетная доска. В одной упаковке 10 м². Чтобы набрать 45 м², потребуется купить 5 упаковок, то есть 50 м² паркетной доски. Стоимость материала составит

50*3200=160 000 рублей. Стоимость установки составит 45*1100=49500 рублей. Общая стоимость равна 160 000+49 500 =209 500 рублей.

б) Ламинат. В одной упаковке 7 м². Чтобы набрать 45 м², потребуется купить 7 упаковок, то есть 49 м² ламината. Стоимость материала составит 49*520 = 25 480 рублей. Стоимость установки составит 45*180=8100 рублей. Общая стоимость равна 25 480+8 100 =33580 рублей.

Таким образом, экономия составит 209 500 – 33 580 =175 920 (рублей).

Ответ: 175 920.

Вот мы и решили задачи 1-5 ОГЭ по математике. Как видите, ничего сверхъестественного. Главное – не бояться, внимательно и вдумчиво читать условие, а также аккуратно считать.

Удачи на экзамене!

Решение 2436. Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.

Задание 1. Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

Решение.

Треть спицы будет равна

25 – 6,2 = 18,8 см

следовательно, длина всей спицы:

18,8∙3 = 56,4 см

Ответ: 56,4

Задание 2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Решение.

Высота h = 53,1 см, проведенная к основанию a = 38 см, дает площадь каждого сегмента, равную:

Так как таких сегментов 8, то получаем полную площадь поверхности:

кв. см

Округляем до десятков, получаем 8070 кв. см.

Ответ: 8070

Задание 3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.

Решение.

Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.

По теореме Пифагора можно записать равенство:

Решаем уравнение относительно R, имеем:

Ответ: 62,5

Задание 4. Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh , где R — радиус сферы, а h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение.

Подставим в формулу площади купола зонта числовые значения, получим:

Округляем до целого, имеем: 9813 см. кв.

Ответ: 9813

Задание 5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение.

Вычислим площадь ткани в кв. см, получим:

S = 35∙100∙80 = 280 000 см. кв.

Площадь клиньев для 29 зонтов, равна:

29∙8∙1050 = 243 600 см. кв.

Площадь обрезков:

280 000 – 243 600 = 36 400 см. кв.

Что составляет:

Ответ: 13

Решение 4136. Длина зонта в сложенном виде равна 26 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,5 см.

Две подруги Ира и Юля задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Ира и Юля сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 40 см. Высота купола зонта h (рис. 2) оказалась равна 26 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 104 см.

Задание 1. Длина зонта в сложенном виде равна 26 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,5 см.

Решение.

Треть спицы будет равна

26 – 6,5 = 19,5 см

следовательно, длина всей спицы:

19,5∙3 = 58,5 см

Ответ: 58,5

Задание 2. Поскольку зонт сшит из треугольников, рассуждала Ира, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Иры, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 55 см. Ответ дайте в квадратных сантиметрах.

Решение.

Высота h = 55 см, проведенная к основанию a = 40 см, дает площадь каждого сегмента, равную:

Так как таких сегментов 8, то получаем полную площадь поверхности:

кв. см

Округляем до десятков, получаем 8800 кв. см.

Ответ: 8800

Задание 3. Юля предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC = R (рис. 2). Ответ дайте в сантиметрах.

Решение.

Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.

По теореме Пифагора можно записать равенство:

Решаем уравнение относительно R, имеем:

Ответ: 65

Задание 4. Юля нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh, где R — радиус сферы, а h — высота сегмента. Рассчитайте площадь поверхности купола способом Юли. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение.

Подставим в формулу площади купола зонта числовые значения, получим:

Округляем до целого, имеем: 10613 см. кв.

Ответ: 10613

Задание 5. Рулон ткани имеет длину 30 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 27 зонтов, таких же, как зонт, который был у Иры и Юли. Каждый треугольник с учётом припуска на швы имеет площадь 1150 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение.

Вычислим площадь ткани в кв. см, получим:

S = 30∙100∙90 = 270 000 см. кв.

Площадь клиньев для 27 зонтов, равна:

27∙8∙1150 = 248 400 см. кв.

Площадь обрезков:

270 000 – 248 400 = 21 600 см. кв.

Что составляет:

Ответ: 8

Решение 5236. Длина зонта в сложенном виде равна 28 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

Два друга Дима и Юра задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Дима и Юра сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 30 см. Высота купола зонта h (рис. 2) оказалась равна 29 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 116 см.

Задание 1. Длина зонта в сложенном виде равна 28 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

Решение.

Треть спицы будет равна

28 – 6,2 = 21,8 см

следовательно, длина всей спицы:

21,8∙3 = 65,4 см

Ответ: 65,4

Задание 2. Поскольку зонт сшит из треугольников, рассуждал Дима, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Димы, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 63,7 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Решение.

Высота h = 63,7 см, проведенная к основанию a = 30 см, дает площадь каждого сегмента, равную:

Так как таких сегментов 12, то получаем полную площадь поверхности:

кв. см

Округляем до десятков, получаем 11470 кв. см.

Ответ: 11470

Задание 3. Юра предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.

Решение.

Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.

По теореме Пифагора можно записать равенство:

Решаем уравнение относительно R, имеем:

Ответ: 72,5

Задание 4. Юра нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Юры. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение.

Подставим в формулу площади купола зонта числовые значения, получим:

Округляем до целого, имеем: 13204 см. кв.

Ответ: 13204

Задание 5. Рулон ткани имеет длину 16 м и ширину 150 см. На фабрике из этого рулона были вырезаны треугольные клинья для 18 зонтов, таких же, как зонт, который был у Димы и Юры. Каждый треугольник с учётом припуска на швы имеет площадь 1000 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение.

Вычислим площадь ткани в кв. см, получим:

S = 16∙100∙150 = 240 000 см. кв.

Площадь клиньев для 18 зонтов, равна:

18∙12∙1000 = 216 000 см. кв.

Площадь обрезков:

240 000 – 216 000 = 24 000 см. кв.

Что составляет:

Ответ: 10

Решение 2536. Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,8 см.

Две подруги Оля и Аня задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Оля и Аня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 28 см. Высота купола зонта h (рис. 2) оказалась равна 27 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 108 см.

Задание 1. Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,8 см.

Решение.

Треть спицы будет равна

27 – 6,8 = 20,2 см

следовательно, длина всей спицы:

20,2∙3 = 60,6 см

Ответ: 60,6

Задание 2. Поскольку зонт сшит из треугольников, рассуждала Оля, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Оли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 59 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Решение.

Высота h = 59 см, проведенная к основанию a = 28 см, дает площадь каждого сегмента, равную:

Так как таких сегментов 12, то получаем полную площадь поверхности:

кв. см

Округляем до десятков, получаем 9910 кв. см.

Ответ: 9910

Задание 3. Аня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC = R (рис. 2). Ответ дайте в сантиметрах.

Решение.

Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.

По теореме Пифагора можно записать равенство:

Решаем уравнение относительно R, имеем:

Ответ: 67,5

Задание 4. Аня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Ани. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение.

Подставим в формулу площади купола зонта числовые значения, получим:

Округляем до целого, имеем: 11445 см. кв.

Ответ: 11445

Задание 5. Рулон ткани имеет длину 20 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 15 зонтов, таких же, как зонт, который был у Оли и Ани. Каждый треугольник с учётом припуска на швы имеет площадь 850 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение.

Вычислим площадь ткани в кв. см, получим:

S = 20∙100∙90 = 180 000 см. кв.

Площадь клиньев для 15 зонтов, равна:

15∙12∙850 = 153 000 см. кв.

Площадь обрезков:

180 000 – 153 000 = 27 000 см. кв.

Что составляет:

Ответ: 15

Решение 5336. Длина зонта в сложенном виде равна 26,5 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,3 см.

Две подруги Катя и Таня задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из десяти отдельных клиньев, натянутых на каркас из десяти спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Катя и Таня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 34 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 110 см.

Задание 1. Длина зонта в сложенном виде равна 26,5 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,3 см.

Решение.

Треть спицы будет равна

26,5 – 6,3 = 20,2 см

следовательно, длина всей спицы:

20,2∙3 = 60,6 см

Ответ: 60,6

Задание 2. Поскольку зонт сшит из треугольников, рассуждала Катя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Кати, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 58,2 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

Решение.

Высота h = 58,2 см, проведенная к основанию a = 34 см, дает площадь каждого сегмента, равную:

Так как таких сегментов 10, то получаем полную площадь поверхности:

кв. см

Округляем до десятков, получаем 9890 кв. см.

Ответ: 9890

Задание 3. Таня предположила, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.

Решение.

Рассмотрим прямоугольный треугольник с катетами d/2 и R-h и гипотенузой R.

По теореме Пифагора можно записать равенство:

Решаем уравнение относительно R, имеем:

Ответ: 73

Задание 4. Таня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Тани. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

Решение.

Подставим в формулу площади купола зонта числовые значения, получим:

Округляем до целого, имеем: 11461 см. кв.

Ответ: 11461

Задание 5. Рулон ткани имеет длину 20 м и ширину 150 см. На фабрике из этого рулона были вырезаны треугольные клинья для 26 зонтов, таких же, как зонт, который был у Кати и Тани. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Решение.

Вычислим площадь ткани в кв. см, получим:

S = 20∙100∙150 = 300 000 см. кв.

Площадь клиньев для 26 зонтов, равна:

26∙10∙1050 = 273 000 см. кв.

Площадь обрезков:

300 000 – 273 000 = 27 000 см. кв.

Что составляет:

Ответ: 9

Источник

Решу ОГЭ 2022 по русскому языку 9 класс тренировочный вариант №7954726:

Тест изложения

Ответы для варианта

Другие тренировочные варианты ОГЭ 2022 по русскому языку:

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Практические задачи №1-5 к ОГЭ по математике

Задание 1.

Задание 2.

Задание 3.

Задание 4.

Задание 5.

РЕКОМЕНДУЕМЫЕ ТОВАРЫ