Авторы: М.Т. Баранов, Т.А. Ладыженская, Л.А. Тростенцова.
Издательство:
Просвещение 2015-2020
Тип: Учебник
Подробный решебник (ГДЗ) по Русскому языку за 7 (седьмой) класс — готовый ответ упражнение — 20. Авторы учебника: Баранов, Ладыженская, Тростенцова. Издательство: Просвещение 2015-2020.
Сложность:
Среднее время решения: 1 мин. 28 сек.
ОГЭ по математике 2022 задание 14: номер 48 | Из заданных последовательност…
35
Из заданных последовательностей выберите геометрическую прогрессию. В ответе запишите знаменатель этой геометрической прогрессии. ($a_{n}$): $a_{1}=5$, $a_{n}:a_{n+1}=2$ (b$_{n}$): 4, 6, 8,10, … $(c_{n}): 1$, ${1} / {2}$, ${1} / {3}$, ${1} / {4}$, …
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
Геометрическая прогрессия задана условиями $b_1=6$, $b_{n+1}=-4{b_n} $. Найдите $b_5$.
В первом ряду театра $20$ мест, а в каждом следующем на $2$ больше, чем в предыдущем. Сколько мест в десятом ряду?
Выписаны первые несколько членов геометрической прогрессии: $0{{,}}4$; $0{{,}}8$; $1{{,}}6$; $…$ Найдите сумму первых $6$ её членов.
Выписаны первые несколько членов геометрической прогрессии: $0{{,}}4$; $0{{,}}8$; $1{{,}}6$; $…$ Найдите сумму первых $6$ её членов.
Автор:
Канакина В.П., Горецкий В.Г.
 #огэ_математика #ёж_математик #огэ_2022
#огэ_математика #ёж_математик #огэ_2022
Запись на занятия
Подробнее о занятиях
Vk
Telegram
Ёжику на корм
Друзья!!! В этом видео вы найдете решение типовых задач №20 на ОГЭ по математике в 2022 году. Все задания взяты с сайта «Сдам ГИА: Решу ОГЭ»
Полезные ссылки:
Видеокурс ОГЭ 2022 Математика
Вторая часть видео
Третья часть видео
Четвёртая часть видео
Пятая часть видео
Подробнее о разложении квадратного трёхчлена на множители (тема 9)
Таймкоды:
00:34 задание 1 № 47
03:22 задание 2 № 311236
05:34 задание 3 № 311243
07:45 задание 4 № 311255
09:05 задание 5 № 311575
11:32 задание 7 № 311582
14:35 задание 8 № 311584
16:35 задание 11 № 311599
20:10 задание 12 № 311654
22:17 задание 16 № 314410
23:42 задание 18 № 338112
Если вы считаете, что Ёжик-математик делает полезное дело, ставьте лайки под видео, пишите комментарии и подписывайтесь на канал. Этим вы поспособствуете продвижению канала.
Всем удачи на экзаменах!!!
Музыка в видео: П.И. Чайковский — «Вальс цветов» (балет «Щелкунчик»)
Главная › ОГЭ 9 класс › Задание 20 ОГЭ. Выражения и уравнения
Автор: Ирина Гайкова
Комментариев нет
989
Telegram
VK
OK
Интересная статья? Поделитесь ею пожалуйста с другими:
Telegram
VK
OK

Хотите обучаться математике индивидуально?
Запишитесь на консультацию.
Мы храним ваши данные в тайне
Оставьте свой комментарий:









 Еще смайлы
Еще смайлы
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий
Имя *
Email *
Вебсайт
Получать новые комментарии по электронной почте. Вы можете подписаться без комментирования.
Нажимая на кнопку «Отправить комментарий», я соглашаюсь с политикой обработки персональных данных
Задание №20 ОГЭ по математике
В данном задании необходимо решить уравнение степени больше двух — это может быть биквадратное или кубическое уравнение. Ниже мы приводим алгоритмы решения типовых заданий.
Алгоритм решения:
- Определить тип уравнения.
- Перенести правую часть уравнения в левую.
- Привести уравнение к виду, при котором можно его многочлен слева разложить на множители.
- Разложить на множители.
- Приравнять каждый множитель к нулю
- Решить полученные уравнения.
- Записать ответ.
Решение:
1. Уравнение четвертой степени.
2. Перенесем правую часть уравнения в левую:
x 4 – (4x – 5) 2 = 0
3. Уравнение уже приведено к виду, при котором можно его левую часть разложить на множители.
4. Данное уравнение разложим на множители по формуле разности квадратов. Получим:
(х 2 – (4х-5))( х 2 + (4х-5)) = 0, или (х 2 – 4х+5)(х 2 + 4х-5) = 0.
5. Приравняем каждый множитель к нулю:
х 2 – 4х+5 = 0 и х 2 + 4х-5 = 0
6. Решим каждое из уравнений по формулам дискриминанта и корней:
Для первого уравнения:
D = b 2 -4ac = 16-20 = – 4, это означает, что первое уравнение х 2 – 4х+5 = 0 не имеет корней.
Для второго уравнения:
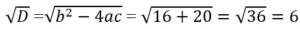
Определим корни второго уравнения:
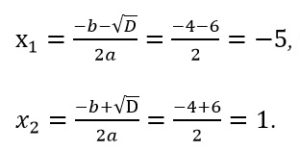 Получили два
Получили два
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Решение:
1. Перед нами уравнение третьей степени общего типа.
2. Найдем делители свободного члена данного уравнения. Это числа: 1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 12; -12;.18; -18; 36; -36.
3. Рассмотрим числа 1; -1; 2; -2; 3; -3. Это наименьшие среди найденных делителей. Подставим их по очереди в уравнение вместо х:
Мы нашли один корень.
4. Теперь выполним деление кубического многочлена на x-3, воспользовавшись схемой Горнера, имеем:
| 1 | 4 | -9 | -36 | |
| 3 | 1 | 7 | 12 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
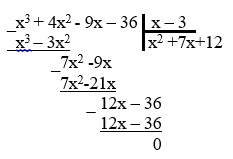
5. После деления получаем квадратный трехчлен:
Составим квадратное уравнение для вычисления оставшихся двух корней:
6. Решим его с помощью формул корней и дискриминанта
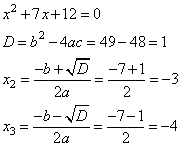
7. Получили три корня 3; -3; -4.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами кубическое уравнение общего вида.
2. Найдем делители свободного члена уравнения. Это числа: 1; -1 и 2; -2.
3. Определим один из корней кубического уравнения среди делителей свободного члена .Для этого подставим каждый из этих делителей вместо x и проверим, какой их них является корнем:
– для x=1: 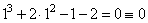 – подходит это и есть один из корней.
– подходит это и есть один из корней.
4. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
| 1 | 2 | -1 | -2 | |
| 1 | 1 | 3 | 2 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
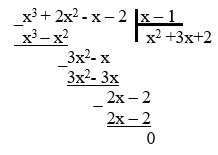
5. Получаем квадратный трехчлен
6. Составим и решим квадратное уравнение для вычисления оставшихся двух корней. Для этого воспользуемся формулами корней квадратного уравнения и дискриминантом.
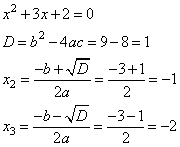
7. Получили три корня -2; -1; 1.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Выполняем замену выражения с х на альтернативную переменную. Это позволит упростить уравнение и привести его к форме обычного квадратного.
- Решаем полученное квадратное уравнения.
- Переходим обратно к выражению с х, для которого была выполнена замена.
- Находим искомые корни уравнения.
Решение:
Это уравнение можно решить с помощью т.Виета. Согласно теореме, имеем:
Возвращаемся к переменной х. Поскольку (х–2) 2 =а, то получим:

это уравнение корней не имеет, т.к. нельзя извлечь
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Корни уравнения: 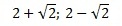
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Используя формулу сокращенного умножения для квадрата разности, раскрываем скобки в левой и правой части неравенства.
- Группируем элементы (слагаемые) неравенства: слагаемые с «х» должны оказаться в левой части, свободные члены – в правой. Приводим подобные.
- Решаем полученное неравенство.
Решение:
х≤|1| → –1≤x≤1 → xϵ[–1; 1] 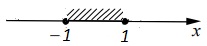
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Из 2-го уравнения выражаем у через х.
- Подставляем полученное выражение для у в 1-е уравнение.
- В полученном уравнении с одной переменной (х) выполняем тождественные преобразования. Приводим его к квадратичному виду.
- Выполняем замену х 2 на а. Решаем полученное квадратное уравнение.
- Возвращаемся от а к х. Находим все значения (корни) для х.
- Определяем соответствующие им значения для у.
- Фиксируем в ответе пары соответствующих корней.
Решение:
Теперь возвращаемся к уравнению, в котором у выражено через х. И вычисляем соответствующие значения для у: 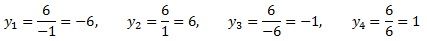 Корни системы: (–1; –6), (1; 6), (–6; –1), (6; 1)Ответ: 16
Корни системы: (–1; –6), (1; 6), (–6; –1), (6; 1)Ответ: 16
pазбирался: Даниил Романович | обсудить разбор | оценить
Нам дано уравнение третьей степени: х 3 + 6х 2 =4х + 24
В данном уравнении перенесем все слагаемые в одну сторону ( в левую), изменяя при этом знаки: х 3 + 6х 2 – 4х – 24=0
Теперь сгруппируем слагаемые: (х 3 + 6х 2 ) – (4х + 24)=0
Вынесем общий множитель за скобки из каждой группы: х 2 (х + 6) – 4(х + 6)=0
Вынесем за скобки выражение (х + 6): (х + 6)(х 2 – 4)=0
Приравняем каждый множитель к нулю и решим полученные уравнения:
х + 6=0 и х 2 – 4=0
х=6 х 2 =4, отсюда х1,2= ± 2
pазбирался: Даниил Романович | обсудить разбор | оценить
Для начала преобразуем нашу дробь, которая дана по условию. Применим правило пропорции, умножив на 5 знаменатель данной дроби:
4 a − 9 b + 3 9 a − 4 b + 3 . . = 5
5(9а – 4b + 3)=4a – 9b+3
Раскроем скобки и перенесем слагаемые с буквами а и b влево, а свободные члены вправо (не забывая изменять при переносе знаки на противоположные): 45a – 20b +15 =4a – 9b+3 45a – 20b – 4a + 9b=3 – 15 Приведем подобные слагаемые: 41a – 11b = – 12 Выпишем выражение, значение которого надо найти: 41a – 11b + 15 и заменим в нем 41a – 11b на число -12, полученное при упрощении нашей дроби: 41 a – 11 b + 15= – 12 + 15=3. Видим, что значение нашего выражения получилось равным 3.Ответ: 3
pазбирался: Даниил Романович | обсудить разбор | оценить
Данное уравнение является квадратным. Но в его условии присутствует квадратный
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.
Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):
х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0
Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:
х 2 − 2 х − 24 = 0
Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.
Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .
pазбирался: Даниил Романович | обсудить разбор | оценить
Имеем дробное неравенство, где решать надо будет только знаменатель. Но для этого посмотрим, что решением неравенства являются числа, которые больше или равны нулю. Для этого наш знаменатель должен быть отрицательным числом, так как числитель – число тоже отрицательное, а при делении двух отрицательных чисел получим число положительное. Далее, знаменатель не должен быть равен нулю, так как на нуль делить нельзя. Следовательно, начнем решение с того, что выпишем знаменатель, который должен быть отрицательным числом:
У нас получилось квадратное неравенство, которое мы и должны решать. Начнем с раскрытия скобок по формуле сокращенного умножения и приведения подобных слагаемых:
Получим квадратное неравенство, для которого надо найти интервал отрицательных чисел ( 0 )
Для этого найдем нули функции, решая с помощью дискриминанта:
Д=(-4) 2 – 4 ∙ 1 ∙ 1 =16-4=12
х 1 = 4 − √ 12 2 . . = 2 ( 2 − √ 3 ) 2 . . = 2 − √ 3
Знаем, что х2 будет отличаться только знаком, получим, что х 2 = 2 + √ 3 Теперь отмечаем числа на числовом луче и показываем интервалы справа налево путем чередования знаков. Видим, что наш интервал отрицательных чисел – от точки ( 2 − √ 3 ) до точки ( 2 + √ 3 ) . 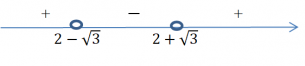 Ответ: ( 2 − √ 3 ; 2 + √ 3 )
Ответ: ( 2 − √ 3 ; 2 + √ 3 )
pазбирался: Даниил Романович | обсудить разбор | оценить
Чтобы решить данное задание, необходимо понимать, что выполнять действия умножение и деление степеней мы можем в том случае, если они имеют одинаковые основания. Поэтому разложим на множители основание 36 нашего числителя так, чтобы вместо 36 были числа 4 и 3, которые есть в знаменателе.
( 3 ∙ 3 ∙ 4 ) n 4 n − 2 ∙ 3 2 n − 1 . .
Теперь представим каждый множитель в виде степени:
3 n ∙ 3 n ∙ 4 n 4 n − 2 ∙ 3 2 n − 1 . .
Разложим знаменатель дроби на множители по свойству степеней
3 n ∙ 3 n ∙ 4 n 4 n ∙ 4 − 2 ∙ 3 2 n ∙ 3 − 1 . .
Теперь можно сократить числитель и знаменатель на 3 n и в 4 n степени
Получим дробь, которую преобразуем по свойству степеней:
. . 1 4 − 2 ∙ 3 − 1 . . = 4 2 ∙ 3 1 1 . . = 16 ∙ 3 = 48
pазбирался: Даниил Романович | обсудить разбор | оценить
Для того чтобы начать решать неравенство, мы должны понимать, интервал каких чисел будем находить – положительных или отрицательных. Для этого перенесем выражение из правой части в левую, изменяя знак на противоположный, и справа от знака «меньше» образуется нуль:
( х − 5 ) 2 − √ 7 ( х − 5 ) 0 Теперь вынесем за скобки общий множитель (х-5), получим: ( х − 5 ) ( х − 5 − √ 7 ) 0 Найдем нули функции, приравнивая каждый множитель к нулю: х − 5 = 0 , откуда х=5 х − 5 − √ 7 = 0 , откуда: х = 5 + √ 7 Отметим эти числа на числовом луче и найдем интервал отрицательных чисел: 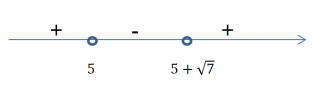 Итак, видно, что необходимый интервал от 5 до ( 5 + √ 7 ) Ответ: ( 5 ; 5 + √ 7 ) Ответ: см. решение
Итак, видно, что необходимый интервал от 5 до ( 5 + √ 7 ) Ответ: ( 5 ; 5 + √ 7 ) Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Разбор задания 20 ОГЭ-2019 по математике
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 20
Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) В любом параллелограмме есть два равных угла.
Решение
Первое утверждение есть аксиома параллельных прямых. Второе утверждение неверно, так как для отрезков с длинами 1, 2, 4 не выполняется неравенство треугольника (сумма длин любых двух сторон меньше длины третьей стороны)
Третье утверждение верно – в параллелограмме противолежащие углы равны.
Подготовка к решению №20 ОГЭ по математике
Разделы: Математика
Класс: 9
Ключевые слова: геометрия , ГИА
Современное общество понимает важность математического образования подрастающего поколения, признает его необходимость. Математика является обязательным предметом на всех этапах школьного обучения с 1 по 11 класс, экзамен по математике является обязательным в 9 и 11 классах. В настоящее время в рамках ОГЭ по математике проводится проверка знаний и по алгебре, и по геометрии. Задачи по геометрии занимают примерно третью часть всех заданий КИМов. Задания базового уровня направлены на проверку знаний основных фактов курса геометрии, умения решать простейшие задачи.
Как помочь каждому школьнику справиться заданиями ГИА, а учителю эффективнее организовать учебный процесс? Не секрет, что прочными математическими знаниями обладают единицы.
Геометрия как учебный предмет играет огромную роль в развитии познавательной активности и любознательности, логического мышления и пространственного воображения учащихся, формирует не только специальные геометрические знания учащихся, но и влияет на общее развитие личности, умение логически мыслить, доказательно обосновывать утверждения в любой сфере деятельности. Каждый учитель старается вернуть интерес к предмету, показать его значимость в различных сферах человеческой деятельности, научить ученика учиться и применять накопленные знания в практической деятельности.
В процессе обучения геометрии важное место занимает проверка теоретических знаний. Необходимость повторения – это требования одной из задач обучения, требующая прочного и сознательного овладения знаниями. Повторение материала осуществляется во всей системе учебного процесса. Формы и виды повторения могут быть разнообразными. Одна из форм повторения – обобщающее повторение. Обобщающее повторение дает возможность осуществлять дифференцируемый подход к учащимся, учитывать их возрастные и индивидуальные особенности, учитывать особенности класса, умения и навыки учащихся.
Учитель сам определяет, что повторять, как повторять и когда повторять, стремясь привести в систему знания и умения учащихся, устранить пробелы в знаниях учащихся, обобщить, систематизировать и окончательно закрепить наиболее существенное из учебного материала.
В своей работе я использую различные методы повторения, в том числе и метод обобщающего повторения, который, как я считаю, является более эффективным при подготовке к ОГЭ учащихся 9 класса. Повторение по геометрии строю на повторении определений, свойств основных геометрических фигур – треугольников, четырехугольников, многоугольников, окружности и круга.
Умение применять теоретические знания при решении задач говорит о большой эффективности такого повторения. Обобщающее повторение способствует повышению качества знаний учащихся.
В течение учебного года по окончании четверти с учащимися провожу зачеты по формулировкам теорем и определений по образцу задания №20 ОГЭ. По окончании года все формулировки собираю воедино и провожу зачет по всему материалу прошедшего учебного года.
В данной работе представлены карточки с формулировками, в которых нужно выбрать верные или неверные утверждения. Каждый ученик на зачете получает не менее 10 карточек. Ему нужно заполнить бланк для заполнения результатов (Приложение 1). Получением зачета является успешное выполнение 9-10 карточек. Для быстрого получения результата зачета для себя готовлю таблицу с правильными ответами (Приложение 2).
Я готовлю к ГИА учащихся много лет. Мой опыт позволяет сделать вывод, что такая форма работы способствует успешной подготовке к сдаче учащимися ГИА.
Карточка 1 (верные/ неверные)
- Сумма длин всех сторон называется площадью многоугольника
- Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности
- Диагонали ромба взаимно перпендикулярны и делят его углы пополам
- Около четырехугольника всегда можно описать окружность
Карточка 2 (верные/ неверные)
- Отрезок, соединяющий любые две соседние вершины, называется диагональю многоугольника
- Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания
- Квадратом называется прямоугольник, у которого все стороны равны
- Около треугольника нельзя описать окружность
Карточка 3 (верные/ неверные)
- Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины
- Катет прямоугольного треугольника есть среднее арифметическое для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла
- Два угла квадрата острые, а два другие — прямые
- Около любого треугольника можно описать окружность
Карточка 4 (верные/ неверные)
- Сумма углов невыпуклого n-угольника равна (n-2)×180°
- Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой
- Диагонали квадрата не равны
- Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность
Карточка 5 (верные/ неверные)
- Две смежные стороны четырехугольника называются противоположными
- Медианы треугольника пересекаются в одной точке, которая делит его медиану в отношении 2:1, считая от вершины
- Равные многоугольники имеют равные периметры
- В любом описанном четырехугольнике суммы противоположных сторон равны
Карточка 6 (верные/ неверные)
- Сумма углов выпуклого четырехугольника равна 180°
- Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна произведению площадей этих многоугольников
- Не во всякий четырехугольник можно вписать окружность
Карточка 7 (верные/ неверные)
- Параллелограммом называется квадрат, у которого противоположные стороны попарно параллельны
- Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны
- Площадь квадрата равна сумме его сторон
- В треугольник можно вписать только одну окружность
Карточка 8 (верные/ неверные)
- В параллелограмме противоположные стороны равны, а противоположные углы — не равны
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны
- Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
- Не в любой треугольник можно вписать окружность
Карточка 9 (верные/ неверные)
- Диагонали параллелограмма точкой пересечения делятся пополам
- Если два угла одного треугольника соответственно равны двум сторонам другого, то такие треугольники подобны
- Число k, равное произведению сходственных сторон подобных треугольников, называется коэффициентом подобия
- Высоты треугольника (или их продолжения) пересекаются в одной точке
Карточка 10 (верные/ неверные)
- Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – трапеция
- Отношение периметров двух подобных треугольников равно квадрату коэффициента подобия
- Средней линией треугольника называется отрезок, соединяющий середины двух его сторон
- Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке
Карточка 11 (верные/ неверные)
- Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм
- Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то такой треугольник равнобедренный
- Синусом острого угла тупоугольного треугольника называется отношение противолежащего катета к гипотенузе
- Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему
Карточка 12 (верные/ неверные)
- Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм
- В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов
- Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему
- Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка
Карточка 13 (верные/ неверные)
- Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие – не параллельны
- Площадь трапеции равна произведению суммы ее оснований на высоту
- Тангенсом прямого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету
- Биссектрисы треугольника пересекаются в одной точке
Карточка 14 (верные/ неверные)
- Параллельные стороны трапеции называются боковыми, а не параллельные – основаниями
- Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность имеют две общие точки
- Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе
Карточка 15 (верные/ неверные)
- Трапеция называется равнобедренной, если ее боковые стороны параллельны
- Если высоты двух треугольников равны, то их площади относятся как основания
- Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку
- Каждая точка биссектрисы неразвернутого угла равноудалена от его углов
Карточка 16 (верные/ неверные)
- Трапеция, один из углов которой прямой, называется прямоугольной
- Площадь прямоугольного треугольника равна половине произведения его катета и гипотенузы
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек
- Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно сумме отрезков другой хорды
Карточка 17 (верные/ неверные)
- Прямоугольником называется параллелограмм, у которого все углы прямые
- Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию
- Прямая, имеющая с окружностью две общие точки, называется касательной к окружности, а их общие точки называются точками касания прямой и окружности
- Центральный угол, опирающийся на полуокружность – прямой
Карточка 18 (верные/ неверные)
- Диагонали прямоугольника равны
- Площадь параллелограмма равна половине произведения его основания на высоту, проведенной к этому основанию
- Угол с вершиной в центре окружности называется ее вписанным углом
- Вписанные углы, опирающиеся на одну и ту же дугу, равны
Карточка 19 (верные/ неверные)
- Если в параллелограмме диагонали равны, то этот параллелограмм-ромб
- Площадь прямоугольника равна произведению его противоположных сторон
- Сумма градусных мер дуг окружности с общими концами равна 360°
- Вписанный угол измеряется половиной дуги, на которую он опирается
Карточка 20 (верные/ неверные)
- Ромбом называется пятиугольник, у которого все стороны равны
- Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки
- Угол, вершина которого лежит на окружности, а сторонами являются диаметры, называется вписанным углом
- Если прямая проходит через конец касательной, лежащей на окружности, и перпендикулярна к этому радиусу, то она является касательной
источники:
http://rosuchebnik.ru/material/oge-po-matematike-zadanie-20/
http://urok.1sept.ru/articles/675702
Задание 1 № 366805
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Город Гранюк | Деревня Астрелка | Хутор Южный | Город Гусевск |
| Цифры |
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.
Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.
Ответ: 1465.
2. Задание 2 № 366806
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Решение.
Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится
 пачек чая.
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
3. Задание 3 № 366807
Найдите площадь (в км2), которую занимает заказник.
Решение.

Площадь заказника равна:

Ответ: 351.
4. Задание 4 № 366808
Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Решение.
Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
 км.
км.
Ответ: 30.
5. Задание 5 № 366809
Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | |||
| Шина вида «А» | |||
| Шина вида «Б» | |||
| Спица | |||
| Педаль вида «А» | |||
| Педаль вида «Б» | |||
| Тормоз вида «А» | нет | ||
| Тормоз вида «Б» | нет | ||
| Набор крепёжных изделий |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Решение.
На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:
 руб.
руб.
Ответ: 5300.
6. Задание 6 № 316314
Найдите значение выражения: 
Решение.
Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.
7. Задание 7 № 317575
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?
1) 
2) 
3) 
4) 
Решение.
Заметим, что  и
и  Проверим все варианты ответа:
Проверим все варианты ответа:
1)  — неверно;
— неверно;
2)  — верно;
— верно;
3)  — верно;
— верно;
4)  — верно.
— верно.
Ответ указан под номером 1.
8. Задание 8 № 353586
Какое из данных ниже чисел является значением выражения 
1) 
2) 
3) 
4) 
Решение.
Последовательно получим:


Ответ: 1
9. Задание 9 № 338500
При каком значении  значения выражений
значения выражений  и
и  равны?
равны?
Решение.
Для ответа на вопрос задачи нужно решить уравнение  Решим его:
Решим его:

Ответ: 2.
10. Задание 10 № 325450
В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
Решение.
Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна 
Ответ: 0,3.
11. Задание 11 № 311406
На рисунке изображён график функции  . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке 
2) 
3) 
4) прямая  пересекает график в точках
пересекает график в точках  и
и 
Решение.
Проверим каждое из утверждений.
1) Функция возрастает на промежутке  — неверно, функция убывает на промежутке
— неверно, функция убывает на промежутке  и затем возрастает на
и затем возрастает на  .
.
2)  — неверно,
— неверно, 

3)  — верно, видно из графика.
— верно, видно из графика.
4) Прямая  пересекает график в точках
пересекает график в точках  и
и  — верно, видно из графика.
— верно, видно из графика.
Таким образом, неверные утверждения находятся под номерами 1 и 2.
Ответ: 12.
12. Задание 12 № 311543
Площадь любого выпуклого четырехугольника можно вычислять по формуле  , где
, где  — длины его диагоналей, а
— длины его диагоналей, а  угол между ними. Вычислите
угол между ними. Вычислите  , если
, если  .
.
Решение.
Выразим  :
:

Подставляя, получаем:

Ответ: 0,4.
13. Задание 13 № 338497
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.

1) 1
2) 2
3) 3
4) 4
Решение.
Решим неравенство методом интервалов:


Правильный ответ указан под номером: 4.
14. Задание 14 № 406645
В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Решение.
Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.
Найдем сумму этой прогрессии:

Ответ: 377 мест.
15. Задание 15 № 340000

В прямоугольном треугольнике  катет
катет  , а высота
, а высота  , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна  Найдите
Найдите 
Решение.
Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Углы  и
и  равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.
16. Задание 16 № 351463
 На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что  Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Решение.
Пусть длина большей дуги  равна
равна  Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.
17. Задание 17 № 169876
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на  .
.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.
———-
В открытом банке иррациональный ответ.
18. Задание 18 № 350842

Найдите угол 
Решение.

Искомый угол  опирается на
опирается на  часть окружности:
часть окружности:  . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.
. Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е. 
Ответ: 22,5
19. Задание 19 № 401617
Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.
Ответ: 13.
20. Задание 20 № 338505
Решите неравенство 
Решение.
Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение 


Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).
Таким образом, ответ 
Ответ: 
Примечание.
Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно, 
21. Задание 21 № 353527
Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли  г 21-процентного раствора, тогда взяли и
г 21-процентного раствора, тогда взяли и  г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится
г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится  г, а во втором —
г, а во втором —  г Концентрация получившегося раствора равна
г Концентрация получившегося раствора равна  или 58%.
или 58%.
Ответ: 58.
22. Задание 22 № 338288
Постройте график функции  И определите, при каких значениях
И определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение.
Упростим выражение:
По теореме, обратной теореме Виета, корни уравнения  равны -1 и -2 соответственно, тогда по формуле
равны -1 и -2 соответственно, тогда по формуле  , получаем:
, получаем:  . Имеем:
. Имеем:

График функции сводится к графику параболы  с выколотой точкой
с выколотой точкой 
Выделим полный квадрат:

Следовательно, график функции получается из графика функции  сдвигом на
сдвигом на  . (см. рис.)
. (см. рис.)

Из графика видно, что прямая  имеет с графиком функции ровно одну общую точку при
имеет с графиком функции ровно одну общую точку при  и
и 
Ответ: −1; 3.
23. Задание 23 № 339395
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.
Решение.
 Угол
Угол  — вписанный, он равен 90° и опирается на дугу
— вписанный, он равен 90° и опирается на дугу  следовательно, дуга
следовательно, дуга  равна 180°, значит, хорда
равна 180°, значит, хорда  — диаметр окружности и
— диаметр окружности и 
Ответ: 16.
24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Решение.
Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.
25. Задание 25 № 311926
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
Решение.

По свойству равнобедренной трапеции  следовательно, треугольники
следовательно, треугольники  и
и  равны. Так как
равны. Так как  =
=  треугольники
треугольники  и
и  равнобедренные, следовательно,
равнобедренные, следовательно,  и
и  — соответствующие медианы этих треугольников. Значит,
— соответствующие медианы этих треугольников. Значит,  Отрезок
Отрезок  соединяет середины диагоналей трапеции, следовательно,
соединяет середины диагоналей трапеции, следовательно,  и прямые
и прямые 
 и
и  параллельны, поэтому,
параллельны, поэтому,  — трапеция. Проведём
— трапеция. Проведём  — высоту трапеции
— высоту трапеции  и
и  — высоту трапеции
— высоту трапеции  . Прямоугольные треугольники
. Прямоугольные треугольники  и
и  подобны, значит,
подобны, значит, 
Площадь трапеции  :
: 
Площадь трапеции 


Ответ: 9.


