Задание 19 номер 341525

Огэ математика 341525

Задание 19 № 402025

Какое из следующих утверждений верно?

1) Треугольник со сторонами 1, 2, 4 существует.

2) Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.

3) Основания любой трапеции параллельны.

Аналоги к заданию № 341525: 402025 402196 403776 Все

Задание 19 № 402196

Какое из следующих утверждений верно?

1) Основания любой трапеции параллельны.

2) Тангенс любого острого угла меньше единицы.

3) Сумма углов любого треугольника равна 360 градусам.

Аналоги к заданию № 341525: 402025 402196 403776 Все

Задание 19 № 403776

Задание 19 № 402025

Задание 19 № 402196

Какое из следующих утверждений верно.

Oge. sdamgia. ru

25.11.2017 7:36:09

2017-11-25 07:36:09

Источники:

Https://oge. sdamgia. ru/test? likes=341525

РЕШУ ГВЭ, математика 9: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Огэ математика 341525

Огэ математика 341525

Огэ математика 341525

Задание 8 № 341525

Какие из следующих утверждений верны?

1) Треугольника со сторонами 1, 2, 4 не существует.

2) Сумма углов любого треугольника равна 360 градусам.

3) Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Треугольника со сторонами 1, 2, 4 не существует» — Верно, сторона треугольника не может быть больше суммы двух других.

2) «Сумма углов любого треугольника равна 360 градусам» — Неверно, сумма углов любого треугольника равна 180 градусам.

3) «Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности» — Верно, центр описанной окружности лежит в точке пересечения серединных перпендикуляров.

Задание 8 № 341525

Задание 8 341525.

Math9-gve. sdamgia. ru

22.07.2017 13:36:17

2017-07-22 13:36:17

Источники:

Https://math9-gve. sdamgia. ru/problem? id=341525

OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Огэ математика 341525

Огэ математика 341525

Огэ математика 341525

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Какое из следующих утверждений верно?

1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

2) В любой прямоугольник можно вписать окружность.

3) Каждая из биссектрис равнобедренного треугольника является его медианой.

В ответе запишите номер выбранного утверждения.

Укажите номера верных утверждений.

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его медианой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Какие из данных утверждений верны? Запишите их номера.

1) Вокруг любого треугольника можно описать окружность.

2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна 180° , то эти прямые параллельны.

3) Площадь треугольника не превышает произведения двух его сторон.

Какие из следующих утверждений верны?

1) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

2) Боковые стороны любой трапеции равны.

3) Один из углов треугольника всегда не превышает 60 градусов.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Укажите номера верных утверждений.

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2) Треугольник со сторонами 1, 2, 4 существует.

3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.

4) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.

Если утверждений несколько, запишите их номера в порядке возрастания.

Укажите номера верных утверждений.

1) Если угол равен 47°, то смежный с ним равен 153°.

2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.

3) Через любую точку проходит ровно одна прямая.

Если утверждений несколько, запишите их номера в порядке возрастания.

Укажите номера верных утверждений.

1) Площадь трапеции равна половине высоты, умноженной на разность оснований.

2) Через любые две точки можно провести прямую.

3) Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Укажите номера верных утверждений.

1) Смежные углы равны.

2) Любые две прямые имеют ровно одну общую точку.

3) Если угол равен 108°, то вертикальный с ним равен 108°.

Если утверждений несколько, запишите их номера в порядке возрастания.

Укажите номера верных утверждений.

1) Диаметр делит окружность на две равные дуги.

2) Параллелограмм имеет две оси симметрии.

3) Площадь треугольника равна его основанию, умноженному на высоту.

Какие из следующих утверждений верны?

1) Один из углов треугольника всегда не превышает 60 градусов.

2) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.

3) Все диаметры окружности равны между собой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Какие из следующих утверждений верны?

1. Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.

2. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

3. Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Укажите номера верных утверждений.

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2) Треугольник со сторонами 1, 2, 4 существует.

3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.

4) В любом параллелограмме диагонали равны.

Какие из следующих утверждений верны?

1) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

2) В тупоугольном треугольнике все углы тупые.

3) Средняя линия трапеции равна полусумме её оснований.

Если утверждений несколько, запишите их номера в порядке возрастания.

Какие из следующих утверждений верны?

1) Треугольника со сторонами 1, 2, 4 не существует.

2) Смежные углы равны.

3) Все диаметры окружности равны между собой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Какое из следующих утверждений верно?

1) Точка касания двух окружностей равноудалена от центров этих окружностей.

2) В параллелограмме есть два равных угла.

3) Площадь прямоугольного треугольника равна произведению длин его катетов.

Если утверждений несколько, запишите их номера в порядке возрастания.

Укажите номера верных утверждений.

Math-oge. sdamgia. ru

02.10.2018 17:30:50

2018-10-02 17:30:50

Источники:

Https://math-oge. sdamgia. ru/test? id=26479681

Источник

верхняя шапка

картинка

Задачи разделены на уровни сложности. Задачи из любого уровня вполне реально встретить на настоящем экзамене ОГЭ, более сложные встретятся если «не повезло».

Сложность у всех задач примерно одинаковая

  1. Какое из следующих утверждений верно?

    1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники равны.

    2) Сумма углов прямоугольного треугольника равна 180°.

    3) Любая медиана равнобедренного треугольника является его высотой.

    В ответе запишите номер выбранного утверждения.

    2. посмотреть ответ

  2. Какие из следующих утверждений верны?
    1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
    2) Треугольник со сторонами 1, 2, 4 существует.
    3) В любом параллелограмме есть два равных угла.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    3. посмотреть ответ

  3. Какое из следующих утверждений верно?
    1) Дана окружность. Через любую точку плоскости можно провести к ней касательную прямую.
    2) Если в параллелограмме некоторый угол равен 90°, то это квадрат.
    3) В любом ромбе найдется угол меньше 120°.

    В ответе запишите номер выбранного утверждения.

    4. посмотреть ответ

  4. Какое из следующих утверждений верно?

    1) Внутренние односторонние углы при пересечении параллельных прямых секущей равны.

    2) Площадь трапеции равна произведению высоты на сумму оснований.

    3) В любом квадрате все углы равны.

    В ответе запишите номер выбранного утверждения.

    5. посмотреть ответ

  5. Какие из следующих утверждений верны?

    1) Сумма катетов длиннее гипотенузы.

    2) Длина суммы векторов длиннее суммы длин самих векторов.

    3) В любом треугольнике найдется острый угол.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    6. посмотреть ответ

  6. Какое из следующих утверждений верно?

    1) Сумма длин трех сторон четырехугольника всегда длиннее четвертой стороны.

    2) В любой выпуклый четырехугольник можно вписать окружность.

    3) Диагонали ромба равны.

    В ответе запишите номер выбранного утверждения.

    7. посмотреть ответ

  7. Какое из следующих утверждений верно?
    1) Площадь треугольника равна произведению стороны на высоту, проведенную к этой стороне.

    2) Треугольники равны, если их соответствующие стороны равны.
    3) У подобных треугольников площади равны.

    В ответе запишите номер выбранного утверждения.

    8. посмотреть ответ

  8. Какое из следующих утверждений верно?

    1) Сумма вертикальных углов равна 180°.

    2) Корень квадратный из площади квадрата равен длине его стороны.

    3) Периметр прямоугольника всегда больше его площади.

    В ответе запишите номер выбранного утверждения.

    9. посмотреть ответ

  9. Какие из следующих утверждений верны?

    1) У подобных треугольников соответствующие углы равны.

    2) В правильном пятиугольнике все углы равны.

    3) Площадь прямоугольника равна квадрату любой его стороны.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    10. посмотреть ответ

  10. Какое из следующих утверждений верно?
    1) В правильном шестиугольнике все углы по 160°.
    2) Не существует треугольника со сторонами 10,12 и 16.
    3) Диагонали прямоугольника равны.

    В ответе запишите номер выбранного утверждения.

    11. посмотреть ответ

  11. Какие из следующих утверждений верны?

    1) В любой прямоугольник можно вписать окружность.

    2) Вписанные углы, опирающиеся на одну дугу окружности, равны.

    3) Если угол между векторами равен 90°, то их скалярное произведение равно нулю.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    12. посмотреть ответ

  12. Какое из следующих утверждений верно?
    1) Косинус угла в прямоугольном треугольнике это отношение прилежащего катета к противолежащему катету.
    2) Катет лежащий против угла в 60° в два раза короче гипотенузы.
    3) Диагонали ромба перпендикулярны.

    В ответе запишите номер выбранного утверждения.

    13. посмотреть ответ

  13. Какие из следующих утверждений верны?
    1) Центр окружности вписанной в треугольник находится на пересечении биссектрис.

    2) В правильном шестиугольнике все стороны равны.
    3) Сумма двух соседних углов параллелограмма равна 180°.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    14. посмотреть ответ

  14. Какие из следующих утверждений верны?
    1) Дана прямая. Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной.
    2) Высоты треугольника пересекаются в одной точке.
    3) Высота треугольника всегда лежит внутри треугольника.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    15. посмотреть ответ

  15. Какое из следующих утверждений верно?
    1) Диагонали ромба пересекаются и точкой пересечения делятся пополам.
    2) Площадь прямоугольника равна произведению двух противоположных сторон.
    3) Длина вектора равна сумме квадратов его координат.

    В ответе запишите номер выбранного утверждения.

    16. посмотреть ответ

  16. Какое из следующих утверждений верно?
    1) Сумма смежных углов равна 180°.
    2) Если скалярное произведение векторов равно нулю, то векторы параллельны.
    3) В любой трапеции есть, по крайней мере, два острых угла.

    В ответе запишите номер выбранного утверждения.

    17. посмотреть ответ

  17. Какие из следующих утверждений верны?
    1) Площадь любого треугольника равна половине произведения сторон на синус угла между ними.

    2) Все точки лежащие на биссектрисе некоторого угла равноудалены от сторон этого угла.

    3) Площадь ромба равна половине произведения сторон.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    18. посмотреть ответ

  18. Какое из следующих утверждений верно?
    1) Если две окружности касаются, то у них радиусы равны.
    2) Периметр прямоугольника равен произведению двух соседних сторон.
    3) Сумма углов пятиугольника равна 540°.

    В ответе запишите номер выбранного утверждения.

    19. посмотреть ответ

  19. Какие из следующих утверждений верны?
    1) Вокруг любого четырехугольника можно описать окружность.
    2) Если некоторая окружность касается прямой, то расстояние от центра окружности до этой прямой равно радиусу окружности.
    3) Если соответственные углы при пересечении двух прямых секущей равны, то прямые параллельны.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    20. посмотреть ответ

  20. Какие из следующих утверждений верны?
    1) Через точку, лежащую на окружности, всегда можно провести касательную к этой окружности.

    2) Длина окружности всегда больше ее радиуса.
    3) Если в треугольнике одна сторона равна половине второй, то в треугольнике есть угол в 30°.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    21. посмотреть ответ

  21. Какое из следующих утверждений верно?
    1) Если в параллелограмме все углы равны, то это квадрат.
    2) Длина самой длинной стороны в треугольнике меньше суммы длин двух других сторон.
    3) Вокруг любого четырехугольника можно описать окружность.

    В ответе запишите номер выбранного утверждения.

    22. посмотреть ответ

  22. Какие из следующих утверждений верны?
    1) Диагональ параллелограмма делит его на два равных треугольника.

    2) Площадь квадрата равна произведению двух его смежных сторон.
    3) Все хорды одной окружности равны между собой.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    23. посмотреть ответ

  23. Какие из следующих утверждений верны?
    1) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
    2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
    3) Любой квадрат является прямоугольником.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    24. посмотреть ответ

  24. Какие из следующих утверждений верны?
    1) Существует прямоугольник, диагонали которого взаимно перпендикулярны.

    2) Каждая из биссектрис равнобедренного треугольника является его медианой.
    3) В любой ромб можно вписать окружность.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    25. посмотреть ответ

  25. Какие из следующих утверждений верны?
    1) Любые два прямоугольных треугольника подобны.
    2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
    3) Стороны треугольника пропорциональны синусам противолежащих углов.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    26. посмотреть ответ

  26. Какие из следующих утверждений верны?
    1) Треугольник со сторонами, длины которых равны 3,4 и 5, является тупоугольным.
    2) Прямоугольник обладает центром симметрии.
    3) Любой прямоугольный треугольник не обладает центром симметрии.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    27. посмотреть ответ

  27. Какие из следующих утверждений верны?
    1) У квадрата ровно две оси симметрии.
    2) Центром симметрии ромба является точка пересечения его диагоналей.
    3) Площадь прямоугольного треугольника меньше произведения его катетов.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    28. посмотреть ответ

  28. Какое из следующих утверждений верно?
    1) В правильный шестиугольник всегда можно вписать окружность.
    2) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
    3) Сумма вертикальных углов равна 180°.

    В ответ запишите номер выбранного утверждения.

    29. посмотреть ответ

  29. Какое из следующих утверждений верно?
    1) Через любые две точки на плоскости можно провести окружность, причем только одну.
    2) У прямоугольного треугольника не может быть оси симметрии.
    3) Диагонали трапеции всегда пересекаются.

    В ответ запишите номер выбранного утверждения.

    30. посмотреть ответ

  30. Какие из следующих утверждений верны?
    1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат.
    2) В параллелограмме есть два равных угла.
    3) Площадь параллелограмма меньше или равна произведению двух его соседних сторон.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    31. посмотреть ответ

  31. Какие из следующих утверждений верны?
    1) Косинус острого угла прямоугольного треугольника равен отношению катета, прилежащего к этому углу, к гипотенузе.
    2) Если в параллелограмме все углы равны, то это прямоугольник.
    3) Все высоты равнобедренного треугольника лежать внутри этого треугольника.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    32. посмотреть ответ

  32. Какое из следующих утверждений верно?
    1) К двум окружностям всегда можно провести две общие касательные.
    2) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник – параллелограмм.
    3) Точка пересечения биссектрис любого треугольника всегда лежит внутри этого треугольника.

    В ответ запишите номер выбранного утверждения.

    33. посмотреть ответ

нижняя шапка

Простой способ вычислить проценты от X

Сколько будет   %

от   ?  

19% от 341525 это: 64889.75

Процент от Разница
1% от 341525 это 3415.25 338109.75
2% от 341525 это 6830.5 334694.5
3% от 341525 это 10245.75 331279.25
4% от 341525 это 13661 327864
5% от 341525 это 17076.25 324448.75
6% от 341525 это 20491.5 321033.5
7% от 341525 это 23906.75 317618.25
8% от 341525 это 27322 314203
9% от 341525 это 30737.25 310787.75
10% от 341525 это 34152.5 307372.5
11% от 341525 это 37567.75 303957.25
12% от 341525 это 40983 300542
13% от 341525 это 44398.25 297126.75
14% от 341525 это 47813.5 293711.5
15% от 341525 это 51228.75 290296.25
16% от 341525 это 54644 286881
17% от 341525 это 58059.25 283465.75
18% от 341525 это 61474.5 280050.5
19% от 341525 это 64889.75 276635.25
20% от 341525 это 68305 273220
21% от 341525 это 71720.25 269804.75
22% от 341525 это 75135.5 266389.5
23% от 341525 это 78550.75 262974.25
24% от 341525 это 81966 259559
25% от 341525 это 85381.25 256143.75
26% от 341525 это 88796.5 252728.5
27% от 341525 это 92211.75 249313.25
28% от 341525 это 95627 245898
29% от 341525 это 99042.25 242482.75
30% от 341525 это 102457.5 239067.5
31% от 341525 это 105872.75 235652.25
32% от 341525 это 109288 232237
33% от 341525 это 112703.25 228821.75
34% от 341525 это 116118.5 225406.5
35% от 341525 это 119533.75 221991.25
36% от 341525 это 122949 218576
37% от 341525 это 126364.25 215160.75
38% от 341525 это 129779.5 211745.5
39% от 341525 это 133194.75 208330.25
40% от 341525 это 136610 204915
41% от 341525 это 140025.25 201499.75
42% от 341525 это 143440.5 198084.5
43% от 341525 это 146855.75 194669.25
44% от 341525 это 150271 191254
45% от 341525 это 153686.25 187838.75
46% от 341525 это 157101.5 184423.5
47% от 341525 это 160516.75 181008.25
48% от 341525 это 163932 177593
49% от 341525 это 167347.25 174177.75
50% от 341525 это 170762.5 170762.5
51% от 341525 это 174177.75 167347.25
52% от 341525 это 177593 163932
53% от 341525 это 181008.25 160516.75
54% от 341525 это 184423.5 157101.5
55% от 341525 это 187838.75 153686.25
56% от 341525 это 191254 150271
57% от 341525 это 194669.25 146855.75
58% от 341525 это 198084.5 143440.5
59% от 341525 это 201499.75 140025.25
60% от 341525 это 204915 136610
61% от 341525 это 208330.25 133194.75
62% от 341525 это 211745.5 129779.5
63% от 341525 это 215160.75 126364.25
64% от 341525 это 218576 122949
65% от 341525 это 221991.25 119533.75
66% от 341525 это 225406.5 116118.5
67% от 341525 это 228821.75 112703.25
68% от 341525 это 232237 109288
69% от 341525 это 235652.25 105872.75
70% от 341525 это 239067.5 102457.5
71% от 341525 это 242482.75 99042.25
72% от 341525 это 245898 95627
73% от 341525 это 249313.25 92211.75
74% от 341525 это 252728.5 88796.5
75% от 341525 это 256143.75 85381.25
76% от 341525 это 259559 81966
77% от 341525 это 262974.25 78550.75
78% от 341525 это 266389.5 75135.5
79% от 341525 это 269804.75 71720.25
80% от 341525 это 273220 68305
81% от 341525 это 276635.25 64889.75
82% от 341525 это 280050.5 61474.5
83% от 341525 это 283465.75 58059.25
84% от 341525 это 286881 54644
85% от 341525 это 290296.25 51228.75
86% от 341525 это 293711.5 47813.5
87% от 341525 это 297126.75 44398.25
88% от 341525 это 300542 40983
89% от 341525 это 303957.25 37567.75
90% от 341525 это 307372.5 34152.5
91% от 341525 это 310787.75 30737.25
92% от 341525 это 314203 27322
93% от 341525 это 317618.25 23906.75
94% от 341525 это 321033.5 20491.5
95% от 341525 это 324448.75 17076.25
96% от 341525 это 327864 13661
97% от 341525 это 331279.25 10245.75
98% от 341525 это 334694.5 6830.5
99% от 341525 это 338109.75 3415.25
100% от 341525 это 341525 0

Как можно рассчитать 19% от 341525

В магазине товар стоит 341525₽, вам дали скидку 19% и вы хотите понять сколько вы сэкономили.

Решение:

Сэкономленная сумма = Цена товара * Скидка в процентах/ 100

Сэкономленная сумма = (19 * 341525) / 100

Сэкономленная сумма = 64889.75₽

Проще говоря, при покупке товара за 341525₽ и скидке в 19%, вы заплатите 276635.25₽ и при этом сэкономите 64889.75₽.

Для рассчета НДС от 341525₽, вы можете использовать Калькулятор НДС онлайн

Расчеты процентов: примеры

  • 18% от 51949
  • 19% от 308986
  • 56% от 312836
  • 80% от 102136
  • 6% от 377282
  • 71% от 13043
  • 21% от 311972
  • 57% от 262828
  • 66% от 6079
  • 50% от 9363
  • 85% от 257795
  • 43% от 357755

percent-calc.com    © 2022

1
Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
Смотреть видеоразбор >>

2
Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
Смотреть видеоразбор >>

3
Биссектриса треугольника делит пополам сторону, к которой проведена.
Смотреть видеоразбор >>

4
Биссектрисы треугольника пересекаются в центре его вписанной окружности.
Смотреть видеоразбор >>

5
В любой прямоугольник можно вписать окружность.
Смотреть видеоразбор >>

6
В любой ромб можно вписать окружность.
Смотреть видеоразбор >>

7
В любой треугольник можно вписать окружность.
Смотреть видеоразбор >>

8
В любой четырёхугольник можно вписать окружность.
Смотреть видеоразбор >>

9
В любом параллелограмме диагонали точкой пересечения делятся пополам.
Смотреть видеоразбор >>

10
В любом прямоугольнике диагонали взаимно перпендикулярны.
Смотреть видеоразбор >>

11
В любом тупоугольном треугольнике есть острый угол.
Смотреть видеоразбор >>

12
В остроугольном треугольнике все углы острые.
Смотреть видеоразбор >>

13
В параллелограмме есть два равных угла.
Смотреть видеоразбор >>

14
В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Смотреть видеоразбор >>

15
В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.
Смотреть видеоразбор >>

16
В прямоугольном треугольнике гипотенуза равна сумме катетов.
Смотреть видеоразбор >>

17
В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов.
Смотреть видеоразбор >>

18
В треугольнике против большего угла лежит большая сторона.
Смотреть видеоразбор >>

19
В треугольнике против большей стороны лежит больший угол.
Смотреть видеоразбор >>

20
В тупоугольном треугольнике все углы тупые.
Смотреть видеоразбор >>

21
Вертикальные углы равны.
Смотреть видеоразбор >>

22
Внешний угол треугольника больше не смежного с ним внутреннего угла.
Смотреть видеоразбор >>

23
Внешний угол треугольника равен сумме его внутренних углов.
Смотреть видеоразбор >>

24
Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Смотреть видеоразбор >>

25
Вокруг любого параллелограмма можно описать окружность.
Смотреть видеоразбор >>

26
Вокруг любого треугольника можно описать окружность.
Смотреть видеоразбор >>

27
Вписанный угол, опирающийся на диаметр окружности, прямой.
Смотреть видеоразбор >>

28
Вписанный угол, опирающийся на диаметр окружности, прямой.
Смотреть видеоразбор >>

29
Все высоты равностороннего треугольника равны.
Смотреть видеоразбор >>

30
Все диаметры окружности равны между собой.
Смотреть видеоразбор >>

31
Все квадраты имеют равные площади.
Смотреть видеоразбор >>

32
Все прямоугольные треугольники подобны.
Смотреть видеоразбор >>

33
Все равнобедренные треугольники подобны.
Смотреть видеоразбор >>

34
Все равносторонние треугольники подобны.
Смотреть видеоразбор >>

35
Все углы прямоугольника равны.
Смотреть видеоразбор >>

36
Все углы ромба равны.
Смотреть видеоразбор >>

37
Все хорды одной окружности равны между собой.
Смотреть видеоразбор >>

38
Все хорды одной окружности равны между собой.
Смотреть видеоразбор >>

39
Всякий равнобедренный треугольник является остроугольным.
Смотреть видеоразбор >>

40
Всякий равносторонний треугольник является остроугольным.
Смотреть видеоразбор >>

41
Всякий равносторонний треугольник является равнобедренным.
Смотреть видеоразбор >>

42
Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
Смотреть видеоразбор >>

43
Две прямые, параллельные третьей прямой, перпендикулярны друг другу.
Смотреть видеоразбор >>

44
Две прямые, перпендикулярные третьей прямой, параллельны друг другу.
Смотреть видеоразбор >>

45
Две прямые, перпендикулярные третьей прямой, перпендикулярны друг другу.
Смотреть видеоразбор >>

46
Диагонали квадрата взаимно перпендикулярны.
Смотреть видеоразбор >>

47
Диагонали квадрата точкой пересечения делятся пополам.
Смотреть видеоразбор >>

48
Диагонали любого прямоугольника делят его на 4 равных треугольника.
Смотреть видеоразбор >>

49
Диагонали любого прямоугольника равны.
Смотреть видеоразбор >>

50
Диагонали параллелограмма равны.
Смотреть видеоразбор >>

51
Диагонали прямоугольника равны.
Смотреть видеоразбор >>

52
Диагонали прямоугольной трапеции равны.
Смотреть видеоразбор >>

53
Диагонали равнобедренной трапеции равны.
Смотреть видеоразбор >>

54
Диагонали ромба перпендикулярны.
Смотреть видеоразбор >>

55
Диагонали ромба равны.
Смотреть видеоразбор >>

56
Диагонали ромба точкой пересечения делятся пополам.
Смотреть видеоразбор >>

57
Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
Смотреть видеоразбор >>

58
Диагональ параллелограмма делит его на два равных треугольника.
Смотреть видеоразбор >>

59
Диагональ равнобедренной трапеции делит её на два равных треугольника.
Смотреть видеоразбор >>

60
Диагональ трапеции делит её на два равных треугольника.
Смотреть видеоразбор >>

61
Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса.
Смотреть видеоразбор >>

62
Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Смотреть видеоразбор >>

63
Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Смотреть видеоразбор >>

64
Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Смотреть видеоразбор >>

65
Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом.
Смотреть видеоразбор >>

66
Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат.
Смотреть видеоразбор >>

67
Если в ромбе один из углов равен 90°, то такой ромб – квадрат.
Смотреть видеоразбор >>

68
Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
Смотреть видеоразбор >>

69
Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник – ромб.
Смотреть видеоразбор >>

70
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
Смотреть видеоразбор >>

71
Если два угла треугольника равны, то равны и противолежащие им стороны.
Смотреть видеоразбор >>

72
Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
Смотреть видеоразбор >>

73
Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Смотреть видеоразбор >>

74
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
Смотреть видеоразбор >>

75
Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Смотреть видеоразбор >>

76
Если две стороны треугольника равны, то равны и противолежащие им углы.
Смотреть видеоразбор >>

77
Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то это квадрат.
Смотреть видеоразбор >>

78
Если диагонали параллелограмма перпендикулярны, то это ромб.
Смотреть видеоразбор >>

79
Если диагонали параллелограмма равны, то он является ромбом.
Смотреть видеоразбор >>

80
Если диагонали параллелограмма равны, то это квадрат.
Смотреть видеоразбор >>

81
Если диагонали параллелограмма равны, то это прямоугольник.
Смотреть видеоразбор >>

82
Если диагонали параллелограмма равны, то это ромб.
Смотреть видеоразбор >>

83
Если один из углов треугольника прямой, то треугольник прямоугольный.
Смотреть видеоразбор >>

84
Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
Смотреть видеоразбор >>

85
Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
Смотреть видеоразбор >>

86
Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
Смотреть видеоразбор >>

87
Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
Смотреть видеоразбор >>

88
Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
Смотреть видеоразбор >>

89
Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.
Смотреть видеоразбор >>

90
Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
Смотреть видеоразбор >>

91
Если три угла одного треугольника равны трём углам другого треугольника, то такие треугольники подобны.
Смотреть видеоразбор >>

92
Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
Смотреть видеоразбор >>

93
Если угол острый, то смежный с ним угол также является острым.
Смотреть видеоразбор >>

94
Из двух хорд окружности больше та, середина которой находится дальше от центра окружности.
Смотреть видеоразбор >>

95
Каждая из биссектрис равнобедренного треугольника является его высотой.
Смотреть видеоразбор >>

96
Каждая из биссектрис равнобедренного треугольника является его медианой.
Смотреть видеоразбор >>

97
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Смотреть видеоразбор >>

98
Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
Смотреть видеоразбор >>

99
Квадрат является прямоугольником.
Смотреть видеоразбор >>

100
Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.
Смотреть видеоразбор >>

101
Любая биссектриса равнобедренного треугольника является его медианой.
Смотреть видеоразбор >>

102
Любая высота равнобедренного треугольника является его биссектрисой.
Смотреть видеоразбор >>

103
Любая медиана равнобедренного треугольника является его биссектрисой.
Смотреть видеоразбор >>

104
Любой квадрат можно вписать в окружность.
Смотреть видеоразбор >>

105
Любой квадрат является прямоугольником.
Смотреть видеоразбор >>

106
Любой квадрат является ромбом.
Смотреть видеоразбор >>

107
Любой параллелограмм можно вписать в окружность.
Смотреть видеоразбор >>

108
Любой прямоугольник можно вписать в окружность.
Смотреть видеоразбор >>

109
Любые два диаметра окружности пересекаются.
Смотреть видеоразбор >>

110
Любые два равносторонних треугольника подобны.
Смотреть видеоразбор >>

111
Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам.
Смотреть видеоразбор >>

112
Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.
Смотреть видеоразбор >>

113
Медиана треугольника делит пополам угол, из которого проведена.
Смотреть видеоразбор >>

114
На плоскости существует единственная точка, равноудалённая от концов отрезка.
Смотреть видеоразбор >>

115
Не существует прямоугольника, диагонали которого взаимно перпендикулярны.
Смотреть видеоразбор >>

116
Один из двух смежных углов острый, а другой тупой.
Смотреть видеоразбор >>

117
Один из углов треугольника всегда не превышает 60°.
Смотреть видеоразбор >>

118
Основания равнобедренной трапеции равны.
Смотреть видеоразбор >>

119
Отношение площадей подобных треугольников равно коэффициенту подобия.
Смотреть видеоразбор >>

120
Площадь квадрата равна произведению двух его смежных сторон.
Смотреть видеоразбор >>

121
Площадь квадрата равна произведению его диагоналей.
Смотреть видеоразбор >>

122
Площадь круга меньше квадрата длины его диаметра.
Смотреть видеоразбор >>

123
Площадь любого параллелограмма равна произведению длин его сторон.
Смотреть видеоразбор >>

124
Площадь параллелограмма равна половине произведения его диагоналей.
Смотреть видеоразбор >>

125
Площадь прямоугольника равна произведению длин всех его сторон.
Смотреть видеоразбор >>

126
Площадь прямоугольника равна произведению длин его смежных сторон.
Смотреть видеоразбор >>

127
Площадь прямоугольного треугольника равна произведению длин его катетов.
Смотреть видеоразбор >>

128
Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.
Смотреть видеоразбор >>

129
Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
Смотреть видеоразбор >>

130
Площадь трапеции равна произведению основания трапеции на высоту.
Смотреть видеоразбор >>

131
Площадь трапеции равна произведению средней линии на высоту.
Смотреть видеоразбор >>

132
Площадь треугольника не превышает произведения двух его сторон.
Смотреть видеоразбор >>

133
Против большей стороны треугольника лежит больший угол.
Смотреть видеоразбор >>

134
Против большей стороны треугольника лежит меньший угол.
Смотреть видеоразбор >>

135
Против равных сторон треугольника лежат равные углы.
Смотреть видеоразбор >>

136
Ромб не является параллелограммом.
Смотреть видеоразбор >>

137
Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.
Смотреть видеоразбор >>

138
Смежные углы равны.
Смотреть видеоразбор >>

139
Средняя линия трапеции параллельна её основаниям.
Смотреть видеоразбор >>

140
Средняя линия трапеции равна полусумме её оснований.
Смотреть видеоразбор >>

141
Средняя линия трапеции равна сумме её оснований.
Смотреть видеоразбор >>

142
Сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон.
Смотреть видеоразбор >>

143
Сумма острых углов прямоугольного треугольника равна 90°.
Смотреть видеоразбор >>

144
Сумма смежных углов равна 180°.
Смотреть видеоразбор >>

145
Сумма углов выпуклого четырёхугольника равна 360°.
Смотреть видеоразбор >>

146
Сумма углов любого треугольника равна 180°.
Смотреть видеоразбор >>

147
Сумма углов любого треугольника равна 360°.
Смотреть видеоразбор >>

148
Сумма углов остроугольного треугольника равна 180°.
Смотреть видеоразбор >>

149
Сумма углов прямоугольного треугольника равна 90°.
Смотреть видеоразбор >>

150
Сумма углов равнобедренного треугольника равна 180°.
Смотреть видеоразбор >>

151
Сумма углов тупоугольного треугольника равна 180°.
Смотреть видеоразбор >>

152
Существует квадрат, который не является прямоугольником.
Смотреть видеоразбор >>

153
Существует квадрат, который не является ромбом.
Смотреть видеоразбор >>

154
Существует параллелограмм, который не является прямоугольником.
Смотреть видеоразбор >>

155
Существует прямоугольник, диагонали которого взаимно перпендикулярны.
Смотреть видеоразбор >>

156
Существует прямоугольник, который не является параллелограммом.
Смотреть видеоразбор >>

157
Существует ромб, который не является квадратом.
Смотреть видеоразбор >>

158
Существуют три прямые, которые проходят через одну точку.
Смотреть видеоразбор >>

159
Тангенс любого острого угла меньше единицы.
Смотреть видеоразбор >>

160
Точка пересечения двух окружностей равноудалена от центров этих окружностей.
Смотреть видеоразбор >>

161
Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Смотреть видеоразбор >>

162
Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Смотреть видеоразбор >>

163
Треугольник с углами 40°, 70°, 70° – равнобедренный.
Смотреть видеоразбор >>

164
Треугольник со сторонами 1, 2 и 4 существует.
Смотреть видеоразбор >>

165
Треугольника со сторонами 1, 2 и 4 не существует.
Смотреть видеоразбор >>

166
У любой прямоугольной трапеции есть два равных угла.
Смотреть видеоразбор >>

167
У любой трапеции боковые стороны равны.
Смотреть видеоразбор >>

168
У любой трапеции боковые стороны равны.
Смотреть видеоразбор >>

169
У любой трапеции основания параллельны.
Смотреть видеоразбор >>

170
У равнобедренного треугольника есть ось симметрии.
Смотреть видеоразбор >>

171
У равнобедренного треугольника есть центр симметрии.
Смотреть видеоразбор >>

172
У равностороннего треугольника есть центр симметрии.
Смотреть видеоразбор >>

173
У равностороннего треугольника три оси симметрии.
Смотреть видеоразбор >>

174
Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
Смотреть видеоразбор >>

175
Угол, опирающийся на диаметр окружности, прямой.
Смотреть видеоразбор >>

176
Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
Смотреть видеоразбор >>

177
Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
Смотреть видеоразбор >>

178
Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
Смотреть видеоразбор >>

179
Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
Смотреть видеоразбор >>

180
Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.
Смотреть видеоразбор >>

181
Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
Смотреть видеоразбор >>

182
Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.
Смотреть видеоразбор >>

183
Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
Смотреть видеоразбор >>

184
Через две различные точки на плоскости проходит единственная прямая.
Смотреть видеоразбор >>

185
Через заданную точку плоскости можно провести единственную прямую.
Смотреть видеоразбор >>

186
Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
Смотреть видеоразбор >>

187
Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
Смотреть видеоразбор >>

Статьи

Основное общее образование

Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)

Математика

Представляем вашему вниманию разбор 19 задания ОГЭ-2019 по математике.

13 ноября 2018

Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Часть 1

Задание 19

Найдите тангенс острого угла, изображённого на рисунке.

Задание 19

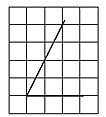
Решение

Выделим прямоугольный треугольник (см. рисунок).

Задание 19. Решение

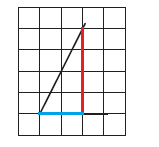
Тангенс есть отношение противолежащего катета к прилежащему, отсюда найдем

Ответ: 2.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену

Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.

Купить

Задание 19 номер 341525

Он-местоимение,выраженное подлежащим
никогда-обстоятельство
не-частица,входящая в роль сказуемого
давал-глагол,выраженный сказуемым
себя-местоимение
в-предлог
обиду-существительное,выраженное дополнением

Задание 19 номер 341525

Скорее всего — да………..

Задание 19 номер 341525

Артист кино великолепно сыграл главную роль в фильме.

Задание 19 номер 341525

Мне с тобой не по пути.
Моей маме поможет не кто иной,как папа
тебе злость не к лицу

Всё варианты 19 задания математика ЕГЭ Профиль 2020admin2020-08-06T14:49:52+03:00

Скачать задания в формате pdf.

Комментарии для сайта Cackle

Категория: 18 (С7) Числа, их свойстваЕГЭ (диагностич. работы)

 Условия заданий 1-19,  ответы

Разбор заданий №13; №14; №15; №16; №17; №18

19. Есть синие и красные карточки. Всего карточек 50 штук. На каждой написаны натуральные числа, среднее арифметическое которых равно 16. Все числа на синих карточках разные. При этом любое число на синей карточке больше, чем любое на красной. Числа на синих увеличили в 2 раза, после чего среднее арифметическое стало равно 31,2.
а) Может ли быть 10 синих карточек?
б) Может ли быть 10 красных карточек?
в) Какое наибольшее количество синих карточек может быть?

Решение:

Пусть есть n синих карточек. Тогда красных – (50-n) штук.

Согласно условию сумма чисел с карточек равна 800.

Упорядочим числа с синих карточек: a_1>a_2>...>a_n.

Упорядочим числа с красных карточек: a_{n+1}geq a_{n+2}geq ...geq a_{50}. Согласно условию a_n>a_{n+1}.

После увеличения чисел на синих карточках имеем:

2(a_1+a_2+...+a_n)+a_{n+1}+a_{n+2}+...+a_{50}=1560.

a) Проверим, может ли быть 10 синих карточек.

n=10, имеем

(a_1+a_2+...+a_{10})+(a_{11}+a_{12}+...+a_{50})=800   (1)

и

2(a_1+a_2+...+a_{10})+(a_{11}+a_{12}+...+a_{50})=1560   (2)

Откуда, вычитая (1) из (2), получаем:

a_1+a_2+...+a_{10}=760  и  a_{11}+a_{12}+...+a_{50}=40.

Пусть a_{11}=a_{12}=...=a_{50}=1, и числа с синих карточек, например, такие: 2;3;4;5;6;7;8;9;10;706.

Может быть 10 синих карточек.

б) Проверим, может ли быть 10 красных карточек.

n=40, имеем

a_1+a_2+...+a_{40}=760  и  a_{41}+a_{42}+...+a_{50}=40.

Поскольку любое число на синей карточке больше, чем любое на красной, то самое маленькое возможное значение числа с синей карточки – это 5. Даже если далее все числа с синих карточек отличаются, будучи упорядоченными, друг от друга на 1, то их сумма оказывается как минимум 5+6+7+...+44, то есть 980, что противоречит условию.

Не может быть 10 красных карточек.

в) Выясним какое наибольшее количество синих карточек может быть, то есть найдем наибольшее значение n при данных условиях.

Имеем

a_1+a_2+...+a_{n}=760  и  a_{n+1}+a_{n+2}+...+a_{50}=40.

760=a_1+a_2+...+a_{n}geq a_n+(a_n+1)+...+(a_n+n-1)=ncdot a_n+frac{n(n-1)}{2}.

Откуда

2a_ncdot n+n^2-nleq 1520.

Заметим, как уже нами было показано, синих карточек, как минимум, может быть 10.  Если их больше десяти, то a_ngeq 3.

Откуда

6n+n^2-nleq 2a_ncdot n+n^2-nleq 1520;

5n+n^2leq 1520;

n^2+5n-1520leq 0;

(n-frac{-5+sqrt{6105}}{2})(n-frac{-5-sqrt{6105}}{2})leq 0.

Откуда

nleq frac{-5+sqrt{6105}}{2},

далее

nleq 36.

Пусть n=36. Учитывая, что a_{37}+a_{38}+...+a_{50}=40, имеем: a_ngeq 4.

Даже если a_1+a_2+...+a_{n}=4+5+...+39=774, то приходим к противоречию с тем, что a_1+a_2+...+a_{n}=760.

Пусть n=35.

Находится подходящий вариант:

a_1=4,a_2=5,...,a_{34}=37,a_{35}=63,

и

a_{36}=a_{37}=...=a_{47}=3,a_{48}=2,a_{49}=a_{50}=1.

Ответ: а) да; б) нет; в) 35.

Источник

В 19 задании из приведенных утверждений необходимо выбрать одно или несколько правильных. Утверждения из общего теоретического курса геометрии, поэтому, какие-то определенные рекомендации здесь дать нельзя, кроме как полного повторения теоретического курса. Другое дело, что если вы точно не знаете какое-либо утверждение, то решить задачу можно наоборот — выбирая и отсеивая неправильные.

Задание OM2001o

Какие из следующих утверждений верны?

  1. Все диаметры окружности равны между собой.
  2. Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
  3. Любые два равносторонних треугольника подобны.

Все диаметры окружности всегда равны между собой – это даже интуитивно понятно. Что касается второго утверждения, то оно неверно – вписанный угол всегда в два раза меньше центрального. А вот третье утверждение тоже верно – треугольники могут быть подобны по трем углам, а у равносторонних треугольников они всегда равны.

Ответ: 13

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM2002o

Какие из следующих утверждений верны?

  1. Все высоты равностороннего треугольники равны.
  2. Существуют три прямые, которые проходят через одну точку.
  3. Если диагонали параллелограмма равны, то он является ромбом.

Первое утверждение верно, так как у равностороннего треугольника все стороны равнозначны, а значит и все элементы, проведенные к ним, тоже. Второе утверждение тоже верно, так как нет ограничений на количество произвольных прямых, проходящих через одну точку. Третье утверждение неверно – если диагонали равны, то это либо прямоугольник, либо квадрат.

Ответ: 12

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM2003o

Какие из следующих утверждений верны?

  1. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
  2. Любой прямоугольник можно вписать в окружность.
  3. Через заданную точку плоскости можно провести единственную прямую.

Первое утверждение верно из общих свойств треугольника – сумма двух сторон всегда больше третьей. Второе утверждение тоже верно – действительно, любой прямоугольник можно вписать в окружность. Третье утверждение неверно, так как я писал уже чуть выше, что нет ограничений на количество произвольных прямых, проходящих через одну точку.

Ответ: 12

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM2004o

Укажите номера верных утверждений.

  1. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
  2. Треугольник со сторонами 1, 2, 4 существует.
  3. Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
  4. В любом параллелограмме диагонали равны.

Проанализируем каждое из утверждений:

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

Да, такое утверждение в геометрии есть, с дополнением ” и только одну” :

“Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой, и причем только одну.”

2) Треугольник со сторонами 1, 2, 4 существует.

Для существования треугольника должно выполняться следующее правило:

Сумма двух сторон всегда больше третьей. В данном случае это не так, так как 1 + 2 < 4

3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.

Действительно, ромб – параллелограмм с равными сторонами, если у него один из углов будет равен 90°, а значит и все остальные, то тогда он станет квадратом.

4) В любом параллелограмме диагонали равны.

Нет, такого утверждения в геометрии нет, они равны только в квадрате и прямоугольнике.

Ответ: 13

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM2005o

Какое из следующих утверждений верно?

  1. Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом.
  2. Смежные углы всегда равны.
  3. Каждая из биссектрис равнобедренного треугольника является его высотой.

Проанализируем каждое утверждение.

1) Это утверждение верно, поскольку равенство и перпендикулярность диагоналей является одним из свойств именно квадрата.

2) Это утверждение неверно. Основание – соответствующая теорема, которой утверждается, что смежные углы в сумме имеют 1800, т.е. дополняют друг друга до развернутого угла. Следовательно, равенство смежных углов может иметь место только в случае, если достоверно известно, что один из них прямой.

3) Утверждение неверно. Высотой является только биссектриса, опущенная на основание равнобедренного треугольника.

Ответ: 1

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM2006o

Какое из следующих утверждений верно?

  1. Если угол острый, то смежный с ним угол также является острым.
  2. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом.
  3. Касательная к окружности параллельна радиусу, проведённому в точку касания.

Выполняем анализ утверждений.

1) Согласно теореме о смежных углах, их сумма всегда равна 1800. Это означает, что любой из смежных углов является разностью 1800 и величины 2-го смежного угла. Если первый смежный угол острый, значит, второй равен разности 1800 и острого угла (т.е. угла, меньшего 900), которая в любом случае окажется больше 900. А угол, больший 900, по определению тупой. Итак, утверждение неверно.

2) Одно из свойств ромба заключается в том, что его диагонали перпендикулярны. Однако и диагонали квадрата тоже пересекаются под прямым углом. Но поскольку квадрат является частным случаем ромба, то и в этом противоречия заданному утверждению нет. Т.е. в целом утверждение верно.

3) Одно из основных св-в касательных к окружности заключается в том, что касательная всегда перпендикулярна к радиусу, проведенному из центра этой окружности в точку касания. Оно противоречит заданному утверждению, поэтому утверждение неверно.

Ответ: 2

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание 19OM21R

Какие из следующих утверждений верны? В ответ запишите номера утверждений без пробелов, запятых и других дополнительных символов.

  1. Сумма углов равнобедренного треугольника равна 180 градусам.
  2. Боковые стороны любой трапеции равны.
  3. Центры вписанной и описанной окружностей треугольника совпадают.

Обращаем внимание на то, что вопрос содержит слово КАКИЕ, что означает нахождение нескольких верных ответов. Итак, первое утверждение является верным, потому что есть теорема о сумме углов треугольника, равной 180 градусов, это не зависит от вида треугольника. Второе утверждение является не верным, так как по определению, только у равнобедренной трапеции боковые стороны равны. Теперь становится понятным, что третье утверждение тоже должно быть верным. Но в доказательство тому мы имеем правила, которые нам говорят о том, что центры окружностей совпадают.

Итак, наши верные утверждения под номерами 1 и 3.

Ответ: 13

pазбирался: Даниил Романович | обсудить разбор | оценить

1 Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части. Смотреть видеоразбор >> 2 Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию. Смотреть видеоразбор >> 3 Биссектриса треугольника делит пополам сторону, к которой проведена. Смотреть видеоразбор >> 4 Биссектрисы треугольника пересекаются в центре его вписанной окружности. Смотреть видеоразбор >> 5 В любой прямоугольник можно вписать окружность. Смотреть видеоразбор >> 6 В любой ромб можно вписать окружность. Смотреть видеоразбор >> 7 В любой треугольник можно вписать окружность. Смотреть видеоразбор >> 8 В любой четырёхугольник можно вписать окружность. Смотреть видеоразбор >> 9 В любом параллелограмме диагонали точкой пересечения делятся пополам. Смотреть видеоразбор >> 10 В любом прямоугольнике диагонали взаимно перпендикулярны. Смотреть видеоразбор >> 11 В любом тупоугольном треугольнике есть острый угол. Смотреть видеоразбор >> 12 В остроугольном треугольнике все углы острые. Смотреть видеоразбор >> 13 В параллелограмме есть два равных угла. Смотреть видеоразбор >> 14 В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности. Смотреть видеоразбор >> 15 В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса. Смотреть видеоразбор >> 16 В прямоугольном треугольнике гипотенуза равна сумме катетов. Смотреть видеоразбор >> 17 В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов. Смотреть видеоразбор >> 18 В треугольнике против большего угла лежит большая сторона. Смотреть видеоразбор >> 19 В треугольнике против большей стороны лежит больший угол. Смотреть видеоразбор >> 20 В тупоугольном треугольнике все углы тупые. Смотреть видеоразбор >> 21 Вертикальные углы равны. Смотреть видеоразбор >> 22 Внешний угол треугольника больше не смежного с ним внутреннего угла. Смотреть видеоразбор >> 23 Внешний угол треугольника равен сумме его внутренних углов. Смотреть видеоразбор >> 24 Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны. Смотреть видеоразбор >> 25 Вокруг любого параллелограмма можно описать окружность. Смотреть видеоразбор >> 26 Вокруг любого треугольника можно описать окружность. Смотреть видеоразбор >> 27 Вписанный угол, опирающийся на диаметр окружности, прямой. Смотреть видеоразбор >> 28 Вписанный угол, опирающийся на диаметр окружности, прямой. Смотреть видеоразбор >> 29 Все высоты равностороннего треугольника равны. Смотреть видеоразбор >> 30 Все диаметры окружности равны между собой. Смотреть видеоразбор >> 31 Все квадраты имеют равные площади. Смотреть видеоразбор >> 32 Все прямоугольные треугольники подобны. Смотреть видеоразбор >> 33 Все равнобедренные треугольники подобны. Смотреть видеоразбор >> 34 Все равносторонние треугольники подобны. Смотреть видеоразбор >> 35 Все углы прямоугольника равны. Смотреть видеоразбор >> 36 Все углы ромба равны. Смотреть видеоразбор >> 37 Все хорды одной окружности равны между собой. Смотреть видеоразбор >> 38 Все хорды одной окружности равны между собой. Смотреть видеоразбор >> 39 Всякий равнобедренный треугольник является остроугольным. Смотреть видеоразбор >> 40 Всякий равносторонний треугольник является остроугольным. Смотреть видеоразбор >> 41 Всякий равносторонний треугольник является равнобедренным. Смотреть видеоразбор >> 42 Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности. Смотреть видеоразбор >> 43 Две прямые, параллельные третьей прямой, перпендикулярны друг другу. Смотреть видеоразбор >> 44 Две прямые, перпендикулярные третьей прямой, параллельны друг другу. Смотреть видеоразбор >> 45 Две прямые, перпендикулярные третьей прямой, перпендикулярны друг другу. Смотреть видеоразбор >> 46 Диагонали квадрата взаимно перпендикулярны. Смотреть видеоразбор >> 47 Диагонали квадрата точкой пересечения делятся пополам. Смотреть видеоразбор >> 48 Диагонали любого прямоугольника делят его на 4 равных треугольника. Смотреть видеоразбор >> 49 Диагонали любого прямоугольника равны. Смотреть видеоразбор >> 50 Диагонали параллелограмма равны. Смотреть видеоразбор >> 51 Диагонали прямоугольника равны. Смотреть видеоразбор >> 52 Диагонали прямоугольной трапеции равны. Смотреть видеоразбор >> 53 Диагонали равнобедренной трапеции равны. Смотреть видеоразбор >> 54 Диагонали ромба перпендикулярны. Смотреть видеоразбор >> 55 Диагонали ромба равны. Смотреть видеоразбор >> 56 Диагонали ромба точкой пересечения делятся пополам. Смотреть видеоразбор >> 57 Диагонали трапеции пересекаются и делятся точкой пересечения пополам. Смотреть видеоразбор >> 58 Диагональ параллелограмма делит его на два равных треугольника. Смотреть видеоразбор >> 59 Диагональ равнобедренной трапеции делит её на два равных треугольника. Смотреть видеоразбор >> 60 Диагональ трапеции делит её на два равных треугольника. Смотреть видеоразбор >> 61 Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса. Смотреть видеоразбор >> 62 Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу. Смотреть видеоразбор >> 63 Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом. Смотреть видеоразбор >> 64 Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом. Смотреть видеоразбор >> 65 Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом. Смотреть видеоразбор >> 66 Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат. Смотреть видеоразбор >> 67 Если в ромбе один из углов равен 90°, то такой ромб – квадрат. Смотреть видеоразбор >> 68 Если в треугольнике есть один острый угол, то этот треугольник остроугольный. Смотреть видеоразбор >> 69 Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник – ромб. Смотреть видеоразбор >> 70 Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны. Смотреть видеоразбор >> 71 Если два угла треугольника равны, то равны и противолежащие им стороны. Смотреть видеоразбор >> 72 Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны. Смотреть видеоразбор >> 73 Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны. Смотреть видеоразбор >> 74 Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны. Смотреть видеоразбор >> 75 Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. Смотреть видеоразбор >> 76 Если две стороны треугольника равны, то равны и противолежащие им углы. Смотреть видеоразбор >> 77 Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то это квадрат. Смотреть видеоразбор >> 78 Если диагонали параллелограмма перпендикулярны, то это ромб. Смотреть видеоразбор >> 79 Если диагонали параллелограмма равны, то он является ромбом. Смотреть видеоразбор >> 80 Если диагонали параллелограмма равны, то это квадрат. Смотреть видеоразбор >> 81 Если диагонали параллелограмма равны, то это прямоугольник. Смотреть видеоразбор >> 82 Если диагонали параллелограмма равны, то это ромб. Смотреть видеоразбор >> 83 Если один из углов треугольника прямой, то треугольник прямоугольный. Смотреть видеоразбор >> 84 Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны. Смотреть видеоразбор >> 85 Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны. Смотреть видеоразбор >> 86 Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны. Смотреть видеоразбор >> 87 Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны. Смотреть видеоразбор >> 88 Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла. Смотреть видеоразбор >> 89 Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны. Смотреть видеоразбор >> 90 Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны. Смотреть видеоразбор >> 91 Если три угла одного треугольника равны трём углам другого треугольника, то такие треугольники подобны. Смотреть видеоразбор >> 92 Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны. Смотреть видеоразбор >> 93 Если угол острый, то смежный с ним угол также является острым. Смотреть видеоразбор >> 94 Из двух хорд окружности больше та, середина которой находится дальше от центра окружности. Смотреть видеоразбор >> 95 Каждая из биссектрис равнобедренного треугольника является его высотой. Смотреть видеоразбор >> 96 Каждая из биссектрис равнобедренного треугольника является его медианой. Смотреть видеоразбор >> 97 Касательная к окружности перпендикулярна радиусу, проведённому в точку касания. Смотреть видеоразбор >> 98 Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон. Смотреть видеоразбор >> 99 Квадрат является прямоугольником. Смотреть видеоразбор >> 100 Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету. Смотреть видеоразбор >> 101 Любая биссектриса равнобедренного треугольника является его медианой. Смотреть видеоразбор >> 102 Любая высота равнобедренного треугольника является его биссектрисой. Смотреть видеоразбор >> 103 Любая медиана равнобедренного треугольника является его биссектрисой. Смотреть видеоразбор >> 104 Любой квадрат можно вписать в окружность. Смотреть видеоразбор >> 105 Любой квадрат является прямоугольником. Смотреть видеоразбор >> 106 Любой квадрат является ромбом. Смотреть видеоразбор >> 107 Любой параллелограмм можно вписать в окружность. Смотреть видеоразбор >> 108 Любой прямоугольник можно вписать в окружность. Смотреть видеоразбор >> 109 Любые два диаметра окружности пересекаются. Смотреть видеоразбор >> 110 Любые два равносторонних треугольника подобны. Смотреть видеоразбор >> 111 Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам. Смотреть видеоразбор >> 112 Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой. Смотреть видеоразбор >> 113 Медиана треугольника делит пополам угол, из которого проведена. Смотреть видеоразбор >> 114 На плоскости существует единственная точка, равноудалённая от концов отрезка. Смотреть видеоразбор >> 115 Не существует прямоугольника, диагонали которого взаимно перпендикулярны. Смотреть видеоразбор >> 116 Один из двух смежных углов острый, а другой тупой. Смотреть видеоразбор >> 117 Один из углов треугольника всегда не превышает 60°. Смотреть видеоразбор >> 118 Основания равнобедренной трапеции равны. Смотреть видеоразбор >> 119 Отношение площадей подобных треугольников равно коэффициенту подобия. Смотреть видеоразбор >> 120 Площадь квадрата равна произведению двух его смежных сторон. Смотреть видеоразбор >> 121 Площадь квадрата равна произведению его диагоналей. Смотреть видеоразбор >> 122 Площадь круга меньше квадрата длины его диаметра. Смотреть видеоразбор >> 123 Площадь любого параллелограмма равна произведению длин его сторон. Смотреть видеоразбор >> 124 Площадь параллелограмма равна половине произведения его диагоналей. Смотреть видеоразбор >> 125 Площадь прямоугольника равна произведению длин всех его сторон. Смотреть видеоразбор >> 126 Площадь прямоугольника равна произведению длин его смежных сторон. Смотреть видеоразбор >> 127 Площадь прямоугольного треугольника равна произведению длин его катетов. Смотреть видеоразбор >> 128 Площадь ромба равна произведению двух его смежных сторон на синус угла между ними. Смотреть видеоразбор >> 129 Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне. Смотреть видеоразбор >> 130 Площадь трапеции равна произведению основания трапеции на высоту. Смотреть видеоразбор >> 131 Площадь трапеции равна произведению средней линии на высоту. Смотреть видеоразбор >> 132 Площадь треугольника не превышает произведения двух его сторон. Смотреть видеоразбор >> 133 Против большей стороны треугольника лежит больший угол. Смотреть видеоразбор >> 134 Против большей стороны треугольника лежит меньший угол. Смотреть видеоразбор >> 135 Против равных сторон треугольника лежат равные углы. Смотреть видеоразбор >> 136 Ромб не является параллелограммом. Смотреть видеоразбор >> 137 Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности. Смотреть видеоразбор >> 138 Смежные углы равны. Смотреть видеоразбор >> 139 Средняя линия трапеции параллельна её основаниям. Смотреть видеоразбор >> 140 Средняя линия трапеции равна полусумме её оснований. Смотреть видеоразбор >> 141 Средняя линия трапеции равна сумме её оснований. Смотреть видеоразбор >> 142 Сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон. Смотреть видеоразбор >> 143 Сумма острых углов прямоугольного треугольника равна 90°. Смотреть видеоразбор >> 144 Сумма смежных углов равна 180°. Смотреть видеоразбор >> 145 Сумма углов выпуклого четырёхугольника равна 360°. Смотреть видеоразбор >> 146 Сумма углов любого треугольника равна 180°. Смотреть видеоразбор >> 147 Сумма углов любого треугольника равна 360°. Смотреть видеоразбор >> 148 Сумма углов остроугольного треугольника равна 180°. Смотреть видеоразбор >> 149 Сумма углов прямоугольного треугольника равна 90°. Смотреть видеоразбор >> 150 Сумма углов равнобедренного треугольника равна 180°. Смотреть видеоразбор >> 151 Сумма углов тупоугольного треугольника равна 180°. Смотреть видеоразбор >> 152 Существует квадрат, который не является прямоугольником. Смотреть видеоразбор >> 153 Существует квадрат, который не является ромбом. Смотреть видеоразбор >> 154 Существует параллелограмм, который не является прямоугольником. Смотреть видеоразбор >> 155 Существует прямоугольник, диагонали которого взаимно перпендикулярны. Смотреть видеоразбор >> 156 Существует прямоугольник, который не является параллелограммом. Смотреть видеоразбор >> 157 Существует ромб, который не является квадратом. Смотреть видеоразбор >> 158 Существуют три прямые, которые проходят через одну точку. Смотреть видеоразбор >> 159 Тангенс любого острого угла меньше единицы. Смотреть видеоразбор >> 160 Точка пересечения двух окружностей равноудалена от центров этих окружностей. Смотреть видеоразбор >> 161 Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка. Смотреть видеоразбор >> 162 Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку. Смотреть видеоразбор >> 163 Треугольник с углами 40°, 70°, 70° – равнобедренный. Смотреть видеоразбор >> 164 Треугольник со сторонами 1, 2 и 4 существует. Смотреть видеоразбор >> 165 Треугольника со сторонами 1, 2 и 4 не существует. Смотреть видеоразбор >> 166 У любой прямоугольной трапеции есть два равных угла. Смотреть видеоразбор >> 167 У любой трапеции боковые стороны равны. Смотреть видеоразбор >> 168 У любой трапеции боковые стороны равны. Смотреть видеоразбор >> 169 У любой трапеции основания параллельны. Смотреть видеоразбор >> 170 У равнобедренного треугольника есть ось симметрии. Смотреть видеоразбор >> 171 У равнобедренного треугольника есть центр симметрии. Смотреть видеоразбор >> 172 У равностороннего треугольника есть центр симметрии. Смотреть видеоразбор >> 173 У равностороннего треугольника три оси симметрии. Смотреть видеоразбор >> 174 Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу. Смотреть видеоразбор >> 175 Угол, опирающийся на диаметр окружности, прямой. Смотреть видеоразбор >> 176 Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника. Смотреть видеоразбор >> 177 Центр описанной около треугольника окружности всегда лежит внутри этого треугольника. Смотреть видеоразбор >> 178 Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника. Смотреть видеоразбор >> 179 Центром вписанной в треугольник окружности является точка пересечения его биссектрис. Смотреть видеоразбор >> 180 Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника. Смотреть видеоразбор >> 181 Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам. Смотреть видеоразбор >> 182 Центры вписанной и описанной окружностей равнобедренного треугольника совпадают. Смотреть видеоразбор >> 183 Центры вписанной и описанной окружностей равностороннего треугольника совпадают. Смотреть видеоразбор >> 184 Через две различные точки на плоскости проходит единственная прямая. Смотреть видеоразбор >> 185 Через заданную точку плоскости можно провести единственную прямую. Смотреть видеоразбор >> 186 Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. Смотреть видеоразбор >> 187 Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой. Смотреть видеоразбор >>

верхняя шапка

картинка

Задачи разделены на уровни сложности. Задачи из любого уровня вполне реально встретить на настоящем экзамене ОГЭ, более сложные встретятся если «не повезло».

Сложность у всех задач примерно одинаковая

  1. Какое из следующих утверждений верно?

    1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники равны.

    2) Сумма углов прямоугольного треугольника равна 180°.

    3) Любая медиана равнобедренного треугольника является его высотой.

    В ответе запишите номер выбранного утверждения.

    2. посмотреть ответ

  2. Какие из следующих утверждений верны?
    1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
    2) Треугольник со сторонами 1, 2, 4 существует.
    3) В любом параллелограмме есть два равных угла.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    3. посмотреть ответ

  3. Какое из следующих утверждений верно?
    1) Дана окружность. Через любую точку плоскости можно провести к ней касательную прямую.
    2) Если в параллелограмме некоторый угол равен 90°, то это квадрат.
    3) В любом ромбе найдется угол меньше 120°.

    В ответе запишите номер выбранного утверждения.

    4. посмотреть ответ

  4. Какое из следующих утверждений верно?

    1) Внутренние односторонние углы при пересечении параллельных прямых секущей равны.

    2) Площадь трапеции равна произведению высоты на сумму оснований.

    3) В любом квадрате все углы равны.

    В ответе запишите номер выбранного утверждения.

    5. посмотреть ответ

  5. Какие из следующих утверждений верны?

    1) Сумма катетов длиннее гипотенузы.

    2) Длина суммы векторов длиннее суммы длин самих векторов.

    3) В любом треугольнике найдется острый угол.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    6. посмотреть ответ

  6. Какое из следующих утверждений верно?

    1) Сумма длин трех сторон четырехугольника всегда длиннее четвертой стороны.

    2) В любой выпуклый четырехугольник можно вписать окружность.

    3) Диагонали ромба равны.

    В ответе запишите номер выбранного утверждения.

    7. посмотреть ответ

  7. Какое из следующих утверждений верно?
    1) Площадь треугольника равна произведению стороны на высоту, проведенную к этой стороне.

    2) Треугольники равны, если их соответствующие стороны равны.
    3) У подобных треугольников площади равны.

    В ответе запишите номер выбранного утверждения.

    8. посмотреть ответ

  8. Какое из следующих утверждений верно?

    1) Сумма вертикальных углов равна 180°.

    2) Корень квадратный из площади квадрата равен длине его стороны.

    3) Периметр прямоугольника всегда больше его площади.

    В ответе запишите номер выбранного утверждения.

    9. посмотреть ответ

  9. Какие из следующих утверждений верны?

    1) У подобных треугольников соответствующие углы равны.

    2) В правильном пятиугольнике все углы равны.

    3) Площадь прямоугольника равна квадрату любой его стороны.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    10. посмотреть ответ

  10. Какое из следующих утверждений верно?
    1) В правильном шестиугольнике все углы по 160°.
    2) Не существует треугольника со сторонами 10,12 и 16.
    3) Диагонали прямоугольника равны.

    В ответе запишите номер выбранного утверждения.

    11. посмотреть ответ

  11. Какие из следующих утверждений верны?

    1) В любой прямоугольник можно вписать окружность.

    2) Вписанные углы, опирающиеся на одну дугу окружности, равны.

    3) Если угол между векторами равен 90°, то их скалярное произведение равно нулю.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    12. посмотреть ответ

  12. Какое из следующих утверждений верно?
    1) Косинус угла в прямоугольном треугольнике это отношение прилежащего катета к противолежащему катету.
    2) Катет лежащий против угла в 60° в два раза короче гипотенузы.
    3) Диагонали ромба перпендикулярны.

    В ответе запишите номер выбранного утверждения.

    13. посмотреть ответ

  13. Какие из следующих утверждений верны?
    1) Центр окружности вписанной в треугольник находится на пересечении биссектрис.

    2) В правильном шестиугольнике все стороны равны.
    3) Сумма двух соседних углов параллелограмма равна 180°.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    14. посмотреть ответ

  14. Какие из следующих утверждений верны?
    1) Дана прямая. Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной.
    2) Высоты треугольника пересекаются в одной точке.
    3) Высота треугольника всегда лежит внутри треугольника.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    15. посмотреть ответ

  15. Какое из следующих утверждений верно?
    1) Диагонали ромба пересекаются и точкой пересечения делятся пополам.
    2) Площадь прямоугольника равна произведению двух противоположных сторон.
    3) Длина вектора равна сумме квадратов его координат.

    В ответе запишите номер выбранного утверждения.

    16. посмотреть ответ

  16. Какое из следующих утверждений верно?
    1) Сумма смежных углов равна 180°.
    2) Если скалярное произведение векторов равно нулю, то векторы параллельны.
    3) В любой трапеции есть, по крайней мере, два острых угла.

    В ответе запишите номер выбранного утверждения.

    17. посмотреть ответ

  17. Какие из следующих утверждений верны?
    1) Площадь любого треугольника равна половине произведения сторон на синус угла между ними.

    2) Все точки лежащие на биссектрисе некоторого угла равноудалены от сторон этого угла.

    3) Площадь ромба равна половине произведения сторон.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    18. посмотреть ответ

  18. Какое из следующих утверждений верно?
    1) Если две окружности касаются, то у них радиусы равны.
    2) Периметр прямоугольника равен произведению двух соседних сторон.
    3) Сумма углов пятиугольника равна 540°.

    В ответе запишите номер выбранного утверждения.

    19. посмотреть ответ

  19. Какие из следующих утверждений верны?
    1) Вокруг любого четырехугольника можно описать окружность.
    2) Если некоторая окружность касается прямой, то расстояние от центра окружности до этой прямой равно радиусу окружности.
    3) Если соответственные углы при пересечении двух прямых секущей равны, то прямые параллельны.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    20. посмотреть ответ

  20. Какие из следующих утверждений верны?
    1) Через точку, лежащую на окружности, всегда можно провести касательную к этой окружности.

    2) Длина окружности всегда больше ее радиуса.
    3) Если в треугольнике одна сторона равна половине второй, то в треугольнике есть угол в 30°.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    21. посмотреть ответ

  21. Какое из следующих утверждений верно?
    1) Если в параллелограмме все углы равны, то это квадрат.
    2) Длина самой длинной стороны в треугольнике меньше суммы длин двух других сторон.
    3) Вокруг любого четырехугольника можно описать окружность.

    В ответе запишите номер выбранного утверждения.

    22. посмотреть ответ

  22. Какие из следующих утверждений верны?
    1) Диагональ параллелограмма делит его на два равных треугольника.

    2) Площадь квадрата равна произведению двух его смежных сторон.
    3) Все хорды одной окружности равны между собой.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    23. посмотреть ответ

  23. Какие из следующих утверждений верны?
    1) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
    2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
    3) Любой квадрат является прямоугольником.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    24. посмотреть ответ

  24. Какие из следующих утверждений верны?
    1) Существует прямоугольник, диагонали которого взаимно перпендикулярны.

    2) Каждая из биссектрис равнобедренного треугольника является его медианой.
    3) В любой ромб можно вписать окружность.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    25. посмотреть ответ

  25. Какие из следующих утверждений верны?
    1) Любые два прямоугольных треугольника подобны.
    2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
    3) Стороны треугольника пропорциональны синусам противолежащих углов.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    26. посмотреть ответ

  26. Какие из следующих утверждений верны?
    1) Треугольник со сторонами, длины которых равны 3,4 и 5, является тупоугольным.
    2) Прямоугольник обладает центром симметрии.
    3) Любой прямоугольный треугольник не обладает центром симметрии.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    27. посмотреть ответ

  27. Какие из следующих утверждений верны?
    1) У квадрата ровно две оси симметрии.
    2) Центром симметрии ромба является точка пересечения его диагоналей.
    3) Площадь прямоугольного треугольника меньше произведения его катетов.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    28. посмотреть ответ

  28. Какое из следующих утверждений верно?
    1) В правильный шестиугольник всегда можно вписать окружность.
    2) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
    3) Сумма вертикальных углов равна 180°.

    В ответ запишите номер выбранного утверждения.

    29. посмотреть ответ

  29. Какое из следующих утверждений верно?
    1) Через любые две точки на плоскости можно провести окружность, причем только одну.
    2) У прямоугольного треугольника не может быть оси симметрии.
    3) Диагонали трапеции всегда пересекаются.

    В ответ запишите номер выбранного утверждения.

    30. посмотреть ответ

  30. Какие из следующих утверждений верны?
    1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат.
    2) В параллелограмме есть два равных угла.
    3) Площадь параллелограмма меньше или равна произведению двух его соседних сторон.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    31. посмотреть ответ

  31. Какие из следующих утверждений верны?
    1) Косинус острого угла прямоугольного треугольника равен отношению катета, прилежащего к этому углу, к гипотенузе.
    2) Если в параллелограмме все углы равны, то это прямоугольник.
    3) Все высоты равнобедренного треугольника лежать внутри этого треугольника.

    В ответ запишите номера выбранных утверждений без пробелов, запятых
    и других дополнительных символов.

    32. посмотреть ответ

  32. Какое из следующих утверждений верно?
    1) К двум окружностям всегда можно провести две общие касательные.
    2) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник – параллелограмм.
    3) Точка пересечения биссектрис любого треугольника всегда лежит внутри этого треугольника.

    В ответ запишите номер выбранного утверждения.

    33. посмотреть ответ

нижняя шапка

Какие из следующих утверждений верны?

1) Треугольника со сторонами 1, 2, 4 не существует.

2) Сумма углов любого треугольника равна 360 градусам.

3) Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Треугольника со сторонами 1, 2, 4 не существует» — верно, сторона треугольника не может быть больше суммы двух других.

2) «Сумма углов любого треугольника равна 360 градусам» — неверно, сумма углов любого треугольника равна 180 градусам.

3) «Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности» — верно, центр описанной окружности лежит в точке пересечения серединных перпендикуляров.

Ответ: 13.

Статьи

Основное общее образование

Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)

Математика

Представляем вашему вниманию разбор 19 задания ОГЭ-2019 по математике.

13 ноября 2018

Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Часть 1

Задание 19

Найдите тангенс острого угла, изображённого на рисунке.

Задание 19

Решение

Выделим прямоугольный треугольник (см. рисунок).

Задание 19. Решение

Тангенс есть отношение противолежащего катета к прилежащему, отсюда найдем

Ответ: 2.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену

Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.

Купить

Источник

Задание 1 № 366805

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты Город Гранюк Деревня Астрелка Хутор Южный Город Гусевск
Цифры        

Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.

Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.

Ответ: 1465.

2. Задание 2 № 366806

Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.

Решение.

Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится

пачек чая.

Таким образом, ребята должны купить 14 пачек чая.

Ответ: 14.

3. Задание 3 № 366807

Найдите площадь (в км2), которую занимает заказник.

Решение.

Площадь заказника равна:

Ответ: 351.

4. Задание 4 № 366808

Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.

Решение.

Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:

км.

Ответ: 30.

5. Задание 5 № 366809

Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.

Продукция Цена в магазине «Вело» (руб.) Цена в магазине «ОК» (руб.) Срок доставки из магазина «ОК» (дни)
Подсветка для спиц
Шина вида «А»
Шина вида «Б»
Спица
Педаль вида «А»
Педаль вида «Б»
Тормоз вида «А» нет
Тормоз вида «Б» нет
Набор крепёжных изделий

Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?

Решение.

На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:

руб.

Ответ: 5300.

6. Задание 6 № 316314

Найдите значение выражения:

Решение.

Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.

7. Задание 7 № 317575

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?

1)

2)

3)

4)

Решение.

Заметим, что и Проверим все варианты ответа:

1) — неверно;

2) — верно;

3) — верно;

4) — верно.

Ответ указан под номером 1.

8. Задание 8 № 353586

Какое из данных ниже чисел является значением выражения

1)

2)

3)

4)

Решение.

Последовательно получим:


Ответ: 1

9. Задание 9 № 338500

При каком значении значения выражений и равны?

Решение.

Для ответа на вопрос задачи нужно решить уравнение Решим его:

Ответ: 2.

10. Задание 10 № 325450

В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.

Решение.

Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна

Ответ: 0,3.

11. Задание 11 № 311406

На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке

2)

3)

4) прямая пересекает график в точках и

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .

2) — неверно,

3) — верно, видно из графика.

4) Прямая пересекает график в точках и — верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

Ответ: 12.

12. Задание 12 № 311543

Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .

Решение.

Выразим :

Подставляя, получаем:

Ответ: 0,4.

13. Задание 13 № 338497

На каком из рисунков изображено решение неравенства

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

Решение.

Решим неравенство методом интервалов:

Правильный ответ указан под номером: 4.

14. Задание 14 № 406645

В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение.

Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.

Найдем сумму этой прогрессии:

Ответ: 377 мест.

15. Задание 15 № 340000

В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите

Решение.

Из прямоугольного треугольника по теореме Пифагора найдём

Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.

16. Задание 16 № 351463

На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.

Решение.

Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.

17. Задание 17 № 169876

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.

———-

В открытом банке иррациональный ответ.

18. Задание 18 № 350842

Найдите угол

Решение.

Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.

Ответ: 22,5

19. Задание 19 № 401617

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Ответ: 13.

20. Задание 20 № 338505

Решите неравенство

Решение.

Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение

Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).

Таким образом, ответ

Ответ:

Примечание.

Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,

21. Задание 21 № 353527

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.

Ответ: 58.

22. Задание 22 № 338288

Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.

Решение.

Упростим выражение:

По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:

График функции сводится к графику параболы с выколотой точкой

Выделим полный квадрат:

Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)

Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и

Ответ: −1; 3.

23. Задание 23 № 339395

Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.

Решение.

Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и

Ответ: 16.

24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.

Решение.

Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.

25. Задание 25 № 311926

В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .

Решение.

По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,

Площадь трапеции :

Площадь трапеции


Ответ: 9.

Источник

  • Задание 18 номер 340184
  • Задание 18 номер 311485
  • Задание 17 номер 324364
  • Задание 17 номер 323902
  • Задание 17 номер 323159