Задание 17 Профильного ЕГЭ по математике — это уравнение, система уравнений или неравенство с параметром. Или несколькими параметрами.
Конечно, за один день научиться решать такие задачи невозможно. И все-таки мы немного расскажем о том, как научиться решать задачи с параметрами. С чего начать. И какие вообще есть методы решения задач с параметрами.
Начнем с хорошей новости. Задача 17 (с параметром) оценивается в целых 4 первичных балла ЕГЭ, которые отлично пересчитываются в тестовые.
Если вы полны решимости получить на ЕГЭ заветные 4 первичных балла за задачу 17 (с параметром), не стоит начинать с реальных экзаменационных задач. Ведь мы хотим получить результат, а не разочарование! Поэтому сначала необходимо повторить следующие темы:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
2. Преобразование графиков функций.
3. Построение графиков функций.
4. Базовые элементы для решения задач с параметрами. Да, мы будем рисовать не только привычные функции. Но еще и окружности, ромбики, полуплоскости и всевозможные их комбинации.
5. Что такое параметр. Простые задачи с параметрами.
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому.
Читайте статью, смотрите видеокурс. И помните, что графический метод — хороший, но не единственный.
Потому что, кроме него, есть и другие:
— Квадратные уравнения и неравенства с параметрами
— Задачи с параметрами. Условия касания
— Метод оценки в задачах с параметрами
— Использование четности функций в задачах с параметрами
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 1, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 5, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 11, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 26, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 18
И не думайте, что это все возможные методы решения задач с параметрами. Их намного больше! Мы дали ссылки на те, которые встречаются чаще всего в задачах ЕГЭ.
Несколько мудрых советов о том, как и зачем решать задачи с параметрами.
1. Чтобы на ЕГЭ уверенно справиться с заданием 17, нужно решить не менее 50 задач с параметрами.
2. Настанет момент, когда вы увидите, что задача с параметром похожи на конструктор, где вы собираете решение из знакомых элементов.
3. Два самых главных секрета решения задач с параметрами. Готовы узнать? Вот они:
— Если в задаче с параметром можно сделать замену переменной — сделайте замену.
— Если задачу с параметром можно решить графически — решите графически.
4. Сколько бы вы ни занимались задачами с параметрами, каким бы отличником ни стали — всегда найдется задача, над которой вы задумаетесь. Вот такая, например:
Задача 1. При каких значениях a системы и
равносильны?
Две системы уравнений с двумя переменными называются равносильными, если они имеют одни и те же решения, или обе системы не имеют решений.
1) При — системы равносильны, так как обе не имеют решений
2) При — второе уравнение имеет решение
которое является решением первой системы.
3) При
Система уравнений
Уравнение задает окружность с центром в начале координат и радиусом
Решениями системы
являются две точки, в которых прямая пересекает окружность, заданную уравнением
А вот уравнение задает семейство параллельных прямых
Мы хотим, чтобы две системы были равносильны, то есть чтобы окружность, заданная уравнением , пересекала только одну из этого семейства прямых, а именно прямую
, и не имела общих точек с другими прямыми из этого семейства.

Меняя параметр а, мы можем менять радиус окружности. Мы хотим, чтобы окружность радиуса не имела общих точек с прямыми, параллельными прямой
, то есть лежала ниже прямой, проходящей через точку А на рисунке, и выше прямой, проходящей через точку В.
Когда же происходит касание в точках A и B?
В случае касания радиус окружности Мы легко находим это из треугольника прямоугольного треугольника СОА, где О — начало координат.
Значит, в случае касания , а если
— касания не происходит.
Объединяя случаи, получим, что системы равносильны, если
Легко? Если справились — вот еще одна интересная задача:
Задача 2. При каких значениях параметра a найдется такое значение параметра , что система уравнений
имеет ровно три различных решения?
Вот решение этой задачи.
Лучше всего осваивать эту непростую тему на нашем Онлайн-курсе подготовки к ЕГЭ на 100 баллов. Или на интенсивах ЕГЭ-Студии в Москве. Удачи, друзья!
Решу огэ 323159

Задание 17 № 323159
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Пусть катеты имеют длины A и B, а гипотенуза — длину Пусть длина высоты, проведённой к гипотенузе равна Найдём длину неизвестного катета из теоремы Пифагора:
Площадь прямоугольного треугольника может быть найдена как половина произведения катетов:
Задание 17 № 323159
Пусть катеты имеют длины a и b, а гипотенуза длину Пусть длина высоты, проведённой к гипотенузе равна Найдём длину неизвестного катета из теоремы Пифагора.
Oge. sdamgia. ru
06.05.2019 18:34:02
2019-05-06 18:34:02
Источники:
Https://oge. sdamgia. ru/problem? id=323159
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу огэ 323159
Решу огэ 323159
Решу огэ 323159
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 6 № 323077
На рисунке изображён график функции Y = F(X) — одной из первообразных функции F(X), определённой на интервале (−3; 5). Найдите количество решений уравнения F(X) = 0 на отрезке [−2; 4].
По определению первообразной на интервале (−3; 5) справедливо равенство
Следовательно, решениями уравнения F(X)=0 являются точки экстремумов изображенной на рисунке функции F(X) На рисунке точки, в которых выделены красным и синим цветом. Из них на отрезке [−2;4] лежат 10 точек (синие точки). Таким образом, на отрезке [−2;4] уравнение имеет 10 решений.
Задание 6 № 323077
—>
Следовательно, решениями уравнения f x 0 являются точки экстремумов изображенной на рисунке функции F x На рисунке точки, в которых выделены красным и синим цветом.
Ege. sdamgia. ru
12.02.2020 5:31:15
2020-02-12 05:31:15
Источники:
Https://ege. sdamgia. ru/problem? id=323077
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу огэ 323159
Решу огэ 323159
Решу огэ 323159
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задания Д2 № 323159
На рисунке изображён график функции и одной из первообразных некоторой функции определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Это задание ещё не решено, приводим решение прототипа.
На рисунке изображён график функции Y = F(X) — одной из первообразных некоторой функции F(X), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения F(X)=0 на отрезке [−2;4].
По определению первообразной на интервале (−3; 5) справедливо равенство
Следовательно, решениями уравнения F(X)=0 являются точки экстремумов изображенной на рисунке функции F(X) Это точки −2,6; −2,2; −1,2; −0,5; 0; 0,4; 0,8; 1,2; 2,2; 2,8; 3,4; 3,8. Из них на отрезке [−2;4] лежат 10 точек. Таким образом, на отрезке [−2;4] уравнение имеет 10 решений.
Задания Д2 № 323159
—>
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Mathb-ege. sdamgia. ru
01.08.2017 15:02:42
2017-08-01 15:02:42
Источники:
Https://mathb-ege. sdamgia. ru/problem? id=323159
Задание 1 № 366805
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Город Гранюк | Деревня Астрелка | Хутор Южный | Город Гусевск |
| Цифры |
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.
Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.
Ответ: 1465.
2. Задание 2 № 366806
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Решение.
Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится
 пачек чая.
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
3. Задание 3 № 366807
Найдите площадь (в км2), которую занимает заказник.
Решение.

Площадь заказника равна:

Ответ: 351.
4. Задание 4 № 366808
Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Решение.
Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
 км.
км.
Ответ: 30.
5. Задание 5 № 366809
Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | |||
| Шина вида «А» | |||
| Шина вида «Б» | |||
| Спица | |||
| Педаль вида «А» | |||
| Педаль вида «Б» | |||
| Тормоз вида «А» | нет | ||
| Тормоз вида «Б» | нет | ||
| Набор крепёжных изделий |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Решение.
На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:
 руб.
руб.
Ответ: 5300.
6. Задание 6 № 316314
Найдите значение выражения: 
Решение.
Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.
7. Задание 7 № 317575
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?
1) 
2) 
3) 
4) 
Решение.
Заметим, что  и
и  Проверим все варианты ответа:
Проверим все варианты ответа:
1)  — неверно;
— неверно;
2)  — верно;
— верно;
3)  — верно;
— верно;
4)  — верно.
— верно.
Ответ указан под номером 1.
8. Задание 8 № 353586
Какое из данных ниже чисел является значением выражения 
1) 
2) 
3) 
4) 
Решение.
Последовательно получим:


Ответ: 1
9. Задание 9 № 338500
При каком значении  значения выражений
значения выражений  и
и  равны?
равны?
Решение.
Для ответа на вопрос задачи нужно решить уравнение  Решим его:
Решим его:

Ответ: 2.
10. Задание 10 № 325450
В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
Решение.
Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна 
Ответ: 0,3.
11. Задание 11 № 311406
На рисунке изображён график функции  . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке 
2) 
3) 
4) прямая  пересекает график в точках
пересекает график в точках  и
и 
Решение.
Проверим каждое из утверждений.
1) Функция возрастает на промежутке  — неверно, функция убывает на промежутке
— неверно, функция убывает на промежутке  и затем возрастает на
и затем возрастает на  .
.
2)  — неверно,
— неверно, 

3)  — верно, видно из графика.
— верно, видно из графика.
4) Прямая  пересекает график в точках
пересекает график в точках  и
и  — верно, видно из графика.
— верно, видно из графика.
Таким образом, неверные утверждения находятся под номерами 1 и 2.
Ответ: 12.
12. Задание 12 № 311543
Площадь любого выпуклого четырехугольника можно вычислять по формуле  , где
, где  — длины его диагоналей, а
— длины его диагоналей, а  угол между ними. Вычислите
угол между ними. Вычислите  , если
, если  .
.
Решение.
Выразим  :
:

Подставляя, получаем:

Ответ: 0,4.
13. Задание 13 № 338497
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.

1) 1
2) 2
3) 3
4) 4
Решение.
Решим неравенство методом интервалов:


Правильный ответ указан под номером: 4.
14. Задание 14 № 406645
В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Решение.
Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.
Найдем сумму этой прогрессии:

Ответ: 377 мест.
15. Задание 15 № 340000

В прямоугольном треугольнике  катет
катет  , а высота
, а высота  , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна  Найдите
Найдите 
Решение.
Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Углы  и
и  равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.
16. Задание 16 № 351463
 На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что  Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Решение.
Пусть длина большей дуги  равна
равна  Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.
17. Задание 17 № 169876
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на  .
.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.
———-
В открытом банке иррациональный ответ.
18. Задание 18 № 350842

Найдите угол 
Решение.

Искомый угол  опирается на
опирается на  часть окружности:
часть окружности:  . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.
. Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е. 
Ответ: 22,5
19. Задание 19 № 401617
Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.
Ответ: 13.
20. Задание 20 № 338505
Решите неравенство 
Решение.
Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение 


Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).
Таким образом, ответ 
Ответ: 
Примечание.
Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно, 
21. Задание 21 № 353527
Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли  г 21-процентного раствора, тогда взяли и
г 21-процентного раствора, тогда взяли и  г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится
г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится  г, а во втором —
г, а во втором —  г Концентрация получившегося раствора равна
г Концентрация получившегося раствора равна  или 58%.
или 58%.
Ответ: 58.
22. Задание 22 № 338288
Постройте график функции  И определите, при каких значениях
И определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение.
Упростим выражение:
По теореме, обратной теореме Виета, корни уравнения  равны -1 и -2 соответственно, тогда по формуле
равны -1 и -2 соответственно, тогда по формуле  , получаем:
, получаем:  . Имеем:
. Имеем:

График функции сводится к графику параболы  с выколотой точкой
с выколотой точкой 
Выделим полный квадрат:

Следовательно, график функции получается из графика функции  сдвигом на
сдвигом на  . (см. рис.)
. (см. рис.)

Из графика видно, что прямая  имеет с графиком функции ровно одну общую точку при
имеет с графиком функции ровно одну общую точку при  и
и 
Ответ: −1; 3.
23. Задание 23 № 339395
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.
Решение.
 Угол
Угол  — вписанный, он равен 90° и опирается на дугу
— вписанный, он равен 90° и опирается на дугу  следовательно, дуга
следовательно, дуга  равна 180°, значит, хорда
равна 180°, значит, хорда  — диаметр окружности и
— диаметр окружности и 
Ответ: 16.
24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Решение.
Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.
25. Задание 25 № 311926
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
Решение.

По свойству равнобедренной трапеции  следовательно, треугольники
следовательно, треугольники  и
и  равны. Так как
равны. Так как  =
=  треугольники
треугольники  и
и  равнобедренные, следовательно,
равнобедренные, следовательно,  и
и  — соответствующие медианы этих треугольников. Значит,
— соответствующие медианы этих треугольников. Значит,  Отрезок
Отрезок  соединяет середины диагоналей трапеции, следовательно,
соединяет середины диагоналей трапеции, следовательно,  и прямые
и прямые 
 и
и  параллельны, поэтому,
параллельны, поэтому,  — трапеция. Проведём
— трапеция. Проведём  — высоту трапеции
— высоту трапеции  и
и  — высоту трапеции
— высоту трапеции  . Прямоугольные треугольники
. Прямоугольные треугольники  и
и  подобны, значит,
подобны, значит, 
Площадь трапеции  :
: 
Площадь трапеции 


Ответ: 9.
Задания 1-5
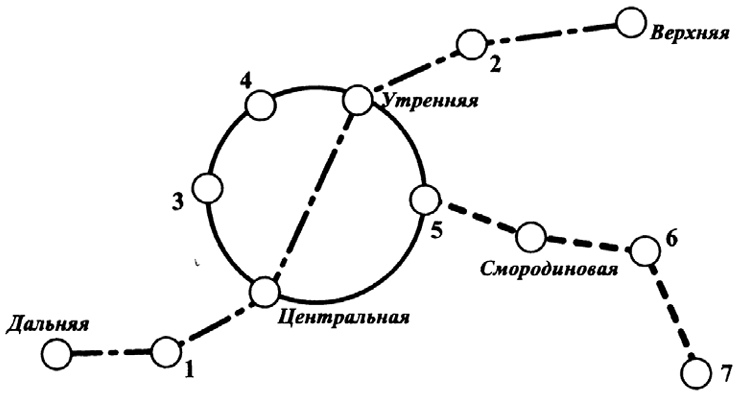
На рисунке (см. выше) изображена схема метро города N. Станция Ветреная расположена между станциями Центральная и Дальняя. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Весёлая. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звёздная. Всего в метрополитене города N есть три станции, от которых тоннель ведёт только в одну сторону — это станции Дальняя, Верхняя и Звёздная. Антон живёт недалеко от станции Надежда.
1. Для станций, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу. В ответе запишите последовательность пяти цифр без пробелов, запятых и других разделительных символов.
| Станции | Весёлая | Ветреная | Звёздная | Птичья | Быстрая |
|---|---|---|---|---|---|
| Цифры |
2. Бригада меняет рельсы на участке между станциями Надежда и Верхняя протяжённостью 12,6 км. Работы начались в пятницу. Каждый рабочий день бригада меняла по 400 метров рельсов. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
3. Территория, находящаяся внутри кольцевой линии, называется Центральным городским районом. Найдите его площадь $$S$$ (в км2), если длина кольцевой ветки равна 42 км. В ответе укажите значение выражения $$Scdotpi$$.
4. Найдите расстояние (в км) между станциями Смородиновая и Хоккейная, если длина Радужной ветки равна 17 км, расстояние от Звёздной до Смородиновой равно 12 км, а от Быстрой до Хоккейной — 15 км. Все расстояния даны по железной дороге.
5. Школьник Антон в среднем в месяц совершает 46 поездок в метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Антон уедет из города и неиспользованные карточки обнуляются. Во сколько рублей обойдётся самый дешёвый вариант?
| Количество поездок | Стоимость карточки (руб.) | Дополнительные условия |
|---|---|---|
| 1 | 40 | школьникам скидка 15% |
| 10 | 370 | школьникам скидка 10% |
| 30 | 1050 | школьникам скидка 10% |
| 50 | 1500 | нет |
| Не ограничено | 2000 | нет |
Ответ: 1) 31745 2) 46 3) 441 4) 10 5) 1482
Скрыть
Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Весёлая. Значит, станция Птичья отмечена на схеме цифрой 4, а станция Весёлая цифрой 3. Станция Ветреная расположена между станциями Центральная и Дальняя, значит, станция Ветреная отмечена на схеме цифрой 1. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звёздная. Следовательно, станция Звёздная отмечена цифрой 7, а станция Быстрая цифрой 5.
Скрыть
$$frac{12,6}{0,4}=31,5$$ дней. При этом каждые 5 дней добавляется ещё 2, то есть ещё 12 дней. Но так как работы начались в пятницу, то ещё +2 дня выходит.
Итого $$32+12+2=46$$ дней.
Скрыть
Сначала найдём радиус окружности:
$$R=frac{L}{2pi}=frac{42}{2pi}=frac{21}{pi}$$.
Теперь найдём площадь:
$$S=pi R^2=picdotfrac{441}{pi^2}=frac{441}{pi}$$.
Таким образом, получаем ответ:
$$Scdotpi=frac{441}{pi}cdotpi=441$$.
Скрыть
Расстояние от Звёздной до Хоккейной равняется $$17-15=2$$ км. Расстояние от Быстрой до Смородиновой равняется $$17-12=5$$ км. Значит, расстояние между станциями Смородиновая и Хоккейная равно $$17-2-5=10$$ км.
Скрыть
Самый дешёвый вариант 6 билетов по 40 и по абонементам на 10 и 30 поездок.
$$40cdot6cdot0,85+(370+1050)cdot0,9=1482$$
