Сложность: 
Среднее время решения: 2 мин. 27 сек.
ЕГЭ по математике 2022 задание 17: номер 46 | Найдите все значения параметр…
45
Найдите все значения параметра $a$, при которых уравнение $√ {a — 2xy} = y — x + 5$ имеет единственное решение.
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
При каких значениях параметра $a$ система
${table15{|x — 2|} + 8{|y + 3|} = 120; x^2 — 4a^2 + 2y + 5 = 4(x — 1) — (y + 2)^2;$
имеет ровно $4$ решения?
При каком значении $a$ множеством решений неравенства
${1+3^x} / {1+3^{-x}}>{3} / {|x+a|}$ является множество всех положительных чисел?
Найдите все значения a, при каждом из которых система неравенств ${table(a — x^2)(a + x — 2)
При каком значении $a$ множеством решений неравенства
${1+2^{-x}} / {1+2^x}>{4} / {√ {x^2+2ax+a^2}}$ является множество всех отрицательных чисел?
Определите,
склоняются или не склоняются приведенные
в скобках названия населенных пунктов,
и поставьте их в нужном падеже.
1)Этим летом мы
гостили сначала в (Яковлево), а затем в
(Путятино), в следующем году будем
отдыхать на даче под (Камышин). 2)Курортная
зона вокруг (Сочи), включающая несколько
городков и поселков, так и называется
– Большие Сочи. 3)Телевизионный фильм
Г.Панфилова «В круге первом» посвящен
событиям 1948-1949гг., происшедшим в
спецтюрьме (Марфино) под Москвой. 4)В
конференции, посвященной проблемам
урбоэкологии, которая состоялась в
этом году в (Ростов-на-Дону), участвовали
делегации из многих городов СНГ, Западной
Европы и Америки. С докладами выступили
представители общественных и научных
организации из (Санкт-Петербург, Кривой
Рог, Гусь-Хрустальный, Петропавловск-Камчатский,
Алма-Ата, Нью-Йорк, Сан-Франциско,
Франкфурт-на-Майне и др.). 5)Авторы книги
очерков «Мир русской усадьбы» знакомят
читателей с (Перемухино, Измайлово,
Знаменское-Губайлово, Марьино, Вороново,
Степановское-Волосово, Локоть-Брасово),
история которых связана с именами таких
известных деятелей России, как
Ю.Ф.Самарин, М.А. Бакунин, К.Д.Бальмонт,
В.Я.Брюсов и др. 6)Один выстрел в (Сараево)
подтолкнул человечество к Первой
мировой войне.
Задание 18
Определите
способ образования следующих
существительных: а)сложение,
б)суффиксальный, в)приставочный,
г)приставочно-суффиксальный,
д)бессуффиксный.
1)бесстрашие
2)главврач
3)глубь
4)Город-герой
5)демонтаж
6)затылок
7)инструктаж
8)контратака
9)материализм
10)объявление
11)плач
12)подснежник
13)пулемет
14)реорганизация
Задание 19
Прочитайте
предложения, объясните характер ошибок.
Сделайте морфологический разбор
выделенных существительных.
1)В
пяти километрах от станции Батыево
находится всемирно известный усадьба-музей
выдающегося русского писателя И.С.
Тургенева. 2)Из кости рога люди стали
вырезать шила, иглы и гарпуны. 3)Умственная
деятельность увеличивает объемы мозга.
4)НАТО был создан по инициативе США в
1949 году. 5)Поздний барокко характеризуется
декоративной пышностью деталей.
6)Бухгалтера предприятий собрались
вместе, чтобы обсудить трудности,
встречающиеся в их работе. 7)В 1913году в
России насчитывалось 19 ясель (550 детей).
8)Из сумчатых млекопитающих наиболее
известно исполинское кенгуру.
9)Этногенез башкиров чрезвычайно сложен.
10)Духовно-рыцарские ордена возникли в
XI-XII
веках в связи с крестовыми походами.
Имя прилагательное Задание 20
Распределите
прилагательные в три столбика:
а)качественные, б)относительные,
в)притяжательные. 1)Большая луна
2)Рыбачьи лодки
3)Ненужные вещи
4)Невская вода
5)Скульптурные
украшения
6)Пеликаний клюв
7)Толстовский
роман
8)Мраморный столик
9)Шекспировы сонеты
10)Неопытный человек
11)Тяжелая ноша
12)Картинная галерея
13)Лисья шуба
14)Картинная поза
Задание 21
Образуйте
все возможные формы степеней сравнения
указанных прилагательных и заполните
таблицу. В случае затруднения обращайтесь
к словарю: Орфоэпический словарь
русского языка: произношение, ударение,
грамматические формы/ С.Н. Борунова,
В.Л.Воронцова, Н.А. Еськова. –М.: Русск.яз.,
1987. –704с.
Сладкий,
плохой, синий, деловой.
| Форма | Стиль речи | ||
| Книжный | общеупотребительный | разговорный | |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Физика А.В. Перышкин
С помощью Интернета подготовьте презентацию «Самые большие астероиды и их движение».
Астероид — небольшое планетоподобное тело Солнечной системы (малая планета). Название «астероид» происходит от греческого слова «подобный звезде». Названы эти объекты были Уильямом Гершелем на основании того, что эти объекты при наблюдении в телескоп выглядели как точки звёзд — в отличие от планет, которые при наблюдении в теле¬скоп выглядят дисками. Точное определение термина «астероид» до сих пор не является установившимся. Термин «малая планета» (или «планетоид») не подходит для определения астероидов, так как указывает и на расположение объекта в Солнечной системе. Однако не все астероиды являются малыми планетами. Одним из способов классификации астероидов является определение размера. Действующая классификация определяет астероиды, как объекты с диаметром более 50 м, отделяя их от метеорных тел, которые выглядят как крупные камни, или могут быть ещё меньше. Классификация опирается на утверждение, что астероиды могут уцелеть при входе в атмосферу Земли и достигнуть её поверхности, в то время, как метеоры, как правило, полностью сгорают в атмосфере.
Несколько тысяч астероидов известны под собственными именами. Полагают, что насчитывается до полумиллиона астероидов с диаметром более полу¬тора километров, а объектов, имеющих размеры более 1 км, в Солнечной системе может находиться от 1.1 до 1.9 миллиона. Большинство орбит астероидов сконцентрировано в поясе астероидов между орбитами Марса и Юпитера на расстояниях от 2,0 до 3,3 а.е. от Солнца. Общая масса всех астероидов главного пояса оценивается в 3,0—3,6 • 1021 кг, что составляет всего около 4 % от массы Луны. Имеются, однако, и астероиды, чьи орбиты лежат ближе к Солнцу, типа группы Амура, группы Аполлона и группы Атена. Кроме того, имеются и более далекие от Солнца, типа центавров. На орбите Юпитера находятся троянцы, которых открыто уже более 1560 (первый открыт в 1906 году). 21 августа 2001 года открыт маленький астероид 2001 QR322 на орбите Нептуна. Через год стало ясно, что это первый «троянец» газового гиганта.
На 2 октября 2001г астрономы всего мира наблюдали 146.677 астероидов. Орбиты 30.716 из них определены и они получили собственные номера. Имена присвоены 8.914 астероидам. В последнее время, в связи с совершенствованием методов астрономических наблюдений, количество открытых астероидов растет в геометрической прогрессии, удваиваясь каждые два года, а вот присвоение новых названий идет с «постоянной скоростью» — примерно 1200 названий в год. По состоянию на 10 января 2010 в базах данных насчитывалось 482419 объектов, у 231665 точно определены орбиты и им присвоен официальный номер. 15615 из них на этот момент имели официально утверждённые наименования.
-
Учебник — часть 1, 2
Автор:
Моро М.И., Бантова М.А.
Издательство:
Просвещение
ГДЗ(готовые домашние задания), решебник онлайн к учебнику по математике за 4 класс авторов Моро, Бантова часть 1 задание(номер) 17 — вариант решения упражнения 17
Часть 1:
ЧИСЛА ОТ 1 ДО 1000:
Нумерация:
1
2
3
4
5
6
7
8
9
10
?
Страница 19. ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:
1
2
3
4
Страница 31. СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ:
1
2
3
Страница 35. ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:
1
2
3
Страница 55. ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:
1
2
3
Страница 58. ПРОВЕРИМ СЕБЯ И ОЦЕНИМ СВОИ ДОСТИЖЕНИЯ:
Вариант 1:
1
2
3
4
5
6
7
8
9
10
Страница 69. ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ:
1
2
3
4
5
6
7
8
9
10
11
12
Страница 70. СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ:
1
2
3
4
Страница 71. Задачи — Расчеты:
1
2
Страница 73. ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:
1
2
3
4
5
6
Страница 74. ПРОВЕРИМ СЕБЯ И ОЦЕНИМ СВОИ ДОСТИЖЕНИЯ:
Вариант 1:
1
2
3
4
5
6
7
8
9
10
Страница 95. ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:
1
2
3
4
5
6
7
8
Страница 96. ПРОВЕРИМ СЕБЯ И ОЦЕНИМ СВОИ ДОСТИЖЕНИЯ:
Вариант 1:
1
2
3
4
5
6
7
8
9
Тексты для контрольных работ:
Страница 98. Задания базового уровня:
1
2
3
4
5
6
7
8
Страница 99. Задания повышенного уровня сложности:
1
2
3
4
5
6
7
8
9
Часть 2:
Страница 9. ЗАДАЧИ-РАСЧЕТЫ:
1
2
3
Страница 10. СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ:
1
2
3
4
Страница 18. СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ:
1
2
3
4
5
6
Страница 23. ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:
1
2
Страница 37. ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:
1
2
ПРОВЕРИМ СЕБЯ И ОЦЕНИМ СВОИ ДОСТИЖЕНИЯ:
Страница 38. Вариант 1:
1
2
3
4
5
6
7
8
9
10
Страница 40. НАШИ ПРОЕКТЫ:
1
2
3
4
5
6
Страница 53. СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ:
1
2
3
4
5
Страница 56. ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ:
1
2
Страница 67. ЧТО УЗНАЛИ. ЧЕМУ НАУЧИЛИСЬ:
1
2
3
4
5
6
7
8
9
10
Страница 68. ЗАДАЧИ-РАСЧЕТЫ:
1
2
3
4
5
6
Страница 78. СТРАНИЧКИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫХ:
1
2
3
4
5
6
7
Страница 89. Выражения и уравнения:
1
2
3
4
5
6
7
8
Страница 94. Правила о порядке выполнения действий:
1
2
3
4
5
6
7
Страница 95. Величины:
1
2
3
4
5
6
Страница 96. Геометрические фигуры:
1
2
3
4
5
6
7
8
9
10
11
12
Материал для расширения и углубления знаний:
Страница 104. Доли:
1
2
3
Страница 105. Единицы площади — ар и гектар:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Страница 108. Диагонали прямоугольника (квадрата) и их свойства:
1
2
3
4
Страница 110. Куб:
1
2
Страница 111. Прямоугольный параллелепипед:
1
2
Страница 112. Пирамида:
1
2
Страница 113. Цилиндр:
1
2
Страница 113. Шар:
1
2
ПРОВЕРИМ СЕБЯ И ОЦЕНИМ СВОИ ДОСТИЖЕНИЯ:
Страница 114. Задания базового уровня:
1
2
3
4
5
6
7
8
Страница 115. Задания повышенного уровня сложности:
1
2
3
4
5
6
7
8
9
Прототипы заданий 17 ОГЭ по математике. Материал для подготовки к ОГЭ.
Для выполнения задания 17 необходимо уметь выполнять действия с геометрическими фигурами, координатами и векторами (находить площади фигур)
Подробнее узнать виды заданий на данной позиции в КИМах можно по кодификатору
| Карточки для отработки задания 17 с ответамиИсточник: math100.ru → скачать |
| Тренинг задания 17 ОГЭ по математике (площадь четырехугольника) → вариант 1 → ответы → вариант 2 → ответы |
| Материалы для отработки задания 17 Автор: Е. А. Ширяева → теория → задания |
| Задания 17 — практика (площадь треугольника) → Скачать вариант 1 → Скачать ответы 1 |
| → Задания по геометрии в ОГЭ по математике |
Решение типовых задач № 17 на ОГЭ по математике
Связанные страницы:
Задание 15 ОГЭ по математике — треугольники, четырёхугольники, многоугольники и их элементы
Задание 13 ОГЭ по математике — неравенства
Задание 16 ОГЭ по математике — окружность, круг и их элементы
Тренировочные варианты ОГЭ 2021 по математике с ответами
Задание 14 ОГЭ по математике — задачи на прогрессии
В 17 задании нас ждут задачи с четырехугольниками, а именно трапецией, ромбами и произвольными параллелограммами. Необходимо знать формулы вычисления площади всех вышеперечисленных четырехугольников, а также их свойства. В демонстрационном варианте ОГЭ предлагается задание, связанное с нахождением площади фигуры. Как найти площадь треугольника, трапеции, параллелограмма, круга и сектора? С одной стороны, мы знаем соответствующие формулы. Для выполнения большинства заданий этого будет вполне достаточно, но иногда надо проявить и определенную сообразительность. В некоторых случаях будет разумно представить заданную геометрическую фигуру как сумму или как разность более простых фигур. Безусловно, площадь измеряется в соответствующих единицах. Например, если длины сторон фигуры заданы в сантиметрах, то вычисляемая площадь автоматически измеряется в квадратных сантиметрах. Чтобы не загромождать условие задачи информацией, которая при ее решении фактически не используется, единицы измерения, если они не существенны, не указаны.
Теория к заданию №18
Приступим к разбору теории. Выпуклый четырехугольник:
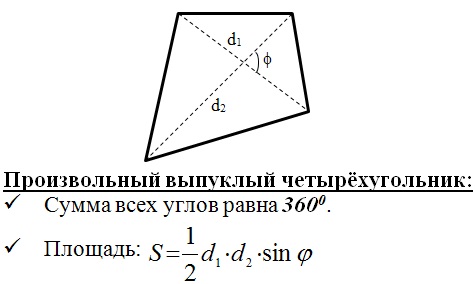
Правильный многоугольник:
- Правильным многоугольником называется многоугольник, у которого все стороны и углы равны между собой.
- Около всякого правильного многоугольника можно описать окружность и в него вписать окружность, причём центры этих окружностей совпадают.
Ниже я привожу формулы для вычисления элементов произвольного правильного многоугольника:
Разберем пример четырехугольника – ромб.
Параллелограмм, все стороны которого равны называется ромбом.
- Диагональ ромба является его осью симметрии.
- Диагонали взаимно перпендикулярны.
- Диагонали являются биссектрисами углов.
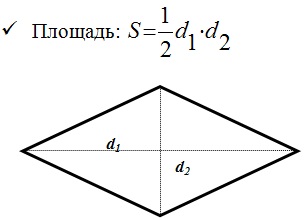Трапеция:
Четырёхугольник, у которого две стороны параллельны, а другие не параллельны, называется трапецией.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите меньший угол параллелограмма.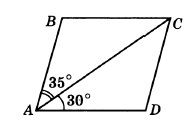
Найдем угол BAD – это сумма углов, на которые диагональ делит этот угол, поэтому:
∠BAD = 35° + 30° = 65°
Вспоминаем, что в параллелограмме противоположные углы равны, а соседние в сумме дают 180°.
Значит:
∠ABC = ∠ADC = 180 – 65 = 115°
∠BAD = ∠BCD = 65°
Так как нас просят найти меньший угол, то это 65.
Ответ: 65
pазбирался: Даниил Романович | обсудить разбор | оценить
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основаниям равен 45°. Найдите площадь трапеции.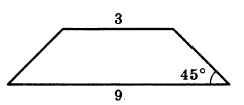
Площадь трапеции равна произведению полусуммы оснований, умноженную на высоту. Основания нам известны из условия, необходимо самим найти высоту:
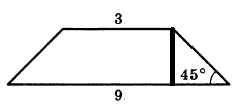
После проведения высоты, у нас получается прямоугольный треугольник. Прямоугольный – потому что высота проводится к основанию под углом 90 градусов. Один из углов равен 45°, значит, и второй тоже, так как сумма острых углов в прямоугольном треугольнике равна 90°. Следовательно, треугольник равнобедренный.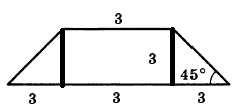
Проведя еще одну высоту, мы получим прямоугольник в центре, та с противоположной стороной, равной основанию 3.
Так как трапеция равнобедренная, то и треугольники равны, значит оставшаяся длина делится пополам:
( 9 – 3 ) / 2 = 3
А так как треугольники равнобедренные, то и высота равна 3.
Отсюда можем найти площадь:
S = ( a + b ) • h / 2 = ( 3 + 9 ) • 3 / 2 = 18
Ответ: 18
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.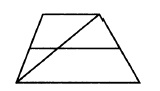
Средняя линия трапеции является еще и средней линией для треугольников, на которые трапецию поделила её диагональ. Средняя линия треугольника равна половине основания, поэтому отрезки, на которые делит диагональ среднюю линию, будут равны:
10 / 2 = 5
11 / 2 = 5,5
Так как нас просят найти больший из отрезков, то ответ 5,5.
Ответ: 5,5
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите площадь трапеции, изображённой на рисунке.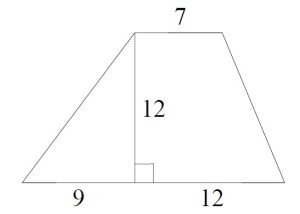
Для решения необходимо помнить и знать формулу для вычисления площади трапеции, а это “полусумма оснований умноженная на высоту”
Непонятно, зачем нам дана информация о значениях длин отрезков, тем не менее решение выглядит так:
- Верхнее основание равно 7
- Нижнее основание равно 9 + 12 = 21
- Полусумма (21 + 7) / 2 = 14
- Высота равна 12
Таким образом, площадь равна 14 • 12 = 168 см²Ответ: 168
pазбирался: Даниил Романович | обсудить разбор | оценить
Сторона ромба равна 4, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь ромба.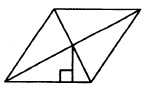
Площадь ромба будем искать по формуле:
S=ah,
где a – сторона ромба, h– высота, опущенная на сторону а.
По условию а=4.
Найдем h. Для этого рассмотрим ∆ОКС и ∆АРС:
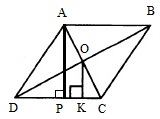
Здесь ОК || АР, причем ОК проходит через середину АС (т.к. АВСD ромб, то его диагонали в т.О делятся пополам). Значит, ОК – ср.линия ∆АРС. Поэтому АР=2ОК. Т.к. пор условию ОК=1, то АР=2·1=2. Т.о., h=АР=2.
Отсюда получаем:
S=4·1=4.
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите величину острого угла параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол, равный 41°. Ответ дайте в градусах.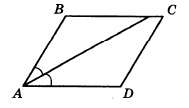
Так как АК биссектриса, то углы ВАК и КАD равны. Обозначим ∠ВАК через х. Поскольку АВСD параллелограмм, то ∠В+∠А=180°. Т.к. АК биссектриса, то ∠А=2х. Тогда ∠В=180°–2х. Рассмотрим ∆АВК:
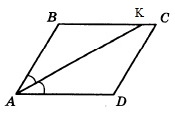
По теореме о сумме углов треугольника ∠ВАК+∠В+∠ВКА=180°
По условию ∠ВКА = 41°
Отсюда получаем:
х+ 180°–2х+410=180°
х–2х=1800–1800–41°
–х=–41°
х=41°
Значит, искомый (острый) ∠А=2·410=82°
Ответ: 82
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.
Для нахождения площади трапеции в справочном материале есть формула
S=a+b2h, для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S=7+112∙7=182∙7=9∙7=63
Ответ: 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Статьи
Основное общее образование
Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)
Математика
Представляем вашему вниманию разбор 17 задания ОГЭ-2019 по математике.
14 ноября 2018
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 17
Найдите длину хорды окружности радиусом 13, если расстояние от центра окружности до хорды равно 5.
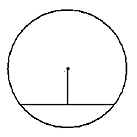
Решение
Рассмотрим треугольник AOB (см. рисунок).
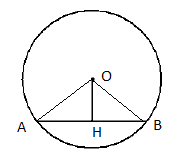
Он равнобедренный (АО = ОВ) и ОН в нем высота (ее длина равна по условию 5). Значит, ОН – медиана по свойству равнобедренного треугольника и АН = НВ. Найдем АН из прямоугольного треугольника АНО по теореме Пифагора:
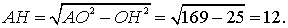
Значит, АВ = 2АН = 24.
Ответ: 24.
ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить
-
Настоящий материал опубликован пользователем Сиразов Фаннур Саматович. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Пожаловаться на материал
-
Автор материала
- На сайте: 4 года и 2 месяца
- Подписчики: 2
- Всего просмотров: 4633
- Всего материалов:
11
Каталог заданий.
Алгебраические выражения
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задание 20 № 47
Сократите дробь 
.
Аналоги к заданию № 47: 311965 340598 340931 341226 Все
Источник: Демонстрационная версия ГИА—2013 по математике., Демонстрационная версия ГИА—2014 по математике.
Раздел кодификатора ФИПИ: 2.2 Действия со степенями.
Решение
·
·
Сообщить об ошибке · Помощь
2
Задание 20 № 311236
Разложите на множители: 
.
Раздел кодификатора ФИПИ: 2.3 Разложение многочленов на множители.
Решение
·
·
Сообщить об ошибке · Помощь
3
Задание 20 № 311243
Сократите дробь 
Раздел кодификатора ФИПИ: 2.3 Разложение многочленов на множители.
Решение
·
·
Сообщить об ошибке · Помощь
4
Задание 20 № 311255
Упростите выражение 
Аналоги к заданию № 311255: 311551 Все
Источник: ГИА-2013. Математика. Диагностическая работа № 1. (вар. 1) 02.10.2012г.
Решение
·
·
Сообщить об ошибке · Помощь
5
Задание 20 № 311575
Упростите выражение: 
.
Аналоги к заданию № 311575: 311579 Все
Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
Задание 1 № 366805
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Город Гранюк | Деревня Астрелка | Хутор Южный | Город Гусевск |
| Цифры |
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
Решение.
Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.
Ответ: 1465.
2. Задание 2 № 366806
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Решение.
Найдём, сколько пакетиков чая ребята потратят за две недели:
Значит, им понадобится
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
3. Задание 3 № 366807
Найдите площадь (в км2), которую занимает заказник.
Решение.
Площадь заказника равна:
Ответ: 351.
4. Задание 4 № 366808
Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Решение.
Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
км.
Ответ: 30.
5. Задание 5 № 366809
Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | |||
| Шина вида «А» | |||
| Шина вида «Б» | |||
| Спица | |||
| Педаль вида «А» | |||
| Педаль вида «Б» | |||
| Тормоз вида «А» | нет | ||
| Тормоз вида «Б» | нет | ||
| Набор крепёжных изделий |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Решение.
На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:
руб.
Ответ: 5300.
6. Задание 6 № 316314
Найдите значение выражения: 
Решение.
Для упрощения вычислений, вынесем общий множитель за скобки:
Ответ: 4,4.
7. Задание 7 № 317575
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.
Какое из приведенных утверждений неверно?
1) 
2) 
3) 
4) 
Решение.
Заметим, что 
и 
Проверим все варианты ответа:
1) — неверно;
2) — верно;
3) — верно;
4) — верно.
Ответ указан под номером 1.
8. Задание 8 № 353586
Какое из данных ниже чисел является значением выражения 
1) 
2) 
3) 
4) 
Решение.
Последовательно получим:
Ответ: 1
9. Задание 9 № 338500
При каком значении 
значения выражений 
и 
равны?
Решение.
Для ответа на вопрос задачи нужно решить уравнение 
Решим его:
Ответ: 2.
10. Задание 10 № 325450
В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
Решение.
Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна 
Ответ: 0,3.
11. Задание 11 № 311406
На рисунке изображён график функции 
. Какие из утверждений относительно этой функции неверны? Укажите их номера.
1) функция возрастает на промежутке 
2) 
3) 
4) прямая 
пересекает график в точках 
и 
Решение.
Проверим каждое из утверждений.
1) Функция возрастает на промежутке — неверно, функция убывает на промежутке 
и затем возрастает на 
.
2) 
— неверно, 
3) 
— верно, видно из графика.
4) Прямая 
пересекает график в точках 
и 
— верно, видно из графика.
Таким образом, неверные утверждения находятся под номерами 1 и 2.
Ответ: 12.
12. Задание 12 № 311543
Площадь любого выпуклого четырехугольника можно вычислять по формуле 
, где 
— длины его диагоналей, а 
угол между ними. Вычислите 
, если 
.
Решение.
Выразим 
:
Подставляя, получаем:
Ответ: 0,4.
13. Задание 13 № 338497
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.
1) 1
2) 2
3) 3
4) 4
Решение.
Решим неравенство методом интервалов:
Правильный ответ указан под номером: 4.
14. Задание 14 № 406645
В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Решение.
Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.
Найдем сумму этой прогрессии:
Ответ: 377 мест.
15. Задание 15 № 340000
В прямоугольном треугольнике 
катет 
, а высота 
, опущенная на гипотенузу, равна 
Найдите 
Решение.
Из прямоугольного треугольника 
по теореме Пифагора найдём 
Углы 
и 
равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
Ответ: 0,2.
16. Задание 16 № 351463
На окружности с центром O отмечены точки A и B так, что 
Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Решение.
Пусть длина большей дуги 
равна 
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Ответ: 2343.
17. Задание 17 № 169876
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на 
.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:
Ответ: 30.
———-
В открытом банке иррациональный ответ.
18. Задание 18 № 350842
Найдите угол
Решение.
Искомый угол опирается на 
часть окружности: 
. Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е. 
Ответ: 22,5
19. Задание 19 № 401617
Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.
Ответ: 13.
20. Задание 20 № 338505
Решите неравенство 
Решение.
Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение 
Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).
Таким образом, ответ 
Ответ:
Примечание.
Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно, 
21. Задание 21 № 353527
Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится 
г, а во втором — 
г Концентрация получившегося раствора равна 
или 58%.
Ответ: 58.
22. Задание 22 № 338288
Постройте график функции 
И определите, при каких значениях 
прямая 
имеет с графиком ровно одну общую точку.
Решение.
Упростим выражение:
По теореме, обратной теореме Виета, корни уравнения 
равны -1 и -2 соответственно, тогда по формуле 
, получаем: 
. Имеем:
График функции сводится к графику параболы 
с выколотой точкой 
Выделим полный квадрат:
Следовательно, график функции получается из графика функции 
сдвигом на 
. (см. рис.)
Из графика видно, что прямая 
имеет с графиком функции ровно одну общую точку при 
и 
Ответ: −1; 3.
23. Задание 23 № 339395
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.
Решение.
Угол 
— вписанный, он равен 90° и опирается на дугу 
следовательно, дуга 
равна 180°, значит, хорда 
— диаметр окружности и 
Ответ: 16.
24. Задание 24 № 155
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Решение.
Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.
25. Задание 25 № 311926
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
Решение.
По свойству равнобедренной трапеции 
следовательно, треугольники и 
равны. Так как 
= 
треугольники и 
равнобедренные, следовательно, 
и 
— соответствующие медианы этих треугольников. Значит, 
Отрезок 
соединяет середины диагоналей трапеции, следовательно, 
и прямые 
и 
параллельны, поэтому, 
— трапеция. Проведём 
— высоту трапеции 
и 
— высоту трапеции 
. Прямоугольные треугольники 
и 
подобны, значит, 
Площадь трапеции 
: 
Площадь трапеции 
Ответ: 9.