Задание 16 номер 356543

Не могу найти по номеру выполняемое многоразовое задание. Да и любые другие по номеру не найти). Пробовал произвольно выбранные задания вызвать по номеру — и ничего!)

Обсуждение

gimmegun

12 Окт 2017 г, в 09:01
редактир. 12 Окт 2017 г, в 09:06

Одной из причин может быть выбор фильтров

По спискам

и

По типу

при поиске.
Если это (эти) задание у Вас в Избранном, то должны быть выбраны фильтры

Избранное

и

Все.

Если выбраны

Все

и

Все

, то задание не покажут.
Если задание не в Избранном, то соответственно наоборот — должны быть выбраны фильтры

Все

и

Все

.
Другой причиной может быть то, что задание выключено или забанено.

Не годится…(( Принцип, который вы описали, до меня добрел)), я им воспользовался, результат=0. Сейчас вот еще на всякий случай попробовал. Взял номер первого попавшегося задания (оно у меня никак не отмечено), выбрал «Все», ввел номер, и тишина…

---

Для обсуждения вопроса/идеи необходима регистрация.

Для таблицы на рис. 13
постройте следующие виды сводных таблиц:

• по учебным
группам подведите итоги по каждому
предмету и виду занятий с привяз­кой
к преподавателю:

средний балл;

количество оценок;

минимальная
оценка;

максимальная
оценка;

• по каждому
преподавателю подведите итоги в разрезе
предметов и номеров учебных групп:

количество оценок;

средний балл;

структура
успеваемости.

Технология работы

1. Проведите
подготовительную работу:

• откройте
  созданную рабочую книгу Spisok
  командой Файл, Открыть;

• вставьте новый
  лист и назовите его Свод;

• выделите блок
  ячеек исходного списка на листе Список,
  начиная от имен полей и вниз до конца
  записей таблицы, и скопируйте их на
  лист Свод.

2. Создайте сводную
таблицу с помощью Мастера сводных таблиц
по шагам:

• установите курсор
  в области данных таблицы;

• выполните команду
  Данные, Сводная таблица.

Этап
1 — выберите источник данных — текущую
таблицу, щелкнув по кнопке <в списке
или базе данных Ехсеl>
и по кнопке <Далее>.

Этап 2 — в строке
Диапазон должен быть отображен блок
ячеек списка (базы дан­ных). Если
диапазон указан неверно, то надо его
стереть и с помощью мыши выделить нужный
блок ячеек.

Этап 3 — постройте
макет сводной таблицы так, как показано
на рис.3.50. Техноло­гия построения
будет одинаковой для всех структурных
элементов и будет состоять в сле­дующем:

• подведите курсор
  к имени поля, находящегося в правой
  стороне макета;

• нажмите левую
  кнопку мыши и, удерживая ее нажатой,
  перетащите элемент с именем поля в одну
  из областей (Страница, Строка, Столбец,
  Данные);

• отпустите кнопку
  мыши, поле должно остаться в этой
  области;

• после установки
  поля в области Данные необходимо два
  раза щелкнуть по нему правой кнопкой
  мыши и в диалоговом окне «Вычисление
  поля сводной таблицы» выбрать операцию
  (функцию) над значением поля.

Этап 4 — выбор
места расположения — существующий
лист.

1. Выполните
   автоформатирование полученной сводной
   таблицы командой Формат, Автоформат.

2. Внесите изменения
   в исходные данные и выполните команду
   Данные, Обновить данные.

3. Повторите процесс
   построения сводной таблицы для п.2
   задания.

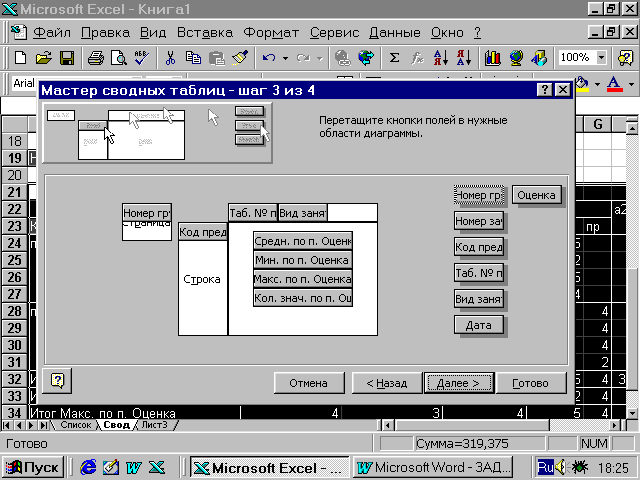
Рис. 18. Пример
макета сводной таблицы

Задание-17

Консолидация данных
по расположению и по категориям.

1. откройте
   книгу Spisok,
   вставьте два листа и переименуйте
   их.

2. Создайте на
   листе Консол.распол. таблицу расчета
   заработной платы (за январь).

3. Скопируйте
   созданную таблицу на тот же лист,
   измените в ней данные. Эта таблица
   будет отражать уровень заработной
   платы за февраль.

4. Выполните
   консолидацию данных по расположению
   и сравните результат с рис. 19.

5. Скопируйте обе
   таблицы (заработная плата за январь
   и за февраль) с листа Консол.распол.
   на лист Консол.категор и измените
   вторую таблицу в соответствии с
   рис.20.

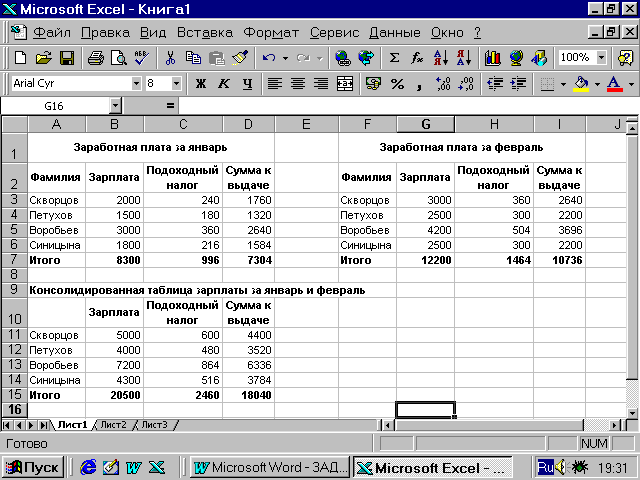
Рис.19. Пример
консолидации данных по расположению

1. Выполните
   консолидацию данных по категориям и
   сравните результат с рис. 20.

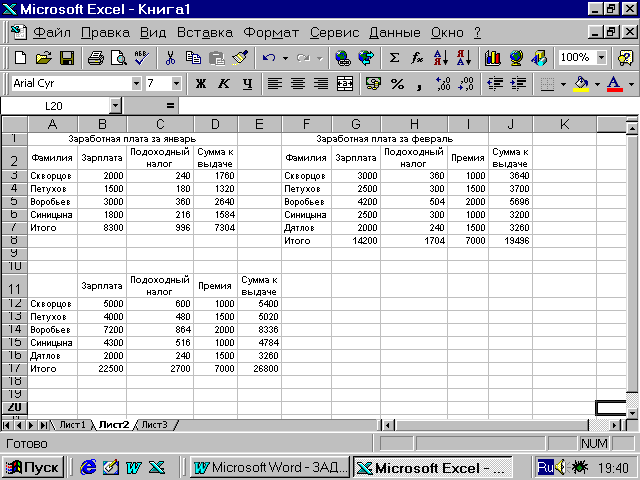
Рис.20. Пример
консолидации данных по категориям

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

7

2 ответа:

0



0

Друзья познаются в беде , у страха глаза велики

0



0

Друзья познаются в беде 

У страха глаза велики

Читайте также

Достоянием русского языка можно считать фразеологизмы. У этих устойчивых речевых выражений нет автора. Они неделимы по смыслу и являются единым целым. В своей речи каждый из нас применяет их часто, хотя и не замечает. С помощью фразеологизмов показывают свое отношение, речь становится яркой и образной.

Все фразеологизмы появились для выражения определенного события или явления. Позднее по различным причинам их стали применять в переносном смысле, но сходном с первоначальным значением. Фразеологизмы бывают как однозначными, так и многозначными, могут иметь синонимы и антонимы. В предложении выражаются одним членом.

Фразеологизмы можно разделить на четыре вида. К первому относятся устойчивые сочетания, имеющие отношение к историческому прошлому народа. Второй вид — это образные речевые обороты, в которых отражаются народные традиции. К следующему виду принадлежат появившиеся от разнообразных ремесел устойчивые комбинации слов. И наконец, последний вид – это крылатые выражения. Устойчивые обороты, входящие в каждую группу, имеют свою уникальную историю происхождения.

Многим из нас помогают фразеологические обороты, как в письменной, так и в устной речи. В произведениях литературы и повседневной речи нам часто приходится употреблять такие сочетания. Так более красочно и эмоционально рассказываем мы о каком-то событии или передаем свое отношение. Например, речевой оборот «рукой подать» означает «недалеко», а фразеологизм «поставить в тупик» заменяет выражение «привести в замешательство».

Таким образом, без фразеологизмов, которые мы используем с самого детства, невозможно представить повседневной речи. Фразеологизмы можно назвать «золотым резервом» русского языка за их эмоциональную окраску и меткость.

Аквалангист плавал , и рыба подплыла незаметно , и потом акула съела эту рыбку

Я решила выбрать Руслана потому, что он храбрый, добрый, сильный, умный, на всё готов ради Людмилы

Мое утро начинается с 6 часов утра.Звенит будильник,встаю,включаю воду в ванной,пока нагревается,иду на кухню и на тощак выпиваю стакан или два кипяченой холодненькой водички.Ставлю чайник,пока умываюсь,он вскипит.Иду умываться,чистить зубы,когда принимаю душ,но обычно я это делаю вечером,перед сном,потом наливаю чайку и иду краситься.Наношу макияж и пью чай одновременно,т.к. времени остается мало.Макияж закончен,выпрямляю волосы,заделываю хвост или оставлю распущенными,одеваюсь,душусь,обуваюсь и иду на работу к 8 часам!!

Когда я стану президентом я буду делать великие дела!Для начала я издам новый закон-все домашние задания за нас,учеников будут делать учителя.А мы будем  учить их и также наказывать как они наказывали раньше нас.После этого я издам указ,чтобы родители разрешали детям играть в компьютер и гулять сколько они хотят.Вскоре я построю лучший в мире космический корабль и подружусь с марсианами.Но это будет еще не скоро,ведь,президентом меня еще не выбрали.Но когда люди осознают,кто лучший они обязательно изберут меня новым президентом!

Задать свой вопрос

  *более 50 000 пользователей получили ответ на «Решим всё»

Условие

vk209029450

2020-01-22 19:31:30

Как решить задания под номером 16 и 17?

предмет не задан
249

О решение…

На нашем сайте такое бывает редко, но решение к данной задаче еще никто не написал.

Что Вы можете сделать?

1. Выставите данный вопрос вновь. Перейдите на главную страницу.
2. Найдите похожую задачу. Используйте поиск.

Написать комментарий

Меню

• Решим всё
• Найти задачу
• Категории
• Статьи
• Тесты
• Архив задач

Присоединяйся в ВК

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

---

С этим файлом связано 3 файл(ов). Среди них: Практическая работа № 1.docx, 0001cd49-c7177f69.pptx, 1 часть повторить!!!!.pdf.
Показать все связанные файлы

---

Подборка по базе: Предпринимательская деятельность. Системный подход в управлении , УП ПМ.03 План задание на практику 6 семестр.doc, практическое задание 1 английский.docx, Практическое задание .docx, Практическая 1. задание 1.docx, Практическое задание №4 по учебному курсу «Налоговый учет и отче, Практическое задание Бизнес-коммуникации.docx, Итоговое задание.doc, Практическое задание по проектированию БД.docx, Практическое задание № 2.docx

---

Новый октябрьский тренировочный вариант (тренировочная работа) №37812190 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.

скачать вариант

скачать ответы

Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812190:

Ответы и решения:

На плане изображено домохозяйство по адресу с. Сосновое, 2-й Зелёный пер, д. 9 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок слева от ворот находится сарай, а справа — гараж. Площадь, занятая гаражом, равна 32 кв. м.

Жилой дом находится в глубине территории. Помимо гаража, жилого дома и сарая, на участке имеется теплица, расположенная на территории огорода (огород отмечен на плане цифрой 5). Все дорожки внутри участка имеют ширину 0,5 м и вымощены тротуарной плиткой размером 1 м × 0,5 м. Перед гаражом имеется площадка, вымощенная той же плиткой.

Задание 1 № 369520 Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Ответ: 1243

Задание 2 № 369521 Тротуарная плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?

Ответ: 29

Задание 3 № 369523 Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.

Ответ: 106

Задание 4 № 369522 Найдите расстояние от сарая до жилого дома (под расстоянием между двумя объектами следует понимать расстояние между их ближайшими точками). Ответ дайте в метрах.

Ответ: 15

Задание 5 № 369524 Хозяин участка хочет сделать пристройку к дому. Для этого он планирует купить 12 тонн силикатного кирпича. Один кирпич весит 3 кг. Цена кирпича и условия доставки всей покупки приведены в таблице. Во сколько рублей обойдётся наиболее дешёвый вариант?

Ответ: 53240

Задание 10 № 311324 Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?

Ответ: 0,18

Задание 11 № 314676 На рисунке изображён график квадратичной функции y = f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера в порядке возрастания.

Ответ: 23

Задание 14 № 394437 Мама договорилась с Димой, что в понедельник он будет учить испанские слова. За первое выученное слово она даст сыну 5конфет, а за каждое следующее слово на 2 конфеты больше, чем за предыдущее. Сколько конфет Дима получит от мамы в понедельник, если он выучит 12 слов?

Ответ: 192

Задание 15 № 339544 В треугольнике ABC BM — медиана и BH – высота. Известно, что AC=216, HC=54 и ∠ ACB=40°. Найдите угол AMB. Ответ дайте в градусах.

Ответ: 140

Задание 16 № 356543 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, AC = 8. Найдите AK.

Ответ: 4

Задание 17 № 323902 Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.

Ответ: 88

Задание 19 № 169915 Какие из следующих утверждений верны? 1) Если угол равен 45°, то вертикальный с ним угол равен 45°. 2) Любые две прямые имеют ровно одну общую точку. 3) Через любые три точки проходит ровно одна прямая. 4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.

Ответ: 1

Задание 21 № 311770 Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?

Ответ: 33

Задание 24 № 339506 Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.

Задание 25 № 339730 Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.

Ответ: 1; 21.

Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:

Тренировочные варианты ОГЭ по математике 9 класс задания с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

1. Задание 1 № 406563

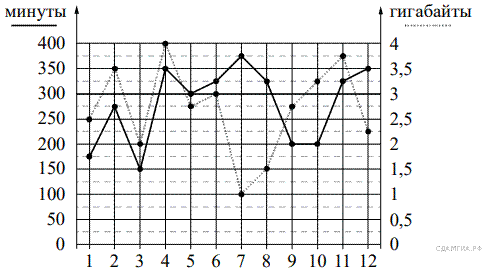
Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета.

Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответе нужно записать

число 51118).

Мобильный интернет	2,5 Гб	3 Гб	3,25 Гб	1 Гб
Номер месяца

На рисунке точками показано количество минут исходящих вызовов и трафик мобильного интернета в гигабайтах, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2019 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.

В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляла 350 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:

• пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ;

• пакет интернета, включающий 3 гигабайта мобильного интернета;

• пакет СМС, включающий 120 СМС в месяц;

• безлимитные бесплатные входящие вызовы.

Стоимость минут, интернета и СМС сверх пакета тарифа указана в таблице.

Исходящие вызовы	3 руб./мин.
Мобильный интернет (пакет)	90 руб. за 0,5 Гб
СМС	2 руб./шт.

Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 110 СМС.

Решение.

Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года.

Из рисунка видно, что 2,5 Гб было потрачено в первый месяц, 3 Гб — потрачено в шестой, 3,25 Гб — в десятый, 1 Гб — в седьмой.

Ответ: 16107.

2. Задание 2 № 406675

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику израсходованных минут и гигабайтов.

ПЕРИОДЫ		ХАРАКТЕРИСТИКИ
А) январь−февраль Б) февраль−март В) август–сентябрь Г) ноябрь–декабрь		1) Расход минут увеличился, а расход гигабайтов уменьшился. 2) Расход гигабайтов увеличился, а расход минут уменьшился. 3) Расход минут увеличился, и расход гигабайтов увеличился. 4) Расход минут уменьшился, и расход гигабайтов уменьшился.

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Решение.

Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года, а сплошной линей — количество минут исходящих вызовов.

За период январь−февраль расход минут увеличился, и расход гигабайтов увеличился.

За период февраль−март расход минут уменьшился, и расход гигабайтов уменьшился.

За период август–сентябрь расход гигабайтов увеличился, а расход минут уменьшился.

За период ноябрь–декабрь расход минут увеличился, а расход гигабайтов уменьшился.

Таким образом, получается соответствие: А — 3, Б — 4, В — 2, Г — 1.

Ответ: 3421.

3. Задание 3 № 406564

Сколько рублей потратил абонент на услуги связи в июне?

Решение.

По рисунку видно, что за июнь абонент потратил 3 Гб интернета, 325 минут исходящих вызовов, и в условии сказано, что за год отправил 110 СМС.

Количество потраченного интернета и СМС не превысило это количество в пакете тарифа, а исходящих вызовов сверх пакета было потрачено 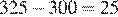минут.

Вычислим стоимость услуг связи, потраченных абонентом в июне:

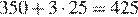рублей.

Ответ: 425.

4. Задание 4 № 406565

Какое наименьшее количество минут исходящих вызовов за месяц было в 2019 году?

Решение.

Сплошной линей на графике показано количество минут исходящих вызовов, израсходованных за каждый месяц года.

Из рисунка видно, что в третьем месяце было потрачено 150 минут, что является наименьшим количеством за 2019 год.

Ответ: 150.

5. Задание 5 № 367694

Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м² площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.

Место	Цена земли (млн руб.)	Цена строительства (млн руб.)	Длина коммуникаций (м)	Стоимость аренды за 1 м2 (руб./месяц)
Центр	64,4
Окраина	11,2

Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.

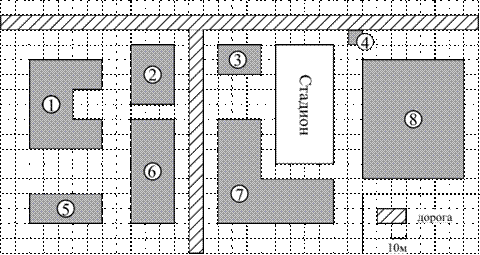
На плане (см. рисунок) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.

Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м². А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.

Решение.

Стоимость постройки ТРК в центре города равна

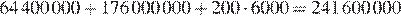рублей.

Стоимость постройки ТРК на окраине города равна

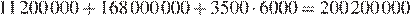рублей.

Разница в стоимости составляет

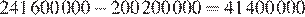рублей.

Разница в стоимости аренды составляет

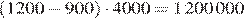рублей.

Значит, более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций через 34,5 месяцев. Округляя, получаем ответ — 35 месяцев.

Ответ: 35.

6. Задание 6 № 203743

Запишите в ответе номера выражений, значения которых положительны.

Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.

Решение.

Найдём значения выражений:

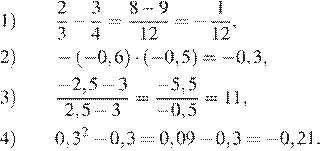
Таким образом, искомое выражение указано под номером 3.

7. Задание 7 № 314800

На координатной прямой отмечены числа а и b. Какое из следующих утверждений неверно?

В ответе укажите номер правильного варианта.

1)

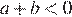
2)

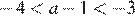
3)

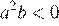
4)

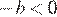
Решение.

Заметим, что 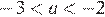и 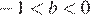, и проверим все варианты ответа:

1) 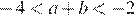, значит, 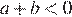— верно.

2) 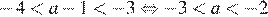— верно.

3) 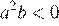— верно, поскольку 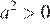, а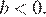

4) 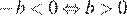— неверно.

Неверным является утверждение 4.

Примечание.

Нетрудно заметить, что справедливо неравенство: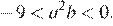

8. Задание 8 № 341704

Найдите значение выражения 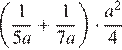при a = 7,7.

Решение.

Упростим выражение:

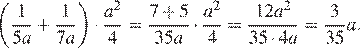
Подставим в полученное выражение значение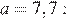

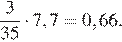
Ответ: 0,66.

9. Задание 9 № 338610

Решите уравнение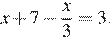

Решение.

Последовательно получаем:

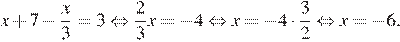
Ответ: −6.

10. Задание 10 № 325541

Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся.

Решение.

Вероятность того, что стрелок промахнётся равна 1 − 0,8 = 0,2. Вероятность того, что стрелок первые два раза попал по мишеням равна 0,8² = 0,64. Откуда, вероятность события, при котором стрелок сначала два раза попадает в мишени, а третий раз промахивается равна 0,64 · 0,2 = 0,128.

Ответ: 0,128.

11. Задание 11 № 193089

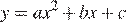Найдите значение по графику функции , изображенному на рисунке.

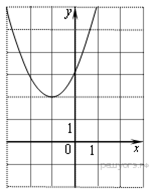
Решение.

Абсцисса вершины параболы равна −1, поэтому 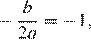откуда 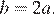Парабола пересекает ось ординат в точке с ординатой 3, поэтому 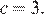Тем самым, уравнение параболы принимает вид 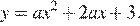Поскольку парабола проходит через точку (−1; 2), имеем:

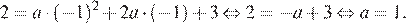
Верный ответ указан под номером 2.

Ответ: 2.

12. Задание 12 № 338396

Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.

Решение.

Найдем расстояние, на котором находится наблюдатель от места удара молнии:

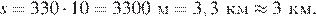
Ответ: 3.

13. Задание 13 № 311312

Решите неравенство .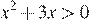

В ответе укажите номер правильного варианта.

1)

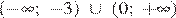
2)

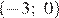
3)

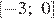
4)

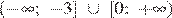
Решение.

Решим данное неравенство:

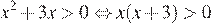. Произведение двух сомножителей будет больше нуля, если его сомножители имеют одинаковый знак.

В данном случае это выполняется при следующих значениях :

1) ;

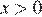2) ;

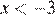Решением неравенства будет являться объединение этих промежутков: 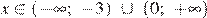, что соответствует первому варианту ответа.

Ответ: 1

14. Задание 14 № 394426

Давление воздуха под колоколом равно 625 мм ртутного столба. Каждую минуту насос откачивает из-под колокола 20% находящегося там воздуха. Определите давление (в мм рт. ст.) через 5 минут после начала работы насоса.

Решение.

Через минуту давление воздуха (в мм рт. ст.) под колоколом станет 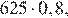через две минуты — 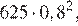…, через 5 минут давление станет 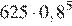или

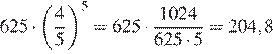мм рт. ст.

Ответ: 204,8.

15. Задание 15 № 348371

Высота BH ромба ABCD делит его сторону AD на отрезки AH = 44 и HD = 11. Найдите площадь ромба.

Решение.

Заметим, что сторона ромба AB = AD = AH + HD = 44 + 11 = 55.

Из прямоугольного треугольника ABH найдем BH по теореме Пифагора:

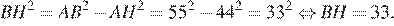
Площадь ромба можно найти как произведение основания на высоту:

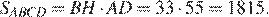
Ответ: 1815.

16. Задание 16 № 339975

Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Решение.

Радиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника 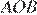по теореме Пифагора найдём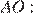

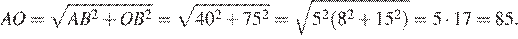
Найдём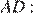

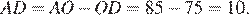
Ответ: 10.

17. Задание 17 № 324017

Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.

Решение.

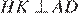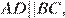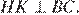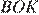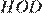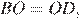
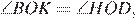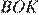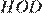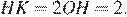Проведём построение и введём обозначения, как показано на рисунке. Учитывая, что и получаем Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники и , они прямоугольные, следовательно, треугольники и равны, откуда то есть высота Найдём площадь ромба как произведение стороны на высоту:

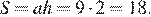
Ответ: 18.

18. Задание 18 № 311485

На квадратной сетке изображён угол 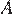. Найдите .

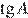Решение.

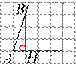
Опустим перпендикуляр BH. Треугольник ABH — прямоугольный. Таким образом,

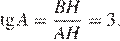
Ответ: 3.

19. Задание 19 № 341676

Какие из следующих утверждений верны?

1) Треугольника со сторонами 1, 2, 4 не существует.

2) Смежные углы равны.

3) Все диаметры окружности равны между собой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

1) «Треугольника со сторонами 1, 2, 4 не существует» — верно, большая сторона треугольника должна быть меньше суммы двух других.

2) «Смежные углы равны» — неверно, смежные углы 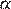и 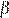связаны соотношением: .

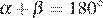3) «Все диаметры окружности равны между собой» — верно.

Ответ: 13.

20. Задание 20 № 311591

Решите уравнение: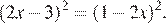

Решение.

Перенесем все члены влево и применим формулу разности квадратов:

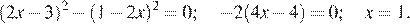
Другой способ. Раскроем скобки, пользуясь формулой квадрата разности:

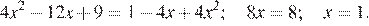
Ответ: 1.

21. Задание 21 № 314507

Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.

Решение.

Пусть скорость пешехода — x км/ч, 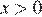, тогда скорость велосипедиста равна (x + 11) км/ч.

Составим таблицу по данным задачи:

	Скорость, км/ч	Время, ч	Расстояние, км
Пешеход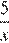
Велосипедист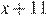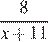

Так как по пути велосипедист сделал остановку на ч., составим уравнение:

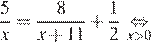
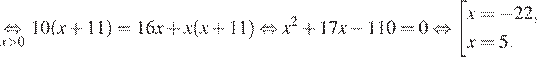
Корень −22 не подходит нам по условию задачи. Скорость пешехода равна 5 км/ч.

Ответ: 5 км/ч.

22. Задание 22 № 353274

Постройте график функции 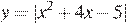. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

Решение.

График данной функции — это график параболы 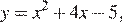отрицательная часть которого отражена относительно оси Этот график изображён на рисунке:

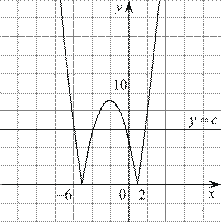
Прямая, параллельная оси абсцисс задаётся формулой 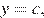где — постоянная. Из графика видно, что прямая может иметь с графиком функции не более четырёх общих точек.

Ответ: 4.

23. Задание 23 № 333321

Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56 .

Решение.

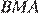Углы и равны как накрест лежащие, углы и равны как вертикальные, следовательно, треугольник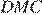и и 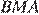подобны по двум углам.

Значит, 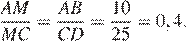Следовательно,

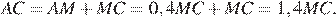
Откуда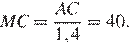

Ответ: 40.

24. Задание 24 № 349626

Окружности с центрами в точках 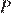и 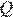не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.

Решение.

Проведём построения и введём обозначения, как показано на рисунке. Пусть 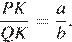Рассмотрим треугольник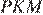и и 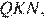они прямоугольные, углы 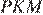и 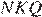равны как вертикальные, следовательно, треугольники подобны, откуда 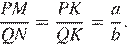Отношение радиусов равно отношению диаметров.

25. Задание 25 № 311708

В прямоугольном треугольнике ABC с прямым углом B, проведена биссектриса угла A. Известно, что она пересекает серединный перпендикуляр, проведённый к стороне BC в точке K. Найдите угол BCK, если известно, что угол ACB равен 40°.

Решение.

Так как биссектриса острого угла A прямоугольного треугольника ABC не может быть перпендикулярна BC, то биссектриса угла A и серединный перпендикуляр к BC имеют ровно одну общую точку.

Пусть N — середина BC. Рассмотрим окружность, описанную около треугольника ABC. Пусть серединный перпендикуляр к BC пересекает меньшую дугу BC в точке L (см. рисунок), тогда точка L является серединой этой дуги, ⌣BL = ⌣LC. Но тогда 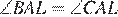как вписанные углы, опирающиеся на равные дуги, а отсюда AL — биссектриса 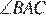. Но это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой 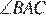. Заметим, что 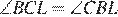как вписанные углы, опирающиеся на равные дуги.

Пусть 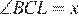. Четырехугольник ACLB — вписанный, поэтому 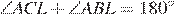, то есть 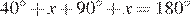, откуда 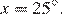Так как точки K и L совпадают,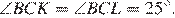

Ответ: 25°.

3568	Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H. а) Докажите, что ∠BB1C1 = ∠BAH. б) Найдите расстояние от центра окружности, описанной около треугольника ABC, до стороны BC, если B1C1=9 и ∠BAC = 60° Решение	Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H. а) Докажите, что ∠BB1C1 = ∠BAH ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 16 Вариант МА2210209
3532	На сторонах AB и CD четырёхугольника ABCD, около которого можно описать окружность, отмечены точки K и N соответственно. Около четырёхугольников AKND и BCNK также можно описать окружность. Косинус одного из углов четырёхугольника ABCD равен 0,25. а) Докажите, что четырёхугольник ABCD является равнобедренной трапецией. б) Найдите радиус окружности, описанной около четырёхугольника AKND, если радиус окружности, описанной около четырёхугольника ABCD, равен 8, AK:KB = 2:5, а BC < AD и BC = 4 Решение	На сторонах AB и CD четырёхугольника ABCD, около которого можно описать окружность, отмечены точки K и N соответственно ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 16
3514	Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F соответственно. Точка D — основание высоты, опущенной из вершины C. I и J — центры окружностей, вписанных в треугольники BCD и ACD. а) Докажите, что I и J лежат на отрезке EF. б) Найдите расстояние от точки C до прямой IJ, если AC=15, BC=20 Решение	Окружность с центром в точке C касается гипотенузы AB прямоугольного треугольника ABC и пересекает его катеты AC и BC в точках E и F соответственно ! 36 вариантов ФИПИ Ященко 2023 Вариант 7 Задание 16
3502	В трапеции ABCD с меньшим основанием BC точки E и F — середины сторон ВC и AD соответственно. В каждый из четырёхугольников ABEF и ECDF можно вписать окружность. а) Докажите, что трапеция ABCD равнобедренная. б) Найдите радиус окружности, описанной около трапеции ABCD, если AB=7, а радиус окружности, вписанной в четырёхугольник ABEF, равен 2,5 Решение	В трапеции ABCD с меньшим основанием BC точки E и F — середины сторон ВC и AD соответственно ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 16
3492	Четырёхугольник ABCD со сторонами BC=7 и AB=CD=20 вписан в окружность радиусом R=16. а) Докажите, что прямые BC и AD параллельны. б) Найдите AD Решение	Четырёхугольник ABCD со сторонами BC=7 и AB=CD=20 вписан в окружность радиусом R=16 ! 36 вариантов ФИПИ Ященко 2023 Вариант 3 Задание 16
3490	Дана равнобедренная трапеция ABCD. На боковой стороне AB и большем основании AD взяты соответственно точки F и E так, что FE параллельно CD, a FC=ED. а) Докажите, что угол BCF равен углу AFE. б) Найдите площадь трапеции ABCD, если DE=5BF, FE=8 и площадь трапеции FCDE равна 27sqrt11 Решение	Дана равнобедренная трапеция ABCD. На боковой стороне AB и большем основании AD взяты соответственно точки F и E так, что FE параллельно CD, a FC=ED ! Досрочный ЕГЭ 2022 по математике 28.03.2022 Задание 16
3477	В параллелограмме ABCD угол ВАС вдвое больше угла CAD. Биссектриса угла BAC пересекает отрезок BC в точке L. На продолжении стороны CD за точку D выбрана такая точка E, что AE=CE. а) Докажите, что AL:BC=AB:BC. б) Найдите EL, если AC=21, tg /_BCA=0,4 Решение	В параллелограмме ABCD угол ВАС вдвое раза больше угла CAD ! 36 вариантов ФИПИ Ященко 2023 Вариант 1 Задание 16 # ЕГЭ 2022 по математике 02.06.2022 основная волна Задание 16 Санкт-Петербург, Центр # Задача-Аналог   3356
3468	На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2. а) Докажите, что площадь четырехугольника МКСN составляет 11/24 площади квадрата ABCD. б) Найдите синус угла между диагоналями четырехугольника МКCN Решение	На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2 ! Тренировочный вариант 399 от Ларина Задание 16
3467	В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е а) Докажите, что AD=CE+CD б) Найдите площадь трапеции ABCD, если АЕ=10, /_BAD=60^@ Решение	В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС ! Тренировочный вариант 398 от Ларина Задание 16
3460	Две окружности пересекаются в точках Р и Q. Через точку Р проведена прямая, пересекающая вторично первую из окружностей в точке А, а вторую – в точке В. Через точку Q также проведена прямая, пересекающая вторично первую окружность в точке С, а вторую – в точке D. а) Докажите, что прямые АС и BD параллельны. б) Найдите наибольшее возможное значение суммы длин отрезков АВ и CD, если расстояние между центрами данных окружностей равно 1 Решение	Две окружности пересекаются в точках Р и Q. Через точку Р проведена прямая, пересекающая вторично первую из окружностей в точке А ! Тренировочный вариант 397 от Ларина Задание 16 # Задача-Аналог   762

Показана страница 1 из 34