 С этим файлом связано 3 файл(ов). Среди них: Практическая работа № 1.docx, 0001cd49-c7177f69.pptx, 1 часть повторить!!!!.pdf.
С этим файлом связано 3 файл(ов). Среди них: Практическая работа № 1.docx, 0001cd49-c7177f69.pptx, 1 часть повторить!!!!.pdf.
 Показать все связанные файлы
Показать все связанные файлы
Подборка по базе: Предпринимательская деятельность. Системный подход в управлении , УП ПМ.03 План задание на практику 6 семестр.doc, практическое задание 1 английский.docx, Практическое задание .docx, Практическая 1. задание 1.docx, Практическое задание №4 по учебному курсу «Налоговый учет и отче, Практическое задание Бизнес-коммуникации.docx, Итоговое задание.doc, Практическое задание по проектированию БД.docx, Практическое задание № 2.docx
1.
1. Задание 16 №
Задание 16 № 311410 311410
Радиус
OB
окружности с центром в точке
O
пересекает хорду
AC
в точке
D
и перпендикулярен ей. Найдите длину хорды
AC
, если
BD
=1см, а радиус окружности равен 5 см.
2.
2. Задание 16 №
Задание 16 № 311488 311488
Найдите величину (в градусах) вписанного угла
α
, опирающегося на хорду
AB
,
равную радиусу окружности.
3.
3. Задание 16 №
Задание 16 № 311681 311681
К окружности с центром в точке
О
проведены касательная
AB
и секущая
AO
. Найдите радиус окружности, если
AB
= 12 см,
AO
= 13 см.
4.
4. Задание 16 №
Задание 16 № 311912 311912
В треугольнике
ABC
угол
C
равен 90°,
AC
= 30 ,
BC
=
Найдите радиус окружности, описанной около этого треугольника.
5.
5. Задание 16 №
Задание 16 № 324324 324324
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
1/7
Образовательный портал «РЕШУ ОГЭ» (
https://math.reshuoge.ru
)
6.
6. Задание 16 №
Задание 16 № 324868 324868
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
7.
7. Задание 16 №
Задание 16 № 339438 339438
Прямая касается окружности в точке
K
. Точка
O
— центр окружности. Хорда
KM
образует с касательной угол, равный 83°. Найдите величину угла
OMK
. Ответ дайте в градусах.
8.
8. Задание 16 №
Задание 16 № 339623 339623
Отрезки
AB
и
CD
являются хордами окружности. Найдите длину хорды
CD
, если
AB
=20, а расстояния от центра окружности до хорд
AB
и
CD
равны соответственно 24 и 10.
9.
9. Задание 16 №
Задание 16 № 339892 339892
Отрезки
AB
и
CD
являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD
, если
AB
= 18,
CD
= 24, а расстояние от центра окружности до хорды
AB
равно 12.
10.
10. Задание 16 №
Задание 16 № 339975 339975
Отрезок
AB
=40 касается окружности радиуса 75 с центром
O
в точке
B
. Окружность пересекает отрезок
AO
в точке
D
. Найдите
AD
11.
11. Задание 16 №
Задание 16 № 340174 340174
На отрезке
AB
выбрана точка
C
так, что
AC
=75 и
BC
=10. Построена окружность с центром
A
, проходящая через
C
. Найдите длину отрезка касательной, проведённой из точки
B
к этой окружности.
2/7
Образовательный портал «РЕШУ ОГЭ» (
https://math.reshuoge.ru
)
12.
12. Задание 16 №
Задание 16 № 340337 340337
Касательные в точках
A
и
B
к окружности с центром
O
пересекаются под углом 72°. Найдите угол
ABO
. Ответ дайте в градусах.
13.
13. Задание 16 №
Задание 16 № 341522 341522
Окружность вписана в квадрат. Найдите площадь квадрата.
14.
14. Задание 16 №
Задание 16 № 102 102
Из точки
А
проведены две касательные к окружности с центром в точке
О
Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки
А
до точки
О
равно 8.
15.
15. Задание 16 №
Задание 16 № 339461 339461
Окружность с центром на стороне
AC
треугольника
ABC
проходит через вершину
C
и касается прямой
AB
в точке
B
. Найдите
AC
, если диаметр окружности равен 7,5, а
AB
= 2.
16.
16. Задание 16 №
Задание 16 № 355413 355413
Радиус окружности, вписанной в трапецию, равен 16. Найдите высоту этой трапеции.
3/7
Образовательный портал «РЕШУ ОГЭ» (
https://math.reshuoge.ru
)
17.
17. Задание 16 №
Задание 16 № 356369 356369
Радиус вписанной в квадрат окружности равен
Найдите диагональ этого квадрата.
18.
18. Задание 16 №
Задание 16 № 356379 356379
Радиус окружности, описанной около квадрата, равен
Найдите радиус окружности, вписанной в этот квадрат.
19.
19. Задание 16 №
Задание 16 № 356399 356399
Сторона квадрата равна 6. Найдите радиус окружности, вписанной в этот квадрат.
20.
20. Задание 16 №
Задание 16 № 356478 356478
Сторона равностороннего треугольника равна
Найдите радиус окружности,
описанной около этого треугольника.
4/7
Образовательный портал «РЕШУ ОГЭ» (
https://math.reshuoge.ru
)
21.
21. Задание 16 №
Задание 16 № 356488 356488
Сторона равностороннего треугольника равна
Найдите радиус окружности, вписанной в этот треугольник.
22.
22. Задание 16 №
Задание 16 № 356498 356498
Радиус окружности, вписанной в равносторонний треугольник, равен 5.
Найдите высоту этого треугольника.
23.
23. Задание 16 №
Задание 16 № 356508 356508
Радиус окружности, описанной около равностороннего треугольника, равен 6.
Найдите высоту этого треугольника.
24.
24. Задание 16 №
Задание 16 № 356518 356518
Радиус окружности, вписанной в равносторонний треугольник, равен
Найдите длину стороны этого треугольника.
5/7
Образовательный портал «РЕШУ ОГЭ» (
https://math.reshuoge.ru
)
25.
25. Задание 16 №
Задание 16 № 356533 356533
Радиус окружности, описанной около равностороннего треугольника, равен
Найдите длину стороны этого треугольника.
26.
26. Задание 16 №
Задание 16 № 356543 356543
Через точку
A
, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке
K
. Другая прямая пересекает окружность в точках
B
и
C
, причём
AB
= 2,
AC
= 8. Найдите
AK
27.
27. Задание 16 №
Задание 16 № 356618 356618
Хорды
AC
и
BD
окружности пересекаются в точке
P
,
BP
=15,
CP
=6,
DP
= 10.
Найдите
AP
28.
28. Задание 16 №
Задание 16 № 369504 369504
На окружности отмечены точки
A
и
B
так, что меньшая дуга
AB
равна 72°. Прямая
BC
касается окружности в точке
B
так, что угол
ABC
острый. Найдите угол
ABC
Ответ дайте в градусах.
6/7
Образовательный портал «РЕШУ ОГЭ» (
https://math.reshuoge.ru
)
29.
29. Задание 16 №
Задание 16 № 406648 406648
Радиус окружности, описанной около квадрата, равен
Найдите радиус окружности, вписанной в этот квадрат.
7/7
Образовательный портал «РЕШУ ОГЭ» (
https://math.reshuoge.ru
)
Новый октябрьский тренировочный вариант (тренировочная работа) №37812194 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
скачать вариант
скачать ответы
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812194:
Ответы и решения:
На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Квартира имеет прямоугольную форму. Вход и выход осуществляются через единственную дверь. При входе в квартиру расположен коридор, отмеченный цифрой 1, а справа находится кладовая комната, которая занимает площадь в 20 кв. м.
Гостиная занимает наибольшую площадь в квартире, а слева от неё находится кухня. Прямо перед гостиной находится детская. В верхнем правом углу схемы находится санузел, отмеченный цифрой 6. Прямо напротив него располагается ванная комната. В санузле и ванной комнате пол выложен плиткой, которая имеет размер 0,5 м × 0,5 м. В квартире стоит одно тарифный счётчик электроэнергии. Имеется возможность установить двухтарифный счётчик.
Задание 2 № 366587 Плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол в ванной комнате и санузле?
Ответ: 36
Задание 3 № 366588 Найдите площадь, которую занимает гостиная. Ответ дайте в квадратных метрах.
Ответ: 42
Задание 4 № 366589 Найдите расстояние от верхнего левого угла квартиры до нижнего правого угла квартиры (расстояние между двумя ближайшими точками по прямой) в метрах.
Ответ: 20
Задание 5 № 366590 Хозяин квартиры планирует заменить в квартире счётчик. Он рассматривает два варианта: однотарифный или двухтарифный счётчики. Цены на оборудование и стоимость его установки, данные о тарифах оплаты, и их стоимости даны в таблице. Обдумав оба варианта, хозяин решил установить двухтарифный электросчётчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счётчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счётчика и однотарифного?
Ответ: 200
Задание 10 № 132738 Миша с папой решили покататься на колесе обозрения. Всего на колесе двадцать четыре кабинки, из них 5— синие, 7— зеленые, остальные— красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Миша прокатится в красной кабинке.
Ответ: 0,5
Задание 14 № 393956 Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000 рублей. Каждый следующий год его прибыль увеличивалась на 300% по сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2003 год?
Ответ: 320000
Задание 15 № 339515 Найдите величину угла DOK, если OK— биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах.
Ответ: 36
Задание 16 № 356508 Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
Ответ: 9
Задание 17 № 356222 На стороне AC треугольника ABC отмечена точка D так, что AD = 3, DC=7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
Ответ: 14
Задание 18 № 339411 На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
Ответ: 1,5
Задание 19 № 311763 Укажите номера верных утверждений. 1) Через любую точку проходит не менее одной прямой. 2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны. 3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
Ответ: 12
Задание 21 № 338972 Два автомобиля одновременно отправляются в 240-километровый пробег. Первый едет со скоростью на 20 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля.
Ответ: 80 км/ч
Задание 23 № 311710 Найдите площадь выпуклого четырёхугольника с диагоналями 3 и 4, если отрезки, соединяющие середины его противоположных сторон, равны.
Задание 25 № 78 Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Ответ: 0,6
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Авторы: Т.А. Ладыженская, Л.А. Тростенцова, А.Д. Дейкина, О.М. Александрова.
Издательство:
Просвещение
Тип: Учебник
Подробный решебник (ГДЗ) по Русскому языку за 8 (восьмой) класс — готовый ответ упражнение — 16. Авторы учебника: Ладыженская, Тростенцова, Дейкина, Александрова. Издательство: Просвещение .
Вы открыли задание номер 16 из решебника на uchim.org.
Другие номера: ГДЗ по русскому языку 8 класс Тростенцова, Ладыженская
← 2 3 4 5 6 7 8 9 10 11 12 13 15 16 17 18 19 20 21 22 23 24 25 26 28 29 30 31 32 33 34 35 37 38 39 40 41 42 43 →
(кликните по решению, если нужно изменить размер)


Открыть номер 16 с телефона
Введите номер задания:
Всё для учебы » ГДЗ бесплатно » ГДЗ по русскому языку 8 класс Тростенцова, Ладыженская » Номер 16 — ГДЗ по русскому языку 8 класс Тростенцова, Ладыженская

ГДЗ(готовые домашние задания), решебник онлайн по физике за 8 класс автора Перышкин упражнение 16, задание 1 — вариант ответа на задание 1
Вопросы к параграфам:
§1
§2
§3
§4
§5
§6
§7
§8
§9
§10
§11
§12
§13
§14
§15
§16
§17
§18
§19
§20
§21
§22
§23
§24
§25
§26
§27
§28
§29
§30
§31
§32
§33
§34
§35
§36
§37
§38
§39
§40
§41
§42
§43
§44
§45
§47
§48
§49
§50
§51
§52
§53
§54
§55
§56
§57
§58
§59
§60
§61
§62
§63
§64
§65
§66
§67
§68
§69
§70
Лабораторные работы:
1
2
3
4
5
6
7
8
9
10
11
Задания к параграфам:
§2
§3
§4
§5
§6
§8
§10
§13
§14
§15
§16
§17
§18
§20
§24
§25
§32
§34
§35
§52
§54
§55
§59
§60
§61
§62
§63
§64
§70
Упражнения:
Упражнение 1:
1
2
Упражнение 2:
1
2
Упражнение 3:
1
2
3
4
Упражнение 4:
1
2
3
Упражнение 5:
1
2
3
Упражнение 6:
1
2
Упражнение 7:
1
2
Упражнение 8:
1
2
3
Упражнение 9:
1
2
3
Упражнение 10:
1
2
3
4
Упражнение 11:
1
2
3
Упражнение 12:
1
2
3
4
5
Упражнение 14:
1
2
3
Упражнение 15:
1
2
3
Упражнение 16:
1
2
3
4
5
6
Упражнение 17:
1
2
3
Упражнение 18:
1
2
Упражнение 19:
1
2
Упражнение 20:
1
2
3
Упражнение 21:
1
2
3
Упражнение 22:
1
2
3
Упражнение 23:
1
2
3
4
Упражнение 24:
1
2
3
Упражнение 25:
1
2
3
4
Упражнение 26:
1
2
3
Упражнение 27:
1
2
Упражнение 28:
1
2
3
Упражнение 30:
1
2
3
4
Упражнение 31:
1
2
3
4
Упражнение 32:
1
2
3
4
Упражнение 33:
1
2
3
4
5
Упражнение 34:
1
2
3
Упражнение 35:
1
2
3
4
Упражнение 36:
1
2
3
Упражнение 37:
1
2
3
4
Упражнение 38:
1
2
Упражнение 39:
1
2
Упражнение 40:
1
2
Упражнение 41:
1
2
3
4
Упражнение 42:
1
2
Упражнение 43:
1
2
Упражнение 44:
1
2
3
Упражнение 45:
1
2
3
4
Упражнение 46:
1
2
3
4
Упражнение 47:
1
2
3
4
5
Упражнение 48:
1
2
Упражнение 49:
1
2
3
4
Для таблицы на рис. 13
постройте следующие виды сводных таблиц:
• по учебным
группам подведите итоги по каждому
предмету и виду занятий с привязкой
к преподавателю:
средний балл;
количество оценок;
минимальная
оценка;
максимальная
оценка;
• по каждому
преподавателю подведите итоги в разрезе
предметов и номеров учебных групп:
количество оценок;
средний балл;
структура
успеваемости.
Технология работы
1. Проведите
подготовительную работу:
-
откройте
созданную рабочую книгу Spisok
командой Файл, Открыть; -
вставьте новый
лист и назовите его Свод; -
выделите блок
ячеек исходного списка на листе Список,
начиная от имен полей и вниз до конца
записей таблицы, и скопируйте их на
лист Свод.
2. Создайте сводную
таблицу с помощью Мастера сводных таблиц
по шагам:
-
установите курсор
в области данных таблицы; -
выполните команду
Данные, Сводная таблица.
Этап
1 — выберите источник данных — текущую
таблицу, щелкнув по кнопке <в списке
или базе данных Ехсеl>
и по кнопке <Далее>.
Этап 2 — в строке
Диапазон должен быть отображен блок
ячеек списка (базы данных). Если
диапазон указан неверно, то надо его
стереть и с помощью мыши выделить нужный
блок ячеек.
Этап 3 — постройте
макет сводной таблицы так, как показано
на рис.3.50. Технология построения
будет одинаковой для всех структурных
элементов и будет состоять в следующем:
-
подведите курсор
к имени поля, находящегося в правой
стороне макета; -
нажмите левую
кнопку мыши и, удерживая ее нажатой,
перетащите элемент с именем поля в одну
из областей (Страница, Строка, Столбец,
Данные); -
отпустите кнопку
мыши, поле должно остаться в этой
области; -
после установки
поля в области Данные необходимо два
раза щелкнуть по нему правой кнопкой
мыши и в диалоговом окне «Вычисление
поля сводной таблицы» выбрать операцию
(функцию) над значением поля.
Этап 4 — выбор
места расположения — существующий
лист.
-
Выполните
автоформатирование полученной сводной
таблицы командой Формат, Автоформат. -
Внесите изменения
в исходные данные и выполните команду
Данные, Обновить данные. -
Повторите процесс
построения сводной таблицы для п.2
задания.
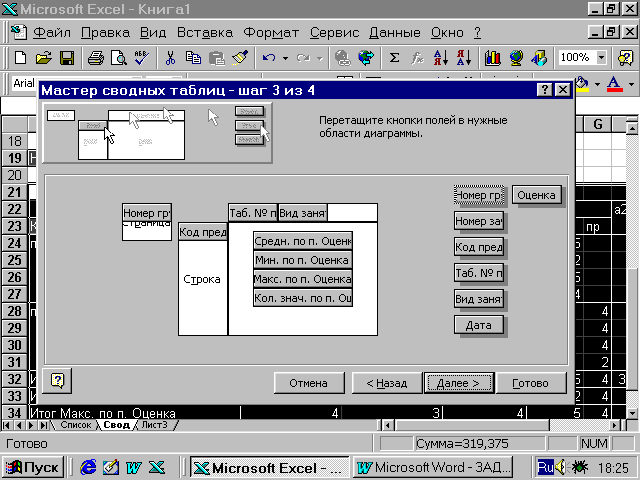
Рис. 18. Пример
макета сводной таблицы
Задание-17
Консолидация данных
по расположению и по категориям.
-
откройте
книгу Spisok,
вставьте два листа и переименуйте
их. -
Создайте на
листе Консол.распол. таблицу расчета
заработной платы (за январь). -
Скопируйте
созданную таблицу на тот же лист,
измените в ней данные. Эта таблица
будет отражать уровень заработной
платы за февраль. -
Выполните
консолидацию данных по расположению
и сравните результат с рис. 19. -
Скопируйте обе
таблицы (заработная плата за январь
и за февраль) с листа Консол.распол.
на лист Консол.категор и измените
вторую таблицу в соответствии с
рис.20.
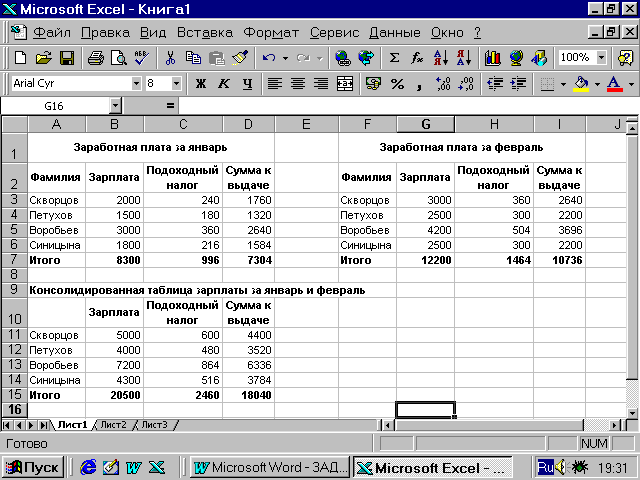
Рис.19. Пример
консолидации данных по расположению
-
Выполните
консолидацию данных по категориям и
сравните результат с рис. 20.
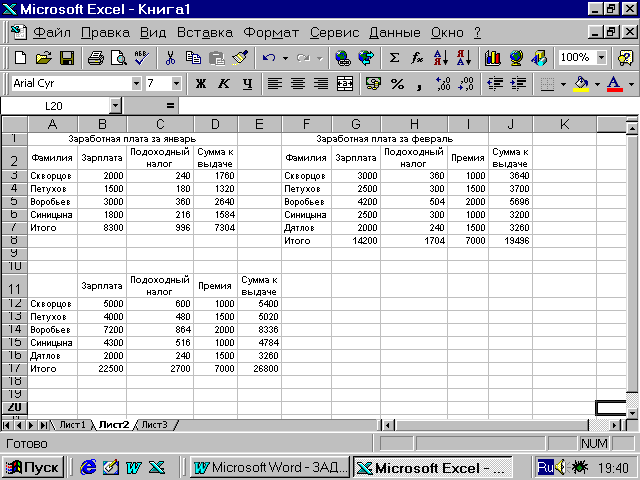
Рис.20. Пример
консолидации данных по категориям
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
![]()
oleg681 год назад
0
0
Развернутый угол — это угол, стороны которого составляют прямую
значит, углы 5:13 в сумме равны 180°
решим пропорцию
5+13=18
180:18=10
угол 1=5*10=50°
угол 2=13*10=130°
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
| Задача №1
| Четырехугольник АВСD вписан в окружность. Угол АВС равен 38°, угол САD равен 33°. Найдите угол АВD. Ответ дайте в градусах. Дано: ∠АВС = 38°, ∠САD = 33°. Найти: ∠АВD. Решение: ∠DBC = ∠DAC = 38°, так как вписанные углы, опирающиеся на одну и ту же дугу DC. ∠АВD = ∠AВC — ∠DBC = 38° — 33° = 5° Ответ: 5. |
| Задача №2
| Площадь круга равна 69. Найдите площадь сектора этого круга, центральный угол которого равен 120°. Дано: Sкруга = 69, угол кругового сектора равен 120°. Найти: Sсектора. Решение:
Ответ: 23. |
| Задача №3
| Угол А четырехугольника АВСD, вписанного в окружность, равен 33°. Найдите угол С этого четырехугольника. Ответ дайте в градусах. Дано: АВСD вписан в окружность, ∠А = 33°. Найти: ∠С. Решение: ∠C = 180° – ∠A = 180° – 33° = 147°, так как сумма противоположных углов вписанного четырехугольника равна 180°. Ответ: 147. |
| Задача №4
| Отрезки АС и BD – диаметры окружности с центром О. Угол АСВ равен 53°. Найдите угол АОD. Ответ дайте в градусах. Дано: АС и BD – диаметры окружности, ∠АСВ = 53°. Найти: ∠ АОD. Решение: 1)∠АCВ = 53° – вписанный угол, опирающийся на ᴗ АВ, поэтому ᴗ АВ = 53° 2 = 106°, так как вписанный угол измеряется половиной дуги, на которую он опирается. 2)BD – диаметр, значит ᴗ ВАD = 180°. 3) ∠ АОD – центральный угол, опирающийся на ᴗ АD, следовательно ∠ АОD = ᴗ АD = 180° – 106° = 74°. Ответ: 74. |
| Задача №5
| Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 20,5. Найдите ВС, если АС = 9. Дано: АВ – d; r = 20,5; АС = 9. Найти: ВС. Решение: ∠C = 90°, так как угол, опирающийся на диаметр, r = 20,5, следовательно АВ = 20,5 2 = 41 По теореме Пифагора АВ2 = АС2 + ВС2 412 = 92 + ВС2 ВС2 = 1681 – 81 ВС2 = 1600 ВС = 40 Ответ: 40. |
| Задача №6
| Точка О – центр окружности, на которой лежат точки А, В и С. Известно, что ∠АВС = 61° и ∠ОАВ = 8°. Найдите угол ВСО. Ответ дайте в градусах. Дано: ∠АВС = 61°, ∠ОАВ = 8°. Найти: ∠ ВСО. Решение: Проведем радиус ОВ, АО = ВО = СО = r. Треугольник АОВ – равнобедренный, значит ∠А = ∠АВО = 8°. Треугольник ВОС – равнобедренный, значит ∠ВСО = ∠ОВС= 61° – 8° = 53°. Ответ: 53. |
| Задача №7
| На окружности с центром О отмечены точки А и В так, что : ∠АОВ = 45°. Длина меньшей дуги равна 91. Найдите длину большей дуги. Дано: ∠АОВ = 45°, длина меньшей дуги равна 91. Найти: длину большей дуги. Решение:
Ответ: 637. |
| Задача №
| Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 77°. Найдите угол С этой трапеции. Ответ дайте в градусах. Дано: АВСD вписана в окружность, АD || ВС, ∠А = 77°. Найти: ∠С. Решение: ∠C = 180° – ∠A = 180° – 77° = 103°, так как сумма противоположных углов вписанного четырехугольника равна 180°. Ответ: 103. |
| Задача №9
| Четырехугольник АВСD описан около окружности, АВ = 8, ВС = 12, СD = 13. Найдите АD. Дано: АВСD описан около окружности, АВ = 8, ВС = 12, СD = 13. Найти: АD. Решение: АD + ВС = АВ + СD, так как суммы противоположных сторон описанного четырехугольника равны. АD + 12 = 8 + 13 АD = 21 – 12 АD = 9 Ответ: 9. |
| Задача №10
| Треугольник АВС вписан в окружность с центром О. Точки О и С лежат в одной полуплоскости относительно прямой АВ. Найдите угол АСВ, если угол АОВ равен 73°. Дано: треугольник АВС вписан в окружность, ∠АОВ = 73°. Найти: ∠АСВ. Решение: ∠ АОВ = 73° – центральный угол, опирающийся на ᴗ АВ, следовательно ᴗ АВ = 73°. ∠АСВ = 73° : 2 = 36, 5° , так как вписанный угол измеряется половиной дуги, на которую он опирается. Ответ: 36,5. |
| Задача №11
| Радиус окружности, вписанной в трапецию, равен 12. Найти высоту этой трапеции. Дано: трапеция вписана в окружность, r = 12. Найти: h. Решение: Высота трапеции равна диаметру вписанной окружности, поэтому h = 2 r = 2 12 = 24 . Ответ: 24. |
| Задача №12
| Сторона АВ треугольника АВС проходит через центр описанной около него окружности . Найдите ∠ А, если ∠В = 44°. Ответ дайте в градусах. Дано: треугольник АВС вписан в окружность, ∠В = 44 °. Найти: ∠А. Решение: ∠C = 90°, так как угол, опирающийся на диаметр, По теореме о сумме углов треугольника ∠А = 180° – (90° + 44°) = 46° Ответ: 46. |
| Задача №13
| Четырехугольник АВСD вписан в окружность. Угол АВD равен 37°, а угол САD равен 58°. Найдите угол АВС. Ответ дайте в градусах. Дано: АВСD вписан в окружность, ∠АВD = 37°, ∠САD = 58°. Найти: ∠АВС. Решение: Вписанный угол измеряется половиной дуги, на которую он опирается. ∠АВD = 37° – вписанный угол, опирающийся на ᴗ АD, поэтому ᴗ АD = 37° 2 = 74°. ∠САD = 58° – вписанный угол, опирающийся на ᴗ СD, поэтому ᴗ СD = 58° 2 = 116°. 3) ᴗ АDС = ᴗ АD + ᴗ DС = 74° + 116° = 190°, значит ∠АВС = 190° : 2 = 95°. Ответ: 95. |
| Задача №14
| Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ = ВС и ∠АВС = 107°. Найдите величину угла ВОС. Ответ дайте в градусах. Дано: АВС вписан в окружность, АВ = ВС, ∠АВС = 107°. Найти: ∠ВОС. Решение: Треугольник АВС равнобедренный, поэтому в нем углы при основании равны, то есть ∠А = ∠АСВ = (180° – 107°) : 2 = 36,5°. ∠ВАС = 36,5° – вписанный угол, опирающийся на ᴗ ВС, поэтому ᴗ ВС = 36,5° 2 = 73°. ∠ ВОС – центральный угол, опирающийся на ᴗ ВС, следовательно ∠ ВОС = ᴗ ВС = 73°. Ответ: 73. |
| Задача №15
| Радиус окружности, вписанной в равносторонний треугольник, равен 6. Найдите высоту этого треугольника. Дано: треугольник АВС описан около окружности, r = 6. Найти: h. Решение: В равностороннем треугольнике любая высота является медианой и биссектрисой и все они пересекаются в одной точке, которая является центром вписанной и описанной окружности. Медианы треугольника точкой пересечения делятся в отношении 2: 1, считая от вершины, значит h = 6 3 = 18. Ответ: 18. |
| Задача №16
| Через точку А, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке К. Другая прямая пересекает окружность в точках В и С, причем АВ = 2, АК = 4. Найдите АС. Дано: АК – касательная, АС – секущая, АВ = 2, АК = 4 Найти: АС. Решение: АК2 = АВ АС 42 = 2 АС АС = 16 : 2 АС = 8 Ответ: 8. |
| Задача №17
| Касательные в точках А и В к окружности с центром О пересекаются под углом 82°. Найдите угол АВО. Ответ дайте в градусах. Дано: касательные в точках А и В пересекаются под углом 82°. Найти: ∠АВО. Решение: Обозначим точку пересечения касательных буквой С . Отрезки касательных СА и СВ равны, значит треугольник АСВ равнобедренный, следовательно ∠САВ = ∠СВА = (180° – 82°) : 2 = 49°. Радиус окружности, проведенный в точку касания, перпендикулярен касательной, поэтому ∠АВС = 90°. ∠АВО = 90° – 49° = 41° Ответ: 41. |





















