Задание 16 номер 339892

---

С этим файлом связано 3 файл(ов). Среди них: Практическая работа № 1.docx, 0001cd49-c7177f69.pptx, 1 часть повторить!!!!.pdf.
Показать все связанные файлы

---

Подборка по базе: Предпринимательская деятельность. Системный подход в управлении , УП ПМ.03 План задание на практику 6 семестр.doc, практическое задание 1 английский.docx, Практическое задание .docx, Практическая 1. задание 1.docx, Практическое задание №4 по учебному курсу «Налоговый учет и отче, Практическое задание Бизнес-коммуникации.docx, Итоговое задание.doc, Практическое задание по проектированию БД.docx, Практическое задание № 2.docx

---

Не могу найти по номеру выполняемое многоразовое задание. Да и любые другие по номеру не найти). Пробовал произвольно выбранные задания вызвать по номеру — и ничего!)

Обсуждение

gimmegun

12 Окт 2017 г, в 09:01
редактир. 12 Окт 2017 г, в 09:06

Одной из причин может быть выбор фильтров

По спискам

и

По типу

при поиске.
Если это (эти) задание у Вас в Избранном, то должны быть выбраны фильтры

Избранное

и

Все.

Если выбраны

Все

и

Все

, то задание не покажут.
Если задание не в Избранном, то соответственно наоборот — должны быть выбраны фильтры

Все

и

Все

.
Другой причиной может быть то, что задание выключено или забанено.

Не годится…(( Принцип, который вы описали, до меня добрел)), я им воспользовался, результат=0. Сейчас вот еще на всякий случай попробовал. Взял номер первого попавшегося задания (оно у меня никак не отмечено), выбрал «Все», ввел номер, и тишина…

---

Для обсуждения вопроса/идеи необходима регистрация.

crsun148

Вопрос по математике:

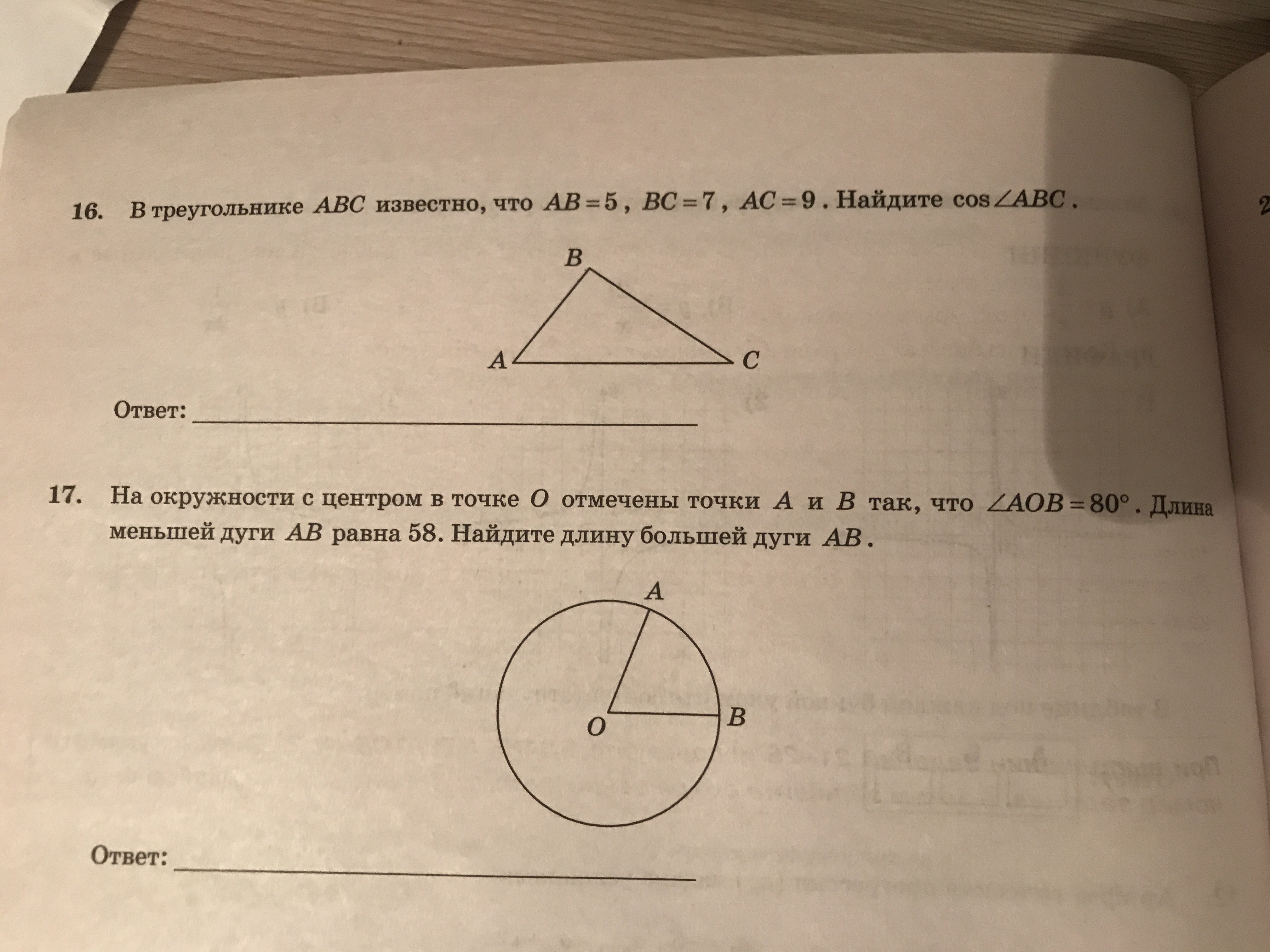
Помогите номер 16 пожалуйста

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 2

kledincrdr988

730-это 100%
803-это 803:730*100%= 110%
110%-100%=10(%)-увеличивалось число жителей

wakns804

Было 730 жителей_это 10 %
803 это 803:730*100=110%
Значит 110-100=10%-Увеличилось число жителей
Ответ:на 10%

Знаете ответ? Поделитесь им!

Гость ?

Как написать хороший ответ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете
  правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не
  побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и
  пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся
  уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
  знаю» и так далее;
• Использовать мат — это неуважительно по отношению к
  пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

• Главная
• Вопросы и ответы
• Помогите плиз.задание номер 16

Сам квадрат
10. 15. 8
9. 11. 13
14. 7. 12
такой должен быть

Для таблицы на рис. 13
постройте следующие виды сводных таблиц:

• по учебным
группам подведите итоги по каждому
предмету и виду занятий с привяз­кой
к преподавателю:

средний балл;

количество оценок;

минимальная
оценка;

максимальная
оценка;

• по каждому
преподавателю подведите итоги в разрезе
предметов и номеров учебных групп:

количество оценок;

средний балл;

структура
успеваемости.

Технология работы

1. Проведите
подготовительную работу:

• откройте
  созданную рабочую книгу Spisok
  командой Файл, Открыть;

• вставьте новый
  лист и назовите его Свод;

• выделите блок
  ячеек исходного списка на листе Список,
  начиная от имен полей и вниз до конца
  записей таблицы, и скопируйте их на
  лист Свод.

2. Создайте сводную
таблицу с помощью Мастера сводных таблиц
по шагам:

• установите курсор
  в области данных таблицы;

• выполните команду
  Данные, Сводная таблица.

Этап
1 — выберите источник данных — текущую
таблицу, щелкнув по кнопке <в списке
или базе данных Ехсеl>
и по кнопке <Далее>.

Этап 2 — в строке
Диапазон должен быть отображен блок
ячеек списка (базы дан­ных). Если
диапазон указан неверно, то надо его
стереть и с помощью мыши выделить нужный
блок ячеек.

Этап 3 — постройте
макет сводной таблицы так, как показано
на рис.3.50. Техноло­гия построения
будет одинаковой для всех структурных
элементов и будет состоять в сле­дующем:

• подведите курсор
  к имени поля, находящегося в правой
  стороне макета;

• нажмите левую
  кнопку мыши и, удерживая ее нажатой,
  перетащите элемент с именем поля в одну
  из областей (Страница, Строка, Столбец,
  Данные);

• отпустите кнопку
  мыши, поле должно остаться в этой
  области;

• после установки
  поля в области Данные необходимо два
  раза щелкнуть по нему правой кнопкой
  мыши и в диалоговом окне «Вычисление
  поля сводной таблицы» выбрать операцию
  (функцию) над значением поля.

Этап 4 — выбор
места расположения — существующий
лист.

1. Выполните
   автоформатирование полученной сводной
   таблицы командой Формат, Автоформат.

2. Внесите изменения
   в исходные данные и выполните команду
   Данные, Обновить данные.

3. Повторите процесс
   построения сводной таблицы для п.2
   задания.

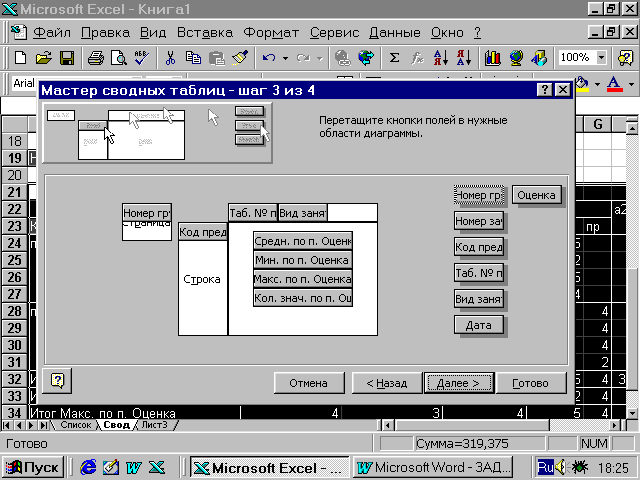
Рис. 18. Пример
макета сводной таблицы

Задание-17

Консолидация данных
по расположению и по категориям.

1. откройте
   книгу Spisok,
   вставьте два листа и переименуйте
   их.

2. Создайте на
   листе Консол.распол. таблицу расчета
   заработной платы (за январь).

3. Скопируйте
   созданную таблицу на тот же лист,
   измените в ней данные. Эта таблица
   будет отражать уровень заработной
   платы за февраль.

4. Выполните
   консолидацию данных по расположению
   и сравните результат с рис. 19.

5. Скопируйте обе
   таблицы (заработная плата за январь
   и за февраль) с листа Консол.распол.
   на лист Консол.категор и измените
   вторую таблицу в соответствии с
   рис.20.

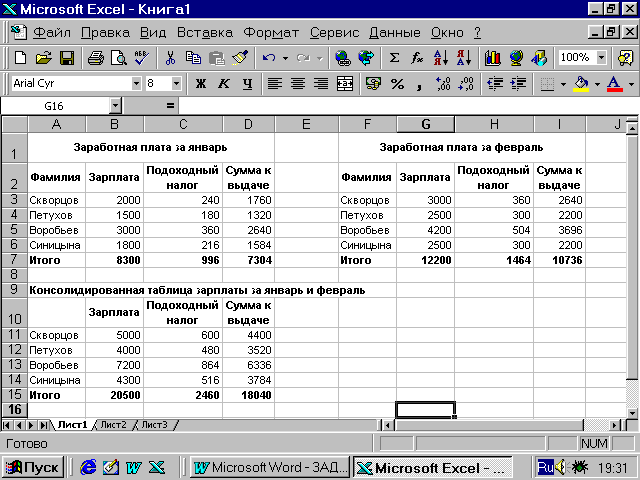
Рис.19. Пример
консолидации данных по расположению

1. Выполните
   консолидацию данных по категориям и
   сравните результат с рис. 20.

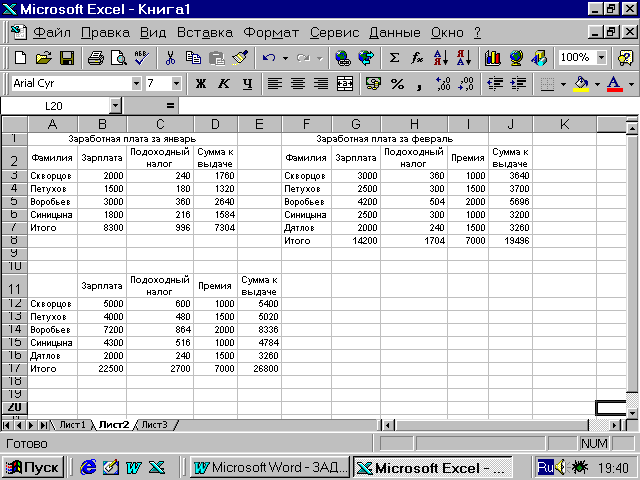
Рис.20. Пример
консолидации данных по категориям

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

oleg681 год назад

0



0

Развернутый угол — это угол, стороны которого составляют прямую 
значит, углы 5:13 в сумме равны 180°
решим пропорцию
5+13=18
180:18=10
угол 1=5*10=50°
угол 2=13*10=130°

Задать свой вопрос

  *более 50 000 пользователей получили ответ на «Решим всё»

Условие

vk209029450

2020-01-22 19:31:30

Как решить задания под номером 16 и 17?

предмет не задан
244

О решение…

На нашем сайте такое бывает редко, но решение к данной задаче еще никто не написал.

Что Вы можете сделать?

1. Выставите данный вопрос вновь. Перейдите на главную страницу.
2. Найдите похожую задачу. Используйте поиск.

Написать комментарий

Меню

• Решим всё
• Найти задачу
• Категории
• Статьи
• Тесты
• Архив задач

Присоединяйся в ВК

Прототипы заданий 16 ОГЭ по математике. Материал для подготовки к ОГЭ.

Для выполнения задания 16 необходимо уметь выполнять действия с геометрическими фигурами, координатами и векторами (окружность, круг и их элементы)

Подробнее узнать виды заданий на данной позиции в КИМах можно по кодификатору

Карточки для отработки задания 16 с ответамиИсточник: math100.ru → скачать

Прототипы задания 16 ОГЭ по математике (окружности) Опубликовано: Гармс Людмила Павловна → скачать

Материалы для отработки задания 16 Автор: Е. А. Ширяева → теория → задания

Задания 16 — практика → Скачать вариант 1 → Скачать ответы 1 → Скачать вариант 2 → Скачать ответы 2

Решение типовых задач № 16 на ОГЭ по математике

Связанные страницы:

Задание 15 ОГЭ по математике — треугольники, четырёхугольники, многоугольники и их элементы

Задание 13 ОГЭ по математике — неравенства

Тренировочные задания по теме «Вероятность» ОГЭ Математика

Тренировочные варианты ОГЭ 2021 по математике с ответами

Задание 14 ОГЭ по математике — задачи на прогрессии

Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 18, CD = 24, а расстояние от центра окружности до хорды AB равно 12.

Спрятать решение

Решение.

Проведём построения и введём обозначения, как показано на рисунке. Рассмотрим треугольники AOH и BOH, они прямоугольные, стороны AO и OB равны как радиусы окружностей, OH — общая, следовательно, треугольники AOH и HOB равны. Откуда Аналогично, равны треугольники COK и KOD, откуда Рассмотрим треугольник BOH, найдём OB по теореме Пифагора:

Рассмотрим треугольник OKD, он прямоугольный, из теоремы Пифагора найдём

Таким образом, расстояние от центра окружности до хорды CD равно 9.

Ответ: 9.

В 16 задании ОГЭ по математике необходимо решить простую задачу по геометрии. Для успешного решения необходимо обладать базовыми знаниями по геометрии вообще, так как сложно выделить какую-то одну тему, по которой даны задания. Это относится ко всему модулю геометрии. Я рекомендую повторить понятия центральные и вписанные углы, свойства касательных к окружности, взаимосвязь между радиусом описанной или вписанной окружности в геометрические фигуры — в первую очередь прямоугольный треугольник и квадрат.

Теория к заданию №16

Несмотря на то, что в задании №16 могут потребоваться любые знания по геометрии, в данном разделе мы разберем теорию по теме “окружность”.

Начнем рассмотрение с понятия вписанная окружность:

1. Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
2. Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d

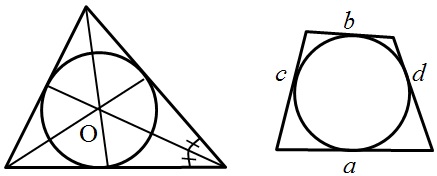
Длинна окружности и площадь:

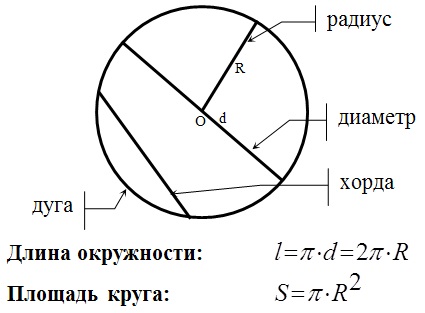
Касательная и секущая:

• Касательная – прямая, имеющая с окружностью одну общую точку.
• Секущая – прямая, имеющая с окружностью две общие точки.

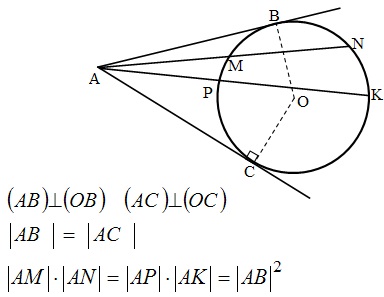Описанная окружность и её свойства:

1. Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
2. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
3. Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
4. Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой.

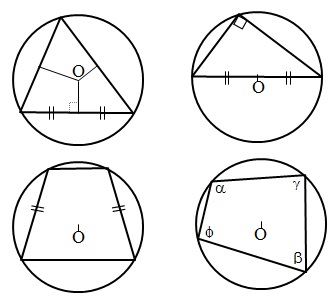
Хорда – отрезок, соединяющий две точки окружности.

• Диаметр, делящий хорду пополам, перпендикулярен хорде.
• В окружности равные хорды равноудалены от центра окружности.
• Отрезки пересекающихся хорд связаны равенством:

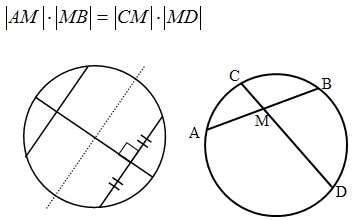
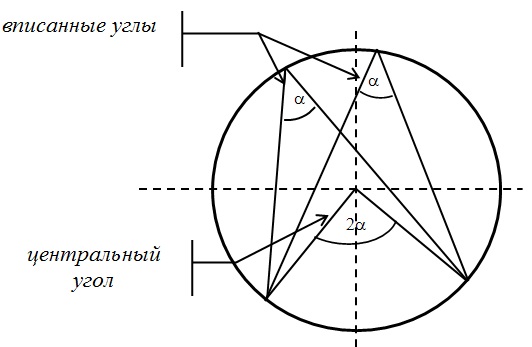
Центральный и вписанный углы:

Ниже я разобрал три различных примера 10 задания. Если у вас остались пожелания, или вы хотите разобрать задачу, которой здесь нет, напишите об этом в комментарии.

Задание OM1701o

Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.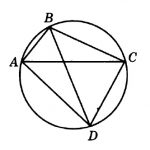

---

Внимательно посмотрим на рисунок. Угол ABC опирается на дугу ADC, а угол CAD – на дугу DC. Угол, который нам необходимо найти – ABD, опирается на дугу AD – которая является частью дуги ADC за вычетом дуги DC. Значит, угол ABD равен разности углов ABC и CAD:

∠ABD = 92 – 60 = 32

Ответ: 32

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1702o

Касательные в точках A и B к окружности с центром O пересекаются под углом 2º. Найдите угол ABO. Ответ дайте в градусах.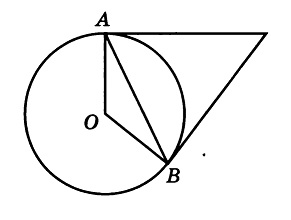

---

Во-первых, касательные равны между собой по длине, а значит треугольник с основанием AB равнобедренный. Угол при вершине этого треугольника равен 2 градуса по условию, значит углы при основании равны:

(180 – 2) / 2 = 89°

Во-вторых, касательные перпендикулярны радиусу, то есть угол между ними и радиусом равен 90 градусов.

Заметим, что угол ABO, который необходимо найти, является частью угла между касательной и радиусом, а именно за вычетом угла, который мы нашли в первом пункте. Значит, этот угол равен:

90 – 89 = 1°

Ответ: 1

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1703o

В треугольнике ABC известно, что AC = 16, BC = 12, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.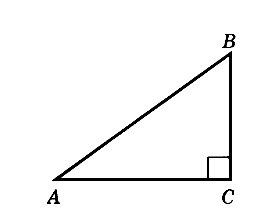

---

Для решения необходимо вспомнить, что центр описанной около прямоугольного треугольника окружности расположен в середине гипотенузы. То есть гипотенуза является диаметром, а её половина – радиусом.

По теореме Пифагора найдем гипотенузу AB:

AB² = BC² + AC² = 12² + 16² = 144 + 256 = 400

AB = √400 = 20

Гипотенуза равна 20, значит радиус – 10.

Ответ: 10

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1704o

Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.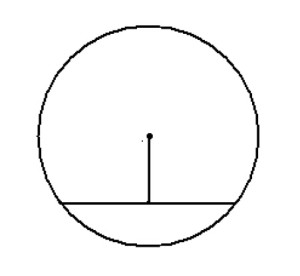

---

Для решения данной задачи необходимо провести радиус окружности к точке начала хорды:

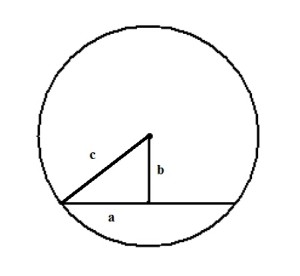
Получаем прямоугольный треугольник, где гипотенуза c – радиус и равна 13 см, b – расстояние до хорды – 5 см. По теореме Пифагора находим катет a:

a² + b² = c²

a² = c² – b² = 13² – 5² = 169 – 25 = 144

Откуда

а = √144 = 12

Но а – лишь половина хорды, поэтому вся хорда равна 2 • а = 24Ответ: 24

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1705o

Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 10. Найдите ВС, если АС=16.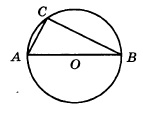

---

Сторона АВ треуг-ка АСВ является диаметром окружности. Это означает, что угол АСВ опирается на диаметр. Тогда угол АСВ равен 90⁰, и, следовательно, ∆АСВ прямоугольный.

Если ∆АСВ прямоугольный, то для нахождения одной из его сторон можно применить т.Пифагора. По т.Пифагора

АС²+ВС²=АВ²  (1)

По условию АС=16, радиус окружности R=10. Если R=10, то АВ=2R=2·10=20.

Тогда из (1) получим:

Ответ: 12

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1706o

Треугольник АВС вписан в окружность с центром в точке О. Найдите угол АСВ, если угол АОВ равен 1130. Ответ дайте в градусах.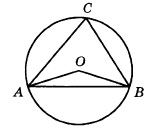

---

Поскольку вершина О угла АОВ лежит в центре окружности, значит, этот угол центральный. А если так, то он равен величине дуги АВ. Т.е. ᴗАВ=113⁰.

Угол АСВ является вписанным. Следовательно, его величина равна половине дуги, на которую он опирается. Из рисунка видно, что оба угла (АОВ и АСВ) опираются на одну и ту же дугу. Т.к.  ᴗАВ=113⁰, то угол АСВ равен

0,5 · ᴗАВ = 0,5 · 113⁰ = 56,5⁰.

Ответ: 56,5

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание 16OM21R

Радиус вписанной в квадрат окружности равен 22√2. Найти диагональ этого квадрата.

---

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22√2, то сторона квадрата будет в два раза больше, т.е. 44√2.

Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44√2. Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а√2, где с – гипотенуза, а – катет. Подставим в неё наши данные:

с=44√2×√2=44√4=44×2=88

Ответ: 88

pазбирался: Даниил Романович | обсудить разбор | оценить

Статьи

Основное общее образование

Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)

Математика

Представляем вашему вниманию разбор 16 задания ОГЭ-2019 по математике.

14 ноября 2018

Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Часть 1

Задание 16

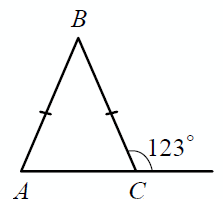
В равнобедренном треугольнике ABC с основанием АС внешний угол при вершине С равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.

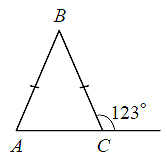
Решение

Треугольник АВС равнобедренный, поэтому угол ВАС равен углу ВСА. Но угол ВСА – смежный с углом в 123°. Следовательно

∠ВАС = ∠ВСА = 180° – 123° = 57°.

Ответ: 57°.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену

Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.

Купить

О категории

Геометрия

Практика (12)

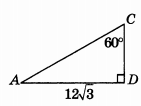
Используя данные, указанные на рисунке, найдите катет CD.

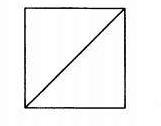
Найдите угол между стороной квадрата и его диагональю.

В равностороннем треугольнике АВС найдите величину острого угла между его высотами.

Медиана равностороннего треугольника равна 12sqrt(3). Найдите его сторону.

Сторона равностороннего треугольника равна 14sqrt(3). Найдите его биссектрису.

В равнобедренном треугольнике АВС с основанием АС биссектриса CF внешнего угла ВСК составляет с лучом СЕ, перпендикулярным к АК, угол 25° (см. рис. 152). Найдите градусную меру угла ВАС.

На рисунке 113 ∠BAD=∠ACD=30° , ∠ABE=∠ADC. Найдите величину ∠BEF в градусах.

В прямоугольном треугольнике АВС гипотенуза АВ = 17 (см. рис. 58), АС = 15. Найдите тангенс угла В.

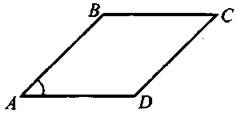
Диагональ BD ромба равна 11 см, а острый угол равен 60 градусов. Найдите периметр ромба в сантиметрах

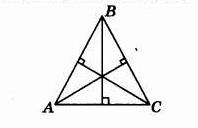
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.

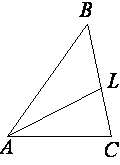
В треугольнике ABC известно, что AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах.

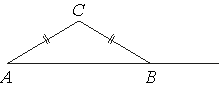
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123 градуса. Найдите величину угла ВАС. Ответ дайте в градусах

Практические задачи с ответами для задания №16 ОГЭ 2022 по математике для 9 класса, центральный и вписанный угол, касательная, хорда, секущая, радиус, окружность, описанная вокруг многоугольника решу ОГЭ онлайн на сайте.

Скачать задание 16 с ответами

Задание 16 ОГЭ 2022 математика 9 класс с ответами окружность:

1)Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 39°. Ответ дайте в градусах.

Ответ: 19,5

2)Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 64°. Ответ дайте в градусах.

Ответ: 32

3)Отрезки AC и BD – диаметры окружности с центром O. Угол ACB равен 25°. Найдите угол AOD. Ответ дайте в градусах.

Ответ: 130

4)Отрезки AC и BD – диаметры окружности с центром О. Угол ACB равен 28°. Найдите угол AOD. Ответ дайте в градусах.

Ответ: 124

5)В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 40°. Найдите вписанный угол ACB. Ответ дайте в градусах.

Ответ: 70

6)В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 38°. Найдите вписанный угол ACB. Ответ дайте в градусах.

Ответ: 71

7)На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что NBA = 36°. Найдите угол NMB. Ответ дайте в градусах.

Ответ: 54

8)На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что NBA = 42°. Найдите угол NMB. Ответ дайте в градусах.

Ответ: 48

9)Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ABC = 56° и OAB = 15°. Найдите угол BCO. Ответ дайте в градусах.

Ответ: 41

10)Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ABC = 62° и OAB = 53°. Найдите угол BCO. Ответ дайте в градусах.

Ответ: 9

11)Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ABC = 76°. Найдите величину угла BOC. Ответ дайте в градусах.

Ответ: 104

12)Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ABC = 57°. Найдите величину угла BOC. Ответ дайте в градусах.

Ответ: 123

13)Четырёхугольник ABCD вписан в окружность. Угол ABC равен 100°, угол CAD равен 31°. Найдите угол ABD. Ответ дайте в градусах.

Ответ: 69

14)Четырёхугольник ABCD вписан в окружность. Угол ABC равен 105°, угол CAD равен 29°. Найдите угол ABD. Ответ дайте в градусах.

Ответ: 76

15)Четырёхугольник ABCD вписан в окружность. Угол ABD равен 10°, угол CAD равен 62°. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 72

16)Четырёхугольник ABCD вписан в окружность. Угол ABD равен 12°, угол CAD равен 71°. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 83

17)На окружности с центром O отмечены точки A и B так, что AOB = 45°. Длина меньшей дуги AB равна 10. Найдите длину большей дуги

Ответ: 70

18)На окружности с центром O отмечены точки A и B так, что AOB = 30°. Длина меньшей дуги AB равна 12. Найдите длину большей дуги.

Ответ: 132

19)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 25°. Ответ дайте в градусах.

Ответ: 65

20)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 27°. Ответ дайте в градусах.

Ответ: 63

21)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 2,5. Найдите AC, если BC = 3.

Ответ: 4

22)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 12,5. Найдите AC, если BC = 7.

Ответ: 24

23)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC = 24.

Ответ: 18

24)Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20,5. Найдите BC, если AC = 9.

Ответ: 40

25)Точка О – центр окружности, ACB = 75°. Найдите величину угла BOA (в градусах).

Ответ: 150

26)Точка О – центр окружности, ACB = 60°. Найдите величину угла BOA (в градусах).

Ответ: 120

27)Центральный угол AOB опирается на хорду AB длиной 11. При этом угол OAB равен 60°. Найдите радиус окружности.

Ответ: 11

28)Центральный угол AOB опирается на хорду AB длиной 17. При этом угол OAB равен 60°. Найдите радиус окружности.

Ответ: 17

29)Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол OAB. Ответ дайте в градусах.

Ответ: 60

30)Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 120

31)Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ABC = 109° и OAB = 48°. Найдите угол BCO. Ответ дайте в градусах.

Ответ: 61

32)Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ABC = 131° и OAB = 53°. Найдите угол BCO. Ответ дайте в градусах.

Ответ: 78

33)В угол C величиной 80° вписана окружность, которая касается сторон угла в точках A и B, точка O – центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Ответ: 100

34)В угол C величиной 73° вписана окружность, которая касается сторон угла в точках A и B, точка O – центр окружности. Найдите угол AOB. Ответ дайте в градусах.

Ответ: 107

35)Касательные в точках A и B к окружности с центром O пересекаются под углом 60°. Найдите угол ABO. Ответ дайте в градусах.

Ответ: 30

36)Касательные в точках A и B к окружности с центром O пересекаются под углом 54°. Найдите угол ABO. Ответ дайте в градусах.

Ответ: 27

37)Хорды AC и BD окружности пересекаются в точке P, BP = 30, CP = 12, DP = 20 . Найдите AP.

Ответ: 50

38)Хорды AC и BD окружности пересекаются в точке P, BP = 4, CP = 12, DP = 24. Найдите AP.

Ответ: 6

39)На окружности отмечены точки A и B так, что меньшая дуга AB равна 142°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 71

40)На окружности отмечены точки A и B так, что меньшая дуга AB равна 96°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 48

41)Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 3, AC = 12. Найдите AK.

Ответ: 6

42)Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 3, AC = 27. Найдите AK.

Ответ: 9

43)Найдите угол АСО, если его сторона СА касается окружности, О – центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 125°.

Ответ: 35

44)Найдите угол АСО, если его сторона СА касается окружности, О – центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 135°.

Ответ: 45

45)Отрезок AB = 8 касается окружности радиуса 6 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Ответ: 4

46)Отрезок AB = 24 касается окружности радиуса 7 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Ответ: 18

47)К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 15, AO = 17.

Ответ: 8

48)К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 8, AO = 10.

Ответ: 6

49)На отрезке AB выбрана точка C так, что AC = 7 и BC = 18. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.

Ответ: 24

50)На отрезке AB выбрана точка C так, что AC = 12 и BC = 8. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведѐнной из точки B к этой окружности.

Ответ: 16

51)Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 64°. Найдите величину угла OMK. Ответ дайте в градусах.

Ответ: 26

52)Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 72°. Найдите величину угла OMK. Ответ дайте в градусах.

Ответ: 18

53)Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 9. Найдите диаметр окружности

Ответ: 30

54)Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 35. Найдите диаметр окружности.

Ответ: 74

55)Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 10.

Ответ: 20

56)Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 5.

Ответ: 2,5

57)Радиус круга равен 3. Найдите его площадь, деленную на π.

Ответ: 9

58)Радиус круга равен 5. Найдите его площадь, деленную на π. 

Ответ: 25

59)Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3 : 4 : 11. Найдите радиус окружности, если меньшая из сторон равна 16.

Ответ: 16

60)Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3 : 7 : 8. Найдите радиус окружности, если меньшая из сторон равна 25.

Ответ: 25

61)В треугольнике ABC известно, что AC = 24, BC = 10, угол C равен 90°. Найдите радиус описанной окружности этого треугольника

Ответ: 13

62)В треугольнике ABC известно, что AC = 4, BC = 3, угол C равен 90°. Найдите радиус описанной окружности этого треугольника.

Ответ: 2,5

63)Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите C, если A = 64°. Ответ дайте в градусах.

Ответ: 26

64)Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите C, если A = 59°. Ответ дайте в градусах.

Ответ: 31

65)Радиус окружности с центром в точке O равен 65, длина хорды AB равна 126. Найдите расстояние от хорды AB до параллельной ей касательной k, если k и AB расположены по разные стороны от центра окружности.

Ответ: 81

66)Радиус окружности с центром в точке O равен 82, длина хорды AB равна 36. Найдите расстояние от хорды AB до параллельной ей касательной k, если k и AB расположены по разные стороны от центра окружности.

Ответ: 162

67)Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Ответ: 8

68)Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Ответ: 10

69)Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.

Ответ: 3

70)Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ = ВС и ∠ABC = 107°. Найдите величину угла ВОС. Ответ дайте в градусах

Ответ: 73

71)Найдите площадь квадрата, описанного вокруг окружности радиуса 6. 

Ответ: 144

72)Найдите площадь квадрата, описанного вокруг окружности радиуса 4. 

Ответ: 64

Смотрите также на нашем сайте:

Задание 15 ОГЭ 2022 математика 9 класс с ответами

Прогрессии задание 14 ОГЭ 2022 математика 9 класс с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Задание 1 № 366805

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	Город Гранюк	Деревня Астрелка	Хутор Южный	Город Гусевск
Цифры

Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.

Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.

Ответ: 1465.

2. Задание 2 № 366806

Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.

Решение.

Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится

пачек чая.

Таким образом, ребята должны купить 14 пачек чая.

Ответ: 14.

3. Задание 3 № 366807

Найдите площадь (в км²), которую занимает заказник.

Решение.

Площадь заказника равна:

Ответ: 351.

4. Задание 4 № 366808

Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.

Решение.

Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:

км.

Ответ: 30.

5. Задание 5 № 366809

Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.

Продукция	Цена в магазине «Вело» (руб.)	Цена в магазине «ОК» (руб.)	Срок доставки из магазина «ОК» (дни)
Подсветка для спиц
Шина вида «А»
Шина вида «Б»
Спица
Педаль вида «А»
Педаль вида «Б»
Тормоз вида «А»		нет
Тормоз вида «Б»	нет
Набор крепёжных изделий

Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?

Решение.

На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:

руб.

Ответ: 5300.

6. Задание 6 № 316314

Найдите значение выражения:

Решение.

Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.

7. Задание 7 № 317575

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?

1)

2)

3)

4)

Решение.

Заметим, что и Проверим все варианты ответа:

1) — неверно;

2) — верно;

3) — верно;

4) — верно.

Ответ указан под номером 1.

8. Задание 8 № 353586

Какое из данных ниже чисел является значением выражения

1)

2)

3)

4)

Решение.

Последовательно получим:

Ответ: 1

9. Задание 9 № 338500

При каком значении значения выражений и равны?

Решение.

Для ответа на вопрос задачи нужно решить уравнение Решим его:

Ответ: 2.

10. Задание 10 № 325450

В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.

Решение.

Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна

Ответ: 0,3.

11. Задание 11 № 311406

На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке

2)

3)

4) прямая пересекает график в точках и

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .

2) — неверно,

3) — верно, видно из графика.

4) Прямая пересекает график в точках и — верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

Ответ: 12.

12. Задание 12 № 311543

Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .

Решение.

Выразим :

Подставляя, получаем:

Ответ: 0,4.

13. Задание 13 № 338497

На каком из рисунков изображено решение неравенства

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

Решение.

Решим неравенство методом интервалов:

Правильный ответ указан под номером: 4.

14. Задание 14 № 406645

В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение.

Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.

Найдем сумму этой прогрессии:

Ответ: 377 мест.

15. Задание 15 № 340000

В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите

Решение.

Из прямоугольного треугольника по теореме Пифагора найдём

Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.

16. Задание 16 № 351463

На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.

Решение.

Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.

17. Задание 17 № 169876

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.

———-

В открытом банке иррациональный ответ.

18. Задание 18 № 350842

Найдите угол

Решение.

Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.

Ответ: 22,5

19. Задание 19 № 401617

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Ответ: 13.

20. Задание 20 № 338505

Решите неравенство

Решение.

Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение

Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).

Таким образом, ответ

Ответ:

Примечание.

Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,

21. Задание 21 № 353527

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.

Ответ: 58.

22. Задание 22 № 338288

Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.

Решение.

Упростим выражение:

По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:

График функции сводится к графику параболы с выколотой точкой

Выделим полный квадрат:

Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)

Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и

Ответ: −1; 3.

23. Задание 23 № 339395

Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.

Решение.

Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и

Ответ: 16.

24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.

Решение.

Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.

25. Задание 25 № 311926

В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .

Решение.

По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,

Площадь трапеции :

Площадь трапеции

Ответ: 9.