Задание 15 номер 339863 - Большой телефонный справочник предприятий

Примеры решения логарифмических, показательных неравенств

Статьи

Основное общее образование

Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)

Математика

Представляем вашему вниманию разбор 15 задания ОГЭ-2019 по математике.

14 ноября 2018

Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Часть 1

Задание 15

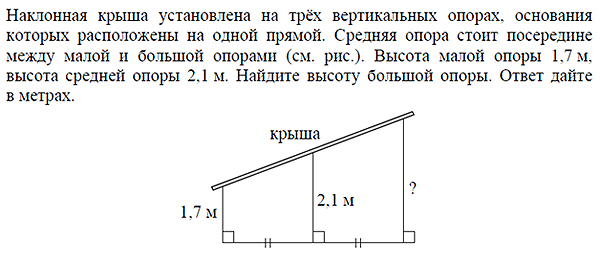
Решение

Фигура, изображенная на рисунке, является прямоугольной трапецией. Средняя опора есть не что иное, как средняя линия трапеции, длина которой вычисляется по формуле

где a, b – длины оснований. Составим уравнение:

b = 2,5.

Ответ: 2,5.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену

Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.

Купить

Номер варианта сайта alexlarin.net:

Условие:

Решите неравенство (2^{2x-x^2-1}+{1over {2^{2x-x^2}-1}}<=2.)

Решение:

Решение во вложении.

Источник — alexlarin.com.

Файл с решением:

Image icon 137_15.png

Маркер СМИ

© 2007 — 2021 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель: Никитенко Евгений Игоревич

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.

Администрация сайта готова оказать поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.

Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.

Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы.

В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.

Теория к заданию №15

Так как задания №16 основаны на теории по теме «треугольники», рассмотрим базовые понятия, определения и формулы.

Вначале предлагаю рассмотреть углы на плоскости:

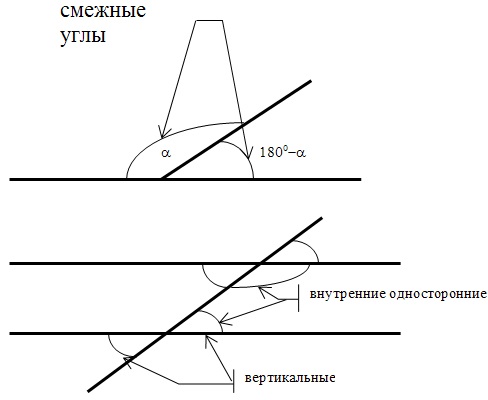
углы на плоскости

Многие задачи построены на нахождении медиан и биссектрис треугольника:

Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.

Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.

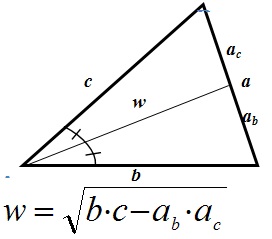биссектриса Медиана:

медиана

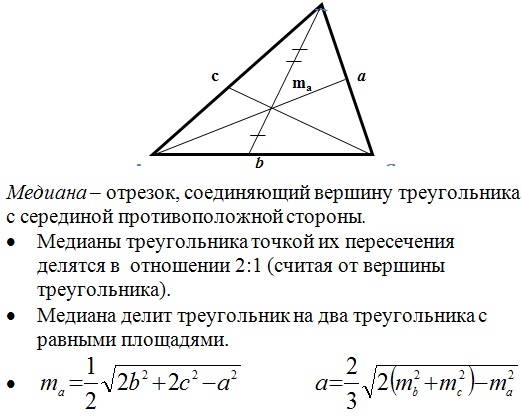
Теперь вспомним основные формулы нахождения площади треугольника:

площадь треугольника

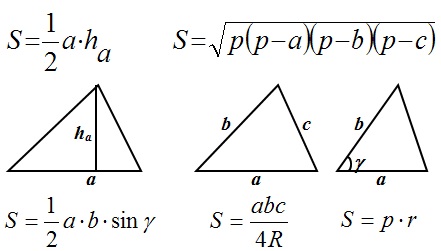
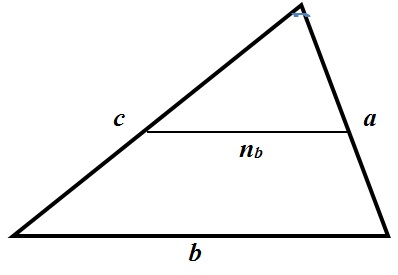
Во многих задачах встречается понятие средняя линия:

Средняя линия – отрезок, соединяющий середины двух сторон треугольника.

Средняя линия параллельна третьей стороне и равна её половине.
Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.

средняя линия

Теперь рассмотрим частные случаи треугольников — равнобедренный, равносторонний, прямоугольный.

Перейдем к рассмотрению равнобедренного треугольника:

Равнобедренный треугольник — треугольник, у которого две стороны равны.

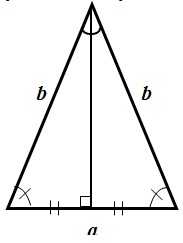
равнобедренный треугольник

Свойства равнобедренного треугольника:

Углы, при основании треугольника, равны.
Высота, проведенная из вершины, является биссектрисой и медианой.

Рассмотрим равносторонний треугольник:

Равносторонний треугольник — треугольник, у которого все стороны равны.

Все углы равны 60°.
Каждая из высот является одновременно биссектрисой и медианой.
Центры описанной и вписанной окружностей совпадают.

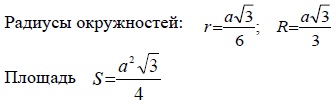равносторонний треугольник Прямоугольный треугольник:

прямоугольный треугольник

Задание OM1601o

В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.

Для решения этого задания достаточно знать правило — сумма углов в треугольнике равна 180°.

Нам известны два угла, значит можем найти третий:

180 — 73 — 48 = 59

Ответ: 59

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1602o

Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.

Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.

Средняя линия — это линия соединяющая середины сторон и параллельная основанию.

Средняя линия равна половине основания, которому она параллельна.

Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC — третьей стороне. А это в свою очередь означает, что она равна половине AC:

MN =½ • AC = 64 / 2 = 32

Ответ: 32

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1603o

В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.

Если в треугольнике две стороны равны — значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:

180 — 122 = 58°

Так как углы при основании равны, значит угол BCA равен углу BAC:

∠BCA = ∠BAC

58° = ∠BCA + ∠BAC = 2 ∠BCA

∠BCA = 58 / 2 = 29°

Ответ: 29

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1604o

Сторона равностороннего треугольника равна 10√3. Найдите его медиану.

Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:

m = ( a • √3 )/ 2

Где m — медиана в равностороннем треугольнике, а a — сторона. Таким образом, для решения данной задачи подставим значение в формулу:

m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15

Ответ: 15

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1605o

Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.

Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:

Сумма острых углов в прямоугольном треугольнике равна 90°.

Следовательно, второй острый угол равен:

90 — 23 = 67°

Ответ: 67

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1606o

В треугольнике ABC известно, что AC = 56, BM — медиана, BM = 48. Найдите AM.

Для решения необходимо вспомнить определение медианы.

Медиана — отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка.

Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^

AM = ½ AC = ½ 56 = 28

Ответ: 28

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1607o

Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.

Формула площади для прямоугольного треугольника выглядит следующим образом:

Площадь прямоугольного треугольника равна половине произведения его катетов.

Это следует из того, что один из катетов является высотой к основанию, которым является второй катет.

Исходя из вышесказанного, можем решить задачу:

S = ½ • 15 • 4 = 30

Ответ: 30

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1608o

Сторона равностороннего треугольника равна 12√3. Найдите его высоту.

Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.

Для медианы, а значит и для высоты, формулу я приводил чуть выше:

m = ( a • √3 )/ 2

Подставим значение:

m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18

Ответ: 18

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1609o

Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.

Воспользуемся теоремой Пифагора:

c² = 12² + 16² = 144 + 256 = 400

c = √400 = 20

Ответ: 20

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1610o

Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.

До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:

m = ( a • √3 )/ 2

Здесь же нам необходимо решить обратную задачу, найти a, если известно m.

Выразим a:

a = ( 2 • m ) / √3

Подставим значение:

a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22

Ответ: 22

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1611o

В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ВАС. Ответ дайте в градусах.

Для решения этого задания нужно помнить два факта:

Внутренний угол с внешним углом дают в сумме 180°
Углы при основании равнобедренного треугольника равны.

Из первого пункта следует, что угол BCA = 180 — 123 = 57°

Из второго — что ∠BCA = ∠BAC = 57°

Ответ: 57

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание 15OM21R

В треугольнике АВС известно, что угол ВАС равен 84⁰, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84⁰:2=42⁰

Ответ: 42

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник

В треугольнике два угла равны 48° и 79°. Найдите третий угол. Ответ дайте в градусах.

Решение:

Сумма углов треугольника равна 180°, поэтому третий угол равен:

180° – (48° + 79°) = 180° – 127° = 53°.

В треугольнике АВС известно, что

— биссектриса. Найдите угол ВАD.

Ответ дайте в градусах.

Решение:
, так как биссектриса делит угол пополам.

Ответ:

В треугольнике АВС известно, что АС = 54,

ВМ – медиана, ВМ = 45. Найдите АМ.

Решение: АМ = 54 : 2 = 27, так как медиана делит противоположную сторону пополам.

Ответ: АМ = 27.

В равнобедренном треугольнике АВС

с основанием АС внешний угол при

вершине С равен 132°. Найдите угол АВС.

Ответ дайте в градусах.

Решение:
.

, так как углы при основании равнобедренного треугольника равны.

, сумма углов треугольника равна 180.

Ответ:

В остроугольном треугольнике АВС

проведена высота ВН,

Найдите угол АВН.

Ответ дайте в градусах.

Решение:

Рассмотрим

значит по теореме о сумме углов треугольника

Ответ:

В треугольнике одна из сторон равна 29, а опущенная на нее высота равна — 12.

Найдите площадь треугольника.

Решение:

Площадь треугольника равна половине произведения основания на высоту, поэтому

Точки М и N являются серединами сторон

АВ и ВС треугольника АВС, сторона

АВ равна 28, сторона ВС равна 44, сторона АС равна 42. Найдите МN.

Решение:

Средняя линия треугольника параллельна одной из сторон треугольника и равна ее половине.

Ответ: 21.

Точки М и N являются серединами сторон

АВ и ВС треугольника АВС соответственно.

Отрезки АN и СМ пересекаются в точке О,

АN = 18, СМ = 21. Найдите ОМ.

Решение:

Точки М и N являются серединами сторон

АВ и ВС, значит медианы,

поэтому поэтому точкой пересечения

делятся в отношении 2 : 1, считая от вершины

Ответ: 7.

Катеты прямоугольного треугольника

равны 12 и 5. Найти гипотенузу этого треугольника.

Решение:

Квадрат гипотенузы равен сумме

квадратов катетов:

Ответ: 13.

В прямоугольном треугольнике катет и гипотенуза соответственно равны 7 и 25.

Найти второй катет этого треугольника.

Решение:

Квадрат гипотенузы равен сумме

квадратов катетов:

Ответ: 24.

В треугольнике АВС угол А равен 45°,

угол В равен 30°, ВС = .Найдите АС.

Решение:

По теореме синусов:

Ответ: 6.

В треугольнике АВС угол С равен 90°,

АС = 14, АВ = 20. Найдите .

Решение:

Синусом острого угла прямоугольного треугольника называется отношение

противолежащего катета к гипотенузе.

Ответ: 0,7.

В треугольнике АВС угол С равен 90°,

ВС = 12, АВ = 15. Найдите .

Решение:

Косинусом острого угла прямоугольного треугольника называется отношение

прилежащего катета к гипотенузе.

Ответ: 0,8.

В треугольнике АВС угол С равен 90°,

АC = 8, ВС = 5. Найдите .

Решение:

Тангенсом острого угла прямоугольного треугольника называется отношение

противолежащего катета к

прилежащему катету.

Ответ: 0,625.

Сторона равностороннего треугольника

равна .Найдите его высоту.

Решение: Высота – медиана и биссектриса.

Ответ: 18.

На стороне треугольника АВС отмечена точка D так, что АD = 5, DС = 15. Площадь треугольника АВС равна 120.

Найдите площадь треугольника ВСD.

Решение:

Площади треугольников, имеющих одинаковые высоты относятся как основания.

Ответ: 90.

В треугольнике АВС АВ = 15, ВС = 8,

Найдите площадь треугольника АВС.

Решение:

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Ответ: 50.

Синус острого угла А треугольника АВС

равен . Найдите косинус угла А.

Решение:

Ответ: 0,75

В треугольнике АВС угол С равен 90°
М – середина АВ, АВ = 42, ВС = 30.

Найдите СМ.

Решение:

В прямоугольном треугольнике середина гипотенузы является центром описанной окружности , значит

СМ = АМ = ВМ = 42 : 2 = 21

Ответ: 21

Биссектриса равностороннего треугольника

равна . Найдите его сторону.

Решение:

Любая биссектриса равностороннего треугольника является его медианой и высотой.

Ответ: 20.

Источник

Автор публикации: Томашова Е.Н.

Вариант № 4413549

1. Задание 1 № 203741. Запишите в ответе номера верных равенств.

Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.

1) [pic]

2) [pic]

3) [pic]

4) [pic]

2. Задание 2 № 314162. Одна из точек, отмеченных на координатной прямой, соответствует числу [pic] Какая это точка?

[pic]

1) точка A

2) точка B

3) точка C

4) точка D

3. Задание 3 № 28. Значение какого из выражений является числом рациональным?

В ответе укажите номер правильного варианта.

1) [pic]

2) [pic]

3) [pic]

4) [pic]

4. Задание 4 № 314548. Найдите корни уравнения [pic]

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

5. Задание 5 № 193091. Найдите значение [pic] по графику функции [pic] изображенному на рисунке.

[pic]

1) [pic]

2) [pic]

3) [pic]

4) [pic]

6. Задание 6 № 314399. Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 528?

7. Задание 7 № 338076. Найдите значение выражения [pic] если [pic]

8. Задание 8 № 338769. Решите неравенство [pic]

В ответе укажите номер правильного варианта.

1) (−∞; 9,5]

2) [−8,5; +∞)

3) [9,5; +∞)

4) (−∞; −8,5]

9. Задание 9 № 339863. Углы B и C треугольника ABC равны соответственно 65° и 85°. НайдитеBC, если радиус окружности, описанной около треугольника ABC, равен 14.

10. Задание 10 № 311956. [pic] Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если уголAOB равен 48°.

11. Задание 11 № 340981. [pic] Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 8 и 15. Найдите длину основания BC.

12. Задание 12 № 311496. [pic] Найдите тангенс угла [pic] треугольника [pic] , изображённого на рисунке.

13. Задание 13 № 119. Укажите номера верных утверждений.

1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.

2) В любом прямоугольнике диагонали взаимно перпендикулярны.

3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

Если утверждений несколько, запишите их номера в порядке возрастания.

14. Задание 14 № 314206. Бизнесмен Петров выезжает из Москвы в Санкт-Петербург на деловую встречу, которая назначена на 9:30. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.

Номер

поезда

Отправление

из Москвы

Прибытие в

Санкт-Петербург

038А

00:43

08:45

020У

00:54

09:02

016А

01:00

08:38

116С

01:00

09:06

Путь от вокзала до места встречи занимает полчаса. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят бизнесмену Петрову.

В ответе укажите номер правильного варианта.

1) 038А

2) 020У

3) 016А

4) 116С

15. Задание 15 № 146. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду. [pic]

16. Задание 16 № 317941. На предприятии работало 240 сотрудников. После модернизации производства их число сократилось до 192. На сколько процентов сократилось число сотрудников предприятия?

17. Задание 17 № 341388. Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 10 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними через 3 часа?

18. Задание 18 № 315183. [pic] На диаграмме представлены семь крупнейших по площади территории (в млн км²) стран мира.

Какое из следующих утверждений верно?

1) Монголия входит в семёрку крупнейших по площади территории стран мира.

2) Площадь территории Индии составляет 8,5 млн км².

3) Площадь Австралии больше площади Канады.

4) Площадь Канады больше площади Индии более, чем в 3 раза.

В ответе запишите номер выбранного утверждения.

19. Задание 19 № 325480. Определите вероятность того, что при бросании кубика выпало число очков, не меньшее 1.

Результат округлите до сотых.

20. Задание 20 № 318357. За 5 минут пешеход прошёл a метров. За сколько минут он пройдёт 120 метров, если будет идти с той же скоростью? Запишите соответствующее выражение.

21. Задание 21 № 311236. Разложите на множители: [pic] .

22. Задание 22 № 314508. На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?

23. Задание 23 № 340600. Постройте график функции [pic] и определите, при каких значениях параметра с прямая y = c имеет с графиком ровно одну общую точку.

24. Задание 24 № 311772. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 16. Найдите её среднюю линию.

25. Задание 25 № 314810. В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA = NA. Докажите, что данный параллелограмм — прямоугольник.

26. Задание 26 № 311705. На каждой из двух окружностей с радиусами 3 и 4 лежат по три вершины ромба. Найдите его сторону.

Вариант № 4413550

1. Задание 1 № 340581. Найдите значение выражения [pic]

2. Задание 2 № 317600. На координатной прямой отмечено число [pic] Расположите в порядке убывания числа [pic] [pic] и [pic]

В ответе укажите номер правильного варианта.

[pic]

1) [pic]

2) [pic]

3) [pic]

4) [pic]

3. Задание 3 № 311806. Укажите наибольшее из следующих чисел:

В ответе укажите номер правильного варианта.

1) [pic]

2) [pic]

3) [pic]

4) [pic]

4. Задание 4 № 314530. Найдите корни уравнения [pic]

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

5. Задание 5 № 340916. Установите соответствие между графиками функций и формулами, которые их задают.

Формулы

1) [pic]

2) [pic]

3) [pic]

4) [pic]

Графики

[pic]

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

6. Задание 6 № 340917. Выписаны первые несколько членов геометрической прогрессии: 17; 68; 272; … Найдите её четвёртый член.

7. Задание 7 № 311471. Упростите выражение [pic] и найдите его значение при [pic]

8. Задание 8 № 311949. Решите систему неравенств [pic]

На каком из рисунков изображено множество её решений?

В ответе укажите номер правильного варианта.

[pic]

9. Задание 9 № 340864. [pic] В треугольнике ABC угол A равен 90°, AC = 6, sin B= 0,3. Найдите BC.

10. Задание 10 № 314811. [pic] Точка О — центр окружности, ∠AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах).

11. Задание 11 № 316284. Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15.

12. Задание 12 № 311683. [pic] Найдите тангенс угла AOB, изображенного на рисунке.

13. Задание 13 № 169935. Какие из следующих утверждений верны?

1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.

2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.

3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.

4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.

Если утверждений несколько, запишите их номера в порядке возрастания.

14. Задание 14 № 333137. В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России с 1 сентября 2013 года.

Превышение

скорости, км/ч

21−40

41−60

61−80

81 и более

Размер штрафа, руб

500

1000

2000

5000

Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 105 км/ч на участке дороги с максимальной разрешённой скоростью 50 км/ч?

1) 500 рублей

2) 1000 рублей

3) 2000 рублей

4) 5000 рублей

15. Задание 15 № 311518. [pic] Из пункта A в пункт B вышел пешеход, и через некоторое время вслед за ним выехал велосипедист. На рисунке изображены графики движения пешехода и велосипедиста. На сколько минут меньше затратил на путь из A в B велосипедист, чем пешеход?

16. Задание 16 № 314405. В течение августа помидоры подешевели на 50%, а затем в течение сентября подорожали на 70%. Какая цена меньше: в начале августа или в конце сентября — и на сколько процентов?

17. Задание 17 № 132758. Какой угол (в градусах) образуют минутная и часовая стрелки часов в 5 ч?

18. Задание 18 № 325362. На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сливочных сухарях. Определите по диаграмме, в каком продукте содержание углеводов наибольшее.

*-к прочему относятся вода, витамины и минеральные вещества.

[pic]

1) какао

2) шоколад

3) фасоль

4) сухари

19. Задание 19 № 311324. Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?

20. Задание 20 № 341717. Площадь четырёхугольника можно вычислить по формуле [pic] , где d1 и d2 — длины диагоналей четырёхугольника, [pic] — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2 = 12, [pic] , а S = 22,5.

21. Задание 21 № 314578. Решите неравенство [pic]

22. Задание 22 № 340966. Первый рабочий за час делает на 5 деталей больше, чем второй, и выполняет заказ, состоящий из 200 деталей, на 2 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?

23. Задание 23 № 314732. Известно, что графики функций [pic] и [pic] имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.

24. Задание 24 № 311249. Основания равнобедренной трапеции равны 8 и 18, а периметр равен 56.

Найдите площадь трапеции.

25. Задание 25 № 311604. Два квадрата имеют общую вершину. Докажите, что отмеченные на рисунке отрезки и равны. [pic]

26. Задание 26 № 311252. Стороны [pic] треугольника [pic] равны [pic] соответственно. Точка [pic] расположена вне треугольника [pic] причем отрезок [pic] пересекает отрезок [pic] в точке, отличной от [pic] Известно, что треугольник с вершинами [pic] и [pic] подобен исходному. Найдите косинус угла [pic] если [pic]

Вариант № 4413551

1. Задание 1 № 314272. Вычислите: [pic]

2. Задание 2 № 314802. На координатной прямой отмечены числа a и b. Какое из следующих утверждений неверно?

[pic]

1) [pic]

2) [pic]

3) [pic]

4) [pic]

3. Задание 3 № 314389. В каком случае числа [pic] и 5 расположены в порядке возрастания?

В ответе укажите номер правильного варианта.

1) [pic]

2) [pic]

3) [pic]

4) [pic]

4. Задание 4 № 314549. Найдите корни уравнения [pic]

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

5. Задание 5 № 314688. Установите соответствие между графиками функций и формулами, которые их задают.

Графики

А)

Б)

В)

[pic]

Формулы

1) [pic]

2) [pic]

3) [pic]

4) [pic]

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

6. Задание 6 № 314620. Геометрическая прогрессия ( [pic] ) задана условиями: [pic] [pic] . Найдите [pic]

7. Задание 7 № 140. Упростите выражение [pic] , найдите его значение при [pic] ; [pic] . В ответ запишите полученное число.

8. Задание 8 № 338599. На каком рисунке изображено решение неравенства [pic]

В ответе укажите номер правильного варианта.

[pic]

1) 1

2) 2

3) 3

4) 4

9. Задание 9 № 323800. [pic] Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

10. Задание 10 № 314807. [pic] Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60° . Найдите длину хорды АВ, если радиус окружности равен 8.

11. Задание 11 № 169862. Сторона квадрата равна 10. Найдите его площадь.

12. Задание 12 № 323750. [pic] Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.

13. Задание 13 № 341410. Какое из следующих утверждений верно?

1) Точка пересечения двух окружностей равноудалена от центров этих окружностей.

2) В параллелограмме есть два равных угла.

3) Площадь прямоугольного треугольника равна произведению длин его катетов.

Если утверждений несколько, запишите их номера в порядке возрастания.

14. Задание 14 № 341333. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года.

Мощность автомобиля
(в л. с.)

Налоговая ставка
(в руб. за л. с. в год)

не более 70

71–100

101–125

126–150

151–175

176–200

201–225

226–250

свыше 250

150

Сколько рублей должен заплатить владелец автомобиля мощностью 142 л. с. в качестве налога за один год?

1) 4970

2) 45

3) 35

4) 6390

15. Задание 15 № 322037. Андрей и Иван соревновались в 50-метровом бассейне на дистанции 100 м. Графики их заплывов показаны на рисунке. По горизонтальной оси отложено время, а по вертикальной – расстояние пловца от старта. Кто быстрее проплыл первую половину дистанции? В ответе запишите, на сколько секунд быстрее он проплыл первую половину дистанции.

[pic]

17. Задание 17 № 96. [pic] От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.

18. Задание 18 № 315142. [pic] На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей.

Какое из следующих утверждений неверно?

1) Пользователей из Украины больше, чем пользователей из Казахстана.

2) Пользователей из России вдвое больше, чем пользователей из Украины.

3) Примерно треть пользователей — не из России.

4) Пользователей из Украины и Беларуси более 3 млн человек.

19. Задание 19 № 325452. Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет менее 4 очков.

20. Задание 20 № 338342. Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта позволяет формула F = 1,8C + 32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 155° по шкале Фаренгейта? Ответ округлите до десятых.

21. Задание 21 № 338713. Решите уравнение [pic]

22. Задание 22 № 341227. Расстояние между пристанями А и В равно 140 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошёл 51 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.

23. Задание 23 № 341342. Постройте график функции [pic] и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.

24. Задание 24 № 314950. [pic] Сторона ромба равна 20, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

25. Задание 25 № 181. [pic] Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.

26. Задание 26 № 340107. Середина M стороны AD выпуклого четырёхугольника равноудалена от всех его вершин. Найдите AD, если BC = 10, а углы B и C четырёхугольника равны соответственно 112° и 113°.

Вариант № 4413552

1. Задание 1 № 316340. Найдите значение выражения:

2. Задание 2 № 341665. Между какими числами заключено число ?

1) 38 и 40

2) 4 и 5

3) 77 и 79

4) 8 и 9

3. Задание 3 № 137276. Какое из следующих выражений равно ?

В ответе укажите номер правильного варианта.

4. Задание 4 № 189. Найдите корни уравнения .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

5. Задание 5 № 316316. На рисунке изображены графики функций вида . Установите соответствие между графиками и знаками коэффициентов и

ГРАФИКИ

[pic]

КОЭФФИЦИЕНТЫ

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

6. Задание 6 № 35. Дана арифметическая прогрессия: Найдите сумму первых десяти её членов.

7. Задание 7 № 311453. Упростите выражение и найдите его значение при . В ответе запишите найденное значение.

8. Задание 8 № 333109. Решите систему неравенств

На каком рисунке изображено множество её решений?

В ответе укажите номер правильного варианта.

[pic]

9. Задание 9 № 339515. [pic] Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах.

10. Задание 10 № 311479. [pic] Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?

11. Задание 11 № 169871. Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба, делённую на .

12. Задание 12 № 340841. [pic] Найдите площадь трапеции, изображённой на рисунке.

13. Задание 13 № 169933. Какие из следующих утверждений верны?

1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

2) Любые два равнобедренных треугольника подобны.

3) Любые два прямоугольных треугольника подобны.

4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.

Если утверждений несколько, запишите их номера в порядке возрастания.

14. Задание 14 № 340924. В таблице даны результаты олимпиад по математике и обществознанию в 10 «А» классе.

Номер ученика

Балл по математике

Балл по биологии

5005

5006

5011

5015

5018

5020

5025

5027

5029

5032

5041

5042

5043

5048

5054

Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 110 или хотя бы по одному предмету набрано не меньше 60 баллов.

Сколько человек из 10 «А», набравших меньше 60 баллов по математике, получат похвальные грамоты?

В ответе укажите номер правильного варианта.

1) 4

2) 5

3) 6

4) 7

15. Задание 15 № 311521. [pic] На рисунке изображен график движения автомобиля из пункта в пункт и автобуса из пункта в пункт . На сколько километров в час скорость автомобиля больше скорости автобуса?

16. Задание 16 № 341018. Спортивный магазин проводит акцию: «Любой джемпер по цене 400 рублей. При покупке двух джемперов — скидка на второй 75%». Сколько рублей придётся заплатить за покупку двух джемперов?

17. Задание 17 № 314808. [pic] Лестницу длиной 2 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?

18. Задание 18 № 315175. [pic] На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей.

Какое из следующих утверждений неверно?

1) Пользователей из Украины больше, чем пользователей из Литвы.

2) Пользователей из Украины меньше четверти общего числа пользователей.

3) Пользователей из Беларуси больше 3 миллионов.

4) Пользователей из России больше, чем из всех остальных стран, вместе взятых.

19. Задание 19 № 311505. В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A?

20. Задание 20 № 341022. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I²R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 588 ватт, а сила тока равна 7 амперам.

21. Задание 21 № 314390. Решите систему уравнений

22. Задание 22 № 314525. Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 3 часа, вернулись обратно через 7 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 5 км/ч?

23. Задание 23 № 314412. Парабола проходит через точки K(0; –5), L(4; 3), M(–3; 10). Найдите координаты её вершины.

24. Задание 24 № 340409. В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ = 86, SQ = 43.

25. Задание 25 № 311606. Два равных прямоугольника имеют общую вершину (см. рис.). Докажите, что площади треугольников и равны. [pic]

26. Задание 26 № 339886. Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1проходит через центр описанной окружности. Найдите угол BAC.

Источник