Примеры решения логарифмических, показательных неравенств
В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.
Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.
Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы.
В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.
Теория к заданию №15
Так как задания №16 основаны на теории по теме «треугольники», рассмотрим базовые понятия, определения и формулы.
Вначале предлагаю рассмотреть углы на плоскости:
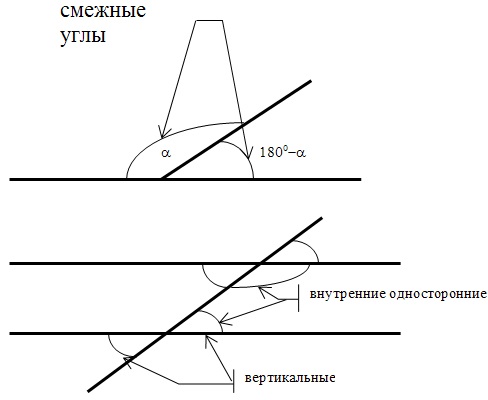
Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
- Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
- Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
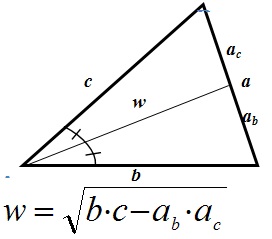 Медиана:
Медиана:
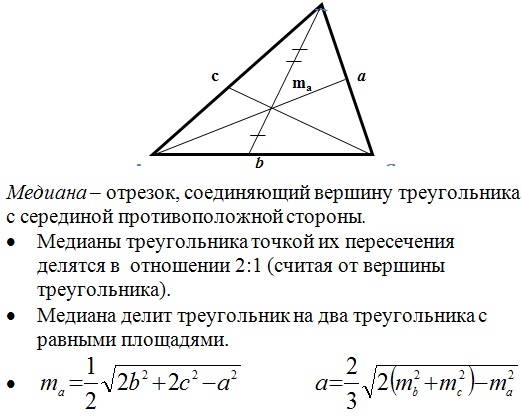
Теперь вспомним основные формулы нахождения площади треугольника:
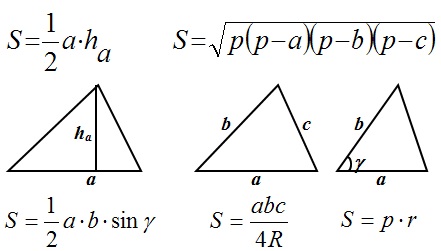
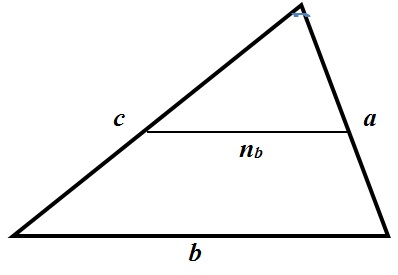
Во многих задачах встречается понятие средняя линия:
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
- Средняя линия параллельна третьей стороне и равна её половине.
- Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
Теперь рассмотрим частные случаи треугольников — равнобедренный, равносторонний, прямоугольный.
Перейдем к рассмотрению равнобедренного треугольника:
Равнобедренный треугольник — треугольник, у которого две стороны равны.
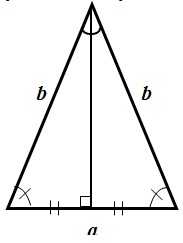
Свойства равнобедренного треугольника:
- Углы, при основании треугольника, равны.
- Высота, проведенная из вершины, является биссектрисой и медианой.
Рассмотрим равносторонний треугольник:
Равносторонний треугольник — треугольник, у которого все стороны равны.
- Все углы равны 60°.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
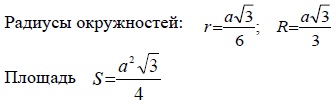 Прямоугольный треугольник:
Прямоугольный треугольник:

Задание OM1601o
В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.
Для решения этого задания достаточно знать правило — сумма углов в треугольнике равна 180°.
Нам известны два угла, значит можем найти третий:
180 — 73 — 48 = 59
Ответ: 59
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1602o
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.
Средняя линия — это линия соединяющая середины сторон и параллельная основанию.
Средняя линия равна половине основания, которому она параллельна.
Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC — третьей стороне. А это в свою очередь означает, что она равна половине AC:
MN =½ • AC = 64 / 2 = 32
Ответ: 32
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1603o
В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.
Если в треугольнике две стороны равны — значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:
180 — 122 = 58°
Так как углы при основании равны, значит угол BCA равен углу BAC:
∠BCA = ∠BAC
58° = ∠BCA + ∠BAC = 2 ∠BCA
∠BCA = 58 / 2 = 29°
Ответ: 29
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1604o
Сторона равностороннего треугольника равна 10√3. Найдите его медиану.
Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
m = ( a • √3 )/ 2
Где m — медиана в равностороннем треугольнике, а a — сторона. Таким образом, для решения данной задачи подставим значение в формулу:
m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15
Ответ: 15
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1605o
Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.
Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно, второй острый угол равен:
90 — 23 = 67°
Ответ: 67
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1606o
В треугольнике ABC известно, что AC = 56, BM — медиана, BM = 48. Найдите AM.
Для решения необходимо вспомнить определение медианы.
Медиана — отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка.
Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^
AM = ½ AC = ½ 56 = 28
Ответ: 28
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1607o
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Это следует из того, что один из катетов является высотой к основанию, которым является второй катет.
Исходя из вышесказанного, можем решить задачу:
S = ½ • 15 • 4 = 30
Ответ: 30
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1608o
Сторона равностороннего треугольника равна 12√3. Найдите его высоту.
Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( a • √3 )/ 2
Подставим значение:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18
Ответ: 18
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1609o
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Воспользуемся теоремой Пифагора:
c² = 12² + 16² = 144 + 256 = 400
c = √400 = 20
Ответ: 20
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1610o
Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.
До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:
m = ( a • √3 )/ 2
Здесь же нам необходимо решить обратную задачу, найти a, если известно m.
Выразим a:
a = ( 2 • m ) / √3
Подставим значение:
a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22
Ответ: 22
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1611o
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ВАС. Ответ дайте в градусах.
Для решения этого задания нужно помнить два факта:
- Внутренний угол с внешним углом дают в сумме 180°
- Углы при основании равнобедренного треугольника равны.
Из первого пункта следует, что угол BCA = 180 — 123 = 57°
Из второго — что ∠BCA = ∠BAC = 57°
Ответ: 57
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание 15OM21R
В треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42
pазбирался: Даниил Романович | обсудить разбор | оценить

© 2007 — 2021 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель: Никитенко Евгений Игоревич
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.
Администрация сайта готова оказать поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены 
За это задание ты можешь получить 3 балла. На решение дается около 25 минут. Уровень сложности: повышенный.
Средний процент выполнения: 2.7%
Ответом к заданию 15 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Необходимо свести сложное неравенство к простейшему. Для этого нужно знать метод замены показательных и тригонометрических функций, помня про ограничения. Знать метод интервалов и метод рационализации для логарифмических, показательных и содержащих модуль неравенств.
Задачи для практики
Задача 1
Окружность с центром $O_1$ радиусом $9$ вписана в треугольник $ABC$. Окружности с центрами $O_2$ и $O_3$ и радиусами ${81} / {25}$ и $1$, которые вписаны в углы треугольника $A$ и $C$ соответственно, касаются первой окружности внешним образом.
а) Докажите, что $∠ C=π-arctg {24} / {7}$.
б) Найдите площадь треугольника $AO_1O_3$.
Решение
a) Обозначим радиусы окружностей $r_1 = 9, r_2 = {81}/{25}, r_3 = 1$, а центры этих окружностей $O_1, O_2, O_3$ соответственно, и проведём радиусы $O_1E, O_2D, O_3F$ к точкам касания со стороной $AC$. Эти радиусы перпендикулярны касательной $AC$.
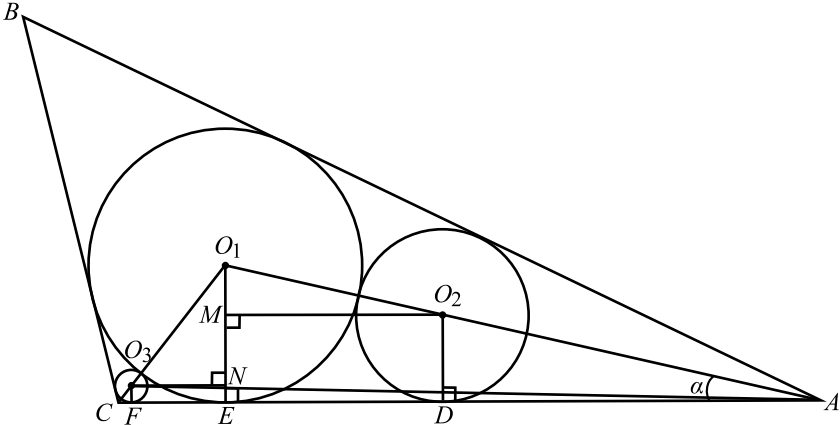
По свойству касательных, проведённых к окружности из одной точки, они образуют одинаковые углы с прямой, проходящей через центр окружности, то есть центры $O_1, O_2$ лежат на биссектрисе угла $A$, а центры $O_1, O_3$ — на биссектрисе угла $C$. Обозначим величину угла $C$ через $2β$. Тогда угол треугольника $O_1CA$ равен $β$.
Проведём $O_3N ⊥O_1E$, тогда $O_3N ‖ FE$ и $O_3N EF$ прямоугольник, $EN = r_3, O_1N = O_1E — EN = r_1 — r_3 = 8. ∠O_1CA = ∠O_1O_3N = β$ как соответственные при $O_3N ‖ AC$, секущая $CO_1$.
Треугольник $O_1O_3N$ прямоугольный, $O_3O_1= r_1 + r_3 = 10, O_3N = √{O_3O_1^2 — O_1N^2} = 6, tgβ = {O_1N}/{O_3N} = {8}/{6} = {4}/{3}$,
$tg 2β = {2 tg β}/{1 — tg^2 β} = {2 · {4}/{3}}/{1 — ({4}/{3})^2} = -{24}/{7}$.
Получили, что угол $C$ тупой. $∠C = π − arctg{24}/{7}$.
б) 1) $tg β = {O_1E}/{EC}, EC = r_1 : tg β = 9 : {4}/{3} = {27}/{4}$.
Обозначим величину угла $O_1AC$ треугольника через $α$. Найдём $EA = r_1 : tg α$.
Проведём $O_2M ⊥O_1E$, тогда аналогично пункту а) $EM = r_2$,
$O_1M = O_1E — EM = r_1 — r_2 = {144}/{25}, O_1O_2= r_1 + r_2 = {306}/{25}$.
$O_2M= √{O_1O_2^2 — O_1M^2} = {270}/{25}, tg α = {O_1M}/{O_2M} = {8}/{15}, AE = r_1 : tg α = 9 : {8}/{15} = {135}/{8}$.
$AC = AE + EC = {189}/{8}$.
$S_{AO_1O_3} = S_{AO_1C}-S_{ACO_3}={1}/{2}r_1· AC-{1}/{2}r_3·AC = {1}/{2}(r_1-r_3) ·AC = 94.5$.
Ответ: 94.5
Задача 2
Две окружности касаются внутренним образом в точке $A$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $BC$ большей окружности вторично пересекает меньшую окружность в точке $D$, отличной от $A$. Лучи $AO$ и $AD$ вторично пересекают б’ольшую окружность в точках $M$ и $N$ соответственно. Точка $C$ лежит на дуге $AN$ большей окружности, не содержащей точку $M$.
а) Докажите, что прямые $MN$ и $BC$ параллельны.
б) Известно, что $sin ∠ AOC = {2√ {2}} / {3}$. Прямые $MC$ и $AN$ пересекаются в точке $K$. Найдите отношение $NK:KA$.
Решение
а) По условию задачи выполним чертёж.
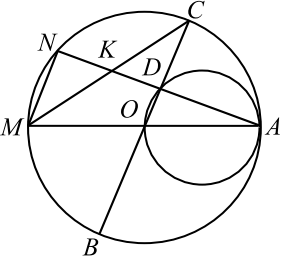
Угол $ANM$ опирается на диаметр $AM$ большей окружности, следовательно, он — прямой. Угол $ADO$ опирается на диаметр $AO$ меньшей окружности, поэтому он тоже прямой. Таким образом, прямые $MN$ и $BC$ перпендикулярны прямой $AN$, значит, они параллельны.
б) Углы $AOC$ и $AMN$ равны как соответственные при параллельных прямых $MN , BC$ и секущей $AM$. Диаметр $BC$ большей окружности перпендикулярен хорде $AN$. Значит, точка $C$ — середина дуги $AN$ (в равнобедренном треугольнике $AON$ высота $OD$ является одновременно медианой и биссектриссой). Следовательно, луч $MC$ является биссектрисой угла $AMN$ прямоугольного треугольника $AMN$, поэтому
${NK}/{KA} = {MN}/{MA} = cos∠AM N = cos∠AOC = √{1-sin^2 ∠AOC} = {1}/{3}$.
Ответ: 1:3
Задача 3
Две окружности касаются внутренним образом в точке $A$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $BC$ большей окружности вторично пересекает меньшую окружность в точке $D$, отличной от $A$. Лучи $AO$ и $AD$ вторично пересекают большую окружность в точках $M$ и $N$ соответственно. Точка $C$ лежит на дуге $AN$ большей окружности, не содержащей точку $M$.
а) Докажите, что прямые $MN$ и $BC$ параллельны.
б) Известно, что $sin ∠ AOC = {√ {5}} / {3}$. Прямые $MC$ и $AN$ пересекаются в точке $K$. Найдите отношение $NK:KA$.
Решение
а) По условию задачи выполним чертёж (см. рис.).
Угол $ANM$ опирается на диаметр $AM$ большей окружности, следовательно, он — прямой. Угол $ADO$ опирается на диаметр $AO$ меньшей окружности, поэтому он тоже прямой. Таким образом, прямые $MN$ и $BC$ перпендикулярны прямой $AN$, значит, они параллельны. б) Углы $AOC$ и $AMN$ равны как соответственные при параллельных прямых $MN$, $BC$ и секущей $AM$. Диаметр $BC$ большей окружности перпендикулярен хорде $AN$. Значит, точка $C$ — середина дуги $AN$ (в равнобедренном треугольнике $AON$ высота $OD$ является одновременно медианой и биссектриссой). Следовательно, луч $MC$ является биссектрисой угла $AMN$ прямоугольного треугольника $AMN$, поэтому
${NK} / {KA} = {MN} / {MA} = cos ∠ AMN = cos ∠ AOC = √ {1 — sin^2 ∠ AOC} = {2} / {3}$.
Ответ: 2:3
Задача 4
В треугольнике $EKP$, в котором все углы острые, проведены высоты $KB$ и $PA$. Из точек $A$ и $B$ на $KB$ и $PA$ опущены перпендикуляры $AM$ и $BN$ соответственно.
а) Докажите, что прямые $MN$ и $KP$ параллельны.
б) Найдите отношение $MN:KP$, если угол $KEP$ равен $45^°$.
Решение
а) $△POB ∼ △KOA$ по первому признаку подобия: $∠PBO = ∠OAK = 90°, ∠BOP = ∠AOK$ как вертикальные.
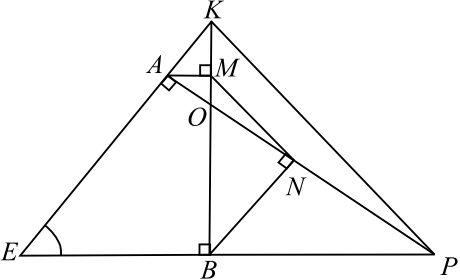
Учитывая, что в подобных треугольниках пропорциональны сходственные стороны и высоты, к ним проведённые, получим ${OP}/{OK} = {BN}/{AM}$ (1).
$△ONB ∼ △AOM$ по первому признаку подобия: $∠BNO = ∠AMO = 90°, ∠BON = ∠AOM$ как вертикальные, отсюда ${ON}/{OM} = {BN}/{AM}$ (2).
Из 1) и 2) следует ${OP}/{OK} = {ON}/{OM}$.
Следовательно, $△OPK ∼ △ONM$ по второму признаку подобия: $∠POK$ — общий, ${OP}/{ON} = {OK}/{OM}$.
Из подобия следует $∠OPK = ∠ONM$ . Углы $OPK$ и $ONM$ соответственные при прямых $PK$ и $NM$ и секущей $OP$ . Следовательно, $PK ‖ MN$ по признаку параллельности прямых.
б) В четырехугольнике $AEBO ∠AEB = 45°$ (по условию) $∠AOB=360°-(∠A +∠B +∠E ) = 360° — 225° = 135°$. В $△AOM ∠AMO = 90°, ∠AOM = 180°-135°=45°, AM=MO$.
Обозначим $OM = x$, тогда $AM = x, AO=OM√2=x√2$.
В $△OAK ∠OAK = 90°, ∠AOM = 45°$, то есть $AO = AK, AO=x√2, KO=AO√2=x√2·√2=2x$.
По доказанному в пункте а) $△OPK ∼ △ONM$, значит, ${MN}/{KP} = {OM}/{OK}$.
Пусть $OM = x, OK = 2x$.
${MN}/{KP}={x}/{2x}=1:2$
Ответ: 1:2
Задача 5
В треугольнике $MNP$, в котором все углы острые, проведены высоты $ME$ и $PF$. Из точек $F$ и $E$ на $ME$ и $PF$ опущены перпендикуляры $FK$ и $EH$ соответственно.
а) Докажите, что прямые $KH$ и $MP$ параллельны.
б) Найдите отношение $MP:KH$, если угол $MNP$ равен $60^°$.
Решение
а) $O$ — точка пересечения высот $ME$ и $PF$. $△POE ∼ △MFO$ по первому признаку подобия: $∠PEO = ∠OFM = 90°, ∠EOP = ∠FOM$ как вертикальные.
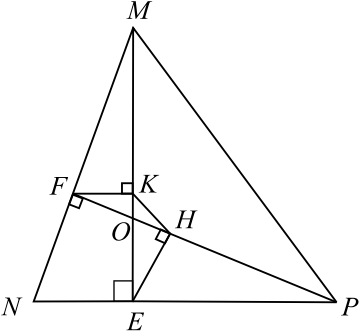
Учитывая, что в подобных треугольниках пропорциональны сходственные стороны и высоты, к ним проведённые, получим ${OP}/{OM} = {EH}/{FK}$ (1).
$△OHE ∼ △FOK$ по первому признаку подобия: $∠EHO = ∠FKO = 90°, ∠EOH = ∠FOK$ как вертикальные, отсюда ${OH}/{OK} = {EH}/{FK}$ (2).
Из 1) и 2) следует ${OP}/{OM} = {OH}/{OK}$.
Следовательно, $△OP M ∼ △OH K$ по второму признаку подобия: $∠P OM$ — общий, ${OP}/{OH} = {OM}/{OK}$.
Из подобия следует $∠OP M = ∠OH K$ . Углы $OP M$ и $OH K$ соответственные при прямых $M P$ и $K H$ и секущей $OP$ . Следовательно, $M P ‖ K H$ по признаку параллельности прямых.
б) В четырехугольнике $N FOE ∠FOE = 360° -(∠90° +∠90° +∠N ) = 360° — 240° = 120°$. В $△FOK ∠FKO = 90°, ∠FOK = 60°$, как смежный с $∠FOE = 120°$, тогда $∠OF K = 30°$.
Обозначим $OK = x$, тогда $FO = 2x$.
В $△OFM ∠M FO = 90°, ∠FOM = 60°, ∠F M O = 30°$, то есть $FO = {1}/{2}M O$, значит, $2x = {1}/{2}M O, M O = 4x$.
По доказанному в пункте а) $△OM P ∼ △OK H$, значит, ${MP}/{K H} = {M O}/{OK} $, но $M O = 4x, OK = x$, следовательно, ${M P}/{K H} = {4x}/{x} = 4 : 1$
Ответ: 4:1
Задача 6
В прямоугольном треугольнике $ABC$ точки $P$ и $K$ — середины катета $BC$ и гипотенузы $AB$ соответственно. Биссектриса угла $BAC$ пересекает прямую $KP$ в точке $R$.
а) Докажите, что точки $A$, $B$, $C$ и $R$ лежат на одной окружности.
б) Найдите отношение площадей треугольников $AKR$ и $BCR$, если $sin ∠ BAC={15} / {17}$.
Решение
а) Отрезок, соединяющий вершину прямого угла и середину гипотенузы, равен половине длины гипотенузы, то есть $AK = K B = K C. AR$ — биссектриса угла $BAC$, значит $∠CAR =∠BAR = α$.
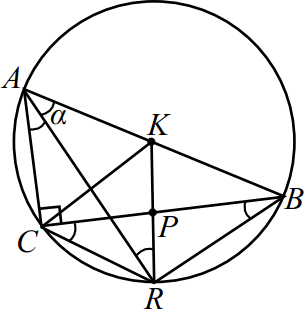
$K P$ — средняя линия $△ABC$, значит, $K P ‖ AC$.
Накрест лежащие углы $CAR$ и $ARK$ равны (секущая $AR$).
В треугольнике $AK R$ равны углы $K AR$ и $K RA$, значит $AK = K R$.
Получим $AK = K B = K C = K R$, значит точки $A, B, C$ и $R$ лежат на окружности с центром $K$.
б) $∠CBR =∠CAR$ и $∠BAR =∠BCR$ (опираются на дуги $C R$ и $BR$ соответственно), таким образом, треугольники $AK R$ и $BC R$ подобны по двум углам. По теореме синусов для треугольника $ABR$ получим ${BR}/{sin ∠RAB} = 2r$, где $r$ — радиус описанной окружности, то есть $2r = AB$. Получили ${BR}/{AB} = sin ∠RAB = sin α$.
Но коэффициент подобия треугольников $AK R$ и $BC R$ равен ${AK}/{BR} = {2AK}/{2BR} = {AB}/{2BR} = {1}/{2 sin α}$.
По условию $sin ∠BAC = sin 2α = {15}/{17}$.
Тогда $cos 2α = √{1 — ({15}/{17})^2} = {8}/{17}$,
$cos 2α = 1 — 2 sin^2 α = {8}/{17}, 2 sin^2 α = {9}/{17}$.
Площади треугольников относятся как квадрат коэффициента подобия, поэтому ${S_{AKR}}/{S_{BCR}} = ({1}/{2sin α})^2 = {1}/{2 · {9}/{17}} = {17}/{18}$.
Ответ: 17:18
Задача 7
В трапеции $ABCD$ боковая сторона $AB$ перпендикулярна основаниям. Из точки $A$ на сторону $CD$ опустили перпендикуляр $AE$. На стороне $AB$ отмечена точка $F$ так, что прямые $BE$ и $FD$ параллельны.
а) Докажите, что прямые $FC$ и $CD$ перпендикулярны.
б) Найдите отношение $BE:FD$, если угол $BCD$ равен $120°$.
Решение
Продолжим боковые стороны трапеции $AB$ и $DC$ до пересечения в точке $S$. Ясно, что $BC$ — меньшее основание, иначе перпендикуляр $AE$ будет падать на продолжение $CD$, а не на саму сторону, что противоречит условию.
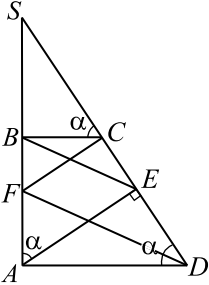
а) Для доказательства перпендикулярности прямых $FC$ и $CD$ достаточно доказать подобие треугольников $SFC$ и $SAE$.
Заметим, что $△SBC ∼ △SAD$ по двум углам ($∠SBC = ∠SAD = 90°, ∠S$ — общий). Тогда ${SB}/{SA} = {SC}/{SD}$, то есть $SB·SD = SA · SC$.
С другой стороны, $△SBE ∼ △SFD$ по двум углам: $∠SBE = ∠SFD$ как соответственные углы при параллельных прямых $BE$ и $FD$ и секущей $SA, ∠S$ — общий.
Тогда ${SB}/{SF} = {SE}/{SD}$, отсюда $SB · SD = SF · SE$.
Следовательно, $SA · SC = SB · SD = SF · SE$.
Тогда $SA · SC = SF · SE, {SA}/{SF} = {SE}/{SC}$.
Отсюда $△SAE ∼ △SFC$ по второму признаку.
Тогда $∠SCF = ∠SEA = 90°, FC ⊥ SD$, что и требовалось доказать.
б) Из подобия треугольников $SBE$ и $SFD$ следует ${BE}/{FD} = {SB}/{SF}$.
$∠BCS = 180° — ∠BCD = 60°, SB = SC sin 60° = {√3}/{2}SC. ∠CSF = 90° — ∠BCS = 30°$. Из $△SFC$ следует, что $CS = SF cos 30° = SF {√3}/{2}$. Тогда $SB = {√3}/{2}SC ={√3}/{2}·{√3}/{2}SF; {SB}/{SF} = {3}/{4} = 0.75$.
Ответ: 0.75
Задача 8
В трапеции $ABCD$ боковая сторона $AB$ перпендикулярна основаниям. Из точки $A$ на сторону $CD$ опустили перпендикуляр $AE$. На стороне $AB$ отмечена точка $F$ так, что прямые $CD$ и $CF$ перпендикулярны. а) Докажите, что прямые $BE$ и $FD$ параллельны. б) Найдите отношение $BE:FD$, если угол $BCD$ равен $150°$.
Решение
Продолжим боковые стороны трапеции $AB$ и $DC$ до пересечения в точке $S$. а) Для доказательства параллельности прямых $BE$ и $FD$ достаточно доказать, что треугольники $SBE$ и $SFD$ подобны (см. рис.). Ясно, что $BC$ — меньшее основание, иначе перпендикуляр $AE$ будет опускаться на продолжение $CD$, а не на саму сторону, что противоречит условию. По условию $FC⊥ CD$ и $AE⊥ CD$, отсюда $FC∥ AE$. Заметим: в прямоугольных треугольниках $SCB$, $SFC$, $SAE$ и $SDA$ угол $S$ общий, значит, $∠ SCB=∠ SFC=∠ SAE=∠ SDA=α$. В каждом из рассматриваемых треугольников выразим $sin α$. $▵ SCB$: $sin α={SB} / {SC}$ (1) $▵ SFC$: $sin α={SC} / {SF}$ (2) $▵ SAE$: $sin α={SE} / {SA}$ (3) $▵ SDA$: $sin α={SA} / {SD}$ (4) Перемножив (1) на (2) и (3) на (4), получим ${SB} / {SC}⋅ {SC} / {SF}=sin^2 α$, ${SB} / {SF}=sin^2α$, ${SE} / {SA}⋅ {SA} / {SD}=sin^2α$, ${SE} / {SD}=sin^2α$. Отсюда ${SB} / {SF}={SE} / {SD}$. Имеем: две стороны $▵ SBE$ пропорциональны двум сторонам $▵ SFD$ и между ними угол $S$ — общий, значит, $▵ SBE∼ ▵ SFD$ по второму признаку подобия. Из подобия следует равенство соответственных углов $SEB$ и $SDF$ при прямых $BE$, $FD$ и секущей $SD$, следовательно, по признаку параллельности прямых $BE∥ FD$. б) Из подобия треугольников $SBE$ и $SFD$ следует ${BE} / {FD}={SB} / {SF}$. В пункте а) доказано ${SB} / {SF}=sin^2 α$, $∠ BCD+α=180°$, $α=180°-150°=30°$. ${BE} / {FD}={SB} / {SF}=sin^2 30°=0{,}5^2=0{,}25$.
Ответ: 0.25
Задача 9
В треугольнике $ABC$ проведена высота $AH$ и медиана $AM$. $AB=2$, $AC=√ {21}$, $AM=2{,}5$.
а) Докажите, что треугольник $ABC$ прямоугольный.
б) Вычислите $HM$.
Решение
а) Достроим треугольник $ABC$ до параллелограмма $ABDC$, как показано на рисунке.
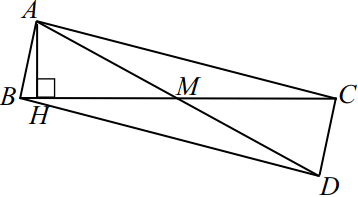
По свойству параллелограмма, верно равенство $2(AB^2 + AC^2) = AD^2 + BC^2$, или $2(AB^2 + AC^2) = (2AM)^2 + BC^2$. Так как по условию $AB = 2, AC = √{21}, AM = 2.5$, то $2(22 + √{21}^2) = (2 · 2.5)^2 + BC^2$, откуда $BC = 5$. Если диагонали параллелограмма равны, то он — прямоугольник, значит, $∠BAC = 90°$ и $△ABC$ прямоугольный.
б) В прямоугольном треугольнике $ABC$ выразим площадь двумя способами: $2S = AB · AC, 2S = BC · AH$, приравнивая правые части этих равенств, находим $AH = {AB·AC}/{BC} = {2 · √21}/{5}$. Катет $HM$ найдём из прямоугольного треугольника $AHM$ по теореме Пифагора: $HM = √{AM^2 − AH^2} = √{2.5^2 −({2 · √21}/{5})^2} = √{{25}/{4} − {84}/{25}} = √{{625 − 336}/{100}} = {17}/{10} = 1.7$.
Ответ: 1.7
Задача 10
В треугольнике $ABC$ точки $K$, $N$, $F$ — середины сторон $AC$, $AB$ и $BC$ соответственно. $AH$ — высота треугольника $ABC$, $∠ CAB=60^°$, $∠ ACB=15^°$.
а) Докажите, что точки $K$, $N$, $F$ и $H$ лежат на одной окружности.
б) Найдите $FH$, если $BC=4√ 3$.
Решение
а) $∠ABC = 180° — (60° + 15°) = 105°$.
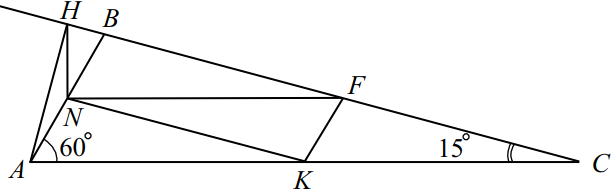
$NH$ — медиана в прямоугольном треугольнике $AHB$, отсюда $NH = NB = AN$.
$∠ABH = 75°, ∠BHN = ∠NBH$ как углы при основании равнобедренного треугольника $NBH , ∠NBH = 75°$.
$FK = {1}/{2}AB, NK = {1}/{2}BC , FN = {1}/{2}AC$ по свойству средней линии треугольника, тогда $△FKN ∼ △ABC$ по трём пропорциональным сторонам, следовательно, $∠NKF = ∠ABC = 105°$.
В четырёхугольнике $NHFK$ найдём сумму противоположных углов: $∠FKN + ∠FHN = 105° + 75° = 180°$, значит, около этого четырёхугольника можно описать окружность, что и требовалось доказать.
б) По теореме синусов для $△NFK: {NK}/{sin∠NFK} = 2R$, где $R$ — радиус окружности, проходящей через точки $K , N , F$ и $H$. Так как $NK = {1}/{2}BC$, то ${BC}/{2sin60°} = 2R = {4√3}/{2} : {√3}/{2} = 4$.
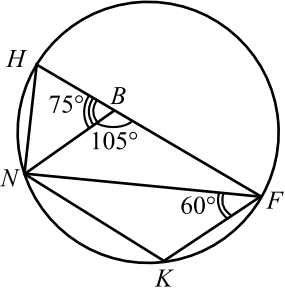
В равнобедренном треугольнике $HNB$ $∠N = 180° — 75°· 2 = 30°$. $∠BNF = ∠BAC = 60°$ как соответственные углы при параллельных прямых $NF$ и $AC$ и секущей $AB$.
В $△HNF ∠HNF = ∠HNB + ∠BNF = 30° + 60° = 90°$, значит $HF$ — диаметр описанной окружности, $HF = 2R = 4$.
Ответ: 4
Задача 11
Две окружности касаются внешним образом в точке $K$. Прямая $AB$ касается первой окружности в точке $A$, а второй — в точке $B$. Прямая $BK$ пересекает первую окружность в точке $D$, прямая $AK$ пересекает вторую окружность в точке $C$.
а) Докажите, что прямые $AD$ и $BC$ параллельны.
б) Найдите площадь $▵ AKB$, если известно, что радиусы окружностей равны $8$ и $2$.
Решение
а) Общая касательная, проведенная к окружностям в точке $K$, пересекает $AB$ в точке $M$. По свойству касательных, проведенных из одной точки, $AM = K M$ и $K M = BM$. Треугольник $AK B$, у которого медиана $K M$ равна половине стороны $AB$, к которой она проведена, прямоугольный, $∠AK B = 90°$. Вписанный угол $AK D$ прямой, поэтому он опирается на диаметр $AD$, значит, $AD ⊥ AB$. Аналогично, получаем, что $BC ⊥ AB$. Следовательно, прямые $AD$ и $BC$ параллельны.
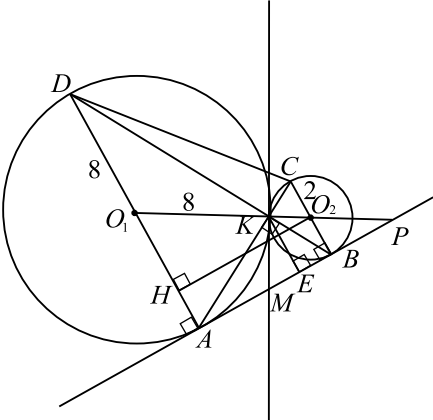
б) Пусть первая окружность имеет радиус $8$, а вторая — радиус $2$.
Проведём $O_2H ⊥ AD$, тогда $O_2HAB$ — прямоугольник и $AH = O_2 B = 2, AB = O_2 H$. Из $△O_1O_2H$ получим $O_2 H^2 = O_1O_2^2 — O_1H^2 = (2 + 8)^2 — (8 — 2)^2 = 64, O_2 H = 8 = AB$.
$△O_2PB ∼ △O_1O_2H$ (по двум углам), ${O_2B}/{O_2P} = {O_1H}/{O_1O_2}; {2}/{O_2P} = {8 — 2}/{8 + 2}; O_2P = {10}/{3}$.
Проведём высоту $KE$ в $△AKB$, получим, что $△O_2BP ∼ △KEP$ (по двум углам). ${KE}/{O_2B} = {KP}/{O_2P}; {KE}/{2} = {2 + {10}/{3}}/{{10}/{3}}; KE = 1.6 · 2 = 3.2$.
$S_{AKB} = {1}/{2}AB · KE = {1}/{2} · 8 · 3.2 = 12.8$.
Ответ: 12.8
Задача 12
Две окружности с центрами $O_1$ и $O_2$ пересекаются в точках $M$ и $N$, причём точки $O_1$ и $O_2$ лежат по разные стороны от прямой $MN$. Продолжение диаметра $AM$ первой окружности и хорды $AN$ этой же окружности пересекают вторую окружность в точках $C$ и $B$ соответственно.
а) Докажите, что треугольники $ANC$ и $O_1MO_2$ подобны.
б) Найдите $MC$, если угол $CMB$ равен углу $NMA$, а радиус второй окружности в $1{,}5$ раза больше радиуса первой и $MN=3$.
Решение
а) $O_1O_2 ⊥ MN, O_1O_2$ делит хорду $MN$ и дугу $MN$ второй окружности пополам.
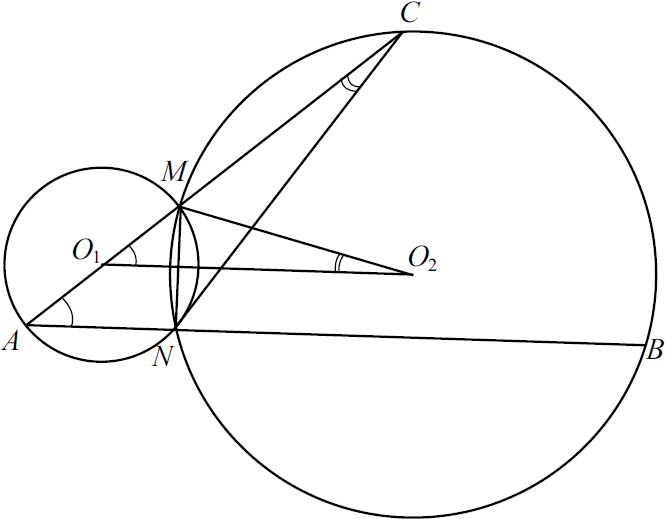
$∠MO_2O_1 = {1}/{2} ︶ MN; ∠ACN = ∠MCN = {1}/{2} ︶ MN = ∠MO_2O_1. ∠ANM = 90°$ как угол, опирающийся на диаметр, поэтому $AN ⊥ MN, O_1O_2 ⊥ MN$, значит, $AN‖ O_1O_2$, откуда $∠MO_1O_2 = ∠MAN$. Итак, $△ACN∼△MO_1O_2$ по двум углам.
б) Введём обозначения: $r$ — радиус меньшей окружности, тогда $1.5r$ -радиус большей окружности.
$∠MNB = 180° — ∠MNA = 90°$, тогда $MB$ — диаметр окружности (проходит через $O_2$). $∠MCB = 90°$, как вписанный угол, опирающийся на диаметр.
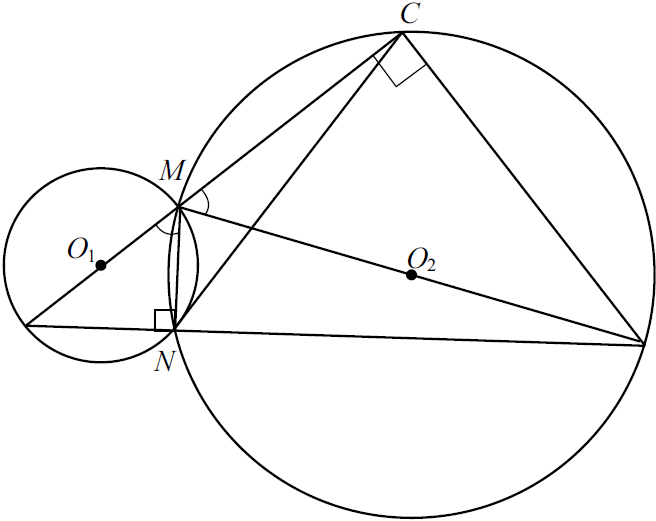
Значит, $△AMN∼△BCM$ по двум углам.
Значит, ${MC}/{MN} = {MB}/{AM}={2⋅3r}/{2⋅2r} =1.5.$
$MC= 1.5·3 = 4.5$.
Ответ:
Задача 13
Две окружности с центрами $O_1$ и $O_2$ пересекаются в точках $M$ и $N$, причём точки $O_1$ и $O_2$ лежат по разные стороны от прямой $MN$. Продолжение диаметра $AM$ первой окружности и хорды $AN$ этой же окружности пересекают вторую окружность в точках $C$ и $B$ соответственно.
а) Докажите, что треугольники $ANC$ и $O_1MO_2$ подобны.
б) Найдите $MC$, если угол $CMB$ равен углу $NMA$, а радиус второй окружности в $2{,}5$ раза больше радиуса первой и $MN=2$.
Решение
а) $O_1O_2 ⊥ MN, O_1O_2$ делит хорду $MN$ и дугу $MN$ второй окружности пополам.
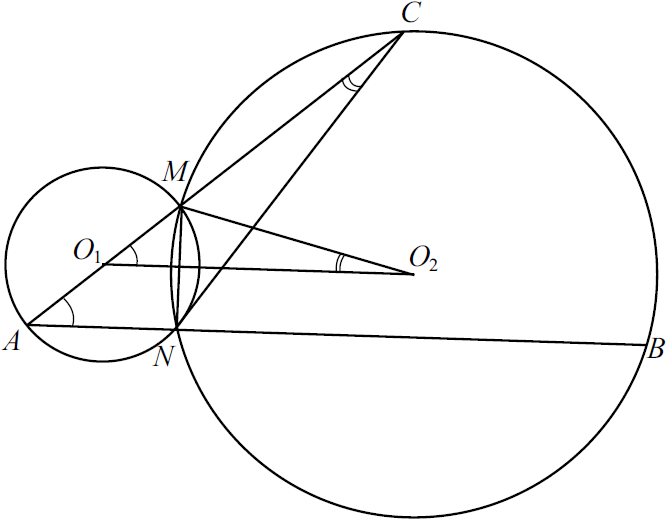
$∠MO_2O_1 = {1}/{2} ︶ MN; ∠ACN = ∠MCN = {1}/{2} ︶ MN = ∠MO_2O_1. ∠ANM = 90°$ как угол, опирающийся на диаметр, поэтому $AN ⊥ MN, O_1O2 ⊥ MN$, значит, $AN‖ O_1O_2$, откуда $∠MO_1O_2 = ∠MAN$. Итак, $△ACN∼△MO_1O_2$ по двум углам.
б) Введём обозначения: $r$ — радиус меньшей окружности, тогда $2.5r$ -радиус большей окружности.
$∠MNB = 180° — ∠ANM = 90°$, тогда $MB$ — диаметр второй окружности (проходит через $O_2$). $∠MCB = 90°$, как вписанный угол, опирающийся на диаметр.
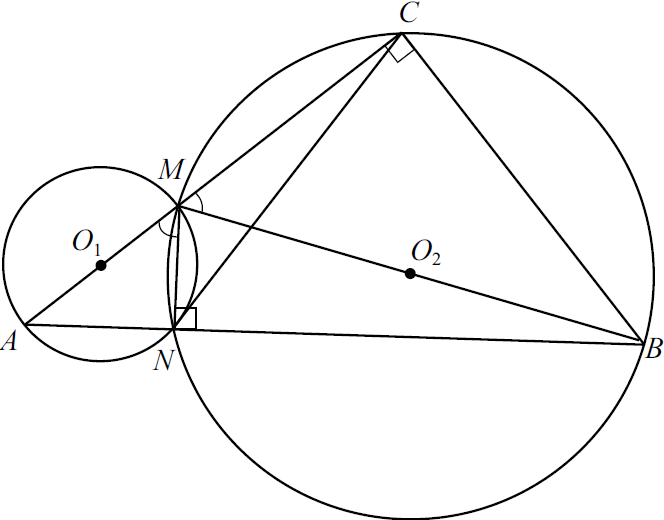
Значит, $△AMN∼△BCM$ по двум углам ($∠ANM = ∠MCB = 90°, ∠AMN = ∠CMB$)
${MC}/{MN} = {MB}/{AM}$, но ${MB}/{AM} = {2·2.5r}/{2r} = 2.5$.
$MC = 2.5·MN = 5$.
Ответ: 5
Задача 14
Основания трапеции равны $7$ и $34$, а её диагонали равны $9$ и $40$.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите площадь трапеции.
Решение
а) Проведём $CE ‖ BD$. $E$ — точка пересечения прямых $AD$ и $CE$. $BCED$ — параллелограмм: $BC ‖ DE$ как прямые, содержащие основания трапеции, $BD ‖ CE$ по построению. $BC = DE = 7$, тогда $AE = AD + DE = 34 + 7 = 41$. Заметим, что для треугольника $ACE$ выполнена теорема Пифагора: $AC^2 + CE^2 = AE^2$, следовательно, $AC ⊥ CE$, а так как $CE ‖ BD$, то $BD ⊥ AC$.
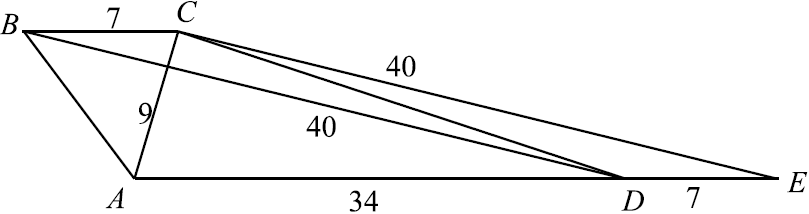
б) Проведём высоту $CH$ трапеции. $CH$ также является высотой треугольника $ACE. CH = {AC·CE}/{AE} = {9·40}/{41}. S_{ABCD} = {AD + BC}/{2}·CH = {34 + 7}/{2}·{9·40}/{41} = 9·20 = 180$.
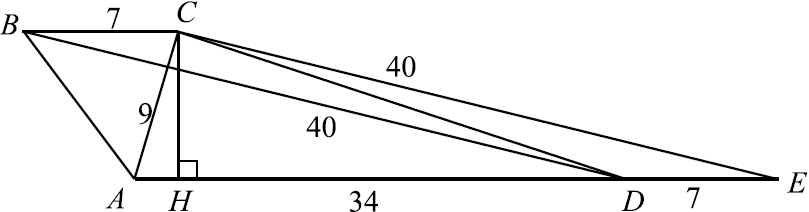
Ответ: 180
Задача 15
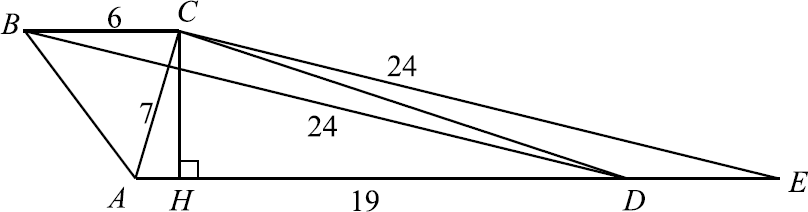
Основания трапеции равны $6$ и $19$, а её диагонали равны $7$ и $24$.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите площадь трапеции.
Решение
а) Проведём $CE ‖ BD$. $E$ — точка пересечения прямых $AD$ и $CE$. $BCED$ — параллелограмм: $BC ‖ DE$ как прямые, содержащие основания трапеции, $BD ‖ CE$ по построению. $BC = DE = 6$, тогда $AE = AD + DE = 19 + 6 = 25$. Заметим, что для треугольника $ACE$ выполнена теорема Пифагора: $AC^2 + CE^2 = AE^2$, следовательно, $AC ⊥ CE$, а так как $CE ‖ BD$, то $BD ⊥ AC$.
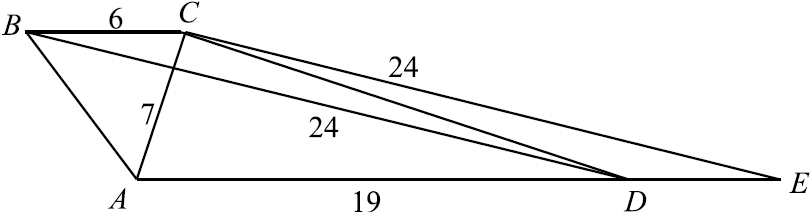
б) Проведём высоту $CH$ трапеции. $CH$ также является высотой треугольника $ACE. CH = {AC·CE}/{AE} = {7·24}/{25}. S_{ABCD} = {AD + BC}/{2}·CH = {19 + 6}/{2}·{7·24}/{25} = 7·12 = 84$.
Ответ: 84
Задача 16
Две окружности касаются внутренним образом в точке $K$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $AB$ большей окружности вторично пересекает меньшую окружность в точке $C$, отличной от $K$. Лучи $KO$ и $KC$ вторично пересекают большую окружность в точках $D$ и $E$ соответственно. Точка $B$ лежит на дуге $EK$ большей окружности, не содержащей точку $D$.
а) Докажите, что прямые $DE$ и $AB$ параллельны.
б) Известно, что $sin∠ KOB = {√ {15}} / {8}$. Прямые $DB$ и $EK$ пересекаются в точке $L$. Найдите отношение $EL:LK$.
Решение
а) $KD$ — диаметр большей окружности ($O ∈ KD$), $O_1$ — центр меньшей окружности, $l$ — общая касательная двух окружностей, проходящая через точку $K$ (см. рис.). $O_1 ∈ KD$. Действительно, $OK⊥ l$, $O_1K⊥ l$ как радиусы, проведённые в точку касания, значит, точки $O$, $K$, $O_1$ лежат на луче $KO$. $∠ DEK=∠ OCK=90°$ как вписанные углы, опирающиеся на диаметры $DK$ и $OK$ соответственно. $C∈ EK$, следовательно, $DE∥ AB$ как два перпендикуляра к одной прямой.
б) Так как диаметр $AB$, перпендикулярный хорде $EK$, делит её пополам, то $CE=CK$, следовательно, $⌣ KB=⌣ BE$ (см. рис.). Угол $EDK$ вписанный, опирается на дугу $EK$, а угол $BOK$ — центральный, опирается на половину дуги $EK$, следовательно, $∠ EDK=∠ BOK=α$; $∠ EDB=∠ BDK$ как вписанные углы, опирающиеся на равные дуги, тогда $DL$ — биссектриса треугольника $DEK$, а по свойству биссектрисы ${EL} / {LK}={DE} / {DK}=cos α=√ {1-sin^2 α}$.
${EL} / {LK}=√ {1-{15} / {64}}={7} / {8}$.
Ответ: fsm78
Задача 17
В остроугольном треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены перпендикуляры $ME$ и $KH$ соответственно. а) Докажите, что прямые $EH$ и $AC$ параллельны. б) Найдите отношение $EH$ к $AC$, если $cos ∠ ABC = {√ {2}} / {4}$.
Решение
а) По условию задачи выполним чертёж.
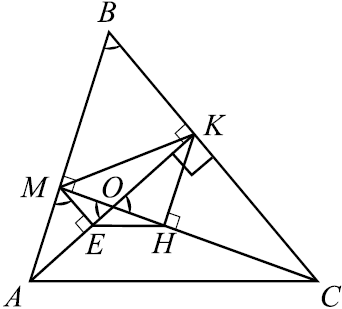
Рассмотрим треугольники $KOH$ и $KOC$. Они подобны как прямоугольные треугольники с общим острым углом $∠KOC$. Значит, ${OH}/{OK} = {OK}/{OC} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OH = {OK^2}/{OC} = ({OK}/{OC})^2·OC = k^2·OC$. Следовательно, ${OH}/{OC} = k^2$.
Аналогично, треугольник $MOE$ подобен треугольнику $MOA$. Тогда ${OE}/{OM} = {OM}/{OA} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OE = {OM^2}/{OA} = ({OM}/{OA})^2·OA = k^2·OA$. Следовательно, ${OE}/{OA} = k^2$.
Треугольники $OEH$ и $OAC$ подобны, так как $∠AOC$ — общий и ${OH}/{OC} = {OE}/{OA}$. Тогда $∠OEH = ∠OAC$, эти углы являются соответственными при прямых $EH$ и $AC$ и секущей $AO$, значит $EH || AC$.
б) Из подобия $OEH$ и $OAC$ следует, что ${EH}/{AC} = {OH}/{OC} = {OE}/{OA} = k^2$. Тогда ${EH}/{AC} = cos^2∠ABC = {2}/{16} ={1}/{8}$. Таким образом, $EH : AC = 1 : 8$.
Ответ: 1:8
Задача 18
В остроугольном треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены перпендикуляры $ME$ и $KH$ соответственно. а) Докажите, что прямые $EH$ и $AC$ параллельны. б) Найдите отношение $EH$ к $AC$, если $sin ∠ ABC = {√ {3}} / {3}$.
Решение
а) По условию задачи выполним чертёж.
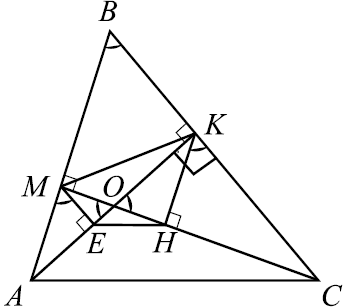
Рассмотрим треугольники $KOH$ и $KOC$. Они подобны как прямоугольные треугольники с общим острым углом $∠KOC$. Значит, ${OH}/{OK} = {OK}/{OC} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OH = {OK^2}/{OC} = ({OK}/{OC})^2·OC = k^2·OC$. Следовательно, ${OH}/{OC} = k^2$.
Аналогично, треугольник $MOE$ подобен треугольнику $MOA$. Тогда ${OE}/{OM} = {OM}/{OA} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OE = {OM^2}/{OA} = ({OM}/{OA})^2·OA = k^2·OA$. Следовательно, ${OE}/{OA} = k^2$.
Треугольники $OEH$ и $OAC$ подобны, так как $∠AOC$ — общий и ${OH}/{OC} = {OE}/{OA}$. Тогда $∠OEH = ∠OAC$, эти углы являются соответственными при прямых $EH$ и $AC$ и секущей $AO$, значит $EH || AC$.
б) Из подобия $OEH$ и $OAC$ следует, что ${EH}/{AC} = {OH}/{OC} = {OE}/{OA} = k^2$. Тогда ${EH}/{AC} = cos^2∠ABC = 1-sin^2∠ABC = 1-{1}/{3} ={2}/{3}$. Таким образом, $EH : AC = 2 : 3$.
Ответ: 2:3
Задача 19
Один из двух отрезков, соединяющих середины противоположных сторон выпуклого четырёхугольника, делит его площадь пополам, а другой — в отношении ${6} / {7}$. а) Докажите, что данный четырёхугольник есть трапеция. б) Укажите отношение двух оснований этой трапеции (меньшего к большему).
Решение
а) Рассмотрим выпуклый четырёхугольник ABCD. Пусть M — середина AB, N — середина CD, причём $S_{AMND} = S_{MBCN}$. Проведём AN и BN. Заметим, что $S_{AMN} = {1}/{2}AM · MNsin∠AMN ={1}/{2}MB · MNsin∠BMN = S_{BMN}$, так как $AM = MB, sin∠AMN = sin(180° — ∠AMN) = sin∠BMN$.
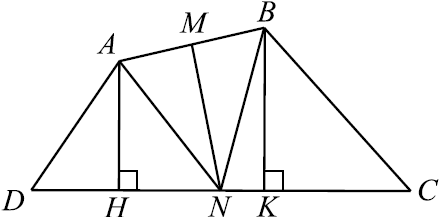
Отсюда $S_{AND} = S_{BNC}(S_{AND} = S_{AMND} — S_{AMN}, S_{BNC} = S_{MBCN} — S_{MBN})$.
Опустим в $△AND$ высоту AH, в $△BNC$ — высоту BK.
Получим ${1}/{2}DN·AH = {1}/{2}NC·BK$, при этом $DN = NC$. Следовательно, $AH = BK$. Но тогда в четырёхугольник $AHKB ∠AHK = ∠BKH = 90°, AH = BK$, то есть $AHKB$ — прямоугольник. Значит, $AB ‖ HK, AB ‖ DC$.
Для доказательства того, что ABCD — трапеция, необходимо доказать, что две другие стороны не параллельны, то есть AD не параллельна BC. Предположим противное. Тогда ABCD — параллелограмм, но тогда отрезок, соединяющий середины AD и BC, делит площадь ABCD пополам, что противоречит условию, так как отношение полученных площадей должно равняться 6 : 7. Отсюда верно ABCD — трапеция.
б) По условию EF делит площадь ABCD на площади, отношение которых равно 6 : 7, а именно $S_{ABFE} : S_{EFCD} = 6 : 7$.
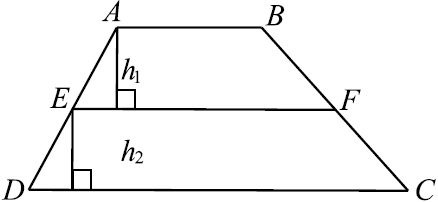
$EF$ — средняя линия, $EF = {AB + CD}/{2}$.
Надо найти AB : CD.
$S_{ABFE} = {AB + EF}/{2}·h_1, S_{EFCD} = {EF + CD}/{2}·h_2$, где $h_1$ — высота $ABFE$, $h_2$ — высота $EFCD$.
Учитывая, что $AB ‖ CD$, а $EF$ — средняя линия и $EF ‖ AB$ и $EF ‖ CD$, то расстояние от $EF$ до $AB$ и от $EF$ до $CD$ равны, то есть $h_1 = h_2$.
Следовательно, ${S_{ABFE}}/{S_{EFCD}} = {{AB + EF}/{2}}/{{EF + CD}/{2}} = {AB + EF}/{EF + CD} = {AB + {AB + CD}/{2}}/{{AB + CD}/{2} + CD} = {3AB + CD}/{3CD + AB}, {3AB + CD}/{3CD + AB} = {6}/{7}, 21AB + 7CD = 18CD + 6AB, 15AB = 11CD, {AB}/{CD} = {11}/{15}$.
$AB : CD = 11 : 15$.
Ответ: 11:15
Задача 20
В выпуклом четырёхугольнике середины противоположных сторон соединены отрезками, причём один из них делит этот четырёхугольник на две равновеликие фигуры, а другой делит площадь в отношении $9:13$. а) Доказать, что данный четырёхугольник является трапецией. б) Найти отношение меньшего основания этой трапеции к большему.
Решение
а) Рассмотрим выпуклый четырёхугольник $QMNP$ (см. рис.). Пусть $E$ — середина $MQ$, $F$ — середина $NP$, причём $S_{MNFE}=S_{EFPQ}$.
Проведём отрезки $EN$ и $EP$. Заметим, что
$S_{▵ EFN}={1} / {2} EF⋅ FNsin ∠ EFN={1} / {2} EF⋅ FP sin ∠ EFP=S_{▵ EFP}$, так как $NF=FP$ и $sin ∠ EFN=sin (180°-∠ EFN)=sin ∠ EFP$. Отсюда $S_{▵ MNE}=S_{▵ EPQ}$ ($S_{▵ MNE}=S_{MNFE}-S_{▵ EFN}$, $S_{▵ EPQ}=S_{EFPQ}-S_{▵ EFP}$). Опустим в $▵ MNE$ высоту $NN_1$, в $▵ EPQ$ — высоту $PP_1$. Получим: ${1} / {2} ME⋅ NN_1={1} / {2} EQ⋅ PP_1$. Но $ME=EQ$, следовательно, $NN_1=PP_1$. Но тогда в четырёхугольнике $N_1NPP_1$ $∠ NN_1P_1=∠ N_1P_1P=90°$, $NN_1=PP_1$, то есть $N_1NPP_1$ — прямоугольник. Значит, $N_1P_1∥ NP$, $MQ∥ NP$. Из предположения о том, что $MN∥ QP$, следует, что отрезок, соединяющий середины сторон $MN$ и $QP$, делит параллелограмм $MNPQ$ на две равновеликие фигуры. Но по условию это не так. Значит, $MN ∦ QP$. Следовательно, $MNPQ$ — трапеция. б) По условию второй отрезок $AB$ делит четырёхугольник так, что площадь $ANPB$ относится к площади $ABQM$ как $9:13$ (см. рис.).
$S_{ANPB}:S_{ABQM}=9:13$. $AB$ — средняя линия трапеции, $AB={NP+MQ} / {2}$. $S_{ANPB}={AB+NP} / {2}⋅ h_1$; $S_{ABQM}={AB+MQ} / {2}⋅ h_2$, где $h_1$ — высота трапеции $ANPB$; $h_2$ — высота трапеции $ABQM$. Так как $NP∥ MQ$, а $AB$ — средняя линия и $AB∥ NP$ и $AB∥ MQ$, то расстояния от $AB$ до $NP$ и от $AB$ до $MQ$ равны, то есть $h_1=h_2$. Отсюда, ${S_{ANPB}} / {S_{ABQM}}={{NP+AB} / {2}} / {{AB+MQ} / {2}}={NP+{NP+MQ} / {2}} / {{NP+MQ} / {2}+MQ}={3NP+MQ} / {3MQ+NP}$, ${3NP+MQ} / {3MQ+NP}={9} / {13}$, $39NP+13MQ=27MQ+9NP$, $30NP=14MQ$, ${NP} / {MQ}={14} / {30}={7} / {15}$.
Ответ: 7:15
В задании №15 требуется решить один из видов неравенств:
- Рациональное неравенство
- Показательное неравенство
- Логарифмическое неравенство, возможно с переменным основанием
- Неравенство с радикалом
- Смешанное неравенство, которое может содержать несколько видов одновременно
Получить за решение этого задания можно 2 первичных балла. Потерять 1 балл можно при вычислительной ошибке, при условии что имеется верная последовательность всех шагов решения.

Статистика выполнения задания №15 по годам
Метод интервалов
- Решить уравнение f(x) = 0. Так мы найдем нули функции, от которых зависит знак неравенства. Удобно отдельно находить нули числителя и нули знаменателя.
- Отметить все полученные корни (нули) на координатной прямой. Получим несколько интервалов.
- Выяснить знак (плюс или минус) функции f(x) на самом правом интервале. Для этого достаточно подставить в f(x) очень большое число, например, 1 000 000.
- Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется. НО есть одно исключение:
При переходе через нуль мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная.
Пример 1
При переходе через нуль мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная.

Пример 2
В случае с нестрогими неравенствами( ≤ , ≥) необходимо включить в интервалы точки, которые являются решением уравнения f(x) = 0;

Пример 3

Знак правого промежутка был «+». Единственный нуль четной степени x = 10, поэтому в этом нуле знак не меняем. В остальных нулях чередуем знак.
Пример неравенства №15

Оформление задачи №15
Еще больше крутых лайфхаков, разборов, ловушек ЕГЭ и теории в нашей группе вконтакте и инсте преподавателей @turboegemath и @turbomath

-
-
Предмет:
Геометрия
-
Автор:
ashantitate174
-
Создано:
3 года назад
Ответы
Знаешь ответ? Добавь его сюда!
-
-
Геометрия1 минута назад
Помогите пожалуйста решить задачу по геометрии, умоляю
-
Математика5 минут назад
У скольких трехзначных чисел сумма цифр равна произведению цифр? Помогите пожалуйста!!!
-
Физика10 минут назад
Помогите решить задачу
-
Литература15 минут назад
ПОМОГИТЕ ПОЖАЛУЙСТА. ПЕЧОРИН, ГЕРОЙ НАШЕГО ВРЕМЕНИ (княжна Мери)
-
Химия20 минут назад
Предмет: Химия. Тема: Классификация неорганических соединений
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Вы не можете общаться в чате, вы забанены.
Чтобы общаться в чате подтвердите вашу почту
Отправить письмо повторно
Вопросы без ответа
-
Математика2 часа назад
ПРЯМОУГОЛЬНИК ДЛИНОЙ 8 СМ И ШИРИНОЙ 4 СМ. КАК ПРОВЕСТИ В ЭТОМ ПРЯМОУГОЛЬНИКЕ ОТРЕЗОК,ЧТОБЫ ПОЛУЧИЛОСЬ ДВА ТРЕУГОЛЬНИКА.
-
Английский язык4 часа назад
перестройте предложения текста употребив страдательный залог.
In January the Fernwood Company hired Martha as a secretary, In March the company sent her to school to study statistics and programming. In April the boss gave her the first raise. Just two months later, he promoted Martha to the position of supervisor of her department. In November they invited her to take a position in the company’s office in England. And in December the company gave her the new job in London.
Топ пользователей
-

Fedoseewa27
20959
-

Sofka
7417
-

vov4ik329
5113
-

DobriyChelovek
4631
-

olpopovich
3461
-

zlatikaziatik
3125
-

manbenzopila
2540
-
Udachnick
1867
-

Zowe
1683
-

NikitaAVGN
1210
Войти через Google
или
Запомнить меня
Забыли пароль?
У меня нет аккаунта, я хочу Зарегистрироваться
Выберите язык и регион
Русский
Россия
English
United States

How much to ban the user?
1 hour
1 day
В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.
Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.
Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы.
В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.
Теория к заданию №15
Так как задания №16 основаны на теории по теме “треугольники”, рассмотрим базовые понятия, определения и формулы.
Вначале предлагаю рассмотреть углы на плоскости:

Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
- Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
- Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
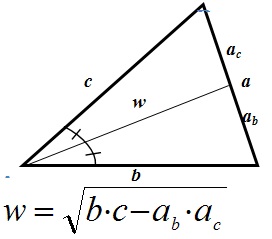 Медиана:
Медиана:

Теперь вспомним основные формулы нахождения площади треугольника:
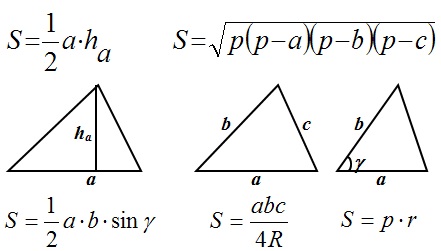
Во многих задачах встречается понятие средняя линия:
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
- Средняя линия параллельна третьей стороне и равна её половине.
- Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.

Теперь рассмотрим частные случаи треугольников – равнобедренный, равносторонний, прямоугольный.
Перейдем к рассмотрению равнобедренного треугольника:
Равнобедренный треугольник – треугольник, у которого две стороны равны.

Свойства равнобедренного треугольника:
- Углы, при основании треугольника, равны.
- Высота, проведенная из вершины, является биссектрисой и медианой.
Рассмотрим равносторонний треугольник:
Равносторонний треугольник – треугольник, у которого все стороны равны.
- Все углы равны 60°.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
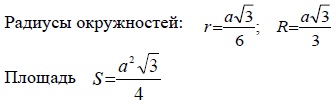 Прямоугольный треугольник:
Прямоугольный треугольник:

В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.
Для решения этого задания достаточно знать правило – сумма углов в треугольнике равна 180°.
Нам известны два угла, значит можем найти третий:
180 – 73 – 48 = 59
Ответ: 59
pазбирался: Даниил Романович | обсудить разбор | оценить
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.
Средняя линия – это линия соединяющая середины сторон и параллельная основанию.
Средняя линия равна половине основания, которому она параллельна.
Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC – третьей стороне. А это в свою очередь означает, что она равна половине AC:
MN =½ • AC = 64 / 2 = 32
Ответ: 32
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.
Если в треугольнике две стороны равны – значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:
180 – 122 = 58°
Так как углы при основании равны, значит угол BCA равен углу BAC:
∠BCA = ∠BAC
58° = ∠BCA + ∠BAC = 2 ∠BCA
∠BCA = 58 / 2 = 29°
Ответ: 29
pазбирался: Даниил Романович | обсудить разбор | оценить
Сторона равностороннего треугольника равна 10√3. Найдите его медиану.
Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
m = ( a • √3 )/ 2
Где m – медиана в равностороннем треугольнике, а a – сторона. Таким образом, для решения данной задачи подставим значение в формулу:
m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15
Ответ: 15
pазбирался: Даниил Романович | обсудить разбор | оценить
Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.
Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно, второй острый угол равен:
90 – 23 = 67°
Ответ: 67
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике ABC известно, что AC = 56, BM — медиана, BM = 48. Найдите AM.
Для решения необходимо вспомнить определение медианы.
Медиана – отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка.
Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^
AM = ½ AC = ½ 56 = 28
Ответ: 28
pазбирался: Даниил Романович | обсудить разбор | оценить
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Это следует из того, что один из катетов является высотой к основанию, которым является второй катет.
Исходя из вышесказанного, можем решить задачу:
S = ½ • 15 • 4 = 30
Ответ: 30
pазбирался: Даниил Романович | обсудить разбор | оценить
Сторона равностороннего треугольника равна 12√3. Найдите его высоту.
Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( a • √3 )/ 2
Подставим значение:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18
Ответ: 18
pазбирался: Даниил Романович | обсудить разбор | оценить
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Воспользуемся теоремой Пифагора:
c² = 12² + 16² = 144 + 256 = 400
c = √400 = 20
Ответ: 20
pазбирался: Даниил Романович | обсудить разбор | оценить
Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.
До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:
m = ( a • √3 )/ 2
Здесь же нам необходимо решить обратную задачу, найти a, если известно m.
Выразим a:
a = ( 2 • m ) / √3
Подставим значение:
a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22
Ответ: 22
pазбирался: Даниил Романович | обсудить разбор | оценить
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ВАС. Ответ дайте в градусах.
Для решения этого задания нужно помнить два факта:
- Внутренний угол с внешним углом дают в сумме 180°
- Углы при основании равнобедренного треугольника равны.
Из первого пункта следует, что угол BCA = 180 – 123 = 57°
Из второго – что ∠BCA = ∠BAC = 57°
Ответ: 57
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42
pазбирался: Даниил Романович | обсудить разбор | оценить
Практические задачи с ответами для задания №15 ОГЭ 2022 по математике для 9 класса, произвольный треугольник, равнобедренный и равносторонний треугольник.
Скачать задание 15 с ответами
Задание 15 ОГЭ 2022 математика 9 класс с ответами треугольники и трапеция:
1)В треугольнике два угла равны 70° и 44°. Найдите его третий угол. Ответ дайте в градусах.
Правильный ответ: 66
2)В треугольнике два угла равны 45° и 86°. Найдите его третий угол. Ответ дайте в градусах.
Правильный ответ: 49
3)В треугольнике ABC угол C равен 125°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Правильный ответ: 55
4)В треугольнике ABC угол C равен 179°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Правильный ответ: 1
5)В треугольнике ABC известно, что BAC = 88°, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Правильный ответ: 44
6)В треугольнике ABC известно, что BAC = 10°, AD – биссектриса. Найдите угол CAD. Ответ дайте в градусах.
Правильный ответ: 5
7)В остроугольном треугольнике ABC проведена высота BH, BAC = 16°. Найдите угол ABH. Ответ дайте в градусах.
Правильный ответ: 74
8)В остроугольном треугольнике ABC проведена высота BH, BAC = 80°. Найдите угол ABH. Ответ дайте в градусах.
Правильный ответ: 10
9)В треугольнике ABC известно, что АС = 14, BM – медиана, BM = 10. Найдите АM.
Правильный ответ: 7
10)В треугольнике ABC известно, что АС = 58, BM – медиана, BM = 37. Найдите АM.
Правильный ответ: 29
11)Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 21, сторона BC равна 22, сторона AC равна 30. Найдите MN.
Правильный ответ: 15
12)Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 66, сторона BC равна 37, сторона AC равна 52. Найдите MN.
Правильный ответ: 26
13)Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB = 48, AC = 42, MN = 28. Найдите AM.
Правильный ответ: 16
14)Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB = 18, AC = 36, MN = 16. Найдите AM.
Правильный ответ: 10
15)Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN = 27, CM = 15. Найдите CO.
Правильный ответ: 10
16)Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN = 30, CM = 9. Найдите AO.
Правильный ответ: 20
17)У треугольника со сторонами 6 и 30 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 15. Чему равна высота, проведённая ко второй стороне?
18)У треугольника со сторонами 12 и 6 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 3. Чему равна высота, проведённая ко второй стороне?
19)В треугольнике ABC проведены медиана BM и высота BH. Известно, что AC = 10 и BC = BM. Найдите AH.
20)В треугольнике ABC проведены медиана BM и высота BH. Известно, что AC = 40 и BC = BM. Найдите AH.
21)В треугольнике АВС углы А и С равны 30° и 70° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
22)В треугольнике АВС углы А и С равны 10° и 64° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
23)Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит еѐ пополам. Найдите сторону АВ, если сторона АС равна 38.
24)Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит еѐ пополам. Найдите сторону АС, если сторона АВ равна 12.
25)Катеты прямоугольного треугольника равны 9 и 12. Найдите гипотенузу этого треугольника.
26)Катеты прямоугольного треугольника равны 7 и 24. Найдите гипотенузу этого треугольника.
27)Один из острых углов прямоугольного треугольника равен 21°. Найдите его другой острый угол. Ответ дайте в градусах.
28)Один из острых углов прямоугольного треугольника равен 43°. Найдите его другой острый угол. Ответ дайте в градусах.
29)В прямоугольном треугольнике катет и гипотенуза равны 7 и 25 соответственно. Найдите другой катет этого треугольника.
30)В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.
31)В треугольнике ABC угол C равен 90°, M – середина стороны AB, AB = 26, BC = 18 . Найдите CM.
32)В треугольнике ABC известно, что AC = 30, BC = 16, угол C равен 90°. Найдите радиус описанной около этого треугольника окружности.
33)Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
34)Диагональ прямоугольника образует угол 86° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
35)Один из углов параллелограмма равен 61°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
36)Один из углов параллелограмма равен 102°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах.
37)Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 33°. Ответ дайте в градусах.
36)Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 16°. Ответ дайте в градусах.
37)Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 70° и 35°. Найдите меньший угол параллелограмма.
38)Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол параллелограмма.
39)Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 10, BD = 22, AB = 9. Найдите DO.
40)Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 16, BD = 20, AB = 5. Найдите DO.
41)В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 8.
42)В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 11.
43)Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
44)Сумма двух углов равнобедренной трапеции равна 94°. Найдите больший угол трапеции. Ответ дайте в градусах.
45)Сумма двух углов равнобедренной трапеции равна 268°. Найдите меньший угол трапеции. Ответ дайте в градусах.
46)Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 62° и 9° соответственно.
47)Основания трапеции равны 2 и 9. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из еѐ диагоналей.
48)Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 54°. Найдите угол B этой трапеции. Ответ дайте в градусах.
49)Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно
50)Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
51)Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 12, BF = 5.
Смотрите также на нашем сайте:
-
Прогрессии задание 14 ОГЭ 2022 математика 9 класс с ответами
-
Тренировочные варианты ОГЭ 2022 по математике 9 класс
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задание 1 № 366805
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Город Гранюк | Деревня Астрелка | Хутор Южный | Город Гусевск |
| Цифры |
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.
Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.
Ответ: 1465.
2. Задание 2 № 366806
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Решение.
Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится
 пачек чая.
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
3. Задание 3 № 366807
Найдите площадь (в км2), которую занимает заказник.
Решение.

Площадь заказника равна:

Ответ: 351.
4. Задание 4 № 366808
Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Решение.
Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
 км.
км.
Ответ: 30.
5. Задание 5 № 366809
Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | |||
| Шина вида «А» | |||
| Шина вида «Б» | |||
| Спица | |||
| Педаль вида «А» | |||
| Педаль вида «Б» | |||
| Тормоз вида «А» | нет | ||
| Тормоз вида «Б» | нет | ||
| Набор крепёжных изделий |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Решение.
На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:
 руб.
руб.
Ответ: 5300.
6. Задание 6 № 316314
Найдите значение выражения: 
Решение.
Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.
7. Задание 7 № 317575
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?
1) 
2) 
3) 
4) 
Решение.
Заметим, что  и
и  Проверим все варианты ответа:
Проверим все варианты ответа:
1)  — неверно;
— неверно;
2)  — верно;
— верно;
3)  — верно;
— верно;
4)  — верно.
— верно.
Ответ указан под номером 1.
8. Задание 8 № 353586
Какое из данных ниже чисел является значением выражения 
1) 
2) 
3) 
4) 
Решение.
Последовательно получим:


Ответ: 1
9. Задание 9 № 338500
При каком значении  значения выражений
значения выражений  и
и  равны?
равны?
Решение.
Для ответа на вопрос задачи нужно решить уравнение  Решим его:
Решим его:

Ответ: 2.
10. Задание 10 № 325450
В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
Решение.
Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна 
Ответ: 0,3.
11. Задание 11 № 311406
На рисунке изображён график функции  . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке 
2) 
3) 
4) прямая  пересекает график в точках
пересекает график в точках  и
и 
Решение.
Проверим каждое из утверждений.
1) Функция возрастает на промежутке  — неверно, функция убывает на промежутке
— неверно, функция убывает на промежутке  и затем возрастает на
и затем возрастает на  .
.
2)  — неверно,
— неверно, 

3)  — верно, видно из графика.
— верно, видно из графика.
4) Прямая  пересекает график в точках
пересекает график в точках  и
и  — верно, видно из графика.
— верно, видно из графика.
Таким образом, неверные утверждения находятся под номерами 1 и 2.
Ответ: 12.
12. Задание 12 № 311543
Площадь любого выпуклого четырехугольника можно вычислять по формуле  , где
, где  — длины его диагоналей, а
— длины его диагоналей, а  угол между ними. Вычислите
угол между ними. Вычислите  , если
, если  .
.
Решение.
Выразим  :
:

Подставляя, получаем:

Ответ: 0,4.
13. Задание 13 № 338497
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.

1) 1
2) 2
3) 3
4) 4
Решение.
Решим неравенство методом интервалов:


Правильный ответ указан под номером: 4.
14. Задание 14 № 406645
В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Решение.
Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.
Найдем сумму этой прогрессии:

Ответ: 377 мест.
15. Задание 15 № 340000

В прямоугольном треугольнике  катет
катет  , а высота
, а высота  , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна  Найдите
Найдите 
Решение.
Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Углы  и
и  равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.
16. Задание 16 № 351463
 На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что  Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Решение.
Пусть длина большей дуги  равна
равна  Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.
17. Задание 17 № 169876
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на  .
.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.
———-
В открытом банке иррациональный ответ.
18. Задание 18 № 350842

Найдите угол 
Решение.

Искомый угол  опирается на
опирается на  часть окружности:
часть окружности:  . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.
. Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е. 
Ответ: 22,5
19. Задание 19 № 401617
Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.
Ответ: 13.
20. Задание 20 № 338505
Решите неравенство 
Решение.
Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение 


Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).
Таким образом, ответ 
Ответ: 
Примечание.
Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно, 
21. Задание 21 № 353527
Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли  г 21-процентного раствора, тогда взяли и
г 21-процентного раствора, тогда взяли и  г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится
г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится  г, а во втором —
г, а во втором —  г Концентрация получившегося раствора равна
г Концентрация получившегося раствора равна  или 58%.
или 58%.
Ответ: 58.
22. Задание 22 № 338288
Постройте график функции  И определите, при каких значениях
И определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение.
Упростим выражение:
По теореме, обратной теореме Виета, корни уравнения  равны -1 и -2 соответственно, тогда по формуле
равны -1 и -2 соответственно, тогда по формуле  , получаем:
, получаем:  . Имеем:
. Имеем:

График функции сводится к графику параболы  с выколотой точкой
с выколотой точкой 
Выделим полный квадрат:

Следовательно, график функции получается из графика функции  сдвигом на
сдвигом на  . (см. рис.)
. (см. рис.)

Из графика видно, что прямая  имеет с графиком функции ровно одну общую точку при
имеет с графиком функции ровно одну общую точку при  и
и 
Ответ: −1; 3.
23. Задание 23 № 339395
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.
Решение.
 Угол
Угол  — вписанный, он равен 90° и опирается на дугу
— вписанный, он равен 90° и опирается на дугу  следовательно, дуга
следовательно, дуга  равна 180°, значит, хорда
равна 180°, значит, хорда  — диаметр окружности и
— диаметр окружности и 
Ответ: 16.
24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Решение.
Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.
25. Задание 25 № 311926
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
Решение.

По свойству равнобедренной трапеции  следовательно, треугольники
следовательно, треугольники  и
и  равны. Так как
равны. Так как  =
=  треугольники
треугольники  и
и  равнобедренные, следовательно,
равнобедренные, следовательно,  и
и  — соответствующие медианы этих треугольников. Значит,
— соответствующие медианы этих треугольников. Значит,  Отрезок
Отрезок  соединяет середины диагоналей трапеции, следовательно,
соединяет середины диагоналей трапеции, следовательно,  и прямые
и прямые 
 и
и  параллельны, поэтому,
параллельны, поэтому,  — трапеция. Проведём
— трапеция. Проведём  — высоту трапеции
— высоту трапеции  и
и  — высоту трапеции
— высоту трапеции  . Прямоугольные треугольники
. Прямоугольные треугольники  и
и  подобны, значит,
подобны, значит, 
Площадь трапеции  :
: 
Площадь трапеции 


Ответ: 9.
