За это задание ты можешь получить 3 балла. На решение дается около 25 минут. Уровень сложности: повышенный.
Средний процент выполнения: 2.7%
Ответом к заданию 15 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Необходимо свести сложное неравенство к простейшему. Для этого нужно знать метод замены показательных и тригонометрических функций, помня про ограничения. Знать метод интервалов и метод рационализации для логарифмических, показательных и содержащих модуль неравенств.
Задачи для практики
Задача 1
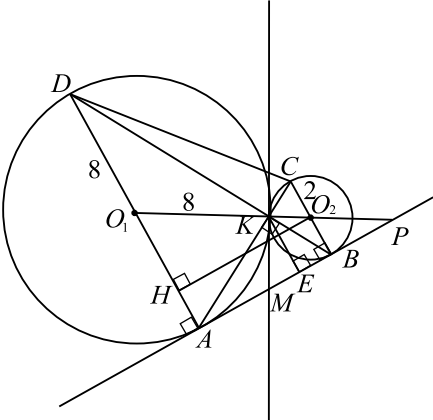
Окружность с центром $O_1$ радиусом $9$ вписана в треугольник $ABC$. Окружности с центрами $O_2$ и $O_3$ и радиусами ${81} / {25}$ и $1$, которые вписаны в углы треугольника $A$ и $C$ соответственно, касаются первой окружности внешним образом.
а) Докажите, что $∠ C=π-arctg {24} / {7}$.
б) Найдите площадь треугольника $AO_1O_3$.
Решение
a) Обозначим радиусы окружностей $r_1 = 9, r_2 = {81}/{25}, r_3 = 1$, а центры этих окружностей $O_1, O_2, O_3$ соответственно, и проведём радиусы $O_1E, O_2D, O_3F$ к точкам касания со стороной $AC$. Эти радиусы перпендикулярны касательной $AC$.
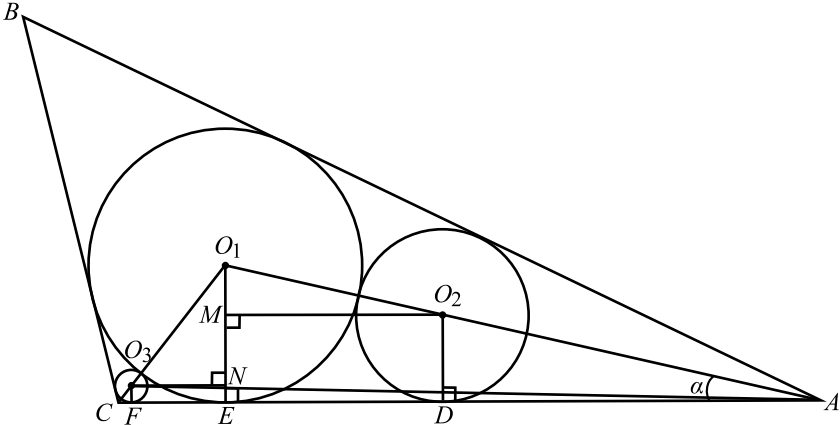
По свойству касательных, проведённых к окружности из одной точки, они образуют одинаковые углы с прямой, проходящей через центр окружности, то есть центры $O_1, O_2$ лежат на биссектрисе угла $A$, а центры $O_1, O_3$ — на биссектрисе угла $C$. Обозначим величину угла $C$ через $2β$. Тогда угол треугольника $O_1CA$ равен $β$.
Проведём $O_3N ⊥O_1E$, тогда $O_3N ‖ FE$ и $O_3N EF$ прямоугольник, $EN = r_3, O_1N = O_1E — EN = r_1 — r_3 = 8. ∠O_1CA = ∠O_1O_3N = β$ как соответственные при $O_3N ‖ AC$, секущая $CO_1$.
Треугольник $O_1O_3N$ прямоугольный, $O_3O_1= r_1 + r_3 = 10, O_3N = √{O_3O_1^2 — O_1N^2} = 6, tgβ = {O_1N}/{O_3N} = {8}/{6} = {4}/{3}$,
$tg 2β = {2 tg β}/{1 — tg^2 β} = {2 · {4}/{3}}/{1 — ({4}/{3})^2} = -{24}/{7}$.
Получили, что угол $C$ тупой. $∠C = π − arctg{24}/{7}$.
б) 1) $tg β = {O_1E}/{EC}, EC = r_1 : tg β = 9 : {4}/{3} = {27}/{4}$.
Обозначим величину угла $O_1AC$ треугольника через $α$. Найдём $EA = r_1 : tg α$.
Проведём $O_2M ⊥O_1E$, тогда аналогично пункту а) $EM = r_2$,
$O_1M = O_1E — EM = r_1 — r_2 = {144}/{25}, O_1O_2= r_1 + r_2 = {306}/{25}$.
$O_2M= √{O_1O_2^2 — O_1M^2} = {270}/{25}, tg α = {O_1M}/{O_2M} = {8}/{15}, AE = r_1 : tg α = 9 : {8}/{15} = {135}/{8}$.
$AC = AE + EC = {189}/{8}$.
$S_{AO_1O_3} = S_{AO_1C}-S_{ACO_3}={1}/{2}r_1· AC-{1}/{2}r_3·AC = {1}/{2}(r_1-r_3) ·AC = 94.5$.
Ответ: 94.5
Задача 2
Две окружности касаются внутренним образом в точке $A$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $BC$ большей окружности вторично пересекает меньшую окружность в точке $D$, отличной от $A$. Лучи $AO$ и $AD$ вторично пересекают б’ольшую окружность в точках $M$ и $N$ соответственно. Точка $C$ лежит на дуге $AN$ большей окружности, не содержащей точку $M$.
а) Докажите, что прямые $MN$ и $BC$ параллельны.
б) Известно, что $sin ∠ AOC = {2√ {2}} / {3}$. Прямые $MC$ и $AN$ пересекаются в точке $K$. Найдите отношение $NK:KA$.
Решение
а) По условию задачи выполним чертёж.
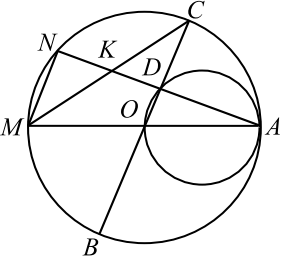
Угол $ANM$ опирается на диаметр $AM$ большей окружности, следовательно, он — прямой. Угол $ADO$ опирается на диаметр $AO$ меньшей окружности, поэтому он тоже прямой. Таким образом, прямые $MN$ и $BC$ перпендикулярны прямой $AN$, значит, они параллельны.
б) Углы $AOC$ и $AMN$ равны как соответственные при параллельных прямых $MN , BC$ и секущей $AM$. Диаметр $BC$ большей окружности перпендикулярен хорде $AN$. Значит, точка $C$ — середина дуги $AN$ (в равнобедренном треугольнике $AON$ высота $OD$ является одновременно медианой и биссектриссой). Следовательно, луч $MC$ является биссектрисой угла $AMN$ прямоугольного треугольника $AMN$, поэтому
${NK}/{KA} = {MN}/{MA} = cos∠AM N = cos∠AOC = √{1-sin^2 ∠AOC} = {1}/{3}$.
Ответ: 1:3
Задача 3
Две окружности касаются внутренним образом в точке $A$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $BC$ большей окружности вторично пересекает меньшую окружность в точке $D$, отличной от $A$. Лучи $AO$ и $AD$ вторично пересекают большую окружность в точках $M$ и $N$ соответственно. Точка $C$ лежит на дуге $AN$ большей окружности, не содержащей точку $M$.
а) Докажите, что прямые $MN$ и $BC$ параллельны.
б) Известно, что $sin ∠ AOC = {√ {5}} / {3}$. Прямые $MC$ и $AN$ пересекаются в точке $K$. Найдите отношение $NK:KA$.
Решение
а) По условию задачи выполним чертёж (см. рис.).
Угол $ANM$ опирается на диаметр $AM$ большей окружности, следовательно, он — прямой. Угол $ADO$ опирается на диаметр $AO$ меньшей окружности, поэтому он тоже прямой. Таким образом, прямые $MN$ и $BC$ перпендикулярны прямой $AN$, значит, они параллельны. б) Углы $AOC$ и $AMN$ равны как соответственные при параллельных прямых $MN$, $BC$ и секущей $AM$. Диаметр $BC$ большей окружности перпендикулярен хорде $AN$. Значит, точка $C$ — середина дуги $AN$ (в равнобедренном треугольнике $AON$ высота $OD$ является одновременно медианой и биссектриссой). Следовательно, луч $MC$ является биссектрисой угла $AMN$ прямоугольного треугольника $AMN$, поэтому
${NK} / {KA} = {MN} / {MA} = cos ∠ AMN = cos ∠ AOC = √ {1 — sin^2 ∠ AOC} = {2} / {3}$.
Ответ: 2:3
Задача 4
В треугольнике $EKP$, в котором все углы острые, проведены высоты $KB$ и $PA$. Из точек $A$ и $B$ на $KB$ и $PA$ опущены перпендикуляры $AM$ и $BN$ соответственно.
а) Докажите, что прямые $MN$ и $KP$ параллельны.
б) Найдите отношение $MN:KP$, если угол $KEP$ равен $45^°$.
Решение
а) $△POB ∼ △KOA$ по первому признаку подобия: $∠PBO = ∠OAK = 90°, ∠BOP = ∠AOK$ как вертикальные.
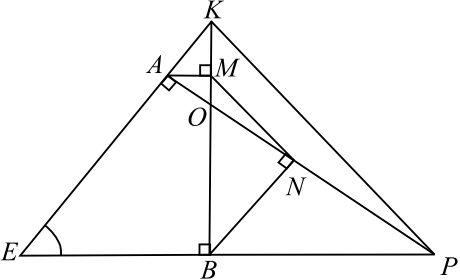
Учитывая, что в подобных треугольниках пропорциональны сходственные стороны и высоты, к ним проведённые, получим ${OP}/{OK} = {BN}/{AM}$ (1).
$△ONB ∼ △AOM$ по первому признаку подобия: $∠BNO = ∠AMO = 90°, ∠BON = ∠AOM$ как вертикальные, отсюда ${ON}/{OM} = {BN}/{AM}$ (2).
Из 1) и 2) следует ${OP}/{OK} = {ON}/{OM}$.
Следовательно, $△OPK ∼ △ONM$ по второму признаку подобия: $∠POK$ — общий, ${OP}/{ON} = {OK}/{OM}$.
Из подобия следует $∠OPK = ∠ONM$ . Углы $OPK$ и $ONM$ соответственные при прямых $PK$ и $NM$ и секущей $OP$ . Следовательно, $PK ‖ MN$ по признаку параллельности прямых.
б) В четырехугольнике $AEBO ∠AEB = 45°$ (по условию) $∠AOB=360°-(∠A +∠B +∠E ) = 360° — 225° = 135°$. В $△AOM ∠AMO = 90°, ∠AOM = 180°-135°=45°, AM=MO$.
Обозначим $OM = x$, тогда $AM = x, AO=OM√2=x√2$.
В $△OAK ∠OAK = 90°, ∠AOM = 45°$, то есть $AO = AK, AO=x√2, KO=AO√2=x√2·√2=2x$.
По доказанному в пункте а) $△OPK ∼ △ONM$, значит, ${MN}/{KP} = {OM}/{OK}$.
Пусть $OM = x, OK = 2x$.
${MN}/{KP}={x}/{2x}=1:2$
Ответ: 1:2
Задача 5
В треугольнике $MNP$, в котором все углы острые, проведены высоты $ME$ и $PF$. Из точек $F$ и $E$ на $ME$ и $PF$ опущены перпендикуляры $FK$ и $EH$ соответственно.
а) Докажите, что прямые $KH$ и $MP$ параллельны.
б) Найдите отношение $MP:KH$, если угол $MNP$ равен $60^°$.
Решение
а) $O$ — точка пересечения высот $ME$ и $PF$. $△POE ∼ △MFO$ по первому признаку подобия: $∠PEO = ∠OFM = 90°, ∠EOP = ∠FOM$ как вертикальные.
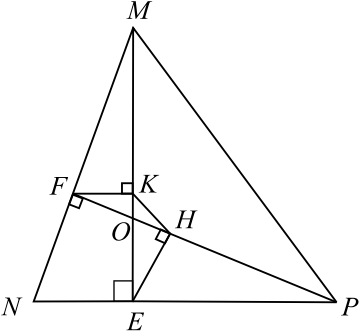
Учитывая, что в подобных треугольниках пропорциональны сходственные стороны и высоты, к ним проведённые, получим ${OP}/{OM} = {EH}/{FK}$ (1).
$△OHE ∼ △FOK$ по первому признаку подобия: $∠EHO = ∠FKO = 90°, ∠EOH = ∠FOK$ как вертикальные, отсюда ${OH}/{OK} = {EH}/{FK}$ (2).
Из 1) и 2) следует ${OP}/{OM} = {OH}/{OK}$.
Следовательно, $△OP M ∼ △OH K$ по второму признаку подобия: $∠P OM$ — общий, ${OP}/{OH} = {OM}/{OK}$.
Из подобия следует $∠OP M = ∠OH K$ . Углы $OP M$ и $OH K$ соответственные при прямых $M P$ и $K H$ и секущей $OP$ . Следовательно, $M P ‖ K H$ по признаку параллельности прямых.
б) В четырехугольнике $N FOE ∠FOE = 360° -(∠90° +∠90° +∠N ) = 360° — 240° = 120°$. В $△FOK ∠FKO = 90°, ∠FOK = 60°$, как смежный с $∠FOE = 120°$, тогда $∠OF K = 30°$.
Обозначим $OK = x$, тогда $FO = 2x$.
В $△OFM ∠M FO = 90°, ∠FOM = 60°, ∠F M O = 30°$, то есть $FO = {1}/{2}M O$, значит, $2x = {1}/{2}M O, M O = 4x$.
По доказанному в пункте а) $△OM P ∼ △OK H$, значит, ${MP}/{K H} = {M O}/{OK} $, но $M O = 4x, OK = x$, следовательно, ${M P}/{K H} = {4x}/{x} = 4 : 1$
Ответ: 4:1
Задача 6
В прямоугольном треугольнике $ABC$ точки $P$ и $K$ — середины катета $BC$ и гипотенузы $AB$ соответственно. Биссектриса угла $BAC$ пересекает прямую $KP$ в точке $R$.
а) Докажите, что точки $A$, $B$, $C$ и $R$ лежат на одной окружности.
б) Найдите отношение площадей треугольников $AKR$ и $BCR$, если $sin ∠ BAC={15} / {17}$.
Решение
а) Отрезок, соединяющий вершину прямого угла и середину гипотенузы, равен половине длины гипотенузы, то есть $AK = K B = K C. AR$ — биссектриса угла $BAC$, значит $∠CAR =∠BAR = α$.
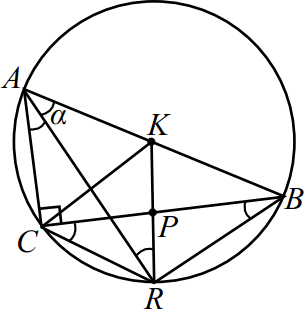
$K P$ — средняя линия $△ABC$, значит, $K P ‖ AC$.
Накрест лежащие углы $CAR$ и $ARK$ равны (секущая $AR$).
В треугольнике $AK R$ равны углы $K AR$ и $K RA$, значит $AK = K R$.
Получим $AK = K B = K C = K R$, значит точки $A, B, C$ и $R$ лежат на окружности с центром $K$.
б) $∠CBR =∠CAR$ и $∠BAR =∠BCR$ (опираются на дуги $C R$ и $BR$ соответственно), таким образом, треугольники $AK R$ и $BC R$ подобны по двум углам. По теореме синусов для треугольника $ABR$ получим ${BR}/{sin ∠RAB} = 2r$, где $r$ — радиус описанной окружности, то есть $2r = AB$. Получили ${BR}/{AB} = sin ∠RAB = sin α$.
Но коэффициент подобия треугольников $AK R$ и $BC R$ равен ${AK}/{BR} = {2AK}/{2BR} = {AB}/{2BR} = {1}/{2 sin α}$.
По условию $sin ∠BAC = sin 2α = {15}/{17}$.
Тогда $cos 2α = √{1 — ({15}/{17})^2} = {8}/{17}$,
$cos 2α = 1 — 2 sin^2 α = {8}/{17}, 2 sin^2 α = {9}/{17}$.
Площади треугольников относятся как квадрат коэффициента подобия, поэтому ${S_{AKR}}/{S_{BCR}} = ({1}/{2sin α})^2 = {1}/{2 · {9}/{17}} = {17}/{18}$.
Ответ: 17:18
Задача 7
В трапеции $ABCD$ боковая сторона $AB$ перпендикулярна основаниям. Из точки $A$ на сторону $CD$ опустили перпендикуляр $AE$. На стороне $AB$ отмечена точка $F$ так, что прямые $BE$ и $FD$ параллельны.
а) Докажите, что прямые $FC$ и $CD$ перпендикулярны.
б) Найдите отношение $BE:FD$, если угол $BCD$ равен $120°$.
Решение
Продолжим боковые стороны трапеции $AB$ и $DC$ до пересечения в точке $S$. Ясно, что $BC$ — меньшее основание, иначе перпендикуляр $AE$ будет падать на продолжение $CD$, а не на саму сторону, что противоречит условию.
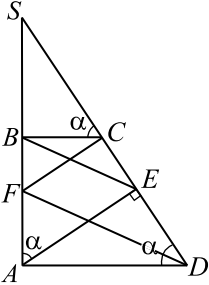
а) Для доказательства перпендикулярности прямых $FC$ и $CD$ достаточно доказать подобие треугольников $SFC$ и $SAE$.
Заметим, что $△SBC ∼ △SAD$ по двум углам ($∠SBC = ∠SAD = 90°, ∠S$ — общий). Тогда ${SB}/{SA} = {SC}/{SD}$, то есть $SB·SD = SA · SC$.
С другой стороны, $△SBE ∼ △SFD$ по двум углам: $∠SBE = ∠SFD$ как соответственные углы при параллельных прямых $BE$ и $FD$ и секущей $SA, ∠S$ — общий.
Тогда ${SB}/{SF} = {SE}/{SD}$, отсюда $SB · SD = SF · SE$.
Следовательно, $SA · SC = SB · SD = SF · SE$.
Тогда $SA · SC = SF · SE, {SA}/{SF} = {SE}/{SC}$.
Отсюда $△SAE ∼ △SFC$ по второму признаку.
Тогда $∠SCF = ∠SEA = 90°, FC ⊥ SD$, что и требовалось доказать.
б) Из подобия треугольников $SBE$ и $SFD$ следует ${BE}/{FD} = {SB}/{SF}$.
$∠BCS = 180° — ∠BCD = 60°, SB = SC sin 60° = {√3}/{2}SC. ∠CSF = 90° — ∠BCS = 30°$. Из $△SFC$ следует, что $CS = SF cos 30° = SF {√3}/{2}$. Тогда $SB = {√3}/{2}SC ={√3}/{2}·{√3}/{2}SF; {SB}/{SF} = {3}/{4} = 0.75$.
Ответ: 0.75
Задача 8
В трапеции $ABCD$ боковая сторона $AB$ перпендикулярна основаниям. Из точки $A$ на сторону $CD$ опустили перпендикуляр $AE$. На стороне $AB$ отмечена точка $F$ так, что прямые $CD$ и $CF$ перпендикулярны. а) Докажите, что прямые $BE$ и $FD$ параллельны. б) Найдите отношение $BE:FD$, если угол $BCD$ равен $150°$.
Решение
Продолжим боковые стороны трапеции $AB$ и $DC$ до пересечения в точке $S$. а) Для доказательства параллельности прямых $BE$ и $FD$ достаточно доказать, что треугольники $SBE$ и $SFD$ подобны (см. рис.). Ясно, что $BC$ — меньшее основание, иначе перпендикуляр $AE$ будет опускаться на продолжение $CD$, а не на саму сторону, что противоречит условию. По условию $FC⊥ CD$ и $AE⊥ CD$, отсюда $FC∥ AE$. Заметим: в прямоугольных треугольниках $SCB$, $SFC$, $SAE$ и $SDA$ угол $S$ общий, значит, $∠ SCB=∠ SFC=∠ SAE=∠ SDA=α$. В каждом из рассматриваемых треугольников выразим $sin α$. $▵ SCB$: $sin α={SB} / {SC}$ (1) $▵ SFC$: $sin α={SC} / {SF}$ (2) $▵ SAE$: $sin α={SE} / {SA}$ (3) $▵ SDA$: $sin α={SA} / {SD}$ (4) Перемножив (1) на (2) и (3) на (4), получим ${SB} / {SC}⋅ {SC} / {SF}=sin^2 α$, ${SB} / {SF}=sin^2α$, ${SE} / {SA}⋅ {SA} / {SD}=sin^2α$, ${SE} / {SD}=sin^2α$. Отсюда ${SB} / {SF}={SE} / {SD}$. Имеем: две стороны $▵ SBE$ пропорциональны двум сторонам $▵ SFD$ и между ними угол $S$ — общий, значит, $▵ SBE∼ ▵ SFD$ по второму признаку подобия. Из подобия следует равенство соответственных углов $SEB$ и $SDF$ при прямых $BE$, $FD$ и секущей $SD$, следовательно, по признаку параллельности прямых $BE∥ FD$. б) Из подобия треугольников $SBE$ и $SFD$ следует ${BE} / {FD}={SB} / {SF}$. В пункте а) доказано ${SB} / {SF}=sin^2 α$, $∠ BCD+α=180°$, $α=180°-150°=30°$. ${BE} / {FD}={SB} / {SF}=sin^2 30°=0{,}5^2=0{,}25$.
Ответ: 0.25
Задача 9
В треугольнике $ABC$ проведена высота $AH$ и медиана $AM$. $AB=2$, $AC=√ {21}$, $AM=2{,}5$.
а) Докажите, что треугольник $ABC$ прямоугольный.
б) Вычислите $HM$.
Решение
а) Достроим треугольник $ABC$ до параллелограмма $ABDC$, как показано на рисунке.
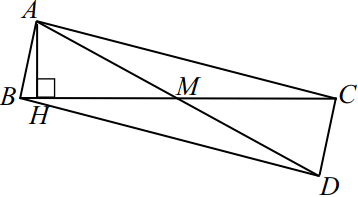
По свойству параллелограмма, верно равенство $2(AB^2 + AC^2) = AD^2 + BC^2$, или $2(AB^2 + AC^2) = (2AM)^2 + BC^2$. Так как по условию $AB = 2, AC = √{21}, AM = 2.5$, то $2(22 + √{21}^2) = (2 · 2.5)^2 + BC^2$, откуда $BC = 5$. Если диагонали параллелограмма равны, то он — прямоугольник, значит, $∠BAC = 90°$ и $△ABC$ прямоугольный.
б) В прямоугольном треугольнике $ABC$ выразим площадь двумя способами: $2S = AB · AC, 2S = BC · AH$, приравнивая правые части этих равенств, находим $AH = {AB·AC}/{BC} = {2 · √21}/{5}$. Катет $HM$ найдём из прямоугольного треугольника $AHM$ по теореме Пифагора: $HM = √{AM^2 − AH^2} = √{2.5^2 −({2 · √21}/{5})^2} = √{{25}/{4} − {84}/{25}} = √{{625 − 336}/{100}} = {17}/{10} = 1.7$.
Ответ: 1.7
Задача 10
В треугольнике $ABC$ точки $K$, $N$, $F$ — середины сторон $AC$, $AB$ и $BC$ соответственно. $AH$ — высота треугольника $ABC$, $∠ CAB=60^°$, $∠ ACB=15^°$.
а) Докажите, что точки $K$, $N$, $F$ и $H$ лежат на одной окружности.
б) Найдите $FH$, если $BC=4√ 3$.
Решение
а) $∠ABC = 180° — (60° + 15°) = 105°$.
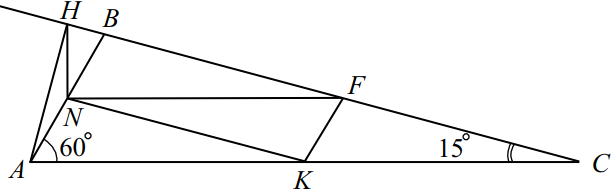
$NH$ — медиана в прямоугольном треугольнике $AHB$, отсюда $NH = NB = AN$.
$∠ABH = 75°, ∠BHN = ∠NBH$ как углы при основании равнобедренного треугольника $NBH , ∠NBH = 75°$.
$FK = {1}/{2}AB, NK = {1}/{2}BC , FN = {1}/{2}AC$ по свойству средней линии треугольника, тогда $△FKN ∼ △ABC$ по трём пропорциональным сторонам, следовательно, $∠NKF = ∠ABC = 105°$.
В четырёхугольнике $NHFK$ найдём сумму противоположных углов: $∠FKN + ∠FHN = 105° + 75° = 180°$, значит, около этого четырёхугольника можно описать окружность, что и требовалось доказать.
б) По теореме синусов для $△NFK: {NK}/{sin∠NFK} = 2R$, где $R$ — радиус окружности, проходящей через точки $K , N , F$ и $H$. Так как $NK = {1}/{2}BC$, то ${BC}/{2sin60°} = 2R = {4√3}/{2} : {√3}/{2} = 4$.
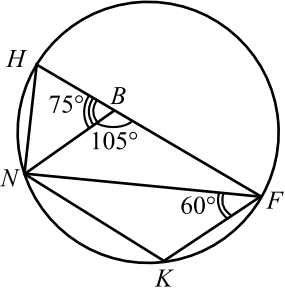
В равнобедренном треугольнике $HNB$ $∠N = 180° — 75°· 2 = 30°$. $∠BNF = ∠BAC = 60°$ как соответственные углы при параллельных прямых $NF$ и $AC$ и секущей $AB$.
В $△HNF ∠HNF = ∠HNB + ∠BNF = 30° + 60° = 90°$, значит $HF$ — диаметр описанной окружности, $HF = 2R = 4$.
Ответ: 4
Задача 11
Две окружности касаются внешним образом в точке $K$. Прямая $AB$ касается первой окружности в точке $A$, а второй — в точке $B$. Прямая $BK$ пересекает первую окружность в точке $D$, прямая $AK$ пересекает вторую окружность в точке $C$.
а) Докажите, что прямые $AD$ и $BC$ параллельны.
б) Найдите площадь $▵ AKB$, если известно, что радиусы окружностей равны $8$ и $2$.
Решение
а) Общая касательная, проведенная к окружностям в точке $K$, пересекает $AB$ в точке $M$. По свойству касательных, проведенных из одной точки, $AM = K M$ и $K M = BM$. Треугольник $AK B$, у которого медиана $K M$ равна половине стороны $AB$, к которой она проведена, прямоугольный, $∠AK B = 90°$. Вписанный угол $AK D$ прямой, поэтому он опирается на диаметр $AD$, значит, $AD ⊥ AB$. Аналогично, получаем, что $BC ⊥ AB$. Следовательно, прямые $AD$ и $BC$ параллельны.
б) Пусть первая окружность имеет радиус $8$, а вторая — радиус $2$.
Проведём $O_2H ⊥ AD$, тогда $O_2HAB$ — прямоугольник и $AH = O_2 B = 2, AB = O_2 H$. Из $△O_1O_2H$ получим $O_2 H^2 = O_1O_2^2 — O_1H^2 = (2 + 8)^2 — (8 — 2)^2 = 64, O_2 H = 8 = AB$.
$△O_2PB ∼ △O_1O_2H$ (по двум углам), ${O_2B}/{O_2P} = {O_1H}/{O_1O_2}; {2}/{O_2P} = {8 — 2}/{8 + 2}; O_2P = {10}/{3}$.
Проведём высоту $KE$ в $△AKB$, получим, что $△O_2BP ∼ △KEP$ (по двум углам). ${KE}/{O_2B} = {KP}/{O_2P}; {KE}/{2} = {2 + {10}/{3}}/{{10}/{3}}; KE = 1.6 · 2 = 3.2$.
$S_{AKB} = {1}/{2}AB · KE = {1}/{2} · 8 · 3.2 = 12.8$.
Ответ: 12.8
Задача 12
Две окружности с центрами $O_1$ и $O_2$ пересекаются в точках $M$ и $N$, причём точки $O_1$ и $O_2$ лежат по разные стороны от прямой $MN$. Продолжение диаметра $AM$ первой окружности и хорды $AN$ этой же окружности пересекают вторую окружность в точках $C$ и $B$ соответственно.
а) Докажите, что треугольники $ANC$ и $O_1MO_2$ подобны.
б) Найдите $MC$, если угол $CMB$ равен углу $NMA$, а радиус второй окружности в $1{,}5$ раза больше радиуса первой и $MN=3$.
Решение
а) $O_1O_2 ⊥ MN, O_1O_2$ делит хорду $MN$ и дугу $MN$ второй окружности пополам.
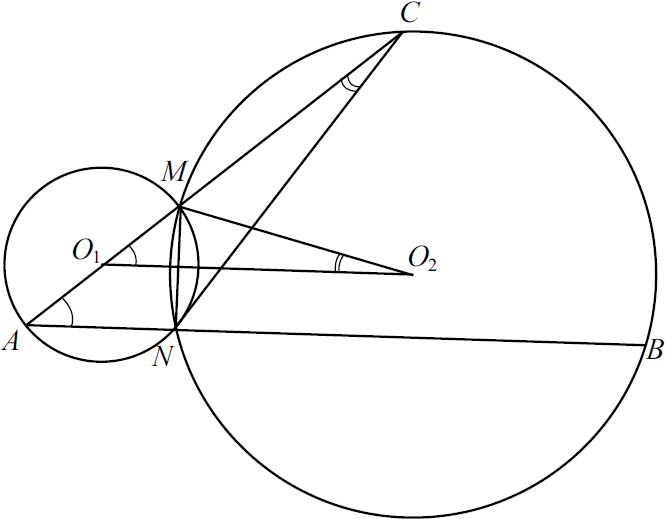
$∠MO_2O_1 = {1}/{2} ︶ MN; ∠ACN = ∠MCN = {1}/{2} ︶ MN = ∠MO_2O_1. ∠ANM = 90°$ как угол, опирающийся на диаметр, поэтому $AN ⊥ MN, O_1O_2 ⊥ MN$, значит, $AN‖ O_1O_2$, откуда $∠MO_1O_2 = ∠MAN$. Итак, $△ACN∼△MO_1O_2$ по двум углам.
б) Введём обозначения: $r$ — радиус меньшей окружности, тогда $1.5r$ -радиус большей окружности.
$∠MNB = 180° — ∠MNA = 90°$, тогда $MB$ — диаметр окружности (проходит через $O_2$). $∠MCB = 90°$, как вписанный угол, опирающийся на диаметр.
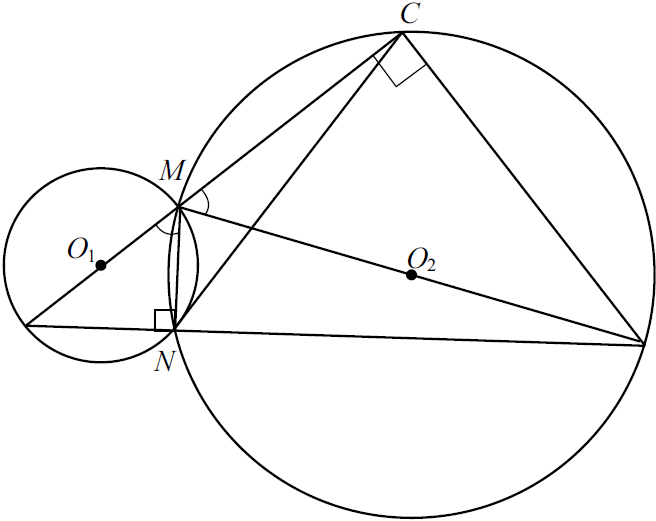
Значит, $△AMN∼△BCM$ по двум углам.
Значит, ${MC}/{MN} = {MB}/{AM}={2⋅3r}/{2⋅2r} =1.5.$
$MC= 1.5·3 = 4.5$.
Ответ:
Задача 13
Две окружности с центрами $O_1$ и $O_2$ пересекаются в точках $M$ и $N$, причём точки $O_1$ и $O_2$ лежат по разные стороны от прямой $MN$. Продолжение диаметра $AM$ первой окружности и хорды $AN$ этой же окружности пересекают вторую окружность в точках $C$ и $B$ соответственно.
а) Докажите, что треугольники $ANC$ и $O_1MO_2$ подобны.
б) Найдите $MC$, если угол $CMB$ равен углу $NMA$, а радиус второй окружности в $2{,}5$ раза больше радиуса первой и $MN=2$.
Решение
а) $O_1O_2 ⊥ MN, O_1O_2$ делит хорду $MN$ и дугу $MN$ второй окружности пополам.
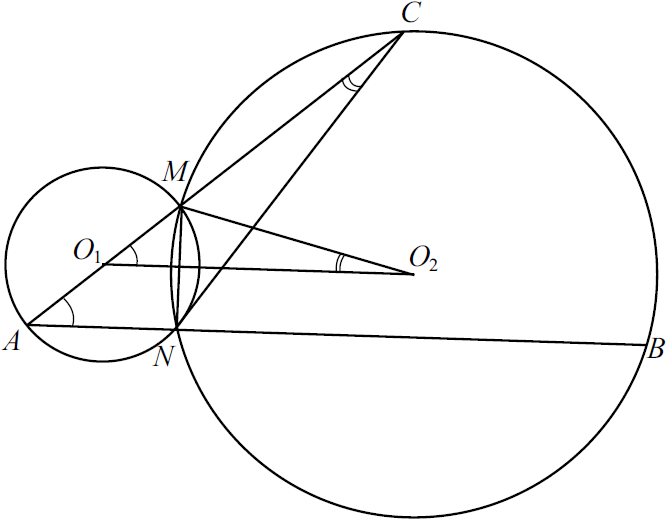
$∠MO_2O_1 = {1}/{2} ︶ MN; ∠ACN = ∠MCN = {1}/{2} ︶ MN = ∠MO_2O_1. ∠ANM = 90°$ как угол, опирающийся на диаметр, поэтому $AN ⊥ MN, O_1O2 ⊥ MN$, значит, $AN‖ O_1O_2$, откуда $∠MO_1O_2 = ∠MAN$. Итак, $△ACN∼△MO_1O_2$ по двум углам.
б) Введём обозначения: $r$ — радиус меньшей окружности, тогда $2.5r$ -радиус большей окружности.
$∠MNB = 180° — ∠ANM = 90°$, тогда $MB$ — диаметр второй окружности (проходит через $O_2$). $∠MCB = 90°$, как вписанный угол, опирающийся на диаметр.
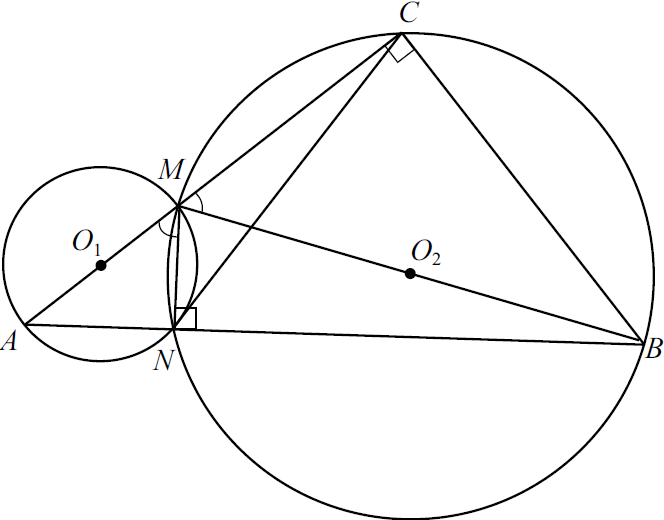
Значит, $△AMN∼△BCM$ по двум углам ($∠ANM = ∠MCB = 90°, ∠AMN = ∠CMB$)
${MC}/{MN} = {MB}/{AM}$, но ${MB}/{AM} = {2·2.5r}/{2r} = 2.5$.
$MC = 2.5·MN = 5$.
Ответ: 5
Задача 14
Основания трапеции равны $7$ и $34$, а её диагонали равны $9$ и $40$.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите площадь трапеции.
Решение
а) Проведём $CE ‖ BD$. $E$ — точка пересечения прямых $AD$ и $CE$. $BCED$ — параллелограмм: $BC ‖ DE$ как прямые, содержащие основания трапеции, $BD ‖ CE$ по построению. $BC = DE = 7$, тогда $AE = AD + DE = 34 + 7 = 41$. Заметим, что для треугольника $ACE$ выполнена теорема Пифагора: $AC^2 + CE^2 = AE^2$, следовательно, $AC ⊥ CE$, а так как $CE ‖ BD$, то $BD ⊥ AC$.
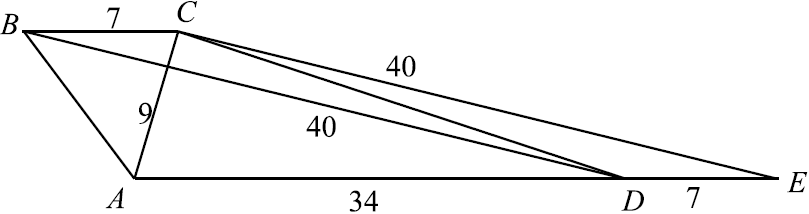
б) Проведём высоту $CH$ трапеции. $CH$ также является высотой треугольника $ACE. CH = {AC·CE}/{AE} = {9·40}/{41}. S_{ABCD} = {AD + BC}/{2}·CH = {34 + 7}/{2}·{9·40}/{41} = 9·20 = 180$.
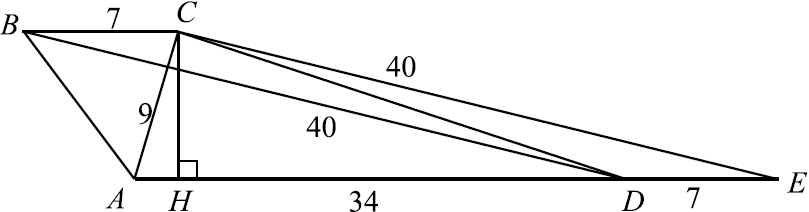
Ответ: 180
Задача 15
Основания трапеции равны $6$ и $19$, а её диагонали равны $7$ и $24$.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите площадь трапеции.
Решение
а) Проведём $CE ‖ BD$. $E$ — точка пересечения прямых $AD$ и $CE$. $BCED$ — параллелограмм: $BC ‖ DE$ как прямые, содержащие основания трапеции, $BD ‖ CE$ по построению. $BC = DE = 6$, тогда $AE = AD + DE = 19 + 6 = 25$. Заметим, что для треугольника $ACE$ выполнена теорема Пифагора: $AC^2 + CE^2 = AE^2$, следовательно, $AC ⊥ CE$, а так как $CE ‖ BD$, то $BD ⊥ AC$.
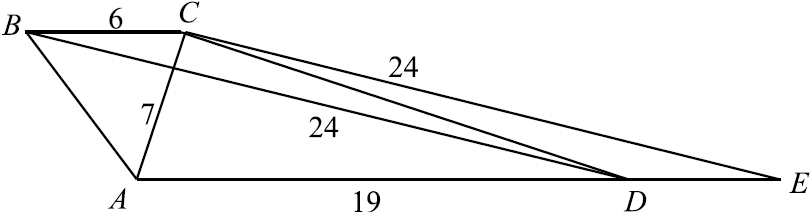
б) Проведём высоту $CH$ трапеции. $CH$ также является высотой треугольника $ACE. CH = {AC·CE}/{AE} = {7·24}/{25}. S_{ABCD} = {AD + BC}/{2}·CH = {19 + 6}/{2}·{7·24}/{25} = 7·12 = 84$.
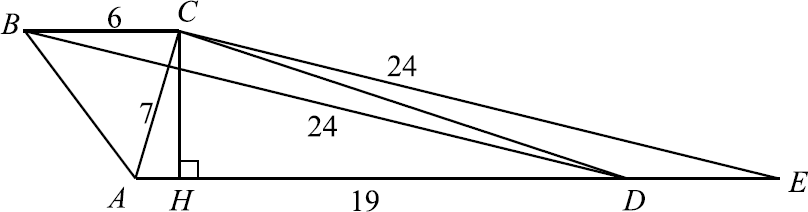
Ответ: 84
Задача 16
Две окружности касаются внутренним образом в точке $K$, причём меньшая окружность проходит через центр $O$ большей. Диаметр $AB$ большей окружности вторично пересекает меньшую окружность в точке $C$, отличной от $K$. Лучи $KO$ и $KC$ вторично пересекают большую окружность в точках $D$ и $E$ соответственно. Точка $B$ лежит на дуге $EK$ большей окружности, не содержащей точку $D$.
а) Докажите, что прямые $DE$ и $AB$ параллельны.
б) Известно, что $sin∠ KOB = {√ {15}} / {8}$. Прямые $DB$ и $EK$ пересекаются в точке $L$. Найдите отношение $EL:LK$.
Решение
а) $KD$ — диаметр большей окружности ($O ∈ KD$), $O_1$ — центр меньшей окружности, $l$ — общая касательная двух окружностей, проходящая через точку $K$ (см. рис.). $O_1 ∈ KD$. Действительно, $OK⊥ l$, $O_1K⊥ l$ как радиусы, проведённые в точку касания, значит, точки $O$, $K$, $O_1$ лежат на луче $KO$. $∠ DEK=∠ OCK=90°$ как вписанные углы, опирающиеся на диаметры $DK$ и $OK$ соответственно. $C∈ EK$, следовательно, $DE∥ AB$ как два перпендикуляра к одной прямой.
б) Так как диаметр $AB$, перпендикулярный хорде $EK$, делит её пополам, то $CE=CK$, следовательно, $⌣ KB=⌣ BE$ (см. рис.). Угол $EDK$ вписанный, опирается на дугу $EK$, а угол $BOK$ — центральный, опирается на половину дуги $EK$, следовательно, $∠ EDK=∠ BOK=α$; $∠ EDB=∠ BDK$ как вписанные углы, опирающиеся на равные дуги, тогда $DL$ — биссектриса треугольника $DEK$, а по свойству биссектрисы ${EL} / {LK}={DE} / {DK}=cos α=√ {1-sin^2 α}$.
${EL} / {LK}=√ {1-{15} / {64}}={7} / {8}$.
Ответ: fsm78
Задача 17
В остроугольном треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены перпендикуляры $ME$ и $KH$ соответственно. а) Докажите, что прямые $EH$ и $AC$ параллельны. б) Найдите отношение $EH$ к $AC$, если $cos ∠ ABC = {√ {2}} / {4}$.
Решение
а) По условию задачи выполним чертёж.
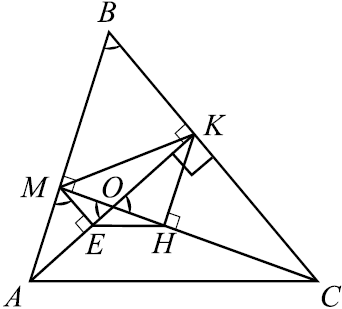
Рассмотрим треугольники $KOH$ и $KOC$. Они подобны как прямоугольные треугольники с общим острым углом $∠KOC$. Значит, ${OH}/{OK} = {OK}/{OC} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OH = {OK^2}/{OC} = ({OK}/{OC})^2·OC = k^2·OC$. Следовательно, ${OH}/{OC} = k^2$.
Аналогично, треугольник $MOE$ подобен треугольнику $MOA$. Тогда ${OE}/{OM} = {OM}/{OA} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OE = {OM^2}/{OA} = ({OM}/{OA})^2·OA = k^2·OA$. Следовательно, ${OE}/{OA} = k^2$.
Треугольники $OEH$ и $OAC$ подобны, так как $∠AOC$ — общий и ${OH}/{OC} = {OE}/{OA}$. Тогда $∠OEH = ∠OAC$, эти углы являются соответственными при прямых $EH$ и $AC$ и секущей $AO$, значит $EH || AC$.
б) Из подобия $OEH$ и $OAC$ следует, что ${EH}/{AC} = {OH}/{OC} = {OE}/{OA} = k^2$. Тогда ${EH}/{AC} = cos^2∠ABC = {2}/{16} ={1}/{8}$. Таким образом, $EH : AC = 1 : 8$.
Ответ: 1:8
Задача 18
В остроугольном треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены перпендикуляры $ME$ и $KH$ соответственно. а) Докажите, что прямые $EH$ и $AC$ параллельны. б) Найдите отношение $EH$ к $AC$, если $sin ∠ ABC = {√ {3}} / {3}$.
Решение
а) По условию задачи выполним чертёж.
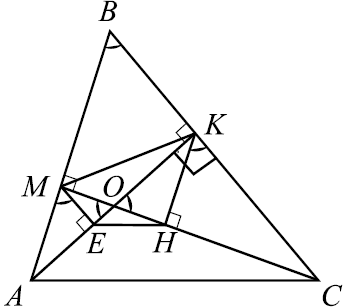
Рассмотрим треугольники $KOH$ и $KOC$. Они подобны как прямоугольные треугольники с общим острым углом $∠KOC$. Значит, ${OH}/{OK} = {OK}/{OC} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OH = {OK^2}/{OC} = ({OK}/{OC})^2·OC = k^2·OC$. Следовательно, ${OH}/{OC} = k^2$.
Аналогично, треугольник $MOE$ подобен треугольнику $MOA$. Тогда ${OE}/{OM} = {OM}/{OA} = sin(90° — ∠ABC) = cos∠ABC = k$. Отсюда следует, что $OE = {OM^2}/{OA} = ({OM}/{OA})^2·OA = k^2·OA$. Следовательно, ${OE}/{OA} = k^2$.
Треугольники $OEH$ и $OAC$ подобны, так как $∠AOC$ — общий и ${OH}/{OC} = {OE}/{OA}$. Тогда $∠OEH = ∠OAC$, эти углы являются соответственными при прямых $EH$ и $AC$ и секущей $AO$, значит $EH || AC$.
б) Из подобия $OEH$ и $OAC$ следует, что ${EH}/{AC} = {OH}/{OC} = {OE}/{OA} = k^2$. Тогда ${EH}/{AC} = cos^2∠ABC = 1-sin^2∠ABC = 1-{1}/{3} ={2}/{3}$. Таким образом, $EH : AC = 2 : 3$.
Ответ: 2:3
Задача 19
Один из двух отрезков, соединяющих середины противоположных сторон выпуклого четырёхугольника, делит его площадь пополам, а другой — в отношении ${6} / {7}$. а) Докажите, что данный четырёхугольник есть трапеция. б) Укажите отношение двух оснований этой трапеции (меньшего к большему).
Решение
а) Рассмотрим выпуклый четырёхугольник ABCD. Пусть M — середина AB, N — середина CD, причём $S_{AMND} = S_{MBCN}$. Проведём AN и BN. Заметим, что $S_{AMN} = {1}/{2}AM · MNsin∠AMN ={1}/{2}MB · MNsin∠BMN = S_{BMN}$, так как $AM = MB, sin∠AMN = sin(180° — ∠AMN) = sin∠BMN$.
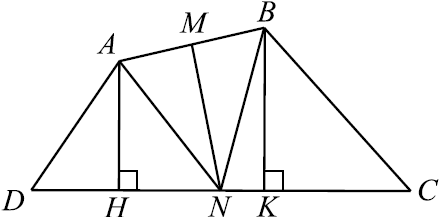
Отсюда $S_{AND} = S_{BNC}(S_{AND} = S_{AMND} — S_{AMN}, S_{BNC} = S_{MBCN} — S_{MBN})$.
Опустим в $△AND$ высоту AH, в $△BNC$ — высоту BK.
Получим ${1}/{2}DN·AH = {1}/{2}NC·BK$, при этом $DN = NC$. Следовательно, $AH = BK$. Но тогда в четырёхугольник $AHKB ∠AHK = ∠BKH = 90°, AH = BK$, то есть $AHKB$ — прямоугольник. Значит, $AB ‖ HK, AB ‖ DC$.
Для доказательства того, что ABCD — трапеция, необходимо доказать, что две другие стороны не параллельны, то есть AD не параллельна BC. Предположим противное. Тогда ABCD — параллелограмм, но тогда отрезок, соединяющий середины AD и BC, делит площадь ABCD пополам, что противоречит условию, так как отношение полученных площадей должно равняться 6 : 7. Отсюда верно ABCD — трапеция.
б) По условию EF делит площадь ABCD на площади, отношение которых равно 6 : 7, а именно $S_{ABFE} : S_{EFCD} = 6 : 7$.
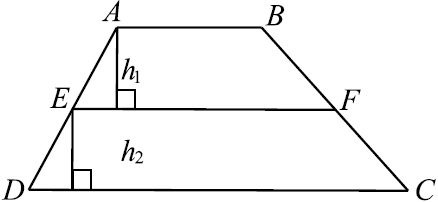
$EF$ — средняя линия, $EF = {AB + CD}/{2}$.
Надо найти AB : CD.
$S_{ABFE} = {AB + EF}/{2}·h_1, S_{EFCD} = {EF + CD}/{2}·h_2$, где $h_1$ — высота $ABFE$, $h_2$ — высота $EFCD$.
Учитывая, что $AB ‖ CD$, а $EF$ — средняя линия и $EF ‖ AB$ и $EF ‖ CD$, то расстояние от $EF$ до $AB$ и от $EF$ до $CD$ равны, то есть $h_1 = h_2$.
Следовательно, ${S_{ABFE}}/{S_{EFCD}} = {{AB + EF}/{2}}/{{EF + CD}/{2}} = {AB + EF}/{EF + CD} = {AB + {AB + CD}/{2}}/{{AB + CD}/{2} + CD} = {3AB + CD}/{3CD + AB}, {3AB + CD}/{3CD + AB} = {6}/{7}, 21AB + 7CD = 18CD + 6AB, 15AB = 11CD, {AB}/{CD} = {11}/{15}$.
$AB : CD = 11 : 15$.
Ответ: 11:15
Задача 20
В выпуклом четырёхугольнике середины противоположных сторон соединены отрезками, причём один из них делит этот четырёхугольник на две равновеликие фигуры, а другой делит площадь в отношении $9:13$. а) Доказать, что данный четырёхугольник является трапецией. б) Найти отношение меньшего основания этой трапеции к большему.
Решение
а) Рассмотрим выпуклый четырёхугольник $QMNP$ (см. рис.). Пусть $E$ — середина $MQ$, $F$ — середина $NP$, причём $S_{MNFE}=S_{EFPQ}$.
Проведём отрезки $EN$ и $EP$. Заметим, что
$S_{▵ EFN}={1} / {2} EF⋅ FNsin ∠ EFN={1} / {2} EF⋅ FP sin ∠ EFP=S_{▵ EFP}$, так как $NF=FP$ и $sin ∠ EFN=sin (180°-∠ EFN)=sin ∠ EFP$. Отсюда $S_{▵ MNE}=S_{▵ EPQ}$ ($S_{▵ MNE}=S_{MNFE}-S_{▵ EFN}$, $S_{▵ EPQ}=S_{EFPQ}-S_{▵ EFP}$). Опустим в $▵ MNE$ высоту $NN_1$, в $▵ EPQ$ — высоту $PP_1$. Получим: ${1} / {2} ME⋅ NN_1={1} / {2} EQ⋅ PP_1$. Но $ME=EQ$, следовательно, $NN_1=PP_1$. Но тогда в четырёхугольнике $N_1NPP_1$ $∠ NN_1P_1=∠ N_1P_1P=90°$, $NN_1=PP_1$, то есть $N_1NPP_1$ — прямоугольник. Значит, $N_1P_1∥ NP$, $MQ∥ NP$. Из предположения о том, что $MN∥ QP$, следует, что отрезок, соединяющий середины сторон $MN$ и $QP$, делит параллелограмм $MNPQ$ на две равновеликие фигуры. Но по условию это не так. Значит, $MN ∦ QP$. Следовательно, $MNPQ$ — трапеция. б) По условию второй отрезок $AB$ делит четырёхугольник так, что площадь $ANPB$ относится к площади $ABQM$ как $9:13$ (см. рис.).
$S_{ANPB}:S_{ABQM}=9:13$. $AB$ — средняя линия трапеции, $AB={NP+MQ} / {2}$. $S_{ANPB}={AB+NP} / {2}⋅ h_1$; $S_{ABQM}={AB+MQ} / {2}⋅ h_2$, где $h_1$ — высота трапеции $ANPB$; $h_2$ — высота трапеции $ABQM$. Так как $NP∥ MQ$, а $AB$ — средняя линия и $AB∥ NP$ и $AB∥ MQ$, то расстояния от $AB$ до $NP$ и от $AB$ до $MQ$ равны, то есть $h_1=h_2$. Отсюда, ${S_{ANPB}} / {S_{ABQM}}={{NP+AB} / {2}} / {{AB+MQ} / {2}}={NP+{NP+MQ} / {2}} / {{NP+MQ} / {2}+MQ}={3NP+MQ} / {3MQ+NP}$, ${3NP+MQ} / {3MQ+NP}={9} / {13}$, $39NP+13MQ=27MQ+9NP$, $30NP=14MQ$, ${NP} / {MQ}={14} / {30}={7} / {15}$.
Ответ: 7:15
В задании №15 требуется решить один из видов неравенств:
- Рациональное неравенство
- Показательное неравенство
- Логарифмическое неравенство, возможно с переменным основанием
- Неравенство с радикалом
- Смешанное неравенство, которое может содержать несколько видов одновременно
Получить за решение этого задания можно 2 первичных балла. Потерять 1 балл можно при вычислительной ошибке, при условии что имеется верная последовательность всех шагов решения.

Статистика выполнения задания №15 по годам
Метод интервалов
- Решить уравнение f(x) = 0. Так мы найдем нули функции, от которых зависит знак неравенства. Удобно отдельно находить нули числителя и нули знаменателя.
- Отметить все полученные корни (нули) на координатной прямой. Получим несколько интервалов.
- Выяснить знак (плюс или минус) функции f(x) на самом правом интервале. Для этого достаточно подставить в f(x) очень большое число, например, 1 000 000.
- Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется. НО есть одно исключение:
При переходе через нуль мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная.
Пример 1
При переходе через нуль мы можем поменять знак на противоположный, если степень выражения, дающего этот нуль, нечетная, и не можем поменять знак, если степень четная.

Пример 2
В случае с нестрогими неравенствами( ≤ , ≥) необходимо включить в интервалы точки, которые являются решением уравнения f(x) = 0;

Пример 3

Знак правого промежутка был «+». Единственный нуль четной степени x = 10, поэтому в этом нуле знак не меняем. В остальных нулях чередуем знак.
Пример неравенства №15

Оформление задачи №15
Еще больше крутых лайфхаков, разборов, ловушек ЕГЭ и теории в нашей группе вконтакте и инсте преподавателей @turboegemath и @turbomath
Новый сентябрьский тренировочный вариант (тренировочная работа) №37446019 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
Ссылка для скачивания варианта: задания (КИМ)
Ответы и решения для варианта: скачать
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37446019
Ответы и решения для заданий ОГЭ 2022
На плане (см. рисунок) изображён район города, в котором проживает Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м 2 и фитнес‐ центр. В 15 м от магазина расположен дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а недалеко от него – мебельный центр площадью 2025 м 2 .
Задание 1 №368420 Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
Правильный ответ: 7521
Задание 2 №368421 Детскую площадку решили покрыть резиновой плиткой размером 1 м × 1 м каждая. Плитка продаётся упаковками по 16 штук. Какое минимальное количество упаковок плитки необходимо приобрести?
Правильный ответ: 352
Задание 3 №368422 Найдите суммарную площадь, которую занимают магазин и фитнес-центр. Ответ дайте в м 2 .
Правильный ответ: 2700
Задание 4 №368424 По периметру детской площадки планируется поставить забор. Найдите его длину (в метрах).
Правильный ответ: 300
Задание 5 №368425 Фирма выбирает место для строительства гостиницы: в центре города или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей. В гостинице планируется сдавать 500 номеров. Стоимость земли, цена строительства гостиницы и средняя стоимость номера даны в таблице. Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько суток после начала сдачи номеров (при условии полной загрузки гостиницы) более высокая стоимость номеров компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций?
Правильный ответ: 203
Задание 10 №316354 Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик из партии бракованный, равна 0,02. Какова вероятность того, что два случайно выбранных из одной партии фонарика окажутся небракованными?
Правильный ответ: 0,9604
Задание 14 №393946 Васе надо решить 434 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней.
Правильный ответ: 57
Задание 15 №323537 Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Правильный ответ: 78
Задание 16 №348379 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.
Правильный ответ: 60
Задание 17 №311480 Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции.
Правильный ответ: 17
Задание 18 №341709 На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AC.
Правильный ответ: 4
Задание 19 №341332 Какое из следующих утверждений верно? 1) Диагонали параллелограмма равны. 2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне. 3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Правильный ответ: 2
Задание 21 №338603 Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Правильный ответ: 75
Задание 24 №333131 Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
Задание 25 №315126 Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Правильный ответ: 14
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:
-
Тренировочный вариант №18 ОГЭ 2022 по математике 9 класс с ответами
-
Тренировочный вариант Ларина №290 ОГЭ 2022 по математике 9 класс
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.
Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.
Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы.
В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.
Теория к заданию №15
Так как задания №16 основаны на теории по теме “треугольники”, рассмотрим базовые понятия, определения и формулы.
Вначале предлагаю рассмотреть углы на плоскости:
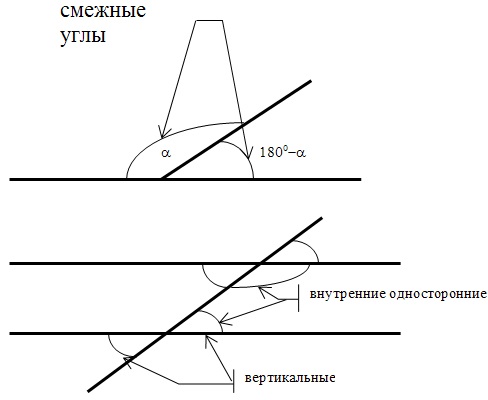
Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
- Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
- Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
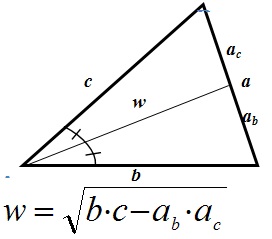 Медиана:
Медиана:
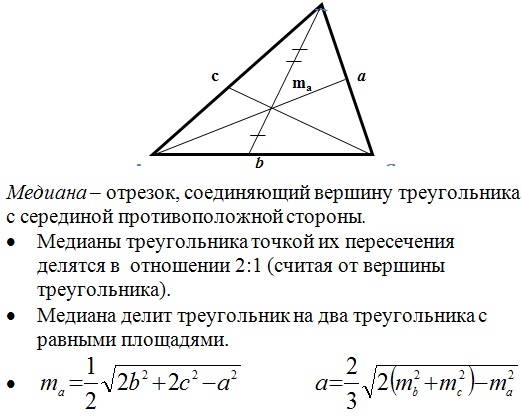
Теперь вспомним основные формулы нахождения площади треугольника:
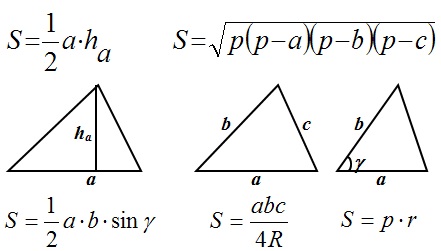
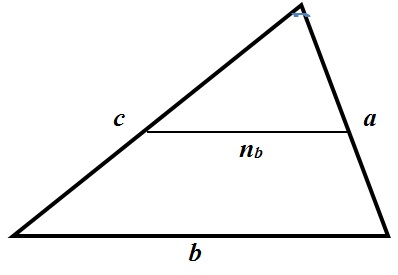
Во многих задачах встречается понятие средняя линия:
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
- Средняя линия параллельна третьей стороне и равна её половине.
- Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
Теперь рассмотрим частные случаи треугольников – равнобедренный, равносторонний, прямоугольный.
Перейдем к рассмотрению равнобедренного треугольника:
Равнобедренный треугольник – треугольник, у которого две стороны равны.
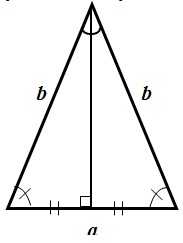
Свойства равнобедренного треугольника:
- Углы, при основании треугольника, равны.
- Высота, проведенная из вершины, является биссектрисой и медианой.
Рассмотрим равносторонний треугольник:
Равносторонний треугольник – треугольник, у которого все стороны равны.
- Все углы равны 60°.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
 Прямоугольный треугольник:
Прямоугольный треугольник:

В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.
Для решения этого задания достаточно знать правило – сумма углов в треугольнике равна 180°.
Нам известны два угла, значит можем найти третий:
180 – 73 – 48 = 59
Ответ: 59
pазбирался: Даниил Романович | обсудить разбор | оценить
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.
Средняя линия – это линия соединяющая середины сторон и параллельная основанию.
Средняя линия равна половине основания, которому она параллельна.
Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC – третьей стороне. А это в свою очередь означает, что она равна половине AC:
MN =½ • AC = 64 / 2 = 32
Ответ: 32
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.
Если в треугольнике две стороны равны – значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:
180 – 122 = 58°
Так как углы при основании равны, значит угол BCA равен углу BAC:
∠BCA = ∠BAC
58° = ∠BCA + ∠BAC = 2 ∠BCA
∠BCA = 58 / 2 = 29°
Ответ: 29
pазбирался: Даниил Романович | обсудить разбор | оценить
Сторона равностороннего треугольника равна 10√3. Найдите его медиану.
Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
m = ( a • √3 )/ 2
Где m – медиана в равностороннем треугольнике, а a – сторона. Таким образом, для решения данной задачи подставим значение в формулу:
m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15
Ответ: 15
pазбирался: Даниил Романович | обсудить разбор | оценить
Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.
Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно, второй острый угол равен:
90 – 23 = 67°
Ответ: 67
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике ABC известно, что AC = 56, BM — медиана, BM = 48. Найдите AM.
Для решения необходимо вспомнить определение медианы.
Медиана – отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка.
Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^
AM = ½ AC = ½ 56 = 28
Ответ: 28
pазбирался: Даниил Романович | обсудить разбор | оценить
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Это следует из того, что один из катетов является высотой к основанию, которым является второй катет.
Исходя из вышесказанного, можем решить задачу:
S = ½ • 15 • 4 = 30
Ответ: 30
pазбирался: Даниил Романович | обсудить разбор | оценить
Сторона равностороннего треугольника равна 12√3. Найдите его высоту.
Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( a • √3 )/ 2
Подставим значение:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18
Ответ: 18
pазбирался: Даниил Романович | обсудить разбор | оценить
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Воспользуемся теоремой Пифагора:
c² = 12² + 16² = 144 + 256 = 400
c = √400 = 20
Ответ: 20
pазбирался: Даниил Романович | обсудить разбор | оценить
Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.
До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:
m = ( a • √3 )/ 2
Здесь же нам необходимо решить обратную задачу, найти a, если известно m.
Выразим a:
a = ( 2 • m ) / √3
Подставим значение:
a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22
Ответ: 22
pазбирался: Даниил Романович | обсудить разбор | оценить
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ВАС. Ответ дайте в градусах.
Для решения этого задания нужно помнить два факта:
- Внутренний угол с внешним углом дают в сумме 180°
- Углы при основании равнобедренного треугольника равны.
Из первого пункта следует, что угол BCA = 180 – 123 = 57°
Из второго – что ∠BCA = ∠BAC = 57°
Ответ: 57
pазбирался: Даниил Романович | обсудить разбор | оценить
В треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42
pазбирался: Даниил Романович | обсудить разбор | оценить
- ОГЭ по математике
Прототипы заданий 15 ОГЭ по математике. Материал для подготовки к ОГЭ.
Для выполнения задания 15 необходимо уметь выполнять действия с геометрическими фигурами, координатами и векторами (треугольники, четырёхугольники, многоугольники и их элементы)
Подробнее узнать виды заданий на данной позиции в КИМах можно по кодификатору
| Карточки для отработки задания 15 с ответамиИсточник: math100.ru → скачать |
| Прототипы задания 15 ОГЭ по математике (треугольники) Опубликовано: Гармс Людмила Павловна → скачать |
| Материалы для отработки задания 15 Автор: Е. А. Ширяева → теория → задания |
| → проверочная работа |
Решение типовых задач № 15 на ОГЭ по математике
Связанные страницы:
Решение заданий варианта №15 из сборника ОГЭ 2021 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. Полный разбор всех заданий. ГДЗ для 9 класса.
ЧАСТЬ 1
![]()
Задание 1-5.
Юра летом отдыхает у дедушки и бабушки в деревне Казаково. Юра с дедушкой собираются съездить на велосипедах в село Бор на железнодорожную станцию. Из Казаково в Бор можно проехать по шоссе до деревни Заулки, где нужно свернуть под прямым углом направо на другое шоссе, ведущее в Бор через посёлок Малахово. Из Казаково в Бор можно проехать через посёлок Малахово и не заезжая в Заулки, но тогда первую часть пути надо будет ехать по прямой лесной дорожке. Есть и третий маршрут: доехать по прямой тропинке мимо пруда до села Шокша и там, повернув налево, по шоссе добраться до Бора.
По шоссе Юра с дедушкой едут со скоростью 15 км/ч, а по лесной дорожке и тропинке 12 км/ч. Расстояние по шоссе от Казаково до Заулок равно 24 км, от Бора до Заулок – 30 км, от Бора до Малахово – 20 км, а от Бора до Шокши – 8 км.
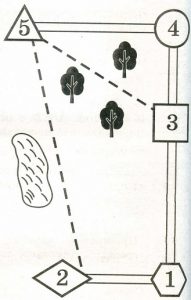
Задание 6.
Найдите значение выражения
Задание 7.
Какое из следующих чисел заключено между числами и
?
1) 0,2
2) 0,3
3) 0,4
4) 0,5
Задание 8.
Найдите значение выражения
Задание 9.
Решите уравнение (5х – 2)(–х + 3) = 0
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Задание 10.
В группе туристов 8 человек. С помощью жребия они выбирают трёх человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?
Задание 11.
Установите соответствие между формулами, которыми заданы функции, и графиками этих функций.
ФОРМУЛЫ
А) у = –х2 + 2х + 4
Б) у = х2 – 2х – 4
В) у = –х2 – 2х + 4
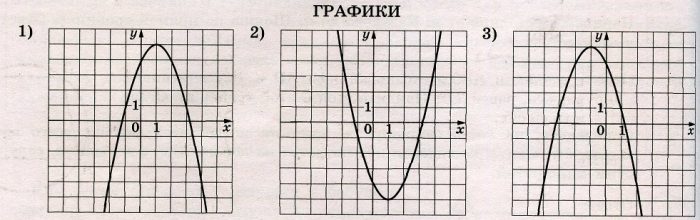
В таблице под каждой буквой укажите соответствующий номер.
Задание 13.
Укажите решение неравенства
x2 – 49 ≥ 0.
1) [–7;7]
2) нет решений
3) (–∞; –7] ∪ [7; +∞)
4) (–∞; +∞)
Задание 14.
К концу 2009 года в городе проживало 53 100 человек. Каждый год число жителей города ‚возрастало на одну и ту же величину. В конце 2018 года в городе проживало 60 390 человек. Какова была численность населения этого города к концу 2015 года?
![]()
Задание 15.
Точки М и N являются серединами сторон АВ и ВС треугольника АВС, сторона АВ равна 73, сторона ВС равна 31, сторона АС равна 42. Найдите МN.
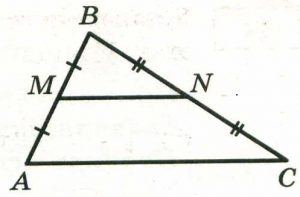
Задание 16.
Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 77°. Найдите угол С этой трапеции. Ответ дайте в градусах.
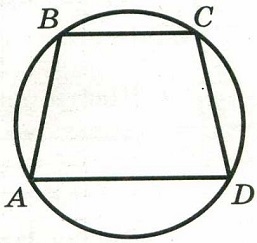
Задание 17.
В ромбе АВСD угол АВС равен 68°. Найдите угол АСD. Ответ дайте в градусах.
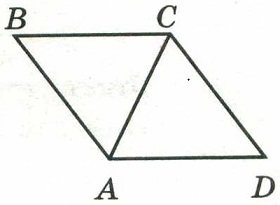
Задание 18.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
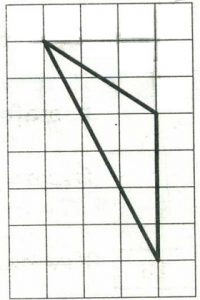
Задание 19.
Какие из следующих утверждений верны?
1) Диагональ параллелограмма делит его на два равных треугольника.
2) Все углы ромба равны.
3) Площадь квадрата равна произведению двух его смежных сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ЧАСТЬ 2
![]()
Задание 20.
Найдите значение выражения 41a – b + 45, если
Задание 21.
Шесть одинаковых рубашек дешевле куртки на 8 %. На сколько процентов девять таких же рубашек дороже куртки?
Задание 22.
Постройте график функции и определите, при каких значениях k прямая у = kх имеет с графиком ровно одну общую точку.
![]()
Задание 23.
Биссектриса угла А параллелограмма АВСD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК = 10, СК = 18.
Задание 24.
Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой СD. Докажите, что CD⊥EF.
Задание 25.
В треугольнике АВС биссектриса ВЕ и медиана АD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника АВС.
Источник варианта: Сборник ОГЭ 2021 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Статьи
Основное общее образование
Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)
Математика
Представляем вашему вниманию разбор 15 задания ОГЭ-2019 по математике.
14 ноября 2018
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 15
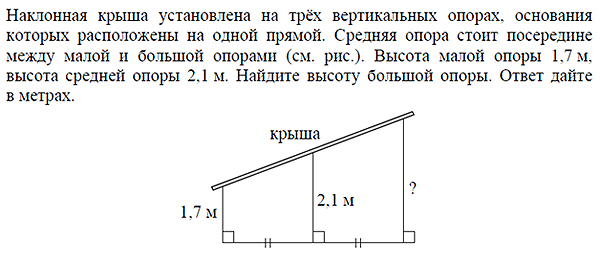
Решение
Фигура, изображенная на рисунке, является прямоугольной трапецией. Средняя опора есть не что иное, как средняя линия трапеции, длина которой вычисляется по формуле

где a, b – длины оснований. Составим уравнение:

b = 2,5.
Ответ: 2,5.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить
ОГЭ по математике №15. Треугольники, четырёхугольники, многоугольники и их элементыadmin2022-03-19T15:42:57+03:00
Скачать файл в формате pdf.
Комментарии для сайта Cackle
|
В треугольнике два угла равны 48° и 79°. Найдите третий угол. Ответ дайте в градусах. | Решение: Сумма углов треугольника равна 180°, поэтому третий угол равен: 180° – (48° + 79°) = 180° – 127° = 53°.
| ||||||
|
В треугольнике АВС известно, что
Ответ дайте в градусах. | Решение: Ответ:
| ||||||
|
В треугольнике АВС известно, что АС = 54, ВМ – медиана, ВМ = 45. Найдите АМ. | Решение: АМ = 54 : 2 = 27, так как медиана делит противоположную сторону пополам. Ответ: АМ = 27.
| ||||||
|
В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 132°. Найдите угол АВС. Ответ дайте в градусах. | Решение:
Ответ:
|
|
В остроугольном треугольнике АВС проведена высота ВН, Найдите угол АВН. Ответ дайте в градусах. | Решение: Рассмотрим значит по теореме о сумме углов треугольника
Ответ:
| ||||||
|
В треугольнике одна из сторон равна 29, а опущенная на нее высота равна — 12. Найдите площадь треугольника. | Решение: Площадь треугольника равна половине произведения основания на высоту, поэтому
| ||||||
|
Точки М и N являются серединами сторон АВ и ВС треугольника АВС, сторона АВ равна 28, сторона ВС равна 44, сторона АС равна 42. Найдите МN. | Решение: Средняя линия треугольника параллельна одной из сторон треугольника и равна ее половине.
Ответ: 21.
| ||||||
|
Точки М и N являются серединами сторон АВ и ВС треугольника АВС соответственно. Отрезки АN и СМ пересекаются в точке О, АN = 18, СМ = 21. Найдите ОМ. | Решение: Точки М и N являются серединами сторон АВ и ВС, значит поэтому поэтому точкой пересечения делятся в отношении 2 : 1, считая от вершины
Ответ: 7.
| ||||||
|
Катеты прямоугольного треугольника равны 12 и 5. Найти гипотенузу этого треугольника. | Решение: Квадрат гипотенузы равен сумме квадратов катетов:
Ответ: 13.
| ||||||
|
В прямоугольном треугольнике катет и гипотенуза соответственно равны 7 и 25. Найти второй катет этого треугольника. | Решение: Квадрат гипотенузы равен сумме квадратов катетов:
Ответ: 24.
| ||||||
|
В треугольнике АВС угол А равен 45°, угол В равен 30°, ВС = | Решение: По теореме синусов:
Ответ: 6.
| ||||||
|
В треугольнике АВС угол С равен 90°, АС = 14, АВ = 20. Найдите | Решение: Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Ответ: 0,7.
| ||||||
|
В треугольнике АВС угол С равен 90°, ВС = 12, АВ = 15. Найдите | Решение: Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Ответ: 0,8.
| ||||||
|
В треугольнике АВС угол С равен 90°, АC = 8, ВС = 5. Найдите | Решение: Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Ответ: 0,625.
| ||||||
|
Сторона равностороннего треугольника равна | Решение: Высота – медиана и биссектриса.
Ответ: 18.
| ||||||
|
На стороне треугольника АВС отмечена точка D так, что АD = 5, DС = 15. Площадь треугольника АВС равна 120. Найдите площадь треугольника ВСD. | Решение: Площади треугольников, имеющих одинаковые высоты относятся как основания.
Ответ: 90.
| ||||||
| В треугольнике АВС АВ = 15, ВС = 8,
Найдите площадь треугольника АВС. | Решение: Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Ответ: 50.
| ||||||
| Синус острого угла А треугольника АВС равен | Решение:
Ответ: 0,75
| ||||||
|
М
В треугольнике АВС угол С равен 90° Найдите СМ. | Решение: В прямоугольном треугольнике середина гипотенузы является центром описанной окружности , значит СМ = АМ = ВМ = 42 : 2 = 21 Ответ: 21
| ||||||
|
Биссектриса равностороннего треугольника равна | Решение: Любая биссектриса равностороннего треугольника является его медианой и высотой.
Ответ: 20.
|
Задание 15 323537 огэ математика

Задание 15 № 323537
Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Введём обозначения, как показано на рисунке. Пусть диагональ BD образует со стороной AB угол 51°. Диагонали прямоугольника точкой пересечения делятся пополам, поэтому треугольник ABO — равнобедренный, откуда получаем, что ∠ABO = ∠BAO = 51°. Сумма углов треугольника равна 180°, откуда ∠ BOA = 180° − 2 · 51° = 78°. Этот угол является острым углом между диагоналями прямоугольника.
Задание 15 № 323537
Сумма углов треугольника равна 180 , откуда BOA 180 2 51 78.
Oge. sdamgia. ru
11.08.2020 19:31:22
2020-08-11 19:31:22
Источники:
Https://oge. sdamgia. ru/test? pid=323537
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задание 15 323537 огэ математика
Задание 15 323537 огэ математика
Задание 15 323537 огэ математика

Задание 15 № 339515
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах.
Углы AOD и DOB — смежные, вместе составаляют развёрнутый угол, следовательно, ∠AOD = 180° − ∠DOB = 180° − 108° = 72°. Поскольку OK — биссектриса угла AOD, ∠AOK = ∠KOD = ∠AOD/2 = 72°/2 = 36°.
Задание 15 № 339515
Задание 15 339515.
Oge. sdamgia. ru
26.09.2020 7:54:19
2020-09-26 07:54:19
Источники:
Https://oge. sdamgia. ru/problem? id=339515
Задание №15 на ОГЭ по математике. Практические задачи по геометрии » /> » /> .keyword { color: red; } Задание 15 323537 огэ математика
Задание №15 на ОГЭ по математике. Практические задачи по геометрии
Задание №15 на ОГЭ по математике. Практические задачи по геометрии
1. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,2 метра от земли. Длина троса равна 4 метра. Найдите расстояние от основания флагштока до места крепления троса на земле. Ответ дайте в метрах.

Решение.
Треугольник на чертеже прямоугольный. Значит, применяем теорему Пифагора.
Расстояние от основания флагштока до места крепления троса на земле равно 2,4 м
2.Какой угол (в градусах) описывает минутная стрелка за 4 минуты?

Решение.
Так как 1 час – это 60 минут, а 1 круг – это 360 градусов, то одна минута соответствует
360 : 60 = 6 градусам на круге.
За 4 минуты минутная стрелка пройдет 6 ∙ 4 = 24 градуса.
Это полезно
Узнаете, чем отличаются официально-деловой, публицистический, научный, художественный и разговорный стили.

Узнаете, чем отличаются официально-деловой, публицистический, научный, художественный и разговорный стили.



Наш онлайн-курс по Физике
Все темы ЕГЭ с нуля
Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале!
Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео
Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали.
Мы обязательно ответим!
Мы заметили, что Вы регулярно пользуетесь нашими материалами для подготовки по физике.
Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале.
Ege-study. ru
23.12.2018 4:23:00
2018-12-23 04:23:00
Источники:
Https://ege-study. ru/ru/oge/materialy/matematika/zadanie-15/
Задание 1 № 366805
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Город Гранюк | Деревня Астрелка | Хутор Южный | Город Гусевск |
| Цифры |
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.
Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.
Ответ: 1465.
2. Задание 2 № 366806
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Решение.
Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится
 пачек чая.
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
3. Задание 3 № 366807
Найдите площадь (в км2), которую занимает заказник.
Решение.

Площадь заказника равна:

Ответ: 351.
4. Задание 4 № 366808
Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Решение.
Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
 км.
км.
Ответ: 30.
5. Задание 5 № 366809
Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | |||
| Шина вида «А» | |||
| Шина вида «Б» | |||
| Спица | |||
| Педаль вида «А» | |||
| Педаль вида «Б» | |||
| Тормоз вида «А» | нет | ||
| Тормоз вида «Б» | нет | ||
| Набор крепёжных изделий |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Решение.
На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:
 руб.
руб.
Ответ: 5300.
6. Задание 6 № 316314
Найдите значение выражения: 
Решение.
Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.
7. Задание 7 № 317575
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?
1) 
2) 
3) 
4) 
Решение.
Заметим, что  и
и  Проверим все варианты ответа:
Проверим все варианты ответа:
1)  — неверно;
— неверно;
2)  — верно;
— верно;
3)  — верно;
— верно;
4)  — верно.
— верно.
Ответ указан под номером 1.
8. Задание 8 № 353586
Какое из данных ниже чисел является значением выражения 
1) 
2) 
3) 
4) 
Решение.
Последовательно получим:


Ответ: 1
9. Задание 9 № 338500
При каком значении  значения выражений
значения выражений  и
и  равны?
равны?
Решение.
Для ответа на вопрос задачи нужно решить уравнение  Решим его:
Решим его:

Ответ: 2.
10. Задание 10 № 325450
В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
Решение.
Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна 
Ответ: 0,3.
11. Задание 11 № 311406
На рисунке изображён график функции  . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке 
2) 
3) 
4) прямая  пересекает график в точках
пересекает график в точках  и
и 
Решение.
Проверим каждое из утверждений.
1) Функция возрастает на промежутке  — неверно, функция убывает на промежутке
— неверно, функция убывает на промежутке  и затем возрастает на
и затем возрастает на  .
.
2)  — неверно,
— неверно, 

3)  — верно, видно из графика.
— верно, видно из графика.
4) Прямая  пересекает график в точках
пересекает график в точках  и
и  — верно, видно из графика.
— верно, видно из графика.
Таким образом, неверные утверждения находятся под номерами 1 и 2.
Ответ: 12.
12. Задание 12 № 311543
Площадь любого выпуклого четырехугольника можно вычислять по формуле  , где
, где  — длины его диагоналей, а
— длины его диагоналей, а  угол между ними. Вычислите
угол между ними. Вычислите  , если
, если  .
.
Решение.
Выразим  :
:

Подставляя, получаем:

Ответ: 0,4.
13. Задание 13 № 338497
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.

1) 1
2) 2
3) 3
4) 4
Решение.
Решим неравенство методом интервалов:


Правильный ответ указан под номером: 4.
14. Задание 14 № 406645
В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Решение.
Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.
Найдем сумму этой прогрессии:

Ответ: 377 мест.
15. Задание 15 № 340000

В прямоугольном треугольнике  катет
катет  , а высота
, а высота  , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна  Найдите
Найдите 
Решение.
Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Углы  и
и  равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.
16. Задание 16 № 351463
 На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что  Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Решение.
Пусть длина большей дуги  равна
равна  Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.
17. Задание 17 № 169876
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на  .
.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.
———-
В открытом банке иррациональный ответ.
18. Задание 18 № 350842

Найдите угол 
Решение.

Искомый угол  опирается на
опирается на  часть окружности:
часть окружности:  . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.
. Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е. 
Ответ: 22,5
19. Задание 19 № 401617
Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.
Ответ: 13.
20. Задание 20 № 338505
Решите неравенство 
Решение.
Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение 


Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).
Таким образом, ответ 
Ответ: 
Примечание.
Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно, 
21. Задание 21 № 353527
Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли  г 21-процентного раствора, тогда взяли и
г 21-процентного раствора, тогда взяли и  г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится
г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится  г, а во втором —
г, а во втором —  г Концентрация получившегося раствора равна
г Концентрация получившегося раствора равна  или 58%.
или 58%.
Ответ: 58.
22. Задание 22 № 338288
Постройте график функции  И определите, при каких значениях
И определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение.
Упростим выражение:
По теореме, обратной теореме Виета, корни уравнения  равны -1 и -2 соответственно, тогда по формуле
равны -1 и -2 соответственно, тогда по формуле  , получаем:
, получаем:  . Имеем:
. Имеем:

График функции сводится к графику параболы  с выколотой точкой
с выколотой точкой 
Выделим полный квадрат:

Следовательно, график функции получается из графика функции  сдвигом на
сдвигом на  . (см. рис.)
. (см. рис.)

Из графика видно, что прямая  имеет с графиком функции ровно одну общую точку при
имеет с графиком функции ровно одну общую точку при  и
и 
Ответ: −1; 3.
23. Задание 23 № 339395
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.
Решение.
 Угол
Угол  — вписанный, он равен 90° и опирается на дугу
— вписанный, он равен 90° и опирается на дугу  следовательно, дуга
следовательно, дуга  равна 180°, значит, хорда
равна 180°, значит, хорда  — диаметр окружности и
— диаметр окружности и 
Ответ: 16.
24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Решение.
Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.
25. Задание 25 № 311926
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
Решение.

По свойству равнобедренной трапеции  следовательно, треугольники
следовательно, треугольники  и
и  равны. Так как
равны. Так как  =
=  треугольники
треугольники  и
и  равнобедренные, следовательно,
равнобедренные, следовательно,  и
и  — соответствующие медианы этих треугольников. Значит,
— соответствующие медианы этих треугольников. Значит,  Отрезок
Отрезок  соединяет середины диагоналей трапеции, следовательно,
соединяет середины диагоналей трапеции, следовательно,  и прямые
и прямые 
 и
и  параллельны, поэтому,
параллельны, поэтому,  — трапеция. Проведём
— трапеция. Проведём  — высоту трапеции
— высоту трапеции  и
и  — высоту трапеции
— высоту трапеции  . Прямоугольные треугольники
. Прямоугольные треугольники  и
и  подобны, значит,
подобны, значит, 
Площадь трапеции  :
: 
Площадь трапеции 


Ответ: 9.




















































