Задание 15 номер 311514

xpinknsa676

xpinknsa676

Вопрос по математике:

Номер 14* и 15* помогите плиз♡♡♡♡♡♡♡

Изображение к вопросу

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

xchosldesy

xchosldesy

15 Б) 1,3,9,27,81. Умножаешь на 3

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

  • Отвечать достоверно на те вопросы, на которые знаете
    правильный ответ;
  • Писать подробно, чтобы ответ был исчерпывающий и не
    побуждал на дополнительные вопросы к нему;
  • Писать без грамматических, орфографических и
    пунктуационных ошибок.

Этого делать не стоит:

  • Копировать ответы со сторонних ресурсов. Хорошо ценятся
    уникальные и личные объяснения;
  • Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
    знаю» и так далее;
  • Использовать мат — это неуважительно по отношению к
    пользователям;
  • Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Условие

15 номер задания

математика 10-11 класс
388

Все решения

Написать комментарий

Задание 15 номер 311514

Обозначим АВС. АС-основание. Проведем высоту с вершины В. Пункт пересечения обозначим Н. Значит АН=26/2=13 см, так как высота в равнобедренном треугольнике является медианой и биссектрисой.  Треугольник АВН-прямоугольный. Угол АВН=60 градусов. Значит угол ВАН=30 градусов, с этого получается, что ВН в два раза меньше, чем АВ, потому что лежит против угла в 30 градусов. Пусть ВН-х см, тогда АВ=2х см. По теореме Пифагора 4х²=х²+169, 3х²=169, х=√169/3 =13/√3. S=1/2*26*13/√3=(169√3)/3 см².

Задание 15 номер 311514

В четырёх маленьких клетках 3*4=12 кроликов.
В пяти больших клетках 9*5=45 кроликов .
вроде так

Задание 15 номер 311514

Ответ:

Купили -8 рулонов обоев.

Длиной по 10м 50 см.

Израсходовали 3/4 части.

Ск. метров обоев осталось-?

10 м 50 см = 1050 см

1) 8*1050=8400 (см) или 84 (м) — обоев всего

2) 8400*3/4=252/4  (см) или 63 (м) — израсходовали

3) 84 — 63 = 21 (м) — осталось

ответ: 21 м обоев остался

Пошаговое объяснение:

Задание 15 номер 311514

U= frac{435}{3} =145 км/ч — скорость вертолета
U=145*3=435 км/ч — скорость самолета
S=435*5=2175 км — пролетел самолет за 5 часов

ОТВЕТ: 2175 км

Случайная величина 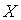 распределена равномерно на отрезке . Тогда случайная величина 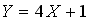   имеет…

другой (не равномерный) вид распределения

равномерное распределение на отрезке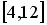

равномерное распределение на отрезке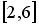  

равномерное распределение на отрезке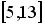  

Условие задачи

Задание 15 номер 311514

Решение

Задание 15 номер 311514

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что (a-b)^2=(b-a)^2 . Используем также условия 3-x>0; x+4>0.

Задание 15 номер 311514

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря, Задание 15 номер 311514.

Поскольку Задание 15 номер 311514

Согласно методу замены множителя, выражение log_{3-x}{(x+4)} заменим
на (3-x-1)(x+4-1).
Получим систему:

Задание 15 номер 311514

Решить ее легко.

Ответ:

x∈[-3;2).

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.

Источник

logo

    • Предмет:

      Геометрия

    • Автор:

      janaemoyer537

    • Создано:

      3 года назад

    Ответы

    Знаешь ответ? Добавь его сюда!

  • geometriya
    Геометрия

    1 минута назад

    Помогите пожалуйста решить задачу по геометрии, умоляю

  • matematika
    Математика

    5 минут назад

    У скольких трехзначных чисел сумма цифр равна произведению цифр? Помогите пожалуйста!!!

  • fizika
    Физика

    10 минут назад

    Помогите решить задачу

  • literatura
    Литература

    15 минут назад

    ПОМОГИТЕ ПОЖАЛУЙСТА. ПЕЧОРИН, ГЕРОЙ НАШЕГО ВРЕМЕНИ (княжна Мери)

  • himiya
    Химия

    20 минут назад

    Предмет: Химия. Тема: Классификация неорганических соединений

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Вы не можете общаться в чате, вы забанены.

Чтобы общаться в чате подтвердите вашу почту
Отправить письмо повторно

Вопросы без ответа

  • matematika
    Математика

    2 часа назад

    ПРЯМОУГОЛЬНИК ДЛИНОЙ 8 СМ И ШИРИНОЙ 4 СМ. КАК ПРОВЕСТИ В ЭТОМ ПРЯМОУГОЛЬНИКЕ ОТРЕЗОК,ЧТОБЫ ПОЛУЧИЛОСЬ ДВА ТРЕУГОЛЬНИКА. 

  • angliiskii-yazyk
    Английский язык

    4 часа назад

    перестройте предложения текста употребив страдательный залог.

    In January the Fernwood Company hired Martha as a secretary, In March the company sent her to school to study statistics and programming. In April the boss gave her the first raise. Just two months later, he promoted Martha to the position of supervisor of her department. In November they invited her to take a position in the company’s office in England. And in December the company gave her the new job in London.

Топ пользователей

  • avatar

    Fedoseewa27

    20959

  • avatar

    Sofka

    7417

  • avatar

    vov4ik329

    5113

  • avatar

    DobriyChelovek

    4631

  • avatar

    olpopovich

    3461

  • avatar

    zlatikaziatik

    3125

  • avatar

    manbenzopila

    2540

  • avatar

    Udachnick

    1867

  • avatar

    Zowe

    1683

  • avatar

    NikitaAVGN

    1210

Войти через Google

или

Запомнить меня

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

Выберите язык и регион

Русский

Россия

English

United States

zoom

How much to ban the user?

1 hour
1 day

Источник

t1609674978aa.png

В треугольнике два угла равны 48° и 79°. Найдите третий угол. Ответ дайте в градусах.

Решение:

Сумма углов треугольника равна 180°, поэтому третий угол равен:

180° – (48° + 79°) = 180° – 127° = 53°.

5

3

t1609674978ab.png

В треугольнике АВС известно, что t1609674978ac.gif

t1609674978ad.gif— биссектриса. Найдите угол ВАD.

Ответ дайте в градусах.

Решение:
t1609674978ae.gif, так как биссектриса делит угол пополам.

Ответ: t1609674978af.gif

3

8

t1609674978ag.png

В треугольнике АВС известно, что АС = 54,

ВМ – медиана, ВМ = 45. Найдите АМ.

Решение: АМ = 54 : 2 = 27, так как медиана делит противоположную сторону пополам.

Ответ: АМ = 27.

2

7

t1609674978ah.pngD

В равнобедренном треугольнике АВС

с основанием АС внешний угол при

вершине С равен 132°. Найдите угол АВС.

Ответ дайте в градусах.

Решение:
t1609674978ai.gif.

t1609674978aj.gif, так как углы при основании равнобедренного треугольника равны.

t1609674978ak.gif, сумма углов треугольника равна 180.

Ответ: t1609674978al.gif

8

4

t1609674978am.png

В остроугольном треугольнике АВС

проведена высота ВН, t1609674978an.gif

Найдите угол АВН.

Ответ дайте в градусах.

Решение:

Рассмотрим t1609674978ao.gif

значит по теореме о сумме углов треугольника

t1609674978ap.gif

Ответ: t1609674978aq.gif

3

4

t1609674978ar.gif

В треугольнике одна из сторон равна 29, а опущенная на нее высота равна — 12.

Найдите площадь треугольника.

Решение:

Площадь треугольника равна половине произведения основания на высоту, поэтому

t1609674978as.gif

1

7

4

t1609674978at.gif

Точки М и N являются серединами сторон

АВ и ВС треугольника АВС, сторона

АВ равна 28, сторона ВС равна 44, сторона АС равна 42. Найдите МN.

Решение:

Средняя линия треугольника параллельна одной из сторон треугольника и равна ее половине.

t1609674978au.gif

Ответ: 21.

2

1

t1609674978av.png

Точки М и N являются серединами сторон

АВ и ВС треугольника АВС соответственно.

Отрезки АN и СМ пересекаются в точке О,

АN = 18, СМ = 21. Найдите ОМ.

Решение:

Точки М и N являются серединами сторон

АВ и ВС, значит t1609674978aw.gifмедианы,

поэтому поэтому точкой пересечения

делятся в отношении 2 : 1, считая от вершины

t1609674978ax.gif

Ответ: 7.

7

t1609674978ay.gif

Катеты прямоугольного треугольника

равны 12 и 5. Найти гипотенузу этого треугольника.

Решение:

Квадрат гипотенузы равен сумме

квадратов катетов:

t1609674978az.gif

Ответ: 13.

1

3

t1609674978ay.gif

В прямоугольном треугольнике катет и гипотенуза соответственно равны 7 и 25.

Найти второй катет этого треугольника.

Решение:

Квадрат гипотенузы равен сумме

квадратов катетов:

t1609674978ba.gif

Ответ: 24.

2

4

t1609674978bb.gif

В треугольнике АВС угол А равен 45°,

угол В равен 30°, ВС = t1609674978bc.gif.Найдите АС.

Решение:

По теореме синусов:

t1609674978bd.gif

Ответ: 6.

8

t1609674978be.png

В треугольнике АВС угол С равен 90°,

АС = 14, АВ = 20. Найдите t1609674978bf.gif.

Решение:

Синусом острого угла прямоугольного треугольника называется отношение

противолежащего катета к гипотенузе.

t1609674978bg.gif

Ответ: 0,7.

0

,

7

t1609674978be.png

В треугольнике АВС угол С равен 90°,

ВС = 12, АВ = 15. Найдите t1609674978bh.gif.

Решение:

Косинусом острого угла прямоугольного треугольника называется отношение

прилежащего катета к гипотенузе.

t1609674978bi.gif

Ответ: 0,8.

0

,

8

t1609674978bj.gif

В треугольнике АВС угол С равен 90°,

АC = 8, ВС = 5. Найдите t1609674978bk.gif.

Решение:

Тангенсом острого угла прямоугольного треугольника называется отношение

противолежащего катета к

прилежащему катету.

t1609674978bl.gif

Ответ: 0,625.

0

,

6

2

5

t1609674978bm.png

Сторона равностороннего треугольника

равна t1609674978bn.gif.Найдите его высоту.

Решение: Высота – медиана и биссектриса.

t1609674978bo.gif

Ответ: 18.

1

8

t1609674978bp.gif

На стороне треугольника АВС отмечена точка D так, что АD = 5, DС = 15. Площадь треугольника АВС равна 120.

Найдите площадь треугольника ВСD.

Решение:

Площади треугольников, имеющих одинаковые высоты относятся как основания.

t1609674978bq.gif

Ответ: 90.

9

0

В треугольнике АВС АВ = 15, ВС = 8,

t1609674978br.gif.

Найдите площадь треугольника АВС.

Решение:

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

t1609674978bs.gif

Ответ: 50.

5

0

Синус острого угла А треугольника АВС

равен t1609674978bt.gif. Найдите косинус угла А.

Решение:

t1609674978bu.gif

Ответ: 0,75

0

,

7

5

t1609674978bv.gift1609674978bw.gif

М

t1609674978bx.gift1609674978bx.gif

В треугольнике АВС угол С равен 90°
М – середина АВ, АВ = 42, ВС = 30.

Найдите СМ.

Решение:

В прямоугольном треугольнике середина гипотенузы является центром описанной окружности , значит

СМ = АМ = ВМ = 42 : 2 = 21

Ответ: 21

2

1

t1609674978bm.png

Биссектриса равностороннего треугольника

равна t1609674978by.gif. Найдите его сторону.

Решение:

Любая биссектриса равностороннего треугольника является его медианой и высотой.

t1609674978bz.gif

Ответ: 20.

2

0
Источник

Простой способ вычислить проценты от X

Сколько будет   %

от   ?  

15% от 311514 это: 46727.1

Процент от — Таблица для 311514

Процент от Разница
1% от 311514 это 3115.14 308398.86
2% от 311514 это 6230.28 305283.72
3% от 311514 это 9345.42 302168.58
4% от 311514 это 12460.56 299053.44
5% от 311514 это 15575.7 295938.3
6% от 311514 это 18690.84 292823.16
7% от 311514 это 21805.98 289708.02
8% от 311514 это 24921.12 286592.88
9% от 311514 это 28036.26 283477.74
10% от 311514 это 31151.4 280362.6
11% от 311514 это 34266.54 277247.46
12% от 311514 это 37381.68 274132.32
13% от 311514 это 40496.82 271017.18
14% от 311514 это 43611.96 267902.04
15% от 311514 это 46727.1 264786.9
16% от 311514 это 49842.24 261671.76
17% от 311514 это 52957.38 258556.62
18% от 311514 это 56072.52 255441.48
19% от 311514 это 59187.66 252326.34
20% от 311514 это 62302.8 249211.2
21% от 311514 это 65417.94 246096.06
22% от 311514 это 68533.08 242980.92
23% от 311514 это 71648.22 239865.78
24% от 311514 это 74763.36 236750.64
25% от 311514 это 77878.5 233635.5
26% от 311514 это 80993.64 230520.36
27% от 311514 это 84108.78 227405.22
28% от 311514 это 87223.92 224290.08
29% от 311514 это 90339.06 221174.94
30% от 311514 это 93454.2 218059.8
31% от 311514 это 96569.34 214944.66
32% от 311514 это 99684.48 211829.52
33% от 311514 это 102799.62 208714.38
34% от 311514 это 105914.76 205599.24
35% от 311514 это 109029.9 202484.1
36% от 311514 это 112145.04 199368.96
37% от 311514 это 115260.18 196253.82
38% от 311514 это 118375.32 193138.68
39% от 311514 это 121490.46 190023.54
40% от 311514 это 124605.6 186908.4
41% от 311514 это 127720.74 183793.26
42% от 311514 это 130835.88 180678.12
43% от 311514 это 133951.02 177562.98
44% от 311514 это 137066.16 174447.84
45% от 311514 это 140181.3 171332.7
46% от 311514 это 143296.44 168217.56
47% от 311514 это 146411.58 165102.42
48% от 311514 это 149526.72 161987.28
49% от 311514 это 152641.86 158872.14
50% от 311514 это 155757 155757
51% от 311514 это 158872.14 152641.86
52% от 311514 это 161987.28 149526.72
53% от 311514 это 165102.42 146411.58
54% от 311514 это 168217.56 143296.44
55% от 311514 это 171332.7 140181.3
56% от 311514 это 174447.84 137066.16
57% от 311514 это 177562.98 133951.02
58% от 311514 это 180678.12 130835.88
59% от 311514 это 183793.26 127720.74
60% от 311514 это 186908.4 124605.6
61% от 311514 это 190023.54 121490.46
62% от 311514 это 193138.68 118375.32
63% от 311514 это 196253.82 115260.18
64% от 311514 это 199368.96 112145.04
65% от 311514 это 202484.1 109029.9
66% от 311514 это 205599.24 105914.76
67% от 311514 это 208714.38 102799.62
68% от 311514 это 211829.52 99684.48
69% от 311514 это 214944.66 96569.34
70% от 311514 это 218059.8 93454.2
71% от 311514 это 221174.94 90339.06
72% от 311514 это 224290.08 87223.92
73% от 311514 это 227405.22 84108.78
74% от 311514 это 230520.36 80993.64
75% от 311514 это 233635.5 77878.5
76% от 311514 это 236750.64 74763.36
77% от 311514 это 239865.78 71648.22
78% от 311514 это 242980.92 68533.08
79% от 311514 это 246096.06 65417.94
80% от 311514 это 249211.2 62302.8
81% от 311514 это 252326.34 59187.66
82% от 311514 это 255441.48 56072.52
83% от 311514 это 258556.62 52957.38
84% от 311514 это 261671.76 49842.24
85% от 311514 это 264786.9 46727.1
86% от 311514 это 267902.04 43611.96
87% от 311514 это 271017.18 40496.82
88% от 311514 это 274132.32 37381.68
89% от 311514 это 277247.46 34266.54
90% от 311514 это 280362.6 31151.4
91% от 311514 это 283477.74 28036.26
92% от 311514 это 286592.88 24921.12
93% от 311514 это 289708.02 21805.98
94% от 311514 это 292823.16 18690.84
95% от 311514 это 295938.3 15575.7
96% от 311514 это 299053.44 12460.56
97% от 311514 это 302168.58 9345.42
98% от 311514 это 305283.72 6230.28
99% от 311514 это 308398.86 3115.14
100% от 311514 это 311514 0

Как можно рассчитать 15% от 311514

В магазине товар стоит 311514₽, вам дали скидку 15% и вы хотите понять сколько вы сэкономили.

Решение:

Сэкономленная сумма = Цена товара * Скидка в процентах/ 100

Сэкономленная сумма = (15 * 311514) / 100

Сэкономленная сумма = 46727.1₽

Проще говоря, при покупке товара за 311514₽ и скидке в 15%, вы заплатите 264786.9₽ и при этом сэкономите 46727.1₽.

Для рассчета НДС от 311514₽, вы можете использовать Калькулятор НДС онлайн

Расчеты процентов: примеры

  • 30 от 2000
  • 30 от 1000
  • 30 от 300
  • 30 от 5000
  • 28% от 265911
  • 40% от 345039
  • 86% от 138345
  • 60% от 338073
  • 24% от 107540
  • 97% от 244897
  • 41% от 392911
  • 85% от 349031
  • 91% от 6436
  • 17% от 206146
  • 9% от 308659
  • 12% от 3069
  • 20 от 40
  • 20 от 4000
  • 40 от 200
  • 12 от 40000

percent-calc.com    © 2023

Источник

Задача 1

В треугольнике $ABC$ стороны $AC$ и $BA$ равны. Внешний угол при вершине $B$ равен $116^°$. Найдите угол $A$. Ответ дайте в градусах.

Задача 2

Прямые $m$ и $n$ параллельны. Найдите $∠ 3$, если $∠ 1=40^°$, $∠ 2=98^°$ (см. рис.). Ответ дайте в градусах.

Задача 3

Найдите величину острого угла параллелограмма $ABCD$, если биссектриса угла $D$ образует со стороной $BC$ угол, равный $53^°$ (см. рис.). Ответ дайте в градусах.

Задача 4

Высота равностороннего треугольника равна $11√ {3}$. Найдите его периметр.

Задача 5

Высота равностороннего треугольника равна $15√ {3}$. Найдите его периметр.

Задача 6

В параллелограмме $ABCD$ диагонали $AC$ и $BD$ пересекаются в точке $O$. Сторона $AD=11$, а расстояние от точки $O$ до этой стороны равно $4$ (см. рис.). Найдите площадь параллелограмма.

Задача 7

В прямоугольном треугольнике $ABC$ катет $BC=12√ {2}$, а высота $CK$, опущенная на гипотенузу, равна $3√ {2}$. Найдите $sin ∠ ABC$ (см. рис.).

Задача 8

На прямой $AB$ взята точка $L$. Луч $LK$ — биссектриса угла $CLB$. Известно, что $∠ KLC=64^°$ (см. рис.). Найдите угол $CLA$. Ответ дайте в градусах.

Задача 9

В треугольнике $ABC$ $AN$ — медиана и $AL$ — высота. Известно, что $BC=68$, $LC=17$ и $∠ BCA=52^°$ (см. рис.). Найдите угол $BNA$. Ответ дайте в градусах.

Задача 10

В треугольнике $ABC$ проведена биссектриса $AE$, угол $AEC$ равен $104^°$, угол $ABC$ равен $82^°$. Найдите угол $ACB$ (см. рис.). Ответ дайте в градусах.

Задача 11

В трапеции $ABCD$ $AB=CD$, $∠ BDA=42^°$ и $∠ BDC=34^°$ (см. рис.). Найдите угол $ABD$. Ответ дайте в градусах.

Задача 12

Сумма двух углов равнобедренной трапеции равна $240^°$. Найдите меньший угол трапеции. Ответ дайте в градусах.

Задача 13

В треугольнике $ABC$ угол $C$ равен $90^°$, $AC=9$, $cos A={1} / {3}$. Найдите $AB$.

Задача 14

В треугольнике $ABC$ стороны $AC$ и $BC$ равны. Внешний угол при вершине $B$ равен $146^°$. Найдите угол $C$. Ответ дайте в градусах.

Задача 15

Прямые $m$ и $n$ параллельны. Найдите $∠ 3$, если $∠ 1=36^°$, $∠ 2=102^°$ (см. рис.). Ответ дайте в градусах.

Задача 16

Найдите величину острого угла параллелограмма $ABCD$, если биссектриса угла $A$ образует со стороной $BC$ угол, равный $23^°$ (см. рис.). Ответ дайте в градусах.

Задача 17

В прямоугольном треугольнике $ABC$ катет $AC=16√ {3}$, а высота $CM$, опущенная на гипотенузу, равна $6√ {3}$. Найдите $sin ∠ BAC$ (см. рис.).

Задача 18

На прямой $AB$ взята точка $F$. Луч $FD$ — биссектриса угла $CFA$. Известно, что $∠ DFC=75^°$ (см. рис.). Найдите угол $CFB$. Ответ дайте в градусах.

Задача 19

В треугольнике $ABC$ $BF$ — медиана и $BK$ — высота. Известно, что $AC=28$, $KC=7$ и $∠ ACB=65^°$ (см. рис.). Найдите угол $AFB$. Ответ дайте в градусах.

Задача 20

Стороны параллелограмма равны $10$ и $15$. Высота, проведённая к меньшей стороне, равна $12$. Найдите высоту, проведённую к большей стороне.

Источник

  • Задание 15 номер 311355
  • Задание 22 номер 593 география
  • Задание 15 номер 311343
  • Задание 15 номер 193
  • Задание 22 номер 1966