Не могу найти по номеру выполняемое многоразовое задание. Да и любые другие по номеру не найти). Пробовал произвольно выбранные задания вызвать по номеру — и ничего!)
Обсуждение
gimmegun
12 Окт 2017 г, в 09:01
редактир. 12 Окт 2017 г, в 09:06
Одной из причин может быть выбор фильтров
По спискам
и
По типу
при поиске.
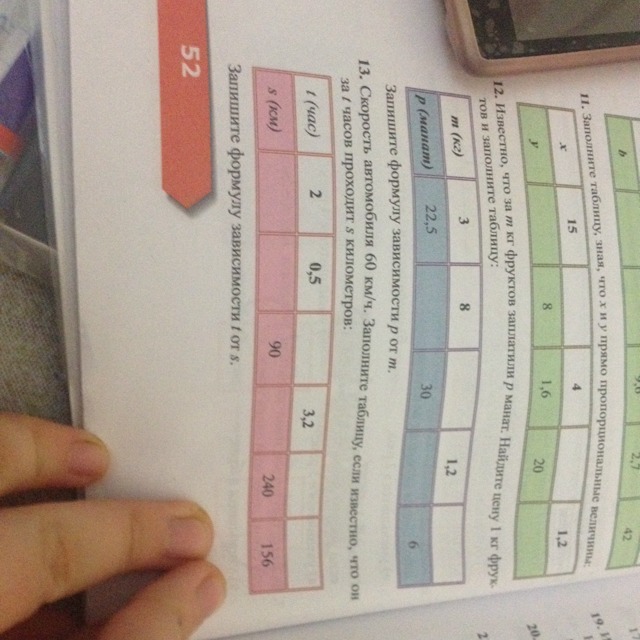
Если это (эти) задание у Вас в Избранном, то должны быть выбраны фильтры
Избранное
и
Все.
Если выбраны
Все
и
Все
, то задание не покажут.
Если задание не в Избранном, то соответственно наоборот — должны быть выбраны фильтры
Все
и
Все
.
Другой причиной может быть то, что задание выключено или забанено.
Не годится…(( Принцип, который вы описали, до меня добрел)), я им воспользовался, результат=0. Сейчас вот еще на всякий случай попробовал. Взял номер первого попавшегося задания (оно у меня никак не отмечено), выбрал «Все», ввел номер, и тишина…
Для обсуждения вопроса/идеи необходима регистрация.
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
Объяснение:
решение во вложении
Ответ подобран нейросетью
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
1)16*6=96
2)96:3=32
Пошаговое объяснение:
Ответ подобран нейросетью
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
32 пакета.
Пошаговое объяснение:
В одном ящике 16кг,а в 6 таких ящиках
1) 6*16=96 кг моркови всего привезли.
В одном пакете 3кг.
2) 96:3=32 пакета с морковью.
Ответ подобран нейросетью
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
5 минут
Объяснение:
Смотри фото
Ответ подобран нейросетью
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
Можно лучший ответ?)))
Ответ подобран нейросетью
Мгновенный доступ
50 баллов
ИЛИ
Доступ после просмотра рекламы
Ответы будут доступны после просмотра рекламы
Пусть 3 1/3 часа -3 часа 20 минут(200 минут) — первый насос
Пусть 1 1/2 раза — представим, как 1,5 раз — второй насос
3 часа 20 минут * 1,5 раза = 300 (мин)
300 — 200 = 100 (мин) или 1 ч. 40 мин.- откачают воду оба насоса
ответ: за 1 ч. 40 мин.
4
1 ответ:
0
0
1) 120
2) 30
3)1,5
4)195
5)4
6)2,8
Читайте также
3 потому что это проходят в 6 классе
1) Площадь всей поверхность Земли = поверхность суши + поверхность воды.
Поверхность воды — неизвестное слагаемое.
Значит находим его так:
Поверхность воды = Площадь всей поверхности Земли — площадь суши
510.000.000 — 149.000.000 = 361.000.000 (км²) (или 361 млн км²)
2) Площадь Азии <u>на</u> 2282 тыс км² <u>больше</u>, чем площадь Северной и Южной Америки вместе.
Площадь Азии = Площадь Северной Америки + площадь Южной Америки + ещё 2282 тыс км²:
24.247.000 + 17.834.000 + 2.282.000 = 44.363.000 (км²) (или 44 млн 363 тыс км²)
3) Площадь Северного Ледовитого океана = Площадь Тихого океана : 12. (так Северный Ледовитый океан меньше Тихого и составляет одну двенадцатую его часть)
180.000.000 : 12 = 15.000.000 (км²) (или 15 млн км²)
(5/8 х — 1/5) *3/4=1 1/3
5/8 х-1/5=4/3 : 3/4
5/8 х — 1/5=4/3 * 4/3
5/8 х — 1/5=16/9
5/8 х=1 7/9+1/5
5/8 х=1 35/45+9/45
5/8 х=1 44/45
х=99/45 : 5/8
х=99/45 * 8/5
х=792/225=3 117/225
1) 300/100 * 28 = 84 квартиры однокомнатных
2) 300 — 84 = 216 квартир 2 и 3комнатных
принмаем за Х количество 3 комнатных, тогда двух будет х *1,7, отсюда
х + х * 1,7 = 216
2,7х = 216
х = 216 / 2,7
х = 80 трёхкомнатных
80 * 1,7 = 136 двухкомнатных
Проверка: 80 + 136 + 84 = 300
29-(34+98-63)
так наверное
Условие
15 номер задания
математика 10-11 класс
386
Все решения
Написать комментарий
| 30 | ||||||||||||||||||||
| В | вариантах | 12.26. | –12.30. | L | – | часть | дуги | линии | ||||||||||||
| x = a cost, | y = a sin t . | |||||||||||||||||||
| 12.26. ∫ | x2 | + y2 | dl;a =1; | π | ≤ϕ ≤ | π | . | |||||||||||||
| 8 | 4 | |||||||||||||||||||
| x2 | + y2 | |||||||||||||||||||
| L | ||||||||||||||||||||
| 12.27. ∫ρ cos 2ϕdl;a =2; | π | ≤ϕ ≤ | π . | |||||||||||||||||
| L | 4 | π . | 2 | |||||||||||||||||
| 12.28. ∫sin 4ϕdl;a =1; 0 ≤ϕ ≤ | ||||||||||||||||||||
| L | 4 | |||||||||||||||||||
| 12.29. ∫ | xy(x2 − y | 2 ) | dl;a = 2; | π | ≤ϕ ≤ | 3π | . | |||||||||||||
| (x2 | + y2 )2 | 8 | 8 | |||||||||||||||||
| L | ||||||||||||||||||||
| 12.30. ∫ρ a2 − ρ2 dl;a =1; | 0 ≤ϕ ≤ π. | |||||||||||||||||||
| L | ||||||||||||||||||||
| рода ∫ f (x, y)dl . | ||||||||||||||||||||
| L | ||||||||||||||||||||
| В | вариантах | 13.1. | –13.6. | L | – | часть | дуги | линии | ||||||||||||
| x = a cost, | y = a sin t . |
13.1. ∫
L
13.2. ∫
L
13.3. ∫
L
13.4. ∫
L
xydl; 0 ≤ t ≤ π4 .
(x + y)2dl; π4 ≤ t ≤π2 .
(x − y)2dl; π6 ≤ t ≤ π3 . xydl; 0 ≤ t ≤π3 ;
| 13.5. ∫ x2dl;0≤ t ≤ | π . | |||
| L | π | 6 | 2π . | |
| 13.6. ∫ y2dl; | ≤ t ≤ | |||
| L | 3 | 3 |
| 31 | |||||||||||||||||||||||||
| В вариантах | 13.7. | – | 13.12. | L | – | часть | дуги | линии | |||||||||||||||||
| x = a cost, y = bsin t . | |||||||||||||||||||||||||
| 13.7. ∫ xydl;0≤ t ≤ | π | ; a = 2;b =1. | |||||||||||||||||||||||
| L | 4 | ||||||||||||||||||||||||
| 13.8. ∫x3 ydl; | π | ≤ t ≤ π ; a =1;b = 2. | |||||||||||||||||||||||
| L | 4 | 2 | |||||||||||||||||||||||
| 13.9. ∫ xy3dl; | π | ≤ t ≤ | π | ;a = | 3;b =1. | ||||||||||||||||||||
| L | x | 4 | 2 | ||||||||||||||||||||||
| 13.10. ∫ | dl; | π | ≤ t ≤ | π | ;a = 2;b =1. | ||||||||||||||||||||
| y | 6 | 3 | |||||||||||||||||||||||
| L | |||||||||||||||||||||||||
| 13.11. ∫ | y | dl;0 | ≤ t ≤ π ;a =1;b = 3. | ||||||||||||||||||||||
| L x | xy | 3 | π ;a =1;b = 3. | ||||||||||||||||||||||
| 13.12. ∫ | dl;0 ≤ t ≤ | ||||||||||||||||||||||||
| 1+8x2 | |||||||||||||||||||||||||
| L | 4 | L | |||||||||||||||||||||||
| В вариантах | 13.13. | – | 13.18. | – | часть | дуги | линии | ||||||||||||||||||
| x = a cos3 t; y = a sin3 t . | |||||||||||||||||||||||||
| 13.13. ∫ xdl;0 ≤ t ≤ | π | ;a =1. | |||||||||||||||||||||||
| L | 2 | ||||||||||||||||||||||||
| 13.14. ∫ ydl; π | ≤ t ≤ π ;a = 2. | ||||||||||||||||||||||||
| L | 4 | 2 | |||||||||||||||||||||||
| 13.15. ∫3 | π | ;a = | 8. | ||||||||||||||||||||||
| xdl;0 ≤ t ≤ | |||||||||||||||||||||||||
| L | 4 | ||||||||||||||||||||||||
| 13.16. ∫ | 3 | π | ≤ t ≤ π ;a = 8. | ||||||||||||||||||||||
| ydl; | |||||||||||||||||||||||||
| L | 6 | 3 | |||||||||||||||||||||||
| 13.17. ∫(x2 / 3 + y2 / 3 )dl;0 ≤ t ≤ π ;a =1. | |||||||||||||||||||||||||
| L | y | 3 | |||||||||||||||||||||||
| 13.18. ∫ | ( | )1/ 3dl;0 | ≤ t ≤ π ;a = 2 / | ||||||||||||||||||||||
| L | x | 4 |
| 32 | ||||||||||||||||||||||||||||||
| В вариантах | 13.19. | – | 13.24. | L | – | часть | дуги | линии | ||||||||||||||||||||||
| x = t cost, y = t sin t . | ||||||||||||||||||||||||||||||
| dl;0 ≤ t ≤ π | ||||||||||||||||||||||||||||||
| 13.19. ∫ | x2 + y2 | . ] | ||||||||||||||||||||||||||||
| L | 2 | |||||||||||||||||||||||||||||
| )dl;≤ t ≤ π . | ||||||||||||||||||||||||||||||
| 13.20. ∫ | (2 + | x2 + y2 | ||||||||||||||||||||||||||||
| L | π | 3 | ||||||||||||||||||||||||||||
| 13.21. ∫ | (x2 + y2 )3/ 2dl; | ≤ t ≤ π . | ||||||||||||||||||||||||||||
| L | dl | 2 | π . | |||||||||||||||||||||||||||
| 13.22. ∫ | dl;0 ≤ t ≤ | |||||||||||||||||||||||||||||
| L | x2 + y2 | 4 | ||||||||||||||||||||||||||||
| 13.23. ∫ | x2 + y2 | dl; | π | ≤ t | ≤ | π | . | |||||||||||||||||||||||
| 1+ x2 + y2 | 6 | 4 | ||||||||||||||||||||||||||||
| L | ||||||||||||||||||||||||||||||
| (1+ x2 + y2 ) | π | π . | ||||||||||||||||||||||||||||
| 13.24. ∫ | x2 + y2 dl; | ≤ t ≤ | ||||||||||||||||||||||||||||
| L | 4 | L | 3 | |||||||||||||||||||||||||||
| В вариантах | 13.25. | – | 13.30. | – | часть | дуги | линии | |||||||||||||||||||||||
| x = t −sin t, | y =1−cost . | |||||||||||||||||||||||||||||
| 13.25. ∫ | ≤ π . | |||||||||||||||||||||||||||||
| ydl;0 ≤ t | ||||||||||||||||||||||||||||||
| L | 2 | |||||||||||||||||||||||||||||
| 13.26. ∫ ydl;0 ≤ t ≤π . | ||||||||||||||||||||||||||||||
| L | ||||||||||||||||||||||||||||||
| 13.27. ∫(y −1)dl;0 ≤ t ≤ 2π . | ||||||||||||||||||||||||||||||
| L | ||||||||||||||||||||||||||||||
| 13.28. ∫ y2dl;0 ≤ t ≤ π . | ||||||||||||||||||||||||||||||
| L | dl | |||||||||||||||||||||||||||||
| 13.29. ∫ | dl;1 ≤ t ≤ 2. | |||||||||||||||||||||||||||||
| 2y | ||||||||||||||||||||||||||||||
| L | ||||||||||||||||||||||||||||||
| 13.30. ∫ dldl; π | ≤ t ≤ π . | |||||||||||||||||||||||||||||
| L | y | 4 | 2 |
33
Задание 14. Вычислить криволинейный интеграл второго рода ∫Р(x, y)dx +Q(x, y)dy .
L
Ввариантах 14.1. – 14.10. L – отрезок прямой AB .
14.1.∫(x + y)dx +(x − y)dy; L : y = x2 ,0 ≤ x ≤1.
L
14.2. ∫ y2dx + x dy; L : y = x +1 ,0≤ x ≤ 2.
| L | ||||||
| 14.3. ∫ | y | dx + x2 | dy; L : y = | ,1 ≤ x ≤ 4. | ||
| x | ||||||
| L x | ||||||
| 14.4. ∫sin ydx + cos 2x dy; L : y = 2x ,0 ≤ x ≤1. | ||||||
| L |
| 14.5. ∫e2 y dx + | ||||
| xdy; L : y = x +1 ,1≤ x ≤ 2. | ||||
| L | ||||
| 14.6. ∫ x cos ydx + sin x dy; L : y = x2 ,0≤ x ≤1. | ||||
| L | x | |||
| 14.7. ∫ xe2 y dx + | ||||
| xdy; L : y = x2 ,1≤ x ≤ 2. | ||||
| L | ||||
| 14.8. ∫ x2e4dx + x3 dy; L : y = x3 ,0 ≤ x ≤1. | ||||
| L |
| 14.9. ∫(y2 +1)dx + x3dy; L : y = | ,0 ≤ x ≤ 2. | |||
| x | ||||
| L | ||||
| 14.10. ∫ dx | + dy ; L : y = x3 | ,1≤ x ≤ 3. | ||
| L y | x2 | – 14.20. L – часть дуги линии | ||
| В вариантах 14.10. | ||||
| x = at, y = bt, z = ct, 0 < t <1. |
14.11. ∫ y2 − x2dx +xydy; L : y = 
x ,0 ≤ x ≤1.
| L | |||||
| 14.12. ∫ | y | dx + | x | dy; L : y = x2 | ,1 ≤ x ≤ 2. |
| L x | y |
| 14.13. ∫ x | x | dy; L : y = x4 ,1≤ x ≤ 4. | ||||
| ydx + | ||||||
| y | ||||||
| L |
| 34 | ||||||||||
| 14.14. ∫ ye−x2 dx + | y2 | dy; L : y = x ,1 ≤ x ≤ 2. | ||||||||
| x | ||||||||||
| L | ||||||||||
| 14.15. ∫sin ydx +cos2 xdy; L : y = x +1 ,0≤ x ≤ 2. | ||||||||||
| L | ||||||||||
| 14.16. ∫ | x + ydx + | y − xdy; L : y = x +1 ,0 ≤ x ≤1. | ||||||||
| L | ||||||||||
| 14.17. ∫ xy2dx +cos | ||||||||||
| xdy; L : y = x ,0 ≤ x ≤ π 2 . | ||||||||||
| L |
14. 18. L∫ x
+y1dx +3
xdy; L : y = x2 ,0 ≤ x ≤1.
| y | dy; L : y = x4 | |||||||
| 14.19. ∫3 x2 ydx + 3 | ,1 ≤ x ≤2. | |||||||
| L | x |
14.20. ∫ x2e y dx + xy dy; L : y = x3 ,0 ≤ x ≤1.
| L | 14.21. – 14.30. L – часть дуги линии | ||||||||||||
| В вариантах | |||||||||||||
| x = R cost, y = R sin t, z = ht, | 0 ≤ t < π . | ||||||||||||
| 14.21. ∫ xsin ydx + | y | cos x3dy; L : y = x2 ,1≤ x ≤ 2. | |||||||||||
| x | |||||||||||||
| L | |||||||||||||
| dy; L : y = x3 ,1 ≤ x ≤ 2. | |||||||||||||
| 14.22. ∫ | y | dx + | x | ||||||||||
| L | x | y | |||||||||||
| 14.23. ∫cos | y | dx + dy | ; L : y = x2 | ,1 ≤ x ≤3. | |||||||||
| L | x | x | dy | ||||||||||
| 14.24. ∫ | ; L : y = x +1,0≤ x ≤1. | ||||||||||||
| 2y − xdx + | |||||||||||||
| 1+ x + y | |||||||||||||
| L |
| 14.25. ∫ x2exy dx + x | ||||||
| ydy; L : y = x2 ,0≤ x ≤1. | ||||||
| L | ||||||
| 14.26. ∫ yex4 dx + dy | ; L : y = x3 ,1 ≤ x ≤ 3. | |||||
| L | xdx | x2 | ||||
| 14.27. ∫ | dx + yxdy; L : y = x2 ,0 ≤ x ≤1. | |||||
| y | ||||||
| L cos2 |
|
В треугольнике два угла равны 48° и 79°. Найдите третий угол. Ответ дайте в градусах. | Решение: Сумма углов треугольника равна 180°, поэтому третий угол равен: 180° – (48° + 79°) = 180° – 127° = 53°.
| ||||||
|
В треугольнике АВС известно, что
Ответ дайте в градусах. | Решение: Ответ:
| ||||||
|
В треугольнике АВС известно, что АС = 54, ВМ – медиана, ВМ = 45. Найдите АМ. | Решение: АМ = 54 : 2 = 27, так как медиана делит противоположную сторону пополам. Ответ: АМ = 27.
| ||||||
|
В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 132°. Найдите угол АВС. Ответ дайте в градусах. | Решение:
Ответ:
|
|
В остроугольном треугольнике АВС проведена высота ВН, Найдите угол АВН. Ответ дайте в градусах. | Решение: Рассмотрим значит по теореме о сумме углов треугольника
Ответ:
| ||||||
|
В треугольнике одна из сторон равна 29, а опущенная на нее высота равна — 12. Найдите площадь треугольника. | Решение: Площадь треугольника равна половине произведения основания на высоту, поэтому
| ||||||
|
Точки М и N являются серединами сторон АВ и ВС треугольника АВС, сторона АВ равна 28, сторона ВС равна 44, сторона АС равна 42. Найдите МN. | Решение: Средняя линия треугольника параллельна одной из сторон треугольника и равна ее половине.
Ответ: 21.
| ||||||
|
Точки М и N являются серединами сторон АВ и ВС треугольника АВС соответственно. Отрезки АN и СМ пересекаются в точке О, АN = 18, СМ = 21. Найдите ОМ. | Решение: Точки М и N являются серединами сторон АВ и ВС, значит поэтому поэтому точкой пересечения делятся в отношении 2 : 1, считая от вершины
Ответ: 7.
| ||||||
|
Катеты прямоугольного треугольника равны 12 и 5. Найти гипотенузу этого треугольника. | Решение: Квадрат гипотенузы равен сумме квадратов катетов:
Ответ: 13.
| ||||||
|
В прямоугольном треугольнике катет и гипотенуза соответственно равны 7 и 25. Найти второй катет этого треугольника. | Решение: Квадрат гипотенузы равен сумме квадратов катетов:
Ответ: 24.
| ||||||
|
В треугольнике АВС угол А равен 45°, угол В равен 30°, ВС = | Решение: По теореме синусов:
Ответ: 6.
| ||||||
|
В треугольнике АВС угол С равен 90°, АС = 14, АВ = 20. Найдите | Решение: Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Ответ: 0,7.
| ||||||
|
В треугольнике АВС угол С равен 90°, ВС = 12, АВ = 15. Найдите | Решение: Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Ответ: 0,8.
| ||||||
|
В треугольнике АВС угол С равен 90°, АC = 8, ВС = 5. Найдите | Решение: Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Ответ: 0,625.
| ||||||
|
Сторона равностороннего треугольника равна | Решение: Высота – медиана и биссектриса.
Ответ: 18.
| ||||||
|
На стороне треугольника АВС отмечена точка D так, что АD = 5, DС = 15. Площадь треугольника АВС равна 120. Найдите площадь треугольника ВСD. | Решение: Площади треугольников, имеющих одинаковые высоты относятся как основания.
Ответ: 90.
| ||||||
| В треугольнике АВС АВ = 15, ВС = 8,
Найдите площадь треугольника АВС. | Решение: Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Ответ: 50.
| ||||||
| Синус острого угла А треугольника АВС равен | Решение:
Ответ: 0,75
| ||||||
|
М
В треугольнике АВС угол С равен 90° Найдите СМ. | Решение: В прямоугольном треугольнике середина гипотенузы является центром описанной окружности , значит СМ = АМ = ВМ = 42 : 2 = 21 Ответ: 21
| ||||||
|
Биссектриса равностороннего треугольника равна | Решение: Любая биссектриса равностороннего треугольника является его медианой и высотой.
Ответ: 20.
|
Вариант 1 Треугольники. Задание ОГЭ 15
| 1 | В треугольнике ABC известно, что BAC=68°, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах. |
| 2 | В треугольнике ABC известно, что АС =14, BM – медиана, BM=10 . Найдите АM |
| 3 | В треугольнике два угла равны 72° и 42°. Найдите его третий угол. Ответ дайте в градусах. |
| 4 | В треугольнике ABC угол C равен 115°. Найдите внешний угол при вершине C. Ответ дайте в градусах |
| 5 | В треугольнике ABC известно, что AB=BC , ABС =106° . Найдите угол BCA. Ответ дайте в градусах |
| 6 | Один из острых углов прямоугольного треугольника равен 19°. Найдите его другой острый угол. Ответ дайте в градусах |
| 7 | В остроугольном треугольнике ABC проведена высота BH, BAC=37° . Найдите угол ABH. Ответ дайте в градусах. |
| 8 | Два катета прямоугольного треугольника равны 4 и 10. Найдите площадь этого треугольника |
| 9 | Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника |
| 10 | На стороне AC треугольника ABC отмечена точка D так, что AD=6, DC=10 . Площадь треугольника ABC равна 48. Найдите площадь треугольника BCD. |
Вариант 2 Треугольники. Задание ОГЭ 15
| 1 | В треугольнике ABC известно, что BAC=82°, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах |
| 2 | В треугольнике ABC известно, что АС =16, BM – медиана, BM=12 . Найдите АM |
| 3 | В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах |
| 4 | В треугольнике ABC угол C равен 177°. Найдите внешний угол при вершине C. Ответ дайте в градусах |
| 5 | В треугольнике ABC известно, что AB=BC , ABС =108° . Найдите угол BCA. Ответ дайте в градусах. |
| 6 | Один из острых углов прямоугольного треугольника равен 21°. Найдите его другой острый угол. Ответ дайте в градусах |
| 7 | В остроугольном треугольнике ABC проведена высота BH, BAC=23° . Найдите угол ABH. Ответ дайте в градусах. |
| 8 | Два катета прямоугольного треугольника равны 14 и 5. Найдите площадь этого треугольника |
| 9 | Сторона треугольника равна 20, а высота, проведённая к этой стороне, равна 9. Найдите площадь этого треугольника |
| 10 | На стороне AC треугольника ABC отмечена точка D так, что AD=2, DC=7 . Площадь треугольника ABC равна 27. Найдите площадь треугольника BCD |
Вариант 3 Треугольники. Задание ОГЭ 15
| 1 | В треугольнике ABC известно, что BAC=26°, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах |
| 2 | В треугольнике ABC известно, что АС =38, BM – медиана, BM=17 . Найдите АM |
| 3 | В треугольнике два угла равны 38° и 89°. Найдите его третий угол. Ответ дайте в градусах |
| 4 | В треугольнике ABC угол C равен 106°. Найдите внешний угол при вершине C. Ответ дайте в градусах |
| 5 | В треугольнике ABC известно, что AB=BC , ABС =132° . Найдите угол BCA. Ответ дайте в градусах |
| 6 | Один из острых углов прямоугольного треугольника равен 85°. Найдите его другой острый угол. Ответ дайте в градусах |
| 7 | В остроугольном треугольнике ABC проведена высота BH, BAC=29° . Найдите угол ABH. Ответ дайте в градусах. |
| 8 | Два катета прямоугольного треугольника равны 16 и 4. Найдите площадь этого треугольника |
| 9 | Сторона треугольника равна 21, а высота, проведённая к этой стороне, равна 4. Найдите площадь этого треугольника |
| 10 | На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7 . Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD. |
Вариант 4 Треугольники. Задание ОГЭ 15
| 1 | В треугольнике ABC известно, что BAC=24 , AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах |
| 2 | В треугольнике ABC известно, что АС=54, BM – медиана, BM=43 . Найдите АM |
| 3 | В треугольнике два угла равны 54° и 58°. Найдите его третий угол. Ответ дайте в градусах. |
| 4 | В треугольнике ABC угол C равен 142°. Найдите внешний угол при вершине C. Ответ дайте в градусах |
| 5 | В треугольнике ABC известно, что AB=BC , ABС =144° . Найдите угол BCA. Ответ дайте в градусах |
| 6 | Один из острых углов прямоугольного треугольника равен 71°. Найдите его другой острый угол. Ответ дайте в градусах |
| 7 | В остроугольном треугольнике ABC проведена высота BH, BAC=55° . Найдите угол ABH. Ответ дайте в градусах. |
| 8 | Два катета прямоугольного треугольника равны 22 и 8. Найдите площадь этого треугольника |
| 9 | Сторона треугольника равна 24, а высота, проведённая к этой стороне, равна 10. Найдите площадь этого треугольника |
| 10 | На стороне AC треугольника ABC отмечена точка D так, что AD=4, DC=8 . Площадь треугольника ABC равна 36. Найдите площадь треугольника BCD. |
Вариант 5 Треугольники. Задание ОГЭ 15
| 1 | В треугольнике ABC известно, что BAC=124°, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах. |
| 2 | В треугольнике ABC известно, что АС=28, BM – медиана, BM=8 . Найдите АM |
| 3 | В треугольнике два угла равны 123° и 9°. Найдите его третий угол. Ответ дайте в градусах. |
| 4 | В треугольнике ABC угол C равен 109°. Найдите внешний угол при вершине C. Ответ дайте в градусах |
| 5 | В треугольнике ABC известно, что AB=BC , ABС =102° . Найдите угол BCA. Ответ дайте в градусах |
| 6 | Один из острых углов прямоугольного треугольника равен 54°. Найдите его другой острый угол. Ответ дайте в градусах |
| 7 | В остроугольном треугольнике ABC проведена высота BH, BAC=67° . Найдите угол ABH. Ответ дайте в градусах. |
| 8 | Два катета прямоугольного треугольника равны 12 и 7. Найдите площадь этого треугольника |
| 9 | Сторона треугольника равна 26, а высота, проведённая к этой стороне, равна 7. Найдите площадь этого треугольника |
| 10 | На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7 . Площадь треугольника ABC равна 60. Найдите площадь треугольника ABD. |
Вариант 6 Треугольники. Задание ОГЭ 15
| 1 | В треугольнике ABC известно, что BAC=168°, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах. |
| 2 | В треугольнике ABC известно, что АС=45, BM – медиана, BM=43 . Найдите АM |
| 3 | В треугольнике два угла равны 45° и 72°. Найдите его третий угол. Ответ дайте в градусах. |
| 4 | В треугольнике ABC угол C равен 98°. Найдите внешний угол при вершине C. Ответ дайте в градусах |
| 5 | В треугольнике ABC известно, что AB=BC , ABС =88° . Найдите угол BCA. Ответ дайте в градусах |
| 6 | Один из острых углов прямоугольного треугольника равен 12°. Найдите его другой острый угол. Ответ дайте в градусах |
| 7 | В остроугольном треугольнике ABC проведена высота BH, BAC=43° . Найдите угол ABH. Ответ дайте в градусах. |
| 8 | Два катета прямоугольного треугольника равны 11 и 6. Найдите площадь этого треугольника |
| 9 | Сторона треугольника равна 31, а высота, проведённая к этой стороне, равна 6. Найдите площадь этого треугольника |
| 10 | На стороне AC треугольника ABC отмечена точка D так, что AD=4, DC=7 . Площадь треугольника ABC равна 55. Найдите площадь треугольника ABD |
Вариант 7 Треугольники. Задание ОГЭ 15
| 1 | В треугольнике ABC известно, что BAC=39°, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах. |
| 2 | В треугольнике ABC известно, что АС=12, BM – медиана, BM=4 . Найдите АM |
| 3 | В треугольнике два угла равны 24° и 52°. Найдите его третий угол. Ответ дайте в градусах. |
| 4 | В треугольнике ABC угол C равен 24°. Найдите внешний угол при вершине C. Ответ дайте в градусах |
| 5 | В треугольнике ABC известно, что AB=BC , ABС =96° . Найдите угол BCA. Ответ дайте в градусах |
| 6 | Один из острых углов прямоугольного треугольника равен 9°. Найдите его другой острый угол. Ответ дайте в градусах |
| 7 | В остроугольном треугольнике ABC проведена высота BH, BAC=59° . Найдите угол ABH. Ответ дайте в градусах. |
| 8 | Два катета прямоугольного треугольника равны 26 и 3. Найдите площадь этого треугольника |
| 9 | Сторона треугольника равна 54, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника |
| 10 | На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=10 . Площадь треугольника ABC равна 39. Найдите площадь треугольника ABD |
Вариант 8 Треугольники. Задание ОГЭ 15
| 1 | В треугольнике ABC известно, что BAC=54°, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах. |
| 2 | В треугольнике ABC известно, что АС=124, BM – медиана, BM=48 . Найдите АM |
| 3 | В треугольнике два угла равны 59° и 58°. Найдите его третий угол. Ответ дайте в градусах. |
| 4 | В треугольнике ABC угол C равен 17°. Найдите внешний угол при вершине C. Ответ дайте в градусах |
| 5 | В треугольнике ABC известно, что AB=BC , ABС =84° . Найдите угол BCA. Ответ дайте в градусах |
| 6 | Один из острых углов прямоугольного треугольника равен 34°. Найдите его другой острый угол. Ответ дайте в градусах |
| 7 | В остроугольном треугольнике ABC проведена высота BH, BAC=80° . Найдите угол ABH. Ответ дайте в градусах. |
| 8 | Два катета прямоугольного треугольника равны 18 и 9. Найдите площадь этого треугольника |
| 9 | Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 21. Найдите площадь этого треугольника |
| 10 | На стороне AC треугольника ABC отмечена точка D так, что AD=2, DC=13 . Площадь треугольника ABC равна 75. Найдите площадь треугольника ABD |
Огэ математика задание 15 номер 311343
В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите.
В равнобедренном треугольнике. Найдите AC, если высота.
В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.
Площадь равнобедренного треугольника равна Угол, лежащий напротив основания равен 120°. Найдите длину боковой стороны.
В треугольнике ABC AC = BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD = AC. Известно, что ∠CAB = 80° и ∠ACB=59∘. Найдите угол DCB. Ответ дайте в градусах.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123.
Oge. sdamgia. ru
12.10.2020 18:02:54
2020-10-12 18:02:54
Источники:
Https://oge. sdamgia. ru/test? theme=34&ttest=true
Преподаватели компьютерной графики, обучение и курсы компьютерной графики в Москве | Репетит-Центр » /> » /> .keyword { color: red; } Огэ математика задание 15 номер 311343
Репетиторы компьютерной графики
Репетиторы компьютерной графики
Компьютерная графика – поистине увлекательный предмет, если научиться его понимать. С его помощью можно освоить различные программы для обработки фотографий или создания наполненных спецэффектами видеороликов. «Компьютерная графика занимает одну из первых позиций в изобразительной деятельности» — это отмечает в своем исследовании учащаяся магистратуры Гуляева Александра Сергеевна.
Никнуть в предмет, стоит нанять хорошего репетитора компьютерной графики в Москве. К тому же, с его помощью можно также сдать зачет или экзамен, если речь идет о предмете, как об одном из профильных в ВУЗе.
Воспользоваться поиском подходящей кандидатуры вы сможете на нашем сайте, где представлено огромное множество анкеты преподавателей, готовых обучить компьютерной графике желающих. Каждая анкета содержит подробную информацию об учителях, их опыте и возможностях. Вы также можете увидеть стоимость занятия для студентов и узнать о возможности проведения его на дому.
С помощью услуг частного репетитора по компьютерной графике, вы:
- Научитесь работать в таких программах, как Photoshop, InDesign, Illustrator и других графических редакторах; Освоите графический дизайн; Успешно подготовитесь к сдаче зачета или экзамена, если вы является студентом профильного ВУЗа, где сдача подобного предмета необходима; Получите весь необходимый материал в виде интерактивных занятий, что позволит сделать процесс обучения интересным и познавательным; Закрепите полученные знания с помощью контрольных точек.
Также вы получите бесценный опыт общения с педагогом в области графического дизайна, что также накладывает определенный отпечаток. Услуги репетитора компьютерной графики в Москве предоставляют специалисты, которые могут научить разнообразным нюансам графического дизайна.
Также вы можете ознакомиться с отзывами тех, кто уже воспользовался услугами. Хотим отметить, что все отзывы абсолютно правдивы, чего нельзя сказать с уверенностью о таких сайтах, как авито или яндекс. услуги.
Если у вас нет возможности заняться поиском подходящей кандидатуры самостоятельно, то мы готовы подобрать лучшего репетитора по компьютерной графике, который удовлетворит всем вашим требованиям и пожеланиям.
Если вы горите желанием познать такой предмет, как графический дизайн, то советуем нанять квалифицированного учителя как можно скорее.
Выезд на дом:
Мытищи
- Образование: Московский автомобильно-дорожный государственный технический университет, 2002 О преподавателе: Частный репетитор по компьютерной графике, обучение в Москве.
Школьники, старшеклассники, студенты, взрослые. Все графические программы — Photoshop, Illustrator и др. Любой уровень от новичка до эксперта (повышение квалификации).
Опыт работы дизайнером — 13 лет в крупных компаниях: X5 retail, LitRes, РЖД, Отто груп россия.
Легко нахожу подход к любому ученику, имею диплом психолога.
Работаю дизайнером более 15 лет.
Выезд на дом:
У себя — метро Щукинская, 10 минут. На выезде — 1500 руб. рассматриваю любые районы Москвы.
- Образование: Всесоюзный юридический заочный институт, факультет правоведения (неоконченное высшее); Московский экстерный гуманитарный университет, факультет культуроведения, магистр – культуры, 1995 год окончания. О преподавателе: Опытный преподаватель по компьютерной графике. Курсы компьютерной графики.
Основы работы на компьютере с «нуля» для детей и взрослых. Работа в интернете, работа с почтой. Полная подготовка художника — дизайнера для работы в рекламных агентствах (РА). Вопросы графического дизайна, основ полиграфии, пре-пресс, макетирования и верстки, Flash-анимации (создание баннров) и WEB-дизайна. Создание сайтов с нуля, ведение интернет-магазинов и работа с их администрированием. Фотошоп (Photoshop) для фотографов (профессионалов и любителей.) Продвижение сайтов (раскрутка в бизнесе) и поисковая оптимизация, контент-менеджмент, CMS (системы администрирования сайтов).
Программы: Word, Excel, Photoshop, Illustrator, Corel Draw, Dreamweaver, PowerPoint и др. .Профессиональный дизайнер – более 10 лет. Арт-директор в рекламных агентствах полного цикла и издательствах – более 5 лет.
Выезд на дом:
Рассмотрю заявки в пределах Москвы, желательно вблизи метро. Удалённые занятия по Skype только для взрослых за.
- Образование: Московский государственный университет дизайна и технологии (1978 г.), бывший технологический институт легкой промышленности. Факультет: дизайн и конструирование изделий из кожи. Балтийская педагогическая академия. О преподавателе: Услуги репетитора по компьютерной графике. Обучение компьютерной графике.
Занимаюсь с учениками от 6 лет и до любого возраста, учитываю способности учащегося, пожелание родителя, составляю индивидуальную методику обучения. С детьми предпочитаю работать в игровой форме, весело и непринуждённо. Для взрослых, которые считают, что у них нет способностей к рисованию, разработала свою методику, мастер-класс, инициируя творческий потенциал ученика. Для абитуриентов разработала ускоренную методику подготовки. Разработала и успешно применяю профессиональное изучение обучение рисунку с простых и легких упражнений по СКАЙП.
Благодаря моей методике ученики осваивают академический рисунок онлайн по СКАЙП для поступления в желаемый ВУЗ. Профорентирую исходя из потенциальных возможностей ученика. Провожу мастер-классы по живописи (масло, акрил, мастихин). Владею методиками (артреабилитация) по восстановлению графических навыков, каллиграфии, подготовки руки к школе для письма. В результате многолетней педагогической практики разработала методику интеллектуального и творческого развития личности с помощью изотворчества. В результате занятий по моей методике у учеников улучшаются математические способности, логическое мышление, пространственное воображение, речевые способности (риторика) и, конечно, изонавыки. Провожу занятия по арттерапии в разных техниках рисунка и живописи. Обучаю основам стиля АНИМЕ и МАНГА. Обучаю по индивидуальной программе компьютерной графике: Corel, Fotoshop. Работаю с детьми, подростками и взрослыми с 1989 года. В клубе «Салют» в своем микрорайоне вела сразу несколько кружков: изостудию, керамический, кукольный театр (дети сами создавали кукол для спектакля «Дядя Фёдор» и сами же в нем играли). Постоянно повышаю свой профессиональный уровень художника — педагога. Посещаю курсы по психологии. Иллюстрирую книги, пишу картины. Участвую в выставках, веду мастер-классы по живописи (масло, акрил, мастихин).
Выезд на дом:
Рассмотрю заявки в пределах Москвы, желательно вблизи метро. Удалённые занятия по Skype только для взрослых за.
Выезд на дом:
У себя — метро Щукинская, 10 минут. На выезде — 1500 руб. рассматриваю любые районы Москвы.
Образование Московский автомобильно-дорожный государственный технический университет, 2002.
Repetit-center. ru
05.04.2017 11:00:15
2017-04-05 11:00:15
Источники:
Https://repetit-center. ru/include/photoshop. php
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Огэ математика задание 15 номер 311343
Огэ математика задание 15 номер 311343
Огэ математика задание 15 номер 311343
Задание 15 № 311320
В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите.
В равностороннем треугольнике ABC все углы равны 60°. Биссектрисы CN и AM делят углы пополам, поэтому = = Сумма углов в треугольнике равна 180°, поэтому Вертикальные углы равны, следовательно,
Задание 15 № 311332
В равнобедренном треугольнике. Найдите AC, если высота.
В равнобедренном треугольнике высота, опущенная на основание делит основание пополам, то есть CH делит AB пополам. Тогда получаем прямоугольный треугольник ACH с двумя известными катетами и гипотенузой которого является искомая По теореме Пифагора найдем
Задание 15 № 311343
В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите.
Медианы в равностороннем треугольнике являются биссектрисами и высотами, поэтому. Треугольник AOK — прямоугольный, поэтому.
Задание 15 № 311680
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.
Углы ACB и BAC равны, т. к. находятся при основании равнобедренного треугольника; пусть один из них равен X. Поскольку сумма углов треугольника равна 180°, имеем: ∠ABC = 180° − X − X. Угол ACB смежен с углом 123°, значит, равен 180° − 123° = 57°. Следовательно, X = 57°, откуда ∠ABC = 180° − 2·57° = 66°.
Задание 15 № 311680
Задание 15 № 311343
В равностороннем треугольнике ABC все углы равны 60.
Oge. sdamgia. ru
20.03.2020 18:26:07
2020-03-20 18:26:07
Источники:
Https://oge. sdamgia. ru/test? theme=34
Решайте и скачайте пробные тренировочные варианты ОГЭ по математике — тесты и варианты за 2022 год (с ответами и решениями заданий) с сайта (не Гущина) — сдам ГИА, решу ОГЭ. Тесты за 9 класс можно смотреть онлайн, а можно распечатать в формате pdf. Многие задачи (упражнения) взяты из КИМов (реальных вариантов) и открытого банка заданий ОГЭ.
Пробный тренировочный вариант ОГЭ по математике.
Часть 1
Модуль — Алгебра
Задание №1
Задание №2
Задание №3
Задание №4
Задание №5
Задание №6
Задание №7
Задание №8
Модуль — Геометрия
Задание №9
Задание №10
Задание №11
Задание №12
Задание №13
Модуль — Реальная математика
Задание №14
Задание №15
Задание №16
Задание №17
Задание №18
Задание №19
Задание №20
Часть 2
Задание №21
Задание №22
Задание №23
Задание №24
Задание №25
Задание №26
ВАЖНО! Никаких реальных вариантов ни до экзамена, ни во время его проведения на сайте нет, не было и не будет.
ЗАПРЕЩЕНО копирование материалов без указания активные ссылки на источник
В случае нарушения авторских прав, правообладателям обращаться по адресу:
Контакты: tolkoexamen@gmail.com
» Физика. Решение задач ОГЭ(ГИА)
Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А (см. рисунок). В точке В наклонная плоскость без излома переходит в наружную поверхность горизонтальной…
Небольшое тело массой M = 0,99 кг лежит на вершине гладкой полусферы. В тело попадает пуля массой m = 0,01 кг, летящая горизонтально со скоростью v0 = 100 м/с, и застревает в нём…
В цилиндре под поршнем находится ненасыщенный пар. Какие процессы будут происходить при опускании поршня и сжатии пара?
Удельная теплота плавления алюминия 3,9 • 105 Дж /кг. Это значит, что для плавления: 1) 1 кг алюминия при любой температуре требуется 3.9 • 105 Дж теплоты; 2) 1 кг алюминия при температуре плавления требуется 3,9 • 105 Дж теплоты; 3) 3,9 кг алюминия при любой температуре требуется 3.9 • 105 Дж теплоты;
Температура кипения воды зависит от: 1) мощности нагревателя; 2) массы воды; 3) давления окружающего воздуха; 4) начальной температуры воды.
В 2 кг воды t 80 °С долили воду t 10 °С, в результате чего установилась температура 35 °С. Чему равна масса долитой воды? Температурой окружающего воздуха пренебречь.
Твердое вещество массой m стали нагревать. На рис. 50 показан график изменения температуры t вещества по мере поглощения им все большего количества теплоты Q. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
В печь поместили некоторое количество алюминия. Диаграмма изменения температуры алюминия с течением времени показана на рис. 49. Печь при постоянном нагреве передает алюминию 2 кДж тепловой энергии в минуту. Какое количество теплоты потребовалось для плавления алюминия, уже нагретого до температуры его плавления? 1) 10 кДж; 2) 30 кДж; 3) 40 кДж; 4) 60 кДж.
С высоты 70 м упал без начальной скорости на металлическую плиту свинцовый осколок. На сколько градусов он нагрелся, если на нагревание пошло 90% механической энергии осколка? Удельная теплоемкость свинца 140 Дж/(кг • °С).
В 1 л воды при 25 °С опустили кусочек стали массой 200 г, нагретой до 200 °С. До какой температуры нагреется вода и охладится сталь в момент установления теплового равновесия? Удельная теплоемкость воды 4200 Дж/(кг • °С), удельная теплоемкость стали 500 Дж /(кг • °С).
Задания
Версия для печати и копирования в MS Word
Задание 15 № 311343
В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите
.
Спрятать решение
Решение.
Медианы в равностороннем треугольнике являются биссектрисами и высотами, поэтому 
. Треугольник AOK — прямоугольный, поэтому 
.
Ответ: 60.
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 3)
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
·
Сообщить об ошибке · Помощь
Автор скрыт
05.05.2021.
Тест. Алгебра, 9 класс
Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного
использования.
Администрация сайта не
проверяет возможные ошибки,
которые могут встретиться в тестах.
Неравенства, системы неравенств:
1. Линейные неравенства;
2. Квадратные неравенства;
3. Рациональные неравенства;
4. Системы неравенств.
Вопрос 1
Решите неравенство 
.
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4) 
Вопрос 2
Решите неравенство
и определите, на каком рисунке изображено множество его решений.
В ответе укажите номер правильного варианта.
Вопрос 3
На каком рисунке изображено множество решений неравенства 
В ответе укажите номер правильного варианта.
Вопрос 4
При каких значениях 
выражение 
принимает положительные значения?
В ответе укажите номер правильного варианта.
| 1) |
| |
| 2) |
| |
| 3) |
| |
| 4) |
|
Вопрос 5
Решите неравенство 4x − 2(7x + 9) < 4.
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4) 
Вопрос 6
При каких значениях x значение выражения 6x + 9 меньше значения выражения 9x − 3?
В ответе укажите номер правильного варианта.
1) x > − 2
2) x < 4
3) x < − 2
4) x > 4
Вопрос 7
Решите неравенство 
В ответе укажите номер правильного варианта.
1) 
2) 
3) ![( минус принадлежит fty; минус 16]](https://oge.sdamgia.ru/formula/svg/4e/4e1bad0a23d6aa4b7f50b065ef38cf85.svg)
4) ![( минус принадлежит fty; 0]](https://oge.sdamgia.ru/formula/svg/eb/eb056e87336a3746cdb956605c767956.svg)
Вопрос 8
При каких значениях x значение выражения 
больше значения выражения 
?
В ответе укажите номер правильного варианта.
1) x > − 10
2) x < − 10
3) x > − 6
4) x < − 6
Вопрос 9
Решите неравенство 
и определите, на каком рисунке изображено множество его решений.
В ответе укажите номер правильного варианта.
Вопрос 10
На каком рисунке изображено множество решений неравенства 
?
В ответе укажите номер правильного варианта.
Вопрос 11
Решите неравенство 
.
В ответе укажите номер правильного варианта.
1) 
2) 
3) ![[0; 1]](https://oge.sdamgia.ru/formula/svg/7c/7c639b435011726883a45253255a3841.svg)
4) ![( минус принадлежит fty; 0] cup [1; плюс принадлежит fty)](https://oge.sdamgia.ru/formula/svg/8a/8a92edb840e76a16cd575d6f3f42eed3.svg)
Вопрос 12
Решите неравенство 
В ответе укажите номер правильного варианта.
1) 
2) 
3) ![[0; 4]](https://oge.sdamgia.ru/formula/svg/f7/f76184ee855a8b328682d18ffeeabfd2.svg)
4) ![( минус принадлежит fty; 0] cup [4; плюс принадлежит fty)](https://oge.sdamgia.ru/formula/svg/2d/2d7e2282b6fad0b6a0d65e6a76e673d9.svg)
Вопрос 13
Решите неравенство 
.
В ответе укажите номер правильного варианта.
1) 
2) 
3) ![( минус принадлежит fty; 0] cup [5; плюс принадлежит fty)](https://oge.sdamgia.ru/formula/svg/e6/e6c5827c315ec03039445931f95757af.svg)
4) ![[0; 5]](https://oge.sdamgia.ru/formula/svg/02/0266dd3a8322c091dd353b1052650224.svg)
Вопрос 14
На каком рисунке изображено множество решений неравенства 
?
В ответе укажите номер правильного варианта.
1) 4 2) 3 3) 2 4) 1
Вопрос 15
Решите неравенство 
В ответе укажите номер правильного варианта.
1) 
2) ![( минус принадлежит fty; минус 19]cup[19; плюс принадлежит fty)](https://oge.sdamgia.ru/formula/svg/07/07a4f39ef693a53c94356b0e3b17c72e.svg)
3) ![[ минус 19;19]](https://oge.sdamgia.ru/formula/svg/a8/a899602133312afdf88edd0c87df011e.svg)
4) 
Вопрос 16
Решение какого из данных неравенств изображено на рисунке?
1) 
2) 
3) 
4) 
Вопрос 17
Укажите неравенство, которое не имеет решений.
| 1) |
| |
| 2) |
| |
| 3) |
| |
| 4) |
|
Вопрос 18
Укажите неравенство, которое не имеет решений.
| 1) |
| |
| 2) |
| |
| 3) |
| |
| 4) |
|
Вопрос 19
Укажите неравенство, решением которого является любое число.
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4) 
Вопрос 20
Укажите неравенство, решением которого является любое число.
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4) 
Вопрос 21
Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4) 
Вопрос 22
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.
Вопрос 23
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.
Вопрос 24
Решите неравенство 
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4) нет решений
Вопрос 25
Укажите решение неравенства 
.
| 1) |
| |
| 2) |
| |
| 3) |
| |
| 4) | нет решений |
![( минус принадлежит fty ; минус 6 ]cup [ 6; плюс принадлежит fty )](https://oge.sdamgia.ru/formula/svg/b7/b72623c62f3bd33afca80de2ed075e81.svg)
![[ минус 6;6 ]](https://oge.sdamgia.ru/formula/svg/e9/e9b1d877c95dbd77a7c0e8c6bfcadc76.svg)
Вопрос 26
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.
Вопрос 27
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.
Вопрос 28
На каком рисунке изображено множество решений неравенства 
?
Вопрос 29
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.
Вопрос 30
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.
Вопрос 31
Укажите решение неравенства 
Вопрос 32
Укажите решение неравенства 
Вопрос 33
Укажите решение системы неравенств 
Вопрос 34
Решите систему неравенств 
На каком из рисунков изображено множество её решений?
В ответе укажите номер правильного варианта.
Вопрос 35
Найдите наименьшее значение 
, удовлетворяющее системе неравенств,
Вопрос 36
Найдите наибольшее значение x, удовлетворяющее системе неравенств
Вопрос 37
Укажите решение системы неравенств 
В ответе укажите номер правильного варианта.
Вопрос 38
Укажите решение системы неравенств 
В ответе укажите номер правильного варианта.
Вопрос 39
Укажите решение системы неравенств
1) 
2) нет решений
3) 
4) 
Вопрос 40
Укажите решение системы неравенств
1) 
2) 
3) 
4) 