Задание 15 номер 193 - Большой телефонный справочник предприятий

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ДЕЛАМ МОЛОДЕЖИ

ПРИКАЗ
от 15 июля 2020 г. N 193

ОБ УТВЕРЖДЕНИИ ПОРЯДКА
ОПРЕДЕЛЕНИЯ НОРМАТИВНЫХ ЗАТРАТ НА ВЫПОЛНЕНИЕ РАБОТ
ФЕДЕРАЛЬНЫМИ ГОСУДАРСТВЕННЫМИ БЮДЖЕТНЫМИ И АВТОНОМНЫМИ
УЧРЕЖДЕНИЯМИ, В ОТНОШЕНИИ КОТОРЫХ ФУНКЦИИ И ПОЛНОМОЧИЯ
УЧРЕДИТЕЛЯ ОСУЩЕСТВЛЯЕТ ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ДЕЛАМ МОЛОДЕЖИ

Во исполнение пункта 28 Положения о формировании государственного задания на оказание государственных услуг (выполнение работ) в отношении федеральных государственных учреждений и финансовом обеспечении выполнения государственного задания, утвержденного постановлением Правительства Российской Федерации от 26 июня 2015 г. N 640 «О порядке формирования государственного задания на оказание государственных услуг (выполнение работ) в отношении федеральных государственных учреждений и финансового обеспечения выполнения государственного задания» (далее — Положение) (Собрание законодательства Российской Федерации, 2015, N 28, ст. 4226; 2020, N 30, ст. 4915), приказываю:

1. Утвердить Порядок определения нормативных затрат на выполнение работ федеральными государственными бюджетными и автономными учреждениями, в отношении которых функции и полномочия учредителя осуществляет Федеральное агентство по делам молодежи (далее — Порядок) (Приложение).

2. Признать утратившим силу приказ Федерального агентства по делам молодежи от 21 января 2019 г. N 10 «Об утверждении Порядка определения нормативных затрат на выполнение работ федеральными государственными бюджетными учреждениями, в отношении которых функции и полномочия учредителя осуществляет Федеральное агентство по делам молодежи» (зарегистрирован в Минюсте России 3 апреля 2019 г. регистрационный номер 54258).

3. Признать утратившим силу приказ Федерального агентства по делам молодежи от 18 ноября 2019 г. N 394 «О внесении изменений в Порядок определения нормативных затрат на выполнение работ федеральными государственными бюджетными учреждениями, в отношении которых функции и полномочия учредителя осуществляет Федеральное агентство по делам молодежи, утвержденный приказом Федерального агентства по делам молодежи от 21 января 2019 г. N 10» (зарегистрирован в Минюсте России 30 января 2020 г. регистрационный номер 57336).

4. Контроль за исполнением настоящего приказа возложить на заместителя руководителя Федерального агентства по делам молодежи П.В. Абрамова.

Руководитель
А.В.БУГАЕВ

Приложение

Утвержден
приказом Федерального агентства
по делам молодежи
от 15 июля 2020 г. N 193

ПОРЯДОК
ОПРЕДЕЛЕНИЯ НОРМАТИВНЫХ ЗАТРАТ НА ВЫПОЛНЕНИЕ РАБОТ
ФЕДЕРАЛЬНЫМИ ГОСУДАРСТВЕННЫМИ БЮДЖЕТНЫМИ И АВТОНОМНЫМИ
УЧРЕЖДЕНИЯМИ, В ОТНОШЕНИИ КОТОРЫХ ФУНКЦИИ И ПОЛНОМОЧИЯ
УЧРЕДИТЕЛЯ ОСУЩЕСТВЛЯЕТ ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ДЕЛАМ МОЛОДЕЖИ

I. Общие положения

1. Настоящий Порядок разработан в целях определения нормативных затрат на выполнение работ федеральными государственными бюджетными и автономными учреждениями, в отношении которых Федеральное агентство по делам молодежи осуществляет функции и полномочия учредителя (далее — Учреждениями) для определения объема субсидии на финансовое обеспечение выполнения государственного задания Учреждениями.

2. Нормативные затраты на выполнение работ определяются при расчете объема финансового обеспечения выполнения государственного задания на выполнение работ Учреждениями и утверждаются Федеральным агентством по делам молодежи.

3. Нормативные затраты на выполнение работ, определяемые в соответствии с настоящим Порядком, учитываются при формировании обоснований бюджетных ассигнований федерального бюджета на очередной финансовый год и плановый период.

II. Состав и расчет нормативных затрат на выполнение работ

4. Нормативные затраты на выполнение работ на соответствующий финансовый год (Nw) рассчитываются по следующей формуле:

где:

Nw — нормативные затраты на выполнение w-й работы на соответствующий финансовый год;

Gj — нормативные затраты, определенные для j-й группы затрат на единицу работы на соответствующий финансовый год, где j — соответствующая группа затрат.

5. При определении нормативных затрат на выполнение работ применяются показатели материальных, технических и трудовых ресурсов, используемых для выполнения работ, по видам затрат исходя из нормативов их потребления, установленных нормативными правовыми актами Российской Федерации, межгосударственными, национальными (государственными) стандартами Российской Федерации, строительными нормами и правилами, санитарными нормами и правилами, стандартами, порядками, регламентами и паспортами выполнения работ в установленной сфере, или на основе усреднения показателей деятельности Учреждения, которое имеет минимальный объем указанных затрат на выполнение работы в установленной сфере (далее — стандарты работ).

6. Нормативные затраты на выполнение работы рассчитываются на работу в целом или в случае установления в государственном задании показателей объема выполнения работы — на единицу объема работы.

7. В состав нормативных затрат на выполнение работ включаются следующие группы затрат (Gj):

7.1. Затраты на оплату труда работников, непосредственно связанных с выполнением работ, и начисления на выплаты по оплате труда работников, непосредственно связанных с выполнением работ.

7.2. Затраты на приобретение материальных запасов и на приобретение движимого имущества (основных средств и нематериальных активов), используемого в процессе выполнения работ, с учетом срока их полезного использования, а также затраты на аренду указанного имущества, которые определяются исходя из фактических объемов потребления материальных запасов за прошлые годы в натуральном или стоимостном выражении с учетом стандартов работ и включают в себя затраты на приобретение материальных запасов, непосредственно используемых для выполнения работ.

7.2.1. Затраты на формирование резерва на полное восстановление состава объектов особо ценного движимого имущества, используемого в процессе выполнения работ (основных средств и нематериальных активов, амортизируемых в процессе оказания работы).

7.3. Затраты на иные расходы, непосредственно связанные с выполнением работ, с учетом стандартов работ <1>.

———————————

<1> Подпункт «в» пункта 29 Положения.

7.4. Затраты на оплату коммунальных услуг, которые определяются исходя из натуральных показателей потребления коммунальных услуг в текущем финансовом году с учетом тарифов очередного финансового года, с учетом изменения площадей в очередном финансовом году по сравнению с отчетным финансовым годом и ввода в эксплуатацию новых площадей (вывода из эксплуатации площадей), требований обеспечения энергоэффективности и энергосбережения, а также с учетом стандартов работ.

Затраты на коммунальные услуги определяются обособленно по видам коммунальных ресурсов:

затраты на холодное водоснабжение и водоотведение;

затраты на горячее водоснабжение;

затраты на теплоснабжение;

затраты на газоснабжение;

затраты на электроснабжение;

прочие затраты на коммунальные услуги.

7.5. Затраты на содержание объектов недвижимого имущества, необходимого для выполнения государственного задания, а также затраты на аренду указанного имущества.

В состав затрат на содержание объектов недвижимого имущества входят:

затраты на эксплуатацию системы охранной сигнализации и пожарной безопасности;

затраты на аренду недвижимого имущества и земельных участков;

затраты на проведение текущего ремонта объектов недвижимого имущества;

затраты на содержание прилегающих территорий;

прочие затраты на содержание объектов недвижимого имущества.

7.6. Затраты на содержание объектов особо ценного движимого имущества, необходимого для выполнения государственного задания, а также затраты на аренду указанного имущества.

В состав затрат на содержание объектов особо ценного движимого имущества входят:

затраты на техническое обслуживание и текущий ремонт объектов особо ценного движимого имущества;

затраты на материальные запасы, потребляемые в рамках содержания особо ценного движимого имущества, не отнесенные к нормативным затратам, непосредственно связанным с оказанием услуг (выполнением работ);

затраты на обязательное страхование гражданской ответственности владельцев транспортных средств;

прочие затраты на содержание объектов особо ценного движимого имущества.

В случае сдачи в аренду с согласия учредителя недвижимого имущества или особо ценного движимого имущества, закрепленного за Учреждениями учредителем или приобретенного Учреждениями за счет средств, выделенных им учредителем на приобретение такого имущества, затраты на содержание соответствующего имущества включаются в состав арендной платы и не учитываются при определении нормативных затрат на содержание имущества <2>.

———————————

<2> Пункт 11 Положения.

7.7. Затраты на формирование в установленном порядке резерва на полное восстановление состава объектов особо ценного движимого имущества, необходимого для общехозяйственных нужд (основных средств и нематериальных активов), с учетом срока их полезного использования, формируемого в размере начисленной годовой суммы амортизации по указанному имуществу, в целях создания источника финансового обеспечения их приобретения, создания, модернизации и (или) дооборудования <3>.

———————————

<3> Подпункт «ж» пункта 29 Положения.

7.8. Затраты на приобретение услуг связи, которые определяются исходя из фактических объемов потребления за прошлые годы в натуральном или стоимостном выражении, с учетом стандартов работ.

Затраты на приобретение услуг связи включают в себя, в том числе, затраты на местную, междугороднюю и международную телефонную связь, интернет, на прочие услуги связи.

7.9. Затраты на приобретение транспортных услуг, которые определяются исходя из фактических объемов потребления за прошлые годы в натуральном или стоимостном выражении, с учетом стандартов работ.

7.10. Затраты на оплату труда работников Учреждения, которые не принимают непосредственного участия в выполнении работ, и начисления на выплаты по оплате труда работников, которые не принимают непосредственного участия в выполнении работ, с учетом стандартов работ.

7.11. Затраты на прочие общехозяйственные нужды, с учетом стандартов работ.

8. Затраты, указанные в подпунктах 7.2.1 и 7.7 настоящего Порядка, рассчитываются на основании годовой расчетной (плановой) суммы амортизации, которая должна начисляться по особо ценному движимому имуществу, используемому в процессе выполнения работы (основные средства и нематериальные активы, амортизируемые в процессе выполнения работ) и необходимому для общехозяйственных нужд (основные средства и нематериальные активы), исходя из срока его полезного использования, установленного с учетом Классификации основных средств, включаемых в амортизационные группы, утвержденной постановлением Правительства Российской Федерации от 1 января 2002 г. N 1 «О Классификации основных средств, включаемых в амортизационные группы» (Собрание законодательства Российской Федерации, 2002, N 1, ст. 52; 2020, N 1, ст. 104), и особенностей условий его эксплуатации (повышенная сменность и (или) агрессивность среды), определяемых исходя из содержания выполняемых работ.

9. Затраты на аренду имущества, включенные в затраты, указанные в пунктах 7.2, 7.5 и 7.6 настоящего Порядка, учитываются в составе указанных затрат в случае, если имущество, необходимое для выполнения государственного задания, не закреплено за Учреждением на праве оперативного управления.

10. В объем финансового обеспечения выполнения государственного задания включаются затраты на уплату налогов, в качестве объекта налогообложения по которым признается имущество Учреждения.

11. В случае если Учреждение оказывает сверх установленного государственного задания государственные услуги (выполняет работы) для физических и юридических лиц за плату, а также осуществляет иную приносящую доход деятельность (далее — платная деятельность), затраты, указанные в пункте 10 настоящего Порядка, рассчитываются с применением коэффициента платной деятельности по формуле:

где:

NУН — затраты на уплату налогов, в качестве объекта налогообложения по которым признается имущество учреждения;

КПД — коэффициент платной деятельности, значение которого с учетом особенностей, установленных Правительством Российской Федерации, определяется как отношение планируемого объема доходов от платной деятельности к общей сумме планируемых поступлений, включающей поступления от субсидии на финансовое обеспечение выполнения государственного задания (далее — субсидия), и доходов от платной деятельности, определяемых с учетом информации об объемах указанных доходов, полученных в отчетном финансовом году, и рассчитывается по формуле:

где:

Vпд(план) — объем доходов от платной деятельности, планируемых к получению в очередном финансовом году с учетом информации об объемах оказываемых услуг (выполняемых работ) в отчетном финансовом году, о получении (прекращении действия) лицензий, иных разрешительных документов на осуществление указанной деятельности, об изменении размера платы (тарифов, цены) за оказываемую услугу (выполняемую работу). Объем планируемых доходов от платной деятельности для расчета коэффициента платной деятельности определяется за вычетом из указанного объема доходов налога на добавленную стоимость в случае, если в соответствии с законодательством Российской Федерации о налогах и сборах операции по реализации услуг (работ) признаются объектами налогообложения;

Vсубсидии(план) — планируемый объем субсидии на очередной финансовый год и плановый период, рассчитанный без применения коэффициента платной деятельности.

12. При расчете коэффициента платной деятельности не учитываются поступления в виде целевых субсидий, предоставляемых из федерального бюджета, грантов, пожертвований, прочих безвозмездных поступлений от физических и юридических лиц, а также средства, поступающие в порядке возмещения расходов, понесенных в связи с эксплуатацией федерального имущества, переданного в аренду (безвозмездное пользование) и в виде платы, взимаемой с потребителя в рамках установленного государственного задания.

III. Утверждение нормативных затрат на выполнение работ
и внесение изменений в утвержденные нормативные затраты
на выполнение работ

13. Значения нормативных затрат на выполнение работ, рассчитанные в соответствии с настоящим Порядком, на очередной финансовый год и на плановый период утверждаются Федеральным агентством по делам молодежи одновременно с утверждением государственного задания не позднее 15 (пятнадцати) рабочих дней со дня отражения на лицевом счете главного распорядителя бюджетных средств, открытом соответствующему главному распорядителю средств федерального бюджета, лимитов бюджетных обязательств на предоставление Учреждениям субсидий на финансовое обеспечение выполнения государственного задания (далее — лимиты бюджетных обязательств).

14. Изменение нормативных затрат в течение срока выполнения государственного задания осуществляется (при необходимости) в случаях, предусмотренных нормативными правовыми актами Российской Федерации (включая внесение изменений в указанные нормативные правовые акты), приводящих к изменению объема финансового обеспечения выполнения государственного задания <4>.

———————————

<4> Пункт 41 Положения.

15. Значения нормативных затрат на выполнение работ (с учетом корректирующих коэффициентов) утверждаются в форме электронного документа в подсистеме бюджетного планирования государственной интегрированной информационной системы управления общественными финансами «Электронный бюджет» путем подписания усиленной квалифицированной электронной подписью лица, имеющего право действовать от имени Учреждения.

Источник

В каком примере к выделенному слову применимо следующее правило: «В кратких пр…

Разбор сложных заданий в тг-канале:

Сложность:

Среднее время решения: 1 мин. 12 сек.

ЕГЭ по русскому языку 2023 задание 15: номер 193 | В каком примере к выделенному…
35

В каком примере к выделенному слову применимо следующее правило: «В кратких прилагательных пишется столько Н, сколько в полных»?

Травы и цветы уже сорва…ы и высуше…ы для гербария.
В институте были сформирова…ы стройотряды.
На скучном уроке ученики невнимательны и рассея…ы.
Дома эти ещё не заселе…ы, квартиры не оборудова…ы.

Объект авторского права ООО «Легион»

Вместе с этой задачей также решают:

Укажите цифру(-ы), на месте которой(-ых) пишется НН.

Глядя на мужчин в дли(1)ых чёрных пальто и широкополых шляпах, на женщин в платьях в пол и придирчиво выбра(2)ых шляпках, можно…

Укажите все цифры, на месте которых пишется одна буква Н.

Среди кадок с брусникой и клюквой, плетё(1)ых корзин с вкусными пряниками ярче солнца блестят, переливаются весе(2)ими кр…

Укажите все цифры, на месте которых пишется НН.

Версаль — знаменитый королевский дворец, окружё(1)ый парком с многочисле(2)ыми фонтанами, его убранство отличалось неслыха(3)ой роск…

Укажите все цифры, на месте которых пишется НН.

История самая обыкнове(1)ая. Но вы, кажется, скло(2)ы придавать ей преувеличе(3)ое значение.

Задание 1

Найдите значение выражения $$(frac{1}{9})^{-2}+19^{-3}:19^{-4}-2019$$

Ответ: 1919

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$(frac{1}{9})^{-2}+19^{-3}: 19^{-4}-2019=$$$$9^{2}+19^{-3-(-4)}-2019=61+19-2019=$$$$100-2019=1919$$

Задание 2

Для квартиры площадью 56 кв. м заказан натяжной потолок белого цвета. Стоимость работ по установке натяжных потолков приведена в таблице.

Цвет потолка	Цена в рублях за 1 м² (в зависмости от площали помещения)
	до 10 м²	от 11 до 30 м²	от 31 до 60 м²	свыше 60 м²
белый	1200	1000	800	600
цветной	1350	1150	950	750

Какова стоимость заказа, если действует сезонная скидка в 5%?

В ответе укажите номер правильного варианта.

1) 4256 рублей

2) 44800 рублей

3) 42 560 рублей

4) 44 995 рублей

Ответ: 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

56*800=44800-стоимость без скидки 44800*0,95=42560-со скидкой, что соответствует 3 варианту ответа

Задание 3

На координатной прямой отмечены числа a, b и c.

Какое из следующих утверждений об этих числах верно?

$$a+b<c$$
$$ab>c$$
$$bc>1$$
$$frac{1}{c}<1$$

Ответ: 1

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

По условию задания: a<0<b<c<1. Пусть a=-0,5; b=0,4; c=0,8

$$a+b<cLeftrightarrow -0,5+0,4<0,8$$-верно
$$ab>c-0,5*0,4>0,8$$-неверно
$$bc>10,4*0,8>1$$-неверно
$$frac{1}{c}<1frac{1}{0,8}<1$$-неверно

Верным является только первый вариант ответа

Задание 4

Значение какого из выражений является числом рациональным?

Варианты ответа

$$sqrt{8}*sqrt{12}$$
$$(sqrt{8}-sqrt{12})(sqrt{8}+sqrt{12})$$
$$frac{sqrt{8}}{sqrt{12}}$$
$$(sqrt{8}+sqrt{12})^{2}$$

Ответ: 2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$sqrt{8-12}=sqrt{96}$$-иррационально
$$(sqrt{8}-sqrt{12})(sqrt{8}+sqrt{12})=8-12=-4$$
$$frac{sqrt{8}}{sqrt{12}}=sqrt{frac{2}{3}}$$-иррационально
$$(sqrt{8}+sqrt{12})^{2}=8+2sqrt{96}+12$$-иррационально

Рациональным является только второй вариант ответа

Задание 5

На графиках показано, как во время телевизионных дебатов между кандидатами А и Б телезрители голосовали за каждого из них. Сколько всего тысяч телезрителей проголосовало за первые 20 минут дебатов?

Ответ: 25

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Кандидат A: 15 Кандидат Б: 10 В сумме : 15+10=25

Задание 6

Решите уравнение $$frac{9}{x-5}=frac{5}{x-9}$$

Ответ: 14

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$9(x-9)=5(x-5)Leftrightarrow$$ $$9x-81=5x-25Leftrightarrow$$ $$4x=56Leftrightarrow$$ $$x=14$$

Задание 7

В в школе учится 1200 учащихся, среди которых 156 отличников. Сколько процентов составляют отличники этой школы?

Ответ: 13

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1200-100% 156-x% $$x=frac{156*100}{1200}=13$$

Задание 8

На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей.

Какие из следующих утверждений неверны?

пользователей из Аргентины больше, чем пользователей из Польши.
пользователей из Аргентины примерно втрое больше, чем пользователей из Парагвая.
пользователей из Аргентины и Беларуси вместе — меньше четверти общего числа пользователей.
пользователей из Бразилии примерно 8 миллионов человек

Ответ: 14

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

верно
не верно
не верно
верно

Задание 9

Аня выбирает трехзначное число. Найдите вероятность того, что оно делится на 11

Ответ: 0,09

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Количество чисел до 999 делящихся на 11: $$999*11=90,(81)Rightarrow 90$$ До 99 — 99:11=9 Всего трехзначных чисел: 999-99=900 $$P=frac{90-9}{900}=frac{81}{900}=0,09$$

Задание 10

Установите соответствие между графиками функций и формулами, которые их задают.

функции

$$y=-frac{6}{x}$$
$$y=-frac{1}{2}x^{2}$$
$$y=frac{1}{2}x-2$$
$$y=-frac{1}{2}x^{2}-2$$

Ответ: 312

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

A — линейная функция $$Rightarrow 3$$

Б — обратная пропорциональность $$Rightarrow 1$$

B — квадратичная вида $$y=-ax^{2}Rightarrow 2$$

Задание 11

Выписаны первые три члена арифметической прогрессии: 20; 13; 6; … Найдите шестой член этой прогрессии.

Ответ: -15

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Найдем разность арифм. Прогрессии : $$d=a_{n+1}-a_{n}=13-20=-7$$ Найдем шестой член используя формулу n-го члена: $$a_{n}=a_{1}+d(n-1)$$ $$a_{6}=2a-7(6-1)=-15$$

Задание 12

Найдите значение выражения $$(x-5)^{2}-x(10+x)$$ при $$x=-frac{1}{20}$$

Ответ: 26

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$(x-5)^{2}-x(10+x)=$$$$x^{2}-10x+25-10x-x^{2}=$$$$-20+25=-20(-frac{1}{20})+25=26$$

Задание 13

Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м³), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T=700 K, P = 20 941,2 Па, V = 9,5 м³.

Ответ: 34,2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Выразим количество вещества из формулы: $$v=frac{PV}{RT}$$ Найдем значение количества вещества: $$v=frac{20941,2*9,5}{8,31*700}=frac{209412*95*10^{-2}}{831*700*10^{-2}}=frac{252*95}{700}=34,2$$

Задание 14

Решите неравенство $$9x^{2}-(3x-5)^{2}leq 5(3x+4)$$

Варианты ответа:

$$[3;+infty)$$
$$[-3;+infty)$$
$$(-infty;3]$$
$$(-infty;-3]$$

Ответ: 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$9x^{2}-(3x-5)^{2}leq 5(3x+4)Leftrightarrow$$$$9x^{2}-9x^{2}+30x-25-25x-20leq 0$$$$15leq 45Leftrightarrow xleq 3$$, что соответствует 3 варианту ответа

Задание 15

Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

Ответ: 49

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Площадь квадрата: $$8^{2}=64$$ Площадь прямоугольника: $$5*3=15$$ $$S=64-15=49$$

Задание 16

Длина хорды окружности равна 12, а расстояние от центра окружности до этой хорды равно 8. Найдите диаметр окружности.

Ответ: 20

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$AH=frac{1}{2}AB=6$$

$$OA=sqrt{OH^{2}+AH^{2}}=$$$$sqrt{6^{2}+8^{2}}=10$$

$$d=2*OA=20$$

Задание 17

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 5 и 8. Найдите длину основания BC.

Ответ: 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Пусть $$BH_{1}left | right |CH$$ и $$BH_{1}=CH$$

Тогда $$AH_{1}=DH=5$$

$$HH_{1}=AH-AH_{1}=8-5=3=BC$$

Задание 18

Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 24 и 26.

Ответ: 120

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$OB=sqrt{26^{2}-24^{2}}=10$$

$$S=frac{1}{2}*10*24=120$$

Задание 19

Катеты прямоугольного треугольника равны $$5sqrt{3}$$ и 5. Найдите синус наименьшего угла этого треугольника.

Ответ: 0,5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$CB>ACRightarrow angle B<angle A$$

$$AB=sqrt{5^{2}+(5sqrt{3})^{2}}=10$$

$$sin A=frac{AC}{AB}=frac{5}{10}=0,5$$

Задание 20

Какие из следующих утверждений верны?

Все равнобедренные треугольники подобны.
Каждая из биссектрис равнобедренного треугольника является его высотой.
Равнобедренный треугольник с углом 60 — равносторонний.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов

Ответ: 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1.нет — только с равными соответствующими друг другу углами 2.нет — только та, что выходит из вершины, противоположной основанию. 3.да

Задание 21

Решите неравенство $$frac{(x+2)(x+1)}{x^{2}-|x|-2}leq -3x$$

Ответ: $$x in (-infty ;-2)cup(-2;frac{2}{3})cup [1; 2)$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Область определения: $$x^{2}-|x|-2neq 0Leftrightarrow$$$$|x|neq 2, |x|neq -1Leftrightarrow$$$$xneq pm 2$$

Раскроем модуль:

1) При $$xgeq 0 Rightarrow$$ $$frac{(x+2)(x+1)}{x^{2}-x-2} leq -3xLeftrightarrow$$ $$frac{(x+2)(x-1)}{(x-2)(x+1)}leq -3xLeftrightarrow$$ $$frac{x+2}{x-2}+3xleq 0$$

Рассматриваем числитель дроби, чтобы разбить его на множители: $$3x^{2}-5x+2=0$$

$$D=25-24=1$$

$$x_{1}=frac{5+1}{6}=1$$

$$x_{2}=frac{5-1}{6}=frac{2}{3}$$

Следовательно,$$frac{(x-frac{2}{3})(x+1)}{x-2}leq 0$$

2) При $$x<0 Rightarrow$$$$frac{(x+2)(x+1)}{x^{2}+x-2}leq -3xLeftrightarrow$$ $$frac{(x+2)(x+1)}{(x+2)(x-1)}+3xleq 0Leftrightarrow$$$$frac{x+1}{x-1}+3xleq 0Leftrightarrow$$ $$frac{x+1+3x^{2}-3x}{x-1}leq 0Leftrightarrow$$ $$frac{3x^{2}-2x+1}{x-1}leq 0$$

Рассмотрим числитель полученной дроби:

$$3x^{2}-2x+1=0$$

$$D=4-12<0$$

Следовательно, числитель данной дроби всегда положителен и не влияет на знак неравенства: $$frac{1}{x-1}leq 0$$

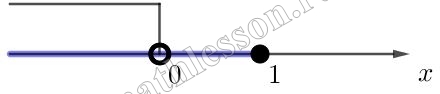
С учетом обрасти опредеделения:

$$x in (-infty ;-2)cup(-2;frac{2}{3})cup [1; 2)$$

Задание 22

Моторная лодка спустилась вниз по течению реки на 20 км и поднялась вверх по притоку еще на 10 км, затратив на весь путь 1 ч 10 мин. На обратный путь лодке потребовалось 1 ч 20 мин. Зная, что скорость реки равна скорости течения притока, найти собственную скорость лодки.

Ответ: 25

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Пусть x-скорость лодки в стоячей воде (кмч ),y кмч — скорость течения

$$left{begin{matrix}frac{20}{x+y}+frac{10}{x-y} =1frac{1}{6} \frac{10}{x+y}+frac{20}{x-y}=1frac{1}{3} end{matrix}right.$$

Умножим второе на 2 и вычтем из первого:

$$frac{10}{x-y}-frac{40}{x-y}=frac{7}{6}-frac{8}{3}$$

$$-frac{30}{x-y}=frac{7-16}{6}=-frac{9}{6}=-frac{3}{2}$$

$$x-y=frac{39*2}{3}=20$$

$$y=x-20$$

Подставим в первое:

$$frac{20}{x+x-20}+frac{10}{x-x+20}=frac{7}{6}$$

$$frac{20}{2x-20}+frac{1}{2}=frac{7}{6}$$

$$frac{10}{x-10}=frac{7-3}{6}=frac{2}{3}$$

$$2(x-10)=30Leftrightarrow$$ $$2x-20=30Leftrightarrow$$ $$2x=50Leftrightarrow$$ $$x=25$$

Задание 23

При каких значениях р вершины парабол $$y=x^{2}-6px+p$$ и $$y=-x^{2}+2px+3$$ расположены по одну сторону от оси х?

Ответ: $$(0 ;frac{1}{9})$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Вершина $$y=x^{2}-6px+p$$: $$x_{01}=-frac{6p}{2}=3p$$, $$y_{01}=9p^{2}-18p^{2}+p=p-9p^{2}$$

Вершина $$y=-x^{2}+2px+3$$: $$x_{02}=-frac{2p}{-2}=p$$, $$y_{02}=-p^{2}+2p^{2}+3=p^{2}+3$$

По одну сторону от OX:

$$left[begin{matrix}left{begin{matrix}y_{01}>0\y_{02}>0end{matrix}right.\left{begin{matrix}y_{01}<0\y_{02}<0end{matrix}right.end{matrix}right.Leftrightarrow$$$$left[begin{matrix}left{begin{matrix}p-9p^{2}>0 \p^{2}+3>0 end{matrix}right. \left{begin{matrix}p-9p^{2}<0 \p^{2}+3<0 end{matrix}right. end{matrix}right.Leftrightarrow$$$$left[begin{matrix}left{begin{matrix}p-9p^{2}>0 \p in R end{matrix}right. \left{begin{matrix}p-9p^{2}<0 \p in varnothing end{matrix}right. end{matrix}right.Leftrightarrow$$$$p(1-9p)>0Leftrightarrow$$ $$pin (0 ;frac{1}{9})$$

Задание 24

В прямоугольном треугольнике, периметр которого равен 36 см, вписана окружность. Гипотенуза делится точкой касания в отношении 2 : 3. Найдите длину гипотенузы.

Ответ: 15

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1) Пусть $$frac{AH}{HB}=frac{2}{3}$$, тогда AH=2x; HB=3x

2) По свойству касательных MB=HB=3x, NA=AH=2x

3) Пусть ON=OH=OM=y, но NC=CM=y. Тогда по т. Пифагора :$$(y+2x)^{2}+(y+3x)^{2}=(5x)^{2}(1)$$

4) т.к. P=36, то $$y+2x+y+3x+5x=36$$, $$2y=36-10xLeftrightarrow y=18-5x$$

Подставим в (1)

$$(18-5x+2x)^{2}+(18-5x+3x)^{2}=25x^{2}$$

$$324-108x+9x^{2}+324-72x+4x^{2}=25x^{2}$$

$$12x^{2}+180x-648=0$$

$$x^{2}+15x-54=0$$

$$left{begin{matrix}x_{1}+x_{2}=-15\x_{1}*x_{2}=-54end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}x_{1}=3\x_{2}=-18end{matrix}right.$$

-18 не может быть, так как длина — число положительное, следовательно, $$5x=5*3=15$$ — длина гипотенузы

Задание 25

Докажите, что в прямоугольном треугольнике произведение длин отрезков, на которые делит гипотенузу точка касания с вписанной окружностью, равна площади треугольника.

Ответ:

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1) Пусть AH=x; HB=y; NO=OM=OH=r. По свойству касательных: AN=AH=x, MB=HB=y

2) $$S_{ABC}=frac{1}{2}AC*CB=$$$$frac{1}{2}(x+r)(y+r)=$$$$frac{1}{2}xy+frac{1}{2}xr+frac{1}{2}yr+frac{1}{2}r^{2}(1)$$

С другой стороны : $$S_{ABC}=2S_{AOH}+2S_{HOB}+S_{CNOM}=$$$$2S_{AOB}+S_{CNOM}=2*frac{1}{2}(x+y)r+r^{2}=xr+yr+r^{2}(2)$$

Приравняем (1) и (2):

$$frac{1}{2}xy+frac{1}{2}xr+frac{1}{2}yr+frac{1}{2}r^{2}=xr+yx+r^{2}$$

$$frac{1}{2}xy=frac{1}{2}xr+frac{1}{2}yr+frac{1}{2}r^{2}|*2$$

$$xy=xr+y^{2}+r^{2}=S_{ABC}$$

Задание 26

В выпуклом четырехугольнике KLMN отрезок MS, соединяющий вершину М с точкой S, расположенной на стороне КN, пересекает диагональ LN в точке О. Известно, что KL : MN = 6 : 7, KM : ON = 2 : 1 и $$angle KLN + angle KMN=180$$. Найдите отношение отрезков MO и OS.

Ответ: $$frac{4}{3}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

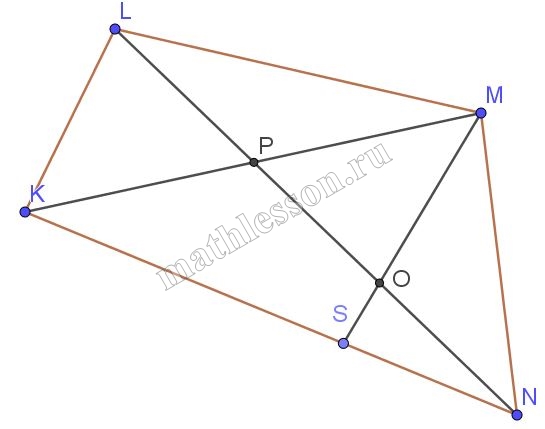
1) Пусть $$KMcap LN=P$$, $$angle KLN=alpha$$ , тогда $$angle KMN=180-alpha$$ ,$$angle LPK=angle MPN=beta$$ (вертикальные)

2) из $$Delta LPK$$ по теореме синусов: $$frac{KP}{sin alpha }=frac{LK}{sin beta }(1)$$

Из $$Delta PMN : frac{PN}{sin (180-alpha )}=frac{MN}{sin beta }$$

С учетом , что $$sin alpha =sin (180-alpha )$$, получаем: $$frac{PN}{sin alpha }=frac{MN}{sin beta }(2)$$

Поделим (1) и (2): $$frac{KP}{PN}=frac{LK}{MN}=frac{6}{7}$$

3) Пусть KM=2y; ON=y, тогда KP=6x, PN=7x, PM=2y-6x, PO=7x-y;

4)По т. Менелая из $$Delta KPN$$ и секущей MS : $$frac{MO}{OS}*frac{SN}{NK}*frac{KP}{PM}=1$$

Пусть $$frac{SO}{OS}=m$$, тогда $$m*frac{SN}{SN+SK}*frac{6x}{2y-6x}=1(3)$$

По т. Менелая из $$Delta KMS$$ и секущей NP: $$frac{NO}{OP}*frac{PM}{MK}*frac{MS}{SN}=1$$

Пусть $$frac{SK}{SN}=n$$, тогда $$frac{SN}{SN+SK}=frac{frac{SN}{SN}}{frac{SN}{SN}+frac{SK}{SN}}=frac{1}{1+n}$$

Получаем: $$frac{y}{7x-y}*frac{2y-6x}{2y}*n=1(4)$$

Выразим в (3) m: $$m=frac{2y-6x}{6x}*(1+n)=frac{(y-3x)(1+n)}{3x}(5)$$

Выразим в (4) n: $$n=frac{y}{y-3x}*frac{7x-y}{y}=frac{7x-y}{y-3x}$$

Выразим в (5): $$m=frac{(y-3x)(1+frac{7x-y}{y-3x})}{3x}=$$$$frac{y-3x+7x-y}{3x}=frac{4x}{3x}=frac{4}{3}$$

Источник

Показать содержание

← Предыдущее

Следующее →

Решебник

§5 / 193

Показать содержание

← Предыдущее

Следующее →

ГДЗ решение к заданию № 193 Математика 5 класс Виленкин Н.Я. Мнемозина 2018 Часть 1, Часть 2 ФГОС бесплатно на гдз.мода!

Источник

В каком примере к выделенному слову применимо следующее правило: «В кратких пр…

Вместе с этой задачей также решают:

Популярные материалы

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Задание 7

Задание 8

Задание 9

Задание 10

Задание 11

Задание 12

Задание 13

Задание 14

Задание 15

Задание 16

Задание 17

Задание 18

Задание 19

Задание 20

Задание 21

Задание 22

Задание 23

Задание 24

Задание 25

Задание 26

Решебник

§5 / 193