Задание 15 номер 132776

Не могу найти по номеру выполняемое многоразовое задание. Да и любые другие по номеру не найти). Пробовал произвольно выбранные задания вызвать по номеру — и ничего!)

Обсуждение

gimmegun

12 Окт 2017 г, в 09:01
редактир. 12 Окт 2017 г, в 09:06

Одной из причин может быть выбор фильтров

По спискам

и

По типу

при поиске.
Если это (эти) задание у Вас в Избранном, то должны быть выбраны фильтры

Избранное

и

Все.

Если выбраны

Все

и

Все

, то задание не покажут.
Если задание не в Избранном, то соответственно наоборот — должны быть выбраны фильтры

Все

и

Все

.
Другой причиной может быть то, что задание выключено или забанено.

Не годится…(( Принцип, который вы описали, до меня добрел)), я им воспользовался, результат=0. Сейчас вот еще на всякий случай попробовал. Взял номер первого попавшегося задания (оно у меня никак не отмечено), выбрал «Все», ввел номер, и тишина…

---

Для обсуждения вопроса/идеи необходима регистрация.

Мгновенный доступ

50 баллов

ИЛИ

Доступ после просмотра рекламы

Ответы будут доступны после просмотра рекламы

Объяснение:

решение во вложении

Ответ подобран нейросетью

Мгновенный доступ

50 баллов

ИЛИ

Доступ после просмотра рекламы

Ответы будут доступны после просмотра рекламы

1)16*6=96

2)96:3=32

Пошаговое объяснение:

Ответ подобран нейросетью

Мгновенный доступ

50 баллов

ИЛИ

Доступ после просмотра рекламы

Ответы будут доступны после просмотра рекламы

32 пакета.

Пошаговое объяснение:

В одном ящике 16кг,а в 6 таких ящиках

1) 6*16=96 кг моркови всего привезли.

В одном пакете 3кг.

2) 96:3=32 пакета с морковью.

Ответ подобран нейросетью

Мгновенный доступ

50 баллов

ИЛИ

Доступ после просмотра рекламы

Ответы будут доступны после просмотра рекламы

5 минут

Объяснение:

Смотри фото

Ответ подобран нейросетью

Мгновенный доступ

50 баллов

ИЛИ

Доступ после просмотра рекламы

Ответы будут доступны после просмотра рекламы

Можно лучший ответ?)))

Ответ подобран нейросетью

Мгновенный доступ

50 баллов

ИЛИ

Доступ после просмотра рекламы

Ответы будут доступны после просмотра рекламы

Пусть 3 1/3 часа -3 часа 20 минут(200 минут) — первый насос

Пусть 1 1/2 раза — представим, как 1,5 раз — второй насос

3 часа 20 минут * 1,5 раза = 300 (мин)

300 — 200 = 100 (мин) или 1 ч. 40 мин.- откачают воду оба насоса

ответ: за 1 ч. 40 мин.

Обвести кружком
номер правильного ответа:

1. Больной ,находящийся
   в сопоре :

1. на вопросы отвечает
   и реагирует на уколы

2. на вопросы не
   отвечает, на уколы реагирует

3. на вопросы не
   отвечает, на уколы не реагирует

Установить
соответствие:

2. Патология
Вынужденное положение

1. Менингит
А. ортопноэ

2. Сердечная
недостаточность Б. С приведенными к
животу

ногами

3. Гидроторакс
В. Лягавой собаки

4. Острый живот
Г. На больном боку

.Д.
Молящегося муллы

Ответ : 1…, 2…, 3…,
4… .

Обвести кружком
номера всех правильных ответов:

3.Акроцианозом
называется синюшность:

1. губ

2. лица

3. мочек ушей

4. кончика носа

5. шеи и верхней
   части грудной клетки

6. ногтей

Дополнить:

4.У больного
,находящегося в лежачем положении, отеки
появляются сначала в области _____________.

5.Видимое на глаз
увеличение щитовидной железы называется

________.

Эталоны ответов
№ 15

15.1. 3.

15.2. 1 В , 2 А , 3 Г , 4 Б
.

15.3. 1,3,4,6.

15.4. крестца

15.5. зоб.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Обозначим АВС. АС-основание. Проведем высоту с вершины В. Пункт пересечения обозначим Н. Значит АН=26/2=13 см, так как высота в равнобедренном треугольнике является медианой и биссектрисой.  Треугольник АВН-прямоугольный. Угол АВН=60 градусов. Значит угол ВАН=30 градусов, с этого получается, что ВН в два раза меньше, чем АВ, потому что лежит против угла в 30 градусов. Пусть ВН-х см, тогда АВ=2х см. По теореме Пифагора 4х²=х²+169, 3х²=169, х=√169/3 =13/√3. S=1/2*26*13/√3=(169√3)/3 см².

В четырёх маленьких клетках 3*4=12 кроликов.
В пяти больших клетках 9*5=45 кроликов .
вроде так

Ответ:

Купили -8 рулонов обоев.

Длиной по 10м 50 см.

Израсходовали 3/4 части.

Ск. метров обоев осталось-?

10 м 50 см = 1050 см

1) 8*1050=8400 (см) или 84 (м) — обоев всего

2) 8400*3/4=252/4  (см) или 63 (м) — израсходовали

3) 84 — 63 = 21 (м) — осталось

ответ: 21 м обоев остался

Пошаговое объяснение:

км/ч — скорость вертолета
км/ч — скорость самолета
км — пролетел самолет за 5 часов

ОТВЕТ: 2175 км

Условие

15 номер задания

математика 10-11 класс
385

Все решения

Написать комментарий

Пятнадцать
и
сто тридцать две тысячи семьсот семьдесят шесть

Сумма	132791
Разность	-132761
Частное	0.0001129722238958848
Остаток от деления	15
Произведение	1991640
Наибольший общий делитель (НОД)	1
Наименьшее общее кратное (НОК)	1991640
Среднее арифметическое	66395.5
Среднее геометрическое	1411.2547608422797
Гипотенуза	132776.00084729167
Простые числа-близнецы?	Нет
Расстояние Левенштейна	5
Общие делители	1
Взаимнопростые числа?	Да
Общие цифры	1

Описание

Пара 15 и 132776 при сложении образуют 132791 . Если вычесть из 15 число 132776 то получается -132761.

Частное от деления 15 на 132776 ~ 0.000113. Остаток от деления – 15. При умножении 15 на 132776 получается число 1991640.

Наибольший общий делитель двух чисел 1 . Для этой пары наименьшим общим кратным (НОК) является число 1991640.

Общий делитель: 1.

Среднее арифметическое: 66395.5 , а среднее геометрическое — 1411.254761.

Это взаимнопростые числа. Общая цифра этой пары чисел: 1.

В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.

Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.

Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы.

В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.

Теория к заданию №15

Так как задания №16 основаны на теории по теме “треугольники”, рассмотрим базовые понятия, определения и формулы.

Вначале предлагаю рассмотреть углы на плоскости:

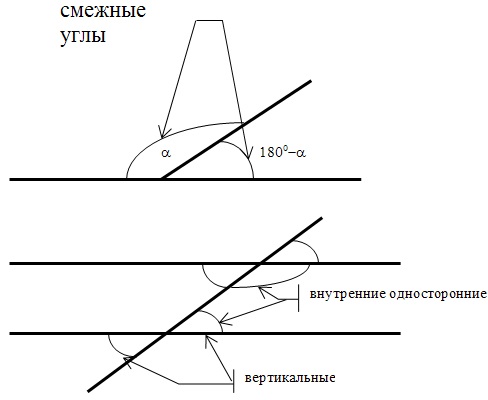
Многие задачи построены на нахождении медиан и биссектрис треугольника:

Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.

• Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
• Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
• Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.

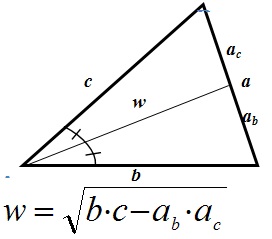Медиана:

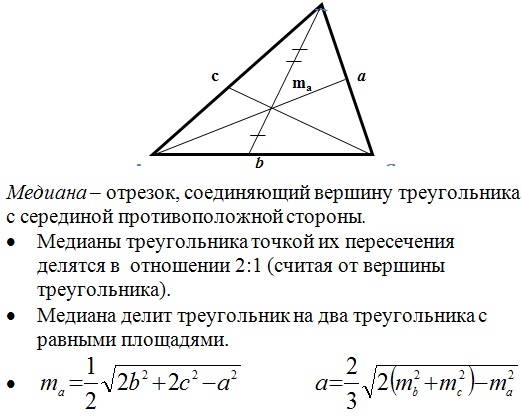
Теперь вспомним основные формулы нахождения площади треугольника:

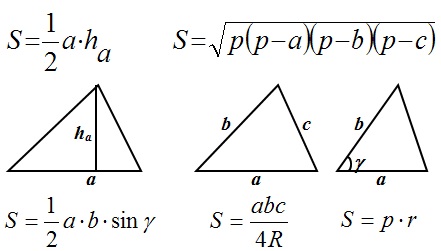
Во многих задачах встречается понятие средняя линия:

Средняя линия – отрезок, соединяющий середины двух сторон треугольника.

• Средняя линия параллельна третьей стороне и равна её половине.
• Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.

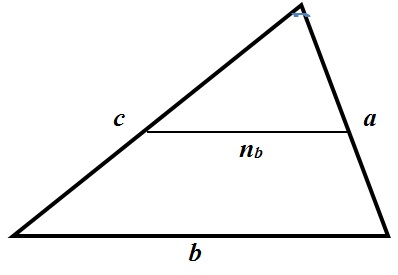
Теперь рассмотрим частные случаи треугольников – равнобедренный, равносторонний, прямоугольный.

Перейдем к рассмотрению равнобедренного треугольника:

Равнобедренный треугольник – треугольник, у которого две стороны равны.

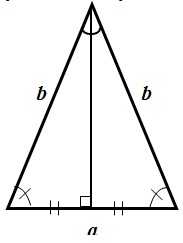
Свойства равнобедренного треугольника:

• Углы, при основании треугольника, равны.
• Высота, проведенная из вершины, является биссектрисой и медианой.

Рассмотрим равносторонний треугольник:

Равносторонний треугольник – треугольник, у которого все стороны равны.

• Все углы равны 60°.
• Каждая из высот является одновременно биссектрисой и медианой.
• Центры описанной и вписанной окружностей совпадают.

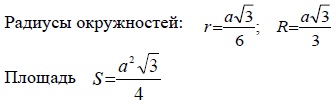Прямоугольный треугольник:

Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Часть 1

Задание 15

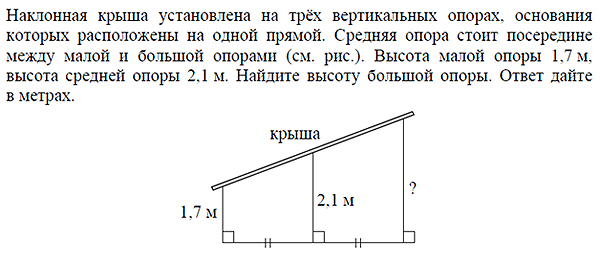
Решение

Фигура, изображенная на рисунке, является прямоугольной трапецией. Средняя опора есть не что иное, как средняя линия трапеции, длина которой вычисляется по формуле

где a, b – длины оснований. Составим уравнение:

b = 2,5.

Ответ: 2,5.

Задание 1 № 366805

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	Город Гранюк	Деревня Астрелка	Хутор Южный	Город Гусевск
Цифры

Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.

Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.

Ответ: 1465.

2. Задание 2 № 366806

Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.

Решение.

Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится

пачек чая.

Таким образом, ребята должны купить 14 пачек чая.

Ответ: 14.

3. Задание 3 № 366807

Найдите площадь (в км²), которую занимает заказник.

Решение.

Площадь заказника равна:

Ответ: 351.

4. Задание 4 № 366808

Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.

Решение.

Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:

км.

Ответ: 30.

5. Задание 5 № 366809

Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.

Продукция	Цена в магазине «Вело» (руб.)	Цена в магазине «ОК» (руб.)	Срок доставки из магазина «ОК» (дни)
Подсветка для спиц
Шина вида «А»
Шина вида «Б»
Спица
Педаль вида «А»
Педаль вида «Б»
Тормоз вида «А»		нет
Тормоз вида «Б»	нет
Набор крепёжных изделий

Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?

Решение.

На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:

руб.

Ответ: 5300.

6. Задание 6 № 316314

Найдите значение выражения:

Решение.

Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.

7. Задание 7 № 317575

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?

1)

2)

3)

4)

Решение.

Заметим, что и Проверим все варианты ответа:

1) — неверно;

2) — верно;

3) — верно;

4) — верно.

Ответ указан под номером 1.

8. Задание 8 № 353586

Какое из данных ниже чисел является значением выражения

1)

2)

3)

4)

Решение.

Последовательно получим:

Ответ: 1

9. Задание 9 № 338500

При каком значении значения выражений и равны?

Решение.

Для ответа на вопрос задачи нужно решить уравнение Решим его:

Ответ: 2.

10. Задание 10 № 325450

В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.

Решение.

Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна

Ответ: 0,3.

11. Задание 11 № 311406

На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке

2)

3)

4) прямая пересекает график в точках и

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .

2) — неверно,

3) — верно, видно из графика.

4) Прямая пересекает график в точках и — верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

Ответ: 12.

12. Задание 12 № 311543

Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .

Решение.

Выразим :

Подставляя, получаем:

Ответ: 0,4.

13. Задание 13 № 338497

На каком из рисунков изображено решение неравенства

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

Решение.

Решим неравенство методом интервалов:

Правильный ответ указан под номером: 4.

14. Задание 14 № 406645

В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение.

Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.

Найдем сумму этой прогрессии:

Ответ: 377 мест.

15. Задание 15 № 340000

В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите

Решение.

Из прямоугольного треугольника по теореме Пифагора найдём

Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.

16. Задание 16 № 351463

На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.

Решение.

Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.

17. Задание 17 № 169876

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.

———-

В открытом банке иррациональный ответ.

18. Задание 18 № 350842

Найдите угол

Решение.

Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.

Ответ: 22,5

19. Задание 19 № 401617

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Ответ: 13.

20. Задание 20 № 338505

Решите неравенство

Решение.

Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение

Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).

Таким образом, ответ

Ответ:

Примечание.

Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,

21. Задание 21 № 353527

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.

Ответ: 58.

22. Задание 22 № 338288

Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.

Решение.

Упростим выражение:

По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:

График функции сводится к графику параболы с выколотой точкой

Выделим полный квадрат:

Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)

Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и

Ответ: −1; 3.

23. Задание 23 № 339395

Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.

Решение.

Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и

Ответ: 16.

24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.

Решение.

Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.

25. Задание 25 № 311926

В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .

Решение.

По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,

Площадь трапеции :

Площадь трапеции

Ответ: 9.