Задания 14. Задачи на прогрессии. Формат 2021
1. Задание 14 № 393942
Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
2. Задание 14 № 393944
Рабочие прокладывают тоннель длиной 500 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра тоннеля. Определите, сколько метров тоннеля проложили рабочие в последний день, если вся работа была выполнена за 10 дней.
3. Задание 14 № 393946
Васе надо решить 434 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней.
4. Задание 14 № 393948
Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.
5. Задание 14 № 393950
Грузовик перевозит партию щебня массой 210 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено за девятый день, если вся работа была выполнена за 14 дней.
6. Задание 14 № 393952
Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам.
7. Задание 14 № 393954
Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней.
8. Задание 14 № 393956
Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000 рублей. Каждый следующий год его прибыль увеличивалась на 300% по сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2003 год?
9. Задание 14 № 393958
Компания «Альфа» начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10 000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?
10. Задание 14 № 394131
Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика на пятый день?
11. Задание 14 № 394303
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?
12. Задание 14 № 394308
В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?
13. Задание 14 № 394309
Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке 15 минут, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на 7 минут. За сколько занятий Андрей проведёт на беговой дорожке в общей сложности 2 часа 25 минут, если будет следовать советам тренера?
14. Задание 14 № 394311
Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв в день 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
15. Задание 14 № 394312
В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах — одно штрафное очко, за каждый последующий — на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?
16. Задание 14 № 394315
Улитка ползет вверх по дереву, начиная от его основания. За первую минуту она проползла 30 см, а за каждую следующую минуту — на 5 см больше, чем за предыдущую. За сколько минут улитка достигнет вершины дерева высотой 5,25 м? В ответе укажите число минут.
17. Задание 14 № 394316
Альпинисты в первый день восхождения поднялись на высоту 1400 м, а затем каждый следующий день поднимались на высоту на 100 м меньше, чем в предыдущий. За сколько дней они покорили высоту 5000 м?
18. Задание 14 № 394318
Клиент взял в банке кредит в размере 50 000 р. на 5 лет под 20% годовых. Какую сумму он должен вернуть в банк в конце срока, если весь кредит с процентами возвращается в банк после срока?
19. Задание 14 № 394319
Бактерия, попав в живой организм, к концу 20-й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т. д. Сколько бактерий окажется в организме через 4 часа, если по истечении четвертого часа в организм из окружающей среды попала еще одна бактерия?
20. Задание 14 № 394320
Однажды богач заключил выгодную, как ему казалось, сделку с человеком, который в течение 15 дней ежедневно должен был приносить по 1000 р., а взамен в первый день богач должен был отдать 10 р., во второй — 20 р., в третий — 40 р., в четвертый — 80 р. и т. д. в течение 15 дней. Сколько денег получил богач и сколько он отдал? Кто выиграл от этой сделки? В ответ запишите, сколько рублей потерял богач за 15 дней.
21. Задание 14 № 394395
На биржевых торгах в понедельник вечером цена акции банка «Городской» повысилась на некоторое количество процентов, а во вторник произошло снижение стоимости акции на то же число процентов. В результате во вторник вечером цена акции составила 99% от ее первоначальной цены в понедельник утром. На сколько процентов менялась котировка акции в понедельник и во вторник?
22. Задание 14 № 394399
Мать дарит дарит каждой из пяти своих дочерей в день рождения, начиная с пяти лет, столько книг, сколько дочери лет. Возрасты пяти дочерей составляют арифметическую прогрессию, разность которой равна 2. Сколько было лет каждой дочери, когда у них составилась библиотека общей численностью в 495 книг? Сколько лет старшей дочери?
23. Задание 14 № 394401
Для асфальтирования участка длиной 99 м используются 2 катка. Первый каток был установлен в одном конце участка, второй — в противоположном. Работать они начали одновременно. Первый каток в каждую минуту проходил 5 м, а второй каток за первую минуту прошел 1,5 м, а за каждую следующую минуту проходил на 0,5 м больше, чем за предыдущую. Через сколько минут катки встретились?
24. Задание 14 № 394402
В сосуде имеется несколько одинаковых кранов, которые открывают один за другим через равные промежутки времени. Через 8 часов после того, как был включен последний кран, сосуд был заполнен. Время, в течение которого были открыты первый и последний краны относятся как 5 : 1. Через сколько времени заполнится сосуд, если открыть все краны одновременно?
25. Задание 14 № 394404
Бригада рабочих могла выполнить всю работу за 24 ч, если бы работали одновременно все рабочие. однако по плану в первый час работал один рабочий, во второй час — 2 рабочих, в третий — 3 и т. д. до тех пор, пока в работу не включились все рабочие. И только несколько часов перед завершением работала вся бригада. Время работы, предусмотренное планом, было бы сокращено на 6 часов, если бы с самого начала работы работала бы вся бригада, за исключением пяти рабочих. Найдите количество рабочих.
26. Задание 14 № 394405
Алик, Миша и Вася покупали блокноты и трехкопеечные карандаши. Алик купил 2 блокнота и 4 карандаша, Миша — блокнот и 6 карандашей, Вася — блокнот и 3 карандаша. Оказалось, что суммы, которые уплатили Алик, Миша и Вася, образуют геометрическую прогрессию. Сколько стоит блокнот?
27. Задание 14 № 394406
Три конькобежца, скорости которых в некотором порядке образуют геометрическую прогрессию, одновременно стартуют (из одного места) по кругу. Через некоторое время второй конькобежец обгоняет первого, пробежав на 400 метров больше его. Третий конькобежец пробегает то расстояние, который пробежал первый к моменту обгона его вторым, за время на ![]() мин больше, чем первый. Найдите скорость первого конькобежца.
мин больше, чем первый. Найдите скорость первого конькобежца.
28. Задание 14 № 394412
Ваня, Миша, Алик и Вадим ловили рыбу. Оказалось, что количества рыб, пойманных каждым из них, образуют в указанном порядке арифметическую прогрессию. Если бы Алик поймал столько же рыб, сколько Вадим, а Вадим поймал бы на 12 рыб больше, то количества рыб, пойманных юношами, образовали бы в том же порядке геометрическую прогрессию. Сколько рыб поймал Миша?
29. Задание 14 № 394430
При свободном падении тело прошло в первую секунду 5 м, а в каждую следующую на 10 м больше. Найдите глубину шахты, если свободно падающее тело достигло его дна через 5 с после начала падения.
30. Задание 14 № 394460
Два приятеля положили в банк по 10000 рублей каждый, причем первый положил деньги на вклад с ежеквартальным начислением 10 %, а второй — с ежегодным начислением 45%. Через год приятели получили деньги вместе с причитающимися им процентами. Кто получил большую прибыль? В ответе напишите «первый» или «второй».
31. Задание 14 № 394464
За изготовление и установку нижнего железобетонного кольца колодца заплатили 234 рубля, а за каждое следующее кольцо платили на 18 рублей меньше, чем за предыдущее. Кроме того, по окончании работы была выплачена премия 360 рублей. Средняя стоимость изготовления и установки одного кольца с учетом премии оказалась равна 202 рубля. Сколько колец было установлено?
32. Задание 14 № 394465
 При хранении бревен их укладывают, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основании положено 12 бревен?
При хранении бревен их укладывают, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основании положено 12 бревен?
Новый октябрьский тренировочный вариант (тренировочная работа) №37812191 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
скачать вариант
скачать ответы
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812191:
Ответы и решения:
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1).
Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт. Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
Задание 1 № 413030 Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Ответ: 56,4
Задание 2 № 413031 Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Ответ: 8070
Задание 3 № 413032 Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что (рис. 2). Ответ дайте в сантиметрах.
Ответ: 62,5
Задание 4 № 413033 Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Ответ: 9813
Задание 5 № 413034 Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Ответ: 13
Задание 7 № 314789 На координатной прямой отмечены числа а и с. Какое из следующих утверждений неверно? В ответе укажите номер выбранного варианта.
Ответ: 1
Задание 10 № 132734 В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
Ответ: 0,2
Задание 14 № 393942 Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Ответ: 8
Задание 15 № 132774 Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Ответ: 70
Задание 16 № 356618 Хорды AC и BD окружности пересекаются в точке P, BP=15, CP = 6, DP = 10. Найдите AP.
Ответ: 25
Задание 17 № 323957 Найдите площадь ромба, если его диагонали равны 14 и 6.
Ответ: 42
Задание 19 № 93 Укажите номера верных утверждений. 1) Существует квадрат, который не является прямоугольником. 2) Если два угла треугольника равны, то равны и противолежащие им стороны. 3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Ответ: 23
Задание 21 № 311600 Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
Ответ: 400 км
Задание 23 № 339619 Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Ответ: 42
Задание 24 № 340104 Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AB и CD в точках P и T соответственно. Докажите, что BP = DT.
Задание 25 № 340129 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 14, BC = 12.
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Сложность:
Среднее время решения: 1 мин. 28 сек.
ОГЭ по математике 2022 задание 14: номер 48 | Из заданных последовательност…
35
Из заданных последовательностей выберите геометрическую прогрессию. В ответе запишите знаменатель этой геометрической прогрессии. ($a_{n}$): $a_{1}=5$, $a_{n}:a_{n+1}=2$ (b$_{n}$): 4, 6, 8,10, … $(c_{n}): 1$, ${1} / {2}$, ${1} / {3}$, ${1} / {4}$, …
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
Геометрическая прогрессия задана условиями $b_1=6$, $b_{n+1}=-4{b_n} $. Найдите $b_5$.
Выписано несколько последовательных членов арифметической прогрессии: $…; 24; x ; -14; -33; …$ Найдите член прогрессии, обозначенный буквой $x$.
В первом ряду театра $20$ мест, а в каждом следующем на $2$ больше, чем в предыдущем. Сколько мест в десятом ряду?
Дана арифметическая прогрессия: $130$; $123$; $116$; $…$ Найдите первый отрицательный член этой прогрессии.
- ОГЭ по математике
Как решать задание 14 ОГЭ по математике? Материал для подготовки к ОГЭ.
Для выполнения задания 14 необходимо уметь решать задачи с прогрессиями.
Задание на работу с последовательностями и прогрессиями (задание 12 в КИМ 2020 г.) заменено на задание с практическим содержанием, направленное на проверку умения применять знания о последовательностях и прогрессиях в прикладных ситуациях (задание 14 в КИМ 2021 г.).
Решение типовых задач № 14 на ОГЭ по математике
| Карточки для отработки задания 14 с ответамиИсточник: math100.ru → скачать (задачи на прогрессии) |
| Прототипы задания 14 ОГЭ по математике Опубликовано: Красникова Г. Д. → скачать |
| Материалы для отработки задания 14 Автор: Е. А. Ширяева → теория → задания |
| Прогрессии — теория Автор: Колесник М.А. → скачать |
| Задание 14 — Презентация Автор: Панина Т.А → скачать |
Виды заданий на данной позиции в КИМах по кодификатору:
— Арифметическая прогрессия. Формула общего члена арифметической прогрессии;
— Формула суммы первых нескольких членов арифметической прогрессии;
— Геометрическая прогрессия. Формула общего члена геометрической прогрессии;
— Формула суммы первых нескольких членов геометрической прогрессии;
— Сложные проценты.
Связанные страницы:
Задание 14 формат огэ по математике 2021, сдам гиа задание 393942, Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Видео Задание 14 формат огэ по математике 2021, сдам гиа задание 393942 канала математика
Показать
Составить предложения из слов: из, страны, весна, грачи, к, чижи, мы, жаворонки, теплые, прилетают.
6·2 ответа
ЗАДАЧА 14
сортировка
по сложности
4. Костя зовёт гостей на день рождения в ресторан. В ресторане в наличии имеются лишь квадратные столики, за которыми умещается не более 4 человек. Если соединить два квадратных стола, то получится стол, за которым умещается до 6 человек. На рисунке изображён случай, когда соединили 3 квадратных столика. В этом случае получился стол вместимостью до 8 человек. Найдите наибольшую вероятность вместимость стола, который получится при соединении 18 квадратных столиков в ряд.
- Вика решила начать делать зарядку каждое утро. В первый день она сделала 20 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 7 дней она сделала всего 203 приседания. Сколько приседаний сделала Вика в пятый день?

2. В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

3. У Лены есть попрыгунчик (каучуковый шар). Она изо всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 320 см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше 7см?

4. Костя зовёт гостей на день рождения в ресторан. В ресторане в наличии имеются лишь квадратные столики, за которыми умещается не более 4 человек. Если соединить два квадратных стола, то получится стол, за которым умещается до 6 человек. На рисунке изображён случай, когда соединили 3 квадратных столика. В этом случае получился стол вместимостью до 8 человек. Найдите наибольшую вероятность вместимость стола, который получится при соединении 18 квадратных столиков в ряд.

5. Даня играет в компьютерную игру. Он играет с 0 очков, а для перехода на следующий уровень ему нужно набрать не менее 100 000 очков. После первых двух минут игры добавляется 2 очка, после следующих двух – 4 очка, после следующих двух – восемь очков и так далее. Таким образом, после каждых двух минут игры количество добавляемых очков удваивается. Через сколько минут Даня перейдёт на следующий

6. При проведении химической реакции в растворе образуется нерастворимый осадок. Наблюдения показали, что каждую минут образуется 0,3 г осадка. Найдите массу осадка (в граммах) в растворе спустя пять минут после начала реакции.

7. Каждый простейший одноклеточный организм инфузория- туфелька размножается делением на 2 части. Сколько инфузорий было первоначально, если после шестикратного деления их стало 320?

8. При хранении брёвен строевого леса их укладывают так, как показано на рисунке. Сколько брёвен находится в одной кладке, если в её основании положено 12 брёвен?

9. Курс воздушных ванн начинают с 15 мин. в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. На какой день продолжительность процедуры достигает 1 час 45 минут?

9.Выписаны первые три члена геометрической прогрессии: 1512; –252; 42; … Найдите сумму первых четырёх ее членов.

10.Грузовик перевозит партию щебня массой 176 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что в первый день было перевезено 6 тонн щебня. Определите, сколько тонн щебня было перевезено в последний день, если вся работа была выполнена за 11 дней.

11.В течение 25 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 7-й день акция стоила 999 рублей, а в 12-й день — 1064 рубля?


Задание 14 формат огэ по математике 2021, сдам гиа задание 393942, Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Видео Задание 14 формат огэ по математике 2021, сдам гиа задание 393942 канала математика
Показать
Решение заданий Варианта №2 из сборника ОГЭ 2022 по математике Ф.Ф. Лысенко, С.О. Иванова 40 тренировочных вариантов. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
![]()
Задание 1-5.
Автомобильное колесо, как правило, представляет из себя металлический диск, с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65R15 (см. рис. 8).
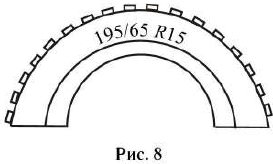
Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 9).
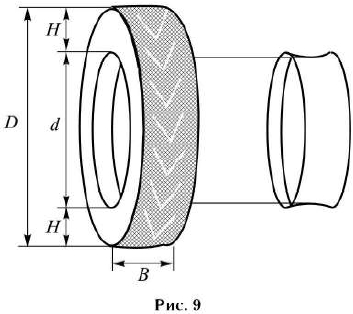
Второе число (число 65 в приведённом примере) – процентное отношение высоты боковины (параметр Н на рисунке 9) к ширине шины, то есть 100·frac{H}{B}.
Последующая буква обозначает тип конструкции шины. В данном примере буква R обозначает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяется шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 175/65R13.
Задание 6.
Найдите значение выражения frac{4}{35}+frac{13}{70}.
Задание 7.
Какое из данных чисел принадлежит отрезку [8; 9]?
1) frac{32}{6}
2) frac{47}{6}
3) frac{55}{6}
4) frac{53}{6}
Задание 8.
Найдите значение выражения (с–3)2·с8 при с = –18.
Задание 9.
Решите уравнение 5 – 2х = –3х.
Задание 10.
В коробке находятся фломастеры: 8 красных, 12 синих и 5 зелёных. Найдите вероятность того, что наудачу взятый фломастер окажется красным.
Задание 11.
Установите соответствие между функциями и их графиками (см. рис. 10).
ФУНКЦИИ
А) у = х + 3
Б) у = 3 – х2
В) y=frac{3}{x}
ГРАФИКИ
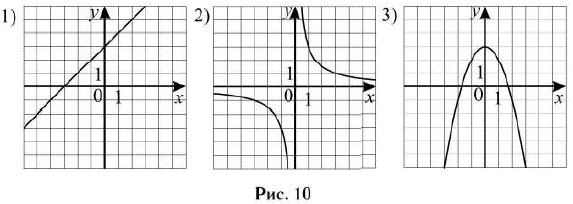
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Расстояние S (в километрах), пройденное спортсменом, можно приближённо вычислить по формуле S = 6t, где t – количество часов в пути. Определите, через какое время спортсмен пройдёт 14 км. Ответ дайте в минутах.
Задание 13.
Укажите решение неравенства 15 – 6(х + 3) < 13 – 2x.
1) (–∞; -frac{1}{4})
2) (–4; +∞)
3) (–∞; -frac{1}{4})
4) (-frac{1}{4}; +∞)
Задание 14.
Регина написала на доске последовательность чисел. Первое число равно 13, а каждое следующее на 13 меньше, чем предыдущее. Найдите сумму первых 82 членов этой последовательности.
![]()
Задание 15.
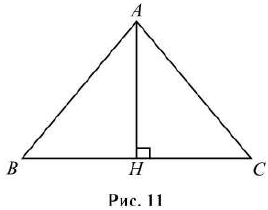
В остроугольном треугольнике АВС проведена высота АН, ∠АСВ = 64° (см. рис. 11). Найдите угол САН. Ответ дайте в градусах.
Задание 16.
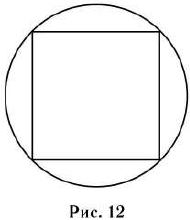
Радиус окружности, описанной около квадрата, равен 5√2 (см. рис. 12). Найдите длину стороны этого квадрата.
Задание 17.
Найдите площадь прямоугольника, если его периметр равен 32 и одна из его сторон на 4 больше другой (см. рис. 13).

Задание 18.
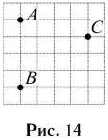
На клетчатой бумаге с размером клетки 1см х 1 см отмечены точки А, В и С (см. рис. 14). Найдите расстояние от точки С до прямой АВ. Ответ дайте в сантиметрах.
Задание 19.
Какие из следующих утверждений верны?
1) Диагонали прямоугольника равны.
2) Все равнобедренные треугольники подобны.
3) Если диагонали параллелограмма перпендикулярны, то это ромб.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ЧАСТЬ 2
![]()
Задание 20.
Решите уравнение х3 + 3х2 = 9х + 27.
Задание 21.
Два мотоциклиста одновременно отправились в 420-километровый мотопробег. Первый едет со скоростью на 10 км/ч больше, чем второй, и прибывает к финишу на 1 час раньше второго. Найдите скорость (в км/ч) первого мотоциклиста.
Задание 22.
Постройте график функции y=-4-frac{x^{4}-2x^{3}}{2x-x^{2}} и определите, при каких значениях p прямая у = р имеет с графиком две общие точки.
![]()
Задание 23.
Высота треугольника разбивает его основание на два отрезка с длинами 4 и 7. Найдите длину этой высоты, если известно, что другая высота треугольника делит её в отношении 2:7, считая от вершины.
Задание 24.
Дан правильный шестиугольник. Докажите, что если середины его сторон последовательно соединить отрезками, то получится правильный шестиугольник.
Задание 25.
Через середину D медианы АК треугольника АВС и вершину В проведена прямая, пересекающая сторону АС в точке Т. Найдите отношение площади треугольника АDТ к площади четырёхугольника СКDТ.
Источник варианта: Сборник ОГЭ 2022 по математике под редакцией Ф.Ф. Лысенко, С.О. Иванова, 40 тренировочных вариантов по новой демоверсии 2022, Легион.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.2 / 5. Количество оценок: 5
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
- ОГЭ по математике
Подборка тренировочных вариантов по математике для 9 класса в формате ОГЭ 2022 с ответами и критериями оценивания.
Соответствуют демоверсии ОГЭ 2022 по математике
Характеристика структуры и содержания КИМ ОГЭ 2022 по математике
Работа содержит 25 заданий и состоит из двух частей.
Часть 1 содержит 19 заданий с кратким ответом; часть 2 – 6 заданий с развёрнутым ответом.
При проверке базовой математической компетентности экзаменуемые должны продемонстрировать владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приёмов решения задач и проч.), умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.
Задания части 2 направлены на проверку владения материалом на повышенном и высоком уровнях. Их назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленных обучающихся, составляющих потенциальный контингент профильных классов.
Эта часть содержит задания повышенного и высокого уровней сложности из различных разделов математики. Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности: от относительно простых до сложных, предполагающих свободное владение материалом и высокий уровень математической культуры.
Смотрите также:
Решаем ОГЭ 192 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина №192 (alexlarin.com)
Решаем ОГЭ 192 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина №192 (alexlarin.com)
Задание 1
Найдите значение выражения $$(1frac{8}{15}-frac{2}{15}):frac{7}{15}$$
Ответ: 3
Скрыть
$$(1*frac{8}{15}-frac{2}{15}):frac{7}{15}=$$$$(frac{23}{15}-frac{2}{15})*frac{15}{7}=$$$$frac{21}{15}*frac{15}{7}=3$$
Задание 2
В нескольких эстафетах, которые проводились в школе, команды показали следующие результаты:
| Команда | I эстафета, мин. | II эстафета, мин. | III эстафета, мин. | IV эстафета, мин. |
| «Непобедимые» | 3,4 | 5,9 | 2,9 | 5,8 |
| «Прорыв» | 4,5 | 4,3 | 3,2 | 5,4 |
| «Чемпионы» | 4,9 | 4,8 | 2,7 | 6,3 |
| «Тайфун» | 3,7 | 4,5 | 2,4 | 5,1 |
За каждую эстафету команда получает количество баллов, равное занятому в этой эстафете месту, затем баллы по всем эстафетам суммируются. Какое итоговое место заняла команда «Чемпионы», если победителем считается команда, набравшая наименьшее количество очков?
В ответе укажите номер правильного варианта.
1) 1
2) 2
3) 3
4) 4
Ответ: 4
Скрыть
Расставим места, которые заняли команды в каждой эстафете:
| Команда | I эстафета, мин. | II эстафета, мин. | III эстафета, мин. | IV эстафета, мин. |
| «Непобедимые» | 1 | 4 | 3 | 3 |
| «Прорыв» | 3 | 1 | 4 | 2 |
| «Чемпионы» | 4 | 3 | 2 | 4 |
| «Тайфун» | 2 | 2 | 1 | 1 |
Тогда суммарные очки для каждой команды:
Непобедимые:11 — 3 место
Прорыв:10 — 2 место
Чемпионы:13 — 4 место
Тайфун:6 — 1 место
Задание 3
Между какими числами заключено число $$2sqrt{5}$$
Варианты ответа
- 9 и 11
- 5 и 6
- 24 и 26
- 4 и 5
Ответ: 4
Скрыть
Представим $$2sqrt{5}$$ в виде корня $$2sqrt{5}=sqrt{2^{2}*5}=sqrt{20}$$. Очевидно что данное число располагается между $$sqrt{16}$$ и $$sqrt{25}$$ или 4 и 5, что соответствует 4 варианту.
Задание 4
Представьте выражение $$frac{(c^{-3})^{-5}}{c^{-10}}$$ в виде степени с основанием c
Варианты ответа
- $$c^{-25}$$
- $$c^{-10}$$
- $$c^{-5}$$
- $$c^{-18}$$
Ответ: 3
Скрыть
$$frac{(c^{-3})^{5}}{c^{-10}}=$$$$frac{c^{-15}}{c^{10}}=$$$$c^{-15-{10}}=c^{-5}$$, что соответствует 3 варианту ответа
Задание 5
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Найдите разность между наименьшим и наибольшим значениями температуры. Ответ дайте в градусах Цельсия.
Ответ: -16
Скрыть
$$t_{min}=8$$ (между 21:00 и 00:00) $$t_{max}=24$$ (между 12:00 и 15:00) $$t_{min}-t_{max}=8-24=-16$$
Задание 6
Решите уравнение $$-2(x+1)-3(2-3x)=34$$
Ответ: 6
Скрыть
$$-2(x+1)-3(2-3x)=34$$ $$-2x-2-6+9x=34$$ $$7x=34+8=42$$ $$x=6$$
Задание 7
Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?
Ответ: 16000000
Скрыть
Частным лицам принадлежит : 100-60=40% Пусть x-сумма в млн.р. 40 млн.р.-100% X млн.р.-40% $$x=frac{40*40}{100}=16$$ млн.р.
Задание 8
На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей. Какие из следующих утверждений неверны?
- пользователей из России больше, чем пользователей из Украины;
- больше трети пользователей сети — из Украины;
- пользователей из Беларуси больше, чем пользователей из Украины;
- пользователей из России больше 4 миллионов человек.
Ответ: 23
Скрыть
- пользователей из России больше, чем пользователей из Украины — верно
- больше трети пользователей сети — из Украины — неверно (сегмент меньше трети круга)
- пользователей из Беларуси больше, чем пользователей из Украины — неверно (сегмент Беларуси меньше)
- пользователей из России больше 4 миллионов человек — верно
Задание 9
На одной тарелке 12 пирожков, 4 из которых с капустой, а на другой тарелке 8 пирожков, 6 из которых с капустой. Из каждой тарелки взяли по одному пирожку. Какова вероятность того, что оба пирожка с капустой?
Ответ: 0,25
Скрыть
Вероятность взять с капустой из первой :$$P_{1}=frac{4}{12}=frac{1}{3}$$ Из второй :$$P_{2}=frac{6}{8}=frac{3}{4}$$ Общая вероятность $$P=P_{1}*P_{2}=$$$$frac{1}{3}*frac{3}{4}=0,25$$
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают.
ФОРМУЛЫ
- $$y=2x$$
- $$y=x^{2}-2$$
- $$y=sqrt{x}$$
- $$y=-frac{2}{x}$$
Ответ: 214
Скрыть
A-парабола $$(y=ax^{2}-b)Rightarrow 2$$ Б-прямая $$(y=kx)Rightarrow 1$$ B-гипербола $$(y=-frac{k}{x})Rightarrow 4$$
Задание 11
Укажите номер первого отрицательного члена арифметической прогрессии: 18; 15; …
Ответ: 8
Скрыть
Первый член прогресси: $$a_{1}=18$$, ее разность: $$d=a_{2}-a_{1}=15-18=-3$$
$$a_{n}a_{1}+d(n-1)=18-3(n-1)=21-3n<0Leftrightarrow $$$$-3n<-21Leftrightarrow n>7$$
Так как $$n in N, n=8$$
Задание 12
Найдите значение выражения $$9b-frac{3a-9b^{2}}{b}$$ при $$a=3sqrt{2}, b=sqrt{8}$$
Ответ: 4,5
Скрыть
$$9b+frac{3a-9b^{2}}{b}=frac{9b^{2}+3a-9b^{2}}{b}=$$$$frac{3a}{b}=frac{3+3sqrt{2}}{sqrt{8}}=$$$$frac{9}{sqrt{4}}=frac{9}{2}=4,5$$
Задание 13
Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта позволяет формула $$F=1,8C+32$$ , где С — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 194по шкале Фаренгейта? Ответ округлите до десятых.
Ответ: 90
Скрыть
Выразим градусы Цельсия из формулы: $$F=1,8C+32Leftrightarrow$$ $$1,8C=F-32Leftrightarrow$$ $$C=frac{F-32}{1,8}$$ Найдем значение: $$C=frac{194-32}{1,8}=90$$
Задание 14
На каком рисунке изображено множество решений неравенства $$x^{2}-2x-3 leq 0$$ Укажите неравенство, которое не имеет решений.
Ответ: 1
Скрыть
$$x^{2}-2x-3leq 0Leftrightarrow f(x)leq 0$$
Пусть $$f(x)=0Leftrightarrow x^{2}-2x-2=0$$ $$left{begin{matrix}x_{1}+x_{2}=2x_{1}*x^{2}=-3end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}x_{1}=3x_{2}=-1end{matrix}right.$$
Отметим точки на прямой ,расставим знаки f(x) на полученных промежутках.

Надо $$f(x) leq 0Leftrightarrow x in [-1; 3]$$, что соответствует 1 варианту ответа
Задание 15
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,6 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 1,5 м. Найдите длину троса. Ответ дайте в метрах.
Ответ: 3,9
Скрыть
$$x=sqrt{3,6^{2}+1,5^{2}}=$$$$sqrt{frac{1296+25}{100}}=$$$$frac{39}{10}=3,9$$
Задание 16
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 42° и 78°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Ответ: 60
Скрыть

$$angle B=42+78=120$$
По свойству углов паралеллограма: $$angle A=180-angle B=180-120=60$$
Задание 17
Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Ответ: 13
Скрыть
Из ABH: $$angle B=90-angle A=30Rightarrow$$ $$AH=frac{1}{2}AB=13$$
$$HD=AD-AH=13$$
Задание 18
Найдите площадь квадрата, если его диагональ равна 8.
Ответ: 32
Скрыть

Пусть AB=BC=a
По т. Пифагора $$Delta ABC$$: $$a^{2}+a^{2}=8^{2}$$
$$2a^{2}=64$$
$$a^{2}=32$$
$$S_{ABCD}=a^{2}=32$$
Задание 19
Найдите угол ABC. Ответ дайте в градусах
Ответ: 45
Скрыть
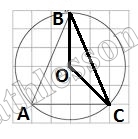
$$angle BOC=cup BC=135$$ $$angle BAC=frac{1}{2}cup BC=frac{135}{2}=67,5=angle BCA$$ $$angle ABC=180-67,5*2=45$$
Задание 20
Какие из следующих утверждений верны?
- Диагонали ромба равны.
- Площадь ромба равна половине произведения его диагоналей.
- Средняя линия трапеции равна половине основания трапеции.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Ответ: 2
Скрыть
1.неверно (перпендикулярно и делятся пополам) 2.Верно 3.Неверно (полусумме оснований)
Задание 21
Решите систему уравнений $$left{begin{matrix}x^{2}+xy+y^{2}=37 x^{3}-y^{3}=37end{matrix}right.$$
Ответ: (-3;-4) (4;3)
Скрыть
$$left{begin{matrix}x^{2}+xy+y^{2}=37x^{3}-y^{3}=37end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}x^{2}+xy+y^{2}=37(x-y)(x^{2}+xy+y^{2})=37end{matrix}right.$$ Поделим второе на первое уравнение :$$x-y=1Leftrightarrow x=1+y$$ $$(1+y)^{2}+(1+y)y+y^{2}=37$$ $$1+2y+y^{2}+y+y^{2}+y^{2}=37$$ $$3y^{2}+3y-36=0|:3$$ $$y^{2}+y-12=0Leftrightarrow$$ $$D=1+48=49Leftrightarrow$$ $$left{begin{matrix}y_{1}=frac{-1+7}{2}=3y_{2}=frac{-1-7}{2}=-4end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}x_{1}=1+3=4x_{2}=1-4=-3end{matrix}right.$$
Задание 22
Велосипедист проехал 25 км. При этом один час он ехал по ровной дороге, а один час – в гору. Какова скорость (в км/ч) велосипедиста по ровной дороге, если каждый километр по ровной дороге он проезжал на 2 минуты быстрее, чем в гору?
Ответ: 15
Скрыть
Пусть t-время 1 км по дороге , тогда $$t+frac{2}{60}$$-время 1 км. в гору. Тогда $$v_{1}=frac{1}{t}$$-скорость по дороге, $$v_{2}=frac{1}{t+frac{1}{30}}$$-скорость в гору. Тогда $$1*frac{1}{t}+1*frac{1}{t+frac{1}{30}}=25$$
$$frac{1}{t}+frac{30}{30t+1}=25Leftrightarrow$$ $$30t+1+30t=25(30t^{2}+t)$$
$$750t^{2}+25t-60t-1=0$$
$$750t^{2}-35t-1=0$$
$$D=1225+3000=65^{2}$$
$$t_{1}=frac{35+65}{1500}=frac{1}{15}$$
$$t_{2}<0$$
Тогда $$v_{1}=frac{1}{frac{1}{5}}=15$$
Задание 23
Постройте график функции $$y=|x^{2}-4x-2|$$ и определите, при каких значениях с прямая $$y=c$$ имеет с графиком три общие точки.
Ответ: 6
Скрыть
Данный график есть парабола $$y=x^{2}-4x-2$$, у которой часть ,которая располагается по Ox отображается симметрично Ox.
Найдем вершину параболы: $$x_{0}=-frac{-4}{2}=2$$ $$y_{0}=left | 4-8-2 right |=6$$
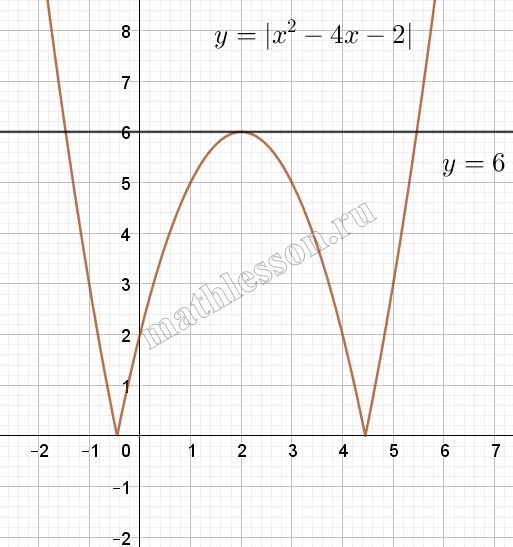
$$y=c$$ — параллельна Ox, тогда при точки при y=6 , то есть c=6
Задание 24
В параллелограмме ABCD биссектриса тупого угла B пересекает сторону АD в точке К. Найти периметр параллелограмма, если АВ = 12 и АК:КD = 4:3
Ответ: 66 или 30
Скрыть
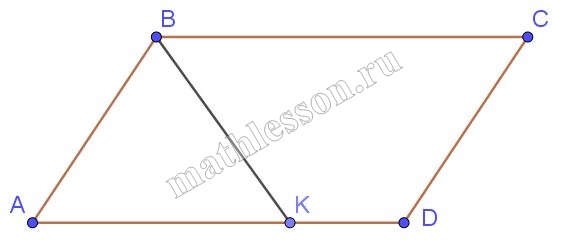
a) Пусть $$Kin AD$$(внутри), тогда:
1) $$angle ABK=angle CBK$$(BK-биссектриса); $$angle CBK=angle AKB$$(накрест лежащие) $$Rightarrow Delta ABK$$-равнобедренный и $$AB = AK$$
2) пусть $$AB=4x =12Rightarrow x=3, KD=3x=9$$$$Rightarrow AD=21$$
3) $$P_{ABCD}=2(12+21)=66$$

b) вне AD. Аналогично $$AK=AB=12$$. Пусть $$DK=3x$$, тогда AK=4x и AD=x. Получаем $$4x=12Rightarrow x=3$$ и $$P_{ABCD}=2(12+3)=30$$
Задание 25
На основаниях АВ и СD вне трапеции построены квадраты. Докажите, что прямая, соединяющая их центры, проходит через точку пересечения диагоналей трапеции.
Ответ:
Скрыть

Пусть $$Kin B_{1}C$$, $$O=BDcap AC$$, $$M=KOcap AD$$
1) $$angle LCK=angle MAN=45$$; $$angle LCO=angle OAN$$(накрест лежащие) $$Rightarrow angle KCA=angle OAD_{1}Rightarrow$$ $$CB_{1}left | right |AD_{1}$$
2) $$angle LKC=angle NMA$$(накрест лежащие) $$Rightarrow Delta KLCsim Delta ANMRightarrow$$ $$frac{KC}{AM}=frac{CL}{AN}=k$$
3) $$LCleft | right |ANRightarrow$$ $$Delta LCOsim Delta ONARightarrow$$ $$frac{LC}{AN}=frac{LO}{ON}=k$$
4) $$LCleft | right |AN Rightarrow$$ $$Delta BLOsim Delta ONDRightarrow$$ $$frac{LO}{ON}=frac{BL}{ND}=k$$
5)т.к. $$frac{LC}{AN}=k$$, $$frac{BL}{ND}=k$$ $$Rightarrow frac{BC}{AD}=k$$,но $$frac{KC}{AM}=k$$ и $$angle KCL=angle MANRightarrow$$ $$Delta KCBsim Delta ADC$$ и если K-центр , то и М-центр
Задание 26
В равнобедренной трапеции ABCD длина боковой стороны АВ равна 2 и длина меньшего основания ВС равна 2. Найдите площадь трапеции, если $$BDperp AB$$.
Ответ: $$3sqrt{3}$$
Скрыть
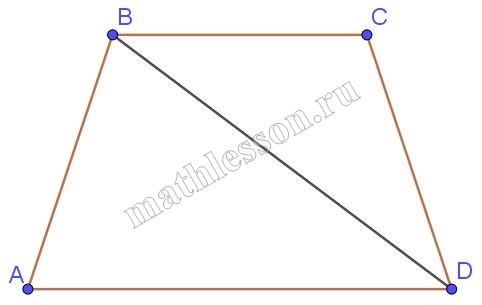
1) Пусть $$angle DBC=alpha$$ , тогда т.к. BC=CD, $$angle BCD=alpha$$, $$angle C=180-2alpha$$
2) По свойству углов трапеции $$angle C+angle D=180Rightarrow$$ $$angle D=180-(180-2alpha )=2alpha$$ $$Rightarrow angle BDA=alpha$$
3) Пусть BD=y. Тогда из $$Delta BCD$$:
$$CD^{2}=BC^{2}+AD^{2}-2BC*AD*cos CBD$$
$$2^{2}=2^{2}+y^{2}-2*2*y*cos alpha Leftrightarrow$$ $$y^{2}-4y*cos alpha =0$$
$$y(y-4cosalpha )=0$$, т.к. y-длина, то $$yneq 0$$, тогда $$y-4cos alpha =0Rightarrow y=4cosalpha$$
4) Из $$Delta ABD$$:
$$frac{AB}{BD}=tgBDARightarrow$$ $$frac{2}{4cosalpha }=tgalpha =frac{sinalpha }{cosalpha }Leftrightarrow$$ $$sinalpha =frac{1}{2}Rightarrow$$ $$alpha =30Rightarrow$$ $$y=4*frac{sqrt{3}}{2}=2sqrt{3}$$
5) $$S_{ABCD}=S_{BCD}+S_{ABD}=$$$$frac{1}{2}*BC*BD*sin CBD+frac{1}{2}*AB*BD=$$$$frac{1}{2}*2*2sqrt{3}*frac{1}{2}+frac{1}{2}*2*2sqrt{3}=$$$$sqrt{3}+2sqrt{3}=3sqrt{3}$$

Образовательный портал для подготовки к экзаменам
Математика
сайты — меню — вход — новости
Задания
Версия для печати и копирования в MS Word
Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Спрятать решение
Решение.
Пусть бригада в первый день покрасила метров забора, во второй —
… , в последний —
метров забора. Тогда
м, а за n дней было покрашено
метров забора.
Поскольку всего было покрашено 240 метров забора, имеем: Таким образом, бригада красила забор в течение 8 дней.
Ответ: 8.

Вход
Регистрация
Что ты хочешь узнать на сайте Знания ком?
Задай вопрос
Математика
Математика — 7 минут назад
. в корзине находятся 20 красных, 15 зеленых шаров. найти вероятность того, что из
четырех выбранных наудачу шаров будет три зеленых
Нет ответа
Ответить
Математика — 7 минут назад
Русаковы сходили в лес за грибами, а затем взвесили собранные
грибы.
марина обратила внимание, что числовые значения масс грибов
образуют последовательность, в которой каждая следующая масса,
начиная со второй, больше предыдущей на одну и ту же величину.
марина собрала меньше всех грибов – 750 г, мама собрала 2 кг 250 г,
костя собрал больше всех – 5 кг 250 г. папа собрал больше грибов,
чем мама.
Нет ответа
Ответить
Математика — 1 день назад
Решите пожалуйста
Нет ответа
Ответить
Математика — 1 день назад
Найди на рисунке диаметр, радиус, хорду и центр окружности.
выбери один или несколько верных вариантов.
Нет ответа
Ответить
Математика — 1 день назад
Помогите пожалуйста!!!!!!!!!!!!!!!
https://skr.sh/i/110123/yrilrwmn.jpg?download=1&name=скриншот%2011-01-2023%2013:45:15.jpg
Нет ответа
Ответить
Математика — 1 день назад
Sos срочно!!! свойство корней!
Нет ответа
Ответить
Математика — 1 день назад
Дремлет чуткий камыш.
тишь — безлюдье вокруг.
чуть приметна тропинка росистая.
куст заденешь плечом —
на лицо тебе вдруг
с листьев брызнет роса серебристая.
нужно склонения всех существительных
Нет ответа
Ответить
Математика — 1 день назад
Помогите решить это задание
Нет ответа
Ответить
Математика — 1 день назад
Срочно пользуюсь значением свойством дроби найдите значение а при котором верно равенство 45/48 = 15/а
1 ответ
Ответить
Математика — 1 день назад
Вычислите: а) 3/7 + (–9/14); б) –5/9 – 1/12; в) –2/3 • 5/8; г) 3/28 : (–5/7).
вычислите: –1/12 • 3/5 – 2/3 : (–10/9).
вычислите, применяя законы умножения: а) –3/7 • 5/13 – 4/7 • 5/13; б) 3/5 • 7/9 – 3/5 • (7/9 – 5/6).
первая бригада может выполнить задание за 24 ч, а вторая – за 48 ч. за сколько часов совместной работы они могут выполнить это задание?
* через два крана бак наполнился за 8 мин. если бы был открыт только первый кран, то бак наполнился бы за 12 мин. за сколько минут наполнился бы бак через один второй кран?
Нет ответа
Ответить
Показать ещё
Все предметы
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
История
Обществознание
Окружающий мир
География
Українська мова
Информатика
Українська література
Қазақ тiлi
Экономика
Музыка
Право
Беларуская мова
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Оʻzbek tili
Кыргыз тили
Астрономия
Физкультура и спорт
Другие предметы
- Сайт
- Главная
- Задать вопрос
- Аккаунт
- Вход
- Регистрация
Войти
У меня нет аккаунта, я хочу
зарегистрироваться
Регистрация
Никнейм
Пароль


