Задание 13 номер 349364

{

Шестнадцатеричная система — 554b4.
Двоичная система — 1010101010010110100.
Посмотрите так же как пишутся десятичные цифры 63, 18, 0, 749, 631, 25, 466, 451, 3932, 4863, 5014, 42321, 82033, 521227, 634348 в различных системах счисления.

Число 349364 в других системах счисления:
2 — 1010101010010110100, 3 — 122202020102, 4 — 1111102310, 5 — 42134424, 6 — 11253232, 7 — 2653361, 8 — 1252264, 9 — 582212, 10 — 349364, 11 — 219534, 12 — 14a218, 13 — c3032, 14 — 91468, 15 — 6d7ae, 16 — 554b4, 17 — 431ee, 18 — 35g52, 19 — 2cheb, 20 — 23d84, 21 — 1gf48, 22 — 1ahi4, 23 — 15g9h, 24 — 116ck, 25 — m8oe, 26 — jml2, 27 — hk6b, 28 — fph8, 29 — e9c1, 30 — cs5e, 31 — bmgp, 32 — al5k.

Информация о цвете #349364

В пространстве цветов RGB, hex #349364 содержит 17.39% красного цвета, 49.16% зелёного и 33.44% синиго процентного содержания цвета.
Тогда как в пространстве цветов CMYK, сщвуржится 46.51 циана (голубого цвета), 0.00 маджента (пурпурного цвета), 23.01 жёлтого и 30.48 чёрного цветов.
Он имеет угол цветового тона 150.32 градусов, насыщенности 47.74% и легкость 39.02%.

Ближайший цвет Web-палитры: #339966.

#349364 Преобразование цвета

Шестнадцатеричное значение цвета #349364 содержит значения в RGB цветах из R:52, G:147, B:100
и CMYK значений C:64, M:0, Y:31, K:42.
Его десятичное значение равно 3445604.

Hex triplet	`#349364`
RGB Decimal	`rgb(52, 147, 100)`
RGB Percent	`rgb(17.39%, 49.16%, 33.44%)`
CMYK	`cmyk(64, 0, 31, 42)`
HSL	`hsl(150.32°, 47.74, 39.02)`
HSV (or HSB)	`hsv(150.32°, 64.63, 57.65)`
Web Safe	`#339966`

CIE-LAB	`54.57, -39.19, 16.90`
XYZ	`14.15, 22.52, 15.65`
xyY	`0.27, 0.43, 22.52`
CIE-LCH	`54.57, 42.68, 156.68`
CIE-LUV	`54.57, -39.69, 28.19`
Hunter-Lab	`47.45, -29.81, 13.66`
Binary	`110100, 10010011, 1100100`

Разделение Добавочный цвет

Цвета по точкам треугольника

Цвет по точкам тетрайдера

Городские номера, которые начинаются на 8349364 и имеют формат вида +7349364XXXX, используются в городах и населённых пунктах, указанных ниже. Кроме того, вы найдёте информацию об операторе, на которого зарегистрированы телефоны с первыми цифрами 8(349364)

Населённые пункты телефонов

Пуровский район
город Губкинский

Операторы номеров с кодом 8(349364)

ООО «Газпром добыча Ноябрьск»
ООО «Пурсатком»
Сибинтек
Теле2

Если нужны более подробные данные по номерам, начинающимся на 349364, выберите следующую цифру по маске:

349 3640XXX
349 3641XXX
349 3642XXX
349 3643XXX
349 3644XXX
349 3645XXX
349 3646XXX
349 3647XXX
349 3648XXX
349 3649XXX

Для электрической
системы, представленной на схеме
7, выполнить
расчет и анализ переходного процесса
для трех режимов.

1. Режим

– трехфазного
КЗ

В заданной точке

для

рассчитать:

– действующие
значения периодической слагаемой тока
короткого замыкания;
–
ударный ток и
мощность КЗ;
– действующие
значения тока двухфазного короткого
замыкания;
действующие значения
периодической слагаемой тока генераторов
Г12,
Г13
посылаемого в место КЗ для трех моментов
времени (результаты представить на
напряжении ступени КЗ 230 кВ):

а)

– для

;

б)

– для

с.;

в)

–

,
принимая

;

–
остаточное напряжение
на шинах генератора Г12
(узел

)
в установившемся режиме КЗ.

2. Режим

– несимметричного
КЗ (для
несимметрии

сопротивление реактора в нейтрали
трансформатора ТТ5 составляет

Ом; между цепями Л3
взаимная индуктивность нулевой
последовательности отсутствует)

В заданной точке

схемы
рассчитать:

– действующее
значение периодической слагаемой тока
КЗ поврежденной фазы;
и

,

– симметричные
составляющие напряжения и остаточные
напряжения неповрежденных фаз;
построить векторные
диаграммы

и

;
симметричные
составляющие напряжения

для узлов:

,

,

,

,
Г12; по
полученным результатам построить эпюры
симметричных составляющих напряжений;
для наглядности
результата напряжения указанных узлов
представить в именованных единицах,
приведенных к ступени генераторного
напряжения (10,5 кВ);

3. Режим

– продольной
несимметрии

В рассматриваемой
схеме осуществляется включение
генераторов ЭСТ1 на параллельную работу
с «системами 2, 3» выключателем В1.
Считая, что такое включение производится
одновременно двумя фазами выключателя,
определить угол (
)
расхождения
эквивалентного вектора ЭДС генераторов
станции ЭСТ1 (
)
и эквивалентного вектора ЭДС «систем
2 и 3» (
)
из условия, что бы ток в цепи выключателя
(
)
составлял

.

Принимая, что при
найденном угле

вектор

опережал
вектор

,
рассчитать:

– падение напряжения
в месте разрыва фазы

;
,
,

– фазные напряжения
на клемме

выключателя В1;
– фазное напряжение
отключенной фазы

на клемме

.

Задание № 14

Для электрической
системы, представленной на схеме
15, выполнить
расчет и анализ переходного процесса
для трех режимов.

1. Режим

– трехфазного
КЗ

В заданной точке

схемы,
которая определена параметром

(выключатель В1
включен), для

рассчитать:

– действующие
значения периодической слагаемой тока
короткого замыкания;
–
ударный ток и
мощность КЗ;
–
остаточное напряжение
на шинах генератора Г4 (узел

);
– действующие
значения периодической слагаемой тока
генератора Г4 для

и

с., приведенные к напряжению ступени
КЗ (110 кВ).

2. Режим

– несимметричного
КЗ

В заданной точке

схемы,
которая определена параметром

(выключатель В1
включен), рассчитать:

– действующее
значение периодической слагаемой тока
КЗ поврежденных фаз;
и

– симметричные
составляющие напряжения и остаточное
напряжение неповрежденной фазы;
построить векторные
диаграммы

и

.

3. Режим

– продольной
несимметрии

Для режима (
),
соответствующего отключению ранее
поврежденных фаз и отключенном
секционном выключателе В1,
рассчитать:

– ток неповрежденной
фазы

на участке

;
– ток фазы

неповрежденной
цепи Л3;
– падение напряжения
в месте разрыва фазы

;
,

– фазные напряжения
в узлах

и

отключенной фазы

выключателя В2.
симметричные
составляющие напряжения

,

,

для узлов:

,

,
«
»,
«
»
«С3»; по
полученным результатам построить эпюры
симметричных составляющих напряжений;
для наглядности
результата напряжения указанных узлов
представить либо в именованных единицах,
приведенных к ступени 115 кВ, либо в
относительных единицах.

К моменту отключения
поврежденных фаз эквивалентный вектор
ЭДС генераторов
Г3, Г4 и С3 (
)
опережала
фазу
эквивалентного
вектора ЭДС генератора Г10 и С2 (
)
на

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Задание 13 номер 349364

Грачи летали — как сеть мелькали.

Задание 13 номер 349364

Все слова образованы по модели Корень — суффикс — окончание. В данном случае у всех трёх слов суффикс -от- , окончание -а, а корни индивидуальные, а именно чист -, добр- и черн-.

Задание 13 номер 349364

Простые:дружный,наветреННыйСуфф.-ЕНН,т.к.приставка),дрЕмота(безуд.гл.-дрЁма),иСкупаться(перед глухим корня -С),лЕденец(безуд.гл-лЁд),оТзвук(приставка),,беСсмыслица(перед глухим корня -С),улуЧшить(сл.сл.луЧше),нЕвнимателЬный(НЕ с прилаг.,Ь для смягчения).

Сложные: ,гОлОлед(безуд.гл.-голый и соед.гласн. перед тв.зв ,легкОмыслеННость( соед.гласн., перед тв.зв ., суфф.-ЕНН) ,верхнЕволжский (соед.гласн.перед мягк.зв.) ,,дЕсятикилометрОвый(без.гл.-дЕсять,ударн.)

Задание 13 номер 349364

Рассказала- удвоенная согл.
улетающей- проверяемая безударная глас. Е (проверим словом полёт)

Задание 13 номер 349364

Бурную реку, главный начальник, зимний вечер, реактивный самолёт.

Задание.

а) Решите уравнение

(1)

б) Укажите корни этого уравнения, принадлежащие отрезку [-3π/2; π/2].

Решение:

а) Решите уравнение

Найдем область допустимых значений уравнения (ОДЗ):

2sinx > 0

sinx > 0

Задание13в2_1

ОДЗ:

Введем новую переменную:

Тогда уравнение (1) примет вид:

4a² – 8a + 3 = 0

Решим квадратное уравнение:

D = 16

a₁ = 3/2, a₂ = 1/2

Вернемся к первоначальной переменной, получим 2 уравнения.

Решим 1 уравнение:

Задание13в1_61

Уравнение не имеет решения, так как — 1 ≤ sinx ≤ 1.

Решим 2 уравнение:

Задание13в2_5

Корни второго уравнения принадлежат ОДЗ.

б) Найдем корни уравнения, принадлежащие отрезку [-3π/2; π/2].

1 способ:

С помощью единичной окружности отберем корни на отрезке [-3π/2; π/2].

Задание13в2_2

Поучаем:

2 способ:

Для первого корня:

Задание13в2_8

Для второго корня:

Задание13в2_9

Ответ:

Задание13в2_10

Рубрики

Демоверсия ЕГЭ по информатике
Демоверсия ЕГЭ по математике
Демоверсия ОГЭ по информатике
Демоверсия ОГЭ по математике
Материалы по аттестации
Решаем ЕГЭ по математике
- Задание 1
- Задание 10
- Задание 11
- Задание 12
- Задание 13
- Задание 14
- Задание 15
- Задание 16
- Задание 2
- Задание 3
- Задание 4
- Задание 5
- Задание 6
- Задание 7
- Задание 8
- Задание 9
Решаем ОГЭ по математике
- Задание 21
- Задание 22
- Задание 24
Скачать экзаменационные варианты по информатике
- ЕГЭ по информатике
- ОГЭ по информатике
Скачать экзаменационные варианты по математике
- ЕГЭ по математике
- ОГЭ по математике
Тематическое планирование

Яндекс.Метрика

Источник

349364 решу огэ

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Для станций, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Станции

Международная

Ломоносовская

Театральная

Проспект славы

Цифры

На рисунке изображена схема метро города N. Станция Театральная расположена между станциями Поперечная и Петровская. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Петровская, Маяковская, Владимирская, Международная, Сельская. Жёлтая ветка включает в себя станции Международная, Ломоносовская, Горная, Проспект славы.

Бригада меняет рельсы на участке между станциями Поперечная и Театральная протяжённостью 13,8 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 300 метров рельсов. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?

Территория, находящаяся внутри кольцевой линии, называется Кировским городским районом. Найдите его площадь S (в км 2 ), если длина кольцевой ветки равна 50 км. В ответе укажите значение выражения S · π.

Найдите расстояние (в км) между станциями Горная и Ломоносовская, если длина Жёлтой ветки равна 54 км, расстояние от Международной до Горной равно 37 км, а от Проспекта славы до Ломоносовской — 44 км. Все расстояния даны по железной дороге.

Школьник Сергей в среднем в месяц совершает 40 поездок в метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Сергей уедет из города и неиспользованные карточки обнуляются. Во сколько рублей обойдётся самый дешёвый вариант?

Количество поездокСтоимость карточки

1	80	Школьникам скидка 15%
10	740	Школьникам скидка 10%
30	2100	Школьникам скидка 10%
50	3200	Нет
Не ограничено	4000	Нет

(руб.)Дополнительные условия

В ответе укажите значение выражения S π.

Math-oge. sdamgia. ru

16.04.2019 23:25:27

2019-04-16 23:25:27

Источники:

Https://math-oge. sdamgia. ru/test? id=36864494

OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 349364 решу огэ

349364 решу огэ

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты

Гостиная

Баня

Гараж

Кухня

Цифры

Инна Сергеевна имеет дом с участком. На рисунке приведён план этого участка.

При входе на участок слева находится гараж площадью 15 м 2 , справа расположена баня. Дом находится внутри участка, имеет форму прямоугольника. Сторона каждой клетки на плане равна 1 метру.

Вход в дом осуществляется через стеклянную дверь. Внутри дома расположены: кухня, гостиная, спальня, детская комната, подсобные помещения.

В центре дома находится гостиная, справа — кухня. Спальня и детская имеют равные площади, подсобные помещения обозначены на плане цифрой 7.

Площадка около входа и дорожки вокруг дома выложены плитками размером 1 м × 1 м, на остальной территории посеяна трава.

Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок понадобилось купить, чтобы выложить все дорожки участка и площадку около входа?

Инна Сергеевна имеет дом с участком. На рисунке приведён план этого участка.

Найдите площадь (в м 2 ), которую занимает жилой дом.

Инна Сергеевна имеет дом с участком. На рисунке приведён план этого участка.

Найдите расстояние от гаража до бани (расстояние между двумя ближайшими точками по прямой) в метрах.

Инна Сергеевна имеет дом с участком. На рисунке приведён план этого участка.

Инна Сергеевна планирует произвести оклейку стен помещений: детской комнаты и спальни — обоями. Она рассмотрела два варианта: флизелиновые и текстильные обои. Данные о стоимости рулона, площади комнат, расходе обоев на комнаты представлены в таблице. Обдумав оба варианта, Инна Сергеевна решила наклеить текстильные обои. На сколько рублей выгоднее наклеить текстильные обои, чем флизелиновые?

Тип обоевСтоимость 1

Флизелиновые	1800	70	7	12 000
Текстильные	2100	70	5	12 500

Рулона (руб.)Площадь стен
Комнат (м 2 )Расход обоев
На 2 комнаты
(рулоны)Стоимость работ
По поклейке обоев
(руб.)

Инна Сергеевна имеет дом с участком. На рисунке приведён план этого участка.

Найдите площадь в м 2 , которую занимает жилой дом.

Math-oge. sdamgia. ru

12.12.2018 5:25:35

2018-12-12 05:25:35

Источники:

Https://math-oge. sdamgia. ru/test? id=37812185

Источник

Задание 1 № 366805

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	Город Гранюк	Деревня Астрелка	Хутор Южный	Город Гусевск
Цифры

Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.

Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.

Ответ: 1465.

2. Задание 2 № 366806

Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.

Решение.

Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится

пачек чая.

Таким образом, ребята должны купить 14 пачек чая.

Ответ: 14.

3. Задание 3 № 366807

Найдите площадь (в км²), которую занимает заказник.

Решение.

Площадь заказника равна:

Ответ: 351.

4. Задание 4 № 366808

Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.

Решение.

Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:

км.

Ответ: 30.

5. Задание 5 № 366809

Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.

Продукция	Цена в магазине «Вело» (руб.)	Цена в магазине «ОК» (руб.)	Срок доставки из магазина «ОК» (дни)
Подсветка для спиц
Шина вида «А»
Шина вида «Б»
Спица
Педаль вида «А»
Педаль вида «Б»
Тормоз вида «А»		нет
Тормоз вида «Б»	нет
Набор крепёжных изделий

Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?

Решение.

На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:

руб.

Ответ: 5300.

6. Задание 6 № 316314

Найдите значение выражения:

Решение.

Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.

7. Задание 7 № 317575

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?

Решение.

Заметим, что и Проверим все варианты ответа:

1) — неверно;

2) — верно;

3) — верно;

4) — верно.

Ответ указан под номером 1.

8. Задание 8 № 353586

Какое из данных ниже чисел является значением выражения

Решение.

Последовательно получим:

Ответ: 1

9. Задание 9 № 338500

При каком значении значения выражений и равны?

Решение.

Для ответа на вопрос задачи нужно решить уравнение Решим его:

Ответ: 2.

10. Задание 10 № 325450

В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.

Решение.

Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна

Ответ: 0,3.

11. Задание 11 № 311406

На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке

4) прямая пересекает график в точках и

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .

2) — неверно,

3) — верно, видно из графика.

4) Прямая пересекает график в точках и — верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

Ответ: 12.

12. Задание 12 № 311543

Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .

Решение.

Выразим :

Подставляя, получаем:

Ответ: 0,4.

13. Задание 13 № 338497

На каком из рисунков изображено решение неравенства

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

Решение.

Решим неравенство методом интервалов:

Правильный ответ указан под номером: 4.

14. Задание 14 № 406645

В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение.

Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.

Найдем сумму этой прогрессии:

Ответ: 377 мест.

15. Задание 15 № 340000

В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите

Решение.

Из прямоугольного треугольника по теореме Пифагора найдём

Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.

16. Задание 16 № 351463

На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.

Решение.

Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.

17. Задание 17 № 169876

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.

———-

В открытом банке иррациональный ответ.

18. Задание 18 № 350842

Найдите угол

Решение.

Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.

Ответ: 22,5

19. Задание 19 № 401617

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Ответ: 13.

20. Задание 20 № 338505

Решите неравенство

Решение.

Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение

Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).

Таким образом, ответ

Ответ:

Примечание.

Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,

21. Задание 21 № 353527

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.

Ответ: 58.

22. Задание 22 № 338288

Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.

Решение.

Упростим выражение:

По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:

График функции сводится к графику параболы с выколотой точкой

Выделим полный квадрат:

Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)

Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и

Ответ: −1; 3.

23. Задание 23 № 339395

Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.

Решение.

Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и

Ответ: 16.

24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.

Решение.

Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.

25. Задание 25 № 311926

В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .

Решение.

По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,

Площадь трапеции :

Площадь трапеции

Ответ: 9.

Источник

Информация о числах

Свойства и характеристики одного числа

Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители…

Свойства пары чисел

Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел…

Триста сорок девять тысяч триста шестьдесят четыре
и
тринадцать

Сумма	349377
Разность	349351
Частное	26874.153846153848
Остаток от деления	2
Произведение	4541732
Наибольший общий делитель (НОД)	1
Наименьшее общее кратное (НОК)	4541732
Среднее арифметическое	174688.5
Среднее геометрическое	2131.1339704485968
Гипотенуза	349364.0002418681
Простые числа-близнецы?	Нет
Расстояние Левенштейна	5
Общие делители	1
Взаимнопростые числа?	Да
Общие цифры	3

Описание

Числа 349364 и 13 при сложении образуют 349377 . При вычитании получается 349351.

При делении 349364 на 13 получается число 26874.153846. Отстатком от деления является число 2. Произведение чисел – 4541732.

Для этой пары наибольшим общим делителем (НОД) является число 1 . Наименьшее общее кратное 4541732.

Общий делитель это 1.

Среднее арифметическое: 174688.5 . Среднее геометрическое для этой пары — 2131.133970.

Эти числа являются взаимнопростыми. 3 — это общая цифра.

Источник

: ОГЭ по математике

Как решать задание 13 ОГЭ по математике? Материал для подготовки к ОГЭ.

Для выполнения задания 13 необходимо уметь решать уравнения, неравенства и их системы.

С видами заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе.

Решение типовых задач № 13 на ОГЭ по математике

Изменения в КИМ 2021 года по сравнению с 2020 годом коснулись задания №13.

В рамках усиления акцента на проверку применения математических знаний в различных ситуациях количество заданий уменьшилось на одно за счет объединения заданий на преобразование алгебраических (задание 13 в КИМ 2020 г.) и числовых выражений (задание 8 в КИМ 2020 г.) в одно задание на преобразование выражений на позиции 8 в КИМ 2021 г.

Связанные страницы:

В задании №13 проверяется умение решать уравнения, неравенства и их системы. Конечно, под такие слова подходит огромный спектр заданий. Уточнение, пожалуй, одно. Надо применять графическое представление решения и показа результатов этого решения. В демонстрационном варианте ОГЭ предложена система двух линейных неравенств и графические представления вариантов ответов. Полезно понимать, что главным здесь является решение конкретных неравенств и понимание геометрического смысла полученного решения.

Теория к заданию №13

Определение:

Неравенством называется выражение вида:
a < b (a ≤ b), a > b (a ≥ b)

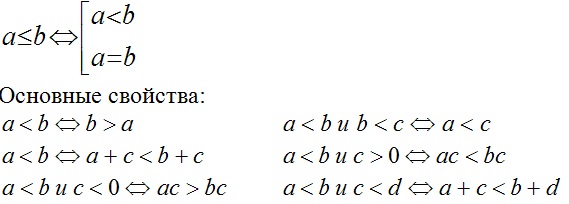
неравенства

Полезным для нас окажется метод интервалов:

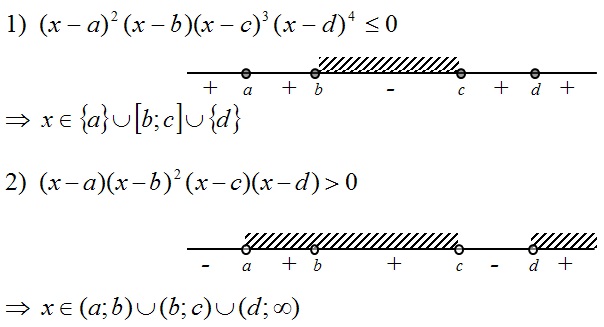
метод интервалов

Задание OM1501o

Укажите решение неравенства: 2 x — 3 ( x — 7) ≤ 3

Для решения линейного неравенства достаточно выполнить действия, аналогичные действию решений линейных уравнений. Однако, в отличие от линейных уравнений следует проявлять внимательность при выполнении операций деления или умножения на отрицательное число – в этих случаях знак неравенства будет меняться на противоположный!

Для решения этого примера вначале раскроем скобки, не забывая, что -3 умножается на -7 и дает + 21:

2 x – 3 x + 21 ≤ 3

Затем приводим подобные, перенося числа в правую сторону:

2 x – 3 x ≤ 3 – 21

– x ≤ -18

Нам необходимо умножить неравенство на -1, чтобы получить диапазон x, не забывая, что при этом меняется знак неравенства:

x ≥ 18

Таким образом, мы получаем, что x должен быть больше либо равен 18.

Ответ: [18;+∞)

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1502o

Укажите множество решений неравенства: 7 x — x² < 0

Существуют несколько способов решения квадратных неравенств, но я приведу самый простой и надежный. В начале выносим x за скобку, так как это неполное квадратное неравенство:

x ( 7 – x ) < 0

Затем находим ноли функции x ( 7 – x ) = 0, приравнивая каждый множитель к нолю:

x = 0

7 – x = 0

Получаем:

x = 0

x = 7

Таким образом, мы получили три интервала:

( -∞ ; 0 )

( 0 ; 7 )

( 7 ; +∞)

Подставим любое значение x из первого интервала и посмотрим на получившийся ответ.

Подставим -1:

x ( 7 – x ) = – 1 ( 7 – (-1) ) = -8

Значение отрицательно, значит в интервале ( -∞ ; 0 ) функция отрицательна, что нам и подходит для ответа, так как в условии:

x ( 7 – x ) < 0

Подставим 1:

x ( 7 – x ) = 1 ( 7 – 1 ) = 6

Значение положительно, и промежуток ( 0 ; 7 ) нам не подходит.

Подставим 8:

x ( 7 – x ) = 8 ( 7 – 8 ) = – 8

Значение отрицательно, и это подходит под условия, следовательно ответ:

( -∞ ; 0 ) и ( 7 ; +∞)

или графически:

Ответ: (-∞;0) и (7;+∞)

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1503o

Укажите множество системы неравенств:

⌈ x — 4 ≥ 0

⌊ x — 0,3 ≥ 1

Решение системы линейных неравенств сводится к решению линейного неравенства с дальнейшим анализом промежутков. В начале действуем аналогично первому случаю: переносим числа в правую часть, оставляя x слева:

⌈ x ≥ 4

⌊ x ≥ 1,3

В отличие от первого примера, решение более простое, но в данном случае нужно сравнить промежутки и выбрать общий. Первое неравенство требует, чтобы x был больше 4, а второе – более 1,3, на координатной прямой это будет выглядеть следующим образом:

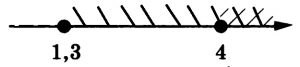
Решение 8 задания ОГЭ по математике

Промежутки перекрывают друг друга начина с 4, значит ответ выглядит следующим образом (не забываем, что неравенство нестрогое):

[ 4 ; + ∞ ) или

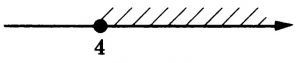
Решение 8 задания ОГЭ по математике

Ответ: [4 ;+∞ )

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1504o

Решите систему неравенств: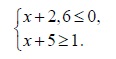

На каком рисунке изображено множество её решений?

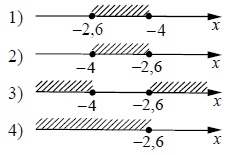
Итак, решим систему неравенств – оставим х в левой части, а остальное перенесём в правую, получим:

х ≤ 0 -2,6

х ≥ 1 – 5

Вычислив, получаем ответ:

х ≤ -2,6

х ≥ -4

Найдем его на координатной прямой – это №2.

Ответ: 2

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1505o

Укажите решение неравенства:

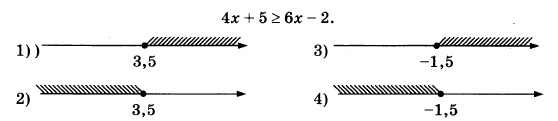
Задание 13 номер 369736 огэ математика

Выполняем тождественные преобразования неравенства и приводим его к простейшему виду. Для этого сначала группируем слагаемые, перенося те, что с «х», в левую сторону, а свободные члены в правую:

4х–6х≥–2–5

Приводим подобные:

–2х≥–7

Находим х. Знак неравенства при этом поменяется на противоположный, поскольку делить будем на –2, т.е. на отрицательное число:

х≤3,5

Далее на коорд.прямой теперь нужно отложить точку со значением 3,5, причем точка будет закрашенная, т.к. знак неравенства нестрогий:

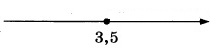
Задание 13 номер 369736 огэ математика

Т.к. знак полученного неравенства «≤», то выделить следует часть прямой слева от точки 3,5:

Это графическое решение соответствует ответу под №2.Ответ: 2

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1506o

Укажите неравенство, решение которого изображено на рисунке.

Задание 13 номер 369736 огэ математика

Тут нужно сразу отметить два важных момента.

Графическим решением неравенств из вариантов ответа является парабола, которая пересекает координатную ось в точках, соответствующих корням неравенств.
Так как все неравенства, представленные в вариантах ответов, имеют нестрогий знак, то точки пересечения корней неравенства с координатной осью будут закрашенными, т.е. входящими в искомые промежутки (решения).

Анализируем неравенства.

1) х²–36≤0

х²≤36

Корни этого неравенства равны ±6. Поскольку знак неравенства «меньше», то для ответа следует взять ту часть параболы, которая располагается ниже коорд.оси. Получаем:

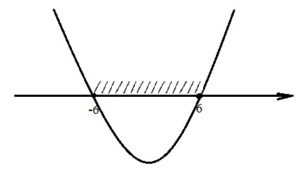
Задание 13 номер 369736 огэ математика

Полученный промежуток-решение не соответствует заданному в качестве ответа в условии.

2) х²+36≥0

х²≥–36

Это неравенство не имеет решений, поскольку для получения решения здесь требуется извлечь корень из отрицательные числа (из –36), а это невозможно.

3) х²–36≥0

х²≥36

Корни неравенства – ±6. Т.к. знак неравенства «больше», то для ответа следует взять ту часть параболы, которая располагается выше координатной оси. Получаем:

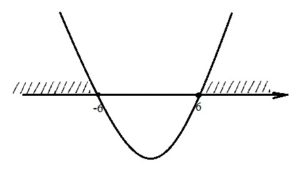
Задание 13 номер 369736 огэ математика

Здесь мы получили полное совпадение полученного решения с тем, которое представлено в условии задания.

4) х²+36≤0

х²≤–36

Тут ситуация такая же, как и во 2-м неравенства. Решений оно не имеет.Ответ: 3

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание 13OM21R

Укажите решение неравенства 8х – х²≥0

[0; +∞)
[8; +∞)
[0; 8]
(-∞;0]∪[8;+∞)

8х – х²≥0

Вынесем -х за скобки: -х(-8 + х) ≥0

Теперь разделим на -1, не забывая изменить знак неравенства на противоположный: х(х – ≤0

Найдем нули функции, приравняв каждый множитель к нулю: х=0 и х – 8=0, найдем х из второго уравнения: х=8.

Итак, имеем нули функции 0 и 8.

Теперь расставляем их на числовом луче и решаем неравенство методом интервалов.

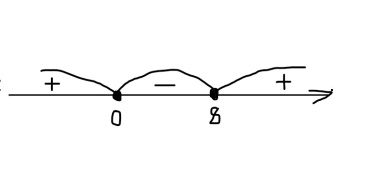
C:UsersУчительDesktopлуч 5.jpg

Теперь находим промежуток чисел, соответствующий неравенству х(х – ≤0, т.е. промежуток отрицательных или равных нулю чисел. Это будет промежуток [0; 8]

В соответствии с его номером, это будет ответ под №3.

Ответ: 3

pазбирался: Даниил Романович | обсудить разбор | оценить

1. Задание 18 № 40

Найдите тангенс угла AOB, изображенного на рисунке.

2. Задание 18 № 311485

На квадратной сетке изображён угол  A. Найдите   тангенс A .

3. Задание 18 № 316348

Найдите тангенс угла, изображённого на рисунке.

4. Задание 18 № 316374

Найдите тангенс угла, изображённого на рисунке.

6. Задание 18 № 340184

Найдите угол ABC. Ответ дайте в градусах.

9. Задание 18 № 348529

Найдите угол BAC. Ответ дайте в градусах.

10. Задание 18 № 348622

Найдите тангенс угла AOB, изображённого на рисунке.

11. Задание 18 № 348734

Найдите тангенс угла AOB, изображённого на рисунке.

12. Задание 18 № 349019

Найдите угол ABC. Ответ дайте в градусах.

14. Задание 18 № 349261

Найдите угол ABC. Ответ дайте в градусах.

17. Задание 18 № 349410

Найдите тангенс угла AOB, изображённого на рисунке.

18. Задание 18 № 349506

Найдите тангенс угла AOB, изображённого на рисунке.

21. Задание 18 № 349593

Найдите тангенс угла AOB, изображённого на рисунке.

22. Задание 18 № 350327

Найдите угол ABC

24. Задание 18 № 350842

Найдите угол ABC

25. Задание 18 № 350906

Найдите угол ABC. Ответ дайте в градусах.

27. Задание 18 № 351332

1. Задание 18 № 66

Найдите тангенс угла А треугольника ABC, изображённого на рисунке.

2. Задание 18 № 92

Найдите тангенс угла B треугольника ABC, изображённого на рисунке.

3. Задание 18 № 196

Найдите тангенс угла С треугольника ABC , изображённого на рисунке.

7. Задание 18 № 311958

На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённой из вершины прямого угла.

11. Задание 18 № 349661

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.

1. Задание 18 № 311356

На рисунке изображен параллелограмм  ABCD. Используя рисунок, найдите   синус angle HBA .

2 Задание 18 № 311400

На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в сантиметрах.

4. Задание 18 № 348499

На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.

5. Задание 18 № 348500

На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.

6. Задание 18 № 349758

На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.

7. Задание 18 № 349925

На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.

Консультация по английскому языку

Английский | Сегодня, 10:14

Разработчики экзаменационных материалов, учителя и выпускники, расскажут, как подготовиться к экзамену, об особенностях заданий в ЕГЭ и ответят на вопросы старшеклассников.

Этапы закрепощения крестьян в России

Крепостное право на Руси появилось позже, чем во многих средневековых европейских королевствах. Это было связано с объективными причинами – низкая плотность населения, зависимость от ордынского ига.

Задания 12-18 досрочного ЕГЭ по математике

3 примера по каждому заданию. Досрочный ЕГЭ по математике прошёл 28 марта.

1 слайд

ГИА — 2016 Задача №13 Киселева Галина Михайловна МБОУ СШ №6 г.Камышин

2 слайд

Укажите номера верных утверждений 1) При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°. 2) Диагонали ромба перпендикулярны. 3) Центром окружности, вписанной в треугольник, является точка пересечения его биссектрис. Вариант 1

3 слайд

Укажите номера верных утверждений 1) Треугольник со сторонами 3 см, 4 см, 5 см является прямоугольным. 2) Если угол равен 120°, то смежный с ним равен 120°. 3) Если расстояние от точки до прямой равно 3, то длина любой наклонной, проведённой из данной точки к прямой, больше 3. Вариант 2

4 слайд

Укажите номера верных утверждений 1) Если угол равен 47°, то смежный с ним равен 153°. 2) Через любую точку проходит ровно одна прямая. 3) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны. Вариант 3

5 слайд

Укажите номера верных утверждений 1) В треугольнике АВС со сторонами АВ = 6,5см, ВС = 5,6см, АС = 8,2см наибольшим является угол В. 2) В равнобедренном треугольнике любая медиана является биссектрисой. 3) Если угол равен 108°, то вертикальный с ним равен 108°. Вариант 4

6 слайд

Укажите номера верных утверждений 1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны. 2) Если в ромбе один из углов равен 90° , то такой ромб — квадрат. 3) Диагональ трапеции делит её на два равных треугольника. Вариант 5

7 слайд

Укажите номера верных утверждений 1) Треугольник, в котором есть два угла 60° и 80°, является равнобедренным. 2) Диагонали прямоугольника равны. 3) У любой трапеции боковые стороны равны. Вариант 6

8 слайд

Укажите номера верных утверждений 1) Вокруг любого треугольника можно описать окружность. 2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат. 3) Площадь трапеции равна произведению средней линии на высоту. Вариант 7

9 слайд

Укажите номера верных утверждений 1) Площадь прямоугольного треугольника равна произведению катетов. 2) Через любые две точки можно провести прямую. 3) Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой. Вариант 8

10 слайд

Укажите номера верных утверждений 1) Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник является параллелограммом. 2) Треугольник со сторонами 6, 7, 12 существует. 3) Сумма вертикальных углов равна 180°. Вариант 9

11 слайд

Укажите номера верных утверждений 1) Площадь ромба равна произведению его диагоналей. 2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны. 3) Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны. Вариант 10

Источник

Информация о цвете #349364

Реклама

#349364 Преобразование цвета

Реклама

Реклама

Населённые пункты телефонов

Операторы номеров с кодом 8(349364)

Если нужны более подробные данные по номерам, начинающимся на 349364, выберите следующую цифру по маске:

Задание № 14

Источники:

349364 решу огэ

349364 решу огэ

Источники:

Информация о числах

Триста сорок девять тысяч триста шестьдесят четыре
и
тринадцать

Описание

Теория к заданию №13

Консультация по английскому языку

Этапы закрепощения крестьян в России

Задания 12-18 досрочного ЕГЭ по математике

Реклама

Реклама

Реклама

Населённые пункты телефонов

Операторы номеров с кодом 8(349364)

Если нужны более подробные данные по номерам, начинающимся на 349364, выберите следующую цифру по маске:

Задание № 14

Источники:

349364 решу огэ

349364 решу огэ

Источники:

Информация о числах

Триста сорок девять тысяч триста шестьдесят четыре и тринадцать

Описание

Теория к заданию №13

Консультация по английскому языку

Этапы закрепощения крестьян в России

Задания 12-18 досрочного ЕГЭ по математике

Триста сорок девять тысяч триста шестьдесят четыре
и
тринадцать