Задание 12 номер 338238

Обвести кружком
номер правильного ответа:

1. Больной, находящийся
в коме:

1. на
вопросы не отвечает, на уколы реагирует

2. на
вопросы не отвечает, на уколы не реагирует

3. на
вопросы отвечает, на уколы реагирует

2. Причина диффузного
цианоза:

1.
замедление тока крови на периферии

2.
нарушение газообмена

Установить
соответствие:

3. Синдром
Положение больного

1. Печеночная
кома А. активное

2.Сердечная
недостаточность Б. пассивное

Г.
вынужденное

Ответ: 1…,2… .

Дополнить:

4. Увеличение в
размерах глазных яблок — __________________ .

5.Незначительные
отеки на голенях — _________________ .

Эталоны ответов
№ 12

12.1. 2.

12.2. 2. Нарушение
газообмена.

12.3. 1 Б, 2 Г .

12.4. экзофтальм

12.5. пастозность

Тестовое задание № 13

Дополнить:

1. Различают
состояния: тяжелое, средней тяжести и
_____________

2. Кожные покровы
могут быть гиперемированными, желтушными,

цианотичными и
_____________ .

Установить
соответствие:

3. Положение больного
Причина

1. ортопноэ
А. Менингит

2. молящегося
муллы Б. Сердечная
нед-ть

3.Лягавой собаки
В. Гидроперикард

Г. Воспаление
брюшины

Ответ: 1…, 2…, 3…
.

4. Вид цианоза
Причина

1. Акроцианоз
А.. Заболевание

дыхательной
системы

2. Диффузный
Б. Заболевание
печени

В. Заболевания
сердца

Ответ: 1…, 2… .

Обвести кружком
номера всех правильных ответов:

5. При исследовании
лимфоузлов оценивают:

1.
величину

2.
консистенцию

3.
болезненность

1. 4.подвижность

Эталоны ответов
№ 13

13.1. удовлетворительное

13.2. бледными

13.3. 1 Б , 2 В , 3 А .

13.4. 1 В ,2 А .

13.5. 1,2,3,4.

Тестовое задание № 14

Дополнить:

1. Положение больного
при неосложненном инфаркте миокарда

_________________ .

2. Крайняя степень
исхудания _________________ .

3. Незначительные
отеки называются _______________ .

Обвести кружком
номер правильного ответа:

1. Больной заторможен,на
   вопросы отвечает не правильно,

плохо ориентируется
в окружающей обстановке в:

1. сопоре

2. коме

3. ступоре

4. помраченном
   сознании

Обвести кружком
номера всех правильных ответов:

5.Ногтевые фаланги
в форме « барабанных палочек» встречаются
при:

1. врожденных пороках
   сердца

2. язвенной болезни

3. гнойных заболеваниях
   легких

4. циррозах печени

5. инфекционнном
   эндокардите

Эталоны ответов
№ 14

14.1. активное

14.2. кахексия

14.3. пастозность

14.4. 3 ступоре

14.5. 1,3,5.

Задание 12 № 202

В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле  , где t — длительность поездки, выраженная в минутах  . Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.

2. Задание 12 № 311326

Площадь параллелограмма   можно вычислить по формуле  , где   — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и  .

3. Задание 12 № 338071

Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 80 см, n = 1600? Ответ выразите в километрах.

4. Задание 12 № 338396

Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.

5. Задание 12 № 341532

Из формулы центростремительного ускорения a = ω²R найдите R (в метрах), если ω = 4 с⁻¹ и a = 64 м/с².

. Задание 12 № 311337

Длину окружности  l можно вычислить по формуле  , где R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать  ).

2. Задание 12 № 311348

Площадь ромба     можно вычислить по формуле   , где     — диагонали ромба (в метрах). Пользуясь этой формулой, найдите диагональ   , если диагональ     равна 30 м, а площадь ромба 120 м².

3. Задание 12 № 311528

Площадь треугольника     можно вычислить по формуле   , где  a — сторона треугольника,  h — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону   , если площадь треугольника равна   , а высота  h  равна 14 м.

4. Задание 12 № 311530

Площадь трапеции     можно вычислить по формуле   , где    — основания трапеции,  h — высота (в метрах). Пользуясь этой формулой, найдите высоту  h, если основания трапеции равны     и   , а её площадь   .

5. Задание 12 № 311535

Радиус вписанной в прямоугольный треугольник окружности можно найти по формуле   , где  a  и  b  — катеты, а  c — гипотенуза треугольника. Пользуясь этой формулой, найдите  b, если     и   .

6. Задание 12 № 311541

Объём пирамиды вычисляют по формуле   , где  S — площадь основания пирамиды,  h — её высота. Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?

7. Задание 12 № 311543

Площадь любого выпуклого четырехугольника можно вычислять по формуле   , где    — длины его диагоналей, а     угол между ними. Вычислите   , если   .

8. Задание 12 № 311824

Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых.

9. Задание 12 № 311920

Центростремительное ускорение при движении по окружности (в м/c² ) можно вычислить по формуле   где   — угловая скорость (в с⁻¹), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с⁻¹, а центростремительное ускорение равно 45 м/c².

10. Задание 12 № 311964

Из закона всемирного тяготения   выразите массу m и найдите её величину (в килограммах), если       и гравитационная постоянная 

11. Задание 12 № 316355

Полную механическую энергию тела (в джоулях) можно вычислить по формуле   где m — масса тела (в килограммах), v — его скорость (в м/с), h — высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а g — ускорение свободного падения (в м/с²). Пользуясь этой формулой, найдите h (в метрах), если       а 

12. Задание 12 № 316914

Мощность постоянного тока (в ваттах) вычисляется по формуле P = I²R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 150 ватт, а сила тока равна 5 амперам.

13. Задание 12 № 318530

Закон Кулона можно записать в виде   где F — сила взаимодействия зарядов (в ньютонах),   и   — величины зарядов (в кулонах), k — коэффициент пропорциональности (в Н·м²/Кл² ), а r — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда   (в кулонах), если   Н·м²/Кл²,   Кл,   м, а   Н.

14. Задание 12 № 338056

Закон всемирного тяготения можно записать в виде   где F — сила притяжения между телами (в ньютонах),   и   — массы тел (в килограммах), r — расстояние между центрами масс (в метрах), а   — гравитационная постоянная, равная 6,67 · 10⁻¹¹ H·м²/кг². Пользуясь формулой, найдите массу тела   (в килограммах), если   Н,   кг, а   м.

15. Задание 12 № 338089

Закон Джоуля–Ленца можно записать в виде Q = I²Rt, где Q — количество теплоты (в джоулях), I — сила тока (в амперах), R — сопротивление цепи (в омах), а t — время (в секундах). Пользуясь этой формулой, найдите время t (в секундах), если Q = 2187 Дж, I = 9 A, R = 3 Ом.

16. Задание 12 № 338238

Площадь четырёхугольника можно вычислить по формуле   где   и   — длины диагоналей четырёхугольника,   — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали   если     a 

17. Задание 12 № 338296

Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м³), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м³.

1. Задание 12 № 46

Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле  , где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.

2. Задание 12 № 311534

Радиус описанной около треугольника окружности можно найти по формуле   , где  a — сторона треугольника,    — противолежащий этой стороне угол, а  R — радиус описанной около этого треугольника окружности. Пользуясь этой формулой, найдите   , если   , а   .

3. Задание 12 № 311536

Длину биссектрисы треугольника, проведённой к стороне  a, можно вычислить по формуле   . Вычислите   ,  если   .

Перейдем к рассмотрению тестового задания ОГЭ по математике — задания №12. В данном задании нам необходимо поработать с формулами — либо просто подставить значения в формулу и провести вычисления, либо вначале выразить неизвестную величину, а затем произвести подстановку.

Задание OM1401o

Мощность постоянного тока (в ваттах) вычисляется по формуле P = I²R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 224 Вт, а сила тока равна 4 А.

---

Выразим сопротивление R:

R = P / I²

Подставим значения в полученную формулу:

R = 224 / 4² = 224 / 16 = 14 ом

Ответ: 14

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1402o

В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле:

С = 6000 + 4100•n,

где n — число колец, установленных в колодце.

Пользуясь этой формулой, рассчитайте стоимость колодца из 7 колец. Ответ укажите в рублях.

---

В данном случае выражать из формулы нам ничего не требуется, поэтому подставим в данную формулу значение n = 7:

С = 6000 + 4100•7 = 6000 + 28700 = 34700

Ответ: 34700

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1403o

Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле:

T = 2 • √l 

где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.

---

Выразим из формулы l, для этого возведем обе части в квадрат, получим:

T ² = 4 • l ,

тогда:

l  = T ² / 4

Подставляя значения из условия, получаем:

l = 3 ² / 4 = 9 / 4 = 2,25

Ответ: 2,25

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1404o

Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой

t_F = 1,8 • t_C + 32,

где t_C — температура в градусах Цельсия, t_F — температура в градусах Фаренгейта.

Какая температура по шкале Фаренгейта соответствует -25° по шкале Цельсия?

---

Подставляем значение -25 в формулу:

t_F = 1,8 • (-25) + 32 = -45 + 32 = -13

Ответ: -13

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1405o

Закон Кулона описывает взаимодействие между двумя электрическими зарядами. Закон можно записать в виде

где F — сила взаимодействия в ньютонах, q₁ и q₂ — величины зарядов в кулонах, k — коэффициент пропорциональности в Н·м²/Кл², а r — расстояние между зарядами в метрах. Пользуясь формулой, найдите величину заряда q₁ (в кулонах), если k=9·10⁹ Н·м²/Кл², q₂=0,004 Кл, r=600 м, F=0,4 Н.

---

Поскольку искомая величина стоит в формуле справа и не является результирующей), необходимо преобразовать эту формулу. Результатом преобразования в данном случае должно стать уравнение, в котором слева будет зафиксировано искомое q₁, а справа – все остальные величины, фигурирующие в начальной формуле.

Для удобства преобразования сначала поменяем местами левую и правую части начальной формулы:

Далее r² из знаменателя слева переносим в числитель справа, а k и q₂ из числителя слева – в знаменатель справа. Получим:

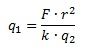
Результат мы получим в кулонах, как и требуется по условию. Основание для этого утверждения таково: т.к. все величины в условии даны в единицах СИ, то и результат будет получен только в СИ, а в этой системе единицей измерения эл.заряда является кулон (Кл).

Подставим в полученную формулу числовые данные из условия и вычислим искомую величину:

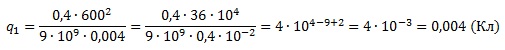Ответ: 0,004

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1406o

Площадь четырёхугольника можно вычислить по формуле:

где d₁ и d₂ – длины диагоналей четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d₂, если d₁=13, sinα=3/13, а S=25,5.

---

Так как искомая величина является в формуле частью выражения справа, то ее необходимо выразить через остальные величины. Тогда получим:

В полученную формулу подставим числовые данные из условия и вычислим искомую диагональ:

Ответ: 17

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание 12OM21R

Площадь четырехугольника можно вычислить по формуле S=d1d2sina2, где d1   и d2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2=16, sin a=25, a S=12,8

---

Для выполнения данного задания надо подставить все известные данные в формулу:

12,8=d1×16×252

В правой части можно сократить 16 и 2 на 2: 12,8=d1×8×251

Теперь умножим 8 на дробь 25, получим 3,2: 12,8=d1×3,2

Найдем неизвестный множитель, разделив 12,8 на 3,2: d1=12,8:3,2=4

Ответ: 4

pазбирался: Даниил Романович | обсудить разбор | оценить

Материал для отработки задания 12 при подготовке к ОГЭ по математике.

Подборка содержит 13 заданий по теме «Числовые последовательности».

→ Скачать задания

→ Скачать ответы

Примеры заданий:

1. Последовательность ( ) an задана условиями a1 = 3, a_{n +1} = a_n — 4 .

Найдите a₅.

Ответ: _____________.

2. Последовательность ( ) cn задана условиями c1 = -4 , c_{n +1} = c_n — 2.

Найдите c₈.

Ответ: _____________.

Связанные страницы:

Задание 14 ОГЭ 2020 по математике — расчёты по формулам

Варианты ОГЭ 2020 по математике

Практико-ориентированные задачи 1-5 ОГЭ 2020 Практика

2 варианта досрочного ОГЭ-2020 по математике от ФИПИ

ОГЭ по математике

Как решать задание 12 ОГЭ по математике? Материал для подготовки к ОГЭ.

Для выполнения задания 12 необходимо уметь осуществлять практические расчёты по формулам; составлять несложные формулы, выражающие зависимости между величинами.

С видами  заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе.

Решение типовых задач № 12 на ОГЭ по математике

Карточки для отработки задания 12 с ответами Источник: math100.ru → скачать

Материалы для отработки задания 12 Автор: Е. А. Ширяева → теория → задания

Практика для отработки задания 12 (презентация) Автор: Духина Марина Васильевна → скачать

Презентация: Решение заданий 12 ОГЭ математикаАвтор: Малявина Алена Сергеевна → скачать

Связанные страницы:

ОГЭ по математике №12. Расчёты по формуламadmin2022-03-19T15:42:57+03:00

Скачать файл в формате pdf.

Комментарии для сайта Cackle

Задание 1 № 366805

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	Город Гранюк	Деревня Астрелка	Хутор Южный	Город Гусевск
Цифры

Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.

Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.

Ответ: 1465.

2. Задание 2 № 366806

Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.

Решение.

Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится

пачек чая.

Таким образом, ребята должны купить 14 пачек чая.

Ответ: 14.

3. Задание 3 № 366807

Найдите площадь (в км²), которую занимает заказник.

Решение.

Площадь заказника равна:

Ответ: 351.

4. Задание 4 № 366808

Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.

Решение.

Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:

км.

Ответ: 30.

5. Задание 5 № 366809

Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.

Продукция	Цена в магазине «Вело» (руб.)	Цена в магазине «ОК» (руб.)	Срок доставки из магазина «ОК» (дни)
Подсветка для спиц
Шина вида «А»
Шина вида «Б»
Спица
Педаль вида «А»
Педаль вида «Б»
Тормоз вида «А»		нет
Тормоз вида «Б»	нет
Набор крепёжных изделий

Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?

Решение.

На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:

руб.

Ответ: 5300.

6. Задание 6 № 316314

Найдите значение выражения:

Решение.

Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.

7. Задание 7 № 317575

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?

1)

2)

3)

4)

Решение.

Заметим, что и Проверим все варианты ответа:

1) — неверно;

2) — верно;

3) — верно;

4) — верно.

Ответ указан под номером 1.

8. Задание 8 № 353586

Какое из данных ниже чисел является значением выражения

1)

2)

3)

4)

Решение.

Последовательно получим:

Ответ: 1

9. Задание 9 № 338500

При каком значении значения выражений и равны?

Решение.

Для ответа на вопрос задачи нужно решить уравнение Решим его:

Ответ: 2.

10. Задание 10 № 325450

В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.

Решение.

Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна

Ответ: 0,3.

11. Задание 11 № 311406

На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке

2)

3)

4) прямая пересекает график в точках и

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .

2) — неверно,

3) — верно, видно из графика.

4) Прямая пересекает график в точках и — верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

Ответ: 12.

12. Задание 12 № 311543

Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .

Решение.

Выразим :

Подставляя, получаем:

Ответ: 0,4.

13. Задание 13 № 338497

На каком из рисунков изображено решение неравенства

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

Решение.

Решим неравенство методом интервалов:

Правильный ответ указан под номером: 4.

14. Задание 14 № 406645

В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение.

Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.

Найдем сумму этой прогрессии:

Ответ: 377 мест.

15. Задание 15 № 340000

В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите

Решение.

Из прямоугольного треугольника по теореме Пифагора найдём

Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.

16. Задание 16 № 351463

На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.

Решение.

Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.

17. Задание 17 № 169876

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.

———-

В открытом банке иррациональный ответ.

18. Задание 18 № 350842

Найдите угол

Решение.

Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.

Ответ: 22,5

19. Задание 19 № 401617

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Ответ: 13.

20. Задание 20 № 338505

Решите неравенство

Решение.

Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение

Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).

Таким образом, ответ

Ответ:

Примечание.

Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,

21. Задание 21 № 353527

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.

Ответ: 58.

22. Задание 22 № 338288

Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.

Решение.

Упростим выражение:

По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:

График функции сводится к графику параболы с выколотой точкой

Выделим полный квадрат:

Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)

Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и

Ответ: −1; 3.

23. Задание 23 № 339395

Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.

Решение.

Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и

Ответ: 16.

24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.

Решение.

Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.

25. Задание 25 № 311926

В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .

Решение.

По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,

Площадь трапеции :

Площадь трапеции

Ответ: 9.

В 12-ом задании мы сталкиваемся с прогрессиями — общими понятиями. Конечно, по каждой теме можно придумать очень сложные задачи, но на самом ОГЭ по этой теме они обычно простые. Главным здесь является понимание, что такое арифметическая и что такое геометрическая прогрессия.

Ответом в задании 12 является целое число или конечная десятичная дробь.

---

Теория к заданию №12

---

Начнем теоретическую справку об определениях прогрессий.

Арифметическая прогрессия:

Последовательность, у которой задан первый член a1, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией.

a_n+1 = a_n + d

где d – разность прогрессии

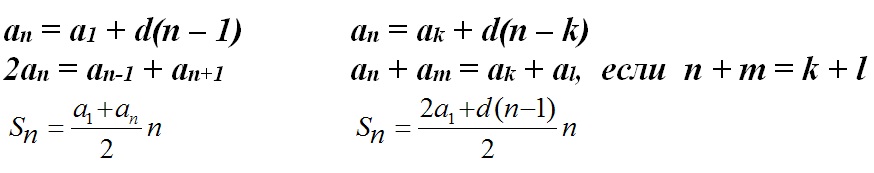
Геометрическая прогрессия:

Последовательность, у которой задан первый член b1 не равен 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q не равное 0, называется геометрической прогрессией.

b_n+1 = b_n q

где q – знаменатель прогрессии

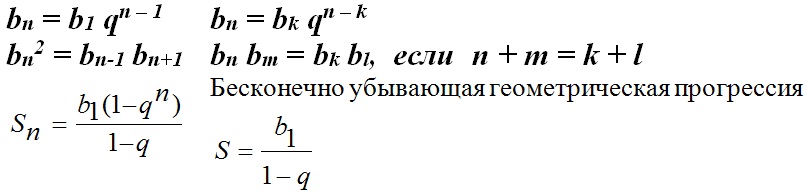
В первом варианте я разобрал, как найти разность арифметической прогрессии, если известны два её члена. Во втором варианте разобрано нахождение неизвестного члена геометрической прогрессии из ряда членов прогрессии. В третьем варианте представлено объяснение по поиску n-ого члена арифметической прогрессии.

---

Разбор типовых вариантов задания №12 ОГЭ по математике.

---

Первый вариант задания (нахождение разности прогрессии)

Дана арифметическая прогрессия a(n) в которой

a (3) = 6,9

a (16) = 26,4

Найдите разность прогрессии.

Решение:

Чтобы найти разность прогрессии в нашем случае, нужно разделить разницу между значениями членов прогрессии на количество членов (в нашем случае — это между 3 и 16).

Находим разницу между значениями  a (3) и a (16):

a (3) — a (16) = 26,4 — 6,9 = 19,5

Находим количество членов:

16 — 3 = 13

Находим разность прогрессии:

19,5 / 13 = 1,5

Ответ: 1,5

---

Второй вариант задания (нахождение неизвестного члена)

Выписано несколько последовательных членов геометрической прогрессии:

-1, x, -49, -343, ….

Найдите x.

Решение:

Для того, чтобы найти x, необходимо вначале вычислить знаменатель прогрессии — для этого необходимо разделить последующий член на предыдущий:

-343 / -49 = 7

Затем, зная знаменатель прогрессии мы можем найти x, разделив последующий член (-49) на уже известный знаменатель 7.

x = -49 / 7 = -7

Ответ: -7

---

Третий вариант задания (нахождение n-ого члена)

Выписаны первые несколько членов арифметической прогрессии:  10, 6, 2, …

Найдите 101 член.

Решение:

Для решения данной задачи воспользуемся формулой, задающей арифметическую прогрессию:

a_n = a₁ + (n-1) • d

В нашем случае:

a₁ = 10

d = 6 — 10 = -4

Подставляем значения в формулу:

a₁₀₁ = 10 + (101-1) • (-4) = -390

Ответ: -390

---

Демонстрационный вариант ОГЭ 2019

В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.

Решение:

В данном задании нас проверяют на знание формулы арифметической прогрессии:

где n — номер члена прогрессии, d — разность, а а1 — первый член.

Решение:

Подставим в общую формулу известные из условия значения:

d = 4,

а1 = 6,

n = 15,

получим:

a15 = 6 + (15 — 1) • 4

вычислив, получаем значение 15 члена:

a15 = 62

Ответ: 62

---

Четвертый вариант задания (нахождение произвольного члена геометрической прогрессии)

Геометрическая прогрессия (b_n) задана условиями:

b₁=–2, b_n+1=2b_n.

Найдите b₇.

Решение:

Искомый 7-й член прогрессии b₇ будем искать по формуле:

b₇=b₁·q⁶.    (1)

Здесь b₁ по условию дано, а знаменатель q нет. Но его можно определить, исходя из определения этой величины. Согласно определению, q=b_n+1/b_n. Используя второе условие задачи, получим, что q=2.

Теперь используем 1-е условие задачи (b₁=–2) и найдем искомую величину по формуле (1):

b₇=–2·2⁶=–2·64=–128.

Ответ: –128

---

Пятый вариант задания (нахождение суммы n членов геометрической прогрессии)

Выписаны первые три члена геометрической прогрессии: 1512; –252; 42; … Найдите сумму первых четырёх ее членов.

Решение:

Сумму произвольного кол-ва членов геометрич.прогрессии будем искать по формуле:

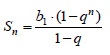
1-й член прогрессии известен из условия и равен b₁=1512. Требуемое число членов n=4.

Знаменатель прогрессии найдем как частное двух соседних членов прогрессии (2-го и 1-го или 3-го и 2-го и т.д.). Найдем его так:

По условию b₂=–252, b₃=42, поэтому

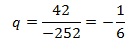
Отсюда получаем:

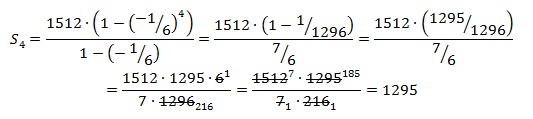
Ответ: 1295