На русском языке:
Триста одиннадцать тысяч восемьсот двадцать четыре рубля пятьдесят одна копейка
На английском языке:
three hundred and eleven thousand, eight hundred and twenty-four rubles and fifty-one kopecks
Сумма НДС 18% (Россия) = 56128.41 прописью:
На русском языке: пятьдесят шесть тысяч сто двадцать восемь рублей сорок одна копейка
На английском языке: fifty-six thousand, one hundred and twenty-eight rubles and forty-one kopecks
Сумма 311824.51 с НДС 18% (Россия) = 367952.92 прописью:
На русском языке: триста шестьдесят семь тысяч девятьсот пятьдесят два рубля девяносто две копейки
На английском языке: three hundred and sixty-seven thousand, nine hundred and fifty-two rubles and ninety-two kopecks
Сумма НДС 10% (Россия) = 31182.45 прописью:
На русском языке: тридцать одна тысяча сто восемьдесят два рубля сорок пять копеек
На английском языке: thirty-one thousand, one hundred and eighty-two rubles and forty-five kopecks
Сумма 311824.51 с НДС 10% (Россия) = 343006.96 прописью:
На русском языке: триста сорок три тысячи шесть рублей девяносто шесть копеек
На английском языке: three hundred and forty-three thousand and six rubles and ninety-six kopecks
Сумма НДС 12% (Казахстан) = 37418.94 прописью:
На русском языке: тридцать семь тысяч четыреста восемнадцать рублей девяносто четыре копейки
На английском языке: thirty-seven thousand, four hundred and eighteen rubles and ninety-four kopecks
Сумма 311824.51 с НДС 12% (Казахстан) = 349243.45 прописью:
На русском языке: триста сорок девять тысяч двести сорок три рубля сорок пять копеек
На английском языке: three hundred and forty-nine thousand, two hundred and forty-three rubles and forty-five kopecks
Сумма НДС 20% (Украина) = 62364.90 прописью:
На русском языке: шестьдесят две тысячи триста шестьдесят четыре рубля девяносто копеек
На английском языке: sixty-two thousand, three hundred and sixty-four rubles and ninety kopecks
Сумма 311824.51 с НДС 20% (Украина) = 374189.41 прописью:
На русском языке: триста семьдесят четыре тысячи сто восемьдесят девять рублей сорок одна копейка
На английском языке: three hundred and seventy-four thousand, one hundred and eighty-nine rubles and forty-one kopecks
Выделить НДС из суммы 311824.51:
Сумма НДС 18% (Россия) = 47566.45 прописью:
На русском языке: сорок семь тысяч пятьсот шестьдесят шесть рублей сорок пять копеек
На английском языке: forty-seven thousand, five hundred and sixty-six rubles and forty-five kopecks
Сумма 311824.51 без НДС 18% (Россия) = 264258.06 прописью:
На русском языке: двести шестьдесят четыре тысячи двести пятьдесят восемь рублей шесть копеек
На английском языке: two hundred and sixty-four thousand, two hundred and fifty-eight rubles and zero kopecks
Сумма НДС 10% (Россия) = 28347.68 прописью:
На русском языке: двадцать восемь тысяч триста сорок семь рублей шестьдесят восемь копеек
На английском языке: twenty-eight thousand, three hundred and forty-seven rubles and sixty-eight kopecks
Сумма 311824.51 без НДС 10% (Россия) = 283476.83 прописью:
На русском языке: двести восемьдесят три тысячи четыреста семьдесят шесть рублей восемьдесят три копейки
На английском языке: two hundred and eighty-three thousand, four hundred and seventy-six rubles and eighty-three kopecks
Сумма НДС 12% (Казахстан) = 33409.77 прописью:
На русском языке: тридцать три тысячи четыреста девять рублей семьдесят семь копеек
На английском языке: thirty-three thousand, four hundred and nine rubles and seventy-seven kopecks
Сумма 311824.51 без НДС 12% (Казахстан) = 278414.74 прописью:
На русском языке: двести семьдесят восемь тысяч четыреста четырнадцать рублей семьдесят четыре копейки
На английском языке: two hundred and seventy-eight thousand, four hundred and fourteen rubles and seventy-four kopecks
Сумма НДС 20% (Украина) = 51970.75 прописью:
На русском языке: пятьдесят одна тысяча девятьсот семьдесят рублей семьдесят пять копеек
На английском языке: fifty-one thousand, nine hundred and seventy rubles and seventy-five kopecks
Сумма 311824.51 без НДС 20% (Украина) = 259853.76 прописью:
На русском языке: двести пятьдесят девять тысяч восемьсот пятьдесят три рубля семьдесят шесть копеек
На английском языке: two hundred and fifty-nine thousand, eight hundred and fifty-three rubles and seventy-six kopecks
Катализатор
| Параметр | Значение |
|---|---|
| Номер артикула: | 311824 |
| Производитель: | Klarius |
| Тип изделия: | Неоригинальный |
| Система выпуска ОГ | с резьбой для лямбда-зонда |

Если доставка автозапчастей составляет более десяти дней, то скорее всего доставка будет осуществляться из-за границы. Просьба уточнять стоимость доставки, т.к. она не включена в стоимость в прайс-листе и может занимать существенную цену
Код автодетали: 311824
| Наличие, шт. Поставщик Поставка, дней Цена, руб. Партия, шт. Дата прайса |
|---|
| Klarius 311824 311824 Катализатор сделать запрос по VIN |
Audi A3 (8P1)
Audi A3 Sportback (8PA)
Рациональное натуральное
шестизначное
число 311824
является составным.
Произведение и сумма цифр: 192, 19.
У числа 10 делителей.
604190 — сумма делителей числа.
311824 и 0.0000032069372466519574 — это обратные числа.
Данное число можно представить произведением простых чисел: 2 * 2 * 2 * 2 * 19489.
Системы счисления:
двоичный вид числа: 1001100001000010000, троичный вид числа: 120211202001, восьмеричный вид числа: 1141020, шестнадцатеричный вид числа: 4C210.
Конвертация из числа байтов это 304 килобайта 528 байтов .
Число азбукой Морзе: …— .—- .—- —.. ..— ….-
Косинус 311824: -0.4871, тангенс 311824: -1.7929, синус 311824: 0.8733.
Число имеет натуральный логарифм: 12.6502.
Десятичный логарифм числа: 5.4939.
558.4120 — корень квадратный, 67.8115 — корень кубический.
Квадрат числа: 9.7234e+10.
3 дня 14 часов 37 минут 4 секунды представляет из себя число секунд 311824.
Нумерологическая цифра этого числа — 1.
Число 311824 (триста одиннадцать тысяч восемьсот двадцать четыре) — шестизначное четное, делится на два, девятнадцать тысяч четыреста восемьдесят девять и само себя.
Т.е число 311824 делится на 2, 19489, 311824, и раскладывается на множители: 2:2:2:2:19489.
Проверка:
311824 : 2 = 155912
155912 : 2 = 77956
77956 : 2 = 38978
38978 : 2 = 19489
19489 : 19489 = 1
Сумма цифр в числе 311824 равна 19, а их умножение (отличных от нуля) — 192.
Обратное число 311824 = 3.206937246652E-6
Двоичная система счисления 3118242: 1001100001000010000
Проверка:
| 262144 | +262144 (218) | 1 |
| 131072 | 0 | |
| 65536 | 0 | |
| 32768 | +32768 (215) | 1 |
| 16384 | +16384 (214) | 1 |
| 8192 | 0 | |
| 4096 | 0 | |
| 2048 | 0 | |
| 1024 | 0 | |
| 512 | +512 (29) | 1 |
| 256 | 0 | |
| 128 | 0 | |
| 64 | 0 | |
| 32 | 0 | |
| 16 | +16 (24) | 1 |
| 8 | 0 | |
| 4 | 0 | |
| 2 | 0 | |
| 1 | 0 |
Примеры:
7472039 + 311824 = 7783863
семь миллионов четыреста семьдесят две тысячи тридцать девять плюс триста одиннадцать тысяч восемьсот двадцать четыре равно семь миллионов семьсот восемьдесят три тысячи восемьсот шестьдесят три
311824 + 3045890 = 3357714
триста одиннадцать тысяч восемьсот двадцать четыре плюс три миллиона сорок пять тысяч восемьсот девяносто равно три миллиона триста пятьдесят семь тысяч семьсот четырнадцать
311824 — 670609 = -358785
триста одиннадцать тысяч восемьсот двадцать четыре минус шестьсот семьдесят тысяч шестьсот девять равно минус триста пятьдесят восемь тысяч семьсот восемьдесят пять
311824 + 1619343 = 1931167
триста одиннадцать тысяч восемьсот двадцать четыре плюс один миллион шестьсот девятнадцать тысяч триста сорок три равно один миллион девятьсот тридцать одна тысяча сто шестьдесят семь
Предыдущее число: 311823 (триста одиннадцать тысяч восемьсот двадцать три), а следующее число — 311825 (триста одиннадцать тысяч восемьсот двадцать пять).
Вы ждали 0.01сек.
БЕСПЛАТНАЯ ДОСТАВКА В ДЁМУ !*
*Пн-Пт после 19-ти, Сб. после 17 часов.Звоните тел./WhatsApp +79899584758.
В прайсе представлены предложения нашего магазина и ближайших складов. Узнать о возможности заказа деталей со сроками поставки более 2-х дней Вы можете по телефонам и WhatsApp.
Просим Вас уточнять наличие и стоимость запчастей по телефонам: +7(989) 958-47-58, 290-47-58 или WhatsApp +79899584758.
Внимание!
Вы можете ввести оригинальный или неоригинальный номер запчасти. На результат поиска не влияет наличие запятых, точек, тире и пробелов. В артикуле должны присутствовать только латинские буквы. Отсутствие результатов поиска может означать, что ваш номер ошибочен или устарел. В этом случае необходимо связаться с менеджером.
Новый сентябрьский тренировочный вариант (тренировочная работа) №37446023 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
Ссылка для скачивания варианта: задания (КИМ)
Ответы и решения для варианта: скачать
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37446023:
Ответы и решения для заданий ОГЭ 2022
На плане (см. рисунок) представлен дизайн‐проект сквера в станице Лужки. Сторона большой клетки равна 2 метра. Участок, отведённый под сквер, имеет квадратную форму. По периметру участка планируется установить забор. С двух сторон сквера будут два входа. Если зайти в сквер, то справа от входа № 1 будет располагаться карусель, а слева — детский игровой комплекс, отмеченный на плане цифрой 5. Дом творчества будет находиться слева, если зайти через вход № 2, а зооуголок — справа. Центр сквера, отмеченный цифрой 4, планируется украсить фонтаном диаметром 2 метра и двумя цветочными клумбами. Рядом с детским игровым комплексом построят кафе, рядом с каруселью — кинотеатр площадью 64 м 2 . За кинотеатром будет оборудована тренажёрная площадка, отмеченная цифрой 8. На территории сквера дорожки шириной 2 м будут выложены тротуарной плиткой размером 1 м × 1 м. Аллея шириной 4 м располагается от входа № 1 до Дома творчества и будет выложена той же плиткой, что и дорожки.
Задание 2 № 367493 Тротуарная плитка продаётся в упаковках по 3 штуки. Сколько упаковок понадобится купить, чтобы выложить аллею от входа № 1 до Дома творчества?
Ответ: 1327
Задание 3 № 367495 Найдите площадь (в м 2 ) земли, которую занимает Дом творчества.
Ответ: 184
Задание 4 № 367496 Найдите наибольший возможный радиус карусели (в метрах).
Ответ: 3
Задание 5 № 367497 По периметру участка планируется установить забор. С двух сторон сквера будут два входа. При обсуждении, каким должен быть забор, рассматривалось два варианта: кованый или комбинированный. Цены на доставку оборудования и на установочные работы, а также стоимость изготовления одного погонного метра забора представлены в таблице. На сколько рублей общая стоимость кованного забора меньше общей стоимости комбинированного забора?
Ответ: 45870
Задание 10 № 311919 Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча — с командой В и с командой С. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда А.
Ответ: 0,25
Задание 12 № 311824 Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C+32 , где C— градусы Цельсия, F— градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых.
Ответ: -14,4
Задание 14 № 394309 Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке 15 минут, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на 7 минут. За сколько занятий Андрей проведёт на беговой дорожке в общей сложности 2 часа 25 минут, если будет следовать советам тренера?
Ответ: 5
Задание 15 № 339375 Точка D на стороне AB треугольника ABC выбрана так, что AD = AC. Известно, что ∠CAB=80° и ∠ ACB=59∘. Найдите угол DCB. Ответ дайте в градусах.
Ответ: 9
Задание 16 № 324868 Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.
Ответ: 14
Задание 17 № 169853 В треугольнике одна из сторон равна 10, а опущенная на нее высота— 5. Найдите площадь треугольника.
Ответ: 25
Задание 18 № 341675 На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.
Ответ: 11
Задание 19 № 314814 Какие из данных утверждений верны? Запишите их номера. 1) Вокруг любого треугольника можно описать окружность. 2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат. 3) Площадь трапеции равна произведению средней линии на высоту. Если утверждений несколько, запишите их номера в порядке возрастания.
Ответ: 123
Задание 21 № 338582 Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.
Ответ: 26
Задание 24 № 333322 Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M. Докажите, что треугольники MBC и MDA подобны.
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:
Тренировочный вариант Ларина №292 ОГЭ 2022 по математике 9 класс с ответами
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задание 12 № 202
В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле ![]() , где t — длительность поездки, выраженная в минутах
, где t — длительность поездки, выраженная в минутах ![]() . Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
. Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
2. Задание 12 № 311326
Площадь параллелограмма ![]() можно вычислить по формуле
можно вычислить по формуле ![]() , где
, где ![]() — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и
— стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и ![]() .
.
3. Задание 12 № 338071
Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 80 см, n = 1600? Ответ выразите в километрах.
4. Задание 12 № 338396
Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.
5. Задание 12 № 341532
Из формулы центростремительного ускорения a = ω2R найдите R (в метрах), если ω = 4 с−1 и a = 64 м/с2.
. Задание 12 № 311337
Длину окружности l можно вычислить по формуле ![]() , где R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать
, где R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать ![]() ).
).
2. Задание 12 № 311348
Площадь ромба ![]() можно вычислить по формуле
можно вычислить по формуле ![]() , где
, где ![]() — диагонали ромба (в метрах). Пользуясь этой формулой, найдите диагональ
— диагонали ромба (в метрах). Пользуясь этой формулой, найдите диагональ ![]() , если диагональ
, если диагональ ![]() равна 30 м, а площадь ромба 120 м2.
равна 30 м, а площадь ромба 120 м2.
3. Задание 12 № 311528
Площадь треугольника ![]() можно вычислить по формуле
можно вычислить по формуле ![]() , где a — сторона треугольника, h — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону
, где a — сторона треугольника, h — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону ![]() , если площадь треугольника равна
, если площадь треугольника равна ![]() , а высота h равна 14 м.
, а высота h равна 14 м.
4. Задание 12 № 311530
Площадь трапеции ![]() можно вычислить по формуле
можно вычислить по формуле ![]() , где
, где ![]() — основания трапеции, h — высота (в метрах). Пользуясь этой формулой, найдите высоту h, если основания трапеции равны
— основания трапеции, h — высота (в метрах). Пользуясь этой формулой, найдите высоту h, если основания трапеции равны ![]() и
и ![]() , а её площадь
, а её площадь ![]() .
.
5. Задание 12 № 311535
Радиус вписанной в прямоугольный треугольник окружности можно найти по формуле ![]() , где a и b — катеты, а c — гипотенуза треугольника. Пользуясь этой формулой, найдите b, если
, где a и b — катеты, а c — гипотенуза треугольника. Пользуясь этой формулой, найдите b, если ![]() и
и ![]() .
.
6. Задание 12 № 311541
Объём пирамиды вычисляют по формуле ![]() , где S — площадь основания пирамиды, h — её высота. Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?
, где S — площадь основания пирамиды, h — её высота. Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?
7. Задание 12 № 311543
Площадь любого выпуклого четырехугольника можно вычислять по формуле ![]() , где
, где ![]() — длины его диагоналей, а
— длины его диагоналей, а ![]() угол между ними. Вычислите
угол между ними. Вычислите ![]() , если
, если ![]() .
.
8. Задание 12 № 311824
Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых.
9. Задание 12 № 311920
Центростремительное ускорение при движении по окружности (в м/c2 ) можно вычислить по формуле ![]() где
где ![]() — угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.
— угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.
10. Задание 12 № 311964
Из закона всемирного тяготения ![]() выразите массу m и найдите её величину (в килограммах), если
выразите массу m и найдите её величину (в килограммах), если ![]()
![]()
![]() и гравитационная постоянная
и гравитационная постоянная ![]()
11. Задание 12 № 316355
Полную механическую энергию тела (в джоулях) можно вычислить по формуле ![]() где m — масса тела (в килограммах), v — его скорость (в м/с), h — высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а g — ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите h (в метрах), если
где m — масса тела (в килограммах), v — его скорость (в м/с), h — высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а g — ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите h (в метрах), если ![]()
![]()
![]() а
а ![]()
12. Задание 12 № 316914
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 150 ватт, а сила тока равна 5 амперам.
13. Задание 12 № 318530
Закон Кулона можно записать в виде ![]() где F — сила взаимодействия зарядов (в ньютонах),
где F — сила взаимодействия зарядов (в ньютонах), ![]() и
и ![]() — величины зарядов (в кулонах), k — коэффициент пропорциональности (в Н·м2/Кл2 ), а r — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда
— величины зарядов (в кулонах), k — коэффициент пропорциональности (в Н·м2/Кл2 ), а r — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда ![]() (в кулонах), если
(в кулонах), если ![]() Н·м2/Кл2,
Н·м2/Кл2, ![]() Кл,
Кл, ![]() м, а
м, а ![]() Н.
Н.
14. Задание 12 № 338056
Закон всемирного тяготения можно записать в виде ![]() где F — сила притяжения между телами (в ньютонах),
где F — сила притяжения между телами (в ньютонах), ![]() и
и ![]() — массы тел (в килограммах), r — расстояние между центрами масс (в метрах), а
— массы тел (в килограммах), r — расстояние между центрами масс (в метрах), а ![]() — гравитационная постоянная, равная 6,67 · 10−11 H·м2/кг2. Пользуясь формулой, найдите массу тела
— гравитационная постоянная, равная 6,67 · 10−11 H·м2/кг2. Пользуясь формулой, найдите массу тела ![]() (в килограммах), если
(в килограммах), если ![]() Н,
Н, ![]() кг, а
кг, а ![]() м.
м.
15. Задание 12 № 338089
Закон Джоуля–Ленца можно записать в виде Q = I2Rt, где Q — количество теплоты (в джоулях), I — сила тока (в амперах), R — сопротивление цепи (в омах), а t — время (в секундах). Пользуясь этой формулой, найдите время t (в секундах), если Q = 2187 Дж, I = 9 A, R = 3 Ом.
16. Задание 12 № 338238
Площадь четырёхугольника можно вычислить по формуле ![]() где
где ![]() и
и ![]() — длины диагоналей четырёхугольника,
— длины диагоналей четырёхугольника, ![]() — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали ![]() если
если ![]()
![]() a
a ![]()
17. Задание 12 № 338296
Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м3.
1. Задание 12 № 46
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле ![]() , где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
, где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
2. Задание 12 № 311534
Радиус описанной около треугольника окружности можно найти по формуле ![]() , где a — сторона треугольника,
, где a — сторона треугольника, ![]() — противолежащий этой стороне угол, а R — радиус описанной около этого треугольника окружности. Пользуясь этой формулой, найдите
— противолежащий этой стороне угол, а R — радиус описанной около этого треугольника окружности. Пользуясь этой формулой, найдите ![]() , если
, если ![]() , а
, а ![]() .
.
3. Задание 12 № 311536
Длину биссектрисы треугольника, проведённой к стороне a, можно вычислить по формуле ![]() . Вычислите
. Вычислите ![]() , если
, если ![]() .
.
Перейдем к рассмотрению тестового задания ОГЭ по математике — задания №12. В данном задании нам необходимо поработать с формулами — либо просто подставить значения в формулу и провести вычисления, либо вначале выразить неизвестную величину, а затем произвести подстановку.
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 224 Вт, а сила тока равна 4 А.
Выразим сопротивление R:
R = P / I2
Подставим значения в полученную формулу:
R = 224 / 42 = 224 / 16 = 14 ом
Ответ: 14
pазбирался: Даниил Романович | обсудить разбор | оценить
В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле:
С = 6000 + 4100•n,
где n — число колец, установленных в колодце.
Пользуясь этой формулой, рассчитайте стоимость колодца из 7 колец. Ответ укажите в рублях.
В данном случае выражать из формулы нам ничего не требуется, поэтому подставим в данную формулу значение n = 7:
С = 6000 + 4100•7 = 6000 + 28700 = 34700
Ответ: 34700
pазбирался: Даниил Романович | обсудить разбор | оценить
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле:
T = 2 • √l
где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
Выразим из формулы l, для этого возведем обе части в квадрат, получим:
T ² = 4 • l ,
тогда:
l = T ² / 4
Подставляя значения из условия, получаем:
l = 3 ² / 4 = 9 / 4 = 2,25
Ответ: 2,25
pазбирался: Даниил Романович | обсудить разбор | оценить
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой
tF = 1,8 • tC + 32,
где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта.
Какая температура по шкале Фаренгейта соответствует -25° по шкале Цельсия?
Подставляем значение -25 в формулу:
tF = 1,8 • (-25) + 32 = -45 + 32 = -13
Ответ: -13
pазбирался: Даниил Романович | обсудить разбор | оценить
Закон Кулона описывает взаимодействие между двумя электрическими зарядами. Закон можно записать в виде
![]()
где F — сила взаимодействия в ньютонах, q1 и q2 — величины зарядов в кулонах, k — коэффициент пропорциональности в Н·м2/Кл2, а r — расстояние между зарядами в метрах. Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9·109 Н·м2/Кл2, q2=0,004 Кл, r=600 м, F=0,4 Н.
Поскольку искомая величина стоит в формуле справа и не является результирующей), необходимо преобразовать эту формулу. Результатом преобразования в данном случае должно стать уравнение, в котором слева будет зафиксировано искомое q1, а справа – все остальные величины, фигурирующие в начальной формуле.
Для удобства преобразования сначала поменяем местами левую и правую части начальной формулы:
![]()
Далее r2 из знаменателя слева переносим в числитель справа, а k и q2 из числителя слева – в знаменатель справа. Получим:
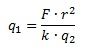
Результат мы получим в кулонах, как и требуется по условию. Основание для этого утверждения таково: т.к. все величины в условии даны в единицах СИ, то и результат будет получен только в СИ, а в этой системе единицей измерения эл.заряда является кулон (Кл).
Подставим в полученную формулу числовые данные из условия и вычислим искомую величину:
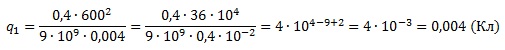 Ответ: 0,004
Ответ: 0,004
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырёхугольника можно вычислить по формуле:
![]()
где d1 и d2 – длины диагоналей четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если d1=13, sinα=3/13, а S=25,5.
Так как искомая величина является в формуле частью выражения справа, то ее необходимо выразить через остальные величины. Тогда получим:
![]()
В полученную формулу подставим числовые данные из условия и вычислим искомую диагональ:
 Ответ: 17
Ответ: 17
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S=d1d2sina2, где d1 и d2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2=16, sin a=25, a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8=d1×16×252
В правой части можно сократить 16 и 2 на 2: 12,8=d1×8×251
Теперь умножим 8 на дробь 25, получим 3,2: 12,8=d1×3,2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d1=12,8:3,2=4
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
- ОГЭ по математике
Как решать задание 12 ОГЭ по математике? Материал для подготовки к ОГЭ.
Для выполнения задания 12 необходимо уметь осуществлять практические расчёты по формулам; составлять несложные формулы, выражающие зависимости между величинами.
С видами заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе.
Решение типовых задач № 12 на ОГЭ по математике
| Карточки для отработки задания 12 с ответами Источник: math100.ru → скачать |
| Материалы для отработки задания 12 Автор: Е. А. Ширяева → теория → задания |
| Практика для отработки задания 12 (презентация) Автор: Духина Марина Васильевна → скачать |
| Презентация: Решение заданий 12 ОГЭ математикаАвтор: Малявина Алена Сергеевна → скачать |
Связанные страницы:
Статьи
Основное общее образование
Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)
Математика
Представляем вашему вниманию разбор 12 задания ОГЭ-2019 по математике
17 октября 2018
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 12
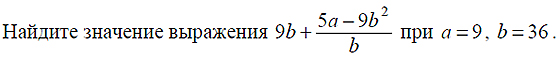
Решение
Вместо того чтобы сразу подставить числа в данное выражение, сначала упростим его, записав в виде рациональной дроби:

Ответ: 1,25.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить
Заец Мирослав Владимирович
учитель математики школы №1317 г. Москвы
Хотите сохранить материал на будущее? Отправьте себе на почту
ОГЭ по математике №12. Расчёты по формуламadmin2022-03-19T15:42:57+03:00
Скачать файл в формате pdf.
Комментарии для сайта Cackle
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Найдите значение выражения .
Ответ:
2
О числах a и c известно, что . Какое из следующих неравенств неверно?
1)
2)
3)
4)
Ответ:
3
Вычислите:
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Ответ:
4
Решите уравнение .
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Ответ:
5
Укажите соответствие между графиками функций и формулами, которые их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
Ответ:
6
Упростите выражение и найдите его значение при
. В ответ запишите полученное число.
Ответ:
7
На каком рисунке изображено множество решений неравенства ?
В ответе укажите номер правильного варианта.
| 1) | 2) |
| 3) | 4) |
1) 1
2) 2
3) 3
4) 4
Ответ:
8
Дорожный знак, изображённый на рисунке, называется «Ограничение высоты». Его устанавливают перед мостами, тоннелями и прочими сооружениями, чтобы запретить проезд транспортного средства, габариты которого (с грузом или без груза) превышают установленную высоту.
Какому из данных транспортных средств этот знак запрещает проезд?
В ответе укажите номер правильного варианта.
1) молоковозу высотой 3770 мм
2) пожарному автомобилю высотой 3400 мм
3) автотопливозаправщику высотой 2900 мм
4) автоцистерне высотой 3350 мм
Ответ:
9
В аэропорту чемоданы пассажиров поднимают в зал выдачи багажа по транспортерной ленте. При проектировании транспортера необходимо учитывать допустимую силу натяжения ленты транспортера. На рисунке изображена зависимость натяжения ленты от угла наклона транспортера к горизонту при расчетной нагрузке. На оси абсцисс откладывается угол подъема в градусах, на оси ординат – сила натяжения транспортерной ленты (в килограммах силы). При каком угле наклона сила натяжения достигает 150 кгс? Ответ дайте в градусах.
Ответ:
10
Городской бюджет составляет 45 млн. р., а расходы на одну из его статей составили 12,5%. Сколько рублей потрачено на эту статью бюджета?
Ответ:
11
Задания Д4 № 31
Завуч школы подвёл итоги контрольной работы по математике в 9-х классах. Результаты представлены на круговой диаграмме.
Какое из утверждений относительно результатов контрольной работы неверно, если всего в школе 120 девятиклассников?
1) Более половины учащихся получили отметку «3».
2) Около четверти учащихся отсутствовали на контрольной работе или получили отметку «2».
3) Отметку «4» или «5» получила примерно шестая часть учащихся.
4) Отметку «3», «4» или «5» получили более 100 учащихся.
В ответ запишите номер выбранного утверждения.
Ответ:
12
Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых.
Ответ:
13
Упростите выражение
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Задание 1 № 366805
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Город Гранюк | Деревня Астрелка | Хутор Южный | Город Гусевск |
| Цифры |
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.
Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.
Ответ: 1465.
2. Задание 2 № 366806
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Решение.
Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится
 пачек чая.
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
3. Задание 3 № 366807
Найдите площадь (в км2), которую занимает заказник.
Решение.

Площадь заказника равна:

Ответ: 351.
4. Задание 4 № 366808
Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Решение.
Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
 км.
км.
Ответ: 30.
5. Задание 5 № 366809
Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | |||
| Шина вида «А» | |||
| Шина вида «Б» | |||
| Спица | |||
| Педаль вида «А» | |||
| Педаль вида «Б» | |||
| Тормоз вида «А» | нет | ||
| Тормоз вида «Б» | нет | ||
| Набор крепёжных изделий |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Решение.
На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:
 руб.
руб.
Ответ: 5300.
6. Задание 6 № 316314
Найдите значение выражения: 
Решение.
Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.
7. Задание 7 № 317575
На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?
1) 
2) 
3) 
4) 
Решение.
Заметим, что  и
и  Проверим все варианты ответа:
Проверим все варианты ответа:
1)  — неверно;
— неверно;
2)  — верно;
— верно;
3)  — верно;
— верно;
4)  — верно.
— верно.
Ответ указан под номером 1.
8. Задание 8 № 353586
Какое из данных ниже чисел является значением выражения 
1) 
2) 
3) 
4) 
Решение.
Последовательно получим:


Ответ: 1
9. Задание 9 № 338500
При каком значении  значения выражений
значения выражений  и
и  равны?
равны?
Решение.
Для ответа на вопрос задачи нужно решить уравнение  Решим его:
Решим его:

Ответ: 2.
10. Задание 10 № 325450
В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.
Решение.
Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна 
Ответ: 0,3.
11. Задание 11 № 311406
На рисунке изображён график функции  . Какие из утверждений относительно этой функции неверны? Укажите их номера.
. Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке 
2) 
3) 
4) прямая  пересекает график в точках
пересекает график в точках  и
и 
Решение.
Проверим каждое из утверждений.
1) Функция возрастает на промежутке  — неверно, функция убывает на промежутке
— неверно, функция убывает на промежутке  и затем возрастает на
и затем возрастает на  .
.
2)  — неверно,
— неверно, 

3)  — верно, видно из графика.
— верно, видно из графика.
4) Прямая  пересекает график в точках
пересекает график в точках  и
и  — верно, видно из графика.
— верно, видно из графика.
Таким образом, неверные утверждения находятся под номерами 1 и 2.
Ответ: 12.
12. Задание 12 № 311543
Площадь любого выпуклого четырехугольника можно вычислять по формуле  , где
, где  — длины его диагоналей, а
— длины его диагоналей, а  угол между ними. Вычислите
угол между ними. Вычислите  , если
, если  .
.
Решение.
Выразим  :
:

Подставляя, получаем:

Ответ: 0,4.
13. Задание 13 № 338497
На каком из рисунков изображено решение неравенства 
В ответе укажите номер правильного варианта.

1) 1
2) 2
3) 3
4) 4
Решение.
Решим неравенство методом интервалов:


Правильный ответ указан под номером: 4.
14. Задание 14 № 406645
В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Решение.
Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.
Найдем сумму этой прогрессии:

Ответ: 377 мест.
15. Задание 15 № 340000

В прямоугольном треугольнике  катет
катет  , а высота
, а высота  , опущенная на гипотенузу, равна
, опущенная на гипотенузу, равна  Найдите
Найдите 
Решение.
Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Углы  и
и  равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:
равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.
16. Задание 16 № 351463
 На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что  Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Длина меньшей дуги AB равна 33. Найдите длину большей дуги.
Решение.
Пусть длина большей дуги  равна
равна  Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.
17. Задание 17 № 169876
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на  .
.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.
———-
В открытом банке иррациональный ответ.
18. Задание 18 № 350842

Найдите угол 
Решение.

Искомый угол  опирается на
опирается на  часть окружности:
часть окружности:  . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.
. Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е. 
Ответ: 22,5
19. Задание 19 № 401617
Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.
Ответ: 13.
20. Задание 20 № 338505
Решите неравенство 
Решение.
Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение 


Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).
Таким образом, ответ 
Ответ: 
Примечание.
Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно, 
21. Задание 21 № 353527
Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть взяли  г 21-процентного раствора, тогда взяли и
г 21-процентного раствора, тогда взяли и  г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится
г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится  г, а во втором —
г, а во втором —  г Концентрация получившегося раствора равна
г Концентрация получившегося раствора равна  или 58%.
или 58%.
Ответ: 58.
22. Задание 22 № 338288
Постройте график функции  И определите, при каких значениях
И определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение.
Упростим выражение:
По теореме, обратной теореме Виета, корни уравнения  равны -1 и -2 соответственно, тогда по формуле
равны -1 и -2 соответственно, тогда по формуле  , получаем:
, получаем:  . Имеем:
. Имеем:

График функции сводится к графику параболы  с выколотой точкой
с выколотой точкой 
Выделим полный квадрат:

Следовательно, график функции получается из графика функции  сдвигом на
сдвигом на  . (см. рис.)
. (см. рис.)

Из графика видно, что прямая  имеет с графиком функции ровно одну общую точку при
имеет с графиком функции ровно одну общую точку при  и
и 
Ответ: −1; 3.
23. Задание 23 № 339395
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.
Решение.
 Угол
Угол  — вписанный, он равен 90° и опирается на дугу
— вписанный, он равен 90° и опирается на дугу  следовательно, дуга
следовательно, дуга  равна 180°, значит, хорда
равна 180°, значит, хорда  — диаметр окружности и
— диаметр окружности и 
Ответ: 16.
24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Решение.
Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.
25. Задание 25 № 311926
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
Решение.

По свойству равнобедренной трапеции  следовательно, треугольники
следовательно, треугольники  и
и  равны. Так как
равны. Так как  =
=  треугольники
треугольники  и
и  равнобедренные, следовательно,
равнобедренные, следовательно,  и
и  — соответствующие медианы этих треугольников. Значит,
— соответствующие медианы этих треугольников. Значит,  Отрезок
Отрезок  соединяет середины диагоналей трапеции, следовательно,
соединяет середины диагоналей трапеции, следовательно,  и прямые
и прямые 
 и
и  параллельны, поэтому,
параллельны, поэтому,  — трапеция. Проведём
— трапеция. Проведём  — высоту трапеции
— высоту трапеции  и
и  — высоту трапеции
— высоту трапеции  . Прямоугольные треугольники
. Прямоугольные треугольники  и
и  подобны, значит,
подобны, значит, 
Площадь трапеции  :
: 
Площадь трапеции 


Ответ: 9.
