Задание 12 номер 311536

Задание 12 огэ математика 311536

Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле, где L — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.

Радиус описанной около треугольника окружности можно найти по формуле, где A — сторона треугольника, — противолежащий этой стороне угол, а R — радиус описанной около этого треугольника окружности. Пользуясь этой формулой, найдите, если, а.

Радиус описанной около треугольника окружности можно найти по формуле, где a сторона треугольника, противолежащий этой стороне угол, а R радиус описанной около этого треугольника окружности.

Oge. sdamgia. ru

15.02.2020 10:42:41

2020-02-15 10:42:41

Источники:

Https://oge. sdamgia. ru/test? theme=70&ttest=true&wclones=1

OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задание 12 огэ математика 311536

Задание 12 огэ математика 311536

Задание 12 огэ математика 311536

Задание 12 № 46

Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле, где L — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.

Подставим в формулу значение T:

Период колебаний математического маятника вычисляется по формуле где G — ускорение свободного падения. При приближенных вычислениях можно принять и использовать формулу, приведенную в условии задачи.

Задание 12 № 46

Период колебания математического маятника T в секундах приближенно можно вычислить по формуле, где l длина нити в метрах.

Oge. sdamgia. ru

13.05.2018 7:11:21

2018-05-13 07:11:21

Источники:

Https://oge. sdamgia. ru/test? theme=70

Длину биссектрисы треугольника проведенной к стороне а можно вычислить по формуле tex l — Школьные » /> » /> .keyword { color: red; } Задание 12 огэ математика 311536

Длину биссектрисы треугольника проведенной к стороне а можно вычислить по формуле если b 1,c 3,l a 1,2

Длину биссектрисы треугольника проведенной к стороне а можно вычислить по формуле если b=1,c=3,l a=1,2

За три дні було продано 425 кг овочів. За перший день було продано в 4рази більше овочів, ніж за другий. За третій день продали на 65 кг більше, ніж з … а другий. Скільки овочів було продано кожного дня?

Чему равна длина третьей стороны треугольника если его периметр равен 32 см, а две его стороны равны 9 см и 11 см? Помогите пожалуйста срочно

В саду растёт 320 деревьев из которых 15 процентов составляют яблони. Сколько яблонь растёт в саду? ​

За третій день продали на 65 кг більше, ніж з а другий.

Znanija. com

20.07.2020 3:40:02

2020-07-20 03:40:02

Источники:

Https://znanija. com/task/6600751

Задания

Версия для печати и копирования в MS Word

Задание 12 № 311536

Длину биссектрисы треугольника, проведённой к стороне  a, можно вычислить по формуле  . Вычислите  ,  если  .

Спрятать решение

Решение.

Выразим из данной формулы :

Подставляя, получаем:

Ответ: 0,8.

Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)

Раздел кодификатора ФИПИ: 1.3 Текстовые задачи.

Спрятать решение

·

·

Сообщить об ошибке · Помощь

На данной странице ответы к сборнику для подготовки к ОГЭ-2016 по математике 36 типовых экзаменационных вариантов под руководством И. В. Ященко.

Варианты с 13 по 23 здесь

Варианты с 24 по 36

---

Ответы:

---

Вариант 1
Номер задания	Ответ	Номер задания	Ответ
1	-2032	14	4
2	1	15	0.6
3	2	16	10
4	-0.1	17	60
5	132	18	13
6	12	19	0.3
7	1.2	20	3
8	3	21	(1;-4); (1.8;0)
9	21	22	15
10	148	23	-5;-11/2
11	64	24	180/13
12	6	26	13
13	13

---

Вариант 2
Номер задания	Ответ	Номер задания	Ответ
1	-1036	14	2
2	3	15	0.4
3	1	16	30
4	-0.4	17	20
5	312	18	24
6	-12	19	0.1
7	-0.9	20	7
8	1	21	(1 ; -6);(2,2 ; 0)
9	24	22	15
10	32	23	-2; -7/4
11	289	24	240/13
12	8	26	15
13	23

---

Вариант 3
Номер задания	Ответ	Номер задания	Ответ
1	3.95	14	2
2	4	15	1.2
3	4	16	640
4	7	17	150
5	231	18	12
6	-2	19	0.65
7	5	20	12
8	1	21	(2 ; 2) ; (2 ; -2)
9	217	22	480
10	8.5	23	4;5
11	45	24	7
12	6	26	13
13	13

Вариант 4
Номер задания	Ответ	Номер задания	Ответ
1	2.06	14	4
2	3	15	0.8
3	2	16	240
4	-3	17	96
5	123	18	24
6	3	19	0.55
7	50	20	9
8	2	21	(2 ; 3) ; (2 ; -3)
9	153	22	540
10	6.5	23	3 ; 4
11	35	24	15
12	6	26	9
13	2

Вариант 5
Номер задания	Ответ	Номер задания	Ответ
1	-3	14	3
2	3	15	12
3	2	16	2640
4	-4	17	60
5	132	18	2
6	135	19	0.56
7	3.5	20	54500
8	2	21	-4; -3; 2
9	74	22	11
10	2500	23	1; 2
11	109	24	8
12	2	26	8.8
13	23

Вариант 6
Номер задания	Ответ	Номер задания	Ответ
1	-1	14	2
2	3	15	8
3	3	16	1320
4	-6	17	30
5	132	18	4
6	192	19	0.25
7	-44.5	20	58500
8	2	21	-5; -4; 3
9	69	22	12
10	1024	23	0;1
11	155	24	9
12	2	26	1.6
13	12

Вариант 7
Номер задания	Ответ	Номер задания	Ответ
1	-380	14	1
2	2	15	5
3	2	16	374.4
4	-0.6	17	6
5	231	18	2
6	-32.4	19	0.4
7	20	20	95
8	1	21	(1 ; 5) ; (-1 ; 5)
9	23	22	16
10	3	23	0 ; 1/4
11	16	24	15
12	8	26	99
13	3

Вариант 8
Номер задания	Ответ	Номер задания	Ответ
1	20	14	3
2	2	15	5
3	2	16	242
4	1.5	17	9
5	312	18	4
6	112	19	0.84
7	21	20	-148
8	3	21	(2 ; 3) ; (-2 ; 3)
9	24	22	25
10	34	23	-8 ; 1/36
11	42	24	7
12	12	26	30
13	1

Вариант 9
Номер задания	Ответ	Номер задания	Ответ
1	8910	14	1
2	3	15	40
3	2	16	50
4	-5	17	1.4
5	231	18	2
6	595	19	0.96
7	-2.5	20	62500
8	1	21	(5 — √2 ; 5 + √2)
9	69	22	10
10	441	23	81
11	109	24	7
12	3	26	12
13	13

Вариант 10
Номер задания	Ответ	Номер задания	Ответ
1	19200	14	2
2	4	15	0.4
3	3	16	45
4	8	17	3
5	312	18	2
6	-625.2	19	0.96
7	-1.7	20	38800
8	1	21	(-1 — √3; -1 + √3)
9	68	22	14
10	154	23	36/49
11	91	24	20
12	3	26	28√3/3
13	12

Вариант 12
Номер задания	Ответ	Номер задания	Ответ
1	2.5	14	2
2	1	15	6
3	4	16	500
4	0.5	17	18
5	213	18	4
6	-4	19	0.5
7	0.2	20	6
8	2	21	(2 ; 1); (-2 ; 1)
9	26	22	480
10	65	23	-6.25; 0; 6.25
11	64	24	18
12	1	26	16
13	23

Рейтинг: 3.0 из 5.0
Проголосовало: 67

Комментарии

Всего комментариев: 0

Статьи

Основное общее образование

Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)

Математика

Представляем вашему вниманию разбор 13 задания ОГЭ-2019 по математике

17 октября 2018

Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Часть 1

Задание 13

Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой t_F = 1,8t_C + 32, где t_C – температура в градусах Цельсия, t_F – температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует –25 градусов по шкале Цельсия?

Решение

Подставим значение –25 в формулу

t_F = 1,8 · (–25) + 32 = –13

Ответ: –13.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену

Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.

Купить

Ответы на тренировочный вариант №36 ОГЭ по математике 2022admin2022-01-21T20:55:44+03:00

Скачать ответы на тренировочный вариант ОГЭ в формате pdf.

Комментарии для сайта Cackle

Задания

Версия для печати и копирования в MS Word

Задание 12 № 311536

Длину биссектрисы треугольника, проведённой к стороне  a, можно вычислить по формуле  . Вычислите  ,  если  .

Спрятать решение

Решение.

Выразим из данной формулы :

Подставляя, получаем:

Ответ: 0,8.

Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)

Раздел кодификатора ФИПИ: 1.3 Текстовые задачи.

Спрятать решение

·

·

Сообщить об ошибке · Помощь

Задание 1 № 366805

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	Город Гранюк	Деревня Астрелка	Хутор Южный	Город Гусевск
Цифры

Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.

Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.

Ответ: 1465.

2. Задание 2 № 366806

Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.

Решение.

Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится

пачек чая.

Таким образом, ребята должны купить 14 пачек чая.

Ответ: 14.

3. Задание 3 № 366807

Найдите площадь (в км²), которую занимает заказник.

Решение.

Площадь заказника равна:

Ответ: 351.

4. Задание 4 № 366808

Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.

Решение.

Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:

км.

Ответ: 30.

5. Задание 5 № 366809

Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.

Продукция	Цена в магазине «Вело» (руб.)	Цена в магазине «ОК» (руб.)	Срок доставки из магазина «ОК» (дни)
Подсветка для спиц
Шина вида «А»
Шина вида «Б»
Спица
Педаль вида «А»
Педаль вида «Б»
Тормоз вида «А»		нет
Тормоз вида «Б»	нет
Набор крепёжных изделий

Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?

Решение.

На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:

руб.

Ответ: 5300.

6. Задание 6 № 316314

Найдите значение выражения:

Решение.

Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.

7. Задание 7 № 317575

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?

1)

2)

3)

4)

Решение.

Заметим, что и Проверим все варианты ответа:

1) — неверно;

2) — верно;

3) — верно;

4) — верно.

Ответ указан под номером 1.

8. Задание 8 № 353586

Какое из данных ниже чисел является значением выражения

1)

2)

3)

4)

Решение.

Последовательно получим:

Ответ: 1

9. Задание 9 № 338500

При каком значении значения выражений и равны?

Решение.

Для ответа на вопрос задачи нужно решить уравнение Решим его:

Ответ: 2.

10. Задание 10 № 325450

В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.

Решение.

Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна

Ответ: 0,3.

11. Задание 11 № 311406

На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке

2)

3)

4) прямая пересекает график в точках и

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .

2) — неверно,

3) — верно, видно из графика.

4) Прямая пересекает график в точках и — верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

Ответ: 12.

12. Задание 12 № 311543

Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .

Решение.

Выразим :

Подставляя, получаем:

Ответ: 0,4.

13. Задание 13 № 338497

На каком из рисунков изображено решение неравенства

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

Решение.

Решим неравенство методом интервалов:

Правильный ответ указан под номером: 4.

14. Задание 14 № 406645

В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение.

Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.

Найдем сумму этой прогрессии:

Ответ: 377 мест.

15. Задание 15 № 340000

В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите

Решение.

Из прямоугольного треугольника по теореме Пифагора найдём

Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.

16. Задание 16 № 351463

На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.

Решение.

Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.

17. Задание 17 № 169876

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.

———-

В открытом банке иррациональный ответ.

18. Задание 18 № 350842

Найдите угол

Решение.

Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.

Ответ: 22,5

19. Задание 19 № 401617

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Ответ: 13.

20. Задание 20 № 338505

Решите неравенство

Решение.

Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение

Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).

Таким образом, ответ

Ответ:

Примечание.

Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,

21. Задание 21 № 353527

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.

Ответ: 58.

22. Задание 22 № 338288

Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.

Решение.

Упростим выражение:

По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:

График функции сводится к графику параболы с выколотой точкой

Выделим полный квадрат:

Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)

Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и

Ответ: −1; 3.

23. Задание 23 № 339395

Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.

Решение.

Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и

Ответ: 16.

24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.

Решение.

Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.

25. Задание 25 № 311926

В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .

Решение.

По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,

Площадь трапеции :

Площадь трапеции

Ответ: 9.

В 12-ом задании мы сталкиваемся с прогрессиями — общими понятиями. Конечно, по каждой теме можно придумать очень сложные задачи, но на самом ОГЭ по этой теме они обычно простые. Главным здесь является понимание, что такое арифметическая и что такое геометрическая прогрессия.

Ответом в задании 12 является целое число или конечная десятичная дробь.

---

Теория к заданию №12

---

Начнем теоретическую справку об определениях прогрессий.

Арифметическая прогрессия:

Последовательность, у которой задан первый член a1, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией.

a_n+1 = a_n + d

где d – разность прогрессии

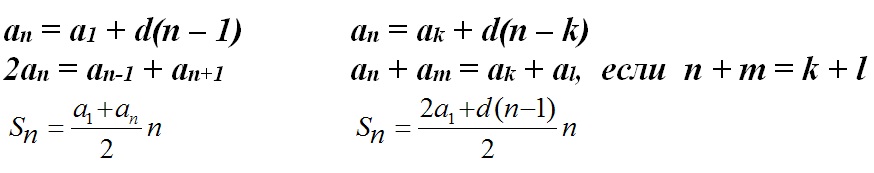
Геометрическая прогрессия:

Последовательность, у которой задан первый член b1 не равен 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q не равное 0, называется геометрической прогрессией.

b_n+1 = b_n q

где q – знаменатель прогрессии

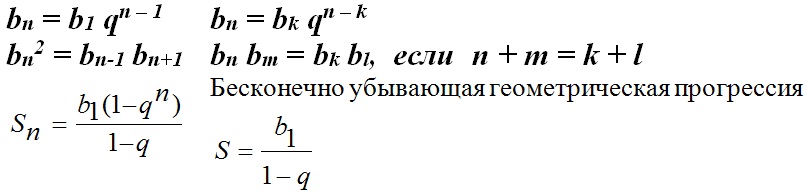
В первом варианте я разобрал, как найти разность арифметической прогрессии, если известны два её члена. Во втором варианте разобрано нахождение неизвестного члена геометрической прогрессии из ряда членов прогрессии. В третьем варианте представлено объяснение по поиску n-ого члена арифметической прогрессии.

---

Разбор типовых вариантов задания №12 ОГЭ по математике.

---

Первый вариант задания (нахождение разности прогрессии)

Дана арифметическая прогрессия a(n) в которой

a (3) = 6,9

a (16) = 26,4

Найдите разность прогрессии.

Решение:

Чтобы найти разность прогрессии в нашем случае, нужно разделить разницу между значениями членов прогрессии на количество членов (в нашем случае — это между 3 и 16).

Находим разницу между значениями  a (3) и a (16):

a (3) — a (16) = 26,4 — 6,9 = 19,5

Находим количество членов:

16 — 3 = 13

Находим разность прогрессии:

19,5 / 13 = 1,5

Ответ: 1,5

---

Второй вариант задания (нахождение неизвестного члена)

Выписано несколько последовательных членов геометрической прогрессии:

-1, x, -49, -343, ….

Найдите x.

Решение:

Для того, чтобы найти x, необходимо вначале вычислить знаменатель прогрессии — для этого необходимо разделить последующий член на предыдущий:

-343 / -49 = 7

Затем, зная знаменатель прогрессии мы можем найти x, разделив последующий член (-49) на уже известный знаменатель 7.

x = -49 / 7 = -7

Ответ: -7

---

Третий вариант задания (нахождение n-ого члена)

Выписаны первые несколько членов арифметической прогрессии:  10, 6, 2, …

Найдите 101 член.

Решение:

Для решения данной задачи воспользуемся формулой, задающей арифметическую прогрессию:

a_n = a₁ + (n-1) • d

В нашем случае:

a₁ = 10

d = 6 — 10 = -4

Подставляем значения в формулу:

a₁₀₁ = 10 + (101-1) • (-4) = -390

Ответ: -390

---

Демонстрационный вариант ОГЭ 2019

В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.

Решение:

В данном задании нас проверяют на знание формулы арифметической прогрессии:

где n — номер члена прогрессии, d — разность, а а1 — первый член.

Решение:

Подставим в общую формулу известные из условия значения:

d = 4,

а1 = 6,

n = 15,

получим:

a15 = 6 + (15 — 1) • 4

вычислив, получаем значение 15 члена:

a15 = 62

Ответ: 62

---

Четвертый вариант задания (нахождение произвольного члена геометрической прогрессии)

Геометрическая прогрессия (b_n) задана условиями:

b₁=–2, b_n+1=2b_n.

Найдите b₇.

Решение:

Искомый 7-й член прогрессии b₇ будем искать по формуле:

b₇=b₁·q⁶.    (1)

Здесь b₁ по условию дано, а знаменатель q нет. Но его можно определить, исходя из определения этой величины. Согласно определению, q=b_n+1/b_n. Используя второе условие задачи, получим, что q=2.

Теперь используем 1-е условие задачи (b₁=–2) и найдем искомую величину по формуле (1):

b₇=–2·2⁶=–2·64=–128.

Ответ: –128

---

Пятый вариант задания (нахождение суммы n членов геометрической прогрессии)

Выписаны первые три члена геометрической прогрессии: 1512; –252; 42; … Найдите сумму первых четырёх ее членов.

Решение:

Сумму произвольного кол-ва членов геометрич.прогрессии будем искать по формуле:

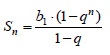
1-й член прогрессии известен из условия и равен b₁=1512. Требуемое число членов n=4.

Знаменатель прогрессии найдем как частное двух соседних членов прогрессии (2-го и 1-го или 3-го и 2-го и т.д.). Найдем его так:

По условию b₂=–252, b₃=42, поэтому

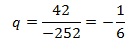
Отсюда получаем:

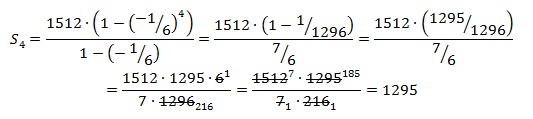
Ответ: 1295