Задание 12 номер 311528 - Большой телефонный справочник предприятий

Новый октябрьский тренировочный вариант (тренировочная работа) №37812183 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.

скачать вариант

скачать ответы

Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812183:

На плане изображено плодоовощное хозяйство, расположенное на территории прямоугольной формы (сторона каждой клетки на плане равна 20 м). Въезд и выезд осуществляются через единственные ворота. При входе на территорию хозяйства слева от ворот находится кукурузное поле. Рядом с ним расположен яблоневый сад.

Также имеется цех по переработке овощей и фруктов, расположенный рядом с полем, засеянным капустой. При входе справа от ворот находится стоянка для грузовиков и сельхозтехники. На территории стоянки расположен склад готовой продукции. Участок с теплицами, в которых выращивают клубнику, граничит с яблоневым садом и капустным полем. К хозяйству подведено электричество.

Задание 1 № 368428 Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Ответ: 2763

Задание 2 № 368429 Урожайность кукурузы в этом хозяйстве в среднем составила 4 тонны с одного гектара земли. Цех по переработке выпускает банки консервированной кукурузы массой нетто основного продукта 280 грамм каждая. Какое максимальное количество банок кукурузы выпустил цех?

Ответ: 17142

Задание 3 № 368430 Найдите суммарную площадь участков земли, занятых под сельскохозяйственные культуры. Ответ дайте в гектарах.

Ответ: 6,44

Задание 4 № 368431 По периметру кукурузного поля планируется поставить забор. Найдите его длину (в метрах).

Ответ: 440

Задание 5 № 368432 Собственник хозяйства рассматривает два варианта водоснабжения: централизованное или автономное из артезианской скважины. Цены на оборудование и стоимость его установки, данные о расходе воды и её стоимости даны в таблице. Обдумав оба варианта, собственник решил оборудовать автономное водоснабжение. Через сколько часов непрерывной работы водоснабжения экономия от использования автономного водоснабжения вместо централизованного компенсирует разность в стоимости установки оборудования и монтажа?

Ответ: 1600

Задание 10 № 132740 У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.

Ответ: 0,75

Задание 12 № 311528 Площадь треугольника можно вычислить по формуле , где — сторона треугольника, — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону , если площадь треугольника равна , а высота равна 14 м.

Ответ: 4

Задание 14 № 393958 Компания «Альфа» начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10 000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?

Ответ: 35000

Задание 15 № 323376 Площадь равнобедренного треугольника равна Угол, лежащий напротив основания равен 120°. Найдите длину боковой стороны.

Ответ: 28

Задание 16 № 311331 Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.

Ответ: 71

Задание 17 № 169913 Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответ укажите площадь, деленную на π.

Ответ: 27

Задание 19 № 341384 Какие из следующих утверждений верны? 1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. 2) Средняя линия трапеции параллельна её основаниям. 3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

Ответ: 23

Задание 21 № 314431 При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?

Ответ: 2/1

Задание 24 № 340341 Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.

Задание 25 № 78 Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.

Ответ: 0,6

Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:

Тренировочный вариант №22 ОГЭ 2022 по математике 9 класс с ответами
Пробный вариант №211004 ОГЭ 2022 по математике 9 класс 100 баллов с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

{

Шестнадцатеричная система — 4c0e8.
Двоичная система — 1001100000011101000.
Посмотрите так же как пишутся десятичные цифры 21, 72, 95, 349, 343, 89, 556, 335, 2230, 6773, 5924, 12086, 63896, 236326, 689858 в различных системах счисления.

Число 311528 в других системах счисления:
2 — 1001100000011101000, 3 — 120211100002, 4 — 1030003220, 5 — 34432103, 6 — 10402132, 7 — 2435150, 8 — 1140350, 9 — 524302, 10 — 311528, 11 — 1a3068, 12 — 130348, 13 — aba49, 14 — 81760, 15 — 62488, 16 — 4c0e8, 17 — 3c6g3, 18 — 2h792, 19 — 277i4, 20 — 1iig8, 21 — 1cd8e, 22 — 175e8, 23 — 12dkg, 24 — mck8, 25 — jnb3, 26 — hilm, 27 — fm92, 28 — e5a0, 29 — cmca, 30 — bg48, 31 — ae59, 32 — 9g78.

Свойства числа 311528

Множители		2 * 2 * 2 * 7 * 5563
Делители	1, 2, 4, 7, 8, 14, 28, 56, 5563, 11126, 22252, 38941, 44504, 77882, 155764, 311528
Количество делителей	16
Сумма делителей	667680
Предыдущее целое	311527
Следующее целое	311529
Простое число?	NO
Предыдущее простое	311473
Следующее простое	311533
311528th простое число	4433047
Является числом Фибоначчи?	NO
Число Белла?	NO
Число Каталана?	NO
Факториал?	NO
Регулярное число?	NO
Совершенное число?	NO
Полигональное число (s < 11)?	NO
Двоичное	1001100000011101000
Восьмеричная	1140350
Двенадцатеричный	130348
Шестнадцатиричная	4c0e8
Квадрат	97049694784
Квадратный корень	558.14693405948
Натуральный логарифм	12.64924450081
Десятичный логарифм	5.493497086947
Синус	0.98357194816311
Косинус	0.18051654435707
Тангенс	5.4486526521224

Математические настройки для вашего сайта

Выберите язык:
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
中文
日本語
한국어

Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером

Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.

Решение

Выполним преобразования и вычислим производную.

y=frac23x^{tfrac32}-6x-5

y’=x^{tfrac12}-6=sqrt{x}-6

Уравнение производной имеет один единственный корень x = 36.

На числовой оси расставим знаки производной и посмотрим как ведет себя функция.

Поведение функции на числовой оси со знаками производной

При переходе через точку x = 36 производная меняет знак с минуса на плюс. Значит x = 36 – точка минимума функции.

Найдем наименьшее значение функции в точке x = 36.

y(36)=frac23cdot 36cdot6-216-5=-77

Наименьшее значение функции равно −77.

Ответ

-77

Задание 12 номер 311528

oleg681 год назад

0

0

Развернутый угол — это угол, стороны которого составляют прямую
значит, углы 5:13 в сумме равны 180°
решим пропорцию
5+13=18
180:18=10
угол 1=5*10=50°
угол 2=13*10=130°

Свойства натурального числа 311528, 0x04C0E8, 0x4C0E8: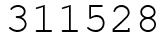
Число 311528.

Рейтинг 0 из 10,
оценок: 0.

Системы счисления, перевод в систему счисления

Десятичное число 311528

311528 в шестнадцатеричной системе счисления

4C0E8
311528 в двоичной системе счисления

1001100000011101000
311528 в восьмеричной системе счисления

1140350

Шестнадцатеричное число 4C0E8

4C0E8 в десятичной системе

311528
4C0E8 в двоичной системе

1001100000011101000
4C0E8 в восьмеричной системе

1140350

Двоичное число 1001100000011101000

1001100000011101000 в десятичной системе

311528
1001100000011101000 в шестнадцатеричной системе

4C0E8
1001100000011101000 в восьмеричной системе

1140350

Восьмеричное число 1140350

1140350 в десятичной системе

311528
1140350 в шестнадцатеричной системе

4C0E8
1140350 в двоичной системе

1001100000011101000

Основные арифметические и алгебраические свойства

Число 311528 на русском языке, number in Russian, число 311528 прописью:

триста одиннадцать тысяч пятьсот двадцать восемь
Четность

Четное число 311528
Разложение на множители, делители числа 311528

2, 2, 2, 7, 5563, 1
Простое или составное число

Составное число 311528
Числа делящиеся на целое число 311528

623056, 934584, 1246112, 1557640, 1869168, 2180696, 2492224, 2803752
Число 311528 умноженное на число два

623056
311528 деленное на число 2

155764
Список 8-ми простых чисел перед числом

311473, 311453, 311447, 311419, 311407, 311393, 311371, 311359
Сумма десятичных цифр

20
Количество цифр

6
Десятичный логарифм 311528

5.493497086947
Натуральный логарифм 311528

12.64924450081
Это число Фибоначчи?

Нет
Число на 1 больше числа 311528,
следующее число

число 311529
Число на 1 меньше числа 311528,
предыдущее число

311527

Степени числа, корни

311528 во второй степени (в квадрате)
(функция x в степени 2 — x²)

97049694784
В третьей степени (в кубе, 311528 в степени 3, x³) равно

30233697316669952
Корень квадратный из 311528

558.14693405948
Корень кубический из числа 311528 =

67.790009637068

Тригонометрические функции, тригонометрия

Синус, sin 311528 градусов, sin 311528°

0.7880107536
Косинус, cos 311528 градусов, cos 311528°

-0.6156614753
Тангенс, tg 311528 градусов, tg 311528°

-1.2799416322
Синус, sin 311528 радиан

0.98357194816311
Косинус, cos 311528 радиан

0.18051654435707
Тангенс, tg 311528 радиан равно

5.4486526521224
311528 градусов, 311528° =

5437.1893121529 радиан
311528 радиан =

17849239.600152 градуса, 17849239.600152°

Контрольные суммы, хэши, криптография

MD-5 хэш(311528)

49447914a8380638815cb4bd092bfe01
CRC-32, CRC32(311528)

2625990
SHA-256 hash, SHA256(311528)

876c52244e6412cda86b5e32657cb274610c08e8bf5592543051714577d32f79
SHA1, SHA-1(311528)

8d3ede2398249ec913706d821ac5f806915f8f90
ГОСТ Р 34.11, GOST R 34.11-94, GOST(311528)

fb21f6f5cca51cb51071f2f4576ea3e8c42867e05b7b23c6796bd0f0d24e54d8
Base64

MzExNTI4

Языки программирования

C++, CPP, C значение 311528

0x04C0E8, 0x4C0E8
Delphi, Pascal значение числа 311528

$04C0E8

Дата и время

Конвертация UNIX timestamp 311528 в дату и время

UTC

воскресенье, 4 января 1970 г., 14:32:08 GMT

в Москве, Россия

воскресенье, 4 января 1970 г., 17:32:08 Московское стандартное время

в Лондоне, Великобритания

воскресенье, 4 января 1970 г., 15:32:08 GMT+01:00

в Нью-Йорке, США

воскресенье, 4 января 1970 г., 9:32:08 Восточно-американское стандартное время

Интернет

Конвертация в IPv4 адрес Интернет

0.4.192.232
311528 в Википедии:

311528

Другие свойства числа

Короткая ссылка на эту страницу, DEC

https://bikubik.com/ru/311528
Короткая ссылка на эту страницу, HEX

https://bikubik.com/ru/x4C0E8
Номер телефона

31-15-28

Цвет по числу 311528, цветовая гамма

html RGB цвет 311528, 16-ричное значение

#04C0E8 — (4, 192, 232)
HTML CSS код цвета #04C0E8

.color-mn { color: #04C0E8; }
.color-bg { background-color: #04C0E8; }

Цвет для данного числа 311528

Здесь вы можете изменить составляющую цвета для данного числа 311528 или цвета 04C0E8:

Источник

Огэ математика 311528

Задание 12 № 311337

Длину окружности L можно вычислить по формуле, где R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать ).

Выразим радиус из формулы длины окружности:

Задание 12 № 311348

Площадь ромба можно вычислить по формуле, где — диагонали ромба (в метрах). Пользуясь этой формулой, найдите диагональ, если диагональ равна 30 м, а площадь ромба 120 м 2 .

Подставим в формулу известные величины:

Задание 12 № 311528

Площадь треугольника можно вычислить по формуле, где A — сторона треугольника, H — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону, если площадь треугольника равна, а высота H равна 14 м.

Задание 12 № 311337

Задание 12 № 311348

Огэ математика 311528.

Oge. sdamgia. ru

26.02.2017 12:09:10

2017-02-26 12:09:10

Источники:

Https://oge. sdamgia. ru/test? theme=27

OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Огэ математика 311528

Огэ математика 311528

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.

Ширина шины (мм)Диаметр диска (дюймы)

13	14	15
165	165/70	165/65	—
175	175/65	175/65; 175/60	—
185	185/65; 185/60	185/60	185/55
195	195/60	195/55	195/55; 195/50

Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 15 дюймам? Ответ дайте в миллиметрах.

Автомобильное колесо, как правило, представляет собой металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.

Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке 2). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр на рисунке 2) к ширине шины, то есть

Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.

За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса D в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.

Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.

Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 165/70 R13.

Огэ математика 311528.

Oge. sdamgia. ru

01.08.2017 5:06:31

2017-08-01 05:06:31

Источники:

Https://oge. sdamgia. ru/test? id=41771045

Решу огэ математика 9 класс 2022 биология — Подготовка к ГИА » /> » /> .keyword { color: red; } Огэ математика 311528

Решу огэ математика 9 класс 2022 биология

Петя записал на доске два различных натуральных числа. Затем он их сложил, перемножил, вычел из большего записанного числа меньшее и разделил большее на меньшее. Сложив четыре полученных результата, Петя получил число 1089. Найдите все такие пары натуральных чисел. В ответ запишите их сумму.

Сразу заметим, что сумма, разность и произведение чисел были натуральными. Поскольку сумма всех четырех результатов оказалась натуральной, частное тоже было целым (и, следовательно, натуральным). Обозначим эти числа за A и Xa. По условию,

Задание 31 № 1822

В ответ запишите их сумму.

Источники:

Решу ОГЭ 2022 тренировочный вариант №37812183 по математике 9 класс с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword < color: red; >Решу огэ математика 9 класс 2022 биология

Решу ОГЭ 2022 тренировочный вариант №37812183 по математике 9 класс с ответами

Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812183:

Ответ: 2763

Ответ: 17142

Ответ: 6,44

Задание 4 № 368431 По периметру кукурузного поля планируется поставить забор. Найдите его длину (в метрах).

Ответ: 440

Ответ: 1600

Ответ: 0,75

Задание 12 № 311528 Площадь треугольника можно вычислить по формуле, где — сторона треугольника, — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону, если площадь треугольника равна, а высота равна 14 м.

Ответ: 4

Ответ: 35000

Ответ: 28

Задание 16 № 311331 Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.

Ответ: 71

Ответ: 27

Ответ: 23

Ответ: 2/1

Решу ОГЭ 2022 тренировочный вариант №37812183 по математике 9 класс с ответами

Ответ: 2763

Ответ: 17142

Ответ: 6,44

Задание 4 № 368431 По периметру кукурузного поля планируется поставить забор. Найдите его длину (в метрах).

Ответ: 440

Ответ: 1600

Ответ: 0,75

Задание 12 № 311528 Площадь треугольника можно вычислить по формуле, где — сторона треугольника, — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону, если площадь треугольника равна, а высота равна 14 м.

Ответ: 4

Ответ: 35000

Ответ: 28

Задание 16 № 311331 Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.

Ответ: 71

Ответ: 27

Ответ: 23

Ответ: 2/1

На плане изображено плодоовощное хозяйство, расположенное на территории прямоугольной формы сторона каждой клетки на плане равна 20 м.

Источники:

2 Средняя линия трапеции параллельна её основаниям.

Dankonoy. com

12.03.2020 18:32:32

2020-03-12 18:32:32

Источники:

Https://dankonoy. com/gia/gia2/archives/8437

Источник

Задание 1 № 366805

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	Город Гранюк	Деревня Астрелка	Хутор Южный	Город Гусевск
Цифры

Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.

Решение.

Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.

Ответ: 1465.

2. Задание 2 № 366806

Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.

Решение.

Найдём, сколько пакетиков чая ребята потратят за две недели:

Значит, им понадобится

пачек чая.

Таким образом, ребята должны купить 14 пачек чая.

Ответ: 14.

3. Задание 3 № 366807

Найдите площадь (в км²), которую занимает заказник.

Решение.

Площадь заказника равна:

Ответ: 351.

4. Задание 4 № 366808

Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.

Решение.

Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:

км.

Ответ: 30.

5. Задание 5 № 366809

Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магизина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.

Продукция	Цена в магазине «Вело» (руб.)	Цена в магазине «ОК» (руб.)	Срок доставки из магазина «ОК» (дни)
Подсветка для спиц
Шина вида «А»
Шина вида «Б»
Спица
Педаль вида «А»
Педаль вида «Б»
Тормоз вида «А»		нет
Тормоз вида «Б»	нет
Набор крепёжных изделий

Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?

Решение.

На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:

руб.

Ответ: 5300.

6. Задание 6 № 316314

Найдите значение выражения:

Решение.

Для упрощения вычислений, вынесем общий множитель за скобки:

Ответ: 4,4.

7. Задание 7 № 317575

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из приведенных утверждений неверно?

Решение.

Заметим, что и Проверим все варианты ответа:

1) — неверно;

2) — верно;

3) — верно;

4) — верно.

Ответ указан под номером 1.

8. Задание 8 № 353586

Какое из данных ниже чисел является значением выражения

Решение.

Последовательно получим:

Ответ: 1

9. Задание 9 № 338500

При каком значении значения выражений и равны?

Решение.

Для ответа на вопрос задачи нужно решить уравнение Решим его:

Ответ: 2.

10. Задание 10 № 325450

В соревнованиях по художественной гимнастике участвуют три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.

Решение.

Всего в соревнованиях участвуют 3 + 3 + 4 = 10 гимнасток. Поэтому вероятность того, что первой будет будет выступать гимнастка из России равна

Ответ: 0,3.

11. Задание 11 № 311406

На рисунке изображён график функции . Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) функция возрастает на промежутке

4) прямая пересекает график в точках и

Решение.

Проверим каждое из утверждений.

1) Функция возрастает на промежутке — неверно, функция убывает на промежутке и затем возрастает на .

2) — неверно,

3) — верно, видно из графика.

4) Прямая пересекает график в точках и — верно, видно из графика.

Таким образом, неверные утверждения находятся под номерами 1 и 2.

Ответ: 12.

12. Задание 12 № 311543

Площадь любого выпуклого четырехугольника можно вычислять по формуле , где — длины его диагоналей, а угол между ними. Вычислите , если .

Решение.

Выразим :

Подставляя, получаем:

Ответ: 0,4.

13. Задание 13 № 338497

На каком из рисунков изображено решение неравенства

В ответе укажите номер правильного варианта.

1) 1

2) 2

3) 3

4) 4

Решение.

Решим неравенство методом интервалов:

Правильный ответ указан под номером: 4.

14. Задание 14 № 406645

В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?

Решение.

Количества мест в рядах представляют собой арифметическую прогрессию с первым членом 17.

Найдем сумму этой прогрессии:

Ответ: 377 мест.

15. Задание 15 № 340000

В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите

Решение.

Из прямоугольного треугольника по теореме Пифагора найдём

Углы и равны как углы с взаимно перпендикулярными сторонами, поэтому их синусы равны:

Ответ: 0,2.

16. Задание 16 № 351463

На окружности с центром O отмечены точки A и B так, что Длина меньшей дуги AB равна 33. Найдите длину большей дуги.

Решение.

Пусть длина большей дуги равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:

Ответ: 2343.

17. Задание 17 № 169876

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.

———-

В открытом банке иррациональный ответ.

18. Задание 18 № 350842

Найдите угол

Решение.

Искомый угол опирается на часть окружности: . Так как угол является вписанный, он равен половине дуги, на которую опирается, т.е.

Ответ: 22,5

19. Задание 19 № 401617

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Ответ: 13.

20. Задание 20 № 338505

Решите неравенство

Решение.

Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение

Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).

Таким образом, ответ

Ответ:

Примечание.

Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно,

21. Задание 21 № 353527

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Пусть взяли г 21-процентного раствора, тогда взяли и г 95-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. В первом растворе содержится г, а во втором — г Концентрация получившегося раствора равна или 58%.

Ответ: 58.

22. Задание 22 № 338288

Постройте график функции И определите, при каких значениях прямая имеет с графиком ровно одну общую точку.

Решение.

Упростим выражение:

По теореме, обратной теореме Виета, корни уравнения равны -1 и -2 соответственно, тогда по формуле , получаем: . Имеем:

График функции сводится к графику параболы с выколотой точкой

Выделим полный квадрат:

Следовательно, график функции получается из графика функции сдвигом на . (см. рис.)

Из графика видно, что прямая имеет с графиком функции ровно одну общую точку при и

Ответ: −1; 3.

23. Задание 23 № 339395

Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16.

Решение.

Угол — вписанный, он равен 90° и опирается на дугу следовательно, дуга равна 180°, значит, хорда — диаметр окружности и

Ответ: 16.

24. Задание 24 № 155

В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.

Решение.

Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM, то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, поэтому треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма этот четырехугольник — параллелограмм.

25. Задание 25 № 311926

В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .

Решение.

По свойству равнобедренной трапеции следовательно, треугольники и равны. Так как = треугольники и равнобедренные, следовательно, и — соответствующие медианы этих треугольников. Значит, Отрезок соединяет середины диагоналей трапеции, следовательно, и прямые и параллельны, поэтому, — трапеция. Проведём — высоту трапеции и — высоту трапеции . Прямоугольные треугольники и подобны, значит,