Задание 11 номер 339254 - Большой телефонный справочник предприятий

Новый октябрьский тренировочный вариант (тренировочная работа) №37812189 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.

скачать вариант

скачать ответы

Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812189:

Ответы и решения:

Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине. Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке 2).

Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр на рисунке 2) к ширине шины, то есть Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции. За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм).

Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры. Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 165/70 R13.

Задание 1 № 407953 Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин. Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 15 дюймам? Ответ дайте в миллиметрах.

Ответ: 185

Задание 2 № 407955 На сколько миллиметров радиус колеса с шиной маркировки 205/55 R14 больше, чем радиус колеса с шиной маркировки 165/65 R14?

Ответ: 5,5

Задание 3 № 408171 На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 195/50 R15?

Ответ: 14,8

Задание 4 № 408172 Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.

Ответ: 561,2

Задание 5 № 408173 На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 175/60 R14? Результат округлите до десятых.

Ответ: 0,8

Задание 10 № 132730 Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет.

Ответ: 0,85

Задание 11 № 339254 На рисунке изображены графики функций вида y = ax 2 + bx + c. Установите соответствие между знаками коэффициентов a и c и графиками функций.

Ответ: 132

Задание 14 № 406316 При проведении химической реакции в растворе образуется нерастворимый осадок. Наблюдения показали, что каждую минуту образуется 0,2 г осадка. Найдите массу осадка (в граммах) в растворе спустя семь минут после начала реакции.

Ответ: 1,4

Задание 15 № 118 В треугольнике ABC угол C прямой, BC = 8 , sin A = 0,4. Найдите AB.

Ответ: 20

Задание 19 № 341384 Какие из следующих утверждений верны? 1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. 2) Средняя линия трапеции параллельна её основаниям. 3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

Ответ: 23

Задание 21 № 338552 Первый велосипедист выехал из посёлка по шоссе со скоростью 18 км/ч. Через час после него со скоростью 16 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 4 часа после этого догнал первого.

Ответ: 24 км/ч

Задание 25 № 340107 Середина M стороны AD выпуклого четырёхугольника равноудалена от всех его вершин. Найдите AD, если BC = 10, а углы B и C четырёхугольника равны соответственно 112° и 113°.

Ответ: 10 корень из 2

Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:

Вариант Ларина №294 ОГЭ 2022 по математике 9 класс с ответами

05.10.2021 математика 9 класс варианты МА2190101-МА2190104 ОГЭ 2022 статград с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

скачать вариант

скачать ответы

Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812189:

Ответы и решения:

Ответ: 185

Ответ: 5,5

Ответ: 14,8

Задание 4 № 408172 Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.

Ответ: 561,2

Ответ: 0,8

Ответ: 0,85

Ответ: 132

Ответ: 1,4

Задание 15 № 118 В треугольнике ABC угол C прямой, BC = 8 , sin A = 0,4. Найдите AB.

Ответ: 20

Ответ: 23

Ответ: 24 км/ч

Ответ: 10 корень из 2

Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:

Вариант Ларина №294 ОГЭ 2022 по математике 9 класс с ответами

05.10.2021 математика 9 класс варианты МА2190101-МА2190104 ОГЭ 2022 статград с ответами

Вариант № 24592967

Задание 1 № 367638

Для станций, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Станции	Кировская	Летняя	Балтийская	Нарвская
Цифры

На рисунке изображена схема метро города N. Станция Кировская Синей ветки расположена между станциями Яблочная и Заводская. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Яблочная, Восточная, Летняя, Площадь победы, Морская. Красная ветка включает в себя станции Балтийская, Банковская, Морская, Восточная и Нарвская.

Решение.

Станция Кировская расположена между станциями Яблочная и Заводская, значит, Кировская отмечена цифрой 3. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Яблочная, Восточная, Летняя, Площадь победы, Морская, следовательно, Летняя отмечена цифрой 2. Красная ветка включает в себя станции Балтийская, Банковская, Морская, Восточная и Нарвская, поэтому Балтийская отмечена цифрой 5, а Нарвская отмечена цифрой 1.

Ответ: 3251.

Задание 2 № 367639

Бригада меняет рельсы на участке между станциями Восточная и Нарвская протяжённостью 16,2 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 600 метров рельсов. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?

Решение.

Заметим, что станция Нарвская отмечена на схеме цифрой 1. Поскольку бригада меняла по 600 метров рельсов в день, на замену рельс на всём участке ушло 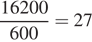дней. Поскольку работы велись только с понедельника по пятницам, на замену рельс на данном участке ушло недель, следовательно, необходимо учитывать 5 · 2 = 10 выходных дней. Значит, проезд между указанными станциями был закрыт дней.

Ответ: 37.

Задание 3 № 367640

Территория, находящаяся внутри кольцевой линии, называется Кировским городским районом. Найдите его площадь S (в км²), если длина кольцевой ветки равна 70 км. В ответе укажите значение выражения S · π.

Решение.

Сначала найдём радиус окружности:

Теперь найдём площадь:

Таким образом, получаем ответ:

Ответ: 1225.

Задание 4 № 367641

Найдите расстояние (в км) между станциями Яблочная и Кировская, если длина Синей ветки равна 48 км, расстояние от Площади победы до Кировской равно 28 км, а от Заводской до Яблочной — 27 км. Все расстояния даны по железной дороге.

Решение.

Расстояние от Кировской до Заводской равняется

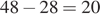км. Расстояние от Площади победы до Яблочной равняется км. Значит, расстояние между станциями Яблочная и Кировская равно км.

Ответ: 7.

Задание 5 № 367642

Школьник Артём в среднем в месяц совершает 45 поездок в метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Артём уедет из города и неиспользованные карточки обнуляются. Во сколько рублей обойдётся самый дешёвый вариант?

Количество поездок	Стоимость карточки (руб.)	Дополнительные условия
1	80	школьникам скидка 15%
10	740	школьникам скидка 10%
30	2100	школьникам скидка 10%
50	3200	нет
Не ограничено	4000	нет

Решение.

Заметим, что последние два вида карточек можно не рассматривать. Сначала Артём должен купить карточку третьего вида, поскольку

Потом Артём должен купить карточку второго вида, поскольку

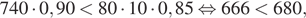
Дальше Артём должен купить пять карточек первого вида, поскольку

Таким образом, самый дешёвый вариант обойдётся в

Ответ: 2896.

Задание 6 № 341487

Найдите значение выражения

Решение.

Вычислим:

Ответ: 0,0000335.

Задание 7 № 205771

О числах и известно, что . Среди приведенных ниже неравенств выберите верные:

В ответе укажите номер правильного варианта.

4) Верно 1, 2 и 3

Решение.

Проверим все варианты ответа:

1) — неверно.

2) — неверно,

3) — верно.

Правильный ответ указан под номером 3.

Задание 8 № 317728

Масса Луны равна 7,35·10²² кг. Выразите массу Луны в млн тонн.

В ответе укажите номер правильного варианта.

1) 7,35⋅10¹⁰ млн т

2) 7,35⋅10¹³ млн т

3) 7,35⋅10¹⁶ млн т

4) 7,35⋅10¹⁹ млн т

Решение.

В одной тонне 10³ кг, 1 миллион — это 10⁶. Преобразуем представленное в условии число:

Правильный ответ указан под номером: 2.

Задание 9 № 338180

Уравнение 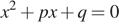имеет корни −6; 4. Найдите

Решение.

По теореме Виета

Ответ: −24.

Задание 10 № 149

На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет.

Решение.

Сергей выучил

25 − 3 = 22 вопроса. Поэтому вероятность того, что ему попадётся выученный билет равна

Ответ: 0,88.

Задание 11 № 339254

На рисунке изображены графики функций вида y = ax² + bx + c. Установите соответствие между знаками коэффициентов a и c и графиками функций.

Коэффициенты

А) a > 0, c < 0

Б) a < 0, c > 0

В) a > 0, c > 0

Графики

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Решение.

Если парабола задана уравнением , то: при то ветви параболы направлены вверх, а при — вниз. Значение c соответствует значению функции в точке x = 0. Следовательно, если график пересекает ось ординат выше оси абсцисс, то значение c положительно, если ниже оси абсцисс — отрицательно.

Таким образом, функциям соответствуют следующие графики: А — 1, Б — 3, В — 2.

Ответ: 132.

Задание 12 № 341203

Последовательность задана формулой Сколько членов в этой последовательности больше 6?

Решение.

Необходимо решить неравенство:

Поскольку n — целые числа, неравенство выполняется при n равном 1, 2, 3 и 4. Таким образом, четыре члена данной последовательности больше 6.

Ответ: 4.

Задание 13 № 338092

Найдите если

Решение.

Имеем:

Ответ: 4.

Задание 14 № 338296

Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м³), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м³.

Решение.

Выразим температуру из закона Клапейрона-Менделеева: Подставляя, получаем:

Ответ: 400.

Задание 15 № 348461

Укажите решение системы неравенств:

Решение.

Решим систему:

Решением системы является вариант 2).

Ответ: 2.

Задание 16 № 311759

Четырёхугольник ABCD вписан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.

Решение.

Углы и опираются на одну дугу следовательно, они равны. Найдём угол

Ответ: 54.

Задание 17 № 339438

Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.

Решение.

Угол, образованный хордой и касательной равен половине дуги, которую он заключает, поэтому величина дуги MK равна 2 · 83° = 166°. Угол MOK — центральный, поэтому он равен величине дуги, на которую опирается. Значит, угол MOK равен 166°. В треугольнике OMK стороны OK и OM равны как радиусы окружности, поэтому треугольник OMK — равнобедренный, следовательно, углы при основании равны. Сумма углов треугольника равна 180°, поэтому ∠OKM = ∠OMK = (180° − ∠KOM)/2 = (180° − 166°)/2 = 7°.

Ответ: 7.

Приведём другое решение.

Найдём угол OKM: OKM = 90° − 83° = 7°. Треугольник OMK — равнобедренный, поэтому угол OMK равен углу OKM и равен 7°

Задание 18 № 169887

Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.

Решение.

Площадь сектора равна:

Ответ: 3.

Задание 19 № 351332

Найдите угол . Ответ дайте в градусах.

Решение.

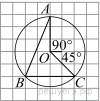
Проведем дополнительные построения. Угол — центральный и равен 135°. Угол опирается на ту же дугу, что и угол , но является вписанным, поэтому равен половине угла т.е. 67,5°.

Ответ: 67,5.

Задание 20 № 67

Укажите номера верных утверждений.

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его медианой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны» — верно по признаку подобия треугольников.

2) «Вертикальные углы равны» — верно, это теорема планиметрии.

3) «Любая биссектриса равнобедренного треугольника является его медианой» — неверно, это утверждение справедливо только для равностороннего треугольника.

Ответ: 12.

Задание 21 № 311237

Решите неравенство .

Решение.

1) Определим знак разности . Так как и , то .

2) Получаем неравенство . Отсюда .

Ответ: . Другая возможная форма ответа: .

Задание 22 № 338552

Первый велосипедист выехал из посёлка по шоссе со скоростью 18 км/ч. Через час после него со скоростью 16 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 4 часа после этого догнал первого.

Решение.

Пусть скорость третьего велосипедиста равна v км/ч, а t ч— момент времени, когда он догнал второго велосипедиста. Начало отсчёта времени — момент, когда первый велосипедист начал движение. Тогда к моменту времени t, когда третий велосипедист догонит второго, второй велосипедист проедет расстояние км, а третий — расстояние км. Аналогично: к моменту времени 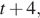когда третий велосипедист догонит первого, первый велосипедист проедет км, а третий, поскольку он был в пути на два часа меньше, проедет км. Составим систему уравнений:

Умножим первое уравнение на а второе — на и вычтем первое уравнение из второго:

По условию задачи подходит только положительный корень, то есть Подставляя t во второе уравнение, найдём искомую скорость:

Ответ: 24 км/ч.

Задание 23 № 314398

Парабола проходит через точки K(0; –5), L(3; 10), M( –3; –2). Найдите координаты её вершины.

Решение.

Одна из возможных форм записи уравнения параболы в общем виде выглядит так: Координата вершины параболы находится по формуле Координата вершины параболы найдётся подстановкой в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов и Подставив координаты точек, через которые проходит парабола, в уравнение параболы, получим систему из трёх уравнений:

Найдём координаты вершины:

Ответ: (−1; −6).

Задание 24 № 340853

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 15, AC = 25.

Решение.

Пусть DC = x. Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем:

откуда

Ответ: 16.

Задание 25 № 77

В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.

Решение.

Прямоугольные треугольники ABE и CDF равны по гипотенузе и острому углу (AB = CD как противолежащие стороны параллелограмма; ∠BAE = ∠DCF как накрест лежащие углы при параллельных прямых AB и CD и секущей AC). Следовательно, BE = DF. Кроме того, BE || DF, т. к. это перпендикуляры к одной прямой. Таким образом, в четырёхугольнике BFDE противолежащие стороны равны и параллельны, поэтому BFDE — параллелограмм.

Задание 26 № 339675

Четырёхугольник ABCD со сторонами AB = 25 и CD = 16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Для решения этой задачи необходимо знание формул тригонометрии.

Решение.

Проведём через точку 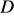прямую, параллельную диагонали Дуги и равны, следовательно, равны и стягивающие их хорды:

Вертикальные углы и равны. Углы и равны как накрест лежащие:

Четырёхугольник вписан в окружность, следовательно, суммы противолежащих углов равны 180°, откуда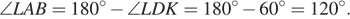

Рассмотрим треугольник По теореме косинусов:

Найдём радиус описанной вокруг треугольника окружности по теореме синусов:

Ответ:

Источник

В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями. Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.

Теория к заданию №11

Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.

На произвольном примере ознакомимся с исследованием функции:

область определения и множество значений
корни и критические точки
промежутки возрастания убывания

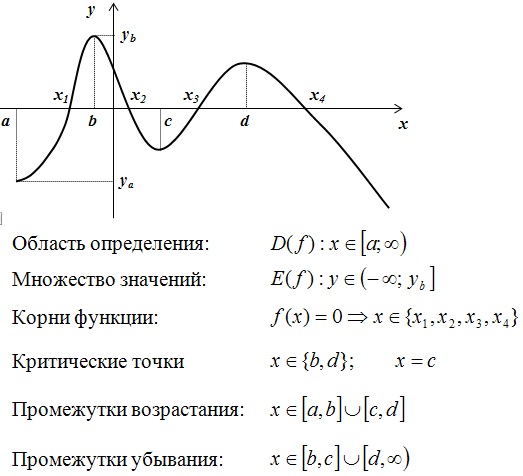
исследование функции

Теперь рассмотрим данный материал на линейной функции:

y = kx + b

где k – угловой коэффициент, b – свободный член

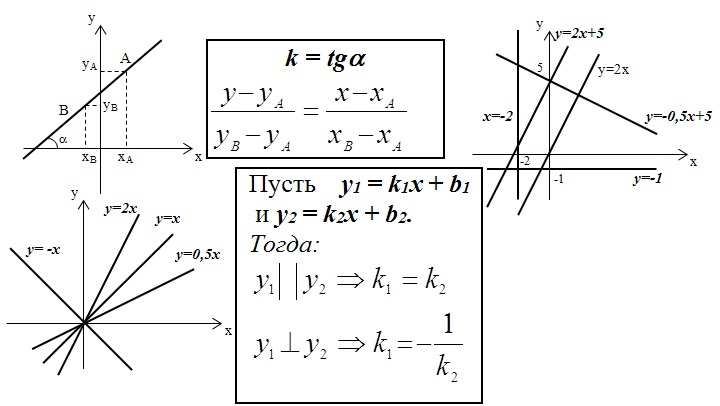
линейная функция

Рассмотрим случай квадратичной функции:

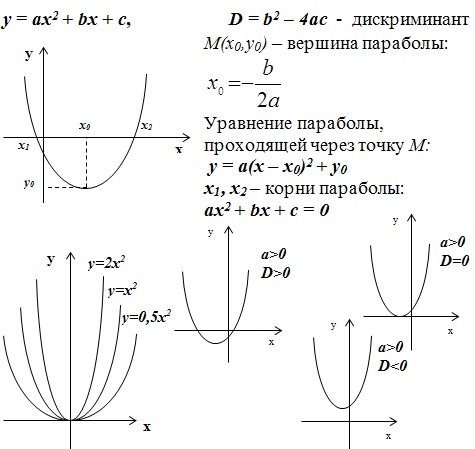
квадратичная функция

Также вспомним, что такое коренная функция и модуль:

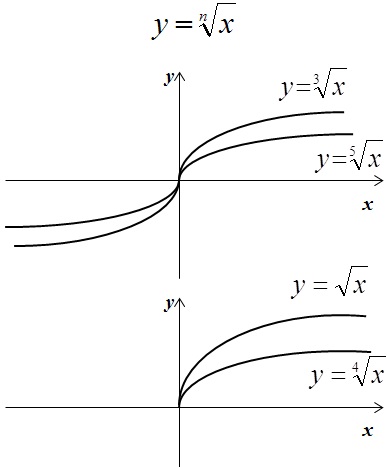
коренная функция

функция модуль

Задание OM1101o

На рисунках изображены графики функций вида

y = ax² + bx + c

Установите соответствие между знаками коэффициентов a и c и графиками функций.

Коэффициенты:

А) a > 0, c > 0

Б) a < 0, c > 0

В) a > 0, c < 0

Графики:

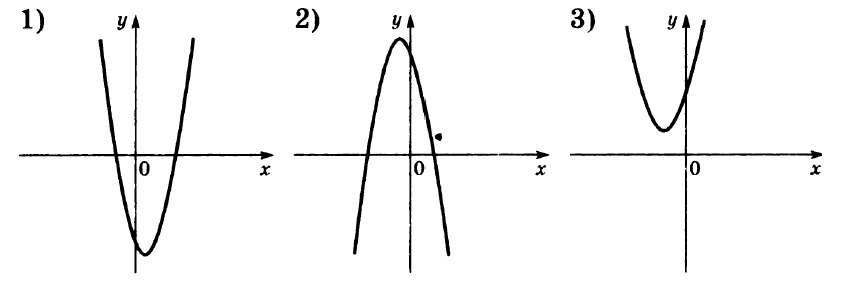
Графики функций огэ по математике 5 задание

Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида

y = ax² + bx + c

Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.

Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.

У первой и третьей ветви направлены вверх, то есть a > 0.

Далее мы смотрим, на что влияет коэффициент c.

Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:

если c > 0, то вершина параболы расположена выше оси х

если c < 0, то вершина параболы расположена ниже оси x

Так, у первой параболы c < 0, у второй и третьей c > 0.

Из всего вышеперечисленного можно найти ответ:

А) 3

Б) 2

В) 1

Ответ: 321

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1102o

Установите соответствие между функциями и их графиками.

Функции:

A) y = -3/x

Б) y = 3/x

В) y = 1/(3x)

Графики:

Графики функций огэ по математике 5 задание

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.

Общие правила:

если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях

Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.

Второе правило, которым я пользуюсь, звучит так:

чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости

и наоборот:

чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.

Ответ:

A) 2

Б) 3

В) 1

Ответ: 231

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1103o

Установите соответствие между функциями и их графиками.

Функции:

A) y = 3x

Б) y = -3x

В) y = (1/3)x

Графики:

Графики функций огэ по математике в 5 задании

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:

y = kx + b

График данной функции зависит от k и b.

если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1

Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.

Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.

Ответ:

A) 2

Б) 3

В) 1

Ответ: 231

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1104o

Установите соответствие между графиками функций и формулами, которые их задают.

5oge 1) y = x²

2) y = x/2

3) y = 2/x

Для решения данной задачи необходимо знать вид графиков функций, а именно:

y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1

x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2

y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2

Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.

Ответ:

А 1

Б 3

В 2

Ответ: 132

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1105o

Установите соответствие между функциями и их графиками.

ФУНКЦИИ

А) у=–х²–4х–3 Б) у=–х²+4х–3 В) у=х²+4х+3

Огэ по математике задание 11 номер 339254

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х² (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.

Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.

Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x₀ отрицателен, значит, А-1, а Б-2.

Ответ: 123

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание OM1106o

На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.

ГРАФИКИ:

Огэ по математике задание 11 номер 339254

КОЭФФИЦИЕНТЫ:

1) k>0, b<0 2) k>0, b>0 3) k<0, b<0

ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>90⁰) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.

У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<90⁰). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.

В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.

Ответ: 213

pазбирался: Даниил Романович | обсудить разбор | оценить

Задание 11OM21R

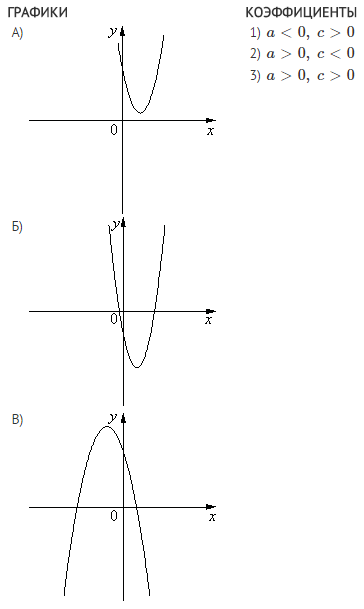
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.

КОЭФФИЦИЕНТЫ

А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0

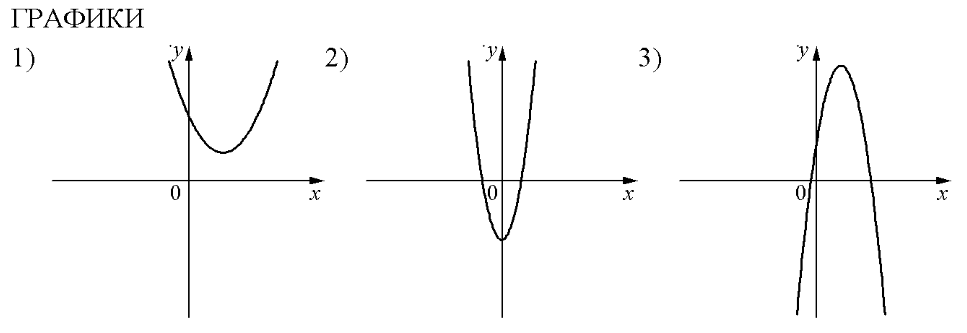
В таблице под каждой буквой укажите соответствующий номер.

Ответ:

Решение

На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).

Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.

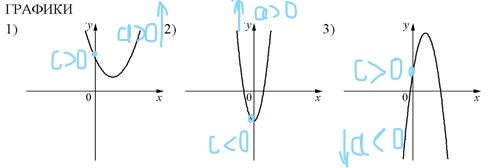
C:UsersУчительDesktopграфик 1.jpg

Теперь расставим в соответствии с указанными коэффициентами:

А) a>0, с >0 – это график №1

Б) а<0; с>0 – это график №3

В) а>0, с<0 – это график №2

Ответ: 132

pазбирался: Даниил Романович | обсудить разбор | оценить

Материалы для отработки задания №11 ОГЭ по математике.

Для выполнения задания 11 необходимо уметь строить и читать графики функций.

Карточки для отработки задания 11 с ответами

Источник: math100.ru

→ скачать

Материалы для отработки задания 11

Автор: Е. А. Ширяева

→ теория

→ задания

Практика для отработки задания 11 (презентация)

Автор: Чагина Юлия Анатольевна

→ скачать

Решение типовых задач № 11 на ОГЭ по математике

С видами заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе

Темы заданий № 10 ОГЭ по математике

Связанные страницы:

Решение заданий 1 — 5 ОГЭ по математике

Задание 9 ОГЭ по математике

Тренировочные задания по теме «Вероятность» ОГЭ Математика

Тренировочные варианты ОГЭ 2021 по математике с ответами

Задание 10 ОГЭ по математике

О категории

Работа с функциями и их графиками

Практика (9)

Установите соответствие между функциями и их графиками.

ФУНКЦИИ

А) y=-12/x
Б) y=1/12x
В) y=12/x

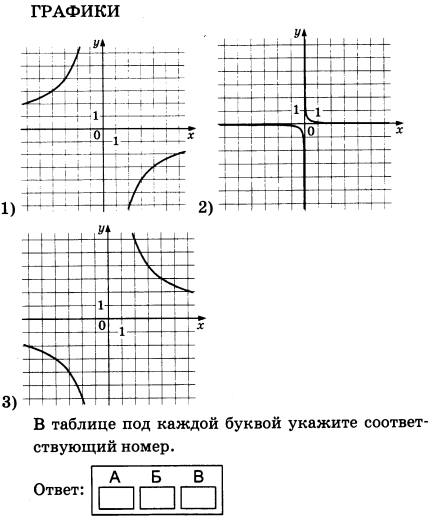
Установите соответствие между графиками функций (см. рис. 56) и формулами, которые их задают.

1) y=2x+1
2) y=5x-3
3) y=-3/x
4) y=x^2+2

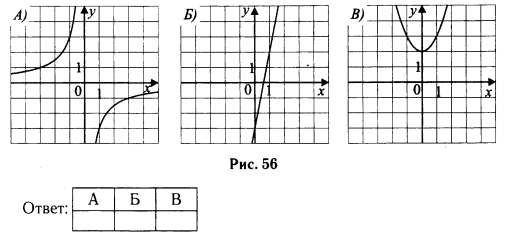
Установите соответствие между функциями и графиками (см. рис. 103).

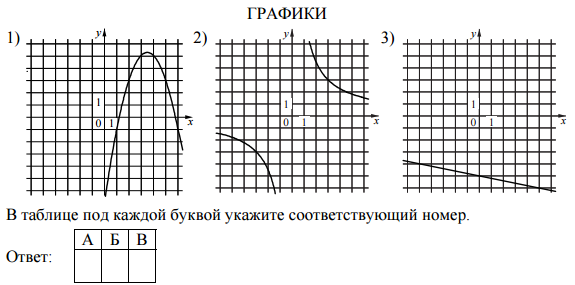
Установите соответствие между функциями и их графиками

ФУНКЦИИ

А) y=-(1/5)x-5
Б) y=-x^2+7x-7
В) y=9/x

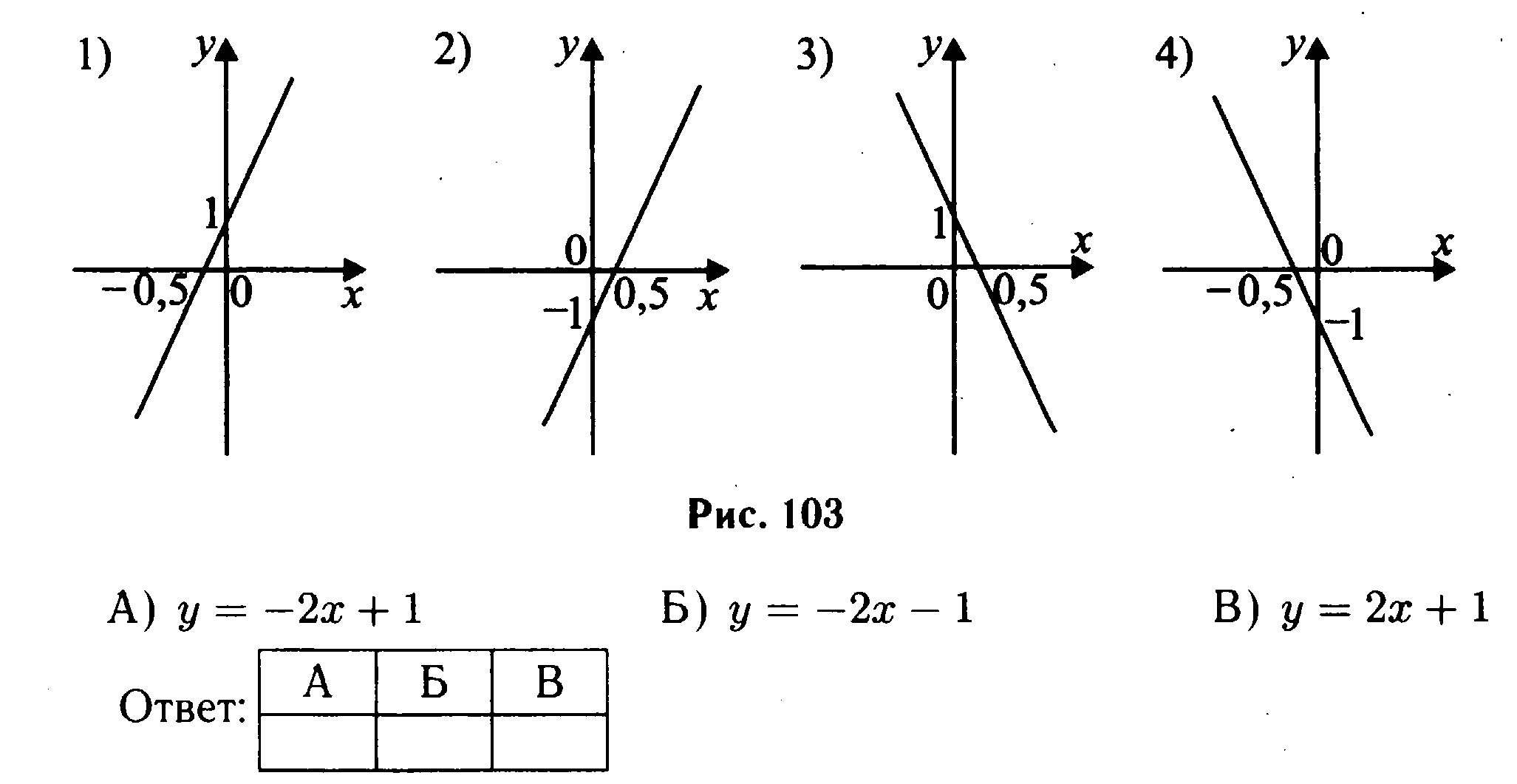
Установите соответствие между графиками функций и формулами, которые их задают.

1) y=-3x
2) y=-x/3
3) y=3-x
4) y=-3/x

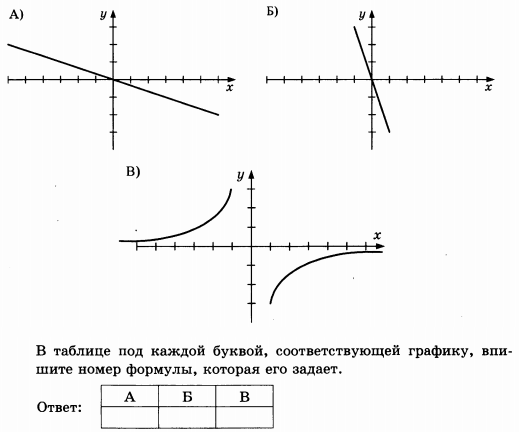
Установите соответствие между графиками функций и формулами, которые их задают.

1) у=2^x
2) y=2+x/3
3) y=1/x
4) y=-4x^2+20x-22

Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.

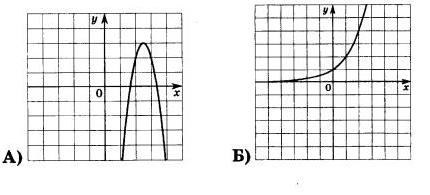
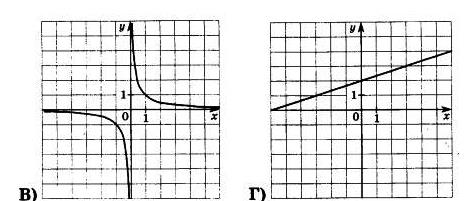
Установите соответствие между графиками функций и формулами, которые их задают.

1) у=3-2х
2) у=-3+2х
3) у=2-х
4) у=2+х

Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.

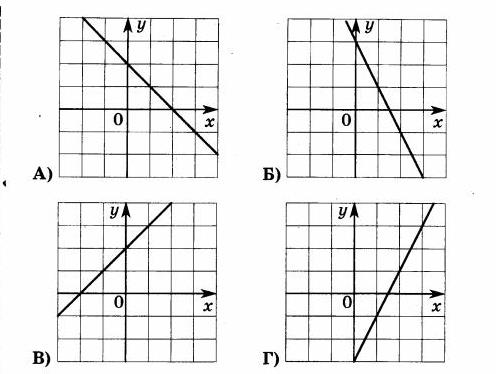
Установите соответствие между графиками функций и формулами, которые их задают.

ФОРМУЛЫ

1) x+3
2) -3x
3) 3
4) 3x

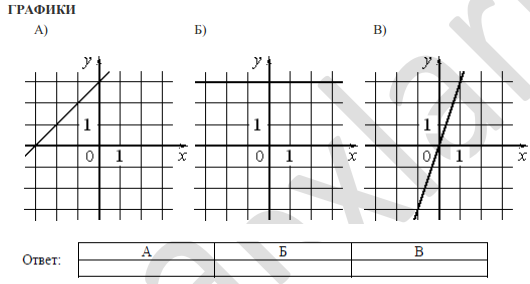
На рисунке изображены графики функций вида y=ax^2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.

Решение.

Если парабола задана уравнением y=ax в степени 2 плюс bx плюс c , то: при a больше 0, то ветви параболы направлены вверх, а при a меньше 0  — вниз. Значение c соответствует значению функции в точке x = 0. Следовательно, если график пересекает ось ординат выше оси абсцисс, то значение c положительно, если ниже оси абсцисс — отрицательно.

Таким образом, функциям соответствуют следующие графики: А — 1, Б — 3, В — 2.

Ответ: 132.

Статьи

Основное общее образование

Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)

Математика

Представляем вашему вниманию разбор 11 задания ОГЭ-2019 по математике

17 октября 2018

Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Часть 1

Задание 11

В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.

Решение

В задаче идет речь об арифметической прогрессии с первым членом a₁ = 6 и разностью d = 4. Формула общего члена

a_n = a₁ + d · (n – 1) = 6 + 4 · 14 = 62.

Ответ: 62.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену

Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.

Купить

Источник