Новый октябрьский тренировочный вариант (тренировочная работа) №37812195 решу ОГЭ 2022 года по математике 9 класс с ответами и решением для подготовки к экзамену, вариант составлен по новой демоверсии ФИПИ.
скачать вариант
скачать ответы
Решу ОГЭ 2022 по математике 9 класс тренировочный вариант №37812195:
Ответы и решения:
Каждый водитель в Российской Федерации должен быть застрахован по программе обязательного страхования гражданской ответственности (ОСАГО). Стоимость полиса получается умножением базового тарифа на несколько коэффициентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, количества предыдущих страховых выплат и других факторов. Коэффициент бонус-малус (КБМ) зависит от класса водителя.
Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год. Сначала водителю присваивается класс 3. Срок действия полиса, как правило, один год. Каждый последующий год класс водителя рассчитывается в зависимости от числа страховых выплат в течение истекшего года, в соответствии со следующей таблицей.
Задание 1 № 369819 Игорь страховал свою гражданскую ответственность три года. В течение первого года была сделана одна страховая выплата, после этого выплат не было. Какой класс будет присвоен Игорю на начало четвёртого года страхования?
Ответ: 3
Задание 2 № 369820 Чему равен КБМ на начало четвёртого года страхования?
Ответ: 1
Задание 3 № 369821 Коэффициент возраста и водительского стажа (КВС) также влияет на стоимость полиса (см. таблицу). Когда Игорь получил водительские права и впервые оформил полис, ему было 22 года. Чему равен КВС на начало 4-го года страхования?
Ответ: 1,04
Задание 4 № 369822 В начале третьего года страхования Игорь заплатил за полис 18585руб. Во сколько рублей обойдётся Игорю полис на четвёртый год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся?
Ответ: 7800
Задание 5 № 369823 Игорь въехал на участок дороги протяжённостью 2,6 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге— 100 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Игорь въехал на участок в 11:10:33, а покинул его в 11:11:51. Нарушил ли Игорь скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой?
Ответ: 20
Задание 10 № 311512 В группе из 20 российских туристов несколько человек владеют иностранными языками. Из них пятеро говорят только по-английски, трое только по-французски, двое по-французски и по английски. Какова вероятность того, что случайно выбранный турист говорит по-французски?
Ответ: 0,25
Задание 11 № 339104 На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
Ответ: 341
Задание 14 № 394312 В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах— одно штрафное очко, за каждый последующий— на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?
Ответ: 21
Задание 16 № 311510 В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B. На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB.
Ответ: 55
Задание 19 № 316286 Укажите номера верных утверждений. 1) Если угол равен 47°, то смежный с ним равен 153°. 2) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны. 3) Через любую точку проходит ровно одна прямая.
Ответ: 2
Задание 21 № 338712 Три бригады изготовили вместе 266 деталей. Известно, что вторая бригада изготовила деталей в 4 раза больше, чем первая и на 5 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.
Ответ: 92
Задание 23 № 311240 Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВС в точках К и Е соответственно. Отрезки АЕ и СК перпендикулярны. Найдите ∠КСВ, если ∠АВС = 20°.
Ответ: 35
Задание 24 № 340341 Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
Задание 25 № 339825 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
Ответ: 168
Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
1. Задание 5 № 311394. Установите соответствие между функциями и их графиками.
А) ![]()
Б) ![]()
В) ![]()
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
А
Б
В
Решение.
Определим вид графика каждой из функций:
A) ![]() уравнение параболы, ветви которой направлены вниз.
уравнение параболы, ветви которой направлены вниз.
Б) ![]() уравнение гиперболы, ветви которой лежат во II и IV четвертях.
уравнение гиперболы, ветви которой лежат во II и IV четвертях.
В) ![]() уравнение прямой, которая проходит через точки (0; −1) и (3; 0).
уравнение прямой, которая проходит через точки (0; −1) и (3; 0).
Таким образом, искомое соответствие: A — 1, Б — 4, В — 2.
Ответ: 142.
Ответ: 142
311394
142
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)
2. Задание 5 № 341040. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
Графики

Коэффициенты
1) k > 0, b < 0
2) k < 0, b < 0
3) k < 0, b > 0
4) k > 0, b > 0
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А
Б
В
Решение.
Если значение функции возрастает с увеличением x, то коэффициент k положителен, если убывает — отрицателен. Значение b соответствует значению функции в точке x = 0, следовательно, если график пересекает ось ординат выше оси абсцисс, то значение b положительно, если ниже оси абсцисс — отрицательно.
Таким образом, коэффициентам соответствуют следующие графики: А — 1, Б — 3, В — 2.
Ответ: 132.
Ответ: 132
341040
132
Источник: СтатГрад: Диагностическая работа по математике 30.09.2014 вариант МА90104.
3. Задание 5 № 193087. График какой из приведенных ниже функций изображен на рисунке?

1) ![]()
2) ![]()
3) ![]()
4) ![]()
Решение.
Ветви изображённой на рисунке параболы направленны вверх, а абсцисса вершины отрицательна. Следовательно, данному графику могут соответсвовать функции ![]() или
или ![]() Выделим полный квадрат в обоих выражениях:
Выделим полный квадрат в обоих выражениях:
![]()
![]()
Графику соответствует вариант под номером 3.
Ответ: 3
193087
3
4. Задание 5 № 311908. Установите соответствие между графиками функций и формулами, которые их задают.

1) ![]()
2) ![]()
3) ![]()
4) ![]()
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
А
Б
В
Решение.
Напомним, что если парабола задана уравнением ![]() , то: при
, то: при ![]() то ветви параболы направлены вверх, а при
то ветви параболы направлены вверх, а при ![]() — вниз; абсцисса вершины параболы вычисляется по формуле
— вниз; абсцисса вершины параболы вычисляется по формуле ![]() парабола пересекает ось Oy в точке с.
парабола пересекает ось Oy в точке с.
Уравнение ![]() задает параболу, ветви которой направлены вверх, абсцисса вершины равна
задает параболу, ветви которой направлены вверх, абсцисса вершины равна ![]() , она пересекает ось ординат в точке 3. Ее график изображен на рисунке А).
, она пересекает ось ординат в точке 3. Ее график изображен на рисунке А).
Уравнение ![]() задает параболу, ветви которой направлены вверх, абсцисса вершины равна
задает параболу, ветви которой направлены вверх, абсцисса вершины равна ![]() , она пересекает ось ординат в точке 3. Такого графика на рисунках нет.
, она пересекает ось ординат в точке 3. Такого графика на рисунках нет.
Уравнение ![]() задает параболу, ветви которой направлены вниз, абсцисса вершины равна
задает параболу, ветви которой направлены вниз, абсцисса вершины равна ![]() , она пересекает ось ординат в точке −3. Ее график изображен на рисунке Б).
, она пересекает ось ординат в точке −3. Ее график изображен на рисунке Б).
Уравнение ![]() задает параболу, ветви которой направлены вниз, абсцисса вершины равна
задает параболу, ветви которой направлены вниз, абсцисса вершины равна ![]() , она пересекает ось ординат в точке −3. Ее график изображен на рисунке В).
, она пересекает ось ординат в точке −3. Ее график изображен на рисунке В).
Тем самым, искомое соответствие: А—1, Б—3, В—4.
Ответ: 134.
Ответ: 134
311908
134
Источник: Тренировочная работа от 19 ноября 2013 Вариант МА90201
5. Задание 5 № 340887. Установите соответствие между графиками функций и формулами, которые их задают.
Формулы
1) ![]()
2) ![]()
3) ![]()
Графики

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А
Б
В
Решение.
Все представленные здесь функции — линейные. Общая формула для уравнения линейной функции: ![]() , если
, если ![]() функция возрастает, если
функция возрастает, если ![]() — убывает. Значению
— убывает. Значению ![]() соответсвует значение функции в точке
соответсвует значение функции в точке ![]()
Уравнение ![]() задаёт убывающую функцию, пересекающую ось ординат в точке 0.
задаёт убывающую функцию, пересекающую ось ординат в точке 0.
Уравнение ![]() задаёт функцию, не пересекающую ось ординат.
задаёт функцию, не пересекающую ось ординат.
Уравнение ![]() задаёт возрастающую функцию, пересекающую ось ординат в точке 1.
задаёт возрастающую функцию, пересекающую ось ординат в точке 1.
Таким образом, установим соответсвие: А — 3, Б — 1, В — 2.
Ответ: 312.
Ответ: 312
340887
312
Источник: Тренировочная работа № 26 ноября 2014 года. Вариант МА90203
6. Задание 5 № 193093. На одном из рисунков изображен график функции ![]() . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
1)

2)

3)

4)

Решение.
Коэффициент ![]() , поэтому ветви параболы направлены вверх. Абсцисса вершины параболы равна:
, поэтому ветви параболы направлены вверх. Абсцисса вершины параболы равна: ![]()
Правильный вариант ответа указан под номером 1.
Ответ: 1
193093
1
7. Задание 5 № 316342. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)![]()
Б)![]()
В)![]()
ГРАФИКИ

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А
Б
В
Решение.
Все представленные здесь функции — гиперболы. Общая формула для уравнения гиперболы: ![]() , если
, если ![]() , то ветви гиперболы располагаются в первой и третьей четвертях, в противном случае — во второй и четвёртой четвертях.
, то ветви гиперболы располагаются в первой и третьей четвертях, в противном случае — во второй и четвёртой четвертях.
Для того, чтобы отличить гиперболы лежащие в одинаковых четвертях нужно подставить какое-нибудь значение ![]() в формулу и проверить, какому графику будет соответствовать полученное значение.
в формулу и проверить, какому графику будет соответствовать полученное значение.
Таким образом, установим соответсвие: А — 1, Б — 4, В — 2.
Ответ: 142
316342
142
Источник: Тренировочная работа 19.02.2014 Вариант МА90501
8. Задание 5 № 193092. Найдите значение ![]() по графику функции
по графику функции ![]() , изображенному на рисунке.
, изображенному на рисунке.

1) ![]()
2) ![]()
3) ![]()
4) ![]()
Решение.
Гипербола проходит через точку (−2;1), поэтому: ![]() Правильный ответ указан под номером 4.
Правильный ответ указан под номером 4.
Ответ: 4.
Ответ: 4
193092
4
9. Задание 5 № 339104. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
Графики

Коэффициенты
1) k < 0, b < 0
2) k < 0, b>0
3) k > 0, b>0
4) k > 0, b<0
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А
Б
В
Решение.
Если значение функции возрастает с увеличением x, то коэффициент k положителен, если убывает — отрицателен. Значение b соответствует значению функции в точке x = 0. Следовательно, если график пересекает ось ординат выше оси абсцисс, то значение b положительно, если ниже оси абсцисс — отрицательно. Таким образом, графикам соответствуют следующие коэффициенты: А — 3, Б — 4, В —1.
Ответ: 341.
Ответ: 341
339104
341
10. Задание 5 № 200515. На одном из рисунков изображен график функции ![]() . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
1)

2)

3)

4)

Решение.
График функции ![]() — парабола. Определим тип каждого графика функции.
— парабола. Определим тип каждого графика функции.
1) На первом рисунке изображена линейная функция.
2) На втором рисунке изображена логарифмическая функция.
3) На третьем рисунке изображена парабола.
4) На четвёртом рисунке изображена гипербола.
Ответ: 3.
Ответ: 3
200515
3
11. Задание 5 № 193094. На одном из рисунков изображен график функции ![]() Укажите номер этого рисунка.
Укажите номер этого рисунка.
1)

2)

3)

4)

Решение.
График функции ![]() проходит через точку (−1; 2). Этому условию удовлетворяет только график, изображённый на рисунке 4.
проходит через точку (−1; 2). Этому условию удовлетворяет только график, изображённый на рисунке 4.
Правильный ответ указан под номером 4.
Ответ: 4
193094
4
12. Задание 5 № 193100. Найдите значение ![]() по графику функции
по графику функции ![]() изображенному на рисунке.
изображенному на рисунке.

Решение.
Парабола пересекает ось ординат в точке с ординатой 1, поэтому ![]() Тем самым, уравнение параболы принимает вид
Тем самым, уравнение параболы принимает вид ![]() Парабола проходит через точки (1; 3) и (−1; 1). Отсюда имеем:
Парабола проходит через точки (1; 3) и (−1; 1). Отсюда имеем:
![]()
Ответ: ![]()
Ответ: 1
193100
1
13. Задание 5 № 193091. Найдите значение ![]() по графику функции
по графику функции ![]() изображенному на рисунке.
изображенному на рисунке.

1) ![]()
2) ![]()
3) ![]()
4) ![]()
Решение.
Значение ![]() — это значение графика при ордината графика при
— это значение графика при ордината графика при ![]() Значит,
Значит, ![]()
Ответ: 4.
Ответ: 4
193091
4
14. Задание 5 № 321867. На рисунке изображены графики функций вида y = ax2 + c. Установите соответствие между графиками и знаками коэффициентов a и c.
ГРАФИКИ
А) 
Б) 
В) 
Г) 
ЗНАКИ КОЭФФИЦИЕНТОВ
1) a > 0, c < 0
2) a < 0, c > 0
3) a > 0, c > 0
4) a < 0, c < 0
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А
Б
В
Г
Решение.
График функции ![]() — парабола. Ветви этой параболы направлены вверх, если
— парабола. Ветви этой параболы направлены вверх, если ![]() и вниз, если
и вниз, если ![]() Значение
Значение ![]() определяет ординату вершины параболы. Если
определяет ординату вершины параболы. Если ![]() то вершина параболы находится над осью абсцисс, а если меньше нуля, то ниже. Таким образом, получаем, ответ: A — 4, Б — 1, В — 2, Г — 3.
то вершина параболы находится над осью абсцисс, а если меньше нуля, то ниже. Таким образом, получаем, ответ: A — 4, Б — 1, В — 2, Г — 3.
Ответ: 4123.
Ответ: 4123
321867
4123
15. Задание 5 № 193090. Найдите значение ![]() по графику функции
по графику функции ![]() , изображенному на рисунке.
, изображенному на рисунке.

1) ![]()
2) ![]()
3) ![]()
4) ![]()
Решение.
Абсцисса вершины параболы равна −1, поэтому ![]() откуда
откуда ![]() Парабола пересекает ось ординат в точке с ординатой 3, поэтому
Парабола пересекает ось ординат в точке с ординатой 3, поэтому ![]() Тем самым, уравнение параболы принимает вид
Тем самым, уравнение параболы принимает вид ![]() Поскольку парабола проходит через точку (−1; 2), имеем:
Поскольку парабола проходит через точку (−1; 2), имеем:
![]()
Таким образом,
![]()
Верный ответ указан под номером 3.
Ответ: 3.
Ответ: 3
193090
3
16. Задание 5 № 340861. Установите соответствие между графиками функций и формулами, которые их задают.
Формулы
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Графики

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А
Б
В
Решение.
Все представленные здесь функции — линейные. Общая формула для уравнения линейной функции: ![]() , если
, если ![]() функция возрастает, если
функция возрастает, если ![]() — убывает. Значению
— убывает. Значению ![]() соответсвует значение функции в точке
соответсвует значение функции в точке ![]()
Уравнение ![]() задаёт функцию, не пересекающую ось абсцисс.
задаёт функцию, не пересекающую ось абсцисс.
Уравнение ![]() задаёт возрастающую функцию, пересекающую ось ординат в точке −3.
задаёт возрастающую функцию, пересекающую ось ординат в точке −3.
Уравнение ![]() задаёт убывающую функцию, пересекающую ось ординат в точке 0.
задаёт убывающую функцию, пересекающую ось ординат в точке 0.
Уравнение ![]() задаёт возрастающую функцию, пересекающую ось ординат в точке 0.
задаёт возрастающую функцию, пересекающую ось ординат в точке 0.
Таким образом, установим соответсвие: А — 3, Б — 2, В — 1.
Ответ: 321.
Ответ: 321
340861
321
Источник: Тренировочная работа № 26 ноября 2014 года. Вариант МА90202
17. Задание 5 № 311316. Укажите соответствие между графиками функций и формулами, которые их задают.

1) ![]()
2) ![]()
3) ![]()
4) ![]()
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
А
Б
В
Решение.
Определим вид графика каждой из функций:
1) ![]() уравнение параболы, ветви которой направлены вверх. Вершина параболы лежит в точке (−1; 2).
уравнение параболы, ветви которой направлены вверх. Вершина параболы лежит в точке (−1; 2).
2) ![]() уравнение прямой, которая проходит через точки (0,5; 0) и (0; 1).
уравнение прямой, которая проходит через точки (0,5; 0) и (0; 1).
3) ![]() уравнение степенной функции с положительным дробным показателем. В точке −1 значение функции равно 0.
уравнение степенной функции с положительным дробным показателем. В точке −1 значение функции равно 0.
4) ![]() уравнение степенной функции с положительным дробным показателем. В точке 1 значение функции равно 0.
уравнение степенной функции с положительным дробным показателем. В точке 1 значение функции равно 0.
Таким образом, искомое соответствие: A — 3, Б — 2, В — 1.
Ответ: 321.
Ответ: 321
311316
321
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 1)
18. Задание 5 № 314718. На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.

1) f( −2) = f(2)
2) f(x)>0 при x<−4 и при x>2
3) Наименьшее значение функции равно −9
Решение.
Проверим каждое утверждение.
1) Значенияе фунцкии в точке −2 меньше значения функции в точке 2. Первое утверждение неверно.
2)f(x)>0 при x<−4 и при x>2. Второе утверждение верно.
2) Наименьшее значение функции равно −9. Третье утверждение верно.
Ответ: 1.
Ответ: 1
314718
1
Источник: Банк заданий ФИПИ
19. Задание 5 № 321919. Установите соответствие между графиками функций и формулами, которые их задают.
А)

Б)

В)

1) ![]()
2) ![]()
3) ![]()
4) ![]()
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
А
Б
В
Решение.
Выделим во всех выражениях полный квадрат:
1) ![]() Ветви параболы направлены вниз, вершина параболы находится в точке
Ветви параболы направлены вниз, вершина параболы находится в точке ![]() Такого графика среди имеющихся — нет.
Такого графика среди имеющихся — нет.
2) ![]() Ветви параболы направлены вниз, вершина параболы находится в точке
Ветви параболы направлены вниз, вершина параболы находится в точке ![]() Такой график изображён на рисунке В).
Такой график изображён на рисунке В).
3) ![]() Ветви параболы направлены вверх, вершина параболы находится в точке
Ветви параболы направлены вверх, вершина параболы находится в точке ![]() Такой график изображён на рисунке Б).
Такой график изображён на рисунке Б).
4) ![]() Ветви параболы направлены вниз, вершина параболы находится в точке
Ветви параболы направлены вниз, вершина параболы находится в точке ![]() Такой график изображён на рисунке А).
Такой график изображён на рисунке А).
Ответ: 432.
Ответ: 432
321919
432
20. Задание 5 № 339254. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты
А) a > 0, c < 0
Б) a < 0, c > 0
В) a > 0, c > 0
Графики

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А
Б
В
othaw436
Вопрос по русскому языку:
Помогите номер 114 задание 4

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
gitrnc50
Утренняя (какая?) морозная(какая?) тишь(что?) Кристальный(Какой?) иней(Что?)Блестит(что делает?)Бело-синими(Какими?) и розовыми(Какаими?)Искорками(Чем?)
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Русский язык.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Русский язык — один из восточнославянских языков, национальный язык русского народа.
В таблице 12
необходимо определить недостающие
суммы в атрибутах бухгалтерского счета.
Таблица 12 -Атрибуты
бухгалтерских счетов
| Счет | Остаток на периода | Оборот по дебету | Оборот по кредиту | Остаток на конец периода | ||
| Дебет | Кредит | Дебет | Кредит | |||
| 01 | 15000 | 1000 | 18000 | |||
| 02 | 5000 | 2500 | 1000 | |||
| 10 | 25000 | 13000 | 35000 | |||
| 50 | 1800 | 1200 | 1000 | |||
| 60 | 4000 | 8000 | 12000 | |||
| 66 | 25000 | 10000 | 15000 | |||
| 80 | 45000 | 15000 | ||||
| 20 | 14569 | 14569 | ||||
| 43 | 2700 | 1600 |
Задание № 12
На основании
данных таблицы 13 составьте бухгалтерский
баланс по форме нетто за январь 201__
г.(табл.14), откройте синтетические счета
по Т-форме: укажите название счета,
кодировку и зафиксируйте начальные
остатки.
Таблица 13 — Остатки
на счетах бухгалтерского учета
организации
на январь 201__ г.
| Наименование и | Сумма, тыс. руб. |
| 1. Основные | 11000 |
| 2. Амортизация | 7000 |
| 3. Материалы (10) | 2000 |
| 4. Основное | 4500 |
| 5. Готовая | 920 |
| 6.Касса (50) | 7 |
| 7.Расчетные счета | 3150 |
| 8. Финансовые | 700 |
| 9. Расчеты с | 1000 |
| 10. Расчеты с | 2000 |
| 11. Расчеты по | 400 |
| Продолжение | |
| 12. Расчеты по | 80 |
| 13. Расчеты по | 30 |
| 14. Расчеты с | 90 |
| 15.Уставный | 9000 |
| 16. Добавочный | 6400 |
| 17. Нераспределённая | +277 |
Таблица 14 —
Бухгалтерский баланс организации на
января 201__ .,тыс.руб.
| Актив | На 1 января | На 1 февраля | Пассив | На 1 января | На 1 февраля |
| I. Внеоборотные | III. Капитал | ||||
| Итого по разделу | |||||
| Итого по разделу | IV. Долгосрочные | ||||
| II. Оборотные | |||||
| Итого по разделу | |||||
| V. Краткосрочные | |||||
| Продолжение | |||||
| Итого по разделу | Итого по разделу | ||||
| Баланс | 17277 | Баланс |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Составить предложения из слов: из, страны, весна, грачи, к, чижи, мы, жаворонки, теплые, прилетают.
6·2 ответа
Тут в основном свойство вертикальных углов и развёрнутый угол


Сегодня 23.01.2022 14:37 свежие новости час назад
Прогноз на сегодня : Огэ по математике задание 11 номер 339104 . Развитие событий.
Актуально сегодня (23.01.2022 14:37): Огэ по математике задание 11 номер 339104
..
1. Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
9041462618282665b80f0416d63c2cfc 96cdab8ddd13b768961ff51daebf848f
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
Огэ по математике задание 11 номер 339104
грохот гис 52 инструкция по применению | спектрум линк инструкция | проект 2 класс на тему о чем может рассказать школьная библиотека | изложение 3 класс сыроежка презентация | tdr 200 firmware | как изменить язык толькл для одного приложения iphome | как подключить видеорегистратор к плафону освещения форд фокус 2 | круз андрей после скачать не бесплатно fb2 | интересные педагогические ситуации и их решение | samsung sgh duos firmware |
Invision Community © 2022 IPS, Inc.
Карта сайт Rss
s
p
Связанных вопросов не найдено
Правильные решения и ответы на любые задания для школьника или студента быстро онлайн. А если не нашли нужное решение или ответ, то задайте свой вопрос нашим специалистам.
В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями. Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.
Теория к заданию №11
Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.
На произвольном примере ознакомимся с исследованием функции:
- область определения и множество значений
- корни и критические точки
- промежутки возрастания убывания
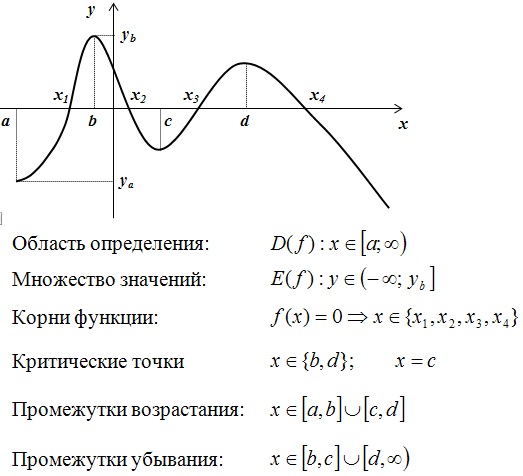
Теперь рассмотрим данный материал на линейной функции:
y = kx + b
где k – угловой коэффициент, b – свободный член
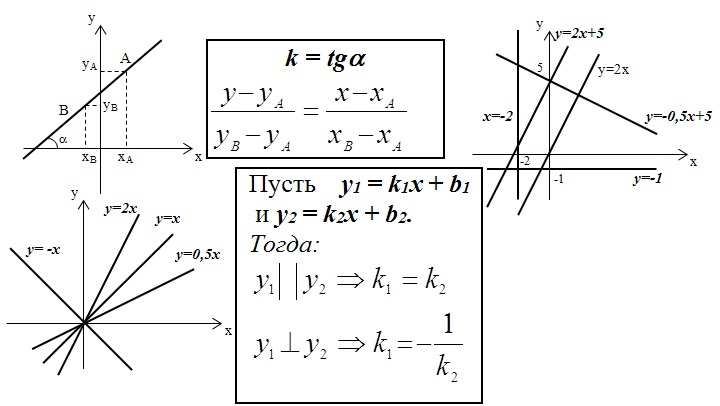
Рассмотрим случай квадратичной функции:
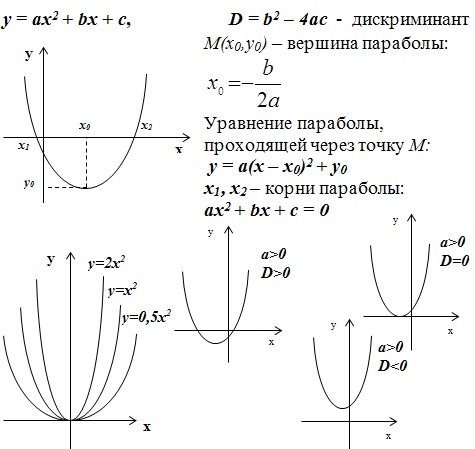
Также вспомним, что такое коренная функция и модуль:
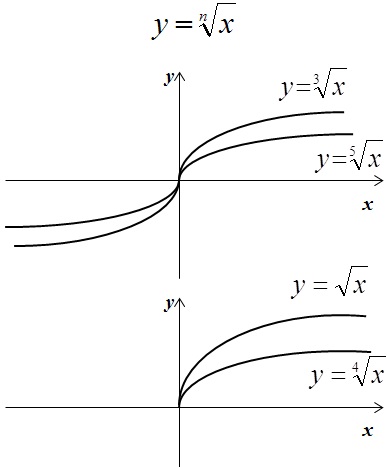

На рисунках изображены графики функций вида
y = ax² + bx + c
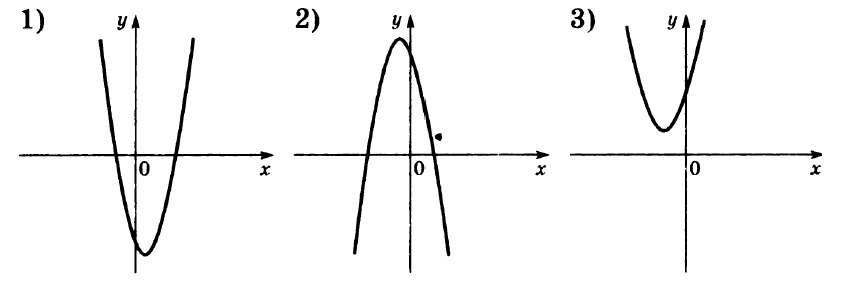
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функции:
A) y = -3/x
Б) y = 3/x
В) y = 1/(3x)
Графики:

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Общие правила:
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
и наоборот:
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между графиками функций и формулами, которые их задают.
 1) y = x²
1) y = x²
2) y = x/2
3) y = 2/x
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.
Ответ:
А 1
Б 3
В 2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:

КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: 213
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
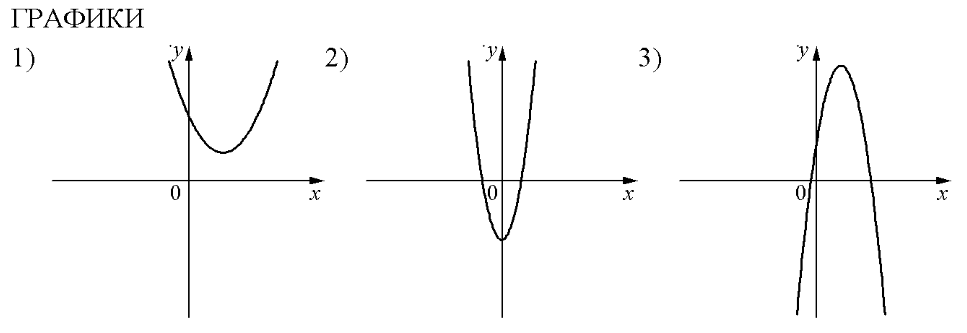
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
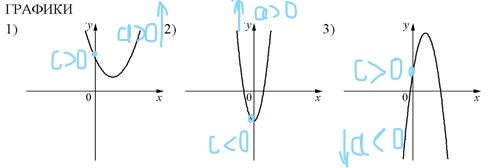
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор | оценить
Материалы для отработки задания №11 ОГЭ по математике.
Для выполнения задания 11 необходимо уметь строить и читать графики функций.
| Карточки для отработки задания 11 с ответами Источник: math100.ru → скачать |
| Материалы для отработки задания 11 Автор: Е. А. Ширяева → теория → задания |
| Практика для отработки задания 11 (презентация) Автор: Чагина Юлия Анатольевна → скачать |
Решение типовых задач № 11 на ОГЭ по математике
С видами заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе
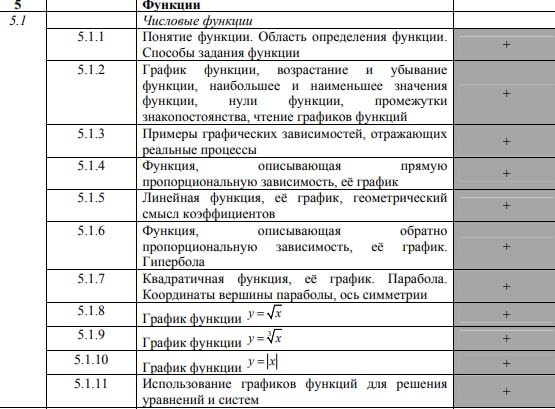
Связанные страницы:
Решение заданий 1 — 5 ОГЭ по математике
Задание 9 ОГЭ по математике
Тренировочные задания по теме «Вероятность» ОГЭ Математика
Тренировочные варианты ОГЭ 2021 по математике с ответами
Задание 10 ОГЭ по математике
Решение заданий Варианта №11 из сборника ОГЭ 2022 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
![]()
Задание 1-5.
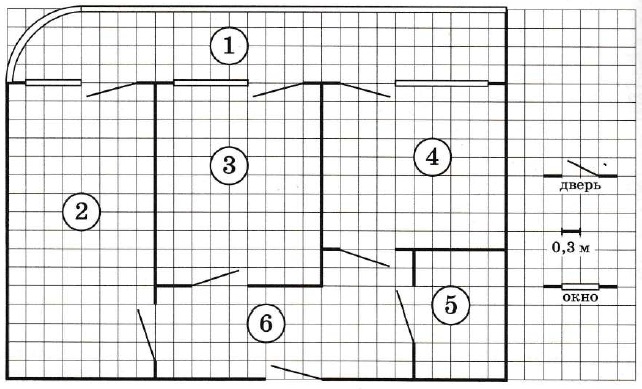 На рисунке изображён план двухкомнатной квартиры с панорамной лоджией в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна (и остекления лоджии), а также указано, что длина стороны клетки на плане соответствует 0,3 м. Вход в квартиру находится в прихожей. Самое большое по площади помещение – гостиная. В спальне, гостиной и кухне есть двери и окна, выходящие на лоджию, но в кухне окно шире, чем в других комнатах. Остекление лоджии со стороны гостиной закруглено. В квартире есть два помещения, в которых нет окон, – это прихожая и санузел.
На рисунке изображён план двухкомнатной квартиры с панорамной лоджией в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна (и остекления лоджии), а также указано, что длина стороны клетки на плане соответствует 0,3 м. Вход в квартиру находится в прихожей. Самое большое по площади помещение – гостиная. В спальне, гостиной и кухне есть двери и окна, выходящие на лоджию, но в кухне окно шире, чем в других комнатах. Остекление лоджии со стороны гостиной закруглено. В квартире есть два помещения, в которых нет окон, – это прихожая и санузел.
Задание 6.
Найдите значение выражения frac{9}{16}:(-frac{3}{40})+4,7.
Задание 7.
Одно из чисел √28, √33, √38, √47 отмечено на прямой А.

Какое это число?
1)√28 2)√33 3)√38 4)√47
Задание 8.
Найдите значение выражения frac{(a^{4})^{-3}}{a^{-15}} при а = 2.
Задание 9.
Найдите корень уравнения (х + 10)2 = (5 – х)2.
Задание 10.
В магазине канцтоваров продаётся 200 ручек: 31 красная, 25 зеленых, 38 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или черной.
Задание 11.
Установите соответствие между формулами, которыми заданы функции, и графиками этих функций.
ФОРМУЛЫ
А) у = –4х2 – 28х – 46
Б) у = 4х2 – 28х + 46
С) у = –4х2 + 28х – 46
ГРАФИКИ
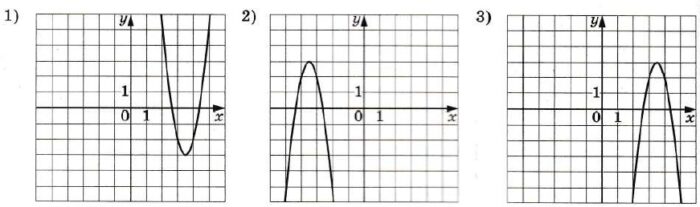
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле a = ω2R, где ω – угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 9 с-1, а центростремительное ускорение равно 243 м/с2. Ответ дайте в метрах.
Задание 13.
Укажите решение неравенства (х + 2)(х – 7) > 0

Задание 14.
В течение 20 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 9-й день акция стоила 888 рублей, а в 13-й день – 940 рублей?
![]()
Задание 15.
Сторона треугольника равна 29, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника.
Задание 16.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 38º, угол CAD равен 33º. Найдите угол ABD. Ответ дайте в градусах.
Задание 17.
Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Задание 18.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Задание 19.
Какие из следующих утверждений верны?
1) Основания любой трапеции параллельны.
2) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
3) Все углы ромба равны.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ЧАСТЬ 2
![]()
Задание 20.
Решите уравнение x6 = –(12 – 8x)3.
Задание 21.
Два велосипедиста одновременно отправились в 208-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым.
Задание 22.
Постройте график функции у = х2 – 4|х| – х и определите, при каких значениях m прямая у = m имеет с графиком не менее одной, но не более трёх общих точек.
![]()
Задание 23.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 6:13:17. Найдите радиус окружности, если меньшая из сторон равна 18.
Задание 24.
Основания ВС и АD трапеции АВСВ равны соответственно 5 и 45, BD = 15. Докажите, что треугольники СВD и ВDА подобны.
Задание 25.
Биссектрисы углов А и В параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если ВС = 6, а расстояние от точки K до стороны АВ равно 6.
Источник варианта: Сборник ОГЭ 2022 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Решение.
Если значение функции возрастает с увеличением x, то коэффициент k положителен, если убывает — отрицателен. Значение b соответствует значению функции в точке x = 0. Следовательно, если график пересекает ось ординат выше оси абсцисс, то значение b положительно, если ниже оси абсцисс — отрицательно. Таким образом, графикам соответствуют следующие коэффициенты: А — 3, Б — 4, В —1.
Ответ: 341.
Статьи
Основное общее образование
Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)
Математика
Представляем вашему вниманию разбор 11 задания ОГЭ-2019 по математике
17 октября 2018
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 11
В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.
Решение
В задаче идет речь об арифметической прогрессии с первым членом a1 = 6 и разностью d = 4. Формула общего члена
an = a1 + d · (n – 1) = 6 + 4 · 14 = 62.
Ответ: 62.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить



