{
Шестнадцатеричная система — 52c93.
Двоичная система — 1010010110010010011.
Посмотрите так же как пишутся десятичные цифры 29, 2, 45, 495, 885, 536, 918, 752, 1048, 6492, 8669, 42575, 30308, 837479, 523612 в различных системах счисления.
Число 339091 в других системах счисления:
2 — 1010010110010010011, 3 — 122020010221, 4 — 1102302103, 5 — 41322331, 6 — 11133511, 7 — 2611414, 8 — 1226223, 9 — 566127, 10 — 339091, 11 — 211845, 12 — 144297, 13 — bb45c, 14 — 8b80b, 15 — 6a711, 16 — 52c93, 17 — 41059, 18 — 342a7, 19 — 2b85h, 20 — 227eb, 21 — 1fcj4, 22 — 19id5, 23 — 14k02, 24 — 10cgj, 25 — lhdg, 26 — j7fp, 27 — h63p, 28 — fceb, 29 — dq5n, 30 — cgn1, 31 — bbqd, 32 — ab4j.
На русском языке:
Триста тридцать девять тысяч девяносто один рубль одиннадцать копеек
На английском языке:
three hundred and thirty-nine thousand and ninety-one ruble and eleven kopeck
Начислить НДС на сумму 339091.11:
Сумма НДС 18% (Россия) = 61036.40 прописью:
На русском языке: шестьдесят одна тысяча тридцать шесть рублей сорок копеек
На английском языке: sixty-one thousand and thirty-six rubles and forty kopecks
Сумма 339091.11 с НДС 18% (Россия) = 400127.51 прописью:
На русском языке: четыреста тысяч сто двадцать семь рублей пятьдесят одна копейка
На английском языке: four hundred thousand, one hundred and twenty-seven rubles and fifty-one kopecks
Сумма НДС 10% (Россия) = 33909.11 прописью:
На русском языке: тридцать три тысячи девятьсот девять рублей одиннадцать копеек
На английском языке: thirty-three thousand, nine hundred and nine rubles and eleven kopecks
Сумма 339091.11 с НДС 10% (Россия) = 373000.22 прописью:
На русском языке: триста семьдесят три тысячи рублей двадцать две копейки
На английском языке: three hundred and seventy-three thousand rubles and twenty-two kopecks
Сумма НДС 12% (Казахстан) = 40690.93 прописью:
На русском языке: сорок тысяч шестьсот девяносто рублей девяносто три копейки
На английском языке: forty thousand, six hundred and ninety rubles and ninety-three kopecks
Сумма 339091.11 с НДС 12% (Казахстан) = 379782.04 прописью:
На русском языке: триста семьдесят девять тысяч семьсот восемьдесят два рубля четыре копейки
На английском языке: three hundred and seventy-nine thousand, seven hundred and eighty-two rubles and zero kopecks
Сумма НДС 20% (Украина) = 67818.22 прописью:
На русском языке: шестьдесят семь тысяч восемьсот восемнадцать рублей двадцать две копейки
На английском языке: sixty-seven thousand, eight hundred and eighteen rubles and twenty-two kopecks
Сумма 339091.11 с НДС 20% (Украина) = 406909.33 прописью:
На русском языке: четыреста шесть тысяч девятьсот девять рублей тридцать три копейки
На английском языке: four hundred and six thousand, nine hundred and nine rubles and thirty-three kopecks
Выделить НДС из суммы 339091.11:
Сумма НДС 18% (Россия) = 51725.76 прописью:
На русском языке: пятьдесят одна тысяча семьсот двадцать пять рублей семьдесят шесть копеек
На английском языке: fifty-one thousand, seven hundred and twenty-five rubles and seventy-six kopecks
Сумма 339091.11 без НДС 18% (Россия) = 287365.35 прописью:
На русском языке: двести восемьдесят семь тысяч триста шестьдесят пять рублей тридцать пять копеек
На английском языке: two hundred and eighty-seven thousand, three hundred and sixty-five rubles and thirty-five kopecks
Сумма НДС 10% (Россия) = 30826.46 прописью:
На русском языке: тридцать тысяч восемьсот двадцать шесть рублей сорок шесть копеек
На английском языке: thirty thousand, eight hundred and twenty-six rubles and forty-six kopecks
Сумма 339091.11 без НДС 10% (Россия) = 308264.65 прописью:
На русском языке: триста восемь тысяч двести шестьдесят четыре рубля шестьдесят пять копеек
На английском языке: three hundred and eight thousand, two hundred and sixty-four rubles and sixty-five kopecks
Сумма НДС 12% (Казахстан) = 36331.19 прописью:
На русском языке: тридцать шесть тысяч триста тридцать один рубль девятнадцать копеек
На английском языке: thirty-six thousand, three hundred and thirty-one ruble and nineteen kopeck
Сумма 339091.11 без НДС 12% (Казахстан) = 302759.92 прописью:
На русском языке: триста две тысячи семьсот пятьдесят девять рублей девяносто две копейки
На английском языке: three hundred and two thousand, seven hundred and fifty-nine rubles and ninety-two kopecks
Сумма НДС 20% (Украина) = 56515.19 прописью:
На русском языке: пятьдесят шесть тысяч пятьсот пятнадцать рублей девятнадцать копеек
На английском языке: fifty-six thousand, five hundred and fifteen rubles and nineteen kopecks
Сумма 339091.11 без НДС 20% (Украина) = 282575.92 прописью:
На русском языке: двести восемьдесят две тысячи пятьсот семьдесят пять рублей девяносто две копейки
На английском языке: two hundred and eighty-two thousand, five hundred and seventy-five rubles and ninety-two kopecks
| Авто | Видео-блоги | ДТП, аварии | Для маленьких | Еда, напитки |
|---|---|---|---|---|
| Животные | Закон и право | Знаменитости | Игры | Искусство |
| Комедии | Красота, мода | Кулинария, рецепты | Люди | Мото |
| Музыка | Мультфильмы | Наука, технологии | Новости | Образование |
| Политика | Праздники | Приколы | Природа | Происшествия |
| Путешествия | Развлечения | Ржач | Семья | Сериалы |
| Спорт | Стиль жизни | ТВ передачи | Танцы | Технологии |
| Товары | Ужасы | Фильмы | Шоу-бизнес | Юмор |
Видео ОГЭ по математике. Задание 9 номер 311381 канала ОГЭ «Ze-Smith» ABC
Показать
Статьи
Основное общее образование
Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)
Математика
Представляем вашему вниманию разбор 11 задания ОГЭ-2019 по математике
17 октября 2018
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 11
В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.
Решение
В задаче идет речь об арифметической прогрессии с первым членом a1 = 6 и разностью d = 4. Формула общего члена
an = a1 + d · (n – 1) = 6 + 4 · 14 = 62.
Ответ: 62.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить
Свойства числа 339091
| Множители | 339091 | |
| Делители | 1, 339091 | |
| Количество делителей | 2 | |
| Сумма делителей | 339092 | |
| Предыдущее целое | 339090 | |
| Следующее целое | 339092 | |
| Простое число? | YES (29119th prime) | |
| Предыдущее простое | 339071 | |
| Следующее простое | 339103 | |
| 339091st простое число | 4856143 | |
| Является числом Фибоначчи? | NO | |
| Число Белла? | NO | |
| Число Каталана? | NO | |
| Факториал? | NO | |
| Регулярное число? | NO | |
| Совершенное число? | NO | |
| Полигональное число (s < 11)? | NO | |
| Двоичное | 1010010110010010011 | |
| Восьмеричная | 1226223 | |
| Двенадцатеричный | 144297 | |
| Шестнадцатиричная | 52c93 | |
| Квадрат | 114982706281 | |
| Квадратный корень | 582.31520673944 | |
| Натуральный логарифм | 12.734023786918 | |
| Десятичный логарифм | 5.5303162630833 | |
| Синус | 0.055313886535711 | |
| Косинус | 0.99846901502065 | |
| Тангенс | 0.055398701114994 |
Математические настройки для вашего сайта
Выберите язык:
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
中文
日本語
한국어
Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.
© 2022
numberempire.com
Все права защищены
Номер варианта сайта alexlarin.net:
Условие:
Три числа составляют арифметическую прогрессию. Если первые два оставить, а к третьему прибавить сумму двух первых, то полученные числа составят геометрическую прогрессию. Найдите знаменатель геометрической прогрессии.
Решение:
Пусть первое число равно (x,) тогда из первого свойства имеем три числа, которые образуют арифметическую прогрессию: (x, x+d, x+2d.)
Согласно второму условию имеем три другие числа, образующие геометрическую прогрессию: (x, x+d, 3x+3d.) Из свойства прогрессии имеем ((x+d)q=3x+3d Rightarrow q=3.)
Ответ 3.
В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями. Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.
Теория к заданию №11
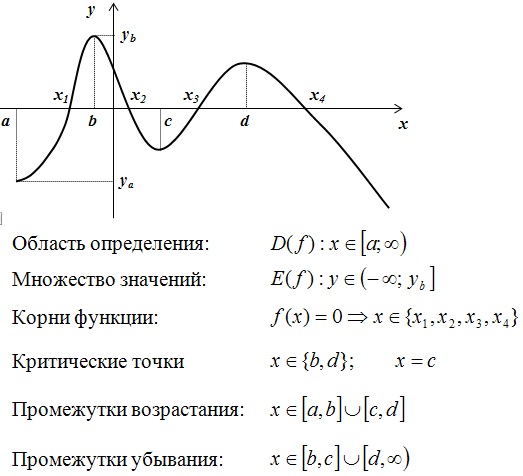
Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.
На произвольном примере ознакомимся с исследованием функции:
- область определения и множество значений
- корни и критические точки
- промежутки возрастания убывания
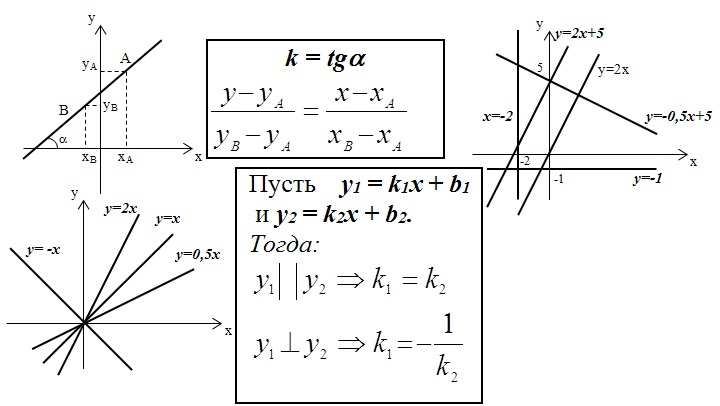
Теперь рассмотрим данный материал на линейной функции:
y = kx + b
где k – угловой коэффициент, b – свободный член
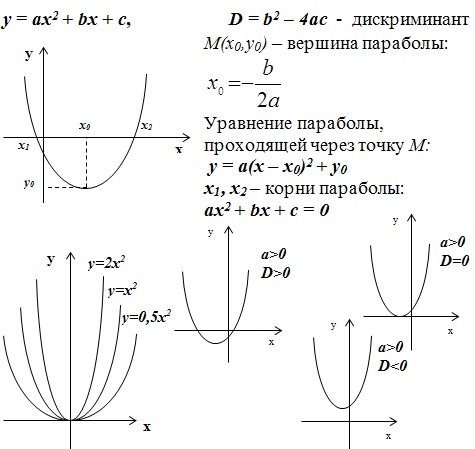
Рассмотрим случай квадратичной функции:
Также вспомним, что такое коренная функция и модуль:
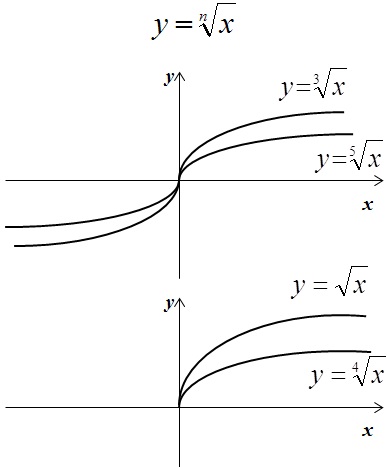

На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
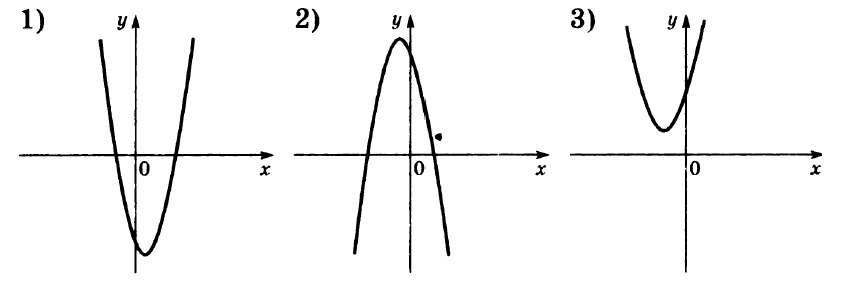
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
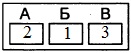
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функции:
A) y = -3/x
Б) y = 3/x
В) y = 1/(3x)
Графики:

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Общие правила:
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
и наоборот:
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между графиками функций и формулами, которые их задают.
 1) y = x²
1) y = x²
2) y = x/2
3) y = 2/x
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.
Ответ:
А 1
Б 3
В 2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:

КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: 213
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
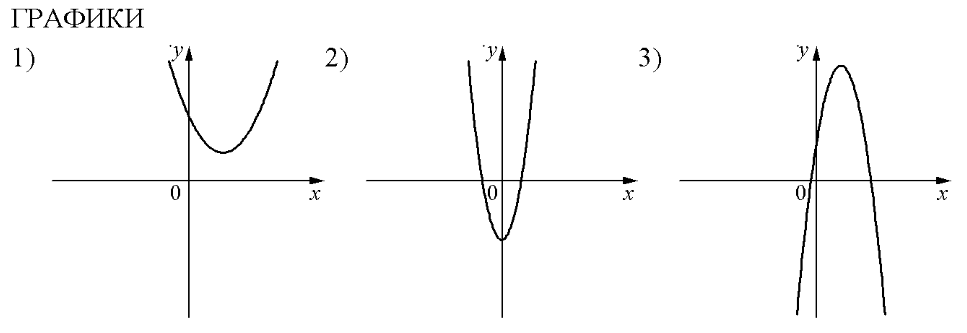
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
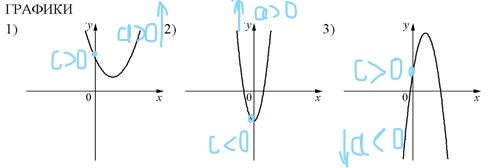
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор | оценить
Материалы для отработки задания №11 ОГЭ по математике.
Для выполнения задания 11 необходимо уметь строить и читать графики функций.
| Карточки для отработки задания 11 с ответами Источник: math100.ru → скачать |
| Материалы для отработки задания 11 Автор: Е. А. Ширяева → теория → задания |
| Практика для отработки задания 11 (презентация) Автор: Чагина Юлия Анатольевна → скачать |
Решение типовых задач № 11 на ОГЭ по математике
С видами заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе
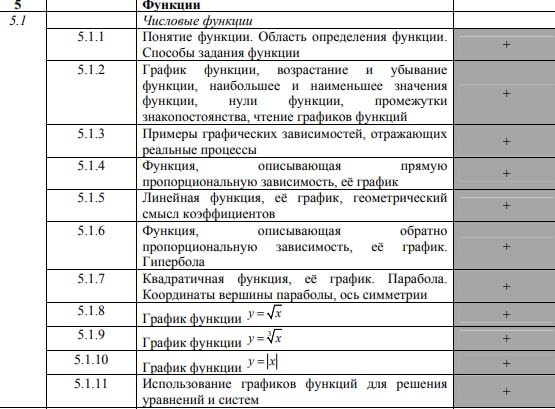
Связанные страницы:
Решение заданий 1 — 5 ОГЭ по математике
Задание 9 ОГЭ по математике
Тренировочные задания по теме «Вероятность» ОГЭ Математика
Тренировочные варианты ОГЭ 2021 по математике с ответами
Задание 10 ОГЭ по математике
| Авто | Видео-блоги | ДТП, аварии | Для маленьких | Еда, напитки |
|---|---|---|---|---|
| Животные | Закон и право | Знаменитости | Игры | Искусство |
| Комедии | Красота, мода | Кулинария, рецепты | Люди | Мото |
| Музыка | Мультфильмы | Наука, технологии | Новости | Образование |
| Политика | Праздники | Приколы | Природа | Происшествия |
| Путешествия | Развлечения | Ржач | Семья | Сериалы |
| Спорт | Стиль жизни | ТВ передачи | Танцы | Технологии |
| Товары | Ужасы | Фильмы | Шоу-бизнес | Юмор |
Видео ОГЭ по математике. Задание 9 номер 311381 канала ОГЭ «Ze-Smith» ABC
Показать
Установите соответствие между функциями и их графиками.
Функции
| А) y = −2x + 4 | Б) y = 2x − 4 | В) y= 2x + 4 |
Графики
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Статьи
Основное общее образование
Линия УМК А. Г. Мерзляка. Алгебра (7-9) (Б)
Математика
Представляем вашему вниманию разбор 11 задания ОГЭ-2019 по математике
17 октября 2018
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Задание 11
В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.
Решение
В задаче идет речь об арифметической прогрессии с первым членом a1 = 6 и разностью d = 4. Формула общего члена
an = a1 + d · (n – 1) = 6 + 4 · 14 = 62.
Ответ: 62.

ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Купить
В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями.
Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.
Задание 11 несложное, тем не менее последние задания придуманы таким образом, чтобы любознательным школьникам было над чем подумать.
Ответом в задании 10 является набор цифр, описывающий соответствие между различными объектами.
Теория к заданию №11
Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.
На произвольном примере ознакомимся с исследованием функции:
- область определения и множество значений
- корни и критические точки
- промежутки возрастания убывания

Теперь рассмотрим данный материал на линейной функции:
y = kx + b
где k – угловой коэффициент, b – свободный член

Рассмотрим случай квадратичной функции:

Также вспомним, что такое коренная функция и модуль:


Я разобрал три случая — случай с параболой и влияние коэффициентов на вид параболы — в первом примере. Во втором примере разобрана гипербола и общие закономерности зависимости общего вида графика от математического выражения. Третий случай рассматривает прямую и варианты её построения в зависимости от коэффициентов.
Разбор типовых вариантов задания №11 ОГЭ по математике
Первый вариант задания (параболы)
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:

Решение:
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Второй вариант задания (гиперболы)
Установите соответствие между функциями и их графиками.
Функции:
A) y = -3/x
Б) y = 3/x
В) y = 1/(3x)
Графики:

Решение:
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Общие правила:
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
и наоборот:
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Ответ:
A) 2
Б) 3
В) 1
Третий вариант задания (линейный график)
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:

Решение:
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Демонстрационный вариант ОГЭ 2019
Установите соответствие между графиками функций и формулами, которые их задают.
 1) y = x²
1) y = x²
2) y = x/2
3) y = 2/x
Решение:
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.
Ответ:
А 1
Б 3
В 2
Четвертый вариант задания (параболы)
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3

Решение:
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэф-т с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: A-1, Б-2, В-3
Пятый вариант задания (линейная функция)
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:

КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
Решение:
Рассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положит.направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: