С этим файлом связано 3 файл(ов). Среди них: Вариант 2Готовый.docx, Вариант 1 Готовый.docx, Тема урока.docx.
Показать все связанные файлы
Подборка по базе: детская литература с практикумом 2 курс 3 семестр практическое з, 1 задание русский.docx, LBD1_1 п. 1,2,4 любых 5 задач 2 задание.doc, Практическое задание №3 Основания и фундаменты.docx, Практическое задание 1_Чижова Л.А.doc, Практическое задание 2_Чижова А.А.doc, Практическое задание 1_Чижова А.А.doc, Наследственное право Задание 13.doc, Комплексное задание.pdf, история задание 1.docx
16. Задание 5 № 339073. Установите соответствие между функциями и их графиками.
Функции
А)  | Б)  | В)  |
Графики
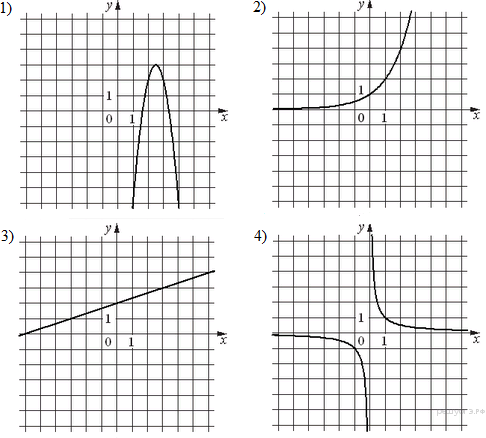
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В |
Решение.
Определим вид графика для каждой из функций.
А) — линейная функция.
Б) — парабола.
В) — гипербола.
Таким образом, искомое соответствие: A — 3, Б — 1, В — 4.
Ответ: 314.
Задание17. Установите соответствие между функциями и их графиками.
Функции
| А) y = −2x + 4 | Б) y = 2x − 4 | В) y= 2x + 4 |
Графики
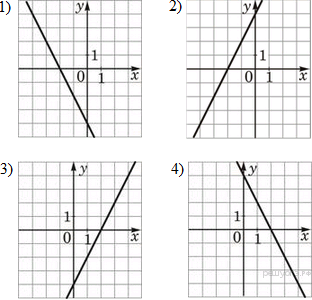
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В |
Решение.
Если прямая задана уравнением 
то при 
функция возрастает, при 
— убывает. Значению соответсвует значение функции в точке 
Уравнение 
задаёт убывающую функцию, пересекающую ось ординат в точке 4.
Уравнение 
задаёт возрастающую функцию, пересекающую ось ординат в точке −4.
Уравнение 
задаёт возрастающую функцию, пересекающую ось ординат в точке 4.
Тем самым, искомое соответствие: А — 4, Б — 3, В — 2.
Ответ: 432.
Задание 18. Установите соответствие между функциями и их графиками.
Функции
А)  | Б)  | В)  |
Графики
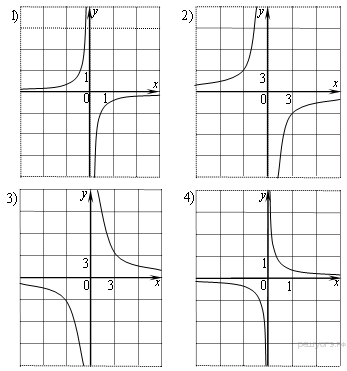
Решение.
Все представленные здесь функции — гиперболы. Общая формула для уравнения гиперболы: 
, если 
, то ветви гиперболы располагаются в первой и третьей четвертях, в противном случае — во второй и четвёртой четвертях.
Для того, чтобы отличить гиперболы лежащие в одинаковых четвертях нужно подставить какое-нибудь значение в формулу и проверить, какому графику будет соответствовать полученное значение.
Таким образом, установим соответсвие: А — 4, Б — 3, В — 2.
Ответ: 432.
Задание 19. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты
| А) a > 0, c < 0 | Б) a < 0, c > 0 | В) a > 0, c > 0 |
Графики
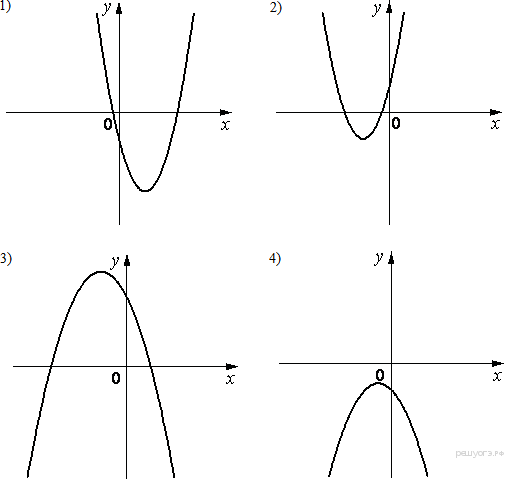
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В |
Решение.
Если парабола задана уравнением 
, то: при 
то ветви параболы направлены вверх, а при 
— вниз. Значение c соответствует значению функции в точке x = 0. Следовательно, если график пересекает ось ординат выше оси абсцисс, то значение c положительно, если ниже оси абсцисс — отрицательно.
Таким образом, функциям соответствуют следующие графики: А — 1, Б — 3, В — 2.
Ответ: 132.
Задание 20. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
Графики
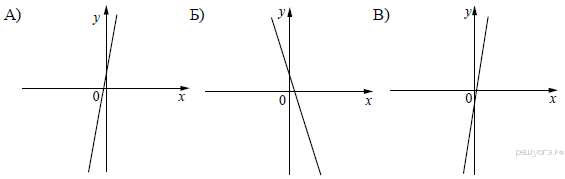
Коэффициенты
| 1) k < 0, b > 0 | 2) k > 0, b > 0 | 3) k < 0, b < 0 | 4) k > 0, b < 0 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В |
Решение.
Если прямая задана уравнением то при функция возрастает, при — убывает. Значению соответсвует значение функции в точке Таким образом, графику A соответствуют коэфициенты 2, Б − 1, В − 4.
Ответ: 214.
Зло — нормативно-оценочная категория нравственного сознания, противоположная понятию добра, обобщённо обозначает нравственно-отрицательное и предосудительное в поступках и мотивах людей и в явлениях действительности. Используется для характеристики, понимания и оценки вреда, ущерба, страданий и так далее
В интернет магазине Пленти Кар Вы можете купить автозапчасти для японских автомобилей (Toyota, Mazda, Honda, Isuzu, Lexus, Mitsubishi, Nissan, Subaru, Suzuki), европейских автомобилей (Ford, BMW, Citroen, Peugeot, Alpha, Lancia, Fiat, Land Rover, Mercedes, Opel, Renault, Rover, Volkswagen, Audi, Skoda, Seat, Volvo, Saab, Jaguar), американских автомобилей (Chevrolet, GM, Chrysler, Cadillac, Hummer, Infiniti, Jeep, Pontiac) и корейских автомобилей (Daewoo, Hyundai, Kia, SsangYong). Если Вы не смогли самостоятельно найти запчасти для Вашего автомобиля, обратитесь к нашим специалистам. Вся информация на сайте носит справочный характер и не является публичной офертой, определяемой статьей 437 ГК РФ.
Политика конфиденциальности | Интеграция с Битрикс24 — maxed.pro
© ПлэнтиКар PlentyCar.ru 2008—2022
620146, Екатеринбург, ул. Фурманова, д. 127.
тел: +7 (343) 204-95-04, 8-800-100-68-40 (многоканальный)
В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями. Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.
Теория к заданию №11
Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.
На произвольном примере ознакомимся с исследованием функции:
- область определения и множество значений
- корни и критические точки
- промежутки возрастания убывания
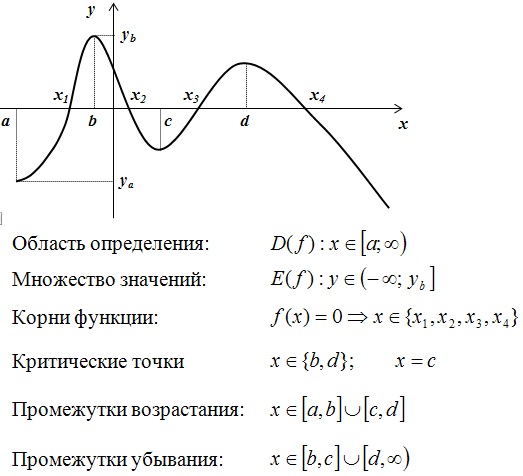
Теперь рассмотрим данный материал на линейной функции:
y = kx + b
где k – угловой коэффициент, b – свободный член
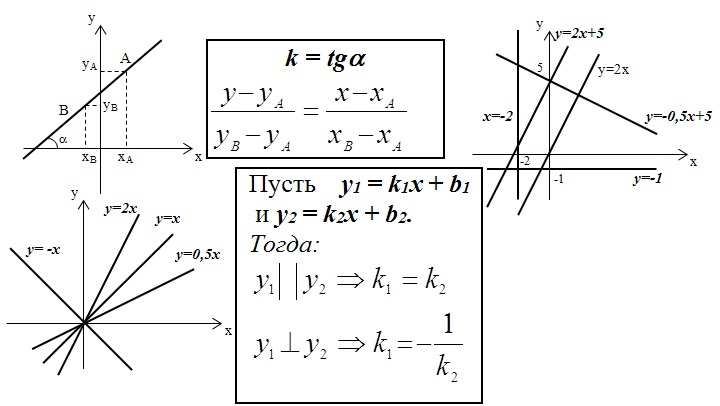
Рассмотрим случай квадратичной функции:
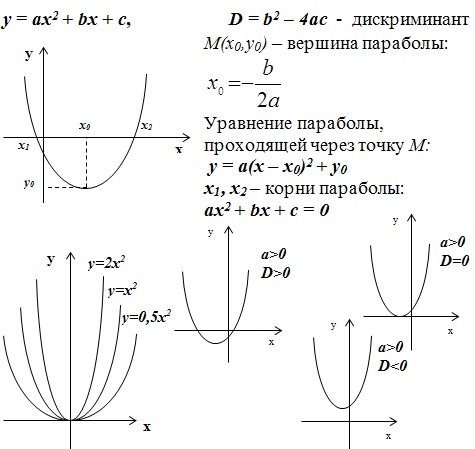
Также вспомним, что такое коренная функция и модуль:
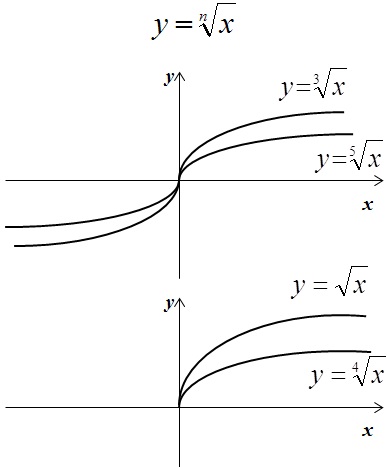
Задание OM1101o
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
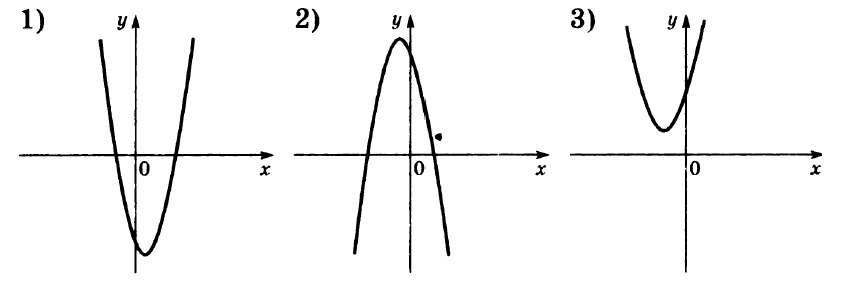
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1102o
Установите соответствие между функциями и их графиками.
Функции:
A) y = -3/x
Б) y = 3/x
В) y = 1/(3x)
Графики:
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Общие правила:
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
и наоборот:
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1103o
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1104o
Установите соответствие между графиками функций и формулами, которые их задают.
1) y = x²
2) y = x/2
3) y = 2/x
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.
Ответ:
А 1
Б 3
В 2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1105o
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM1106o
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:
КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: 213
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание 11OM21R
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
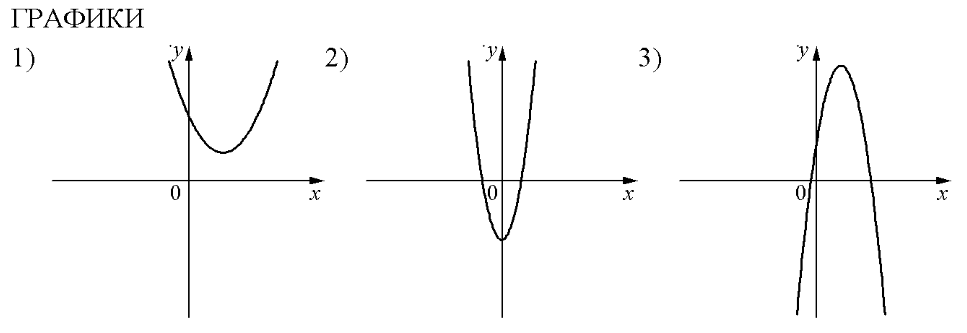
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
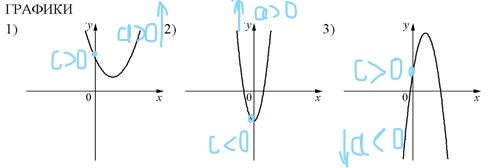
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 — это график №1
Б) а<0; с>0 — это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор | оценить
Материалы для отработки задания №11 ОГЭ по математике.
Для выполнения задания 11 необходимо уметь строить и читать графики функций.
| Карточки для отработки задания 11 с ответами Источник: math100.ru → скачать |
| Материалы для отработки задания 11 Автор: Е. А. Ширяева → теория → задания |
| Практика для отработки задания 11 (презентация) Автор: Чагина Юлия Анатольевна → скачать |
Решение типовых задач № 11 на ОГЭ по математике
С видами заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе
Связанные страницы:
Решение заданий 1 — 5 ОГЭ по математике
Задание 9 ОГЭ по математике
Тренировочные задания по теме «Вероятность» ОГЭ Математика
Тренировочные варианты ОГЭ 2021 по математике с ответами
Задание 10 ОГЭ по математике
В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями. Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.
Теория к заданию №11
Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.
На произвольном примере ознакомимся с исследованием функции:
- область определения и множество значений
- корни и критические точки
- промежутки возрастания убывания
Теперь рассмотрим данный материал на линейной функции:
y = kx + b
где k – угловой коэффициент, b – свободный член
Рассмотрим случай квадратичной функции:
Также вспомним, что такое коренная функция и модуль:
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функции:
A) y = -3/x
Б) y = 3/x
В) y = 1/(3x)
Графики:
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Общие правила:
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
и наоборот:
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между графиками функций и формулами, которые их задают.
1) y = x²
2) y = x/2
3) y = 2/x
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.
Ответ:
А 1
Б 3
В 2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:
КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: 213
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор | оценить
Каталог заданий.
Растяжения и сдвиги
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задание 11 № 34
Установите соответствие между графиками функций и формулами, которые их задают.
1) 
2) 
3) 
4) 
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
Аналоги к заданию № 34: 314771 314772 321919 321920 322008 60 86 112 138 190 … Все
Источник: Демонстрационная версия ГИА—2013 по математике.
Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.
Решение
·
·
Сообщить об ошибке · Помощь
2
Задание 11 № 193087
График какой из приведенных ниже функций изображен на рисунке?
Аналоги к заданию № 193087: 198175 193088 197665 197695 197725 197755 197785 197815 197845 197875 … Все
Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.
Решение
·
·
Сообщить об ошибке · Помощь
3
Задание 11 № 193093
На одном из рисунков изображен график функции 
. Укажите номер этого рисунка.
Аналоги к заданию № 193093: 200515 201145 193094 193095 193096 199705 199735 199765 199795 199825 … Все
Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.
Решение
·
·
Сообщить об ошибке · Помощь
4
Задание 11 № 193097
На одном из рисунков изображена парабола. Укажите номер этого рисунка.
Аналоги к заданию № 193097: 202195 193098 201235 201265 201295 201325 201355 201385 201415 201445 … Все
Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.
Решение
·
·
Сообщить об ошибке · Помощь
5
Задание 11 № 198175
График какой из приведенных ниже функций изображен на рисунке?
Аналоги к заданию № 193087: 198175 193088 197665 197695 197725 197755 197785 197815 197845 197875 … Все
Раздел кодификатора ФИПИ: 4.3 Определение свойств функций.
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О категории
Работа с функциями и их графиками
Практика (9)
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) y=-12/x
Б) y=1/12x
В) y=12/x
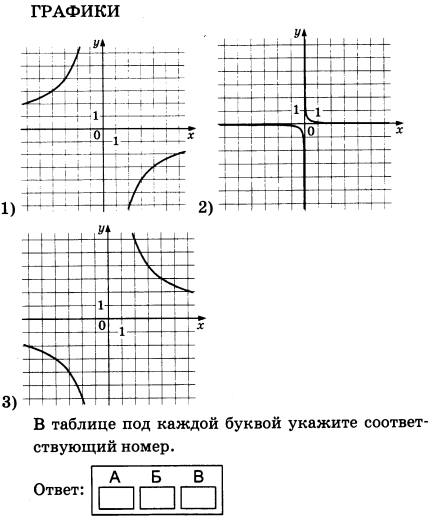
Установите соответствие между графиками функций (см. рис. 56) и формулами, которые их задают.
1) y=2x+1
2) y=5x-3
3) y=-3/x
4) y=x^2+2
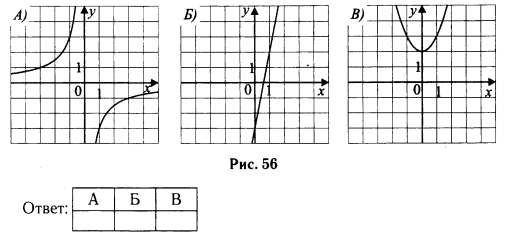
Установите соответствие между функциями и графиками (см. рис. 103).
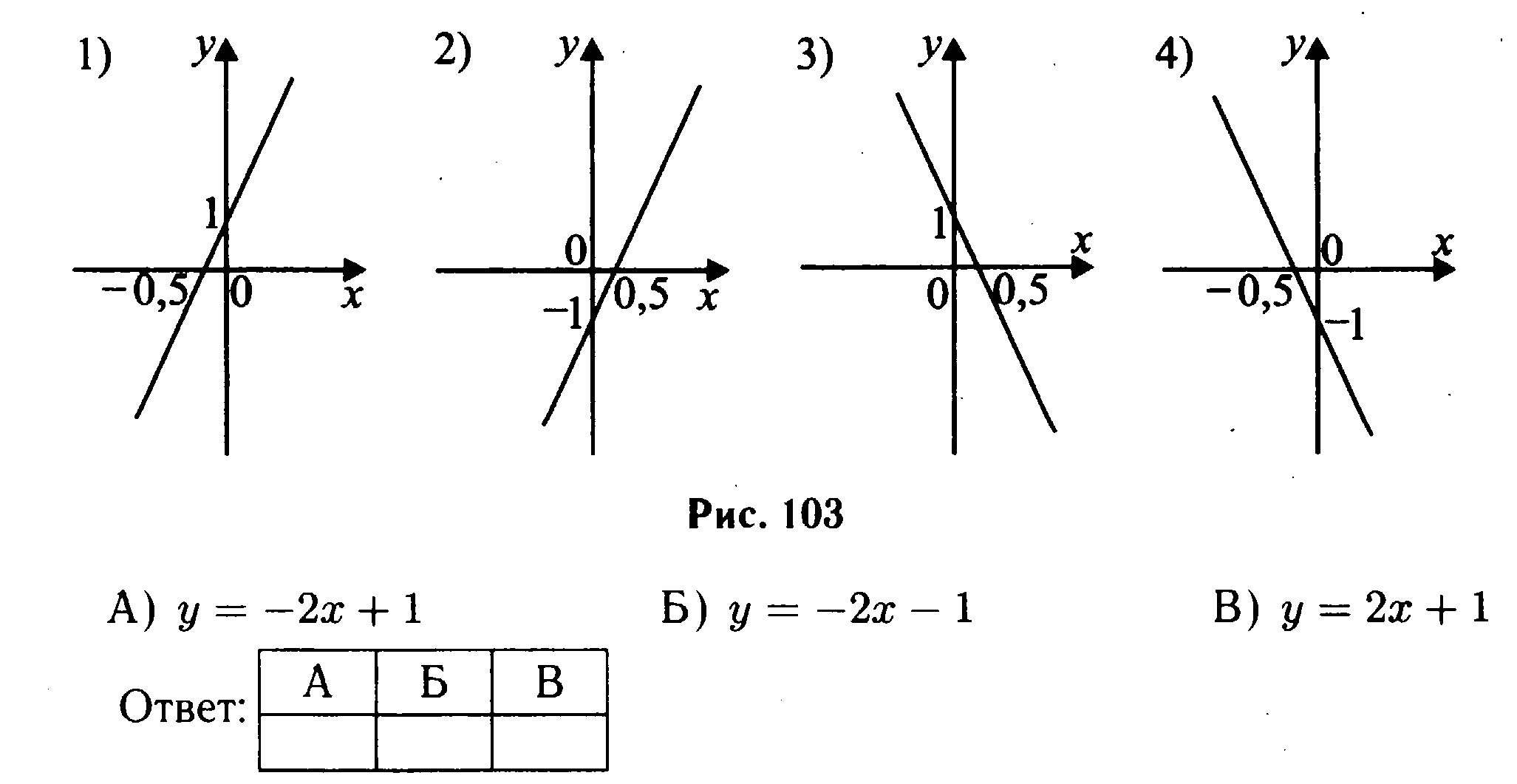
Установите соответствие между функциями и их графиками
ФУНКЦИИ
А) y=-(1/5)x-5
Б) y=-x^2+7x-7
В) y=9/x
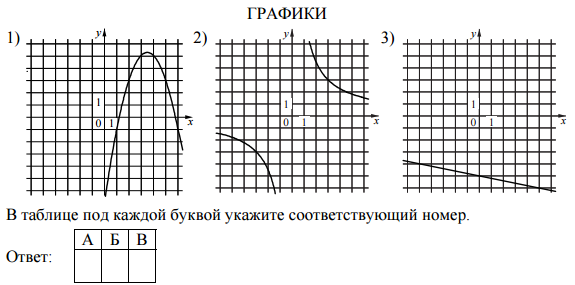
Установите соответствие между графиками функций и формулами, которые их задают.
1) y=-3x
2) y=-x/3
3) y=3-x
4) y=-3/x
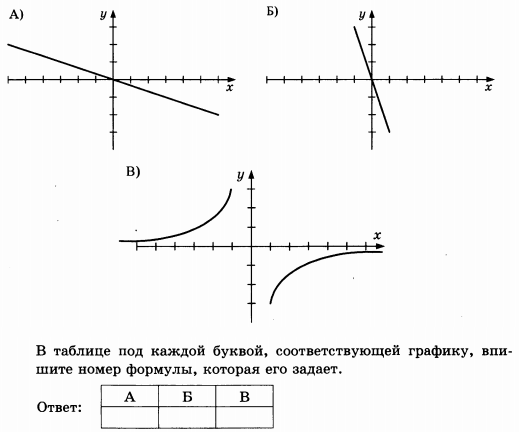
Установите соответствие между графиками функций и формулами, которые их задают.
1) у=2^x
2) y=2+x/3
3) y=1/x
4) y=-4x^2+20x-22
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
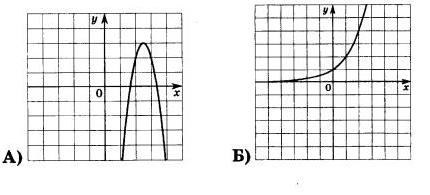
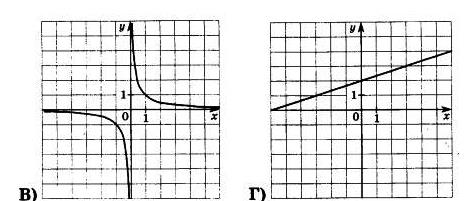
Установите соответствие между графиками функций и формулами, которые их задают.
1) у=3-2х
2) у=-3+2х
3) у=2-х
4) у=2+х
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
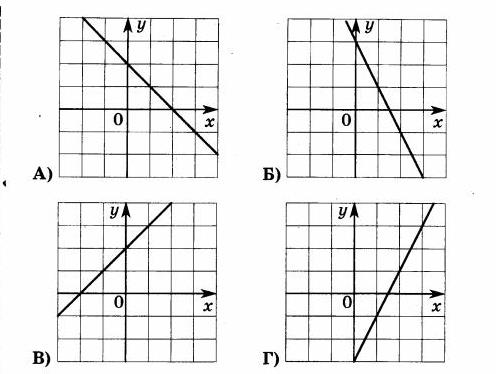
Установите соответствие между графиками функций и формулами, которые их задают.
ФОРМУЛЫ
1) x+3
2) -3x
3) 3
4) 3x
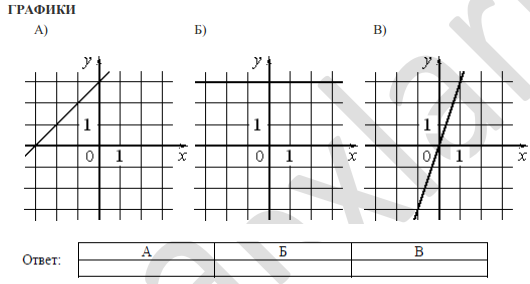
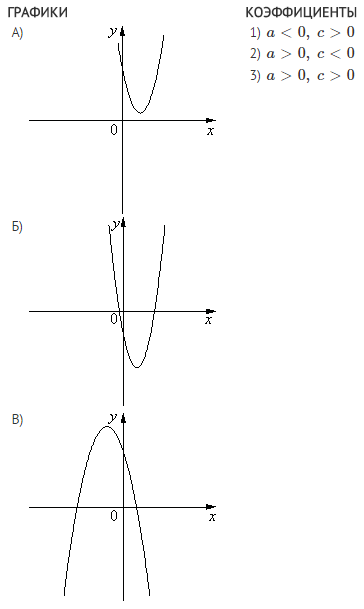
На рисунке изображены графики функций вида y=ax^2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
1 слайд
Задание 11 Графики Заданиена установление соответствия между графиками функций и формулами, которые их задают.
3 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. ОТВЕТ. 231 А Б В А Б В 2 3 1
4 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. ОТВЕТ. 123 А Б В А Б В 1 2 3
7 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. ОТВЕТ. 321 2 3 1 А Б В
8 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. А Б В
9 слайд
На рисунке изображены графики функций вида у= кх + b . Установите соответствие между графиками функций и знаками коэффициентов. В таблице под каждой буквой укажите соответствующий номер. А Б В
11 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. А Б В
12 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. А Б В
15 слайд
Установите соответствие между графиками функций и знаками коэффициентов. В таблице под каждой буквой укажите соответствующий номер. А Б В
16 слайд
Установите соответствие между графиками функций и знаками коэффициентов. В таблице под каждой буквой укажите соответствующий номер. А Б В
17 слайд
Установите соответствие между графиками функций и знаками с и D. В таблице под каждой буквой укажите соответствующий номер. А Б В
20 слайд
Установите соответствие между графиками функций и формулами, которые их задают. В таблице под каждой буквой укажите соответствующий номер. А Б В
Задание № 11.
Политика. Выбор позиций из списка.
Как выполнить задание № 11. РЕКОМЕНДАЦИИ.
Комментарий задания.
Задание № 11 включает в себя вопросы по теме: «Политическая сфера общества». Необходимо из списка выбрать особенности, типы, виды и пр., характеризующие определённое понятие по данной теме.
Алгоритм выполнения.
1.Внимательно прочитайте задание.
2.Из вопроса выделите главное – о каком конкретно понятии идёт речь.
3.Внимательно вдумывайтесь в каждое предложение предполагаемого ответа. Посмотрите, какие особенности или типы понятия даны в ответах.
4.Запишите ответ цифрами, ещё раз проверив его.
Разберём конкретный пример.
11. В государстве Z президент избирается членами обеих палат парламента. Какая дополнительная информация свидетельствует о том, что государство Z является парламентской республикой? Выберите из списка нужные позиции и запишите цифры, под которыми они указаны.
1) Парламент является постоянно действующим органом.
2) Парламент может отправить правительство в отставку.
3) Правительство несет ответственность перед президентом.
4) Главой правительства становится лидер победившей на выборах в парламент партии.
5) Парламент избирается на основе всеобщего и равного избирательного права.
6) Главной функцией правительства является разработка и принятие законов.
Пояснение.
Сначала чётко определяем, какова суть вопроса: особенности парламентской республики.
Вспомним теорию.
Парламентская республика — разновидность республики с перевесом полномочий в пользу парламента. В парламентской республике правительство отвечает только перед парламентом, а не перед президентом.
Разберём каждое высказывание.
1) Парламент является постоянно действующим органом — нет, неверно.
Данный признак характерен для любого вида республик, а не только для парламентской.
2) Парламент может отправить правительство в отставку — да, верно.
Парламент имеет полномочие отправить правительство в отставку в парламентской республике.
3) Правительство несет ответственность перед президентом — нет, неверно.
Правительство несет ответственность перед президентом только в президентской республике, в смешанной – и перед президентом , и перед парламентом, а в парламентской – только перед парламентом.
4) Главой правительства становится лидер победившей на выборах в парламент партии — да, верно.
Да именно лидер победившей на выборах в парламент партии становится главой правительства.
5) Парламент избирается на основе всеобщего и равного избирательного права — нет, неверно.
Данный признак характерен для всех видов республик.
6) Главной функцией правительства является разработка и принятие законов — нет, неверно.
Нет, правительство – исполнительный орган, а не законодательный.
Ответ: 24.
Вернутьсяк списку тестов по обществознанию ЕГЭ
- ОГЭ по математике
Подборка тренировочных вариантов по математике для 9 класса в формате ОГЭ 2023 с ответами и критериями оценивания.
Изменений относительно 2022 года нет, потому актуальны и варианты прошлого года.
Тренировочные варианты ОГЭ 2023 по математике
| alexlarin.net | уровень 1 | уровень 2 |
| вариант 327 | larin22-oge-327-1 | larin22-oge-327 |
| вариант 328 | larin22-oge-328-1 | larin22-oge-328 |
| вариант 329 | larin23-oge-329-1 | larin23-oge-329 |
| вариант 330 | larin23-oge-330-1 | larin23-oge-330 |
| вариант 331 | larin23-oge-331-1 | larin23-oge-331 |
| вариант 332 | larin23-oge-332-1 | larin23-oge-332 |
| вариант 333 | larin23-oge-333-1 | larin23-oge-333 |
| вариант 334 | larin23-oge-334-1 | larin23-oge-334 |
| вариант 335 | larin23-oge-335-1 | larin23-oge-335 |
| вариант 336 | larin23-oge-336-1 | larin23-oge-336 |
| вариант 337 | larin23-oge-337-1 | larin23-oge-337 |
| вариант 338 | larin23-oge-338-1 | larin23-oge-338 |
| вариант 339 | larin23-oge-339-1 | larin23-oge-339 |
| вариант 340 | larin23-oge-340-1 | larin23-oge-340 |
| вариант 341 | larin23-oge-341-1 | larin23-oge-341 |
| вариант 342 | larin23-oge-342-1 | larin23-oge-342 |
| вариант 343 | larin23-oge-343-1 | larin23-oge-343 |
| math100.ru | |
| Вариант 54 | math100-oge-54 |
| Вариант 55 | math100-oge-55 |
| Вариант 56 | math100-oge-56 |
| Вариант 57 | math100-oge-57 |
| Вариант 58 | math100-oge-58 |
| Вариант 59 | math100-oge-59 |
| Вариант 60 | math100-oge-60 |
| Вариант 61 | math100-oge-61 |
| Вариант 62 | math100-oge-62 |
| Вариант 63 | math100-oge-63 |
| Вариант 64 | math100-oge-64 |
| Вариант 65 | math100-oge-65 |
| Вариант 66 | math100-oge-66 |
| Вариант 67 | math100-oge-67 |
| Вариант 68 | math100-oge-68 |
| Вариант 69 | math100-oge-69 |
| Вариант 70 | math100-oge-70 |
| Вариант 71 | math100-oge-71 |
| time4math.ru | |
| Варианты 1-2 | ответы |
| Варианты 3-4 | ответы |
| Варианты 5-6 | ответы |
| Варианты 7-8 | |
| vk.com/pezhirovschool | |
| Вариант 1 (с решением) | скачать |
| Вариант 2 (с решением) | скачать |
| Вариант 3 (с решением) | скачать |
| Вариант 4 (с решением) | скачать |
| Вариант 5 (с ответами) | скачать |
| vk.com/oge100ballov | |
| variant 1 | скачать |
| variant 2 | скачать |
| variant 3 | скачать |
| yagubov.ru | |
| вариант 33 (сентябрь) | скачать |
| вариант 34 (октябрь) | скачать |
| вариант 35 (ноябрь) | скачать |
| вариант 36 (декабрь) | скачать |
| vk.com/math.studying | |
| вариант 1 | ответы |
| вариант 2 | ответы |
| vk.com/matematicalate | |
| variant 1 | скачать |
| variant 2 | скачать |
| variant 3 | скачать |
Характеристика структуры и содержания КИМ ОГЭ 2023 по математике
Работа содержит 25 заданий и состоит из двух частей.
Часть 1 содержит 19 заданий с кратким ответом; часть 2 – 6 заданий с развёрнутым ответом. При проверке базовой математической компетентности экзаменуемые должны продемонстрировать владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приёмов решения задач и проч.), умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.
Задания части 2 направлены на проверку владения материалом на повышенном и высоком уровнях. Их назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленных обучающихся, составляющих потенциальный контингент профильных классов.
Эта часть содержит задания повышенного и высокого уровней сложности из различных разделов математики.
Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности: от относительно простых до сложных, предполагающих свободное владение материалом и высокий уровень математической культуры.
Связанные страницы: