В таблице 12
необходимо определить недостающие
суммы в атрибутах бухгалтерского счета.
Таблица 12 -Атрибуты
бухгалтерских счетов
| Счет | Остаток на периода | Оборот по дебету | Оборот по кредиту | Остаток на конец периода | ||
| Дебет | Кредит | Дебет | Кредит | |||
| 01 | 15000 | 1000 | 18000 | |||
| 02 | 5000 | 2500 | 1000 | |||
| 10 | 25000 | 13000 | 35000 | |||
| 50 | 1800 | 1200 | 1000 | |||
| 60 | 4000 | 8000 | 12000 | |||
| 66 | 25000 | 10000 | 15000 | |||
| 80 | 45000 | 15000 | ||||
| 20 | 14569 | 14569 | ||||
| 43 | 2700 | 1600 |
Задание № 12
На основании
данных таблицы 13 составьте бухгалтерский
баланс по форме нетто за январь 201__
г.(табл.14), откройте синтетические счета
по Т-форме: укажите название счета,
кодировку и зафиксируйте начальные
остатки.
Таблица 13 — Остатки
на счетах бухгалтерского учета
организации
на январь 201__ г.
| Наименование и | Сумма, тыс. руб. |
| 1. Основные | 11000 |
| 2. Амортизация | 7000 |
| 3. Материалы (10) | 2000 |
| 4. Основное | 4500 |
| 5. Готовая | 920 |
| 6.Касса (50) | 7 |
| 7.Расчетные счета | 3150 |
| 8. Финансовые | 700 |
| 9. Расчеты с | 1000 |
| 10. Расчеты с | 2000 |
| 11. Расчеты по | 400 |
| Продолжение | |
| 12. Расчеты по | 80 |
| 13. Расчеты по | 30 |
| 14. Расчеты с | 90 |
| 15.Уставный | 9000 |
| 16. Добавочный | 6400 |
| 17. Нераспределённая | +277 |
Таблица 14 —
Бухгалтерский баланс организации на
января 201__ .,тыс.руб.
| Актив | На 1 января | На 1 февраля | Пассив | На 1 января | На 1 февраля |
| I. Внеоборотные | III. Капитал | ||||
| Итого по разделу | |||||
| Итого по разделу | IV. Долгосрочные | ||||
| II. Оборотные | |||||
| Итого по разделу | |||||
| V. Краткосрочные | |||||
| Продолжение | |||||
| Итого по разделу | Итого по разделу | ||||
| Баланс | 17277 | Баланс |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
![]()
oleg681 год назад
0
0
Развернутый угол — это угол, стороны которого составляют прямую
значит, углы 5:13 в сумме равны 180°
решим пропорцию
5+13=18
180:18=10
угол 1=5*10=50°
угол 2=13*10=130°

Задачи разделены на уровни сложности. Задачи из любого уровня вполне реально встретить на настоящем экзамене ЕГЭ, более сложные встретятся если «не повезло».
Сложность 1 (легкие задачи)
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
Сложность 2 (средние по сложности задачи)
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
Сложность 3 (более сложные задачи)
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()
посмотреть ответ
видеоурок по поиску максимумов и минимумов
![]()
видеоурок по поиску наибольшего и наименьшего значений
![]()

1 способ
Для того, чтобы найти коэффициент , достаточно найти на рисунке точку, принадлежащую графику функции (желательно, чтобы это была точка с целыми координатами).
Подставим в формулу координаты этой точки вместо
и
и найдем
.
Возьмем в качестве примера точку ().
Взяв любую другую точку, принадлежащую графику функции, получим такой же ответ.
2 способ
Коэффициент показывает скорость изменения функции. Мы видим, что при увеличении
на единицу,
увеличивается (по абсолютному значению) на
единицы, то есть в два раза больше. Следовательно,
.
Так как на рисунке функция убывающая, значит, .
Таким образом получили, что,
В девятом задании модуля алгебра ОГЭ по математике нам предлагают решить уравнения. Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными. Судя по материалам ОГЭ и практике проведения экзамена, наиболее вероятным заданием может быть решение линейного или квадратного уравнения. Тем не менее мы рассмотрим задания по всей этой тематике. Сложность заданий как всегда возрастает от задания к заданию. Ответом в задании №9 является целое число или конечная десятичная дробь.
Теория к заданию №9
Ниже я привел теорию по решениям линейных и квадратных уравнений:
Схема решения, правила и алгоритм действий при решении линейного уравнения:

Схема решения, правила и порядок действий при решении квадратного уравнения:

В трех типовых вариантах я разобрал данные случаи – в первом варианте вы найдете подробные указания по решению линейных уравнений, во втором разобран пример решения неполного квадратного уравнения, а в третьем – решение полного квадратного уравнения с вычислением дискриминанта.
Найдите корень уравнения:
10 ( x — 9 ) = 7
Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.
Для начала следует раскрыть скобки: 10x – 90 = 7
Затем переносим 90 в правую часть (не забываем поменять знак):
10x = 7 + 90
10x = 97
Затем делим обе части на 10:
x = 9,7
Ответ: 9,7
pазбирался: Даниил Романович | обсудить разбор | оценить
Решите уравнение:
3 x² + 12 x = 0
Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:
x ( 3 x + 12 ) = 0
Произведение множителей тогда равно нулю, когда один из множителей равен нолю:
x = 0
или
3 x + 12 = 0
3 x = -12
x = -4
Так как в ответе просят указать наименьший корень, то это -4.
Ответ: -4
pазбирался: Даниил Романович | обсудить разбор | оценить
Решите уравнение:
8 x² — 10x + 2 = 0
Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:
4 x² — 5x + 1 = 0
Далее вычисляем дискриминант:
D = b² — 4ac
D = 5² — 4 •4•1 = 9
Вычисляем корни:
x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25
x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1
Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25
Ответ: 0,25
pазбирался: Даниил Романович | обсудить разбор | оценить
Решите уравнение:
7х — 9 = 40
В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой – всё, что известно переносим в правую часть, всё, что неизвестно – оставляем в левой. Далее выполняем необходимое арифметическое действие.
Решение:
7х – 9 = 40
Переносим 9 в правую часть (не забываем про смену знака):
7х = 40 + 9, что эквивалентно
7х = 49
х в нашем случае – это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:
х = 49/7, откуда
х = 7
Ответ: 7
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите корень уравнения:![]()
режде всего, исключим корень, который не входит в ОДЗ:
x+6≠0 → х≠–6
Далее решаем уравнение. Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает вид пропорции:
![]()
Применим правило пропорции. Перемножим между собой крайние ее члены и средние:
1·1=(х+6)·2
Выполним умножение в левой части уравнения и раскроем скобки справа:
1=2х+12
Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:
2х+12=1
Переносим 12 из левой части в правую:
2х=1–12
2х=–11
Находим корень:
х=–11/2=–5,5
ОДЗ это значение не исключает, поэтому оно является искомым результатом.Ответ: -5,5
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите корень уравнения:![]()
Обе части уравнения приводим к единому знаменателю 12:
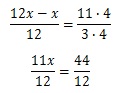
Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем:
11х=44
х=44:11
х=4
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор | оценить
Найти корень уравнения 2 + 3х= – 7х – 5
Имеем линейное уравнение:
2 + 3х= – 7х – 5
Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.
Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.
Запись решения выглядит так:
2 + 3х= – 7х – 5
3х + 7х= – 5 – 2
10х= –7
х=–7:10
х=–0,7
Ответ: –0,7
pазбирался: Даниил Романович | обсудить разбор | оценить
Материалы для отработки задания №11 ОГЭ по математике.
Для выполнения задания 11 необходимо уметь строить и читать графики функций.
| Карточки для отработки задания 11 с ответами Источник: math100.ru → скачать |
| Материалы для отработки задания 11 Автор: Е. А. Ширяева → теория → задания |
| Практика для отработки задания 11 (презентация) Автор: Чагина Юлия Анатольевна → скачать |
Решение типовых задач № 11 на ОГЭ по математике
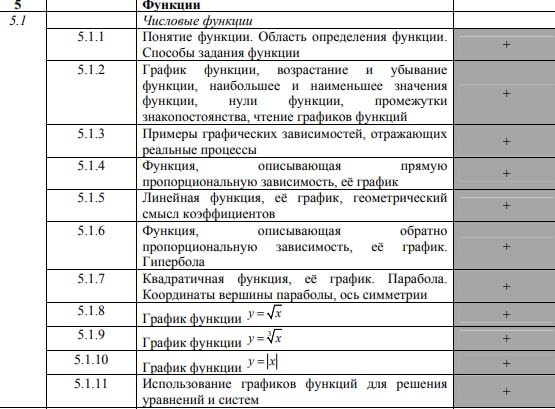
С видами заданий на данной позиции в КИМах можно подробнее ознакомиться в кодификаторе
Связанные страницы:
Решение заданий 1 — 5 ОГЭ по математике
Задание 9 ОГЭ по математике
Тренировочные задания по теме «Вероятность» ОГЭ Математика
Тренировочные варианты ОГЭ 2021 по математике с ответами
Задание 10 ОГЭ по математике
ОГЭ по математике 9 класс 2020-2021 года под редакцией И. В. Ященко — Вариант 1
При написании данной работы «ОГЭ по математике 2020-2021. Вариант 1» было использовано пособие «ОГЭ 2020-2021. Математика. 14 вариантов. Типовые тестовые задания от разработчиков ОГЭ / И. Р. Высоцкий, Л. О. Рослова, Л. В. Кузнецова, В. А. Смирнов, А. В. Хачатурян, С. А. Шестаков, Р. К. Гордин, А. С. Трепалин, А. В. Семенов, П. И. Захаров; под редакцией И. В. Ященко. — М.: Издательство «Экзамен», МЦНМО, 2020-2021″.
Часть 1
Модуль «Алгебра»
[latexpage]
- Найдите значение выражения [frac{3}{4} + frac{7}{25}]
Показать решение
Решение:
Чтобы сложить две дроби, их необходимо привести к общему знаменателю. В данном случае — это число 100:
[
frac{3}{4} + frac{7}{25} = frac{3 * 25}{4 * 25} + frac{7 * 4}{25 * 4} = frac{75}{100} + frac{28}{100} = frac{75 + 28}{100} = frac{103}{100} = 1,03
]
Ответ:
1,03
- В нескольких эстафетах, которые проводились в школе, команды показали следующие результаты.
| Команда | I эстафета, баллы | II эстафета, баллы | III эстафета, баллы | IV эстафета, баллы |
| «Удар» | 3 | 3 | 2 | 4 |
| «Рывок» | 1 | 4 | 4 | 2 |
| «Взлёт» | 4 | 2 | 1 | 3 |
| «Спурт» | 2 | 1 | 3 | 1 |
При подведении итогов баллы каждой команды по всем эстафетам суммируются. Побеждает команда, набравшая наибольшее количество баллов. Какая команда заняла третье место?
- «Удар»
- «Рывок»
- «Взлёт»
- «Спурт»
Показать решение
Решение:
В первую очередь суммируем баллы, набранные каждой командой
«Удар» = 3 + 3 + 2 + 4 = 12
«Рывок» = 1 + 4 + 4 + 2 = 11
«Взлёт» = 4 + 2 + 1 + 3 = 10
«Спурт» = 2 + 1 + 3 + 1 = 7
Судя по результату: первое место у команды «Удар», второе — у команды «Рывок», а третье — у команды «Взлёт».
Ответ:
Третье место заняла команда «Влёт», номер 3.
- На координатной прямой точки A, B, C и D соответсвуют числам: -0,74; -0,047; 0,07; -0,407 .

Какой точке соответствует число -0,047 ?
- A
- B
- C
- D
Показать решение
Решение:
На координатной прямой положительные числа находятся справа от начала координат, а отрицательные — слева. Значит единственное положительное число 0,07 соответсвует точке D. Самое большое отрицательное число — это -0,74, а значит оно соответсвует точке А. Учитывая, что оставшееся число -0,047 больше числа -0,407, то и принадлежат они точкам C и D соотвественно. Отобразим это на чертеже:

Ответ:
Число -0,047 соответсвует точке С, номер 3.
- Найдите значение выражения
[
sqrt{64} + (sqrt{6,4})^2
]
Показать решение
Решение:
В данном примере необходимо проявить смекалку. Если корень из 64 равен 8, поскольку 82 = 64, то корень из 6,4 найти простым путём достаточно сложно. Однако, после нахождения корня из числа 6,4 его нужно тут же возвести в квадрат. Таким образом, два действия: нахождение квадратного корня и возведение в квадрат аннулируют друг друга. Поэтому получаем:
[
sqrt{64} + (sqrt{6,4})^2 = 8 + 6,4 = 14,4
]
Ответ:
14,4
- На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 140 миллиметрам ртутного столба. Ответ дайте в километрах.
Показать решение
Решение:
Найдем на графике линию соответствующую 140 мм ртутного столба. Далее определим место её пересечения с кривой зависимости атмосферного давления от высоты над уровнем моря. На графике прекрасно видно это место пересечения. Проведем от точки пересечения вниз прямую до шкалы высот. Искомая величина 11 километров.

Ответ:
Атмосферное давление равно 140 миллиметрам ртутного столба на высоте 11 километров.
- Решите уравнение x2 + 6 = 5х
Если уравнение имеет более одного корня, в ответ напишите меньший из корней.
Показать решение
Решение
x2 + 6 = 5х
Перед нами обычное квадратное уравнение:
x2 + 6 — 5х = 0
Для его решения необходимо найти дискриминант:
D = b2 — 4ac
D = 25 — 24=1
х1 = 5 — 1/2 = 2
х2 = 5 + 1/2 = 3
х = 2,3.
Ответ
Наименьший корень данного уравнения: 2
- Поступивший в продажу в феврале мобильный телефон стоил 2800 рублей. В сентябре он стал стоить 2520 рублей. На сколько процентов снизилась цена на мобильный телефон в период с февраля по сентябрь?
Показать решение
Решение
Итак, 2800 рублей — 100%
2800 — 2520 = 280 (р) — сумма на которую подешевел телефон
280 / 2800 * 100 = 10 (%)
Ответ
Цена на мобильный телефон в период с февраля по сентябрь снизилась на 10%
- На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.

Какие из следующих утверждений неверны?
1) Канада — крупнейшая по площади территории страна мира.
2) Площадь территории Индии составляет 3,3 млн км2.
3) Площадь территории Китая больше площади территории Австралии.
4) Площадь территории Канады больше площади территории США на 1,5 млн км2.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Показать решение
Решение
Исходя из графика, Канада уступает по площади России, а значит первое утверждение неверное.
Над гистограммой Индии указана площадь 3,3 млн км2, что соответсвует второму утверждению.
Площадь территории Китая согласно графика равна 9,6 млн км2, а площадь Австралии — 7,7 млн км2, что соответсвует утверждению в третьем пункте.
Площадь территории Канады равна 10,0 млн км2, а площадь США — 9,5 млн км2, т.е. почти равны. А значить утверждение 4 неверное.
Ответ
14
- В каждом двадцать пятом пакете сока согласно условиям акции под крышкой есть приз. Призы распределены случайно. Вера покупает пакет сока. Найдите вероятность того, что Вера не найдет приз в своём пакете.
Показать решение
Решение
Решение данной задачи основано на классической формуле определения вероятности:
[
P(A) = frac{m}{n}
]
где, m — число благоприятных исходов события, а n — общее количество исходов
Получаем
[
P(A) = frac{1}{25} = 0.04
]
Таким образом, вероятность того, что Вера не найдёт приз составит 24/25 или
[
1 — 0,04 = 0,96
]
Ответ
Вероятность того, что Вера не найдёт приз составит 0,96
- Установите соответствие между функциями и их графиками.
Функции:
А) [ y = -frac{12}{x} ] Б) [ y = frac{1}{12x} ] В) [ y = frac{12}{x} ]
Графики:

В таблице под каждой буквой укажите соответсвующий номер.
Показать решение
Решение
- Изображённая на рисунке 1 гипербола расположена во второй и четвёртой четвертях, следовательно, данному графику может соответсвовать функция А. Выполним проверку: a) при х = -6, y = -(12/-6) = 2; б) при х = -2, y = -(12/-2) = 6; в) при х = 2, y = -(12/2) = -6; г) при х = 6, y = -(12/6) = -2. Что и требовалось доказать.
- Изображённая на рисунке 2 гипербола расположена в первой и третьей четвертях, следовательно, данному графику может соответсвовать функция Б. Выполнение проверки проведите самостоятельно, по аналогии с первым примером.
- Изображённая на рисунке 3 гипербола расположена в первой и третьей четвертях, следовательно, данному графику может соответсвовать функция В. Выполним проверку: a) при х = -6, y = (12/-6) = -2; б) при х = -2, y = (12/-2) = -6; в) при х = 2, y = (12/2) = 6; г) при х = 6, y = (12/6) = 2. Что и требовалось доказать.
Ответ
А — 1 ; Б — 2 ; В — 3
- Арифметическая прогрессия (an) задана условиями:
a1 = -9, an+1 = an + 4.
Найдите сумму первых шести её членов.
Показать решение
Решение
a1 = -9, an+1 = an + 4.
an + 1=an + 4 ⇒ d = 4
an = a1 + d(n-1)
a6 = a1 + d(n-1) = –9 + 4(6 – 1) = –9 + 20 = 11
S6 = (a1 + a6)∙6 / 2
S6 = (a1 + a6)∙3
S6 = ( –9 + 11)∙3 = 6
Ответ
6
- Найдите значение выражения
[ (2 + c)^2 — c(c — 4) ] при [ c = -frac{1}{8} ]
Показать решение
Решение
Раскрываем скобки. Не забываем, что первая скобка — это квадрат суммы.
[
(2 + c)^2 — c(c — 4 ) = 4 + 4c + c^2 — c^2 + 4c = 4 + 8c
]
при [c=-1/8 ]
[
4 + 8(-frac{1}{8}) = 4 — frac{8}{8} = 4 — 1 = 3
]
Ответ
3
- Площадь четырёхугольника можно вычислить по формуле
[
S = frac{d_1d_2sin a}{2}
]
где d1 и d2 — длины диагоналей четырёхугольника, a — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если
[
d_1 = 7, sin a = frac{6}{11}, S = 21
]
Показать решение
Решение
[
d_2 = frac{2S}{d_1 sin a} = frac{2 * 21}{7 * frac{6}{11}} = frac{42}{ frac{42}{11}}
]
Помните правило, если у нас трёх-этажная дробь, то нижнее значение переносится наверх
[
frac{42}{ frac{42}{11}} = frac{42 * 11}{42} = 11
]
Ответ
11
- Укажите решение неравенства
[
6 — 7x le 3x -7
]
| [ 1) [0,1; +infty); ] | [ 2) (-infty;1,3]; ] |
| [ 3) [1,3;+infty); ] | [ 4) (-infty;0,1] ] |
Показать решение
Решение
Для решения данного неравенства необходимо сделать следующее:
а) перенесём член 3х в левую часть неравенства, а 6 — в правую часть, не забыв поменять знаки на противоположные. Получим:
[ -3x — 7x le -7 — 6 ]
[ -10x le -13 ]
б) Умножим обе части неравенства на отрицательное число -1 и заменим знак неравенства на противоположный.
[ -10x(-1) le -13(-1) ]
[ 10x ge 13 ]
в) найдём значение х
[ x ge 13:10 ]
[ x ge 1,3 ]
г) множеством решений данного неравенства будет числовой промежуток от 1,3 до +∞, что соответсвует ответу 3)
Ответ
3
Модуль «Геометрия»
- Пожарную лестницу длиной 17 м приставили к окну шестого этажа дома. Нижний конец лестницы стоит от стены на 8 м. На какой высоте расположено окно? ответ дайте в метрах.

Показать решение
Решение
На рисунке мы видим обычный прямоугольный треугольник состоящий из гипотенузы (лестница) и двух катетов (стена дома и земля. Для нахождения длины катета воспользуемся теоремой Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2 = a2 + b2
отюда
[ a = sqrt {c^2 — b^2} ]
[ a = sqrt {17^2 — 8^2} = sqrt {289 — 64} = sqrt {225} = 15]
Итак, окно расположено на высоте 15 метров
Ответ
15
- В треугольнике ∆ABC известно, что AB = 8, BC = 10, AC = 14. Найдите cos∠ABC
Показать решение
Решение
Для решения данной задачи необходимо воспользоваться теоремой косинусов. Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
 a2 = b2 + c2 – 2bc cosα
a2 = b2 + c2 – 2bc cosα
АС² = АВ² + ВС² — 2·АВ·ВС·cos∠ABC
14² = 8² + 10² — 2·8·10·cos∠ABC
196 = 64 + 100 — 160·cos∠ABC
160·cos∠ABC = 164 — 196
160·cos∠ABC = — 32
cos∠ABC = — 32 / 160 = -0,2
Ответ
cos∠ABC = -0,2
- На окружности с центром в точке О отмечены точки A и B так, что ∠AOB = 15о. Длина меньшей дуги AB равна 48. Найдите длину большей дуги AB.
Показать решение
Решение
 Известно, что круг составляет 360о. Исходя из этого, 15о составляет:
Известно, что круг составляет 360о. Исходя из этого, 15о составляет:
360о / 15о = 24 — кол-во сегментов в круге по 15о
Итак, 15о составляют 1/24 часть всей окружности, значит оставшаяся часть круга:
[ frac{24}{24} — frac{1}{24} = frac{23}{24} ]
т.е. оставшиеся 345о (360о — 15о = 345о) составляют 23-ю часть всей окружности
Если длина меньшей дуги AB равна 48, то длина большей дуги AB составит:
48 * 23 = 1104
Ответ
1104
- В трапеции ABCD известно, что AB = CD, ∠BDA = 35о и ∠BDC = 58о. Найдите угол ∠ABD. Ответ дайте в градусах.
Показать решение
Решение

По условию задачи перед нами равнобедренная трапеция. Углы в основании равнобедренной трапеции (верхнем и нижним) равны.
∠ADC = 35 + 58 = 93°
∠DAB = ∠ADC = 93°
Теперь рассмотрим треугольник ∆ABD в целом. Нам известно, что сумма углов треугольника равна 180 °. Отсюда:
∠ABD = 180 – ∠ADB – ∠DAB = 180 – 35 – 93 = 52 °.
Ответ
52°
- На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.

Показать решение
Решение
Площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h):
[ S = frac{1}{2} a h ]
где,
a — длина основания треугольника
h — высота треугольника.
Из рисунка мы видим, что основание треугольника равно 6 (клеткам), а высота — 3 (клеткам). Исходя из чего получаем:
[ S = frac{1}{2} a h = frac{1}{2} * 6 * 3 = frac{1}{2} * 18 = frac{18}{2} = 9 ]
Ответ
9
- Какое из следующих утверждений верно?
- Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.
- Каждая из биссектрис равнобедренного треугольника является его медианой.
- Сумма углов любого треугольника равна 360о.
В ответ запишите номер выбранного утверждения.
Показать решение
Решение
Данное задание не является задачей. Вопросы, перечисленные здесь необходимо знать наизусть и уметь на них отвечать.
- Это утверждение абсолютно верно.
- Неверно, поскольку согласно свойствам равнобедренного треугольника у него может быть только одна медиана — это биссектриса, проведенная к основанию. Она же является и высотой треугольника.
- Неверно, поскольку сумма углов любого треугольника равна 180о.
Ответ
1
Часть 2
Модуль «Алгебра»
- Решите уравнение
[ x^2 — 3x + sqrt{6 — x} = sqrt{6 — x} + 28 ]
Показать решение
Решение
[ x^2 — 3x + sqrt{6 — x} = sqrt{6 — x} + 28 ]
Перенесем выражение √6-x с правой стороны в левую
[ x^2 — 3x + sqrt{6 — x} — sqrt{6 — x} = 28 ]
Сократим оба выражения √6-x
[ x^2 — 3x = 28 ]
Перенесём 28 в левую часть уравнения
[ x^2 — 3x — 28 = 0 ]
Перед нами обычное квадратное уравнение.
Область допустимых значений в данном случае составляет: 6 — х ≥ 0 ⇒ x ≤ 6
Для решения уравнения, необходимо найти дискриминант:
D = b2 — 4ac
D = 9 + 112 = 121 = 112
х1 = (3 + 11)/2 = 14/2 = 7 — не является решением
х2 = (3 — 11)/2 = -8/2 = -4
х = -4
Ответ
-4
- Теплоход проходит по течению реки до пункта назначения 210 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 9 часа, а в пункт отправления теплоход возвращается через 27 часов после отплытия из него.
Показать решение
Решение
Пусть
х — это собственная скорость теплохода, тогда
х + 4 — скорость теплохода по течению
х — 4 — скорость теплохода против течения
27 — 9 = 18 (ч) — время движения теплохода из пункта отправления в пункт назначения и обратно без учета стоянки
210 * 2 = 420 (км) — общее расстояние, пройденное теплоходом
Исходя из выше сказанного получим уравнение:
[ frac{210}{x+4} + frac{210}{x-4} = 18 ]
приводим к общему знаменателю и решаем:
[ frac{210 (x-4)}{(x+4)(x-4)} + frac{210(x+4)}{(x-4)(x+4)} = 18 ]
[ 210(x-4) + 210(x+4) = 18(x+4)(x-4) ]
[ 210x + 210x = 18(x^2 -16) ]
[ 420x = 18x^2 -288) ]
[ 18x^2 — 420x — 288 = 0]
Для дальнейшего решения уравнения, необходимо найти дискриминант:
[ D = 420^2 — 4 * 18 * (-288) = 197 136 = 444^2 ]
[ x = frac{ 420 pm 444 }{2 * 18 }]
[ x = frac{ 420 + 444 }{36}]
[ x = frac{864}{36}]
[ x = 24 ]
Собственная скорость теплохода составляет 24 км/ч
Ответ
24 км/ч
- Постройте график функции
[
y =
left{ begin{array}{crl}
x^2 + 4x + 4 & xge-5,
-frac {45}{x} &x<-5
end{array}
]
и определите, при каких значениях m прямая y = m имеет с графиком одну или две общие точки.
Показать решение
Решение

На рисунке выше изображены два графика, соответствующие представленным функциям:
y = x2 + 4x +4 (график, изображенный красной линией)
y = -45/x (график, изображенный синий линией)
Рассмотрим обе функции:
- y=x2+4x+4 на промежутке [–5;+∞) – это квадратичная функция, графиком является парабола, а=1 > 0 – ветви направлены вверх. Если мы её сократим по формуле квадрата суммы двух чисел, то получим: у=(х+2)2 – сдвиг графика влево на 2 единицы, что и видно из графика.
- у=–45/х – это обратная пропорциональность, график гипербола, ветви расположены во 2 и 4 четвертях.
На графике хорошо видно, что прямая у=m имеет с графиком одну общую точку при m=0 и m > 9 и две общие точки при m=9, т.е. ответ: m=0 и m≥9, проверяем:
Одна общая точка в вершине параболы y = x2 + 4x +4
x0 = -b/2a = -4/2 = -2
y0 = -22 + 4(-2) + 4 = 4 — 8 +4 = 0 ⇒ с = 0
Две общие точки при х = – 5 ; у = 9 ⇒ с = 9
Ответ
0; [9;+∞)
- Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 24, а расстояние от центра окружности до хорд AB и CD равны соответсвенно 16 и 12.
Показать решение
Решение
 Треугольники ∆АОВ и ∆СОD являются равнобедренными.
Треугольники ∆АОВ и ∆СОD являются равнобедренными.
AK = BK = AB / 2 = 24 / 2 = 12
Отрезки ОК и ОМ являются высотами и медианами.
По теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов, имеем
OB2 = OK2 + BK2
OB2 = 162 + 122 = 256 + 144 = 400
OB = 20
Учитывая, что OB — это радиус, имеем:
OB = OA = OC = OD = 20
Из треугольника ∆СОМ по теореме Пифагора получаем:
CM2 = OC2 – OM2
CM2 = 202 – 122 = 400 – 144 = 256
CM = 16
CD = CM * 2 = 16 * 2 = 32
Длина хорды CD равна 32.
Ответ
32
- В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке О. Докажите, что площади треугольников ∆AOB и ∆COD равны
Показать решение
Решение

Пусть AD — нижнее основание трапеции, а BC — верхнее, тогда AD>BC.
Найдем площади треугольников ∆ABD и ∆DCA:
S ∆ABD = 1/2 AD ∙ h1
S ∆DCA = 1/2 AD ∙ h2
Учитывая, что величина основания AD и высота обоих треугольников одинаковые, заключаем, что площади этих треугольников равны:
S ∆ABD = S ∆DCA
Каждый из треугольников ∆ABD и ∆DCA состоят из двух других треугольников:
S ∆ABO + S ∆AOD = S ∆ABD (сумма площадей внутренних треугольников S ∆ABO и S ∆AOD равна площади треугольника S ∆ABD)
S ∆DCO + S ∆AOD = S ∆DCA (сумма площадей внутренних треугольников S ∆DCO и S ∆AOD равна площади треугольника S ∆DCA)
Если площади треугольников S ∆ABD и S ∆DCA равны, то и сумма площадей их внутренних треугольников также равны. Отсюда получаем,:
S ∆ABO + S ∆AOD = S ∆DCO + S ∆AOD
в данном равенстве с обеих сторон фигурирует один и тот же треугольник — S ∆AOD, что позволяет нам сократить его. Получаем следующее равенство:
S ∆ABO = S ∆DCO
Что и требовалось доказать.
Ответ
S ∆ABO = S ∆DCO
- На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 9, MD = 6, H — точка пересечения высот треугольника ABC. Найдите AH.
Показать решение
Решение

Для начала начертим треугольник и полуокружность, как сказано в условии задачи (рис.1).
Отметим точку пересечения окружности со стороной АС буквой F (рис.2)
BF — является высотой треугольника ∆ABC, так как для окружности ∠BFC — это вписанный угол, который опирается на дугу в 180° (BC — диаметр), следовательно:
∠BFC=180°/2=90°
Согласно теореме «о двух секущих», имеем: AF * AC = AM * AK
Теперь рассмотрим хорду MK.
Отрезок BC — это перпендикуляр к отрезку MK, проходящий через центр окружности, следовательно BC — это серединный перпендикуляр.
Это значит, BC делит хорду MK пополам, т.е. MD = KD = 6 (см. условие задачи)
Рассмотрим треугольники ∆AHF и ∆ACD.
Угол ∠DAC для обоих треугольников является общим.
А углы ∠AFH и ∠ADC равны, кроме того — это прямые углы.
Следовательно, согласно первому признаку подобия треугольников, данные треугольники подобны.
Отсюда, по определению подобия, мы можем записать: AC / AH = AD / AF => AC * AF = AD * AH
Ранее мы рассматривали равенство (по теореме двух секущих) AF * AC = AM * AK, из которой получаем
AM * AK = AD * AH
AH = (AM * AK) / AD
Из рисунка находим:
AM = AD — MD = 9 — 6 = 3
AK = AD + KD = 9 + 6 =15
Отсюда:
AH = 3 * 15 / 9 = 45 / 9 = 5
Ответ: AH = 5
Ответ
5
ОГЭ по математике №11. Графики функцийadmin2022-03-19T15:42:57+03:00
Скачать файл в формате pdf.
Комментарии для сайта Cackle
![]()
|
| 1. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/diagn_9kl.doc 2. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/А12.docx 3. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/А13.docx 4. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/А3 %.docx 5. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/А5.docx 6. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/Варианты ГИА слабым.doc 7. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_01.doc 8. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_02.doc 9. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_03.doc 10. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_04.doc 11. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_05.doc 12. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_06.doc 13. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_07.doc 14. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_08.doc 15. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_09.doc 16. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_10.doc 17. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_11.doc 18. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_12.doc 19. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_13.doc 20. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_14.doc 21. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_15.doc 22. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_16.doc 23. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_17.doc 24. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/ГИА по темам/ГИА_18.doc 25. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/инд. карта 9.кл..doc 26. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/тренажёр 9кл 1А.docx 27. /Методические рекомендации по подготовке к ГИА тьютора Придача В.И/числовые неравенства.docx | Диагностическая карта по проверке усвоения тем по алгебре ученика (цы) 9 класса моу сош № Решите уравнения1 Задание А13 Решите неравенство Задачи на проценты А3 1. Андрей выбирает трехзначное число. Найдите вероятность того, что оно делится на 33 №1. Укажите выражение, значение которого является наименьшим Гиа. 2012 год. Прототипы задания 1 Задание 2 (№206046) Задание 3 (№137243) Гиа 2012 год прототипы задания 4 Гиа. 2012 год. Прототипы задания 5 Задание 6 (№137268) Задание 7 (№137294) Гиа. 2012 год. Прототипы задания 8 Гиа. 2012 год. Прототипы задания 9 Задание 9 (№132785) Гиа. 2012 год. Прототипы задания 10 Гиа. 2012 год. Прототипы задания 11 Гиа. 2012 год. Прототипы задания 12 Гиа. 2012 год. Прототипы задания 13 Гиа. 2012 год. Прототипы задания 14 Задание 15 (№169915) Задание 16 (№169838) Гиа. 2012 год. Прототипы задания 17 Задание 17 (№193087) Задание 18 (№206194) Чтение графика реальной зависимости 44. в десятичную перевести 1. Одна из точек, отмеченных на координатной прямой, соответствует числу. Какая это точка? |
ГИА. 2012 год. Прототипы задания 17
Задание 17 (№ 193087)
График какой из приведенных ниже функций изображен на рисунке?

| 1. | 2. | 3. | 4. |
Задание 17 (№ 193088)
График какой из приведенных ниже функций изображен на рисунке?

| 1. | 2. | 3. | 4. |
Задание 17 (№ 193089)
Найдите значение ![]() по графику функции
по графику функции ![]() , изображенному на рисунке.
, изображенному на рисунке.

| 1. | -1 | 2. | 1 | 3. | 2 | 4. | 3 |
Задание 17 (№ 193090)
Найдите значение ![]() по графику функции
по графику функции ![]() , изображенному на рисунке.
, изображенному на рисунке.

| 1. | -2 | 2. | 1 | 3. | 2 | 4. | 3 |
Задание 17 (№ 193091)
Найдите значение ![]() по графику функции
по графику функции ![]() , изображенному на рисунке.
, изображенному на рисунке.

| 1. | -3 | 2. | 1 | 3. | 2 | 4. | 3 |
Задание 17 (№ 193092)
Найдите значение ![]() по графику функции
по графику функции ![]() , изображенному на рисунке.
, изображенному на рисунке.

| 1. | 2 | 2. | 3. | 4. | -2 |
Задание 17 (№ 193093)
На одном из рисунков изображен график функции ![]() . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
| 1. |  | 2. |  | 3. |  | 4. |  |
Задание 17 (№ 193094)
На одном из рисунков изображен график функции ![]() . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
| 1. |  | 2. |  | 3. |  | 4. |  |
Задание 17 (№ 193095)
На одном из рисунков изображен график функции ![]() . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
| 1. |  | 2. |  | 3. |  | 4. |  |
Задание 17 (№ 193096)
На одном из рисунков изображен график функции ![]() . Укажите номер этого рисунка.
. Укажите номер этого рисунка.
| 1. |  | 2. |  | 3. |  | 4. |  |
Задание 17 (№ 193097)
На одном из рисунков изображена парабола. Укажите номер этого рисунка.
| 1. |  | 2. |  | 3. |  | 4. |  |
Задание 17 (№ 193098)
На одном из рисунков изображена гипербола. Укажите номер этого рисунка.
| 1. |  | 2. |  | 3. |  | 4. |  |
Задание 17 (№ 193099)
Найдите значение ![]() по графику функции
по графику функции ![]() , изображенному на рисунке.
, изображенному на рисунке.

Задание 17 (№ 193100)
Найдите значение ![]() по графику функции
по графику функции ![]() , изображенному на рисунке.
, изображенному на рисунке.

Задание 17 (№ 193101)
Найдите значение ![]() по графику функции
по графику функции ![]() , изображенному на рисунке.
, изображенному на рисунке.

Задание 17 (№ 193102)
Найдите значение ![]() по графику функции
по графику функции ![]() , изображенному на рисунке.
, изображенному на рисунке.

Похожие:
 | Методические рекомендации для подготовки к гиа в 2013 году. В ней описана структура экзамена, основные особенности. Данное пособие поможет учителям качественно подготовить учеников к экзамену … |  | Анализ результатов пробного гиа по математике 11 апреля 2012 год Гиа поматематике. Задания выполняли 12 учащихся 9 класса мбоу «Обильновская сош» |
 | 31. 01. 2012 Домашнее задание: с. 17 задания для повторения 01. 02. 2012 Домашнее задание: с. 18 все задания |  | Инструкция по заполнению бланков ответов гиа-9 в 2012 г. Ответы на задания типа А В средней части бланка ответов №1 расположены поля для записи ответов на задания типа а с выбором ответа из предложенных вариантов…. |
 | Документи 1. /муниципальное задание 2012/3 квартал.doc 2. /муниципальное… |  | Документи 1. /егэ/В10.pdf 2. /егэ/прототипы заданий… |
 | Документи 1. /Задания/Авторские решения/Задание 1.doc 2. /Задания/Задание… |  | Егэ по химии – 2012. Задания с (Мысленный эксперимент) В 2012 году задание с 2 предложено в новом формате. В условии задания предложено описание конкретного химического эксперимента, ход… |
 | Отчет об исполнении муниципального задания за 2012 год Причины отклонения (в случае, если задание исполнено менее чем на 45% или более чем на 55%) |  | Мкоу «Еландинская основная общеобразовательная школа» План подготовки учащихся к гиа (2012 – 2013 учебный год) Предварительное знакомство уч-ся и родителей с документами гиа-2012г,анализ итогов гиа-2012г |
 | Школьный этап олимпиады по географии 2012-2013 учебный год Задания для 9 классов Задание 1 Определите географические объекты: 2 моря, 1 пролив, 2 залива, 1 остров, 2 полуострова, 5 рек, 1 канал, 2 озера, и 4 города |
Разместите кнопку на своём сайте:
Документы
База данных защищена авторским правом ©lib2.podelise.ru 2000-2013
При копировании материала обязательно указание активной ссылки открытой для индексации.
обратиться к администрации

![Найдите наибольшее значение функции y=-x^3+x^2+x+2 на отрезке [0;2].](https://www.mathm.ru/zad/ege/zad11/1.png)
![Найдите наименьшее значение функции y=2x^3-15x^2+24x-2 на отрезке [0;5].](https://www.mathm.ru/zad/ege/zad11/32.png)
![Найдите наибольшее значение функции y=ln(x+1)-x+3на отрезке [-0,5;3].](https://www.mathm.ru/zad/ege/zad11/2.png)


![Найдите наименьшее значение функции y=4√x-x-2 на отрезке [0;1].](https://www.mathm.ru/zad/ege/zad11/5.png)
![Найдите наименьшее значение функции y=e^x (2x+2)на отрезке [-1;0].](https://www.mathm.ru/zad/ege/zad11/6.png)
![Найдите наименьшее значение функции y=e^x (x^2-2)на отрезке [-2;0].](https://www.mathm.ru/zad/ege/zad11/7.png)
![Найдите наибольшее значение функции y=1/π sinπx-x/2+3+1/6-√3/2π на отрезке [0;1].](https://www.mathm.ru/zad/ege/zad11/8.png)
![Найдите наименьшее значение функции y=tg x-x+3 на отрезке [0;π/4].](https://www.mathm.ru/zad/ege/zad11/9.png)
![Найдите наименьшее значение функции y=e^x (3x^2-2x+2) на отрезке [-1;3].](https://www.mathm.ru/zad/ege/zad11/10.png)

![Найдите наибольшее значение функции y=e^(2-x) (x-1)на отрезке [0;5].](https://www.mathm.ru/zad/ege/zad11/12.png)
![Найдите наибольшее значение функции y=ln(2-x)^2+2x-2на отрезке [0;1,5].](https://www.mathm.ru/zad/ege/zad11/13.png)

![Найдите наименьшее значение функции y=-2 cosx+3x-1 на отрезке [0;π].](https://www.mathm.ru/zad/ege/zad11/15.png)
![Найдите наименьшее значение функции y=12 sin(x)+5cos(x)+1. на отрезке [-π;π].](https://www.mathm.ru/zad/ege/zad11/44.png)
![Найдите наибольшее значение функции y=3 sin(x)+4cos(x)-2. на отрезке [0;2π].](https://www.mathm.ru/zad/ege/zad11/45.png)

![Найдите наименьшее значение функции y=x-√(4x-3).на отрезке [0,75;4].](https://www.mathm.ru/zad/ege/zad11/35.png)


![Найдите наименьшее значение функции y=ln(x^2-x+1)-x+4. на отрезке [0;2].](https://www.mathm.ru/zad/ege/zad11/43.png)



![Найдите наибольшее значение функции y=e^(2x-2) (x^2-4x+4).на отрезке [0;3].](https://www.mathm.ru/zad/ege/zad11/38.png)
![Найдите наименьшее значение функции y=e^(-3x-2) (x^2-6x+9).на отрезке [0;5,5].](https://www.mathm.ru/zad/ege/zad11/39.png)


![Найдите наименьшее значение функции y=e^(-x) (x^2-x+1)-1/e+2.на отрезке [0;2,1].](https://www.mathm.ru/zad/ege/zad11/40.png)


![Найдите наибольшее значение функции y=(x+1)^2 (x+4) на отрезке [-5;-1].](https://www.mathm.ru/zad/ege/zad11/24.png)


![Найдите наименьшее значение функции y=2√3 cos(2x)+2√3 x-(5√3 π)/6.на отрезке [0;π].](https://www.mathm.ru/zad/ege/zad11/46.png)

![Найдите наименьшее значение функции y=|x-5|+|x-4|. на отрезке [0;10].](https://www.mathm.ru/zad/ege/zad11/42.png)
![Найдите наименьшее значение функции y=4|x-1| √x+x^2-2x+2.на отрезке [0;4,5].](https://www.mathm.ru/zad/ege/zad11/41.png)


![Найдите наименьшее значение функции y=√(x^2+2x+2)-4 на отрезке [-4;0].](https://www.mathm.ru/zad/ege/zad11/29.png)


