Дано натуральное число A. Определите, каким по счету числом Фибоначчи оно является, то есть выведите такое число n, что φn = A. Если А не является числом Фибоначчи, выведите число -1.
a = int(input())
if a == 0:
print(0)
else:
fib_prev, fib_next = 0, 1
n = 1
while fib_next <= a:
if fib_next == a:
print(n)
break
fib_prev, fib_next = fib_next, fib_prev + fib_next
n += 1
else:
print(-1)
Числа Фибоначчи – это ряд чисел, в котором каждое последующее число равно сумме двух предыдущих:
1, 1, 2, 3, 5, 8, 13 и т. д.
То есть последовательность всегда начинается с двух единиц. А каждое следующее число является определяется по формуле:

Для определения чисел Фибоначчи часто используется рекурсивный алгоритм:
- Если n = 1 или n = 2, вернуть 1 (поскольку первый и второй элементы ряда Фибоначчи равны 1).
- Вызвать рекурсивно функцию с аргументами n-1 и n-2.
- Результат двух вызовов сложить и вернуть полученное значение.
Реализация с использованием рекурсии
Реализация на Си
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int fibonacci(int N) // рекурсивная функция
{
if (N == 1 || N == 2)
return 1; // первые 2 числа равны 1
return fibonacci(N — 1) + fibonacci(N — 2); // складываем предыдущие 2 числа
}
int main()
{
int N;
printf(«N=»);
scanf(«%d», &N); // вводим число N
for (int i = 1; i <= N; i++) // В цикле выводим N чисел Фибоначчи
printf(«%d «, fibonacci(i));
getchar(); getchar();
return 0;
}
Результат выполнения

У решения с рекурсией есть большая проблема: пересекающиеся вычисления. Когда вызывается fibonacci(N), то подсчитываются значения функции N-1 и для N-2. Но если требуется вычислить fibonacci(N-1), то значения для N-2 и N-3 вычисляются заново.
Поэтому поставленную задачу определения чисел Фибоначчи можно решить без использования рекурсии.
Реализация с использованием цикла
В этом алгоритме используется свойство, что для определения следующего числа Фибоначчи используются только два предыдущих значения.
Алгоритм при этом будет следующий
- Ввести номер N определяемого элемента.
- Проинициализировать два первых элемента a и b значениями 1, и если N<=2 вывести 1
- Выполнять нижеследующие действия N-2 раза
- Сложить a и b, присвоив результат третьей переменной c.
- Поменять начальные значения: a = b, b = c
- Вывести значение b.
Реализация на Си
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <stdio.h>
int main()
{
int N;
printf(«N=»); // вводим число N
scanf(«%d», &N);
int a = 1, b = 1, c;
if (N <= 2) // Первые два числа (a и b) равны 1
printf(«1 «);
else
{
for (int i = 3; i <= N; i++)
{
c = a + b; // вычисляем следующее число как сумму двух предыдущих
a = b; b = c; // перемещаем два предыдущих числа
}
printf(«%d «, b); // выводим последнее число
}
getchar(); getchar();
return 0;
}
Результат выполнения — такой же, как в предыдущем случае.
Назад: Алгоритмизация
Сегодня предлагаю решить разминочную задачу по информатике на циклы.
Задача: Вывести на экран элемент ряда Фибоначчи по его порядковому номеру. Например, если на ввод поступило число 7, то программа должна вывести 13.
Пояснение: Ряд Фибоначчи — это последовательность натуральных чисел, где каждое последующее число является суммой двух предыдущих: 1 1 2 3 5 8 13 21 34 55 89 …
Решение:
Для реализации программы будем использовать современный язык программирования C#. Данный язык в большинстве случаев подходит для участия в экзаменах и олимпиадах по информатике. Программа будет являться консольным приложением.
Т.к. в задаче не указаны никакие ограничение на максимальное значения введённого числа, то будем использовать самый емкий тип данный для целых положительных чисел — ulong. Диапазон данного типа: 0 : 18446744073709551615.
Реализация программы выглядит следующим образом (дополнительный код, связанный с консольным приложением опущен):
static void Main(string[] args)
{
ulong n = 0;
ulong res = 1;
ulong temp = 0;
//Считываем строку с клавиатуры
//и преобразовываем её в ulong
n = Convert.ToUInt64(Console.ReadLine());
for (ulong i = 1; i
В переменной res всегда формируется новый член последовательности. В переменной temp предыдущий член.
На этом всё! Не забывайте информатику и программирование!

Задача по информатике. Гуси и кролики.
Всем привет! Сегодня решим задачу по информатике «Гуси и кролики»…
Категория: Задачи Подкатегория: —
Дата: 15-01-2018 в 16:47:34
2
Задача
Вывести на экран ряд чисел Фибоначчи, состоящий из n элементов.
Числа Фибоначчи – это элементы числовой последовательности
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …, в которой каждое последующее число равно сумме двух предыдущих.
Решение
Описание переменных:
n – количество элементов ряда;
a, b – значения двух последних элементов ряда;
c – буферная («запасная») переменная;
i – счетчик.
Алгоритм решения задачи:
1. Получить значение n.
2. Присвоить a и b значения 0 и 1 соответственно (это первые числа ряда Фибоначчи). Вывести их на экран.
3. Начиная с 3-го элемента по n,
a. выводить на экран сумму a и b,
b. сохранить значение переменной b в c,
c. записать в b сумму a и b,
d. присвоить a значение с.
Программа на языке Паскаль:
var a,b,c,i,n: integer; begin write('n = '); readln(n); a := 0; write(a,' '); b := 1; write(b,' '); for i:=3 to n do begin write(a+b,' '); c := b; b := a + b; a := c end; readln end.
Условие
Дано натуральное число A. Определите, каким по счету числом Фибоначчи оно является, то есть выведите такое число n, что φn = A. Если А не является числом Фибоначчи, выведите число -1.
Решение задачи от разработчиков на Python:
Copy to Clipboard
Другая реализация задачи на Python:
Смотреть видео — Задача «Номер числа Фибоначчи» решение на Python
Делитесь с друзьями ссылкой на ответ и задавайте вопросы в комментариях! 👇
Задача «Список квадратов»
Условие
По данному целому числу N распечатайте все квадраты натуральных чисел, не превосходящие N, в порядке возрастания.

Задача «Минимальный делитель»
Условие
Дано целое число, не меньшее 2. Выведите его наименьший натуральный делитель, отличный от 1.

d
Задача «Утренняя пробежка»
Условие
В первый день спортсмен пробежал x километров, а затем он каждый день увеличивал пробег на 10% от предыдущего значения. По данному числу y определите номер дня, на который пробег спортсмена составит не менее y километров.
Программа получает на вход действительные числа x и y и должна вывести одно натуральное число.

Задача «Длина последовательности»
Условие
Программа получает на вход последовательность целых неотрицательных чисел, каждое число записано в отдельной строке. Последовательность завершается числом 0, при считывании которого программа должна закончить свою работу и вывести количество членов последовательности (не считая завершающего числа 0). Числа, следующие за числом 0, считывать не нужно.

Задача «Сумма последовательности»
Условие
Определите сумму всех элементов последовательности, завершающейся числом 0. В этой и во всех следующих задачах числа, следующие за первым нулем, учитывать не нужно.

Задача «Среднее значение последовательности»
Условие
Определите среднее значение всех элементов последовательности, завершающейся числом 0.

Задача «Максимум последовательности»
Условие
Последовательность состоит из натуральных чисел и завершается числом 0. Определите значение наибольшего элемента последовательности.

Задача «Индекс максимума последовательности»
Условие
Последовательность состоит из натуральных чисел и завершается числом 0. Определите индекс наибольшего элемента последовательности. Если наибольших элементов несколько, выведите индекс первого из них. Нумерация элементов начинается с нуля.

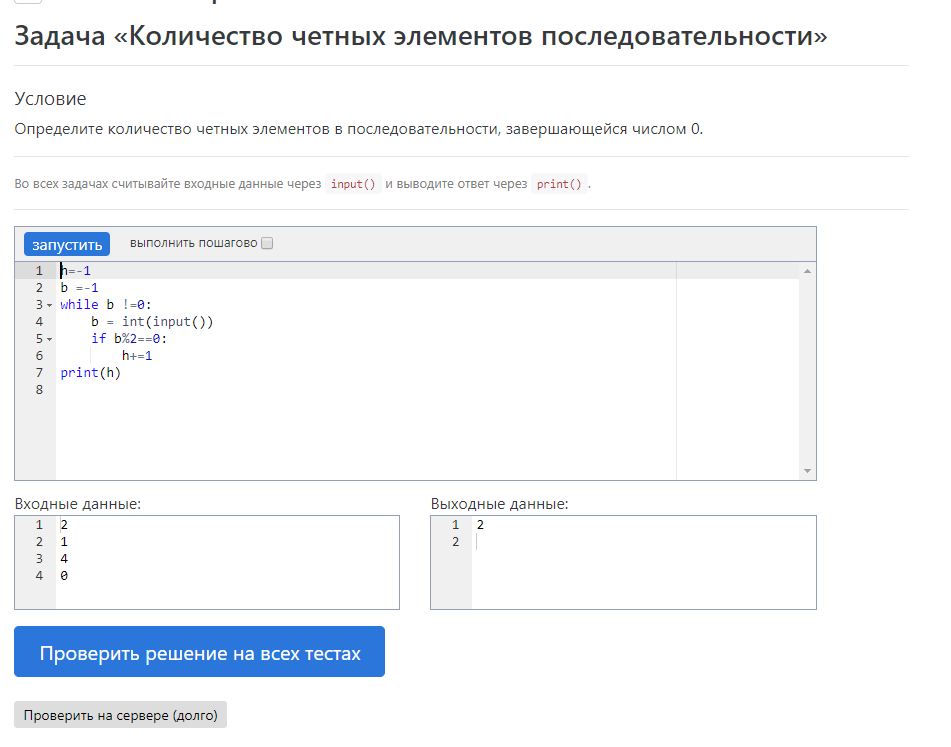
Задача «Количество четных элементов последовательности»
Условие
Определите количество четных элементов в последовательности, завершающейся числом 0.
Задача «Количество элементов, которые больше предыдущего»
Условие
Последовательность состоит из натуральных чисел и завершается числом 0. Определите, сколько элементов этой последовательности больше предыдущего элемента.

Задача «Второй максимум»
Условие
Последовательность состоит из различных натуральных чисел и завершается числом 0. Определите значение второго по величине элемента в этой последовательности. Гарантируется, что в последовательности есть хотя бы два элемента.

Задача «Количество элементов, равных максимуму»
Условие
Последовательность состоит из натуральных чисел и завершается числом 0. Определите, сколько элементов этой последовательности равны ее наибольшему элементу.

Задача «Числа Фибоначчи»
Условие
Последовательность Фибоначчи определяется так:
φ0 = 0, φ1 = 1, φn = φn−1 + φn−2.
По данному числу n определите n-е число Фибоначчи φn.

Задача «Номер числа Фибоначчи»
Условие
Дано натуральное число A. Определите, каким по счету числом Фибоначчи оно является, то есть выведите такое число n, что φn = A. Если А не является числом Фибоначчи, выведите число -1.

Задача «Максимальное число идущих подряд равных элементов»
Условие
Дана последовательность натуральных чисел, завершающаяся числом 0. Определите, какое наибольшее число подряд идущих элементов этой последовательности равны друг другу.

Задача «Стандартное отклонение»
Условие
Дана последовательность натуральных чисел x1x1, x2x2, …, xnxn. Стандартным отклонением называется величинаσ=(x1−s)2+(x2−s)2+…+(xn−s)2n−1−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√σ=(x1−s)2+(x2−s)2+…+(xn−s)2n−1где s=x1+x2+…+xnns=x1+x2+…+xnn — среднее арифметическое последовательности.
Определите стандартное отклонение для данной последовательности натуральных чисел, завершающейся числом 0.

На чтение 3 мин Просмотров 627 Опубликовано 18 июня, 2022 Обновлено 18 июня, 2022
Числа Фибоначчи – это ряд чисел, в котором каждое следующее число равно сумме двух предыдущих.
1, 1, 2, 3, 5, 8, 13, …
Иногда ряд начинают с нуля.
0, 1, 1, 2, 3, 5, 8, …
В данном случае мы будем придерживаться первого варианта.

Содержание
- Вычисление n-го числа ряда Фибоначчи с помощью цикла while
- Вывод чисел Фибоначчи циклом for
- Рекурсивное вычисление n-го числа ряда Фибоначчи
Вычисление n-го числа ряда Фибоначчи с помощью цикла while
Присвоим переменным fib1 и fib2 значения двух первых элементов ряда, то есть единицы.
Получим от пользователя номер элемента, значение которого требуется вычислить. Присвоим номер элемента переменной n.
Поскольку значения первых двух элементов ряда Фибоначчи нам уже известны и вычисления начинаем с третьего, количество проходов по телу цикла должно быть на 2 меньше значения n, то есть n - 2.
Если пользователь вводит 1 или 2, тело цикла ни разу не выполняется, на экран выводится исходное значение fib2.
В теле цикла выполнять следующие действия:
- Сложить fib1 и fib2, присвоив результат переменной для временного хранения данных, например, fib_sum.
- Переменной fib1 присвоить значение fib2.
- Переменной fib2 присвоить значение fib_sum.
После окончания работы цикла вывести значение fib2 на экран.
fib1 = 1
fib2 = 1
n = input("Номер элемента ряда Фибоначчи: ")
n = int(n)
i = 0
while i < n - 2:
fib_sum = fib1 + fib2
fib1 = fib2
fib2 = fib_sum
i = i + 1
print("Значение этого элемента:", fib2)Пример выполнения программы:
Номер элемента ряда Фибоначчи: 10
Значение этого элемента: 55Компактный вариант кода:
fib1 = fib2 = 1
n = input("Номер элемента ряда Фибоначчи: ")
n = int(n) - 2
while n > 0:
fib1, fib2 = fib2, fib1 + fib2
n -= 1
print("Значение этого элемента:", fib2)Вывод чисел Фибоначчи циклом for
В данном случае выводится не только значение искомого элемента ряда Фибоначчи, но и все числа до него включительно. Для этого вывод значения fib2 помещен в цикл.
fib1 = fib2 = 1
n = int(input())
print(fib1, fib2, end=' ')
for i in range(2, n):
fib1, fib2 = fib2, fib1 + fib2
print(fib2, end=' ')Пример выполнения:
10
1 1 2 3 5 8 13 21 34 55 Рекурсивное вычисление n-го числа ряда Фибоначчи
- Если n = 1 или n = 2, вернуть в вызывающую ветку единицу, так как первый и второй элементы ряда Фибоначчи равны единице.
- Во всех остальных случаях вызвать эту же функцию с аргументами n — 1 и n — 2. Результат двух вызовов сложить и вернуть в вызывающую ветку программы.
def fibonacci(n):
if n in (1, 2):
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
print(fibonacci(10))
Допустим, n = 4. Тогда произойдет рекурсивный вызов fibonacci(3) и fibonacci(2). Второй вернет единицу, а первый приведет к еще двум вызовам функции: fibonacci(2) и fibonacci(1). Оба вызова вернут единицу, в сумме будет два. Таким образом, вызов fibonacci(3) возвращает число 2, которое суммируется с числом 1 от вызова fibonacci(2). Результат 3 возвращается в основную ветку программы. Четвертый элемент ряда Фибоначчи равен трем: 1 1 2 3.
( 1 оценка, среднее 5 из 5 )
