 2013г.ВыбранВыбрать
2013г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №457 по учебнику Математика. 5 класс : учебник для учащихся общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 31 издание 2013г.
 2019г.ВыбранВыбрать
2019г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №457 по учебнику Математика. 5 класс : учебник для учащихся общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37 издание 2019г.
Условие
20132019г.
От деревни до города велосипедист ехал 4 ч со скоростью 12 км/ч. Сколько времени он потратит на обратный путь по той же дороге, если увеличит скорость на 4 км/ч?
От деревни до города велосипедист ехал 4 ч со скоростью 12 км/ч. Сколько времени он потратит на обратный путь по той же дороге, если увеличит скорость на 4 км/ч?
Решение 1
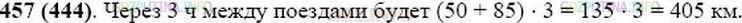
Решение 1
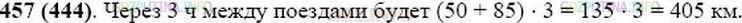
Решение 2

Решение 2

Решение 3

Решение 3

Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
Показать содержание
← Предыдущее
Следующее →
Решебник №1
глава 1 / 457

Решебник №2
глава 1 / 457

Решебник №3
глава 1 / 457


Решебник №4
глава 1 / 457


Решебник №6
глава 1 / 457

Решебник №7
глава 1 / 457

Показать содержание
← Предыдущее
Следующее →
Задание 456. а) Проведите необходимые измерения и найдите площадь: тетрадного листа, крышки стола, классной доски, классной комнаты, спортивной площадки.
б) Что больше: площадь классной доски или 1 $м^2$; площадь классной комнаты или 1 сотка; площадь спортивной площадки или 1 гектар?
Решение
а) 1) 15 * 21 = 315 $(см^2)$ − площадь тетрадного листа;
2) 8 * 15 = 120 $(дм^2)$ − площадь крышки стола;
3) 10 * 17 = 170 $(дм^2)$ − площадь классной доски;
4) 5 * 8 = 40 $(м^2)$ − площадь классной комнаты;
5) 70 * 20 = 1400 $(м^2)$ − площадь спортивной площадки.
Ответ: 315 $см^2$; 120 $дм^2$; 170 $дм^2$; 40 $м^2$; 1400 $м^2$.б) 1) 1 $м^2$ = 100 $дм^2$;
100 $дм^2$ < 170 $дм^2$ − площадь классной доски больше, чем 1 $м^2$;
2) 1 сотка − 100 $м^2$;
100 $м^2$ > 40 $м^2$ − 1 сотка больше, чем площадь классной комнаты;
3) 1 га = 10000 $м^2$;
10000 $м^2$ > 1400 $(м^2)$ − 1 га больше, чем площадь спортивной площадки.
Ответ: площадь классной доски; 1 сотка; 1 га.
Задание 457. а) У прямоугольного участка земли ширина 25 м, а длина 60 м. Какова площадь участка? Ответ выразите в сотках.
б) Поле имеет форму прямоугольника со сторонами 500 м и 380 м. Какова площадь поля? Ответ выразите в гектарах.
Решение
а) 25 * 60 = 1500 $(м^2)$ = 15 (соток) − площадь участка.
Ответ: 15 соток.б) 500 * 380 = 190000 $(м^2)$ = 19 (га) − площадь поля.
Ответ: 19 га.
Задание 458. Многоугольники на рисунке 7.30,а−б разбиты на два прямоугольника. Вычислите площадь каждого многоугольника. Перенесите один из них в тетрадь и покажите, как еще можно разбить этот многоугольник на прямоугольники.
Решение
а) 3 * 3 + 1 * 5 = 9 + 5 = 14 $(см^2)$ − площадь фигуры.
Ответ: 14 $см^2$.б) 4 * 2 + 3 * 2 = 8 + 6 = 14 $(см^2)$ − площадь фигуры.
4 * 3 + 1 * 2 = 12 + 2 = 14 $(см^2)$ − площадь фигуры.
Ответ: 14 $см^2$.
Задание 459. На рисунке 7.31 закрашенная часть квадрата тоже квадрат. Найдите его площадь. Начертите квадрат, площадь которого равна 8 кв.ед.
Решение
1) 2 * 2 = 4 (кв.ед.) − площадь большого квадрата;
2) 4 : 2 = 2 (кв.ед.) − площадь закрашенного квадрата.
3) Если площадь закрашенного квадрата будет равна 8 кв.ед., то:
8 * 2 = 16 (кв.ед) − будет равна площадь большого квадрата и;
16 = 4 * 4 − значит, 4 ед. будет длина стороны большого квадрата.
Ответ: 2 кв.ед. − площадь закрашенного квадрата.
Задание 460. Начертите в тетради круг радиусом 3 см. Оцените площадь круга в квадратных сантиметрах. С помощью квадратной сетки попытайтесь оценить эту площадь более точно.
Решение
S ≈ 2 * 6 + 4 * 2 + 2 * 2 + 4 = 12 + 8 + 4 + 4 = 28 $(см^2)$ − примерная площадь круга.
Ответ: S ≈ 28 $см^2$
Задание 461. а) Периметр прямоугольника равен 30 см, одна из его сторон в 4 раза больше другой. Найдите площадь этого прямоугольника.
б) Периметр прямоугольника равен 28 см, одна из его сторон на 2 см больше другой. Найдите площадь этого прямоугольника.
Решение
а) Пусть ширина прямоугольника составляет 1 часть, тогда:
1) 1 * 4 = 4 (части) − составляет длина прямоугольника;
2) (1 + 4) * 2 = 5 * 2 = 10 (частей) − составляет периметр прямоугольника;
3) 30 : 10 = 3 (см) − ширина прямоугольника;
4) 3 * 4 = 12 (см) − длина прямоугольника;
5) 3 * 12 = 36 $(см^2)$ − площадь прямоугольника.
Ответ: 36 $см^2$.б) 1) 28 : 2 = 14 (см) − сумма двух смежных сторон прямоугольника;
2) 14 − 2 = 12 (см) − была бы сумма двух смежных сторон, если бы стороны были одинаковы;
3) 12 : 2 = 6 (см) − ширина прямоугольника;
4) 6 + 2 = 8 (см) − длина прямоугольника;
5) 6 * 8 = 48 $(см^2)$ − площадь прямоугольника.
Ответ: 48 $см^2$.
Задание 462. ЗАДАЧА−ИССЛЕДОВАНИЕ
1) Площадь прямоугольника равна 36 $см^2$. Какими могут быть длины его сторон, если они выражены в сантиметрах? Рассмотрите все возможные варианты.
2) Для каждого варианта длин сторон вычислите периметр прямоугольника. Какой из этих прямоугольников имеет наибольший периметр?
Решение
1) 36 = 1 * 36;
36 = 2 * 18;
36 = 3 * 12;
36 = 4 * 9;
36 = 6 * 6.
Ответ: длины сторона прямоугольника, площадь которого 36 $см^2$, могут быть:
1 см и 36 см;
2 см и 18 см;
3 см и 12 см;
4 см и 9 см;
6 см и 6 см, то есть прямоугольник может быть квадратом со стороной 6 см.2) 1) (1 + 36) * 2 = 37 * 2 = 74 (см) − периметр прямоугольника со сторонами 1 см и 36 см;
2) (2 + 18) * 2 = 20 * 2 = 40 (см) − периметр прямоугольника со сторонами 2 см и 18 см;
3) (3 + 12) * 2 = 15 * 2 = 30 (см) − периметр прямоугольника со сторонами 3 см и 12 см;
4) (4 + 9) * 2 = 13 * 2 = 26 (см) − периметр прямоугольника со сторонами 4 см и 9 см;
5) 6 * 4 = 24 (см) − периметр квадрата со стороной 6 см;
6) 74 > 40 > 30 > 26 > 24 − периметр прямоугольника со сторонами 1 см и 36 см наибольший.
Ответ: 74 см, 40 см, 30 см, 26 см, 24 см; периметр прямоугольника со сторонами 1 см и 36 см наибольший.





