
Авторы: , В.Б. Полонский, М.С. Якир.
Издательства:
Просвещение, Вентана-граф 2016-2021
Тип: Учебник, Алгоритм успеха
Подробный решебник (ГДЗ) по Математике за 5 (пятый) класс — готовый ответ номер — 302. Авторы учебника: Мерзляк, Полонский, Якир. Издательство: Вентана-граф 2016-2021.
Условие /
номер / 302
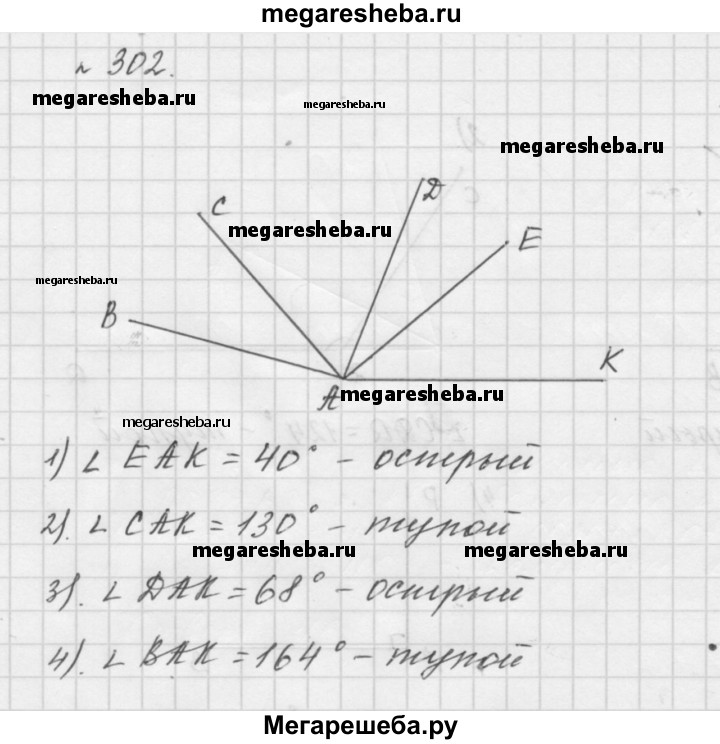
302. Проведите луч. Отложите от этого луча угол, градусная мера которого равна:
1) 40°;
2) 130°;
3) 68°;
4) 164°. Определите вид каждого из построенных углов.
Решебник №1 к учебнику 2015 / номер / 302
Решебник к учебнику 2021 / номер / 302

Видеорешение / номер / 302
Решебник №2 к учебнику 2015 / номер / 302

Оцените решебник:
4.4/5

20150
- Категория: ГДЗ Математика учебник 5 класс Бунимович, Дорофеев, Суворова
Задание 302. а) Сколько треугольников на рисунке 5.27?
б) Сколько четырехугольников на рисунке 5.28?
в) Найдите все 35 треугольников на рисунке 5.29.
Решение
а) Ответ: 6 треугольников
б) Ответ: 9 четырехугольников
в) AOB, BOF, CFG, AOK, AKE, EKH, EHD, HDG, DGC, CGF, BFC, AFB, ACB, BOC, AKB, ABE, AOE, AEH, EKD, AED, EDC, EGD, HDC, DBC, DFC, GCB, ACD, BED, CAE, ACH, EOC, BKD, FAD, GBE, ACE.
Задание 303. ЗАДАЧА−ИССЛЕДОВАНИЕ
Число диагоналей многоугольника можно подсчитать так:
• найти число диагоналей, выходящих из одной вершины, − их на 3 меньше, чем вершин (рисунок справа);
• умножить это число на число вершин;
• разделить результат на 2 (объясните почему).
Сколько диагоналей у семиугольника? десятиугольника? стоугольника? У какого многоугольника 9 диагоналей?
Решение
При подсчете каждая диагональ учитывается 2 раза, так как диагональ соединяет 2 вершины многоугольника и подсчет выполняется для каждой вершины. Поэтому полученный результат нужно разделить на 2.
Семиугольник:
1) 7 − 3 = 4 (диагонали) − выходит из каждой вершины;
2) 4 * 7 = 28 (диагоналей) − удвоенное количество;
3) 28 : 2 = 14 (диагоналей) − в семиугольнике.Десятиугольник:
1) 10 − 3 = 7 (диагоналей) − выходит из каждой вершины;
2) 7 * 10 = 70 (диагоналей) − удвоенное количество;
3) 70 : 2 = 35 (диагоналей) − в десятиугольнике.Стоугольник:
1) 100 − 3 = 97 (диагоналей) − выходит из каждой вершины;
2) 97 * 100 = 9700 (диагоналей) − удвоенное количество;
3) 9700 : 2 = 4850 (диагоналей) − в стоугольнике.Пусть a (вершин) в многоугольнике, тогда:
1) a − 3 (диагоналей) − выходит из каждой вершины;
2) a(a − 3) (диагоналей) − удвоенное количество;
3) a(a − 3) : 2 = 9 (диагоналей) − в многоугольнике;
a(a − 3) = 9 * 2
a(a − 3) = 18
18 = 3 * 6 = 9 * 2
Путем подбора можно вычислить, что a = 6, т.к.:
6 * (6 − 3) = 18
6 * 3 = 18
Значит у шестиугольника 9 диагоналей.Ответ: 14 диагоналей; 35 диагоналей; 4850 диагоналей; у шестиугольника.
Задание 304. Найдите периметр треугольника, изображенного на рисунке 5.30.
Решение
P = 3 + 4 + 5 = 12 (см)
Ответ: 12 см.
Задание 305. Чему равен периметр треугольника ABC со сторонами:
а) AB = 3 см, BC = 4 см 5 мм, AC = 5 см 3 мм;
б) AB = BC = 4 см, AC = 7 см 3 мм;
в) AB = BC = AC = 9 см?
Решение
а) P = AB + BC + AC = 3 см + 4 см 5 мм + 5 см 3 мм = (3 + 4 + 5) см + (5 + 3) мм = 12 см 8 мм
Ответ: 12 см 8 ммб) P = AB + BC + AC = 4 см + 4 см + 7 см 3 мм = (4 + 4 + 7) см + 3 мм = 15 см 3 мм
Ответ: 15 см 3 ммв) P = AB + BC + AC = 9 + 9 + 9 = 27 см
Ответ: 27 см
Задание 306. Выполнив необходимые измерения, найдите периметр многоугольников, изображенных на рисунках 5.25, 5.26.
Решение
P DHFE = DH + HF + FE + EP = 1 см 5 мм + 2 см 5 мм + 2 см 5 мм + 1 см 5 мм = (1 + 2 + 2 + 1) см + (5 + 5 + 5 + 5) мм = 6 см + 20 мм = 6 см + 2 см = 8 см;
P TKMNP = TK + KM + MN + NP + PT = 2 см + 1 см 5 мм + 1 см 5 мм + 2 см + 1 см = (2 + 1 + 1 + 2 + 1) см + (5 + 5) мм = 7 см + 10 мм = 7 см + 1 см = 8 см.
Ответ: 8 см; 8 см.
Задание 307. Выполнив необходимые измерения, найдите периметр четырехугольник, изображенного на рисунке 5.31.
Решение
P ABCD = AB + BC + CD + DA = 4 см 5 мм + 3 см 1 мм + 4 см 3 мм + 4 см = (4 + 3 + 4 + 4)см + (5 + 1 + 3)мм = 15 см + 9 мм = 15 см 9 мм
Ответ: 15 см 9 мм.
Задание 308. Периметр четырехугольника KOPT равен 17 см, KO = 5 см, OP = 6 см, PT = KT. Найдите сторону KT.
Решение
P KOPT = KO + OP + PT + KT, тогда:
1) KO + OP = 5 см + 6 см = 11 (см);
2) PT + KT = P KOPT − (KO + OP) = 17 см − 11 см = 6 (см);
3) KT = (PT + KT) : 2 = 6 : 2 = 3 (см).
Ответ: 3 см.

 Ответы к учебнику за пятый класс «Математика. Арифметика и геометрия», авторы учебника: Е.А.Бунимович, Г.В.Дорофеев, С.Б.Суворова. Мы ни на минуту не сомневаемся, что вы и самостоятельно можете с легкостью выполнить все эти задания, найти ответы и решить все задачи без нашего решебника. Но ГДЗ на 7 гуру поможет вам очень быстро проверить, правильно ли выполнено домашнее задание.
Ответы к учебнику за пятый класс «Математика. Арифметика и геометрия», авторы учебника: Е.А.Бунимович, Г.В.Дорофеев, С.Б.Суворова. Мы ни на минуту не сомневаемся, что вы и самостоятельно можете с легкостью выполнить все эти задания, найти ответы и решить все задачи без нашего решебника. Но ГДЗ на 7 гуру поможет вам очень быстро проверить, правильно ли выполнено домашнее задание.
В учебнике вам может встретиться обозначение дроби через косую черту, например 1/2. В тетрадь это записывать как $frac12$.
Если дроби приводятся к общему знаменателю, числитель и знаменатель умножают на одно и то же число, и это число мелко пишут над дробью: 1/2(3 = 3/6. Это то же самое, что $frac{1^{(3}}{2;;}=frac36$
Запись смешанных дробей: 3_1/2 это то же самое что $3frac12$.
ПЕРЕЙТИ К СПИСКУ СТРАНИЦ УЧЕБНИКА МАТЕМАТИКА 5 КЛАСС БУНИМОВИЧ >>
Показать содержание
← Предыдущее
Следующее →
Решебник 1
глава 2 / §12 / 302

Решебник 2
глава 2 / §12 / 302

Решебник 3
глава 2 / §12 / 302

Решебник 4
глава 2 / §12 / 302

Решебник 5
глава 2 / §12 / 302







Решебник 6
глава 2 / §12 / 302

Решебник 7
глава 2 / §12 / 302

Показать содержание
← Предыдущее
Следующее →
Все ГДЗ по
Математике
5 класс
Алгоритм успеха
