Алгебра. Мерзляк 9 класс Контрольная 2 в 4-х вариантах с ответами. Контрольная работа по алгебре в 9 классе «Функция. Квадратичная функция, её график и свойства» для УМК Мерзляк, Полонский, Якир. Транскрипт заданий. Ответы на все варианты.
Вернуться к Списку контрольных работ (Оглавление)
Алгебра 9 класс (УМК Мерзляк)
Контрольная работа № 2
Тема: Функция. Квадратичная функция, её график и свойства
Вариант 1 (задания)

Вариант 2 (задания)
- Функция задана формулой f(х) = х2/4 – х. Найдите: 1) f(–2) и f(3); 2) нули функции.
- Найдите область определения функции f (х) = (х + 2)/(х2 + х – 20).
- Постройте график функции f (х) = х2 – 2х – 8. Используя график, найдите:
1) область значений функции;
2) промежуток возрастания функции;
3) множество решений неравенства f (x) < 0. - Постройте график функции: 1) f (х) = √x – 2; 2) f (х) = √[х – 2].
- Найдите область определения функции f (х) = √[х – 1] + 2/(x2 – 9).
- При каких значениях b и c вершина параболы у = 3х2 + bx + c находится в точке A (–2; 1)?
Вариант 3 (задания)
- Функция задана формулой f (х) = х2/2 – 3х. Найдите: 1) f (2) и f (–3); 2) нули функции.
- Найдите область определения функции f (х) = (x – 5)/(x2 + x – 6).
- Постройте график функции f (х) = х2 – 2х – 3. Используя график, найдите:
1) область значений функции;
2) промежуток убывания функции;
3) множество решений неравенства f (x) < 0. - Постройте график функции: 1) f (х) = √x + 3; 2) f (х) = √[x + 3].
- Найдите область определения функции f (х) = √[х – 3] + 4/(x2 – 25).
- При каких значениях b и c вершина параболы у = –2х2 + bx + c находится в точке A (2; 1)?
Вариант 4 (задания)
- Функция задана формулой f (х) = х2/5 – 6х. Найдите: 1) f (5) и f (–1); 2) нули функции.
- Найдите область определения функции f (х) = (х + 6)/(х2 – 3 х – 4)
- Постройте график функции f (х) = х2 – 8х + 7. Используя график, найдите:
1) область значений функции;
2) промежуток возрастания функции;
3) множество решений неравенства f (x) > 0. - Постройте график функции: 1) f (х) = √х + 2; 2) f (х) = √[х + 2].
- Найдите область определения функции f (х) = √[x + 3] + 8/(х2 – 36).
- При каких значениях b и c вершина параболы у = –4х2 + bx + c находится в точке A (3; 1)?
ОТВЕТЫ на контрольную № 2
ОТВЕТЫ на Вариант 1
№ 1. Функция задана формулой f(x) = 1/3 • x2 – 2x. Найдите: 1) f(–6) и f(2); 2) нули функции.
ОТВЕТ: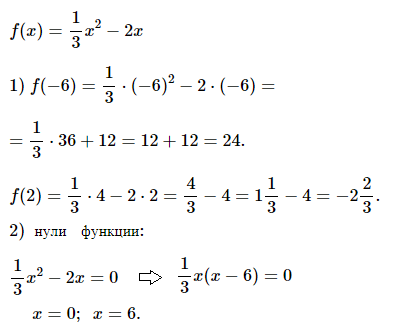
№ 2. Найдите область определения функции f(x) = (x – 4)/(x2 – x – 6).
Нажмите на спойлер, чтобы увидеть ОТВЕТ
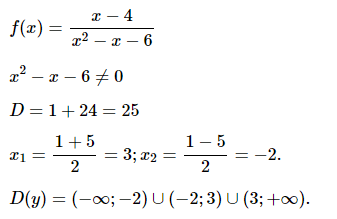
№ 3. Постройте график функции f(x) = x2 – 4x + 3. Используя график, найдите:
1) область значений функции;
2) промежуток убывания функции;
3) множество решений неравенства f(x) > 0.
Нажмите на спойлер, чтобы увидеть ОТВЕТ
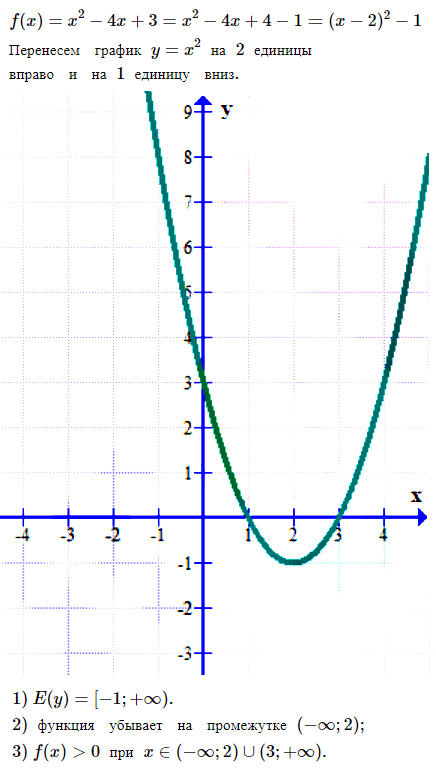
№ 4. Постройте график функции: 1) f (x) = √x +1; 2) f (x) = √[x + 1].
Нажмите на спойлер, чтобы увидеть ОТВЕТ
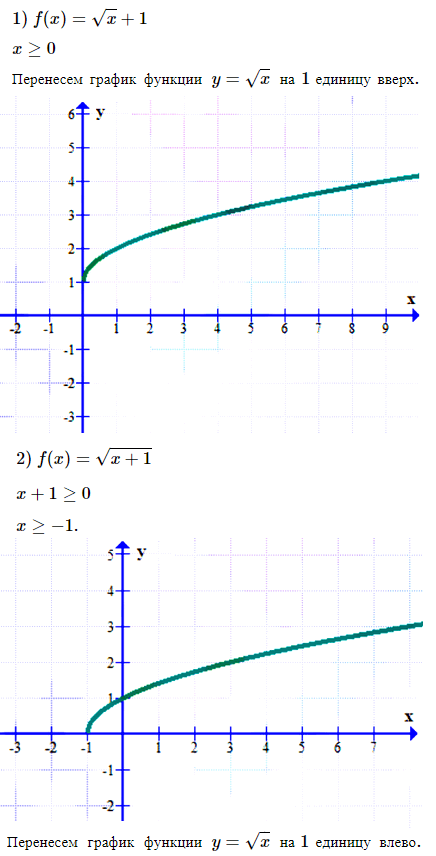
№ 5. Найдите область определения функции f (x) = √[x – 2] + 7/(x2 – 16).
Нажмите на спойлер, чтобы увидеть ОТВЕТ
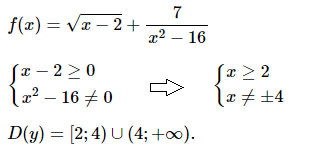
№ 6. При каких значениях b и c вершина параболы y = 2х2 + bx + c находится в точке A (–3; –2)?
Нажмите на спойлер, чтобы увидеть ОТВЕТ
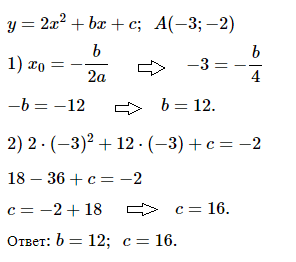
ОТВЕТЫ на Вариант 2
№ 1. Функция задана формулой f(х) = х2/4 – х.
Найдите: 1) f(–2) и f(3); 2) нули функции.
ОТВЕТ: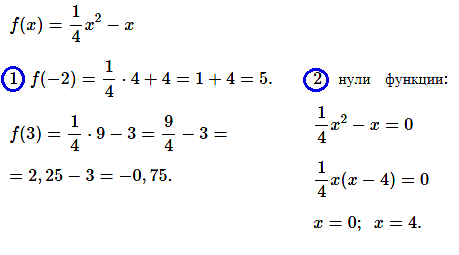
№ 2. Найдите область определения функции f (х) = (х + 2)/(х2 + х – 20).
Нажмите на спойлер, чтобы увидеть ОТВЕТ
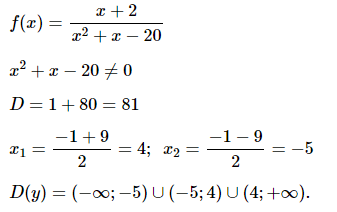
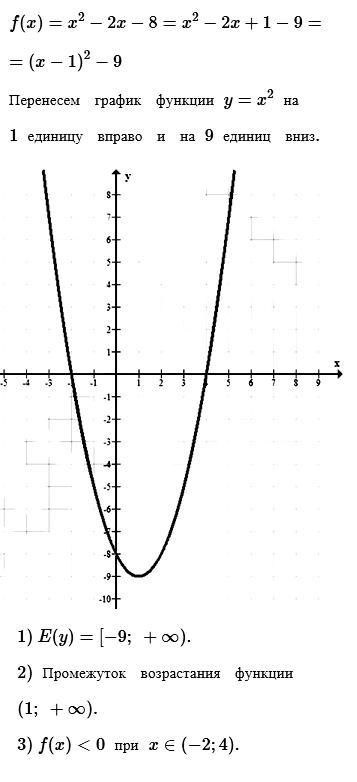
№ 3. Постройте график функции f (х) = х2 – 2х – 8. Используя график, найдите:
1) область значений функции;
2) промежуток возрастания функции;
3) множество решений неравенства f (x) < 0.
Нажмите на спойлер, чтобы увидеть ОТВЕТ
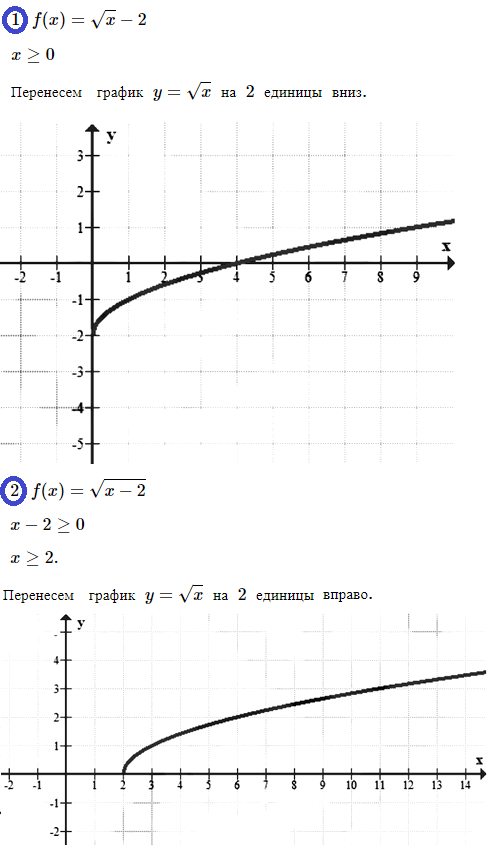
№ 4. Постройте график функции: 1) f (х) = √x – 2; 2) f (х) = √[х – 2].
Нажмите на спойлер, чтобы увидеть ОТВЕТ
№ 5. Найдите область определения функции f (х) = √[х – 1] + 2/(x2 – 9).
Нажмите на спойлер, чтобы увидеть ОТВЕТ
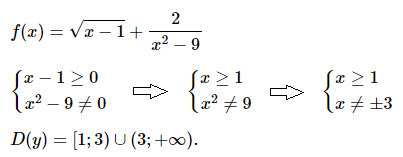
№ 6. При каких значениях b и c вершина параболы у = 3х2 + bx + c находится в точке A (–2; 1)?
Нажмите на спойлер, чтобы увидеть ОТВЕТ
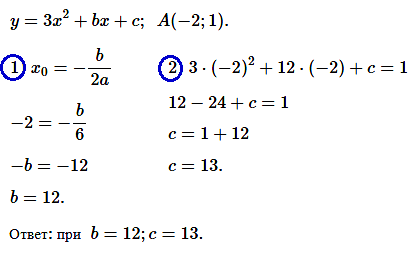
ОТВЕТЫ на Вариант 3
№ 1. Функция задана формулой f (х) = х2/2 – 3х. Найдите: 1) f (2) и f (–3); 2) нули функции.
ОТВЕТ: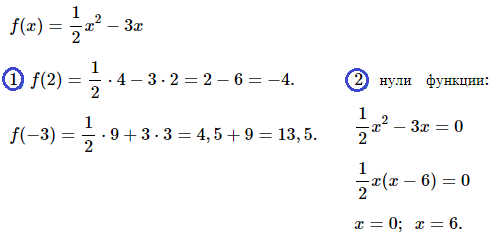
№ 2. Найдите область определения функции f (х) = (x – 5)/(x2 + x – 6).
Нажмите на спойлер, чтобы увидеть ОТВЕТ
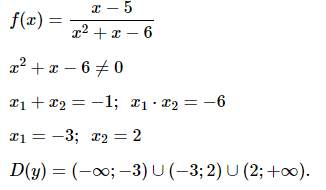
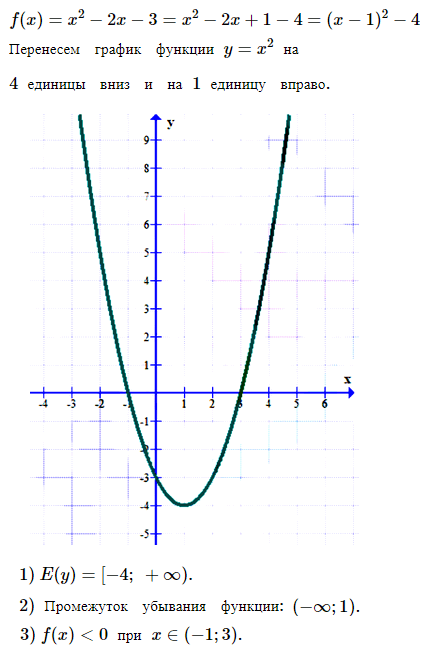
№ 3. Постройте график функции f (х) = х2 – 2х – 3. Используя график, найдите:
1) область значений функции;
2) промежуток убывания функции;
3) множество решений неравенства f (x) < 0.
Нажмите на спойлер, чтобы увидеть ОТВЕТ
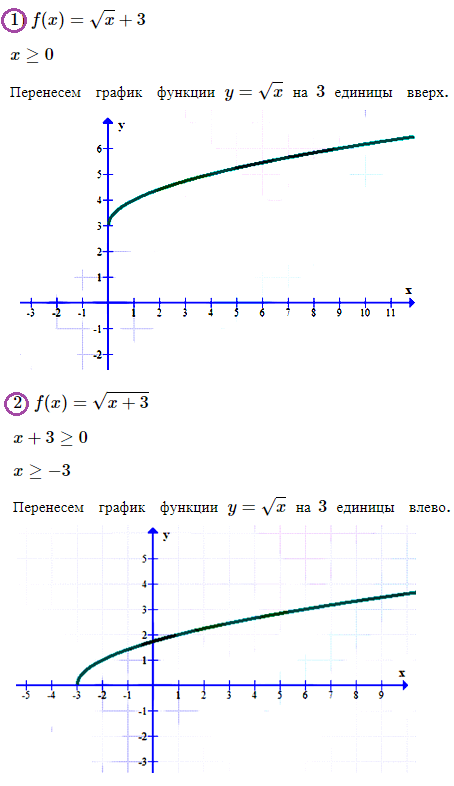
№ 4. Постройте график функции: 1) f (х) = √x + 3; 2) f (х) = √[x + 3].
Нажмите на спойлер, чтобы увидеть ОТВЕТ
№ 5. Найдите область определения функции f (х) = √[х – 3] + 4/(x2 – 25).
Нажмите на спойлер, чтобы увидеть ОТВЕТ
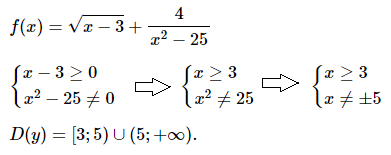
№ 6. При каких значениях b и c вершина параболы у = –2х2 + bx + c находится в точке A (2; 1)?
Нажмите на спойлер, чтобы увидеть ОТВЕТ
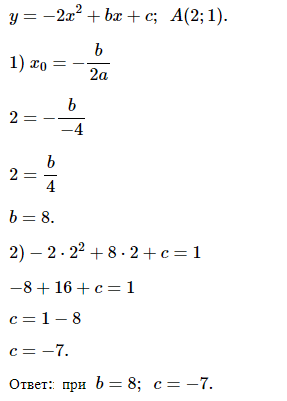
ОТВЕТЫ на Вариант 4
№ 1. Функция задана формулой f (х) = х2/5 – 6х. Найдите: 1) f (5) и f (–1); 2) нули функции.
ОТВЕТ: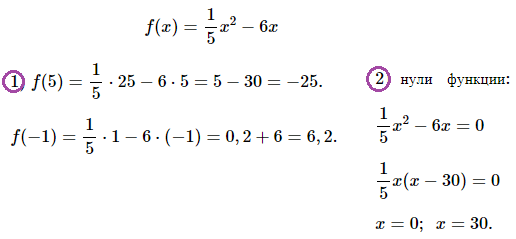
№ 2. Найдите область определения функции f (х) = (х + 6)/(х2 – 3 х – 4)
Нажмите на спойлер, чтобы увидеть ОТВЕТ
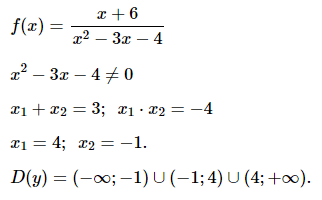
№ 3. Постройте график функции f (х) = х2 – 8х + 7. Используя график, найдите:
1) область значений функции;
2) промежуток возрастания функции;
3) множество решений неравенства f (x) > 0.
Нажмите на спойлер, чтобы увидеть ОТВЕТ
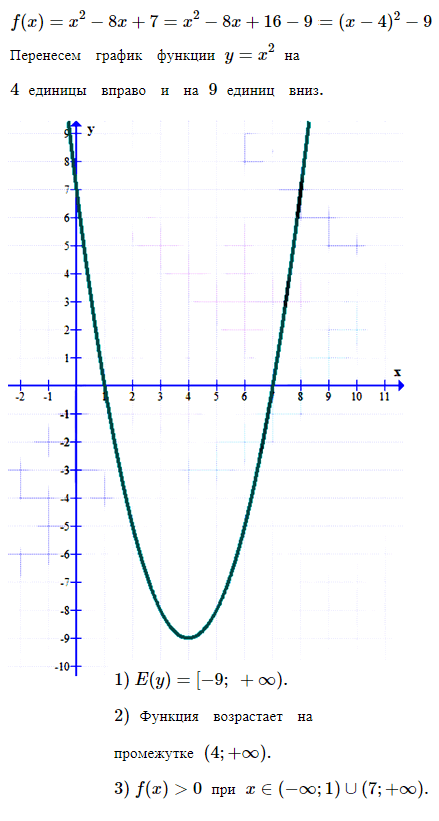
№ 4. Постройте график функции: 1) f (х) = √х + 2; 2) f (х) = √[х + 2].
Нажмите на спойлер, чтобы увидеть ОТВЕТ
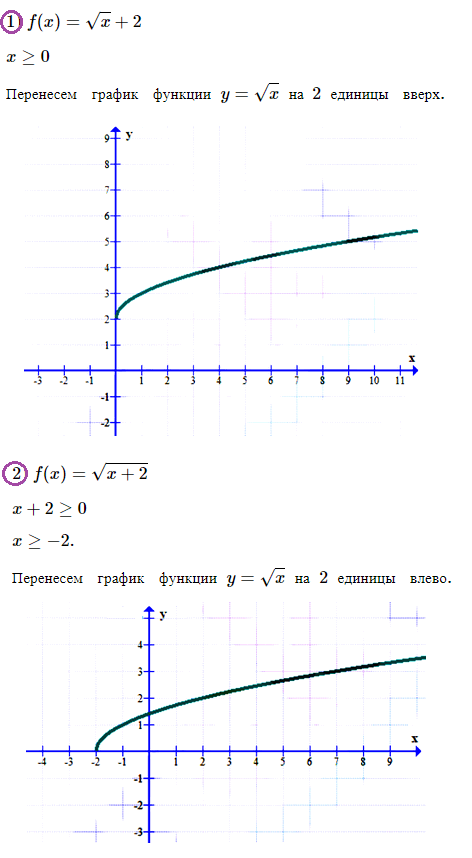
№ 5. Найдите область определения функции f (х) = √[x + 3] + 8/(х2 – 36).
Нажмите на спойлер, чтобы увидеть ОТВЕТ
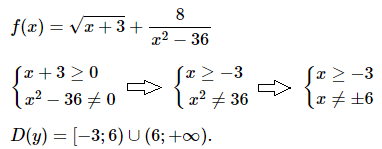
№ 6. При каких значениях b и c вершина параболы у = –4х2 + bx + c находится в точке A (3; 1)?
Нажмите на спойлер, чтобы увидеть ОТВЕТ
Вернуться к Списку контрольных работ по алгебре 9 класс (Мерзляк)
Вы смотрели: Алгебра. Мерзляк 9 класс Контрольная 2 в 4-х вариантах. Контрольная работа по математике в 9 классе «Функция. Квадратичная функция, её график и свойства» по УМК Мерзляк, Полонский, Якир.
Цитаты из пособия «Алгебра 9 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.
Контрольная работа 2 по алгебре «Квадратичная функция. Степенная функция. Корень n-ой степени» с ответами по УМК Макарычев (Просвещение). Поурочное планирование по алгебре для 9 класса. Глава I. КВАДРАТИЧНАЯ ФУНКЦИЯ. Урок 22. Контрольная работа по теме «Квадратичная функция. Степенная функция. Корень n-ой степени». Алгебра 9 Макарычев Контрольная № 2.
Смотреть Список контрольных по алгебре в 9 классе по УМК Макарычев
«Квадратичная функция. Степенная функция. Корень n-ой степени»
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
Общая характеристика контрольной работы
Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).
При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, оценка «4» — четырех задач и оценка «3» — трех задач. Одна задача является резервной (или запасной) и дает некоторую свободу выбора учащимся. При таких же критериях оценки за решение задач вариантов 3, 4 дается дополнительно 0,5 балла, вариантов 5, 6 — 1 балл (т. е. оценку «5» можно получить за правильное решение четырех задач).
Контрольная работа. Варианты 1, 2

Контрольная работа. Варианты 3, 4

Контрольная работа. Варианты 5, 6

ОТВЕТЫ на контрольную работу № 2
Ответы на Вариант 1
№ 1. Постройте график функции у = x2 – 6х + 3. Укажите координаты вершины параболы.
ОТВЕТ: (3; –6).
№ 2. Найдите область значений функции у = –x2 – 8х + 1.
ОТВЕТ: (–∞; 17].
№ 3. Определите координаты точек пересечения параболы у = 1/4 • x2 и прямой у = 5х – 16.
ОТВЕТ: (4; 4), (16; 64).
№ 4. Найдите а и постройте график функции у = –x2 + ах + 3, если известно, что он проходит точку (2; –5).
ОТВЕТ: а = –2.
№ 5. Вычислите 6 3√[–1/8] + 20 4√[5 1/16].
ОТВЕТ: 27.
№ 6. Постройте трафик функции у = |х + 1| – 1.
ОТВЕТ: Сдвиг графика у = |х| на одну единицу влево и на одну единицу вниз.
Ответы на Вариант 2
№ 1. Постройте график функции у = х2 + 8х + 5. Укажите координаты вершины параболы.
ОТВЕТ: (–4; –11).
№ 2. Найдите область значений функции у = –x2 + 6х + 2.
ОТВЕТ: (–∞; 11].
№ 3. Определите координаты точек пересечения параболы у = 1/5 • х2 и прямой у = 20 – 3х.
ОТВЕТ: (–20; 80), (5; 5).
№ 4. Найдите а и постройте график функции у = x2 + ах – 3, если известно, что он проходит точку (–2; 5).
ОТВЕТ: а = –2.
№ 5. Вычислите 12 3√[–1/27] + 15 4√[3 13/81].
ОТВЕТ: 16.
№ 6. Постройте график функции у = |х – 1| + 1.
ОТВЕТ: Сдвиг графика у = |х| на одну единицу вправо и на одну единицу вверх.
Ответы на Вариант 3
№ 1. Найдите область значений функции у = –2x2 + 4х – 7, если х ∈ [–1; 2].
ОТВЕТ: [–13; –51].
№ 2. Найдите область определения и область значений функции у = 3√[2х – 4] + 4х – 2.
ОТВЕТ: х ∈ [2; ∞), у ∈ [6; ∞).
№ 3. Вычислите наибольшее значение функции y = 4/(x2 – 6x + 11) + 7.
ОТВЕТ: у = 9.
№ 4. Вычислите 6 4√[7 58/81] + 4 3√[–3 3/8].
ОТВЕТ: 4.
№ 5. Упростите выражение 2√x(1/(√x – 5) + 1/(√x + 5)) + 100/(25 – x).
ОТВЕТ: 4.
№ 6. Постройте график функции у = –|х + 1| + 2.
ОТВЕТ: Сдвиг графика у = –|х| на одну единицу влево и на две единицы вверх.
Ответы на Вариант 4
№ 1. Найдите область значений функции у = –3x2 – 6х + 3, если х ∈ [–2; 1].
ОТВЕТ: [–4; 8].
№ 2. Найдите область определения и область значений функции у = 2√[3x – 6] + 6х – 5.
ОТВЕТ: х ∈ [2; ∞), у ∈ [7; ∞).
№ 3. Вычислите наибольшее значение функции y = 8/(x2 – 4x + 6) + 1.
ОТВЕТ: у = 5.
№ 4. Вычислите 4 4√[5 1/16] + 6 3√[–2 10/27].
ОТВЕТ: –2.
№ 5. Упростите выражение 3√x(1/(√x – 4) + 1/(√x + 4)) + 96/(16 – x).
ОТВЕТ: 6.
№ 6. Постройте график функции у = –|х – 2| + 1.
ОТВЕТ: Сдвиг графика у = –|х| на две единицы вправо и на одну единицу вверх.
Решения и ответы на Вариант 5
№ 1. Определите расстояние между осями симметрии графиков функции у = –x2 + 2х + 1 и у = 2x2 + 12х + 5.
Решение:

ОТВЕТ: 4.
№ 2. Найдите область определения и область значений функции y = 4√[3x – 6] + 2x2 + 4x – 5.
Решение:

ОТВЕТ: D(у) = [2; +∞), Е(у) = [11; +∞).
№ 3. Найдите наибольшее значение функции у = (3x2 – 6х + 23) / (x2 – 2х + 5). При каком значении х оно достигается?
Решение:

ОТВЕТ: Ответ: уmах = 5 при х = 1.
№ 4. Постройте график функции у = x2 – 5|х| + 4.
Решение:

№ 5. Упростите выражение (x – 15)/( √[x + 1] – 4) – (x – 3)/(2 + √[x + 1]).
Решение:

ОТВЕТ: 6.
№ 6. При каких значениях b и с точка A(–1; –10) является вершиной параболы у = 2х2 + bх + с?
Решение:

ОТВЕТ: b = 4, с = –8.
Решения и ответы на Вариант 6
№ 1. Определите расстояние между осями симметрии графиков функции у = x2 – 4х + 3 и у = –3x2 – 12х – 7.
Решение:

ОТВЕТ: 4.
№ 2. Найдите область определения и область значений функции у = 3√[2х – 4] + 4х2 – 8х + 5.
Решение:

ОТВЕТ: D(y) = [2; +∞), Е(у) = [5; ∞).
№ 3. Найдите наименьшее значение функции у = (5x2 + 10x + 14)/(x2 + 2x + 4). При каком значении х оно достигается?
Решение:

ОТВЕТ: уmах = 3 при х = –1.
№ 4. Постройте график функции у = x2 – 4[х| + 3.
Решение:

№ 5. Упростите выражение (x – 4)/(√[x – 3] + 1) – (x – 12)/(3 + √[x – 3]).
Решение:

ОТВЕТ: 2.
№ 6. При каких значениях b и с точка А(1; –8) является вершиной параболы у = –3x2 + bx + с?
Решение:

ОТВЕТ: b = 6, с = –11.
Вы смотрели: Алгебра 9 Макарычев Контрольная № 2 с ответами. Поурочное планирование по алгебре для 9 класса по УМК Макарычев (Просвещение). Глава I. КВАДРАТИЧНАЯ ФУНКЦИЯ. Урок 22. Контрольная работа по теме «Квадратичная функция. Степенная функция. Корень n-ой степени» + РЕШЕНИЯ и ОТВЕТЫ.
Смотреть Список контрольных по алгебре в 9 классе по УМК Макарычев
Алгебра 9 Мерзляк. Контрольная работа 2 «Функция. Квадратичная функция, её график и свойства» по алгебре в 9 классе с ответами, УМК Мерзляк, Полонский, Якир и др (Алгоритм успеха). Цитаты из пособия «Алгебра 9 класс. Дидактические материалы/ Мерзляк, Полонский, Рабинович и др. — М.: Вентана-Граф» использованы в учебных целях. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
Контрольная работа по алгебре № 2
«Функция. Квадратичная функция, её график и свойства»

Виды заданий (транскрипт):
- Функция задана формулой f(x) = х2/2 + 3х. Найдите: 1) f(2) и f(-1); 2) нули функции.
- Найдите область определения функции:
- Постройте график функции f(x) = х2 + 2х — 3. Используя график, найдите: 1) область значений данной функции; 2) промежуток возрастания функции; 3) множество решений неравенства f(x) > 0.
- Постройте график функции:
- При каких значениях р и q вершина параболы у = х2 + рх + q находится в точке A (-4; 6)?
ОТВЕТЫ на контрольную работу
ОТВЕТЫ на Вариант 1
№ 1. 1) 8; –2,5; 2) 0; –6.
№ 2. 1) (–∞; 4) ∪ (4; 6) ∪ (6; +∞); 2) [–5; –2) ∪ (–2; 2) ∪ (2; +∞).
№ 3. 1) [–4; +∞); 2) (–1; +∞]; 3) при x<–3 и x>1.
№ 5. Ответ: p = 8; q = 22.
ОТВЕТЫ на Вариант 2
№ 1. 1) 9; –5/3; 2) 0; –6.
№ 2. 1) (–∞; -2) U (–2;  U (8; +∞); 2) [–4; –3) U (–3; 3) U (3; +∞).
U (8; +∞); 2) [–4; –3) U (–3; 3) U (3; +∞).
№ 3. 1) [–9; +∞); 2) (–∞; -2]; 3) при x∈(–5; 1).
№ 5. Ответ: p = –6; q = 2.
Вы смотрели: Алгебра 9 Мерзляк. Контрольная работа 2 «Функция. Квадратичная функция, её график и свойства» по алгебре в 9 классе с ответами, УМК Мерзляк, Полонский, Якир и др (Алгоритм успеха). Цитаты из пособия использованы в учебных целях.
Вернуться к Списку контрольных работ по алгебре 9 класс (Мерзляк)
Если Вы считаете, что какое-то задание решено не правильно, то укажите в комментарии ниже № варианта, № задания и своё решение! В противном случае Ваш комментарий не будет напечатан.
