Контрольная работа № 1
Тригонометрические преобразования выражений.
Цель: проверка знаний и практических умений обучающихся.
1 вариант
А1. Вычислите: sin 30˚
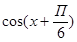1)0,5; 2) 1; 3) 
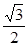; 4) 
.
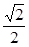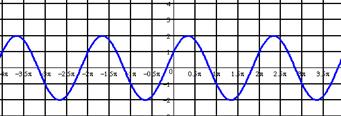
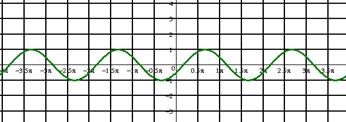А2. На каком из чертежей изображён график функции у =
Рис 1 Рис 2
А3.Найдите значение выражения: 2sin 30˚+6 cos 60˚ — 3ctg 30˚ + 9 tg 30˚
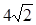1)4; 2) – 4; 3)6; 4)
А 4. Упростите, используя формулы приведения: cos(π-α)∙cos(2π-α)+cos²α
1) 2cos²α; 2)1; 3)0; 4)2sin²α.
А5. Постройте график функции y = 3sinx и укажите область определения
и область значений функции.
А6. Определите знак выражения: sin110˚·cos 110˚
1) + ; 2)- ; 3) 0; 4) нет верного ответа.
В. По заданному значению тригонометрической функции, найдите значение
ctg α, если sin α=0,8 и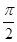 
< α < π.
С. Докажите тождество:
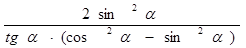= tg2α
Контрольная работа № 1
Тригонометрические преобразования выражений.
Цель: проверка знаний и практических умений обучающихся.
2 вариант
А1. Вычислите: cos 30˚
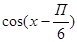1)0,5; 2) 1; 3) 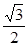; 4) .
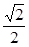А2. На каком из чертежей изображён график функции у =
А3.Найдите значение выражения: 2 cos 30˚- 6 sin 30˚ — ctg 30˚ + 9 tg 45˚
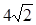1)4; 2) – 4; 3)6; 4) .
А 4. Упростите, используя формулы приведения: sin (π-α)∙cos( 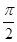— α)+cos²α
1) 2cos²α; 2)1; 3)0; 4)2sin²α.
А5. Постройте график функции y = 1 + cosx и укажите область определения и о
множество значений функции.
А6. Определите знак выражения: sin100˚· cos 100˚.
1) +; 2) -; 3) 0; 4)нет верного ответа.
В. По заданному значению тригонометрической функции, найдите значение tg α,
если cos α= 0,8 и 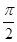< α < π
С. Докажите тождество:
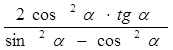= — tg2α
Контрольная работа «Тригонометрия»
Вариант № 1.
1. Выразите в радианах: а) 10°; б) 210°.
2. Выразите в градусах: а) 
; б) 
.
3. Вычислить значение каждой из тригонометрических функций, если: 
.
4. Упростите выражение: 
;
5. Докажите тождество: 
;
6. Вычислите значение sin2x, если cosx =
и 
– 
; 2) ; 3) 
; 4) – .
7. Найдите значение выражения 
при 
8. Упростите выражение 
9. Найдите значение выражения: 
при x=
а)
; б) 
; в) 
; г) 0.
10. Вычислите: 
а) 
; б) 
; в) ; г)1.
11. Решите уравнение 
а) π2n; б) 
; в) πn; г) 0.
12. Решите уравнение 
а) π2+πn; б) πn; в) π2n; г) πn+2πn.
13. Решите уравнение 
а) x=(-1)n+1π3+πn; б) x=(-1)nπ6+πn; в) x=(-1)nπ3+πn; г) x=(-1)n+1π2+πn.
14. Решите уравнение 
а) x=π3+πn; б) x=π2+2πn; в) x=π6+2πn; г) x=2π3+πn.
15. Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют … числа t.
16. Угол в один радиан – это … угол, опирающийся на дугу, длина которой равна радиусу окружности.
17. Какая из тригонометрических функции является четной функцией?
18. Решите уравнение 
.
Вариант № 2.
1. Выразите в радианах: а) 15°; б) 225°.
2. Выразите в градусах: а) 
; б) 
.
3. Вычислить значение каждой из тригонометрических функций, если: 
.
4. Упростите выражение: 
;
5. Докажите тождество: 
;
6. Вычислите значение cos2
, если sin = – и 
– ; 2) ; 3) – 0,5 ; 4) 0,5.
7. Найдите значение выражения 
при cos =
8. Упростите выражение 
9. Найдите значение выражения: 
при x=
а) 1; б) 0,5; в) 
; г) 1,5.
10. Вычислите: 
а)0; б) 
; в)1; г) 
.
11. Решите уравнение 
а) π2n; б) π2+2πn; πn. в) 2π3+2πn; 2πn.; г) π+2πn; πn.
12. Решите уравнение 
а) π2n; б) 2πn, в) π3+πn; г) πn.
13. Решите уравнение 
а) ±π2n; б) ±π2+2πn; в) ±π4+2πn; г) ±π+2πn; πn.
14. Решите уравнение 
а) π2 +2πn; б) 2πn. в) π3+πn; г) π+2πn.
15. Если точка М числовой окружности соответствует числу t, то ординату точки М называют … числа t. 16. Если функция ограничена и снизу и сверху, то её называют … . 17. Какие тригонометрические функции являются нечетными функциями?
18. Решите уравнение 
. Записать полное решение.
Эталон ответов
контрольной работы «Тригонометрия»
Вариант № 1 Вариант № 2
1. π18, 7π6 1. π12, 5π4
2. 12,140 2. 15,120
3. -513, -123, -512 3. -2√65, 2√6, √612
4. 1cos2α 4. — tg2α
5. верное 5. верное
6. 4 6. -12
7. -1,4 7. 1,5
8.1 8. 1
9.г, 9. а,
10.г, 10.а,
11.в, 11.в,
12.б, 12.б,
13.а, 13.в,
14.б, 14.г,
15.косинусом, 15.синусом,
16.центральный, 16.ограниченной,
17.косинус, 17.синус, тангенс, котангенс.
18. х = 2πп 18. х = π2 + 2πп
х = —arcctg7+πп х = arcctg13+πп
Критерии оценивания
Отметка «2» выставляется, если выполнено менее 10 (от 1 до 9) заданий работы.
Отметка «3» выставляется, если верно выполнено 10 — 13 заданий работы.
Отметка «4» выставляется, если верно выполнено 14 — 16 заданий работы.
Отметка «5» выставляется, если верно выполнено 17-18 заданий работы.
Контрольная работа по теме «Тригонометрические выражения»
| Предмет: | Математика |
|---|---|
| Категория материала: | Конспекты |
| Автор: |
Данная разработка рекомендована для проведения контрольной работы по алгебре по теме «Тригонометрические выражения». Задания составлены в соответствии с Государственным стандартом. Разработка предназначена для студентов первого курса профессиональных училищ со слабой математической подготовкой.
Проверяется умение выполнять преобразования выражений, применяя основные формулы тригонометрии; умение вычислять значение функции по заданному значению аргумента.
В этой разработке представлены два варианта контрольной работы, критерии оценки и ответы на данные задания.
Контрольная работа по теме
«Тригонометрические выражения»
1 вариант
Выразить в радианах: 54°, 210°;Выразить в градусах: ;Определить знак выражения:cos 940°;Выразить функцию угла от 0° до 90°:sin 390°cos 120°Вычислить остальные тригонометрические функции, если Вычислить:;Упростить выражение:
2 вариант
Выразить в радианах: 15°, 320°;Выразить в градусах: ;Определить знак выражения:sin 570°;Выразить функцию угла от 0° до 90°:sin 420°cos 300°Вычислить остальные тригонометрические функции, если Вычислить:;Упростить выражение:
Критерии оценки:
оценка «отлично» выставляется обучающемуся, за правильное решение 7 заданий;оценка «хорошо» — за правильное решение 6 заданий;оценка «удовлетворительно» — за правильное решение 5 заданий;оценка «неудовлетворительно» — решено менее 4 заданий.
Ответы:
1 вариант
2 вариант
2.18°, 72°
9°, 108°
c. >0
3.a.
| Тип материала: | Документ Microsoft Word (docx) |
|---|---|
| Размер: | 22.23 Kb |
| Количество скачиваний: | 58 |
Скачать
Просмотров: 159
Похожие материалы
- План урока по теме «Пропорция» 6 класс.
- Конспект урока по геометрии по теме «Признаки параллельности двух прямых»
- Конспект урока по теме «Геометрическая прогрессия»
- Презентация по алгебре 7 класс свойства степени
- Урок математики 5 класс Смешанные числа. Сложение и вычитание.
- Урок по геометрии в 10 классе «Аксиомы стереометрии»
- Технологические карты уроков. 7 класс. Разложение многочленов на множители
- Урок математики в 1 классе. Тема «Решение задач на разностное сравнение чисел»
- Конспект по алгебре на тему «Арифметическая прогрессия»(9класс)
- Конспект внеклассного мероприятия по математике «Олимпийский математический урок» 6 класс
Все материалы взяты из открытых источников сети Интернет. Все права принадлежат авторам материалов.
По вопросам работы сайта обращайтесь через форму обратной связи.
Вариант1
1.Найти область определения и множество
значений функции у=5 cos х .
2. Выяснить является функция у=2sin x – tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( — 2п; 2п) и решить уравнение
sin x = 0,5.
4.Найти наибольшее и наименьшее значения
функции у= 6sin x cos х + 3
5. Построить график функции у= cos х + 2.
При каких значениях функция убывает;
возрастает?
Вариант2
1.Найти область определения и множество
значений функции у=0,5 sin х .
2. Выяснить является функция у=2cos x – x
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( — 2п; 2п) и решить уравнение
cos x = -0,5.
4.Найти наибольшее и наименьшее значения
функции у= 6cosx — 6sinх + 3
5. Построить график функции у= sin х + 2.
При каких значениях функция убывает;
возрастает?
Вариант3
1.Найти область определения и множество
значений функции у= cos х + 4
2. Выяснить является функция у = 3sin x + tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( — 2п; 2п) и решить уравнение
sin x = -1.
4.Найти наибольшее и наименьшее значения
функции у= 8sin x cos х — 2
5. Построить график функции у= cos х — 1.
При каких значениях функция убывает;
возрастает?
Вариант6
1.Найти область определения и множество
значений функции у=sin х — 3
2. Выяснить является функция у = cos x +3 x
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( — 2п; 2п) и решить уравнение
cos x = -1.
4.Найти наибольшее и наименьшее значения
функции у= 5cosx — 5sinх + 2
5. Построить график функции у= sin х — 1.
При каких значениях функция убывает;
возрастает?
Вариант5
1.Найти область определения и множество
значений функции у= 5cos х .
2. Выяснить является функция у=sin x –5 tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( — 2п; 2п) и решить уравнение
sin x = 1.
4.Найти наибольшее и наименьшее значения
функции у= 10sin x cos х + 2 .
5. Построить график функции у= cos х + 1.
При каких значениях функция убывает;
возрастает?
Вариант6
1.Найти область определения и множество
значений функции у=sin х + 2
2. Выяснить является функция у=2cos x – x
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( — 2п; 2п) и решить уравнение
cos x = 1.
4.Найти наибольшее и наименьшее значения
функции у= 8cosx — 8sinх + 3
5. Построить график функции у= sin х + 1.
При каких значениях функция убывает;
возрастает?
Вариант7
1.Найти область определения и множество
значений функции у=cos х + 11
2. Выяснить является функция у=sin x –2tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( — 2п; 2п) и решить уравнение
sin x = 1.
4.Найти наибольшее и наименьшее значения
функции у= 6sin x cos х + 3
5. Построить график функции у= cos х + 3.
При каких значениях функция убывает;
возрастает?
Вариант8
1.Найти область определения и множество
значений функции у=0,5 sin х .
2. Выяснить является функция у=2cos x – x
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( — 2п; 2п) и решить уравнение
cos x = -1.
4.Найти наибольшее и наименьшее значения
функции у= 6cosx — 6sinх + 3
5. Построить график функции у= sin х +3.
При каких значениях функция убывает;
возрастает?
Алгебра 10 Колмогоров Контрольная 1
Контрольная работа № 1 по алгебре с ответами для учащихся 10 класса по УМК Колмогоров (базовый уровень). Настоящая проверочная работа «Тригонометрические функции любого угла. Основные тригонометрические формулы» в 2-х вариантах является важным дополнением к учебнику по алгебре и началам анализа для 10–11 классов под редакцией Колмогорова А.Н. Алгебра 10 Колмогоров Контрольная 1. Ответы адресованы родителям. К сложным заданиям указаны решения.
Цитаты из пособия «Алгебра и начала математического анализа. 10 класс. Контрольные работы в НОВОМ формате / Ю.П. Дудницын, А.В. Семенов; [под общ. ред. А.В. Семенова]; Московский центр непрерывного математического образования» использованы в учебных целях.
Алгебра 10 класс (Колмогоров)
Контрольная работа № 1
К-1. Вариант 2 (транскрипт)
Часть 1
- Вычислите сумму значений выражений А и В, если A = cos 45° • ctg 90° + 2sin 30°, В = 3tg (π/4) + sin π • cos(π/6).
- Гипотенуза AB треугольника ABC равна 12. ∠C = 90°, sinB = √5/3. Найдите длину катета ВС.
- Упростите выражение 1 – sin a • cos a • ctg a.
- Найдите значение выражения (1 + sin a)(1 – sin a)/sin2a, если tg a = 1/2.
Часть 2
- Докажите тождество ((sin a – cos a)2 –1)/(sin2a – cos2a – 1) + ctg ( 3π/2 + a) = 0.
- Найдите наибольшее значение выражения 3 – sin (π + a).
- Существует ли значение a, при котором cos a = (1 – √6)/√10 и sin a = 4√6/√5? Ответ поясните.
Ответы на контрольную работу № 1
Смотреть ОТВЕТЫ на Вариант 1
Смотреть ОТВЕТЫ на Вариант 2
Вы смотрели: Контрольная работа № 1 по алгебре с ответами для учащихся 10 класса «Тригонометрические функции любого угла. Основные тригонометрические формулы» в 2-х вариантах. Алгебра 10 Колмогоров Контрольная 1. Ответы адресованы родителям.
Вернуться к списку контрольных работ по алгебре в 10 классе (Колмогоров)
При оценивании выполнения заданий следует обращать внимание не только на правильность ответа, но и на правильность решения. В отличие от основной школы учащегося нужно ориентировать на получение правильного ответа «законными» способами, а не искать, за что бы похвалить. Разумная последовательность и даже жесткость предъявляемых требований в оценивании выполнения заданий с последующей корректировкой знаний позволит учащемуся получить знания школьного курса алгебры и начал анализа, сдать экзамен (в любой форме) и продолжать обучение в высшем учебном заведении.