Вариант1
1.Найти область определения и множество
значений функции у=5 cos х .
2. Выяснить является функция у=2sin x – tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( — 2п; 2п) и решить уравнение
sin x = 0,5.
4.Найти наибольшее и наименьшее значения
функции у= 6sin x cos х + 3
5. Построить график функции у= cos х + 2.
При каких значениях функция убывает;
возрастает?
Вариант2
1.Найти область определения и множество
значений функции у=0,5 sin х .
2. Выяснить является функция у=2cos x – x![]()
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( — 2п; 2п) и решить уравнение
cos x = -0,5.
4.Найти наибольшее и наименьшее значения
функции у= 6cos![]() x — 6sin
x — 6sin![]() х + 3
х + 3
5. Построить график функции у= sin х + 2.
При каких значениях функция убывает;
возрастает?
Вариант3
1.Найти область определения и множество
значений функции у= cos х + 4
2. Выяснить является функция у = 3sin x + tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( — 2п; 2п) и решить уравнение
sin x = -1.
4.Найти наибольшее и наименьшее значения
функции у= 8sin x cos х — 2
5. Построить график функции у= cos х — 1.
При каких значениях функция убывает;
возрастает?
Вариант6
1.Найти область определения и множество
значений функции у=sin х — 3
2. Выяснить является функция у = cos x +3 x![]()
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( — 2п; 2п) и решить уравнение
cos x = -1.
4.Найти наибольшее и наименьшее значения
функции у= 5cos![]() x — 5sin
x — 5sin![]() х + 2
х + 2
5. Построить график функции у= sin х — 1.
При каких значениях функция убывает;
возрастает?
Вариант5
1.Найти область определения и множество
значений функции у= 5cos х .
2. Выяснить является функция у=sin x –5 tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( — 2п; 2п) и решить уравнение
sin x = 1.
4.Найти наибольшее и наименьшее значения
функции у= 10sin x cos х + 2 .
5. Построить график функции у= cos х + 1.
При каких значениях функция убывает;
возрастает?
Вариант6
1.Найти область определения и множество
значений функции у=sin х + 2
2. Выяснить является функция у=2cos x – x![]()
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( — 2п; 2п) и решить уравнение
cos x = 1.
4.Найти наибольшее и наименьшее значения
функции у= 8cos![]() x — 8sin
x — 8sin![]() х + 3
х + 3
5. Построить график функции у= sin х + 1.
При каких значениях функция убывает;
возрастает?
Вариант7
1.Найти область определения и множество
значений функции у=cos х + 11
2. Выяснить является функция у=sin x –2tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( — 2п; 2п) и решить уравнение
sin x = 1.
4.Найти наибольшее и наименьшее значения
функции у= 6sin x cos х + 3
5. Построить график функции у= cos х + 3.
При каких значениях функция убывает;
возрастает?
Вариант8
1.Найти область определения и множество
значений функции у=0,5 sin х .
2. Выяснить является функция у=2cos x – x![]()
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( — 2п; 2п) и решить уравнение
cos x = -1.
4.Найти наибольшее и наименьшее значения
функции у= 6cos![]() x — 6sin
x — 6sin![]() х + 3
х + 3
5. Построить график функции у= sin х +3.
При каких значениях функция убывает;
возрастает?
Алгебра 10 Колмогоров Контрольная 1
Контрольная работа № 1 по алгебре с ответами для учащихся 10 класса по УМК Колмогоров (базовый уровень). Настоящая проверочная работа «Тригонометрические функции любого угла. Основные тригонометрические формулы» в 2-х вариантах является важным дополнением к учебнику по алгебре и началам анализа для 10–11 классов под редакцией Колмогорова А.Н. Алгебра 10 Колмогоров Контрольная 1. Ответы адресованы родителям. К сложным заданиям указаны решения.
Цитаты из пособия «Алгебра и начала математического анализа. 10 класс. Контрольные работы в НОВОМ формате / Ю.П. Дудницын, А.В. Семенов; [под общ. ред. А.В. Семенова]; Московский центр непрерывного математического образования» использованы в учебных целях.
Алгебра 10 класс (Колмогоров)
Контрольная работа № 1

К-1. Вариант 2 (транскрипт)
Часть 1
- Вычислите сумму значений выражений А и В, если A = cos 45° • ctg 90° + 2sin 30°, В = 3tg (π/4) + sin π • cos(π/6).
- Гипотенуза AB треугольника ABC равна 12. ∠C = 90°, sinB = √5/3. Найдите длину катета ВС.
- Упростите выражение 1 – sin a • cos a • ctg a.
- Найдите значение выражения (1 + sin a)(1 – sin a)/sin2a, если tg a = 1/2.
Часть 2
- Докажите тождество ((sin a – cos a)2 –1)/(sin2a – cos2a – 1) + ctg ( 3π/2 + a) = 0.
- Найдите наибольшее значение выражения 3 – sin (π + a).
- Существует ли значение a, при котором cos a = (1 – √6)/√10 и sin a = 4√6/√5? Ответ поясните.
Ответы на контрольную работу № 1
Смотреть ОТВЕТЫ на Вариант 1
Смотреть ОТВЕТЫ на Вариант 2
Вы смотрели: Контрольная работа № 1 по алгебре с ответами для учащихся 10 класса «Тригонометрические функции любого угла. Основные тригонометрические формулы» в 2-х вариантах. Алгебра 10 Колмогоров Контрольная 1. Ответы адресованы родителям.
Вернуться к списку контрольных работ по алгебре в 10 классе (Колмогоров)
При оценивании выполнения заданий следует обращать внимание не только на правильность ответа, но и на правильность решения. В отличие от основной школы учащегося нужно ориентировать на получение правильного ответа «законными» способами, а не искать, за что бы похвалить. Разумная последовательность и даже жесткость предъявляемых требований в оценивании выполнения заданий с последующей корректировкой знаний позволит учащемуся получить знания школьного курса алгебры и начал анализа, сдать экзамен (в любой форме) и продолжать обучение в высшем учебном заведении.
Контрольная работа по теме: Тригонометрические функции. 10 класс.
Вариант 1.
1. Найдите значение выражения:
; 4) 0.
2. Сравните с нулём выражения: sin 120
0
, cos 195
0
, ctg 359
0
.
Выберите правильную серию ответов:
1) + – – 2) – – + 3) + + – 4) + – +
3. Вычислите:
234
cos6
22
ctgtg
; 3) 6; 4) 0.
4. Упростите выражение:
2
3
cossin
ctg
1) – cos
2
; 2) cos
2
; 3) sin
2
; 4) – sin
2
.
5. Упростите выражение: sin
*
cos
*
ctg – 1
1) 0; 2) cos
2
; 3) – sin
2
; 4) sin
2
.
6. Упростите выражение:
1) sin – cos ; 2) –2 ctg 2; 3) tg 2; 4) 0,5 ctg 2.
7. Вычислите: 2sin 15
0
*
cos 15
0
1)
; 4) 0.
9. Представив 105
0
как 60
0
+ 45
0
, вычислите sin 105
0
.
1)
Контрольная работа по теме: Тригонометрические функции. 10 класс.
Вариант 2.
1. Найдите значение выражения:
; 4) 1,5.
2. Сравните с нулём выражения: sin 187
0
, cos 215
0
, tg 80
0
.
Выберите правильную серию ответов:
1) + – + 2) – + + 3) – – + 4) – + –
3. Вычислите:
6
cos
2
3
sin30cos4
2
sin5
2
.
4. Упростите выражение:
2
3
2
3
sin
cos
tg
tg
1) tg
2
; 2) —tg
2
; 3) -ctg
2
; 4) ctg
2
.
5. Упростите выражение:
1) – sin
; 2) sin ; 3) – 2cos ; 4) sin
– 2cos .
6. Упростите выражение:
1) ctg
2
; 2) tg
2
; 3) – tg
2
; 4) – ctg
2
.
7. Вычислите:
; 4) 0.
8. Вычислите: cos 150
0
1)
.
9. Представив 15
0
как 45
0
– 30
0
, вычислите cos 15
0
.
1)
Контрольная работа по теме: Свойства функции. 10 класс.
1 вариант
1. Найдите область определения функции
.
2. Найдите область значений функции у = cos x +2
1) [-1;1]; 2)[-2;2]; 3) [0;2]; 4) [1;3].
3. Проверьте функцию на четность у = х
4
+ cos x
1) четная; 2) нечетная; 3) ни четная, ни нечетная; 4) периодическая.
4. Найдите нули функции
1) 0; 2) 1; 3) 0; 1; 4) нет.
5. По графику некоторой функции у= f (x) найдите промежутки возрастания
1) [-3;-2] U [2;5]; 2) [-3;5]; 3) [-2;2]; 4) [2;5].
6. Найдите наименьший положительный период функции
1) π; 2) 2 π; 3) 0,5 π; 4) 4 π.
7. Найдите наименьшее значение функции у = х
2
+ 3х – 1
1) -1; 2) -3,25; 3) -1,5; 4) 1,25.
8. Укажите график функции у = (х-1)
2
+4
1) 2) 3) 4)
9. Найдите промежутки, на которых у>0
1) (-2;2); 2) [-2;0)U(2;4); 3) [-2;-1) U (2;4]; 4)
[0;3].
10. Дана функция f (x)= x
3
-2ax + 8 . Известно, что f (1) = 5. Найдите f (-2).
1) 16; 2) 0; 3) 8; 4) -8.
11. Укажите функцию, которой соответствует данный график
1)
Контрольная работа по теме: Свойства функции. 10 класс.
2 вариант
1. Найдите область определения функции и
.
2. Найдите область значений функции у = sin x -2
1) [-1:1]; 2)[-3:-1]; 3) (-2;0); 4) [-2;2].
3. Проверьте функцию на четность:
1) четная; 2) нечетная; 3) ни четная, ни нечетная; 4) убывающая.
4. Найдите нули функции
1) 3; 2) -3; 3) 0; 4) -5.
5. По графику некоторой функции
у= f (x) найдите промежутки возрастания
1)[-2;3]U [2;4]; 2) [-3;5]; 3) [0;3]; 4) (-1;2).
6. Найдите наименьший положительный период функции у = tg 4x
1) 2π; 2)
; 3) 0,5 π; 4) 4 π.
7. Найдите наименьшее значение функции у = —х
2
+ 5х – 9
1)
; 2) -9; 3) 1,5; 4) 9,75.
8. Укажите график функции у = -2x-3
1) 2) 3) 4)
9. Найдите промежутки, на которых у<0
1) (-1;3); 2) [-3;1]U[4;5];
3) (-3;-1); 4) [1;4].
10. Дана функция f (x)= x
3
+5x -a . Известно, что f (2) = 15. Найдите f (-1).
1) -3; 2) -9; 3) -8; 4) 0.
11. Укажите функцию, которой соответствует данный график
1)
Контрольная работа по теме: Тригонометрические уравнения и неравенства. 10 класс.
1 вариант
1. Вычислите: arcsin (
.
3. Решите уравнение: sin x —
4. Решите уравнение: cos 2x=1
1)
5. Укажите уравнение, которому соответствует решение:
:
1) tg x = 1; 2) cos x = 0; 3) sin x = -1; 4) ctg x =
.
6. На каком из рисунков показано решение неравенства: cos x <
?
1) 2) 3) 4)
7. Решите неравенство: tg x ≥
8. Решите уравнение: 6sin
2
x + sin x – 1 = 0
1)
m
т
т
т
3
1
arcsin)1(
)
6
()1(
.
9. Решите уравнение: 2sin
2
x —
sin 2x =0
10. Решите систему:
Контрольная работа по теме: Тригонометрические уравнения и неравенства. 10 класс.
2 вариант
1. Вычислите: arcsin (
.
3. Решите уравнение: sin x +
4. Решите уравнение: ctg (x+
5. Укажите уравнение, которому соответствует решение:
:
1) ctg x = -1; 2) cos x = 0; 3) cos x = -1; 4) tg x = 1.
6. На каком из рисунков показано решение неравенства: sin x ≥
?
1) 2) 3) 4)
7. Решите неравенство: ctg x ≥
8. Решите уравнение: cos
2
x — 4sin x + 3 = 0
1)
sin
2
x -3sin x cos x =0
10. Решите систему:
Контрольная работа по теме: Производная. Применение производной. 10 класс.
1 Вариант.
1. Найдите производную функции
2. Найдите значение производной функции
1) 1; 2) 0; 3) 0,5; 4) -1.
3. Для какой функции найдена производная
4. Найдите значение углового коэффициента касательной, проведенной к графику функции
1) -3; 2) 0; 3) 3; 4) 5.
5. Найдите
4) 0.
6. Напишите уравнение касательной к графику функции
1) у = — 3х – 3; 2) у = 8х+13; 3) у = — 8х – 3; 4) у = — 8х +13.
7. Найдите скорость и ускорение точки в момент времени
c., если она движется
прямолинейно по закону
8. Определите точку максимума функции
9. По графику производной функции 1
укажите количество промежутков 1 3
убывания функции
10. Найдите наибольшее и наименьшее значение функции
11. Найдите производную функции
Контрольная работа по теме: Производная. Применение производной. 10 класс.
2 Вариант.
1. Найдите производную функции
2. Найдите значение производной функции
3. Для какой функции найдена производная
4. Найдите значение углового коэффициента касательной, проведенной к графику функции
1) -6; 2) 4; 3) 6; 4)
-5. 5. Найдите
. 6. Напишите уравнение касательной к графику функции
.
1) у = — 9х – 6; 2) у = — 3х — 6; 3) у = 9х+16; 4) у = 9х — 6.
7. Найдите скорость и ускорение точки в момент времени
cек., если она движется
прямолинейно по закону
8. Определите минимум функции
у
9. По графику производной функции
укажите длину промежутка возрастания 0 1 х
функции
10. Укажите наибольшее и наименьшее значение функции
.
11. Вычислите производную функции
Контрольная работа по теме: Применение непрерывности и производной. 10 класс.
1 Вариант.
1. Найдите тангенс угла наклона касательной, проведенной к графику функции
1) -1,5; 2) 3; 3) -3; 4) — 4,5.
2. Решите неравенство:
.
3. Напишите уравнение касательной к графику функции
1) у = – 12х + 17; 2) у = 12х – 17; 3) у = 19х – 38; 4) у = 12х+32.
4. Решите неравенство
5. Найдите скорость и ускорение точки в момент времени t = 1cек., если она движется
прямолинейно по закону
.
6. Определите абсциссы точек, в которых угловой коэффициент касаcтельной к графику
функции
;,
6
1
ккх
к
sin2.
7. Решите неравенство
;42;26;
8. Вычислите с помощью формул приближенные значения выражений:
а)
Контрольная работа по теме: Применение непрерывности и производной. 10 класс.
2 Вариант.
1. Найдите тангенс угла наклона касательной, проведенной к графику функции
1) -6; 2) 4; 3) 6; 4) -5.
2. Решите неравенство:
.;21;12;).4.2;11;2).3.2;11;2).2.2;11;2).1
3. Напишите уравнение касательной к графику функции
.69).4.169).3.63).2.69).1 хухухуху
.1;03;).4.;13;).3.;13;).2.;10;3).1
5. Найдите скорость и ускорение точки в момент времени t = 1 cек., если она движется
прямолинейно по закону
.
17
8
).4.
8
6
).3.
18
12
).2.
18
8
).1
2222
сма
см
сма
см
сма
см
сма
см
6. Определите абсциссы точек, в которых угловой коэффициент касательной к графику
функции
.,2
2
).4.,
6
1).3.,2
3
)..2.,
6
1)..1
1
хххх
.4;01;2).4.4;01;2).3.;40;12;).2.0;11;2).1
8. Вычислите с помощью формул приближенные значения выражений:
Итоговая контрольная работа 10 класс.
А
1
Вычислите:
.
А
2
Упростите выражение: 5 – 8sin
2
32
0
– 8cos
2
32
0
1) – 3 cos 64
0
; 2) 5 – 8cos 64
0
; 3) 13; 4) – 3.
A
3
Упростите выражение:
.
А
4
Найдите значение выражения:
; 4) 6.
A
5
Решите неравенство:
1) (–∞; — 4 )U[0;3]; 2) ( — 4; 0]U[3; +∞); 3) [3; +∞); 4) (–∞; — 4 ).
A
6
Решите уравнение: sinx – cos
2
x = sin
2
x
1)
.
А
7
Тело движется прямолинейно по закону
(расстояние измеряется в
метрах). Вычислите скорость движения в момент времени t = 4 сек.
1) 1 м/с; 2) 0 м/с; 3) 32 м/с; 4) – 9 м/с.
А
8
Вычислите f ‘ (-2), если f (x) = (7x + 12 )
3
1) – 12; 2) 28; 3) 12; 4) 84.
А
9
Укажите промежутки возрастания функции
у = f(x), заданной графиком на отрезке [a; b].
1) [a; — 1,5]; 2) [1; b];
3) [- 1,5; 1]; 4) [0; 1].
А
10
Функции у = f (x) и у = g (x) заданы графиками
на промежутке [— 7; 3 ]. Укажите те значения х,
при которых f (x)
g (x).
1) [- 7; — 6] U [- 3; 0];
2) [- 6; — 3] U [ 0; 3];
3) [ — 7; — 4] U [ — 2; 3];
4) [ — 7; — 5] U [ — 3; 0] U [ 2; 3].
В
1
Упростите выражение:
2
2
2
sin1
sin2
ctgtg
В
2
Сколько корней имеет уравнение:
В
3
На рисунке изображён график функции
f (x) = ax
2
+ bx + c и четыре прямые. Одна
из этих прямых – график производной
данной функции. Укажите номер этой прямой.
В
4
При каком наибольшем значении а функция
f (x) =
x
3
– ax
2
+ ax + 7 возрастает на всей
числовой прямой?
В
5
Найдите максимум функции
У =
В
6
Найдите разность между наибольшим и наименьшим значениями функции
У = 5,2
С
2
Найдите множество значений функции у = cos2x, если х
С
3
Найдите все целые значения выражения
2
1
3
14sin
32coscos
2
9
cos48cos4sin
72
x
xxxxx
С
4
Найдите целые корни уравнения: ( 6 – х )∙( х – 2 )∙( х + 3 )∙( х + 9 ) = 24х
2
Контрольная работа по теме: Первообразная и интеграл. 11класс.
1 Вариант.
A
1
Определите функцию, для которой F(x) = x
2
– sin2x – 1 является первообразной:
1) f(x) =
; 2) f(x) = 2x – 2cos2x; 3) f(x) = 2x +
cos2x + x.
A
2
Найдите первообразную для функции. F (x) = 4х
3
+ cos x
1) F(x) = 12x
2
– sinx + c; 2) F(x) = 4x
3
+ sinx + c; 3) F(x) = x
4
– sinx + c; 4) F(x) = x
4
+ sinx + c.
A
3
Для функции f(x) = х
2
найдите первообразную F, принимающую заданное значение в
заданной точке F (- 1) = 2
1) F(x) =
.
A
4
Точка движется по прямой так, что её скорость в момент времени t равна V (t) = t + t
2
.
Найдите путь, пройденный точкой за время от 1 до 3 сек, если скорость измеряется в м
/сек. 1) 18 м; 2) 12
.
А
6
Найдите площадь криволинейной трапеции, ограниченной линиями у = – х
2
+ 3 и у = 0
1) 4
.
А
7
Найдите площадь фигуры, ограниченной линиями у =
.
А
8
Вычислите площадь фигуры, ограниченной графиком функции у = 2 – х
2
, касательной к
этому графику в его точке с абсциссой х = — 1 и прямой х = 0
1) 1
В
2
Найдите сумму абсцисс точек пересечения графиков функции у = (х – 1)(х + 2) и её
первообразной, если одна из этих точек находится на оси ординат.
С
1
Найдите ту первообразную функции f(x) = 3х – 1 , для которой уравнение F(x) = 5
имеет единственный корень.
Контрольная работа по теме: Первообразная и интеграл. 11класс.
2 Вариант.
А
1
Определите функцию, для которой F(x) = – cos
— x
3
+ 4 является первообразной:
1) f(x) = — sin
— 3x
2
.
A
2
Найдите первообразную для функции f(x) = x
2
– sinx
1) F(x) =
— cos x + c; 2) F(x) = 2x – cosx + c; 3) F(x) =
+ sinx + c.
A
3
Для функции f(x) = 2x — 2 найдите первообразную F, график которой проходит через точку
А(2;1)
1) F(x) = — х
2
– 2х – 1; 2) F(x) = х
2
+ 2х + 2; 3) F(x) = 2х
2
– 2; 4) F(x) = х
2
– 2х + 1.
А
4
Точка движется по прямой так, что её скорость в момент времени t равна V (t) =3 + 0,2 t.
Найдите путь, пройденный точкой за время от 1 до 7 сек., если скорость измеряется в м
/сек
1) 22, 8 м; 2) 29 м; 3) 23 м; 4) 13 м.
А
5
Вычислите
.
А
6
Найдите площадь криволинейной трапеции, ограниченной линиями у = 2х
2
, у = 0, х = 2
1) 5
.
А
7
Найдите площадь фигуры, ограниченной линиями у = 5 – х
2
, у = 1
1) 16; 2) 5
.
А
8
Вычислите площадь фигуры, ограниченной графиком функции у = – х
2
+ 3, касательной к
этому графику в его точке с абсциссой х = 1 и прямой х = 0.
1) 2
В
2
Найдите сумму абсцисс точек пересечения графиков функции у = (х – 3)(х + 2) и её
первообразной, если одна из этих точек находится на оси ординат.
С
1
Найдите ту первообразную функции f(x) = 2х + 5 , для графика которой прямая
у = 7х – 3 является касательной.
Контрольная работа по теме: Обобщение понятия степени. 11класс.
1 Вариант.
А
1
Вычислите:
; 4) – 11.
А
2
Представьте выражение в виде степени числа х (х > 0):
1) х
1
; 2) х
2
; 3) х
0,99
; 4) х
10,9
.
А
3
Упростите выражение:
ааа
11
4
1
4
1
1) – 4; 3 2) – 4; 3) 3; 4) нет корней.
А
6
Упростите выражение:
5,3
5,35,1
5,2
8,0
4
5
9
1
4
В
2
Найдите значение выражения при m = — 5
2
1
2
3
2
1
2
1
2
1
2
1
2
1
2
1
1
1
1
m
m
m
m
m
m
В
3
Решите систему уравнений:
15225
6235
ху
ух
Найдите у – х, где (х;у) – решение системы.
С
1
Решите уравнение:
Контрольная работа по теме: Обобщение понятия степени. 11класс.
2 Вариант.
А
1
Вычислите:
; 3) 11 ; 4. 9.
А
2
Представьте выражение в виде степени числа х (х > 0):
; 3) х
0
; 4) х
1
.
А
3
Упростите выражение:
1) – 1; 2) 2х
– 1
;
3). 2; 4).
1) 3; 2) 1; 3; 3) – 3; 4) нет корней.
А
6
Упростите выражение:
5,4
5,4
3
4
)2,1(
6
5
8
1
В
2
Найдите значение выражения при а = 16, в = 9
2
1
2
1
4
1
4
1
4
1
4
1
4
1
4
1
44
:
ваа
ва
ва
в
ва
а
В
3
Решите систему уравнений:
.
Найдите у – х, если (х;у) – решение системы.
С
1
Решите уравнение:
Контрольная работа по теме: Показательная функция. 11 класс.
1 вариант
А
1
. Упростите выражение:
1) 1; 2) а; 3) а
2/3
; 4) а
3/2
.
А
2
. Укажите промежуток, которому принадлежат корни уравнения: 6
3х+1
=1/36
1) (-2,25; -1,5); 2) (-1,5; -0,75); 3) (-0,75; 0); 4) корней нет.
А
3
. Вычислите: (10
—10
·100
6
)
-1
1) 0,0001; 2) -100; 3) 0,01; 4) -10000.
А
4.
Решите неравенство: 8
3х/5
≥0,5
1) (-∞; -5/3]; 2) [-5/3; +∞); 3)[-5/9; +∞); 4) (-∞; -5/9].
А
5.
Найдите область определения функции: у =
1) (-∞; 0,2); 2) (-∞; -0,6); 3) (-∞; 5]; 4)[0,2; +∞);
А
6.
График какой из перечисленных функций изображён на рисунке
1) у = (0,5)
х
; 2) у = 2
х
; 3) у = log
2
х; 4) у = log
0,5
х.
В
1.
Найдите произведение корней уравнения
В
2
. Решите систему уравнений
Найдите значение х
0
+2у
0
, где (х
0 ;
у
0
) — решение системы.
В
3
. Укажите целое решение неравенства (х — 6)(8
х—6
— 64) < 0 .
В
4
. Найдите наименьшее значение функции
С
1.
Решите уравнение: 5 · 25
х
– (5х — 31) · 5
х
+ 6 – х = 0.
С
2
. Решите неравенство:
Контрольная работа по теме: Показательная функция. 11 класс.
2 вариант
А
1
. Вычислите: (4/25)
-3/2
+0,25
1) 15,875; 2) 0,186; 3) 0,01; 4) 7,75.
А
2
. Упростите выражение
; 2) -3; 3) 9; 4) 3.
А
3 .
Решите неравенство:
А
4
. Укажите промежуток, которому принадлежит корень уравнения 8
х – 1
= 4
1) ( 0,5 ; 1,25); 2) (1,25 ; 1,5 ); 3) (1,5 ; 1,75); 4) (1,75 ; 2,5).
А
5.
Найдите область определения функции: у =
А
6.
На одном из рисунков изображён график функции
. Укажите этот рисунок.
1) 2) 3) 4)
В
1.
Найдите наименьший корень уравнения 2
2х+1
— 7 · 10
х
+ 5
2х+1
=0
В
2
.Решите систему уравнений
8
1
2
1
1282
12ух
ух
.
Найдите значение 2х
0
—у
0
, где (х
0 ;
у
0
)-решение системы.
В
3
. Укажите целое решение неравенства (х — 6)(8
х—6
— 64) < 0 .
В
4
. Найдите наименьшее значение функции
1
3
1
3
1
5
96624
х
х
х
х
х
х
Контрольная работа по теме: Логарифмическая функция.
Логарифмические уравнения и неравенства. 11 класс.
1 Вариант.
А
1
. Найдите значение выражения
1) 6; 2) 27; 3) 12; 4) 54.
А
2
. Укажите промежуток, которому принадлежит корень уравнения
.3ln3ln4ln xx
); 4) ( 2; 4 ).
А
3
. Найдите область определения функции
A
4
. Найдите значение выражения log
3
(9b), если log
3
b = 5.
1) 25; 2) 10; 3) -8; 4) 7.
А
5
. Решите неравенство log
2
( 1 – 0,3
В
1
. Укажите наименьшее целое число из области определения функции
В
2
. Найдите произведение корней уравнения
011111211
2
5
2
5
loglog2
xx
.
В
3
. Найдите значение выражения
.1004,025,0
8lg
2lg2lg
— решение системы уравнений
.
32
02log
2
1
yx
yx
.3
1
1
2log4
32
3
3log3
66
xx
, при которых область определения функции
5,0
5,4
log21
45,0
axaxay
ax
x
x
содержит ровно три целых числа.
Контрольная работа по теме: Логарифмическая функция.
Логарифмические уравнения и неравенства. 11 класс.
2 Вариант.
А
1
. Найдите значение выражения
1) 1; 2) -9; 3) 3; 4) -1,5.
А
2
. Укажите промежуток, которому принадлежит корень уравнения
.
1) ( -4; -2); 2) ( 6; 8); 3) ( 3; 6); 4) ( -8; -6).
А
3
. Найдите область определения функции y = log
0,1
(0,01 –
.
1) 1; 2) -7; 3) -1; 4) 7.
А
5
. Решите неравенство
В
1
. Найдите наименьшее значение функции
В
2
. Найдите наибольшее целое решение неравенства
В
3
. Найдите значение выражения
— решение системы уравнений
.
53
02log
2
1
yx
yx
.12
3
13
2log3
72
13
1log2
22
xx
С
3
. Найдите все положительные, не равные 1, значения
, при которых область
определения функции
5,0
5,4
log5,0log5,04
axaaay
ax
x
xa
не содержит
двузначных натуральных чисел.
Контрольная работа за полугодие. 11 класс.
Вариант I
Часть 1
При выполнении заданий части 1 в бланке ответов №1 под номером выполняемого вами
задания А
1
– А
10
поставьте знак «
» в клеточку, номер которой соответствует номеру
выбранного вами ответа.
А
1
Упростите выражение
.
А
2
Найдите значение выражения
1) 6,25; 2) 625; 3) 25; 4) 12,5.
А
3
Вычислите
; 4) -12.
А
4
Упростите выражение
4sin5cos
2
cos4cos5sin
.
А
5
Укажите первообразную функции
.
А
6
Найдите угловой коэффициент касательной, проведённой к графику функции
.
1) 0; 2) 4; 3) 1; 4) -2.
А
7
На рисунке изображены графики функций, заданных на отрезках
. Укажите
график четной функции.
А
8
Укажите множество решений неравенства
.
А
9
Укажите промежуток, которому принадлежат корни уравнения
.
А
10
Найдите площадь фигуры, ограниченной
линиями
;
4) 1.
Часть 2
Ответом к каждому заданию этой части будет некоторое число. Это число надо
вписать в бланк ответов №1 справа от номера задания (В
1
—В
5
), начиная с первой
клеточки. Каждую цифру или знак минус отрицательного числа пишите в отдельной
клеточке строго по образцу из верхней части бланка. Единицы измерений писать не
нужно. Если ответ получится в виде дроби, то её надо округлить до ближайшего целого
числа.
В
1
При каком значении а функция
имеет максимум в точке х
0
= 1,5?
В
2
На рисунке изображён график производной
функции
на монотонность
и в ответе укажите длину промежутка возрастания.
В
3
Решите систему уравнений. Найдите х
0
+ у
0
, если (х
0
; у
0
) – решение системы.
В
5
Найдите число корней уравнения
.
Часть 3
Для записи ответов к заданиям этой части (С
1
—С
3
) используйте бланк ответов №2.
Запишите сначала номер задания, а затем полное решение.
С
1
Решите уравнение
С
3
Найдите все значения р, при которых уравнение
не имеет
корней.
Контрольная работа за полугодие. 11 класс.
Вариант II
Часть 1
При выполнении заданий части 1 в бланке ответов №1 под номером выполняемого вами
задания А
1
– А
10
поставьте знак «
» в клеточку, номер которой соответствует номеру
выбранного вами ответа.
А
1
Упростите выражение
представьте в виде степени с основанием
1) 0,0012; 2) 0,12; 3) 0,012; 4) 1,2.
А
4
Найдите множество значений функции
.
А
5
Найдите все решения уравнения
укажите первообразную, график которой проходит через
точку М (-3; 0).
1)
.
А
7
Найдите производную функции
.
А
8
Определите число целых неотрицательных решений неравенства
1) 10; 2) 12; 3) 8; 4) 11.
А
9
Укажите промежуток, которому принадлежат корни уравнения
.
А
10
Функция задана графиком. Укажите область
определения функции.
1)
.
Часть 2
Ответом к каждому заданию этой части будет
некоторое число. Это число надо вписать в бланк ответов №1 справа от номера задания
(В
1
—В
5
), начиная с первой клеточки. Каждую цифру или знак минус отрицательного числа
пишите в отдельной клеточке строго по образцу из верхней части бланка. Единицы
измерений писать не нужно. Если ответ получится в виде дроби, то её надо округлить
до ближайшего целого числа.
В
1
Пусть (х
0
; у
0
) – решение системы.
Найдите х
0
—у
0
.
В
2
На рисунке изображён график производной
функции
и в ответе укажите число промежутков возрастания.
В
3
Вычислите:
278132627001,0
2
3
4
5
0
3
1
2
3
1
.
В
4
Найдите число корней уравнения
020cos10cos10sin5 xxxxtg
.
В
5
При каком значении n функция
имеет максимум в точке х
0
= —3
?
Часть 3
Для записи ответов к заданиям этой части (С
1
—С
3
) используйте бланк ответов №2.
Запишите сначала номер задания, а затем полное решение.
С
1
Решите уравнение
5,015,05,05,0525,0
11
xxx
.
С
3
Найдите все значения р, при которых уравнение
имеет хотя бы один корень.
Контрольная работа по теме:
Производная и первообразная
показательной и логарифмической функций. 11 класс.
Вариант I.
А
1
. Найдите производную функции
.
А
2
. На каком из рисунков изображен график производной функции
1) 2) 3) 4)
А
3
. Найдите значение производной функции
.
А
4
. Найдите угловой коэффициент касательной, проведённой к
графику функции
.
1) 1; 2) 2; 3) 3; 4) 0.
А
5
. Касательной к графику функции
В
1
. Найдите значение С первообразной F функции
), если F(1) = 3.
В
2
. Найдите произведение критических точек функции
.
В
3
. Найдите промежутки монотонности функции
.
В ответе укажите длину промежутка убывания.
С
1
. Найдите наименьшее значение функции
.
С
2
. Найдите общий вид первообразной для функции
)1,05)(1,05()(
xxxx
xf
и определите, при каких
значениях С первообразная при любых значениях х
отрицательна.
Контрольная работа по теме:
Производная и первообразная
показательной и логарифмической функций. 11 класс.
Вариант II.
А
1
. Найдите производную функции
.
А
2
. На каком из рисунков изображен график производной функции
1) 2) 3) 4)
А
3
. Найдите значение производной функции
; 4) 0.
А
4
. Найдите угловой коэффициент касательной, проведённой к
графику функции
.
1) 1,4; 2) 2; 3) 7; 4) 12.
А
5
. Касательной к графику функции
В
1
. Найдите значение С первообразной F функции
,
если F(0) = 2.
В
2
. Найдите сумму критических точек функции
В
3
. Найдите промежутки монотонности функции
.
В ответ выпишите количество промежутков монотонности.
С
1
. Найдите наименьшее значение функции
.
С
2
. Найдите общий вид первообразной для функции
)35,0)(35,0()(
xxxx
xf
и определите, при каких
значениях С первообразная при любых значениях х
положительна.
Контрольная работа «Тригонометрия»
Вариант № 1.
1. Выразите в радианах: а) 10°; б) 210°.
2. Выразите в градусах: а)  ; б)
; б)  .
.
3. Вычислить значение каждой из тригонометрических функций, если: 
 .
.
4. Упростите выражение:  ;
;
5. Докажите тождество:  ;
;
6. Вычислите значение sin2x, если cosx = и
и 
–  ; 2)
; 2)  ; 3)
; 3)  ; 4) –
; 4) –  .
.
7. Найдите значение выражения  при
при 
8. Упростите выражение 
9. Найдите значение выражения:  при x=
при x=
а) ; б)
; б)  ; в)
; в)  ; г) 0.
; г) 0.
10. Вычислите: 
а)  ; б)
; б)  ; в)
; в)  ; г)1.
; г)1.
11. Решите уравнение 
а) π2n; б)  ; в) πn; г) 0.
; в) πn; г) 0.
12. Решите уравнение 
а) π2+πn; б) πn; в) π2n; г) πn+2πn.
13. Решите уравнение 
а) x=(-1)n+1π3+πn; б) x=(-1)nπ6+πn; в) x=(-1)nπ3+πn; г) x=(-1)n+1π2+πn.
14. Решите уравнение 
а) x=π3+πn; б) x=π2+2πn; в) x=π6+2πn; г) x=2π3+πn.
15. Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют … числа t.
16. Угол в один радиан – это … угол, опирающийся на дугу, длина которой равна радиусу окружности.
17. Какая из тригонометрических функции является четной функцией?
18. Решите уравнение  .
.
Вариант № 2.
1. Выразите в радианах: а) 15°; б) 225°.
2. Выразите в градусах: а)  ; б)
; б)  .
.
3. Вычислить значение каждой из тригонометрических функций, если: 
 .
.
4. Упростите выражение:  ;
;
5. Докажите тождество:  ;
;
6. Вычислите значение cos2 , если sin
, если sin = –
= –  и
и 
–  ; 2)
; 2)  ; 3) – 0,5 ; 4) 0,5.
; 3) – 0,5 ; 4) 0,5.
7. Найдите значение выражения  при cos
при cos =
= 
8. Упростите выражение 
9. Найдите значение выражения:  при x=
при x=
а) 1; б) 0,5; в)  ; г) 1,5.
; г) 1,5.
10. Вычислите: 
а)0; б)  ; в)1; г)
; в)1; г)  .
.
11. Решите уравнение 
а) π2n; б) π2+2πn; πn. в) 2π3+2πn; 2πn.; г) π+2πn; πn.
12. Решите уравнение 
а) π2n; б) 2πn, в) π3+πn; г) πn.
13. Решите уравнение 
а) ±π2n; б) ±π2+2πn; в) ±π4+2πn; г) ±π+2πn; πn.
14. Решите уравнение 
а) π2 +2πn; б) 2πn. в) π3+πn; г) π+2πn.
15. Если точка М числовой окружности соответствует числу t, то ординату точки М называют … числа t. 16. Если функция ограничена и снизу и сверху, то её называют … . 17. Какие тригонометрические функции являются нечетными функциями?
18. Решите уравнение  . Записать полное решение.
. Записать полное решение.
Эталон ответов
контрольной работы «Тригонометрия»
Вариант № 1 Вариант № 2
1. π18, 7π6 1. π12, 5π4
2. 12,140 2. 15,120
3. -513, -123, -512 3. -2√65, 2√6, √612
4. 1cos2α 4. — tg2α
5. верное 5. верное
6. 4 6. -12
7. -1,4 7. 1,5
8.1 8. 1
9.г, 9. а,
10.г, 10.а,
11.в, 11.в,
12.б, 12.б,
13.а, 13.в,
14.б, 14.г,
15.косинусом, 15.синусом,
16.центральный, 16.ограниченной,
17.косинус, 17.синус, тангенс, котангенс.
18. х = 2πп 18. х = π2 + 2πп
х = —arcctg7+πп х = arcctg13+πп
Критерии оценивания
Отметка «2» выставляется, если выполнено менее 10 (от 1 до 9) заданий работы.
Отметка «3» выставляется, если верно выполнено 10 — 13 заданий работы.
Отметка «4» выставляется, если верно выполнено 14 — 16 заданий работы.
Отметка «5» выставляется, если верно выполнено 17-18 заданий работы.
-
Найдите значение
выражения:
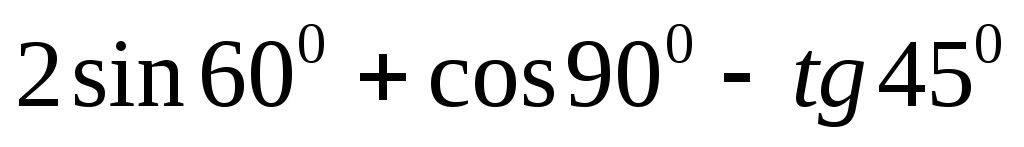
1)![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
0.
-
Сравните с нулём
выражения: sin
1200,
cos
1950,
ctg
3590.
Выберите
правильную серию ответов:
1)
+ – – 2)
– – + 3)
+ + – 4)
+ – +
-
Вычислите:

1)
12; 2)
![]() ;
;
3)
6; 4)
0.
-
Упростите выражение:

1)
– cos2;
2)
cos2;
3)
sin2;
4)
–
sin2.
-
Упростите выражение:
sin
*
cos
* ctg
– 1
1)
0; 2)
cos2;
3)
– sin2;
4)
sin2.
-
Упростите выражение:
1)
sin
– cos ;
2)
–2 ctg 2;
3)
tg 2;
4)
0,5 ctg 2.
-
Вычислите: 2sin
150 *
cos
150
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
-
Вычислите: cos
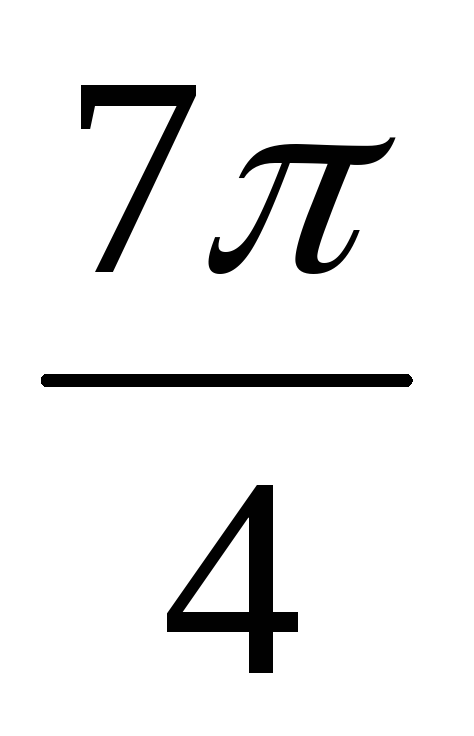
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
0.
-
Представив 1050
как 600 +
450,
вычислите sin
1050.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
-
Дано: sin
= –
где
 .
.
Найдите tg
2
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
Контрольная работа по теме: Тригонометрические функции. 10 класс. Вариант 2.
-
Найдите значение
выражения:

1)
2,5; 2)
0,5; 3)
![]() ;
;
4)
1,5.
-
Сравните с нулём
выражения: sin
1870,
cos
2150,
tg
800.
Выберите
правильную серию ответов:
1)
+ – + 2)
– + + 3)
– – + 4)
– + –
-
Вычислите:

1)
![]() ;
;
2) —![]() ;
;
3) —![]() ;
;
4)
![]() .
.
-
Упростите выражение:

1)
tg2;
2)
-tg2;
3)
-ctg2
;
4)
ctg2.
-
Упростите
выражение: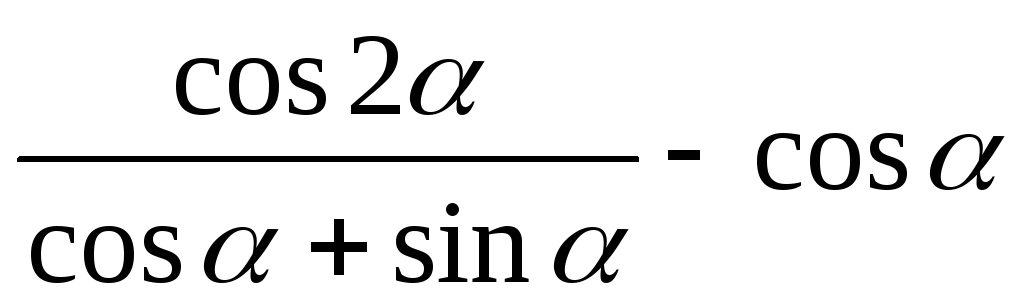
1)
– sin
;
2)
sin ;
3)
– 2cos ;
4)
sin
– 2cos .
-
Упростите выражение:

1)
ctg2;
2)
tg2;
3)
– tg2;
4)
– ctg2.
-
Вычислите:

1)
 ;
;
2)
 ;
;
3)
 ;
;
4) 0. -
Вычислите: cos
 1500
1500
1)
 ;
;
2)
 ;
;
3)
 ;
;
4)
 .
. -
Представив 150
как 450
–
300,
вычислите cos
150.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
-
Дано: cos
= –
где
 .
.
Найдите ctg
2
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.![]()
Контрольная работа по теме: Свойства функции. 10 класс.
1 Вариант
1.
Найдите область определения функции
![]()
![]()
1)![]()
2)
![]()
3)
![]()
4)
![]() .
.
2.
Найдите область значений функции у =
cos
x
+2
1)
[-1;1]; 2)[-2;2];
3)
[0;2]; 4)
[1;3].
3.
Проверьте функцию на четность у = х4+
cos
x
1)
четная; 2)
нечетная; 3)
ни четная, ни нечетная; 4)
периодическая.
4.
Найдите нули функции
![]()
1)
0; 2)
1; 3)
0; 1; 4)
нет.
5 .
.
По графику некоторой функции у= f
(x)
найдите промежутки возрастания
1)
[-3;-2] U
[2;5]; 2)
[-3;5]; 3)
[-2;2]; 4)
[2;5].
6.
Найдите наименьший положительный
период функции
![]()
1)
π;![]()
2)
2 π; 3)
0,5 π; 4)
4 π.
7.
Найдите наименьшее значение функции
у = х2
+ 3х – 1
1)
-1; 2)
-3,25; 3)
-1,5; 4)
1,25.
8.
Укажите график функции у = (х-1)2+4


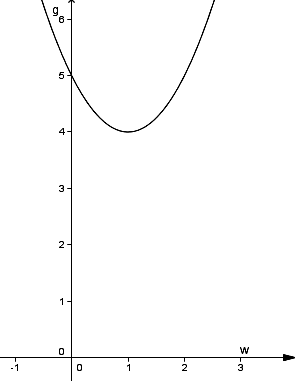

1)
2) 3)
4)
9.
Найдите промежутки, на которых у>0

1)
(-2;2); 2)
[-2;0)U(2;4);
3)
[-2;-1) U
(2;4]; 4)
[0;3].
10.
Дана функция f
(x)=
x3-2ax
+ 8 . Известно, что f
(1) = 5. Найдите f
(-2).
1)
16; 2)
0; 3)
8; 4)
-8.
11.
Укажите функцию, которой соответствует
данный график

1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
