Контрольная работа номер 1 делимость чисел

Контрольная работа №1.6

Делимость натуральных чисел

Вариант 1

1.
Из
чисел 387, 756, 829, 2 148 выпишите те, которые делятся нацело:

1)
на 2;

2)
на 9.

2.
Разложите
число 756 на простые множители.

3.
Найдите
наибольший общий делитель чисел:

1)
24 и 54;

2)
72 и 264.

4.
Найдите
наименьшее общее кратное чисел:

1)
16 и 32;

 2)
15 и 8;

3)
16 и 12.

5.
Докажите,
что числа 272 и 1 365 — взаимно простые.

6.
Вместо
звёздочки в записи 1 52* поставьте цифру так, чтобы полученное число было
кратным 3 (рассмотрите все возможные случаи).

7.
Петя
расставил книги поровну на 12 полках, а потом переставил их, тоже поровну, на 8
полок. Сколько книг было у Пети, если известно, что

их было больше 100, но меньше 140?

Контрольная работа №1.6

Делимость натуральных чисел

Вариант 2

1.
Из
чисел 405, 972, 865, 2 394 выпишите те, которые делятся нацело:

1)
на 5;

2)
на 9.

2.
Разложите
число 1 176 на простые множители.

3.
Найдите
наибольший общий делитель чисел:

1)
27 и 36;

2)
168 и 252.

4.
Найдите
наименьшее общее кратное чисел:

1)
11 и 33;

2)
9 и 10;

3)
18 и 12.

5.
Докажите,
что числа 297 и 304 — взаимно простые.

6.
Вместо
звёздочки в записи 1 99* поставьте цифру так, чтобы полученное число было
кратным 3 (рассмотрите все возможные случаи).

7.
Собранный
урожай яблок фермер может разложить поровну в корзины по 12 кг или в ящики по
15 кг. Сколько килограммов яблок собрал

фермер, если известно, что их было больше
150 кг, но меньше 200 кг?

Контрольная работа №1.6

Делимость натуральных чисел

Вариант 3

1.
Из
чисел 703, 492, 675, 3 258 выпишите те, которые делятся нацело:

1)
на 2;

2)
на 9.

2.
Разложите
число 1 848 на простые множители.

3.
Найдите
наибольший общий делитель чисел:

1)
32 и 56;

 2)
378 и 450.

4.
Найдите
наименьшее общее кратное чисел:

1)
17 и 34;

2)
8 и 25;

 3)
15 и 12.

5.
Докажите,
что числа 325 и 792 — взаимно простые.

6.
Вместо
звёздочки в записи 2 00* поставьте цифру так, чтобы полученное число было
кратным 3 (рассмотрите все возможные случаи).

7.
Учеников
шестых классов, которых больше 120, но меньше 150,

можно
отвезти на экскурсию или микроавтобусами по 12 человек, или микроавтобусами по
16 человек, при этом в обоих случаях пустых мест в микроавтобусах не будет.
Сколько шестиклассников едет на экскурсию?

Контрольная работа №1.6

Делимость натуральных чисел

Вариант 4

1.
Из
чисел 584, 810, 729, 4 635 выпишите те, которые делятся нацело:

1)
на 5;

 2)
на 9.

2.
Разложите
число 1 890 на простые множители.

3.
Найдите
наибольший общий делитель чисел:

1)
40 и 64;

 2)
162 и 270.

4.
Найдите
наименьшее общее кратное чисел:

1)
18 и 36;

2)
12 и 35;

 3)
16 и 24.

5.
Докажите,
что числа 308 и 585 — взаимно простые.

6.
Вместо
звёздочки в записи 1 43* поставьте цифру так, чтобы полученное число было
кратным 3 (рассмотрите все возможные случаи).

7.
Туристы,
отправляясь в поход, планировали пройти весь маршрут за

12
дней, преодолевая ежедневно одно и то же целое число километров.

Однако
им удалось пройти весь маршрут за 9 дней, преодолевая ежедневно одно и то же
целое число километров. Какова длина всего маршрута, если известно, что она
больше 100 км, но меньше 120 км?

 Решения
контрольной работы №1

6
класса УМК А.Г.Мерзляк

Вариант1

1.1) 756; 2 148; 2) 387; 756.

2. 756=7*3*3*3*2*2

3.1) НОД (24; 54) = 6; 2) НОД (72;264) =
24

4. 1) НОК (16; 32) = 32; 2) НОК (15; =
120; 3) НОК (16; 12) =48

5. Доказательство: 272 = 2*131; 1365 = 3*5*7*13.
Среди простых множителей разложения нет общих делителей, кроме 1, значит, по
определению эти числа взаимно простые.

6. 1+5+2=8, значит, вместо * могут стоят
цифры 1, 4, 7. Ответ: 1 521: 1 524; 1 527.

7. Количество книг кратно числам 12 и 8.
Их количество больше 100, но меньше 140. Только одно число попадает в этот
промежуток – это 120, оно кратно 12 и 8.

Ответ: У Пети было 120 книг.

Вариант
2

1.     1)
405; 865; 2)405; 972; 2 394.

2.     1 176
= 2*2*2*3*7*7

3.     1)
НОД (27; 36) = 9; 2) НОД (168; 252) = 84

4.     1)
НОК (11; 33) = 33; 2) НОК (10; 9) = 90; 3) НОК (18; 12) =36

5.     Доказательство:
297 = 11*3*3*3; 304 = 2⁴*19. Среди простых множителей разложения нет
общих делителей, кроме 1, значит, по определению эти числа взаимно простые.

6.     1+9+9=19,
значит, вместо * могут стоят цифры 2, 5, 8. Ответ: 1 992; 1995; 1 998.

7.     Количество
урожая кратно числам 12 и 15. Их количество больше 150, но меньше 200. Только
одно число попадает в этот промежуток – это 180, оно кратно 12 и 15.

Ответ: Фермер собрал 180
кг яблок.

Вариант
3

1.1) 492; 3 258; 2) 675; 3 258.

2. 1 848=11*7*3*2*2*2

3.1) НОД (32; 56) = 8; 2) НОД (378;450) =
18

4. 1) НОК (17; 34) = 34; 2) НОК (25; = 200;
3) НОК (15; 12) =60.

5. Доказательство: 325 = 5*5*13; 792 = 2*2*2*3*3*11.
Среди простых множителей разложения нет общих делителей, кроме 1, значит, по
определению эти числа взаимно простые.

6.2+0+0=21, значит, вместо * могут стоят
цифры 1, 4, 7. Ответ: 2 001; 2 004; 2 007.

7. Количество учащихся кратно числам 12 и 16.
Их количество больше 120, но меньше 150. Только одно число попадает в этот
промежуток – это 144, оно кратно 12 и 16.

Ответ: На экскурсию едет 144
шестиклассника.

Вариант
4

1.     1)
810; 4 635; 2) 810; 729; 4 635.

2.     1 890
= 2*3*3*3*5*7

3.     1)
НОД (40; 64) = 8; 2) НОД (162; 270) = 54

4.     1)
НОК (18; 36) = 36; 2) НОК (12; 35) = 420; 3) НОК (16; 24) =48

5.     Доказательство:
308 = 11*7*2*2; 585 = 13*5*3*3. Среди простых множителей разложения нет общих
делителей, кроме 1, значит, по определению эти числа взаимно простые.

6.     1+4+3=8,
значит, вместо * могут стоят цифры 1, 4, 7. Ответ: 1 431; 1 434; 1 437.

7.     Длина
маршрута кратно числам 12 и 9. Он больше 100 км, но меньше 120 км. Только одно
число попадает в этот промежуток – это 108, оно кратно 12 и 9.

Ответ: Длина всего
маршрута составляет 108 км.

                              1 вариант.

1). Разложите на простые множители число 990, 1655.

2). Найдите наибольший общий делитель и наименьшее общее кратное чисел 192 и 108.

3). Докажите, что числа:

а). 260 и 285 не взаимно простые;

б). 301 и 585 взаимно простые.

4). Выполните действия: 355,1 : 0,67 + 0,83 ∙ 15.

5). Найдите наибольший общий делитель числителя и знаменателя дроби  и сократите эту дробь.

6).  В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке,  15 — в районной. Сколько учеников не являются читателями школьной библиотеки?

                                   2 вариант.

1). Разложите на простые множители число 660, 1550.

2). Найдите наибольший общий делитель и наименьшее общее кратное чисел 144 и 216.

3). Докажите, что числа:

а). 255 и 240 не взаимно простые;

б). 392 и 675 взаимно простые.

4). Выполните действия: 268,8 : 0,56 + 6,44 ∙ 12.

5). Найдите наибольший общий делитель числителя и знаменателя дроби  и сократите эту дробь.

6). Каждый ученик в классе изучает английский или немецкий язык, или оба этих языка. Английский язык изучают 25 человек, немецкий — 27 человек, а тот и другой — 18 человек. Сколько всего учеников в классе?

                              1 вариант.

1). Разложите на простые множители число 990, 1655.

2). Найдите наибольший общий делитель и наименьшее общее кратное чисел 192 и 108.

3). Докажите, что числа:

а). 260 и 285 не взаимно простые;

б). 301 и 585 взаимно простые.

4). Выполните действия: 355,1 : 0,67 + 0,83 ∙ 15.

5). Найдите наибольший общий делитель числителя и знаменателя дроби  и сократите эту дробь.

6).  В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке,  15 — в районной. Сколько учеников не являются читателями школьной библиотеки?

                                   2 вариант.

1). Разложите на простые множители число 660, 1550.

2). Найдите наибольший общий делитель и наименьшее общее кратное чисел 144 и 216.

3). Докажите, что числа:

а). 255 и 240 не взаимно простые;

б). 392 и 675 взаимно простые.

4). Выполните действия: 268,8 : 0,56 + 6,44 ∙ 12.

5). Найдите наибольший общий делитель числителя и знаменателя дроби  и сократите эту дробь.

6). Каждый ученик в классе изучает английский или немецкий язык, или оба этих языка. Английский язык изучают 25 человек, немецкий — 27 человек, а тот и другой — 18 человек. Сколько всего учеников в классе?

Категория: ГДЗ Математика 6 класс дидактические материалы Мерзляк. Контрольные и самостоятельные работы с ответами ✔

Контрольная работа № 1 по теме «Делимость натуральных чисел»

Вариант 1

1. Из чисел 387, 756, 829, 2 148 выпишите те, которые делятся нацело:

1) на 2; 2) на 9.

2. Разложите число 756 на простые множители.

3. Найдите наибольший общий делитель чисел:

1) 24 и 54; 2) 72 и 264.

4. Найдите наименьшее общее кратное чисел:

1) 16 и 32; 2) 15 и 8; 3) 16 и 12.

5. Докажите, что числа 272 и 1 365 — взаимно простые.

6. Вместо звёздочки в записи 1 52* поставьте цифру так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).

7. Петя расставил книги поровну на 12 полках, а потом переставил их, тоже поровну, на 8 полок. Сколько книг было у Пети, если известно, что их было больше 100, но меньше 140?

Вариант 2

1. Из чисел 405, 972, 865, 2 394 выпишите те, которые делятся нацело:

1) на 5; 2) на 9.

2. Разложите число 1 176 на простые множители.

3. Найдите наибольший общий делитель чисел:

1) 27 и 36; 2) 168 и 252.

4. Найдите наименьшее общее кратное чисел:

1) 11 и 33; 2) 9 и 10; 3) 18 и 12.

5. Докажите, что числа 297 и 304 — взаимно простые.

6. Вместо звёздочки в записи 1 99* поставьте цифру так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).

7. Собранный урожай яблок фермер может разложить поровну в корзины по 12 кг или в ящики по 15 кг. Сколько килограммов яблок собрал фермер, если известно, что их было больше 150 кг, но меньше 200 кг?

Вариант 3

1. Из чисел 703, 492, 675, 3 258 выпишите те, которые делятся нацело:

1) на 2; 2) на 9.

2. Разложите число 1 848 на простые множители.

3. Найдите наибольший общий делитель чисел:

1) 32 и 56; 2) 378 и 450.

4. Найдите наименьшее общее кратное чисел:

1) 17 и 34; 2) 8 и 25; 3) 15 и 12.

5. Докажите, что числа 325 и 792 — взаимно простые.

6. Вместо звёздочки в записи 2 00* поставьте цифру так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).

7. Учеников шестых классов, которых больше 120, но меньше 150, можно отвезти на экскурсию или микроавтобусами по 12 человек, или микроавтобусами по 16 человек, при этом в обоих случаях пустых мест в микроавтобусах не будет. Сколько шестиклассников едет на экскурсию?

Вариант 4

1. Из чисел 584, 810, 729, 4 635 выпишите те, которые делятся нацело:

1) на 5; 2) на 9.

2. Разложите число 1 890 на простые множители.

3. Найдите наибольший общий делитель чисел:

1) 40 и 64; 2) 162 и 270.

4. Найдите наименьшее общее кратное чисел:

1) 18 и 36; 2) 12 и 35; 3) 16 и 24.

5. Докажите, что числа 308 и 585 — взаимно простые.

6. Вместо звёздочки в записи 1 43* поставьте цифру так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).

7. Туристы, отправляясь в поход, планировали пройти весь маршрут за 12 дней, преодолевая ежедневно одно и то же целое число километров. Однако им удалось пройти весь маршрут за 9 дней, преодолевая ежедневно одно и то же целое число километров. Какова длина всего маршрута, если известно, что она больше 100 км, но меньше 120 км?

Математика 6 Ершова КР-01

Контрольная работа № 1 по математике 6 класс «Делимость чисел» с ответами для любому УМК Дорофеев в 6-ти вариантах трех уровней сложности. Дидактические материалы для школьников, учителей и родителей. Математика 6 Ершова КР-01.

Математика 6 класс (любой УМК)

Контрольная работа № 1 «Делимость чисел»

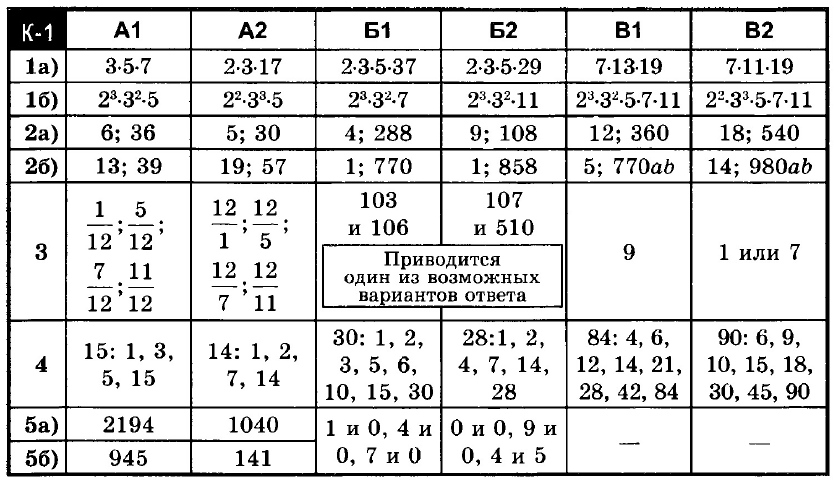
Вариант А1

1. Разложите на простые множители числа: а) 105; б) 360.
2. Найдите наибольший общий делитель и наименьшее общее кратное чисел: а) 12 и 18; б) 13 и 39.
3. Запишите все правильные дроби со знаменателем 12, в которых числитель и знаменатель – взаимно простые числа.
4. Найдите значение выражения и выпишите все делители этого числа: 20,5 • 0,4 + 21,76 : 3,2.
5. Дано число 21 945. Вычеркните в данном числе
   а) одну цифру так, чтобы полученное число делилось на 2;
   б) две цифры так, чтобы полученное число делилось на 9.

Вариант А2

1. Разложите на простые множители числа: а) 102; б) 540.
2. Найдите наибольший общий делитель и наименьшее общее кратное чисел: а) 10 и 15; б) 19 и 57.
3. Запишите все неправильные дроби с числителем 12, в которых числитель и знаменатель – взаимно простые числа.
4. Найдите значение выражения и выпишите все делители этого числа: 36,6 • 0,5 – 12,04 : 2,8.
5. Дано число 10 401. Вычеркните в данном числе
   а) одну цифру так, чтобы полученное число делилось на 5;
   б) две цифры так, чтобы полученное число делилось на 3.

Вариант Б1

1. Разложите на простые множители числа: а) 1110; б) 504.
2. Найдите наибольший общий делитель и наименьшее общее кратное чисел: а) 32 и 36; б) 14 и 55.
3. Составьте из цифр 0, 1, 3, 6 пару трехзначных взаимно простых чисел (цифры в одном числе не должны повторяться). Ответ обоснуйте.
4. Найдите значение выражения и выпишите все делители этого числа: (12,4 • 9,5 – 36,8) : 2,7.
5. Замените звездочки цифрами так, чтобы число *32* делилось на 30. Укажите все возможные решения.

Вариант Б2

1. Разложите на простые множители числа: а) 870; б) 792.
2. Найдите наибольший общий делитель и наименьшее общее кратное чисел: а) 27 и 36; б) 26 и 33.
3. Составьте из цифр 0, 1, 5, 7 пару трехзначных взаимно простых чисел (цифры в одном числе не должны повторяться). Ответ обоснуйте.
4. Найдите значение выражения и выпишите все делители этого числа: (10,32 : 4,3 + 8,8) • 2,5.
5. Замените звездочки цифрами так, чтобы число 81** делилось на 45. Укажите все возможные решения.

Вариант В1

1. Разложите на простые множители числа: а) 1729; б) 27720.
2. Найдите наибольший общий делитель и наименьшее общее кратное чисел: а) 36, 60 и 72; б) 70а и 55b, где а и b – простые числа больше 10.

1. Замените звездочки четырьмя одинаковыми цифрами так, чтобы числа 1** и *4* были взаимно простыми. Укажите все возможные решения.
2. Найдите значение выражения и выпишите все составные делители этого числа: (40,8+4,324:0,46) • 1,5+8,7.
3. Известно, что а, b, с – простые числа, причем произведение аbс нечетно. Докажите, что сумма а + b + с также нечетна.

Вариант В2

1. Разложите на простые множители числа: а) 1463; б) 41580.
2. Найдите наибольший общий делитель и наименьшее общее кратное чисел: а) 36, 54 и 90; б) 98а и 1406, где а и b – простые числа больше 10.

1. Замените звездочки четырьмя одинаковыми цифрами так, чтобы числа *3* и 6** были взаимно простыми. Укажите все возможные решения.
2. Найдите значение выражения и выпишите все составные делители этого числа: (55,08:1,8–7,8) • 6,5–58,2.
3. Известно, что а, b, с – простые числа, причем сумма а + b + с четна. Докажите, что произведение abc также четно.

---

Математика 6 Ершова КР-01.
Ответы на контрольную работу:

---

Вы смотрели: Контрольная работа № 1 по математике 6 класс «Делимость чисел» с ответами для любому УМК Дорофеев в 6-ти вариантах. Дидактические материалы для школьников, учителей и родителей. Математика 6 Ершова КР-01.

Вернуться к Списку контрольных работ по математике для 6 класса

Цитаты из учебного пособия «Самостоятельные и контрольные работы по математике для 6 класса / Ершова А.П., Голобородько В.В. — М.: ИЛЕКСА» использованы на сайте в незначительных объемах, исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). ОТВЕТЫ на контрольную работу адресованы родителям для проверки знаний учащихся.

Контрольная работа № 1 по математике 6 класс «Делимость натуральных чисел» с ответами и решениями по УМК Мерзляк, Полонский, Якир (Вариант 2). Дидактические материалы для учителей, школьников и родителей при дистанционном обучении. Математика 6 Мерзляк КР-1 В2.

КР-1. Вариант 2 (транскрипт заданий)

1. Из чисел 135, 240, 594, 3 251 выпишите те, которые делятся нацело: 1) на 5; 2) на 9.
2. Разложите число 1 584 на простые множители.
3. Найдите наибольший общий делитель чисел: 1) 36 и 63; 2) 180 и 312.
4. Найдите наименьшее общее кратное чисел: 1)15 и 30; 2) 8 и 35; 3) 10 и 16.
5. Докажите, что числа 945 и 208 – взаимно простые.
6. Вместо звёздочки в записи 2 38* поставьте такую цифру, чтобы полученное число было кратно 3 (рассмотрите все возможные случаи).
7. Катя собирает фигурки лошадок. Их можно расставить поровну на 9 полках, а можно, тоже поровну, – на 15 полках. Сколько фигурок у Кати, если известно, что их больше 110, но меньше 140?

---

Математика 6 Мерзляк КР-1 В2 ОТВЕТЫ:

ОТВЕТЫ на Вариант 2

№1.   1) на 5:  135, 240             2) на 9:   135, 594
№2.   1584 = 2×2×2×2×3×3×11 = 2⁴×3²×11
№3.   1) НОД (36; 63) = 3×3 = 9          2) НОД (180; 312) = 2×2×3 = 12
№4.   1) НОК (3; 6) = 6      2) НОК (28; 9) = 252         3) НОК (10; 16) = 2⁴×5 = 80
№5.   НОД (945; 208) = 1. Нет общих делителей => 945 и 208 — взаимно простые.
№6.   2382, 2385, 2388
№7.   НОК (9; 15) = 45.     45×3=135.     110<135<140.    Ответ: 135 фигурок.

Смотреть РЕШЕНИЯ заданий в тетради

---

Математика 6 Мерзляк КР-1 В2. Контрольная работа по математике в 6 классе «Делимость натуральных чисел» с ответами и решениями по УМК Мерзляк, Полонский, Якир. Дидактические материалы для учителей, школьников и родителей при дистанционном обучении.
Другой вариант: КР-1 Вариант 1

В учебных целях использованы цитаты из пособия: «Математика 6 класс. Дидактические материалы/ А.Г. Мерзляк, В.Б. Полонский, Е.М.Рабинович и др. — М.: Вентана-Граф» . Представленная контрольная работа ориентирована на УМК Мерзляк и др. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия.

Вернуться на страницу: Контрольные работы по математике в 6 классе Мерзляк (Оглавление)