Как зашифровать номер телефона в тексте

Ни для кого не секрет, что нашу современную жизнь представить без цифр просто невозможно. С их помощью не только обозначаются номера домов и квартир или указываются цены в магазинах. Перечислить все возможные сферы применения этих десяти символов просто невозможно.

Вполне естественно, что цифры и числа нашли широкое применение и в криптографии. Так, например, отдельными числами можно заменять буквы, создавая шифры, которые трудно разгадать. Такие шифры, которые специалисты называют числовыми, относятся к одним из самых распространенных и интересных шифров. На первый взгляд криптограммы, созданные с помощью числовых систем шифрования, выглядят как набор ничего не значащих цифр.

Простой числовой шифр

Перед тем как приступить к созданию шифрованных сообщений с помощью простого числового шифра, необходимо составить шифровальную таблицу. В верхней строке такой таблицы записываются буквы алфавита, а в нижней — числа. При этом первую букву можно обозначить произвольно выбранным числом, а каждую последующую букву надо обозначить числом, большим, чем предыдущее, на 1,2 или 3.

Например, в русском алфавите букву А можно обозначить числом 27, а числа, предназначенные для обозначения каждой из последующих букв алфавита, увеличивать на 2. В таком случае шифровальная таблица будет выглядеть так:

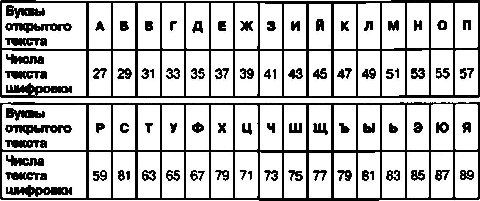
В качестве примера зашифруем с помощью этой таблицы открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ.

Вместо буквы С запишем соответствующее ей в таблице число 61. Вместо буквы Е запишем соответствующее ей число 37, вместо буквы К — число 47 и так далее. В результате получится следующая криптограмма:

61 37 47 59 37 63 53 55 37 61 55 55 29 77 37 53 43 37

Для большей скрытности этот текст можно произвольно разделить на группы цифр, например вот так:

6137 4759 3763 5355 3761 5555 2977 3753 4337

Перед расшифровкой полученный в данном случае шифрованный текст надо разбить на пары цифр, а затем с помощью приведенной выше шифровальной таблицы заменить цифры на соответствующие буквы.

Шифр гласных букв

Не представляет особых трудностей шифрование сообщений с помощью так называемого шифра гласных букв.

При использовании такого шифра гласные буквы в алфавите нумеруются цифрами от 1 до 9. При этом, например, в русском алфавите буква А обозначается цифрой 1, буква Е — цифрой 2, буква И — цифрой 3 и так далее. Затем каждой согласной букве присваивается свой номер, который определяется ее положением относительно ближайшей к ней с левой стороны в алфавите гласной буквы.

Так, например, буква Б — первая согласная буква, расположенная справа от буквы А имеющей номер 1. Поэтому букве Б присваивается число 11. Буква Д — четвертая справа от буквы А, ее обозначают числом 14. Буква Н — пятая справа от гласной буквы И, обозначенной числом 3. Поэтому букве Н должно соответствовать число 35. В соответствии с этим правилом выбираются числа, которыми будут заменены остальные буквы алфавита.

Для быстрого создания шифрованных сообщений с помощью шифра гласных букв можно составить вот такую шифровальную таблицу:

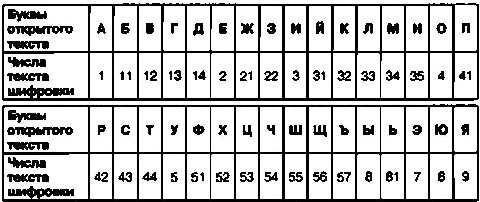
Теперь достаточно в открытом тексте заменить буквы на соответствующие числа, записываемые через точку, и шифровка готова.

В качестве примера попробуем с помощью приведенной выше таблицы зашифровать открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ Сначала необходимо заменить букву С на соответствующее ей число 43, затем букву Е — на число 2, букву К — на число 32 и так до конца текста. В результате зашифрованное сообщение будет выглядеть вот так

43.2.32.42.2.44.35.4.2 43.4.4.11.56.2.35.3.2

Или без пробелов:

43.2.32.42.2.44.35.4.2.43.4.4.11.56.235.3.2

Расшифровка такой криптограммы при использовании заранее составленной таблицы также не будет долгой и затруднительной.

Календарный шифр

Для создания криптограмм с помощью календарного шифра сначала также надо составить шифровальную таблицу. В верхней строке такой таблицы записываются буквы алфавита, а в нижней — числа от 1 до 32. В таком случае наша таблица будет выглядеть так:

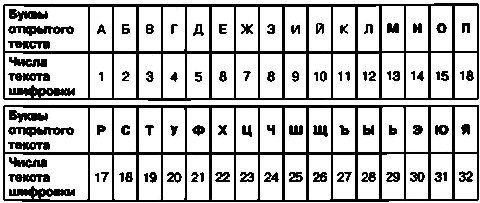
В качестве примера зашифруем с помощью календарного шифра открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ

Вместо буквы С запишем соответствующее ей в таблице число 18. Вместо буквы Е запишем соответствующее ей число 6, вместо буквы К — число 11 и так далее. В результате получится следующая криптограмма:

18.6.11.17.6.19.14.15.6.18.15.15.2.26.6.14.9.6

Но на этом процесс шифрования не заканчивается. Теперь выберем какой-либо месяц календаря и каждый день недели обозначим соответствующей буквой. Например, понедельнику будет соответствовать буква П, вторнику — буква В, среде — буква С, четвергу — буква 4, пятнице — буква П, субботе — буква С, воскресенью — буква В.

Поскольку названия некоторых дней недели начинаются с одинаковых букв, для их различия можно применить цифры. Например, понедельнику будет соответствовать сочетание П1, вторнику — сочетание В1, среде — сочетание С1, четвергу — буква Ч, пятнице сочетание П2, субботе — сочетание С2, воскресенью — сочетание В2.

Шифрование открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ начнется с первой буквы, которой в таблице соответствует число 18. Если 18-е число выбранного месяца выпадет на четверг третьей недели, то первую букву в открытом тексте, а именно букву С, следует заменить на сочетание 43. Таким образом, шифрованное сообщение будет начинаться со знаков 43. Если же 18-е число выбранного месяца выпадет на пятницу третьей недели, то сообщение будет начинаться с сочетания П23. В том случае, когда 18-е число окажется, например, понедельником четвертой недели, то шифровку начнут знаки П14. Таким же образом следует заменить остальные буквы открытого текста.

Например, если для шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ выбрать календарь на март 2012 года, то порядок шифрования будет следующим.

Сначала в соответствии с приведенной выше таблицей необходимо перевести буквы в цифры. В результате из открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ получим:

18.6.11.17.6.19.14.15.6.18.15.15.2.26.6.14.9.6

Теперь с помощью календаря на март 2012 года следует зашифровать числа в дни недели.

Число 18 в марте 2012 года — воскресенье третьей недели, поэтому его надо обозначить как В23.

Число 6 — вторник второй недели, этот день обозначается как В12.

Число 11 в марте 2012 года — воскресенье второй недели, поэтому его надо заменить на сочетание В22.

Для удобства в работе, после того как будут выбраны месяц и год шифровальную таблицу можно дополнить строкой, в которой будет непосредственно указано, на какие сочетания букв и цифр следует заменять соответствующие буквы открытого текста.

В результате шифровальная таблица с использованием календаря на март 2012 года примет следующий вид:

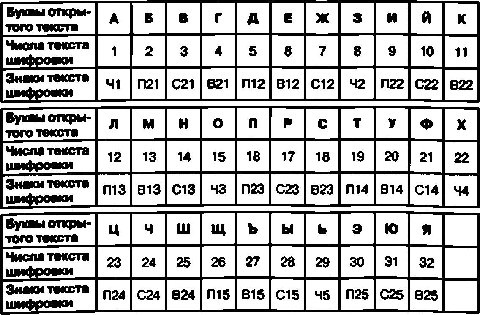
Теперь с помощью такой таблицы зашифровать любое сообщение будет очень просто. Достаточно всего лишь для каждой буквы открытого текста найти соответствующее сочетание знаков для шифровки и выполнить замену. Так, например, открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ после шифрования с помощью календарного шифра с использованием календаря на декабрь 2005 года будет преобразован вот в такую криптограмму:

В23.В12.В22.С23.В12.П14.С13.ЧЗ.В12 В23.ЧЗ.ЧЗ.П21.П15.В12.С13.П22.В12

Или без пробелов:

В23.В12.В22.С23.В12.П14.С13.ЧЗ.В12.В23.ЧЗ.ЧЗ.П21.П15.В12.С13.П22.В12

Дешифровка такого сообщения производится в обратном порядке. Сначала дни недели переводятся в числа месяца, а затем — в буквы открытого текста Естественно, для расшифровки получателю необходимо знать месяц и год, используемые в шифре. Если же заранее составить приведенную выше таблицу, то процесс расшифровки займет всего лишь несколько минут.

Наблюдательный читатель заметит, что в приведенной таблице для обозначения букв алфавита используются 32 числа, хотя в каждом месяце года дней не более, чем 31. Все правильно. Однако в данной таблице ошибок нет. Просто при применении календарного шифра используется маленькая хитрость, заключающаяся в том, что недостающие дни берутся как бы из следующего месяца.

Если посмотреть на букву Я, которая имеет в таблице порядковый номер 32, то она обозначена сочетанием В25. А это означает воскресенье пятой недели. В то же время в календаре на декабрь 2005 года мы не найдем такой даты, поскольку последний, 31-й день этого месяца приходится на субботу пятой недели. Но это не страшно. Из таблицы пользователь точно знает, что буква Я заменена на сочетание В25. Точно так же заполняются соответствующие ячейки таблицы при использовании месяцев с меньшим количеством дней, от 28 до 30 дней.

Использование несуществующих дат лишь запутает того, кто без ведома и разрешения отправителя захочет разгадать такую шифровку. Главное, чтобы тот, кому такое сообщение предназначается, знал об этих маленьких хитростях.

5.5. Книжные шифры

Среди специалистов так называемые книжные шифры считаются сравнительно стойкими системами шифрования. Дело в том, что взломать подобный шифр и расшифровать созданную с его помощью криптограмму, не зная книги, использовавшейся при шифровании, неспециалисту практически невозможно.

В то же время созд ание шифрованных сообщений с помощью книжных шифров не представляет особого труда даже для начинающих пользователей. Для этого достаточно взять какую-либо книгу, по определенному правилу обозначить отдельные буквы текста этой книги числами и выполнить замену букв открытого текста на соответствующие им числа. Не обязательно, чтобы книга, используемая для шифрования, была широко известной. Однако она обязательно должна быть у получателя сообщения, который должен знать и правило шифрования.

Необходимо добавить, что во избежание ошибок книга, находящаяся у получателя сообщения и используемая для дешифрования, должна быть точно такой же, что и книга, имеющаяся у отправителя. Это означает, что обе книги должны быть полностью идентичны, с тем же количеством страниц и тем же размещением текста на них.

Простой книжный шифр

Знакомство с книжными шифрами следует начать с простого книжного шифра.

Перед началом работы необходимо выбрать книгу и страницу, которые будут использоваться для шифрования. Это может быть, например, первая страница первой части третьего тома романа «Война и мир» Льва Николаевича Толстого. Для шифрования простого сообщения достаточно воспользоваться первыми двумя абзацами текста.

«С конца 1811 года началось усиленное вооружение и сосредоточение сил Западной Европы, и в 1812 году силы эти — миллионы людей (считая тех, которые перевозили и кормили армию) двинулись с Запада на Восток, к границам России, к которым точно так же с 1811 года стягивались силы России. 12 июня силы Западной Европы перешли границы России, и началась война, то есть совершилось противное человеческому разуму и всей человеческой природе событие. Миллионы людей совершали друг против друга такое бесчисленное количество злодеяний, обманов, измен, воровства, подделок и выпуска фальшивых ассигнаций, грабежей, поджогов и убийств, которого в целые века не соберет летопись всех судов мира и на которые в этот период времени люди, совершавшие их, не смотрели как на преступления.

Что произвело это необычайное событие? Какие были причины его? Историки с наивной уверенностью говорят, что причинами этого события были обида, нанесенная герцогу Ольденбургскому, несоблюдение континентальной системы, властолюбие Наполеона, твердость Александра, ошибки дипломатов и т. п.»

Все слова текста, напечатанного на этой странице бессмертного произведения великого русского классика, за исключением дат, следует пронумеровать. В результате текст примет следующий вид:

«С(1) конца(2) 1811 года(3) началось(4) усиленное(5) вооружение(6) и(7) сосредоточение(8) сил(9) Западной(10) Европы(11), и(12) в(13) 1812году(14)силы(15)эти(16) — миллионы(17) людей(18) (считая(19) тех(20), которые(21) перевозили(22) и(23) кормили(24) армию(25),) двинулись(26) с(27) Запада(28) на(29) Восток(30), к(31) границам(32) России(33), к(34) которым(35) точно(36) так(37) же(38) с(39) 1811 года(40) стягивались(41) силы(42) России(43). 12 июня(44) силы(45) Западной(46) Европы(47) перешли(48) границы(49) России(50), и(51) началась(52) война(53), то(54) есть(55) совершилосъ(56) противное(57) человеческому(58) разуму(59) и(60) всей(61) человеческой(62) природе(63) событие(64). Миллионы(65) людей(66) совершали(67) друг(68) против(69) друга(70) такое(71) бесчисленное(72) количество(73) злодеяний(74), обманов(75), измен(76), воровства(77), подделок(78) и(79) выпуска(80) фальшивых(81) ассигнаций(82), грабежей(83), поджогов(84) и(85) убийств(86), которого(87) в(88) целые(89) века(90) не(91) соберет(92) летопись(93) всех(94) судов(95) мира(96) и(97) на(98) которые(99) в(100) этот(101) период(102) времени(ЮЗ) люди(104), совершавшие(105) их(106), не(107) смотрели(108) как(109) на(110) преступления(111).

Что(112) произвело(113) это(114) необычайное(115) событием(116)? Какие(117) были(118) причины(119) его(120)? Историки(121) с(122) наивнойМ23) уверенностью(124) говорятМ25), что(126) причинамиМ?7) этого(128) события(129) были(130) обида(131), нанесеннаяМ32) герцогу(133) Ольденбургскому(134), несо6людение(135) контентальной(136) системы(137), властолюбие(138) Наполеона(139), твердость(140) Александра(141), ошибки(142) дипламатов(143) ит.(144) п.(145).

Алгоритм шифрования при использовании простого книжного шифра заключается в том, что цифра 1 обозначает первую букву первого слова, то есть в рассматриваемом примере букву С. Цифра 2 соответствует первой букве второго слова — букве К и так далее. Например, число 38 соответствует букве Ж, а число 81 — букве Ф.

Наблюдательный читатель заметит, что одной и той же букве соответствуют разные числа. Так, например, букве Г соответствуют числа 3,14,32 и др. В этом заключается одно из достоинств книжного шифра. Поскольку одну и ту же букву открытого текста в криптограмме можно заменить разными числами, разгадать такую криптограмму с помощью методов частотного анализа невозможно.

В качестве примера попробуем зашифровать с помощью простого книжного шифра открытый текст СЕКРЕТНОЕ ПОСЛАНИЕ. Итак, если в данном открытом тексте заменить буквы на соответствующие им числа из приведенного выше текста, то полученная криптограмма будет выглядеть так:

1.11.87.33.47.71.107.75.55. 22.134.108.93.25.91.121.120

Для того чтобы расшифровать это сообщение, получатель должен в аналогичной книге на известной ему странице пронумеровать все слова, а затем произвести замену указанных в криптограмме чисел на соответствующие буквы.

Усовершенствованный книжный шифр

При практическом применении рассмотренного ранее простого книжного шифра пользователь, без сомнения, столкнется с одной трудно разрешимой проблемой. Она заключается в том, что в русском алфавите есть буквы, с которых начинается лишь небольшое число слов, таких как, например, буква Ы. Найти такие слова в подавляющем числе книг просто невозможно. В то же время в русском языке практически вообще нет слов, которые начинались бы с таких букв, как Ъ или Ь. Однако незначительное усовершенствование простого книжного шифра позволяет решить эту задачу.

В усовершенствованном книжном шифре для замены каждой буквы открытого текста используются два числа, записываемые через тире. При этом первое число означает порядковый номер слова в тексте, а второе число означает номер буквы в этом слове.

Так, например, в приведенном ранее тексте первой страницы первой части третьего тома романа «Война и мир» Л. Н. Толстого число 2–4 соответствует четвертой букве второго слова, то есть букве Ц Таким же образом определяются числа для других букв. Число 46-8 соответствует в данном темпе букве Й, число 134-3 — букве Ь, число 49-7 — букве Ы и так далее.

Теперь, если в открытом тексте СЕКРЕТНОЕ ПОСЛАНИЕ заменить буквы на соответствующие им числа в соответствии с рассматриваемым алгоритмом шифрования, то полученная криптограмма будет выглядеть так:

4–7.48-2.117-1.83-2.89-5.137-4.57-7.101-3.67-4. 48-1.123-6.82-3.74-2.117-2.124-7.119-3.20-2

Расшифровка такой криптограммы для получателя сообщения не представляет труда. Достаточно в аналогичной книге на определенной странице пронумеровать все слова, а затем произвести замену указанных в криптограмме чисел на соответствующие буквы. В то же время несанкционированный пользователь разгадать подобную шифрограмму не сможет.

5.6. Тайны решеток и таблиц

Уже в древние века наши предки для создания шифрованных сообщений использовали специальные системы шифрования, основу которых составляли так называемые решетки, в отдельные клетки которых в определенном порядке записывались буквы алфавита.

Не менее известны и шифры, при применении которых используются специальные таблицы, ячейки которых также заполняются буквами алфавита При этом шифровальные таблицы с одинаковым количеством строк и столбцов получили название квадратов.

Шифры с использованием всевозможных шифровальных таблиц и решеток постоянно совершенствовались и усложнялись. В то же время эти шифры благодаря простоте их составления и применения может использовать даже неподготовленный пользователь.

В зависимости от используемых алгоритмов данные системы шифрования можно разделить на шифры замены и шифры перестановки. При этом среди шифров замены на основе таблиц следует отметить, например, квадрат Полибия, так называемый шифр «Большой крест» и др.

Простая шифровальная таблица

Данный шифр является одним из самых простых. Его основу составляет таблица, ячейки которой заполнены буквами алфавита. Для русского алфавита такая шифровальная таблица может состоять из шести столбцов по пять строк в каждом, которая будет выглядеть следующим образом:

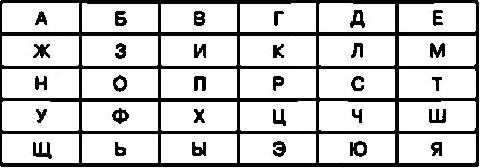
Теперь эту таблицу следует дополнить еще одним столбцом, который заполнен буквами, и строкой, заполненной цифрами. При этом буквы и цифры могут быть абсолютно любыми. Для начала заполним ячейки дополнительной строки цифрами от 1 до 6, а ячейки дополнительного столбца заполним буквами от А до Д.

В итоге шифровальная таблица примет следующий вид:

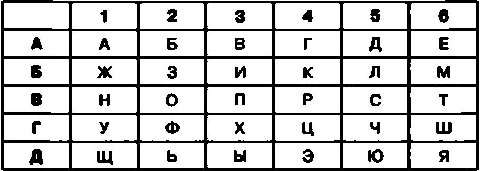
Правило шифрования заключается в том, что каждую букву открытого текста необходимо заменить на комбинацию буквы и цифры. При этом буква в криптограмме соответствует строке, а цифра — столбцу, на пересечении которых расположена ячейка с соответствующей буквой открытого текста.

Так, например, в данной таблице ячейка с буквой С находится на пересечении строки В и столбца 5. Поэтому при шифровании открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ с помощью рассматриваемого шифра буква С должна быть заменена на сочетание или группу В5. Таким же образом букву Е открытого текста надо заменить на А6, букву К — на Б4 и так далее. В результате шифрования криптограмма примет следующий вид:

В5.А6.Б4.В4.А6.В6.В1 В2.А6. В5.В2.В2.А2.Д1.А6.В1.БЗ.А6.

Для расшифровки такой криптограммы следует использовать точно такую же таблицу с аналогичным расположением букв в ячейках. При этом каждая комбинация буквы и цифры шифрограммы должна быть заменена на букву, расположенную в соответствующей ячейке на пересечении строки и столбца, обозначенных этой буквой и этой цифрой. В рассматриваемом примере вместо комбинации В5 следует записать букву С, вместо А6 — букву Е и так далее, пока не будет расшифрован весь текст.

В одном из вариантов такого шифра для обозначения строк также можно использовать цифры. При этом шифровальная таблица будет выглядеть вот так:

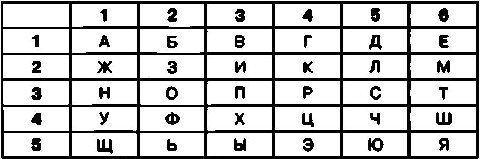
После шифрования открытого текста с помощью приведенного выше алгоритма криптограмма будет состоять из нескольких пар или групп цифр. При этом в каждой группе первая цифра обозначает строку, а вторая цифра — столбец, на пересечении которых расположена ячейка с соответствующей буквой открытого текста.

Так например, в результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ криптограмма примет следующий вид:

35.16.24.34.16.36.31.32.16. 35.32.32.12.51.16.31.23.16.

Расшифровка такой криптограммы заключается в замене пар или групп цифр буквами, находящимися в тех ячейках таблицы, строки и столбцы для которых обозначены соответствующими цифрами.

Таблица с паролем

В приведенных ранее примерах шифров буквы в ячейки шифровальных таблиц вписывались в том порядке, в каком они расположены в алфавите. Естественно, стойкость таких шифров оставляет желать лучшего. Поэтому чаще всего при применении различных шифровальных систем, основанных на использовании таблиц, буквы алфавита в ячейки таких таблиц вписываются в случайном порядке или в соответствии с определенным правилом. Главное, чтобы порядок заполнения ячеек был известен получателю.

Наиболее удобным вариантом будет конечно же тот, когда ячейки заполнены в абсолютно произвольном порядке, а получатель уже имеет готовую таблицу с записанными в ячейки буквами. Однако в этом случае велик риск того, что такая шифровальная таблица может оказаться в руках незаконного пользователя со всеми вытекающими последствиями. Поэтому желательно, чтобы отправитель и получатель сообщения не хранили у себя шифровальную таблицу, а лишь знали, по какому правилу она составляется. При необходимости на основании такого правила всегда можно составить шифровальную таблицу, с ее помощью зашифровать или расшифровать сообщение, а затем эту таблицу уничтожить.

Одним из способов заполнения таблиц является использование паролей. Для составления такой таблицы сначала необходимо выбрать пароль или кодовое слово. При этом желательно, чтобы в пароле не было повторяющихся букв. Конечно же данная рекомендация не является обязательной. После этого буквы пароля вписываются в первые ячейки таблицы, а остальные ячейки заполняются оставшимися, не использованными в пароле, буквами алфавита.

Так, например, если в качестве пароля выбрано слово ПАРОДИЯ, то шифровальная таблица примет следующий вид;

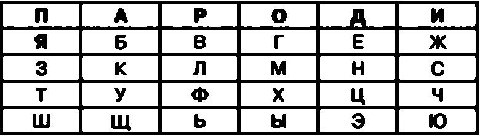
Если теперь эту таблицу дополнить еще одним столбцом, заполненным буквами, и строкой, заполненной цифрами, то можно воспользоваться одним из рассмотренных ранее алгоритмов шифрования.

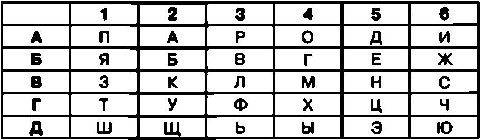
При использовании этого шифра каждую букву открытого текста необходимо заменить на комбинацию буквы и цифры. При этом буква в криптограмме соответствует строке, а цифра — столбцу таблицы, на пересечении которых расположена ячейка с соответствующей буквой открытого текста.

В результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ таким шифром криптограмма примет следующий вид:

В6.Б5.В2.АЗ.Б5.Г1.В5.А4.Б5. В6.А4.А4.Б2.Д2.Б5.В5.А6.Б5.

Таким же образом можно зашифровать сообщение с помощью таблицы, в которой для обозначения столбцов и строк используются только цифры.

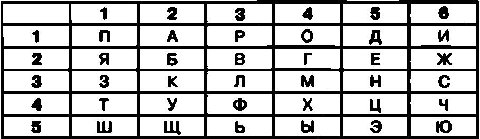
В этом случае после шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ криптограмма будет выглядеть так:

36.25.32.13.25.41.35.14.25. 36.14.14.22.52.25.35.16.25.

При выборе пароля желательно, чтобы в нем не было повторяющихся букв, поскольку в этом случае упрощается создание шифровальной таблицы. Конечно желанная рекомендация не является обязательной. Можно использовать слова и с повторяющимися буквами, только при заполнении таблицы такие буквы следует пропустить.

Так, например, если в качестве пароля выбрано слово ПЕРЕПРАВА, то повторяющиеся буквы Е, П, Р и В не записываются в ячейки, а пропускаются. При этом шифровальная таблица примет следующий вид:

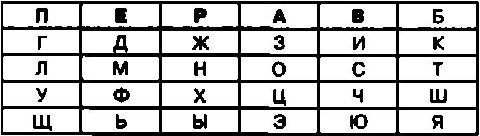
Если теперь данную таблицу дополнить еще одним столбцом, заполненным буквами, и строкой, заполненной цифрами, то можно воспользоваться уже упоминавшимся алгоритмом шифрования.

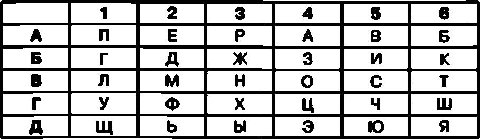
Напомним, что при использовании этого шифра правило шифрования заключается в том, что каждую букву открытого текста необходимо заменить на комбинацию буквы и цифры. При этом буква в криптограмме соответствует строке, а цифра — столбцу, на пересечении которых расположена ячейка с соответствующей буквой открытого текста. В результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ таким шифром криптограмма примет следующий вид:

В5.А2.Б6.АЗ.А2.В6.ВЗ.В4.А2. В5.В4.В4.А6.Д1.А2.ВЗ.Б5.А2.

И в этой таблице для обозначения строк можно использовать цифры. При этом порядок применения алгоритма шифрования не отличается от рассмотренных ранее шифров.

Для того чтобы усложнить незаконному пользователю задачу взлома шифра, вместо повторяющихся в пароле букв в ячейки можно вписывать оставшиеся буквы алфавита. Так, например, при использовании в качестве пароля слова ПЕРЕПРАВА повторяющиеся буквы Е, П, Р и В не записываются в ячейки. Вместо них в соответствующие ячейки вставляются не вошедшие в пароль следующие буквы алфавита Для рассматриваемого пароля вместо второй буквы Е следует записать букву Б, вместо второй буквы П — букву Г, вместо второй буквы Р — букву Д и так далее. При этом шифровальная таблица примет следующий вид:

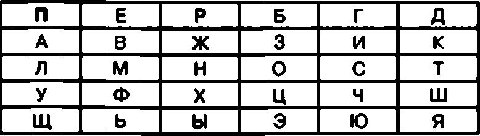
Такую таблицу можно использовать для шифрования сообщений в соответствии как с рассмотренными ранее алгоритмами шифрования, так и с другими.

Следует отметить, что паролем может служить не только отдельное слово, но и целая фраза. Эго может быть известная поговорка или пословица, цитата или строка из стихотворения. При этом правила заполнения ячеек шифровальной таблицы буквами алфавита остаются такими же, как и для уже упоминавшихся таблиц с простым паролем.

Так, например, при использовании в качестве пароля фразы ПРИКАЗЫ НЕ ОБСУЖДАЮТСЯ шифровальная таблица может выглядеть следующим образом:

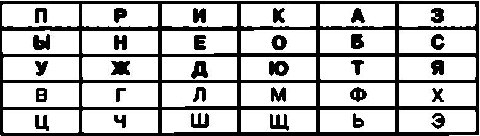
Такую таблицу также можно использовать для шифрования сообщений в соответствии как со всеми рассмотренными ранее алгоритмами шифрования, так и с другими.

Квадрат Полибия

Одну из первых систем шифрования, в которой использовалась таблица, описал древнегреческий историк Полибий. Точно неизвестно, является ли талантливый писатель автором этого шифра. Тем не менее специалисты называют этот шифр «квадратом Полибия». Еще до наступления нашей эры этот шифр широко применялся как греками, так и римлянами.

При использовании данного шифра составляется таблица, которая, например, для английского алфавита состоит из пяти столбцов по пять строк в каждом. В каждую клетку этой таблицы в произвольном порядке вписывается одна из букв алфавита. Необходимо отметить, что для русского алфавита, содержащего большее количество букв, шифровальная таблица должна содержать не менее 30 клеток. Эго может быть, например, таблица из шести столбцов по пять строк в каждом.

Алгоритм шифрования заключается в том, что при преобразовании открытого текста в криптограмму необходимо найти в таблице ячейку с нужной буквой и вставить в шифрованный текст букву, располагающуюся в нижней от нее ячейке в том же столбце. Если же буква открытого текста оказывается в ячейке нижней строки, то в шифрограмму следует записать букву из верхней ячейки того же столбца.

В качестве при мера зашифруем с помощью шифра «квадрат Полибия» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ. Перед началом работы необходимо составить шифровальную таблицу, которая может выглядеть, например, вот так:

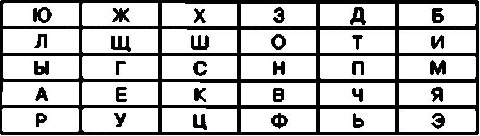
Теперь следует найти клетку с первой буквой открытого текста Эго буква С, ячейка с которой расположена в третьей строке третьего столбца. В соответствии с алгоритмом шифрования вместо этой буквы в криптограмму необходимо записать букву, расположенную в нижней от нее ячейке в том же столбце, то есть вместо буквы С — букву К. Таким же образом букву Е открытого текста надо заменить на букву У, букву К на букву Ц и так далее. Не следует забывать о том, что в случае если буква открытого текста окажется в ячейке нижней строки, то в шифрограмму следует записать букву из самой верхней ячейки того же столбца. Например, буква Р должна быть заменена в криптограмме на букву Ю.

В результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕс помощью рассматриваемого шифра криптограмма примет следующий вид:

КУЦЮУПВНУ КННИГУВМУ

Для расшифровки получатель сообщения должен использовать точно такую же таблицу с аналогичным расположением букв в ячейках. При этом каждая буква шифрограммы должна быть заменена на букву, расположенную в верхней от нее ячейке в том же столбце.

В рассматриваемом примере вместо буквы К следует записать букву С, вместо буквы У — букву Е и так далее, пока не будет расшифрован весь текст. Если же буква из криптограммы в таблице занимает верхнюю ячейку, то ее следует заменить на букву, находящуюся в самой нижней ячейке того же столбца.

Шифр «Большой крест»

Первые упоминания о шифре, в некоторых источниках называемом «Большой крест», относятся к XVIII столетию. Необходимо отметить, что в отдельных зарубежных изданиях автору встречались варианты этого шифра с весьма экзотическими названиями. Например, название одного из вариантов можно перевести на русский язык как шифр «Загончики для поросят».

Шифр «Большой крест» прост и в то же время очень эффективен. Неподготовленный незаконный пользователь, желающий прочитать сообщение, зашифрованное с помощью данного шифра замены, вряд ли сможет сразу догадаться, как его взломать. В связи с ограниченным объемом данной книги далее будут рассмотрены лишь некоторые варианты шифра «Большой крест».

Практическое использование данного шифра следует начать с составления специальной шифровальной таблицы, которая будет выглядеть как несколько решеток. В одном из вариантов такая таблица может иметь вид, показанный на рис. 5.1.

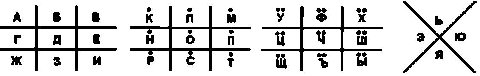
Рис. 5.1 Шифровальная таблица для шифра «Большой крест»

В качестве примера зашифруем с помощью шифра «Большой крест» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ. Если заменить буквы открытого текста соответствующими им символами ячеек решетки, то получится промежуточный результат, показанный на рис. 5.2.

В окончательном виде криптограмма для открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ будет выглядеть так, как показано на рис. 5.3.

Рис. 5.2 Промежуточный результат шифрования с помощью шифра «Большой крест»

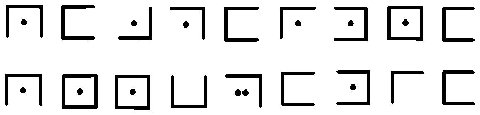
Рис. 5.3 Криптограмма для открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ полученная в результате использования шифра «Большой крест»

Если с помощью рассматриваемого шифра зашифровать открытый текст ИЛЛЮЗИЯ, то криптограмма примет вид показанный на рис. 5.4.

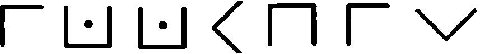
Рис. 5.4 Криптограмма для открытого текста ИЛЛЮЗИЯ, полученная в результате использования шифра «Большой крест»

Для того чтобы расшифровать приведенные криптограммы, достаточно составить аналогичную шифровальную таблицу и заменить символы на соответствующие им буквы.

Необходимо отметить, что комбинаций расположения букв в ячейках решеток может быть довольно много. Поэтому законный пользователь для шифрования сообщений при желании может придумать свой, оригинальный вариант шифра «Большой крест».

5.7. Перестановки в таблицах

В шифрах, основу которых составляют таблицы, применяются самые разнообразные алгоритмы шифрования. Ранее были рассмотрены несколько простых систем шифрования, в которых используются специальные таблицы, ячейки которых заполняются буквами алфавита.

При этом составление криптограммы заключается в замене букв открытого текста в соответствии с определенными правилами.

В то же время существует множество шифров, при работе с которыми также составляются таблицы, однако ячейки этих таблиц заполняются не всеми буквами алфавита, а только буквами открытого текста. Алгоритм шифрования при использовании таких шифров заключается в том, что строки и столбцы в таблице с открытым текстом переставляются или перемешаются в соответствии с определенным правилом.

Простая перестановка

Одним из шифров, основанных на перестановке строк и столбцов в таблице с открытым текстом, является шифр простой перестановки. Создание криптограммы при использовании данного шифра следует начать с составления таблицы, в ячейки которой необходимо вписать по строкам буквы открытого текста. При этом количество строк и столбцов в такой шифровальной таблице выбирается произвольно. После заполнения таблицы буквы в криптограмму выписываются по столбцам, сначала из первого столбца, затем из второго и так далее.

В качестве примера зашифруем с помощью этого шифра открытый текст МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО. При выборе таблицы, состоящей из пяти строк и шести столбцов, ее ячейки будут заполнены следующим образом:

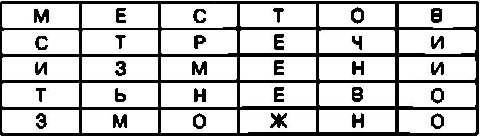
Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первого столбца, затем из ячеек второго столбца и так далее.

В окончательном виде криптограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО будет выглядеть так:

МСИТЗ ЕТЗЬМ СРМНО ТЕЕЕЖ ОЧНВН ВИИОО

Если записать эту криптограмму без пробелов, то она примет следующий вид:

МСИТЗЕТЗЫИСРМНОТЕЕЕЖОЧНВНВИИОО

Для расшифровки такого шифрованного сообщения достаточно в таблицу аналогичных размеров по столбцам вписать буквы криптограммы, а затем по строкам прочитать открытый текст. Естественно, для этого получатель сообщения должен знать размер таблицы.

Перестановка с паролем

Не менее интересен более сложный способ шифрования, который можно назвать перестановкой с паролем. При использовании этого шифра столбцы или строки в таблице, заполненной буквами открытого текста, перемещаются на определенное количество позиций по определенному правилу. Порядок перемещения столбцов или строк в таблице должен быть известен получателю сообщения.

Как и в рассмотренном ранее шифре простой перестановки, создание криптограммы при использовании данного шифра следует начать с составления таблицы, в ячейки которой необходимо вписать по строкам буквы открытого текста. При этом количество строк и столбцов в такой шифровальной таблице выбирается произвольно.

В качестве примера зашифруем с помощью этого шифра открытый текст МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО. При выборе таблицы, состоящей из пяти строк и шести столбцов, ее ячейки будут заполнены следующим образом:

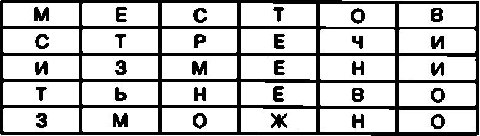
Если пользователь решил произвести перестановку столбцов, то к этой таблице следует добавить еще две строки. В ячейки первой добавленной строки необходимо вписать буквы пароля. В ячейки второй строки записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля.

Если в качестве пароля выбрать, например, слово ПРИВЕТ, то шифровальная таблица будет выглядеть вот так:

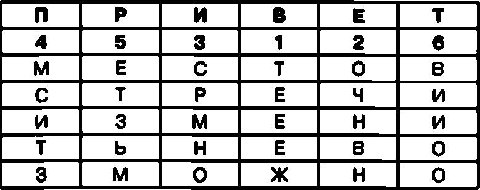
После этого необходимо переставить столбцы в таблице так, чтобы цифры во второй строке располагались по порядку. В результате такой перестановки таблица примет следующий вид:

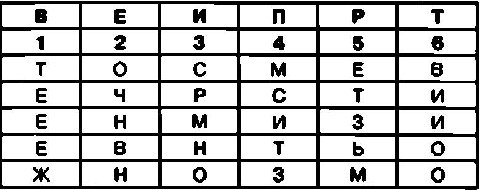
Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек третьей строки, затем из ячеек четвертой строки и так далее.

В окончательном виде криптограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО будет выглядеть так:

ТОСМЕВ ЕЧРСТИ ЕНМИЗИ ЕВНТЬО ЖНОЗМО

Для того чтобы расшифровать эту шифрограмму, получатель сообщения, зная пароль, должен сначала составить аналогичную шифровальную таблицу, во второй строке которой записываются цифры по порядку, а в первой — соответствующие этим цифрам буквы пароля. Остальные ячейки следует заполнить по строкам буквами криптограммы. Если теперь переставить столбцы таблицы так, чтобы буквы в верхней строчке образовали пароль, то в строках таблицы получатель сообщения сможет прочитать открытый текст.

Таким же образом в таблице с открытым текстом можно произвести перестановку строк. В этом случае к первоначальной таблице следует добавить еще два столбца. При этом в ячейки первого добавленного столбца необходимо вписать буквы пароля. В ячейки второго столбца записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля.

Если в качестве пароля выбрать, например, слово ВЕСНА, то шифровальная таблица для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО примет следующий вид:

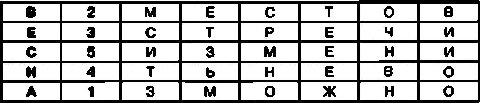
После этого необходимо переставить строки в таблице так, чтобы цифры во втором столбце располагались по порядку. В результате такой перестановки таблица примет следующий вид:

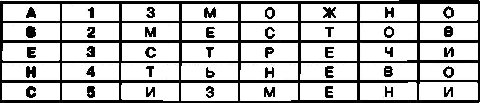
Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек третьего столбца, затем из ячеек четвертого столбца и так далее.

В окончательном виде шифрограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО будет выглядеть так:

ЗМСТИ МЕТЬЗ ОСРНМ ЖТЕЕЕ НОЧВН ОВИОИ

Для расшифровки этой криптограммы получатель сообщения, зная пароль, должен сначала составить аналогичную шифровальную таблицу, во втором столбце шторой записываются цифры по порядку, а в первом — соответствующие этим цифрам буквы пароля. Остальные ячейки следует заполнить по столбцам буквами криптограммы. Если теперь переставить строки таблицы так, чтобы буквы в первом столбце образовали пароль, то в строках таблицы получатель сообщения сможет прочитать открытый текст.

При выборе пароля желательно, чтобы в нем не было повторяющихся букв, поскольку в этом случае упрощается создание шифровальной таблицы. Конечно желанная рекомендация не является обязательной. Можно использовать слова и с повторяющимися буквами, только при заполнении таблицы номера таким буквам присваиваются слева направо.

Двойная перестановка

Следует признать, что рассмотренные ранее системы шифрования, в которых применяется перестановка столбцов и строк шифровальной таблицы, ячейки которой заполнены буквами открытого текста, имеют сравнительно низкую стойкость. Для специалистов взлом таких шифров не представляет особого труда. В то же время неподготовленный незаконный пользователь на разгадку подобного шифра будет вынужден затратить немало времени. Задача взлома шифра значительно усложнится, если отправитель сообщения воспользуется так называемым шифром двойной перестановки.

При использовании шифра двойной перестановки в таблице, заполненной буквами открытого текста, на определенное количество позиций по определенному правилу перемещаются как столбцы, так и строки.

В качестве примера зашифруем с помощью этого шифра открытый текст МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО. Если пользователь решил воспользоваться шифром двойной перестановки, то к уже знакомой шифровальной таблице, состоящей из пяти строк и шести столбцов, следует добавить еще две строки и два столбца. При этом ячейки таблицы будут заполнены следующим образом:

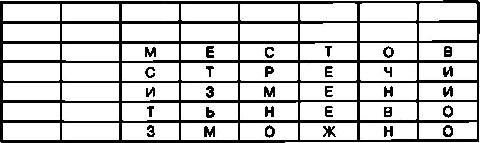
В ячейки первой добавленной строки необходимо вписать буквы пароля для перестановки столбцов. В ячейки второй строки записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля. Если в качестве пароля для перестановки столбцов выбрать, например, слово ПРИВЕТ, то шифровальная таблица будет выглядеть вот так:

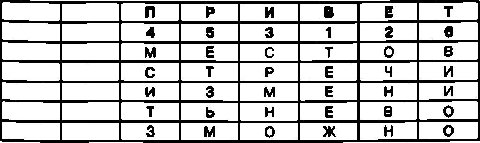
В ячейки первого добавленного столбца необходимо вписать буквы пароля для перестановки строк. В ячейки второго столбца записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля. Если в качестве пароля для перестановки строк выбрать, например, слово ВЕСНА, то шифровальная таблица примет следующий вид:

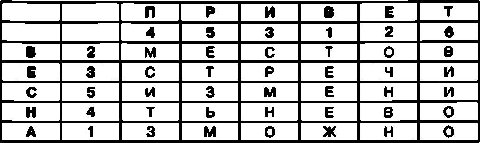
Для создания криптограммы сначала необходимо переставить столбцы в таблице так, чтобы цифры во второй строке располагались по порядку. В результате такой перестановки таблица примет следующий вид:

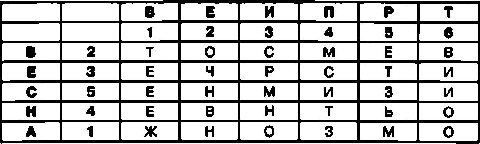
После этого следует переставить строки в таблице так, чтобы цифры во втором столбце располагались по порядку. После выполнения такой перестановки таблица будет выглядеть вот так:

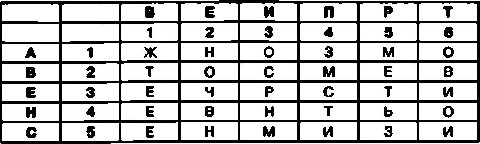
Теперь дпя создания шифрограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки ит. д. В окончательном виде криптограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО будет выглядеть так:

ЖНОЗМО ТОСМЕВ ЕЧРСТИ ЕВНТЬО ЕНМИЗИ

Для того чтобы расшифровать эту шифрограмму, получатель сообщения должен знать пароли для перемещения столбцов и строк Затем необходимо составить аналогичную шифровальную таблицу. Во второй строке этой таблицы записываются цифры по порядку, а в первой — соответствующие этим цифрам буквы пароля для перемещения столбцов. Во втором столбце таблицы записываются цифры по порядку, а в первом — соответствующие этим цифрам буквы пароля для перемещения строк. Остальные ячейки следует заполнить по строкам буквами криптограммы. Теперь необходимо переставить столбцы таблицы так, чтобы буквы в первой строке образовали пароль для перемещения столбцов. После этого достаточно переставить строки таблицы так, чтобы буквы в первом столбце образовали пароль для перемещения строк и в строках таблицы получатель сообщения сможет прочитать открытый текст.

В процессе шифрования буквы из ячеек шифровальной таблицы можно выписать и по столбцам, сначала из ячеек первого столбца, затем из ячеек второго столбца и так далее. В этом случае криптограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО примет следующий вид:

ЖТЕЕЕ НОЧВН ОСРНМ ЗМСТИ МЕТЬЗ ОВИОИ

Однако в этом случае порядок действий при дешифровании незначительно изменится. При составлении таблицы получатель сообщения, как и в рассмотренном ранее примере, во второй строке должен записать цифры по порядку, а в первой — соответствующие этим цифрам буквы пароля для перемещения столбцов. Во втором столбце таблицы записываются цифры по порядку, а в первом — соответствующие этим цифрам буквы пароля для перемещения строк. Однако остальные ячейки следует заполнить буквами криптограммы не по строкам, а по столбцам.

После этого, как и в рассмотренном ранее примере, необходимо переставить столбцы таблицы так, чтобы буквы в первой строке образовали пароль для перемещения столбцов. Теперь достаточно переставить строки таблицы так, чтобы буквы в первом столбце образовали пароль для перемещения строк, и в строках таблицы получатель сообщения сможет прочитать открытый текст.

5.8. Магические квадраты

В Средние века широкое распространение получили шифры, основу которых составляли так называемые магические квадраты.

В математике магическими квадратами называются таблицы с одинаковым количеством строк и столбцов. В каждую ячейку такой таблицы вписывается какое-либо число, при этом сумма всех чисел, расположенных в одном столбце, в одной строке и на одной диагонали, составляет одно и то же число.

Необходимо отметить, что для шифрования проще всего использовать магические квадраты, в ячейки которых записываются числа по порядку без повторов, начиная от цифры 1 и до числа, которое определяется количеством ячеек в данном квадрате. При этом не следует забывать о том, что для шифрования длинных сообщений потребуются таблицы большего размера. Так, например, для шифрования открытого текста, состоящего из 16 знаков, достаточно воспользоваться магическим квадратом размером 4×4, а для шифрования текста, содержащего 64 знака, потребуется таблица размером 8×8.

При использовании шифров, основанных на магических квадратах, алгоритм шифрования заключается в том, что в ячейки таблицы вместо цифр магического квадрата по определенному правилу вписываются буквы и знаки открытого текста После того как все ячейки будут заполнены, текст криптограммы выписывается из таблицы по строкам или по столбцам.

Простейший магический квадрат

Как известно, чем меньше столбцов и строк в квадратной таблице, тем меньше вариантов построения на ее основе магического квадрата Так, например, для таблицы, состоящей из трех столбцов и трех строк, известен всего лишь один вариант заполнения ячеек цифрами от 1 до 9, в результате которого получится магический квадрат. Такая таблица будет выглядеть так:

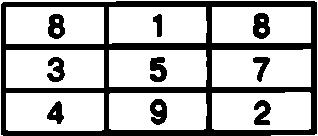
Нетрудно подсчитать, что сумма цифр в каждом столбце, в каждой строке и в каждой большой диагонали составляет одно и то же число и равна 15.

При использовании шифров, основанных на магических квадратах, один из простейших алгоритмов шифрования заключается в том, что в ячейки таблицы вместо цифр магического квадрата вписываются по порядку буквы открытого текста. Так, например, вместо цифры 1 в соответствующую ей ячейку следует записать первую букву сообщения, вместо цифры 2 — вторую букву, вместо цифры 3 — третью букву и так далее.

В качестве примера зашифруем с помощью этого магического квадрата открытый текст РАЗВЕДЧИК При этом в ячейку с цифрой 1 следует записать букву Р, в ячейку с цифрой 2 — букву А, в ячейку с цифрой 3 — букву 3 и так до конца сообщения. В результате таблица примет следующий вид:

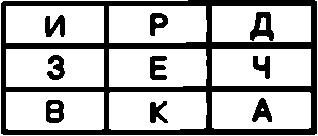
Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки и так далее.

В окончательном виде криптограмма для открытого текста РАЗВЕДЧИК будет выглядеть так:

ИРД ЗЕЧ ВКА

Получив такую шифрограмму, получатель для расшифровки сообщения должен сначала заполнить таблицу буквами криптограммы, а затем из соответствующих ячеек выписать буквы открытого текста в порядке, определяемом цифрами используемого магического квадрата.

Необходимо отметить, что утверждение о существовании лишь одного магического квадрата размером 3×3 для цифр от 1 до 9 не касается случаев, когда другие магические квадраты могут быть образованы из первоначального с помощью поворота таблицы или отражения строк и столбцов.

Один из таких производных квадратов может выглядеть следующим образом:

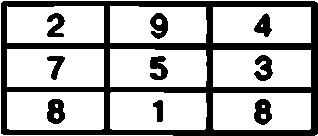
Такой магический квадрат также с успехом можно использовать для шифрования коротких сообщений в соответствии с приведенным выше алгоритмом.

Индийский квадрат

В одном из древних индийских храмов исследователи обнаружили квадратную таблицу, которая при более подробном изучении оказалась одним из самых первых известных магических квадратов. По мнению некоторых историков, эта таблица была создана в XII веке.

Ячейки данной таблицы, состоящей из четырех столбцов и четырех строк, заполнены числами от 1 до 16 так, что сумма всех чисел, расположенных в одном столбце, в одной строке и на одной диагонали, составляет одно и то же число, а именно 34. Более того, сумма чисел в четырех ячейках, образующих квадратные таблицы внутри данного магического квадрата, также составляет 34.

Порядок заполнения ячеек в этой таблице выглядит следующим образом:

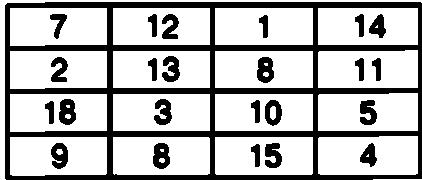
Естественно, что такой магический квадрат также можно использовать для шифровки короткого сообщения, содержащего до шестнадцати знаков.

В качестве примера зашифруем, например, открытый текст СЕКРЕТНАЯ ВСТРЕЧА. Для шифрования данного сообщения с использованием рассмотренного ранее алгоритма необходимо сначала вставить в ячейки таблицы вместо цифр буквы открытого текста. При этом вместо цифры 1 в соответствующую ячейку следует вставить первую букву открытого текста, в рассматриваемом примере это будет буква С. Вместо цифры 2 в соответствующую ячейку следует вставить вторую букву открытого текста, то есть букву Е, и так далее.

В результате такой замены шифровальная таблица примет следующий вид:

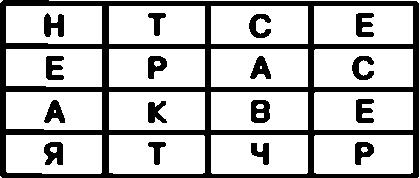
Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки и так далее.

В окончательном виде криптограмма для открытого текста СЕКРЕТНАЯ ВСТРЕЧА будет выглядеть так:

НТСЕ ЕРАС АКВЕ ЯТЧР

Для того чтобы расшифровать эту шифрограмму, получатель сообщения должен сначала заполнить таблицу известных ему размеров буквами криптограммы, а затем из соответствующих ячеек выписать буквы открытого текста в порядке, определяемом цифрами используемого магического квадрата.

По утверждению некоторых источников, классических магических квадратов размером 4×4 существует всего 12. При этом другие магические квадраты тех же размеров могут быть образованы из первоначального, например с помощью поворота таблицы или отражения строк и столбцов. Общее число таких производных магических квадратов разными специалистами оценивается от нескольких сотен до нескольких тысяч. С учетом того, что любой из упомянутых магических квадратов может быть использован для шифрования сообщения, задача взлома шифра для незаконного пользователя с помощью подбора необходимой таблицы вручную становится практически невыполнимой.

Квадрат Эйлера

Известный математик, астролог и криптограф Леонард Эйлер, долгое время работавший в России в XVIII веке, является автором известной таблицы, состоящей из восьми столбцов и восьми строк.

Все клетки так называемого квадрата Эйлера заполнены числами от 1 до 64 так, что сумма всех чисел, расположенных в одном столбце и в одной строке, составляет одно и то же число, а именно 260. Более того, если данную таблицу разделить на четыре квадратные таблицы, то и в каждой из них сумма чисел в ячейках одного столбца и одной строки также будет одинакова и составит 130. Таким же свойством обладает и квадрат размером 4×4, составленный из ячеек, расположенных в центральной части большой таблицы.

Порядок заполнения ячеек в квадрате Эйлера выглядит следующим образом:

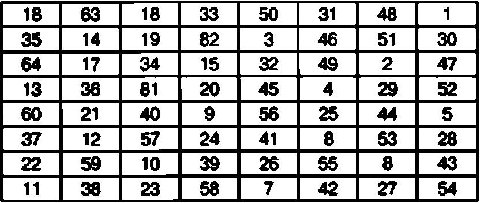
Нетрудно заметить, что с математической точки зрения данная таблица не является классическим магическим квадратом, поскольку суммы чисел в ячейках, образующих диагонали, не равны между собой. В то же время квадрат Эйлера можно использовать для шифрования сравнительно длинных сообщений, используя алгоритм шифрования, рассмотренный ранее для классических магических квадратов.

Магический квадрат 9×9

Как отмечалось ранее, для шифрования длинных сообщений необходимо использовать таблицы большего размера. При этом не следует забывать о том, что чем больше столбцов и строк в квадратной таблице, тем больше вариантов построения на ее основе магического квадрата. Данный факт значительно усложняет незаконному пользователю задачу расшифровки сообщений, зашифрованных, например, с помощью магического квадрата размером 4×4.

Естественно, применение магических квадратов, например, размером 9×9 обеспечивает еще более высокую степень защиты и уменьшает вероятность того, что сообщение будет прочитано тем, кому оно не предназначено.

Один из вариантов такого квадрата имеет следующий вид:

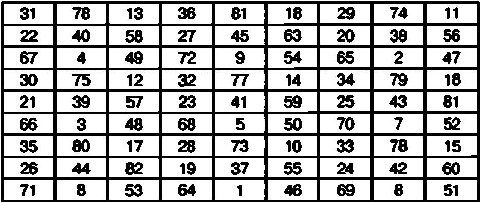
Как и упоминавшийся квадрат Эйлера, данный магический квадрат также можно использовать для шифрования длинных сообщений, используя рассмотренный ранее алгоритм шифрования для классических магических квадратов. При этом открытый текст может содержать до 81 знака.

5.9. Трафарет в системах шифрования

Для создания шифрованных сообщений можно использовать специальные трафареты, которые представляют собой, например, лист бумаги с вырезанными в произвольном порядке отверстиями. Необходимо отметить, что в настоящее время известно множество систем шифрования, в которых применяются различные способы создания и использования таких трафаретов. Естественно, при применении таких шифров получатель криптограммы должен не только иметь точно такой же трафарет, но и хорошо знать правила работы с ним.

Один из вариантов простого шифра с использованием трафарета применял, например, великий русский писатель А. С. Грибоедов в начале XIX века. На лист бумаги он с помощью трафарета наносил текст сообщения, а затем уже без трафарета дополнял текст так, чтобы получилось вполне невинное письмо.

Трафаретные шифры неоднократно упоминаются и в произведениях авторов детективных романов. Среди более сложных шифров с трафаретами следует отметить, например, так называемую решетку Кардано.

Простой шифр с трафаретом

При использовании такого способа шифрования сначала необходимо сделать трафарет из листа бумаги с вырезанными в нем отверстиями. Для этого удобно воспользоваться листом бумаги в клеточку, в котором отдельные клетки следует вырезать в произвольном порядке.

Так, например, трафарет для шифрования сообщений может выглядеть так, как показано на рис. 5.5.

Рис. 5.5 Один из вариантов трафарета для шифрования сообщений

На представленном рисунке черным цветом закрашены ячейки, которые следует вырезать.

В качестве примера зашифруем с помощью данного трафарета открытый текст СЕКРЕТНОЕ ПИСЬМО. Для этого сначала необходимо наложить трафарет на чистый лист бумаги и в вырезанных прямоугольниках вписать буквы открытого текста.

В результате на листе получится следующая надпись:

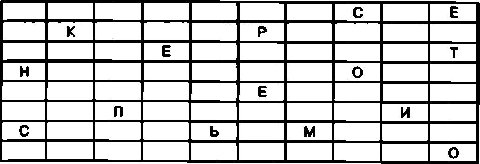
Теперь для создания криптограммы достаточно убрать трафарет и между буквами открытого текста вписать любые другие буквы в произвольном порядке. В этом случае криптограмма может принять следующий вид:

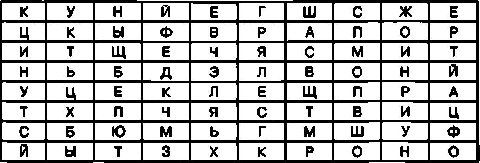
Для того чтобы запутать незаконного пользователя, буквы можно вписать так, чтобы получился какой-либо вполне обычный текст.

При расшифровке такой криптограммы получателю сообщения достаточно наложить аналогичный трафарет на лист с текстом и в вырезанных ячейках прочитать открытый текст.

Необходимо отметить, что при использовании данного шифра для шифровки сравнительно коротких сообщений при создании трафарета необходимо обратить внимание на то, чтобы количество вырезанных клеточек было не меньше, чем количество букв в открытом тексте. Для шифровки длинных сообщений можно сделать трафарет с большим количеством вырезанных ячеек или же один и тот же трафарет использовать несколько раз.

Решетка Кардано

Более сложной системой шифрования, в которой также используется трафарет определенной формы, является шифр, называемый решеткой Кардано. Название этого шифра произошло от имени его автора, итальянского математика и философа Джероламо Кардано. Именно он в далеком 1566 году водной из своих работ опубликовал описание рассматриваемого шифра.

Основу простейшей решетки Кардано составляет трафарет, выполненный в форме квадратной таблицы. При этом ячейки в данном трафарете вырезаются так, чтобы после поворота трафарета вокруг центральной оси буквы, записанные в ячейках на подложенном листе бумага, не перекрывались. Другими словами, при четырех поворотах трафарета на 90? ячейки, перекрыв все клетки таблицы, ни разу не должны оказаться в одном и том же месте.

Рис. 5.8 Решетка Кардано размером 4×4

Так, например, вариант такого трафарета размером 4×4 имеет вид, изображенный на рис. 5.6.

На представленном рисунке черным цветом закрашены ячейки, которые следует вырезать.

В качестве примера зашифруем с помощью решетки Кардано открытый текст СЕКРЕТНАЯ ВСТРЕЧА Шифрование данного сообщения необходимо начать с заполнения ячеек таблицы буквами открытого текста Для этого наложим трафарет на лист с таблицей и в вырезанные ячейки впишем первые буквы открытого текста. В рассматриваемом примере это первые четыре буквы, а именно буквы С, Е, К и Р.

В результате надпись на листе будет выглядеть так:

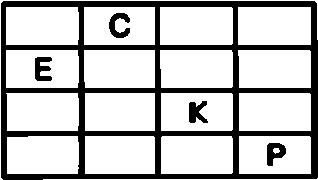
После этого повернем трафарет по часовой стрелке на 90? и в свободные ячейки вновь запишем следующие четыре буквы открытого текста В рассматриваемом примере это буквы Е, Т, Н и А

Теперь повернем трафарет по часовой стрелке еще на 90? и в свободные ячейки вновь запишем следующие четыре буквы открытого текста а именно буквы Е, П, И и С.

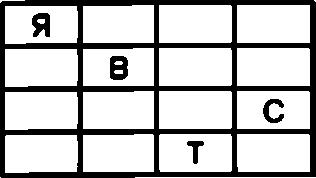
Следующий поворот трафарета также следует провести по часовой стрелке еще на 90?, а свободные ячейки заполнить оставшимися четырьмя буквами открытого текста

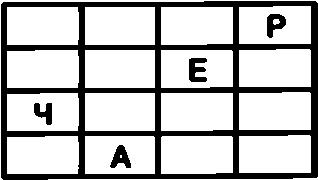
После заполнения всех свободных ячеек и снятия трафарета на листе бумаги останется шифровальная таблица которая имеет следующий вид:

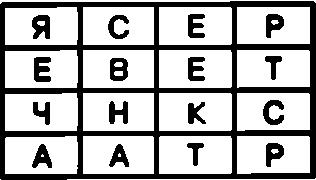
Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки и так далее. В окончательном виде криптограмма для открытого текста СЕКРЕТНАЯ ВСТРЕЧА будет выглядеть так:

ЯСЕР ЕВЕТ ЧНКС ААТР

Для того чтобы расшифровать эту шифрограмму, получатель сообщения должен сначала заполнить таблицу известных ему размеров буквами криптограммы. Затем необходимо наложить на заполненную таблицу трафарет и, поворачивая его по часовой стрелке на 90?, последовательно выписать из открывающихся ячеек буквы открытого текста.

Рис. 5.7 Решетка Кардано размером 6×6

Если пользователю потребуется зашифровать открытый текст, содержащий большое количество знаков, то решетку Кардано размером 4×4 можно использовать неоднократно.

В то же время для шифрования длинных сообщений любой желающий может составить и использовать решетку Кардано практически любых размеров.

Один из вариантов решетки Кардано размером 6×6 имеет вид, изображенный на рис. 5.7.

На представленном рисунке черным цветом закрашены ячейки, которые следует вырезать. Порядок пользования этим трафаретом аналогичен ранее рассмотренному.

Остается добавить, что применение решеток Кардано обеспечивает сравнительно высокую степень защиты и уменьшает вероятность того, что сообщение будет прочитано неподготовленным незаконным пользователем. Однако для специалиста взлом такого шифра не представляет особых трудностей.

5.10. Биграммные шифры

Одной из особенностей рассмотренных ранее систем шифрования является то, что в них каждая буква открытого текста шифруется отдельно. Однако еще в Средние века некоторые ученые предложили шифры с использованием алгоритмов, обеспечивающих одновременное шифрование сразу двух букв сообщения. Такие шифры стали называться биграммными.

Одно из первых описаний биграммного шифра было опубликовано немецким ученым И. Тритемиусом в начале XVI века Однако некоторые специалисты считают, что первое заслуживающее внимания описание биграммного шифра привел итальянец Д. Порта в 1563 году в книге «О тайной переписке».

Необходимо отметить, что биграммные шифры, несмотря на более высокую степень защищенности, по сравнению с другими использовавшимися в то время системами шифрования, в течение примерно 300 лет почти не применялись. И лишь в XIX веке одновременно в нескольких европейских странах началась активная работа над созданием оригинальных биграммных шифров. Так, например, в России над своим вариантом биграммного шифра работал талантливый криптограф и изобретатель П. Ф. Шиллинг, а в Британии — Ч. Ветстоун.

Название одного из биграммных шифров, придуманного в XIX веке, связано с именем министра почт Британской империи барона Л. Плейфера (L Playfair). Шифр «Playfair» был настолько удачным, что в различных версиях применялся англичанами и во время Первой мировой войны уже в XX столетии.

При использовании шифра «Playfair» алгоритм шифрования заключается в том, что открытый текст разделяется на пары букв, после чего каждая пара по определенному правилу заменяется на пару букв криптограммы. При этом в процессе шифрования необходимо использовать таблицу, заполненную буквами соответствующего алфавита.

В оригинальном шифре «Playfair» для английского алфавита применяется таблица размером 5×5 с паролем Playfair. Для русского алфавита можно использовать, например, уже рассмотренную ранее таблицу с паролем ПАРОДИЯ:

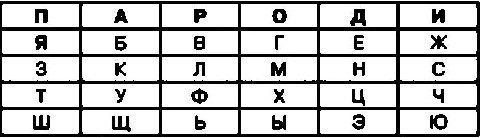
В качестве примера зашифруем с помощью шифра «Playfair» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ.

Как уже отмечалось, сначала шифруемое сообщение необходимо разбить на пары букв, которые часто называются группами. В рассматриваемом примере после выполнения данного преобразования открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ примет следующ ий вид;

СЕ КР ЕТ НО ЕС ОО БЩ ЕН ИЕ

Необходимо отметить, что в соответствии с алгоритмом шифрования пара или группа букв, состоящая из одной и той же буквы, должна быть разделена буквой X или буквой У.

В то же время одной из указанных букв следует дополнить открытый текст в том случае, если последняя группа букв будет неполной.

С учетом данных требований в рассматриваемом примере открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ, разделенный на пары букв, будет выглядеть вот так:

СЕ КР ЕТ НО ЕС ОХ ОБ ЩЕ НИ ЕХ

Теперь каждую пару букв следует зашифровать отдельно с помощью составленной ранее шифровальной таблицы, ячейки которой должны быть заполнены буквами алфавита по определенному правилу. В нашем примере это приведенная выше таблица с паролем ПАРОДИЯ.

Сначала в таблице надо найти каждую из двух букв, входящих в состав подлежащей шифрованию группы. Затем следует мысленно построить четырехугольник, в двух противоположных вершинах которого находятся две шифруемые буквы открытого текста Две буквы, оказавшиеся в двух других вершинах этого прямоугольника, являются составной частью криптограммы. При этом каждая буква пары открытого текста заменяется буквой криптограммы, лежащей с ней в одной строке.

Так, например, в рассматриваемом примере при шифровании первой пары букв, а именно букв СЕ, в криптограмму следует записать буквы НЖ, вместо букв КР — буквы ЛА, вместо букв ЕТ — буквы ЯЦ и так далее.

В случае если обе буквы какой-либо группы открытого текста находятся в одном столбце таблицы, то в криптограмму записываются буквы, находящиеся под ними, то есть в соответствующих ячейках следующей строки.

Так, в рассматриваемом примере при шифровании группы ОХ открытого текста в криптограмму записывается пара ГЫ Если же при этом одна из пары букв открытого текста окажется в нижней строке столбца, то в шифрограмме эта буква должна быть заменена на букву, находящуюся в верхней строке этого столбца.

В случае, если обе буквы какой-либо группы открытого текста находятся в одной строке таблицы, то в криптограмму записываются буквы, находящиеся справа от них, то есть в соответствующих ячейках следующего столбца.

Так, например, при шифровании группы ТХ открытого текста в криптограмму записывается пара УЦ. Если же при этом одна из пары букв открытого текста окажется в крайнем правом столбце строки, то в шифрограмме эта буква должна быть заменена на букву, находящуюся в первом столбце этой строки.

По окончании шифрования криптограмма открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ примет следующий вид:

НЖ ЛА ЯЦ МД ЖН ГЫ АГ ЭБ СД ГЦ

Для дешифрования такого сообщения получатель сначала должен с помощью известного ему правила или пароля составить таблицу, а затем, используя указанные выше правила, заменить пары или группы букв криптограммы на соответствующие им пары или группы букв открытого текста.

Шифр «Двойной квадрат»

Помимо шифра «Playfair», в том же XIX веке был изобретен биграммный шифр, получивший название «Двойной квадрат». Однако, в отличие от шифра «Playfair», при применении шифра «Двойной квадрат» в процессе шифрования используется не одна, а две таблицы, ячейки которых заполнены буквами алфавита.

В то же время алгоритмы шифрования указанных шифров очень похожи: открытый текст разделяется на пары букв, после чего каждая пара по определенному правилу заменяется на пару букв криптограммы.

Перед началом шифрования открытого текста с помощью шифра «Двойной квадрат» необходимо составить две таблицы, заполненные буквами алфавита Для русского алфавита можно использовать, например, уже рассмотренные ранее таблицы с паролем ПАРОДИЯ и с паролем ПРИКАЗЫ НЕ ОБСУЖДАЮТСЯ, которые следует расположить рядом:

В качестве примера зашифруем с помощью шифра «Двойной квадрат» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ

Как уже отмечалось, сначала шифруемое сообщение необходимо разбить на пары букв. В рассматриваемом примере после выполнения данного преобразования открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ примет следующий вид:

СЕ КР ЕТ НО ЕС 00 БЩ ЕН ИЕ

В соответствии с алгоритмом шифрования пара букв, состоящая из одной и той же буквы, должна быть разделена буквой X или буквой У. В то же время одной из указанных букв следует дополнить открытый текст в том случае, если последняя группа букв будет неполной.

С учетом данных требований в рассматриваемом примере открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ, разделенный на пары букв, будет выглядеть вот так:

СЕ КР ЕТ НО ЕС ОХ ОБ ЩЕ НИ ЕХ

Теперь каждую пару или группу букв следует зашифровать отдельно. Для этого сначала надо найти эти две буквы в таблицах, при этом первая буква биграммы должна находиться в левой таблице, а вторая — в правой. После этого необходимо в двух таблицах построить четырехугольник, в двух противоположных вершинах которого находятся две шифруемые буквы открытого текста. Две буквы, оказавшиеся в двух других вершинах этого прямоугольника, являются составной частью криптограммы. При этом каждая буква пары открытого текста заменяется буквой криптограммы, лежащей с ней в одной строке, но в другой таблице.

Так, например, в рассматриваемом примере при шифровании первой пары букв, а именно букв СЕ, в криптограмму следует записать буквы ДЖ, вместо букв КР — буквы ЖА, вместо букв ЕГ — буквы БН и так далее.

При использовании данного шифра возможна ситуация, когда обе буквы какой-либо группы открытого текста окажутся в одной строке таблиц В этом случае в криптограмму вместо первой буквы биграммы открытого текста записывается буква, находящаяся в том же столбце той же строки второй таблицы. Вместо второй буквы биграммы открытого текста в криптограмму записывается буква, находящаяся в том же столбце той же строки первой таблицы.

Так, в рассматриваемом примере при шифровании группы ЕС открытого текста в криптограмму записывается пара БЖ.

Если же при этом одна из пары букв открытого текста окажется в крайнем правом столбце строки, то в шифрограмме эта буква должна быть заменена на букву, находящуюся в первом столбце этой строки.

По окончании шифрования криптограмма открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ примет следующий вид:

ДЖ ЖА БН ЮЕ БЖ ЗХ АГ ШБ ДД СЦ

Для дешифрования такого сообщения получатель сначала должен с помощью известных ему правил или паролей составить две таблицы, а затем, используя указанные выше правила, заменить пары или группы букв криптограммы на соответствующие им пары или группы открытого текста. При этом первая буква биграммы шифрованного текста должна находиться в правой таблице, а вторая — в левой.