
Авторы: , М.К. Потапов, Н.Н. Решетников, А.В. Шевкин.
Издательство:
Просвещение 2015-2022
Тип: Учебник, МГУ — школе
Подробный решебник (ГДЗ) по Алгебре за 7 (седьмой) класс — готовый ответ номер — 193. Авторы учебника: Никольский, Потапов, Решетников, Шевкин. Издательство: Просвещение 2015-2022.
Условие /
номер / 193
193. Напишите алгебраическое выражение, с помощью которого вычисляется: а) путь при равномерном движении, если скорость движущегося тела и, время движения t; б) площадь прямоугольника длины а, ширины b; в) периметр прямоугольника длины k, ширины t; г) длина окружности радиуса r; д) площадь круга радиуса R; е) объём прямоугольного параллелепипеда с длиной рёбер а, b и с.
Решебник к учебнику 2022 / номер / 193

Видеорешение / номер / 193
Решебник к учебнику 2015 / номер / 193

Оцените решебник:
4.4/5

2562
Показать содержание
← Предыдущее
Следующее →
Решебник №1
упражнение / 193

Решебник №2
упражнение / 193

Решебник №3
упражнение / 193

Показать содержание
← Предыдущее
Следующее →
Все ГДЗ по
Алгебре
7 класс
МГУ — школе
-
Готовые домашние задания
-
7 класс -
Алгебра -
Никольский -
193
Показать содержание
- ГДЗ к рабочей тетради по алгебре 7 класс Журавлев С.Г. можно найти тут
- ГДЗ к рабочей тетради по алгебре за 7 класс Потапов М.К. можно найти тут
- ГДЗ к дидактическим материалам по алгебре за 7 класс Потапов М.К. можно найти тут
- ГДЗ к тематическим тестам по алгебре за 7 класс Чулков П.В. можно найти тут
Решебник к учебнику 2022/ номер / 193
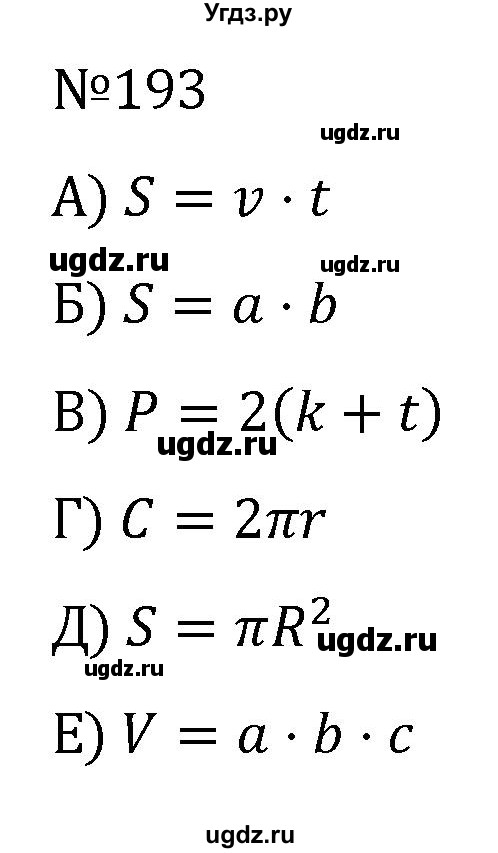
Видеорешение/ номер / 193
Решебник к учебнику 2015/ номер / 193

Ответы к теме 4.2. Буквенные выражения
Задание 191
а) Что называют буквенным выражением? Приведите примеры.
б) Может ли буквенное выражение состоять из одной буквы?
в) Можно ли называть число алгебраическим выражением?
г) Что называют суммой, разностью, произведением, частным двух данных алгебраических выражений? Приведите примеры.
д) Можно ли опускать знак умножения при записи произведения алгебраических выражений?
Решение
а) Если в числовом выражении некоторые (или все) числа заменить буквами (разные числа − разными буквами), то получится буквенное выражение.
Например:
a + b − 8 = 25;
$frac{x}{5 + y} = 22$.б) Буквенное выражение может состоять из одной буквы.
в) Число не является буквенным выражением.
г) Если два данных алгебраических выражения соединить знаком сложения, вычитания, умножения или деления, то получим алгебраическое выражение, которое называют соответственно суммой, разность, произведением или частным данных алгебраических выражений.
Например:
(8a − 2) + (2b + 3) − сумма;
(8a − 2) − (2b + 3) − разность;
(8a − 2) * (2b + 3) − произведение;
$frac{8a — 2}{2b + 3}$ − частное.д) Знак умножения при записи произведения алгебраических выражений можно опустить.
Задание 192
а) В числовом выражении $frac{2 * 5 — 5 : 3}{7 * 5 — 1}$ замените число 5 буквой a. Запишите полученное алгебраическое выражение.
б) В числовом выражении 4 * (6 * 3 − 6) − 6 * (4 * 3 − 4) замените число 4 буквой a, число 6 − буквой b. Запишите полученное алгебраическое выражение.
Решение
а) $frac{2 * a — a : 3}{7 * a — 1}$
б) a * (b * 3 − b) − b * (a * 3 − a)
Задание 193
Напишите алгебраическое выражение, с помощью которого вычисляется:
а) путь при равномерном движении, если скорость движущегося тела v, время движения t;
б) площадь прямоугольника длины a, ширины b;
в) периметр прямоугольника длины k, ширины t;
г) длина окружности радиуса r;
д) площадь круга радиуса R;
е) объем прямоугольного параллелепипеда с длиной ребер a, b и c.
Решение
а) S = v * t
б) S = ab
в) P = 2(k + t)
г) C = 2πR
д) $S = πR^2$
е) V = abc
Задание 194
Напишите сумму, разность, произведение и частное двух алгебраических выражений (a + b) и (3 − c).
Решение
(a + b) + (3 − c) − сумма;
(a + b) − (3 − c) − разность;
(a + b)(3 − c) − произведение;
$frac{a + b}{3 — c}$ − частное.
Задание 195
Алгебраическое выражение 2n, где n − любое натуральное число, задает натуральные числа, делящиеся на 2 (четные числа). Напишите алгебраическое выражение, задающее:
а) целые числа, делящиеся нацело на 5;
б) натуральные числа, делящиеся на 5 с остатком 3.
Решение
а) 5n, где n − целое число.
б) 5n + 3, где n − натуральное число.
Задание 196
а) Два брата коллекционируют почтовые марки. У старшего брата в n раз больше марок, чем у младшего, а всего у них 150 марок. Сколько марок у каждого?
б) Разделите отрезок, длина которого a см, в отношении b : c.
в) Разделите отрезок, длина которого a см, так, чтобы одна его часть была в n раз больше другой.
Решение
а) Пусть x (марок) − у младшего брата, тогда:
xn (марок) − у старшего брата.
Так как, всего у них 150 марок, составим уравнение:
x + xn = 150
x(1 + n) = 150
$x = frac{150}{1 + n}$ (марок) − у младшего брата;
$xn = frac{150n}{1 + n}$ (марок) − у старшего брата.
Ответ: $frac{150}{1 + n}$ − у младшего; $frac{150n}{1 + n}$ − у старшего.б) 1) $a : (b + c) = frac{a}{b + c}$ (см) − приходится на 1 часть;
2) $frac{a}{b + c} * b$ (см) − длина одной части отрезка;
3) $frac{a}{b + c} * c$ (см) − длина другой части отрезка.
Ответ: $frac{a}{b + c} * b$ см и $frac{a}{b + c} * c$ см.в) Пусть x (см) − длина меньшей части, тогда:
xn (см) − длина большей части.
Так как, общая длина отрезка a см, составим уравнение:
x + xn = a
x(1 + n) = a
$x = frac{a}{1 + n}$ (см) − длина меньшей части;
$xn = frac{an}{1 + n}$ (см) − длина большей части.
Ответ: $frac{a}{1 + n}$ см и $frac{an}{1 + n}$ см
Задание 197
а) Турист шел 2 ч со скоростью x км/ч и 3 ч со скоростью y км/ч. Определите среднюю скорость туриста на пройденном участке пути.
б) Турист шел a ч со скоростью 5 км/ч и b ч со скоростью 4 км/ч. Определите среднюю скорость туриста на пройденном участке пути.
Решение
а) 1) 2x + 3y (км) − всего прошел турист;
2) 2 + 3 = 5 (ч) − всего шел турист;
3) $frac{2x + 3y}{5}$ (км/ч) − средняя скорость туриста.
Ответ: $frac{2x + 3y}{5}$ км/чб) 1) 5a + 4b (км) − всего прошел турист;
2) a + b (ч) − всего шел турист;
3) $frac{5a + 4b}{a + b}$ (км/ч) − средняя скорость туриста.
Ответ: $frac{5a + 4b}{a + b}$ км/ч
