Вместо звездочки запишите такой многочлен, чтобы после приведения подобных членов полученный многочлен
3
x
2
+
5
x
2
y
+
7
x
−
8
y
+
15
+
∗
не содержал:
1) членов с
x
2
;
2) членов с переменной x;
3) членов с переменной y.
reshalka.com
Алгебре 7 класс Мерзляк. Номер №324
Решение 1
∗
=
−
(
3
x
2
+
5
x
2
y
)
=
−
3
x
2
−
5
x
2
y
, тогда:
3
x
2
+
5
x
2
y
+
7
x
−
8
y
+
15
+
(
−
3
x
2
−
5
x
2
y
)
=
3
x
2
+
5
x
2
y
+
7
x
−
8
y
+
15
−
3
x
2
−
5
x
2
y
=
(
3
x
2
−
3
x
2
)
+
(
5
x
2
y
−
5
x
2
y
)
+
7
x
−
8
y
+
15
=
7
x
−
8
y
+
15
Решение 2
∗
=
−
(
3
x
2
+
5
x
2
y
+
7
x
)
=
−
3
x
2
−
5
x
2
y
−
7
x
, тогда:
3
x
2
+
5
x
2
y
+
7
x
−
8
y
+
15
+
(
−
3
x
2
−
5
x
2
y
−
7
x
)
=
(
3
x
2
−
3
x
2
)
+
(
5
x
2
y
−
5
x
2
y
)
+
(
7
x
−
7
x
)
−
8
y
+
15
=
−
8
y
+
15
Решение 3
∗
=
−
(
5
x
2
y
−
8
y
)
=
−
5
x
2
y
+
8
y
, тогда:
3
x
2
+
5
x
2
y
+
7
x
−
8
y
+
15
+
(
−
5
x
2
y
+
8
y
)
=
3
x
2
+
5
x
2
y
+
7
x
−
8
y
+
15
−
5
x
2
y
+
8
y
=
3
x
2
+
(
5
x
2
y
−
5
x
2
y
)
+
(
8
y
−
8
y
)
+
7
x
+
15
=
3
x
2
+
7
x
+
15
Авторы: , В. Б. Полонский, М. С. Якир.
Издательство:
Вентана-граф 2016
Тип: Учебник
Подробный решебник (ГДЗ) по Алгебре за 7 (седьмой) класс — готовый ответ номер — 324. Авторы учебника: Мерзляк, Полонский, Якир. Издательство: Вентана-граф 2016.
Условие /
номер / 324
324. Вместо звёздочки запишите такой многочлен, чтобы после приведения подобных членов многочлен Зx^2 + 5х^2у + 7х — 8у + 15 + » не содержал:
1) членов с х^2;
2) членов с переменной x;
3) членов с переменной у.
Решебник №1 / номер / 324
Видеорешение / номер / 324
Решебник №2 / номер / 324
Решебник №3 / номер / 324
Оцените решебник:
4.4/5
1632
-
Главная
-
ГДЗ
- 7 класс
- Алгебра
-
Мерзляк учебник
- 324
Вернуться к содержанию учебника
Упражнения § 9. Страница 64
Вопрос
Вместо звездочки запишите такой многочлен, чтобы после приведения подобных членов многочлен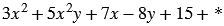 
не содержал:
1) членов с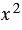 
;
2) членов с переменной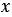 
;
3) членов с переменной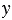 
.
Подсказка
Вспомните:
- Что называют многочленом.
- Что называют одночленом.
- Сложение и вычитание многочленов.
- Правила раскрытия скобок, подобные слагаемые.
- Противоположные числа.
- Правила сложения рациональных чисел.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника