Не могу найти по номеру выполняемое многоразовое задание. Да и любые другие по номеру не найти). Пробовал произвольно выбранные задания вызвать по номеру — и ничего!)
Числа
Вычисления
Алгебраические выражения
1.Значение какого из выражений является числом рациональным?
1) 2) 3) 4)
Решение.
Упростим каждое выражение.
1)
2)
3)
4)
Рациональным является значение первого выражения.
Ответ: 1
Источник: Демонстрационная версия ГИА—2013 по математике.
Задание 4 № 137268
2.Расположите в порядке возрастания числа: ; ; 5,5.
1) 2)
3) 4)
Решение.
Возведём каждое из чисел в квадрат:
Сравним квадраты заданных чисел:
Следовательно,
Правильный ответ указан под номером 4.
Ответ: 4
Задание 4 № 137269
3.Расположите в порядке убывания числа: ; ; 5,5.
1) 2)
3) 4)
Решение.
Возведём каждое из чисел в квадрат:
Сравним квадраты заданных чисел:
Следовательно,
Правильный ответ указан под номером 2.
Ответ: 2
Задание 4 № 287934
4.Расположите в порядке возрастания:
1) 3)
2) ; 4)
Решение.
Поскольку: получаем:
Правильный ответ указан под номером 2.
Ответ: 2
Задание 4 № 287943
5.Расположите в порядке возрастания:
1) , , 2) , ,
3) , , 4) , ,
Решение.
Упростим заданные числовые выражения:
Заметим, что Поэтому правильный ответ указан под номером 1.
Ответ: 1
Задание 4 № 287944
6.Расположите в порядке убывания:
1) 2)
3) 4)
Решение.
Упростим заданные числовые выражения:
Сравним полученные дроби, приведя их к наименьшему общему знаменателю:
Правильный ответ указан под номером 2.
Ответ: 2
Задание 4 № 311750
7.Укажите наибольшее из следующих чисел:
1) 2) 3) 4)
Решение.
Чтобы ответить на вопрос, возведём в квадрат числа
Поскольку имеем: Таким образом, наибольшее число 5.
Правильный ответ указан под номером 3.
Ответ: 3
Источник: МИОО: Диагностическая работа по математике 01.10.2013 вариант МА90101.
Задание 4 № 314246
8.Сравните числа и 16.
1) 2)
3)
Решение.
В силу цепочки неравенств
первое число меньше второго.
Правильный ответ указан под номером 1.
Ответ: 1
Источник: Банк заданий ФИПИ
Задание 4 № 314250
9.Какое из чисел больше: или
1) 2)
3)
Решение.
В силу цепочки неравенств
первое число больше второго.
Правильный ответ указан под номером 3.
Ответ: 3
Источник: Банк заданий ФИПИ
Задание 4 № 314367
10.Значение какого из данных выражений является наименьшим?
1) 2) 3) 4)
Решение.
Возведём каждое число в квадрат и сравним квадраты этих чисел:
Поскольку имеем:
Наименьшим является выражение под номером 4.
Ответ: 4
Источник: Банк заданий ФИПИ
Задание 4 № 314377
11.В каком случае числа и 6 расположены в порядке возрастания?
1) 2)
3) 4)
Решение.
Числа положительны, возведём их в квадрат и сравним квадраты этих чисел:
Поскольку имеем:
Числа расположены в порядке возрастания во втором варианте ответа.
Ответ: 2
Источник: Банк заданий ФИПИ
Задание 4 № 314448
12.Сравните числа и 12.
1) 2)
3)
Решение.
В силу цепочки неравенств
первое число меньше второго.
Правильный ответ указан под номером 1.
Ответ: 1
Источник: Банк заданий ФИПИ
Задание 4 № 314453
13.Какое из чисел больше: или ?
1) 2)
3)
Решение.
В силу цепочки неравенств
первое число меньше второго.
Правильный ответ указан под номером 1.
Ответ: 1
Источник: Банк заданий ФИПИ
Задание 4 № 316557
14.Значение какого из выражений является числом иррациональным?
1) 2)
3) 4)
Решение.
Упростим каждое выражение.
1)
2)
3)
4)
Иррациональным является значение четвёртого выражения.
Ответ: 4
Задание 4 № 316603
15.Расстояние от Юпитера — одной из планет Солнечной системы — до Солнца равно 778,1 млн км. Как эта величина записывается в стандартном виде?
1) 7,781·1011 2) 7,781·108
3) 7,781·1010 4) 7,781·109
Решение.
Число, записанное в стандартном виде, имеет вид: где Преобразуем число к стандартному виду:
Правильный ответ указан под номером: 2.
Ответ: 2
Источник: Банк заданий ФИПИ
Задание 4 № 316624
16.На рулоне обоев имеется надпись, гарантирующая, что длина полотна обоев находится в пределах 10 ± 0,05 м. Какую длину не может иметь полотно при этом условии?
1) 10,23 2) 10,05 3) 9,96 4) 10,03
Решение.
Запись, приведённая в условии, указывает на то, что длина рулона обоев находится в пределах от 9,95 м до 10,05 м. В этот интервал не попадает значение 10,23.
Правильный ответ указан под номером: 1.
Ответ: 1
Задание 4 № 317295
17.Какое из чисел является иррациональным?
1) 2) 3) 4) ни одно из этих чисел
Решение.
Преобразуем числа:
Корень из 10 является иррациональным числом, поэтому число — иррационально.
Правильный ответ указан под номером: 3.
Ответ: 3
Задание 4 № 317301
18.Какое из чисел является рациональным?
1) 2) 3) 4) Все эти числа иррациональны.
Решение.
Преобразуем числа:
Корень из 10 является иррациональным числом, поэтому числа и иррациональны. Число является рациональным числом.
Правильный ответ указан под номером: 2.
Ответ: 2
Задание 4 № 317368
19.Значение какого из чисел является наибольшим?
1) 2) 3) 4)
Решение.
Возведём числа в квадрат:
Сравним квадраты этих чисел. Заметим, что следовательно,
Таким образом, наибольшее число указано под номером 3.
Правильный ответ указан под номером: 3.
Ответ: 3
Задание 4 № 317586
20.Какое из следующих чисел является наименьшим?
1) 1,7·10−3 2) 2,3·10−4 3) 4,5·10−3 4) 8,9·10−4
Решение.
Числа здесь представлены в стандартном виде. Поэтому из них наименьшим будет то, которое имеет наименьший показатель степени десяти. Если показатели равны, то наименьшим будет число, имеющее наименьшую мантиссу. Таким образом, среди представленных чисел наименьшее —
Правильный ответ указан под номером: 2.
Ответ: 2
Задание 4 № 317587
21.Какое из следующих чисел является наибольшим?
1) 1,8·10−3 2) 4,7·10−4 3) 2,9·10−5 4) 9,5·10 −3
Решение.
Числа здесь представлены в стандартном виде. Поэтому из них наибольшим будет то, которое имеет наибольший показатель степени десяти. Если показатели равны, то наибольшим будет число, имеющее наибольшую мантиссу. Таким образом, получаем, что среди представленных чисел наибольшее —
Правильный ответ указан под номером: 4.
Ответ: 4
Задание 4 № 317728
22.Масса Луны равна 7,35·1022 кг. Выразите массу Луны в млн тонн.
1) 7,35⋅1010 млн т 2) 7,35⋅1013 млн т
3) 7,35⋅1016 млн т 4) 7,35⋅1019 млн т
Решение.
В одной тонне 103 кг, 1 миллион — это 106. Преобразуем представленное в условии число:
Правильный ответ указан под номером: 2.
Ответ: 2
Задание 4 № 317741
23.Численность населения Китая составляет 1,3·109 человек, а Вьетнама — 8,5·107 человек. Во сколько раз численность населения Китая больше численности населения Вьетнама?
1) примерно в 6,5 раз 2) примерно в 15 раз
3) примерно в 150 раз 4) примерно в 1,5 раза
Решение.
Разделим численность населения Китая на численность населения Вьетнама:
Таким образом, численность населения Китая примерно в 15 раз больше численности населения Вьетнама.
Правильный ответ указан под номером: 2.
Ответ: 2
Задание 4 № 317753
24.Расстояние от Земли до Солнца равно 147,1 млн км. В каком случае записана эта же величина?
1) 1,471⋅1010 км 2) 1,471⋅108 км
3) 1,471⋅107 км 4) 1,471⋅106 км
Решение.
Запишем 141,7 млн в стандартом виде:
Правильный ответ указан под номером: 2.
Ответ: 2
Задание 4 № 318729
25.Значение какого выражения является рациональным числом?
1) 2) 3) 4)
Решение.
Преобразуем выражения:
Числа являются иррациональными, поэтому первое, второе и четвёртое выражения иррациональны. Число 6 можно представить в виде дроби поэтому оно рационально.
Правильный ответ указан под номером: 3.
Ответ: 3
Источник: Банк заданий ФИПИ
Задание 4 № 318753
26.Значение какого из данных выражений является наименьшим?
1) 2) 3) 4)
Решение.
Возведём числа в квадрат:
Заметим, что поэтому Таким образом, — наименьшее из представленных чисел.
Правильный ответ указан под номером: 4.
Ответ: 4
Задание 4 № 337271
27.Найдите значение выражения
1) 2) 3) 4)
Решение.
Используем свойства степени:
Правильный ответ указан под номером: 1.
Ответ: 1
Задание 4 № 337291
28.В лабораторию купили электронный микроскоп, который даёт возможность различать объекты размером до Выразите эту величину в миллиметрах.
1) 0,002 2) 0,0002 3) 0,00002 4) 0,000002
Решение.
Вспомним, что в одном сантиметре 10 миллиметров:
Правильный ответ указан под номером: 3.
Ответ: 3
Задание 4 № 337311
29.Между какими числами заключено число
1) 8 и 9 2) 72 и 74 3) 24 и 26 4) 4 и 5
Решение.
Сравним квадраты приведённых в условии чисел:
Число 73 лежит между числами 64 и 81, поэтому заключено между числами 8 и 9.
Правильный ответ указан под номером 1.
Ответ: 1
Задание 4 № 337389
30.Какое из данных чисел принадлежит промежутку [6; 7]?
1) 2) 3) 4)
Решение.
Возведём все числа в квадрат:
Заметим, что следовательно, Таким образом, число принадлежит промежутку [6; 7].
Правильный ответ указан под номером: 4.
Ответ: 4
Задание 4 № 342023
31.Значение какого из выражений является числом иррациональным?
1) 2)
3) 4)
Решение.
Найдем значения выражений:
1)
2)
3)
4)
Иррациональным является значение выражения, указанного под номером 4.
Ответ: 4.
Ответ: 4
Задание 4 № 348601
32.Площадь территории России составляет км , а Нигерии — км . Во сколько раз площадь территории России больше площади территории Нигерии?
1) примерно в 18 раз 2) примерно в 180 раз
3) примерно в 1,8 раза 4) примерно в 5,4 раза
Решение.
Площадь территории России примерно в раз больше площади Нигерии. Правильный ответ указан под номером: 1.
Ответ: 1
Ответ: 1
Задание 4 № 348955
33.Площадь территории России составляет 1,7 · 107 км2, а Великобритании — 2,6⋅105 км2. Во сколько раз площадь территории России больше площади территории Великобритании?
1) примерно в 65 раз 2) примерно в 650 раз
3) примерно в 6,5 раза 4) примерно в 1,5 раза
Решение.
Площадь территории России примерно в раз больше площади Великобритании.
Ответ: 1
Ответ: 1
Задание 4 № 351591
34.В лабораторию купили электронный микроскоп, который даёт возможность различать объекты размером до Выразите эту величину в миллиметрах.
1) 0,0000027 2) 0,000027 3) 0,00027 4) 0,027
Вычисления
1.Найдите значение выражения
1) 2) 3) 4) 4
Решение.
Последовательно получаем:
Правильный ответ указан под номером 1.
Ответ: 1
Задание 4 № 137281
2.Вычислите:
1) 2) 3) 4)
Решение.
Используя формулы и получаем:
Правильный ответ указан под номером 4.
Ответ: 4
Задание 4 № 137285
3.Найдите значение выражения .
Решение.
Упростим выражение, разложив подкоренные выражения на множители и вынесем за знак корня полные квадраты чисел:
Ответ: 220.
Ответ: 220
Задание 4 № 316255
4.Найдите значение выражения при а = 6.
Решение.
Упростим выражение:
(при ).
Найдём значение полученного выражения при
Ответ: 0,5.
Ответ: 0,5
0,5
Источник: Диагностическая работа 01.10.2013 Вариант МА90106
Задание 4 № 317389
5.Найдите значение выражения
1) 5 2) 3) 4) 40
Решение.
Найдём значение выражения:
Правильный ответ указан под номером: 1.
Ответ: 1
Источник: Банк заданий ФИПИ
Задание 4 № 318630
6.Чему равно значение выражения
.
1) 6 2) 12 3) 18 4) 36
Решение.
Используем свойства степени:
Правильный ответ указан под номером: 3.
Ответ: 3
Задание 4 № 333111
7.Найдите значение выражения .
Решение.
Приведём к общему знаменателю:
Ответ: 2,18.
Ответ: 2,18
2,18
Источник: МИОО: Диагностическая работа по математике 17.04.2014 вариант МА90605
Задание 4 № 337339
8.Найдите значение выражения
1) 198 2) 3) 3564 4) 2178
Решение.
Найдём значение выражения:
Правильный ответ указан под номером: 1.
Ответ: 1
Задание 4 № 337462
9.Найдите значение выражения
1) 360 2) 3) 4)
Решение.
Найдём значение выражения:
Правильный ответ указан под номером: 4.
Ответ: 4
Задание 4 № 337692
10.Найдите значение выражения (1,7 · 10− 5)(2 · 10− 2).
1) 0,0000034 2) 34000000000
3) 0,000000034 4) 0,00000034
Решение.
Раскроем скобки и перегруппируем множители:
Правильный ответ указан под номером: 4.
Ответ: 4
Задание 4 № 337700
11.Найдите значение выражения
1) 2) 3) 4) 90
Решение.
Найдём значение выражения:
Правильный ответ указан под номером: 4.
Ответ: 4
Задание 4 № 337782
12.Найдите значение выражения
1) 2) 22 3) 4)
Решение.
Применим формулу квадрата суммы:
Правильный ответ указан под номером: 3.
Ответ: 3
Задание 4 № 341194
13.Найдите значение выражения
1) 2600000 2) 0,000026 3) 0,0000026 4) 0,00026
Решение.
Раскроем скобки и перегруппируем множители:
Правильный ответ указан под номером: 2.
Ответ: 2
Источник: Банк заданий ФИПИ
Задание 4 № 349896
14.Найдите значение выражения
1) 2) 3) 4)
Решение.
Найдем значение выражения:
Ответ: 2
Ответ: 2
Задание 4 № 352963
15.Какое из данных ниже чисел является значением выражения ?
1) 2) 3) 4)
Решение.
Найдем значение выражения:
Ответ: 2
Ответ: 2
Источник: Банк заданий ФИПИ
Задание 4 № 353384
16.Найдите значение выражения
Решение.
Найдем значение выражения:
Ответ: 1951,1
Ответ: 1951,1
1951,1
Задание 4 № 355406
17.Какое из данных ниже чисел является значением выражения
1) 16 2) 3) −16 4)
Алгебраические выражения
1.Какое из следующих выражений равно ?
1) 2) 3) 4)
Решение.
При делении степеней с одинаковыми основаниями их показатели вычитаются. Таким образом, правильный ответ под номером 1.
Ответ: 1
Задание 4 № 137276
2.Какое из следующих выражений равно ?
.
1) 2) 3) 4)
Решение.
Пользуясь свойствами степеней получаем:
Правильный ответ указан под номером 1.
Ответ: 1
Задание 4 № 137278
3.Представьте выражение в виде степени с основанием c.
1) 2) 3) 4)
Решение.
Используя формулы и , получаем:
Правильный ответ указан под номером 2.
Ответ: 2
Задание 4 № 137279
4.Представьте выражение в виде степени с основанием x.
1) 2) 3) 4)
Решение.
Используя формулы получаем:
Правильный ответ указан под номером 3.
Ответ: 3
Задание 4 № 137280
5.Найдите значение выражения при .
1) −125 2) 125 3) 4)
Решение.
Упростим выражение используя формулы , и :
Подставим значение :
Правильный ответ указан под номером: 2.
Ответ: 2
Задание 4 № 137292
6.Сравните числа x и y, если , . В ответ запишите большее число.
Решение.
Приведем второе число к десятичному виду и сравним. Воспользуемся формулой
Тем самым,
Ответ: 0,000064.
Ответ: 0,000064
0,000064
Задание 4 № 318723
7.Какому из следующих выражений равна дробь
1) 2) 3) 4)
Решение.
Используем свойства степени:
Правильный ответ указан под номером: 4.
Ответ: 4
Задание 4 № 338098
8.Представьте выражение в виде степени с основанием
1) <img adsbygoogle=»» data-ad-client=»ca-pub-7892686117861611″ data-ad-slot=»7781263272″ src=»http://konspekta.net/lektsia</div><center>%0D%0A%0D%0A%0D%0A<ins%20class=»>
Тоже самое , практически, чтт и в разборе.
Значение:
·Числительные-помогают нам посчитать , определить число и такде выражают колличество.
·Морф.пр : пост.пр : разряд(колличественное , порядковое) ; непост.пр : падеж , по структуре(простое,составное,сложное)
·Синтаксическая роль :
-для колличественных : В корзине лежало два яблока.(как существ.)Мы купили пять яблок.(как дополнение)
-для порядковых : Начался первый урок.(как определение)
Удачи★
Твой wi-fi
При выполнении задания 8 ОГЭ по математике необходимо: знать свойства степеней и корней, уметь сравнивать рациональные и иррациональные числа, применять формулы сокращённого умножения.
Пример 1. Найдите значение выражения . В ответе укажите номер правильного варианта.
1) 84 2) 2352 3) 4) 252
Решение. Произведение корней равно корню из произведения, т. е. . Тогда
Ответ: 1.
Пример 2. Найдите значение выражения . В ответе укажите номер правильного варианта.
1) 2) 3) 4)
Ответ: 3.
Пример 3. На рулоне обоев имеется надпись, гарантирующая, что длина полотна обоев находится в пределах 10 ± 0,05 м. Какую длину не может иметь полотно при этом условии?
В ответе укажите номер правильного варианта.
1) 10,03 2) 10,05 3) 9,96 4) 10,08
Решение. Длина рулона находится в интервале от 10 — 0,05 = 9,95 м до 10 + 0,05 = 10,05 м. Таким образом, только число 10,08 не попадает в этот диапазон.
Ответ: 4.
Пример 4. Сравните числа и 14. В ответе укажите номер правильного варианта.
1) 2) 3)
Решение. Очевидно, что равенство между заданными числами невозможно. Предположим, что справедливо неравенство Возведём обе части неравенства в квадрат и проведём соответствующие преобразования:
Полученное неравенство неверно, а это значит, что предположение неверно. Тогда верно неравенство .
Ответ: 1.
Пример 5. Укажите наименьшее из чисел. В ответе укажите номер правильного варианта.
1) 2) 3) 4)
Решение. Сравним сначала первые три числа, представив их в виде корней:
1) 2) 3)
Из этих чисел наименьшим является . Осталось сравнить его с четвёртым значением.
Результат очевиден. Наименьшим оказалось число под номером 4.
Ответ: 4.
Пример 6. Представьте выражение в виде степени с основанием m. В ответе укажите номер правильного варианта.
1) 2) 3) 4)
Решение. Используем свойства степеней:
Ответ: 2.
Пример 7. Вычислите . В ответе укажите номер правильного варианта.
1) 2) 3) 4)
Решение. Используем свойства степеней:
Ответ: 3.
Пример 8. Какое из чисел является иррациональным? В ответе укажите номер правильного варианта.
1) 2) 3) 4) все числа иррациональны
Решение. Если в результате вычислений или преобразований всё равно остаётся корень, то число является иррациональным:
1) (рациональное число)
2) (иррациональное число)
3) (рациональное число)
Ответ: 2.
Пример 9. Какое из числовых выражений является рациональным? В ответе укажите номер правильного варианта.
1) 2) 3) 4)
Решение. Если в результате вычислений корень «исчезнет», то число является рациональным:
1) (иррациональное число)
2) (иррациональное число)
3) (иррациональное число)
4) (рациональное число)
Ответ: 4.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 8 ОГЭ по математике. Числа, вычисления и алгебраические выражения.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.01.2023
Найдите значения выражений
| 1 | Найдите значение выражения frac{a^2-81}{2a^2+18a} при a=4,5 | Смотреть видеоразбор >> |
| 2 | Найдите значение выражения frac{a^2-25b^2}{5ab}:(frac{1}{5b}-frac{1}{a}) при a = 8 frac{1}{16}, b = 6 frac{3}{16} | Смотреть видеоразбор >> |
| 3 | Найдите значение выражения frac{a^2-4b^2}{2ab}:(frac{1}{2b}-frac{1}{a}) при a = 5 frac{11}{17}, b = 7 frac{3}{17} | Смотреть видеоразбор >> |
| 4 | Найдите значение выражения frac{5ac^2}{a^2-4c^2} cdot frac{a-2c}{ac} при a = 5,2, c = -2,4 | Смотреть видеоразбор >> |
| 5 | Найдите значение выражения frac{64b^2+128b+64}{b}:(frac{4}{b}+4) при b=-frac{15}{16} | Смотреть видеоразбор >> |
| 6 | Найдите значение выражения (frac{y}{x-y}+frac{x}{x+y}):(frac{1}{x^2}+frac{1}{y^2})-frac{y^4}{x^2-y^2} при x = sqrt{7}, y = sqrt{3} | Смотреть видеоразбор >> |
| 7 | Найдите значение выражения frac{a}{a^2-b^2}:frac{a}{ab + b^2} при a = 1,1 и b = 0,6 | Смотреть видеоразбор >> |
| 8 | Найдите значение выражения frac{(m-n+1)^2-(m-1+n)^2}{4m} cdot (n+1) при m = 1 frac{12}{13}, n = sqrt{2} | Смотреть видеоразбор >> |
| 9 | Найдите значение выражения (a^3-16a) cdot (frac{1}{a+4}-frac{1}{a-4}) при a = -45 | Смотреть видеоразбор >> |
| 10 | Найдите значение выражения (frac{1}{a}+frac{1}{b}) cdot ((a+b)^2-frac{a^3-b^3}{a-b}) при a = 2-sqrt{5}, b = sqrt{5}-1 | Смотреть видеоразбор >> |
| 11 | Упростите выражение frac{c^2+4c+4}{c^2-4}:(c+2) | Смотреть видеоразбор >> |

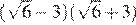 2)
2) 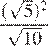 3)
3) 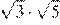 4)
4) 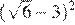
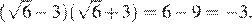
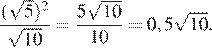
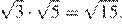
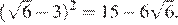
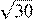 ;
; 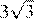 ; 5,5.
; 5,5.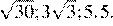 2)
2) 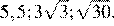
 4)
4) 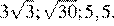
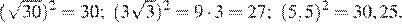
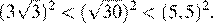
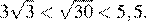
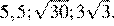
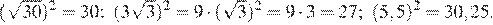
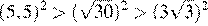
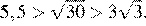
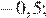
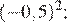
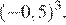
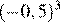 3)
3) 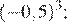
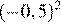
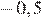 ;
; 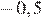
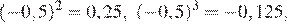 получаем:
получаем: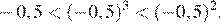
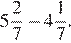
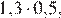
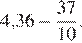
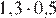 ,
, 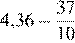 ,
, 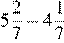 2)
2) 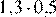 ,
, 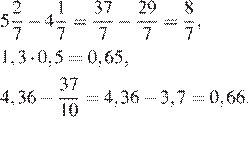
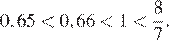 Поэтому правильный ответ указан под номером 1.
Поэтому правильный ответ указан под номером 1.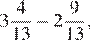
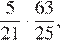
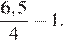
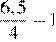 2)
2) 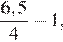
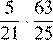
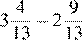 4)
4) 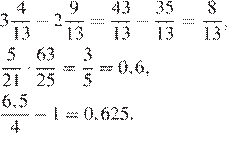
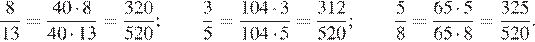
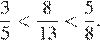
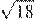 2)
2) 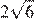 3)
3)  4)
4) 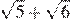
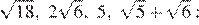
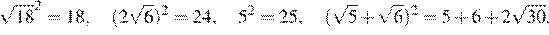
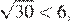
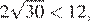 имеем:
имеем: 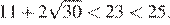 Таким образом, наибольшее число 5.
Таким образом, наибольшее число 5.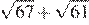 и 16.
и 16.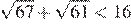 2)
2) 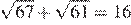
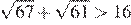
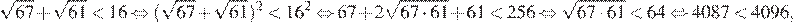
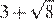 или
или 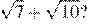
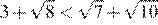 2)
2) 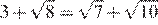
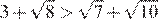
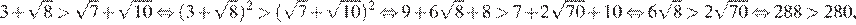
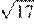 2)
2) 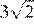 3)
3) 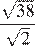 4)
4) 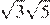
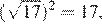
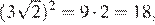
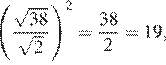
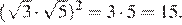
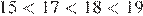 имеем:
имеем: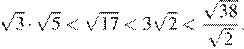
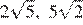 и 6 расположены в порядке возрастания?
и 6 расположены в порядке возрастания?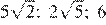 2)
2) 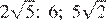
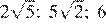 4)
4) 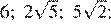
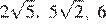 положительны, возведём их в квадрат и сравним квадраты этих чисел:
положительны, возведём их в квадрат и сравним квадраты этих чисел: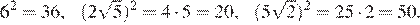
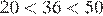 имеем:
имеем: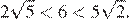
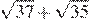 и 12.
и 12.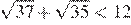 2)
2) 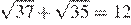
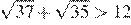
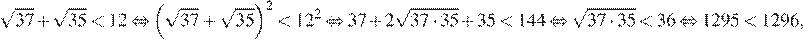
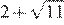 или
или 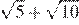 ?
?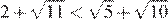 2)
2) 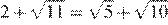
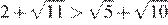
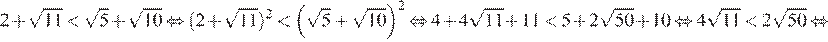
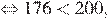
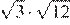 2)
2) 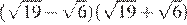
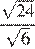 4)
4) 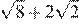
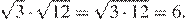
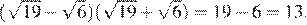
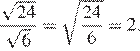
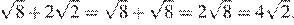
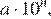 где
где 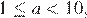
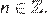 Преобразуем число к стандартному виду:
Преобразуем число к стандартному виду: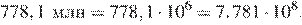
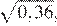
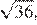
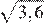 является иррациональным?
является иррациональным?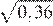 2)
2) 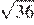 3)
3) 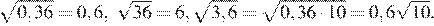
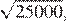
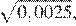
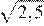 является рациональным?
является рациональным?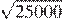 2)
2) 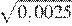 3)
3) 
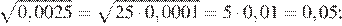
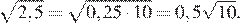
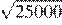 и
и 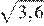 2)
2) 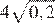 3)
3) 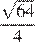 4)
4) 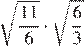
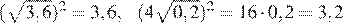
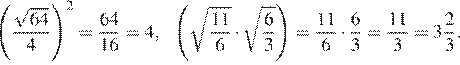
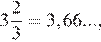 следовательно,
следовательно,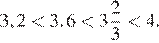
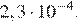
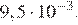
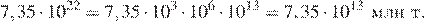
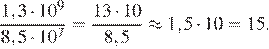
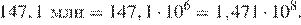
 2)
2) 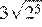 3)
3) 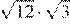 4)
4) 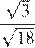
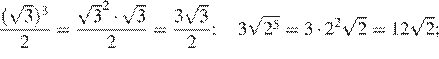
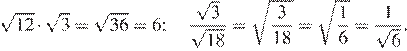
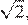
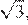
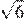 являются иррациональными, поэтому первое, второе и четвёртое выражения иррациональны. Число 6 можно представить в виде дроби
являются иррациональными, поэтому первое, второе и четвёртое выражения иррациональны. Число 6 можно представить в виде дроби 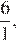 поэтому оно рационально.
поэтому оно рационально.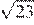 2)
2) 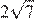 3)
3) 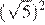 4)
4) 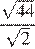
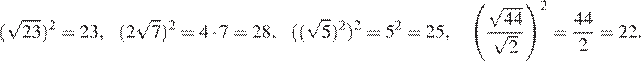
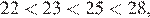 поэтому
поэтому 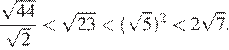 Таким образом,
Таким образом, 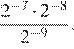
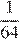 2)
2) 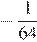 3)
3) 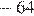 4)
4) 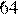
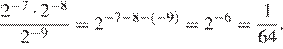
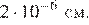 Выразите эту величину в миллиметрах.
Выразите эту величину в миллиметрах.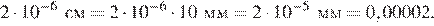
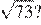
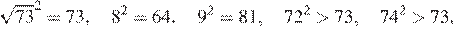
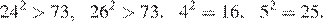
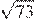 заключено между числами 8 и 9.
заключено между числами 8 и 9.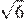 2)
2) 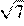 3)
3) 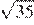 4)
4) 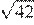
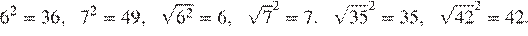
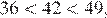 следовательно,
следовательно, 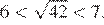 Таким образом, число
Таким образом, число 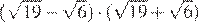
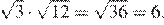
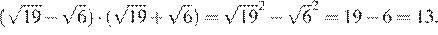
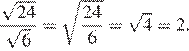
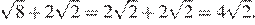
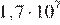 км
км 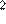 , а Нигерии —
, а Нигерии — 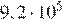 км
км 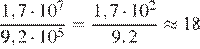 раз больше площади Нигерии. Правильный ответ указан под номером: 1.
раз больше площади Нигерии. Правильный ответ указан под номером: 1.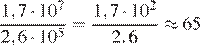 раз больше площади Великобритании.
раз больше площади Великобритании.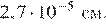 Выразите эту величину в миллиметрах.
Выразите эту величину в миллиметрах.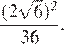
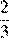 2)
2) 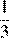 3)
3) 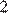 4) 4
4) 4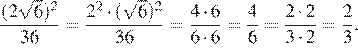
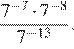
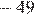 2)
2) 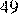 3)
3) 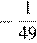 4)
4) 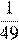
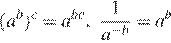 и
и 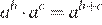 получаем:
получаем: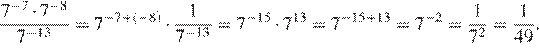
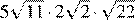 .
.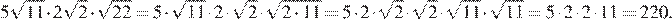
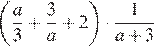 при а = 6.
при а = 6.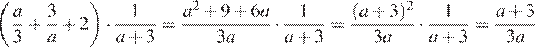 (при
(при 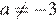 ).
).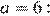
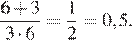
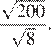
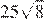 3)
3) 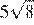 4) 40
4) 40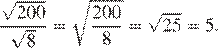
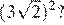
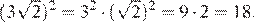
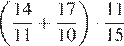 .
.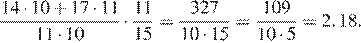
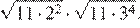
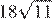 3) 3564 4) 2178
3) 3564 4) 2178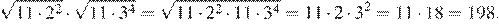
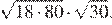
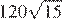 3)
3) 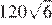 4)
4) 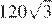
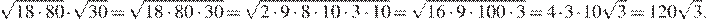
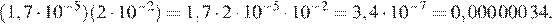
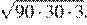
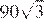 2)
2) 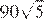 3)
3) 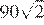 4) 90
4) 90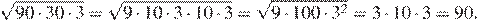
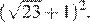
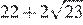 2) 22 3)
2) 22 3) 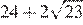 4)
4) 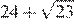
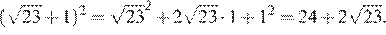
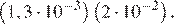
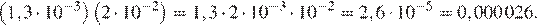
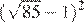
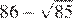 2)
2) 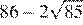 3)
3) 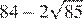 4)
4) 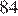
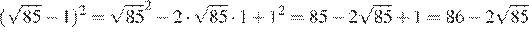
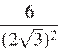 ?
? 2)
2)  3)
3)  4)
4) 
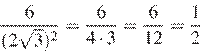
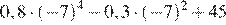
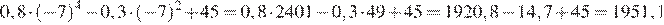
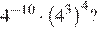
 3) −16 4)
3) −16 4) 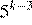 ?
?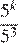 2)
2) 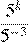 3)
3) 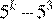 4)
4) 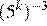
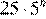 ?
?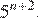 2)
2) 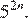 3)
3) 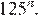 4)
4) 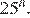
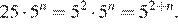
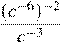 в виде степени с основанием c.
в виде степени с основанием c.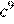 2)
2) 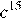 3)
3) 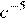 4)
4) 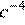
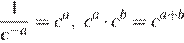 и
и 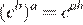 , получаем:
, получаем: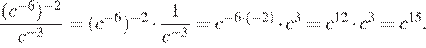
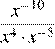 в виде степени с основанием x.
в виде степени с основанием x.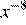 2)
2) 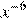 3)
3) 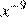 4)
4) 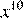
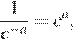
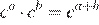 получаем:
получаем: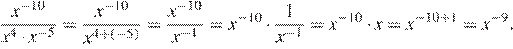
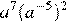 при
при 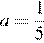 .
.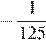 4)
4) 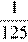
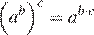 ,
, 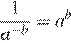 и
и 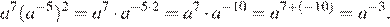
 :
: 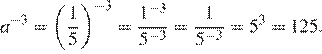
 ,
, 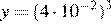 . В ответ запишите большее число.
. В ответ запишите большее число.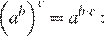
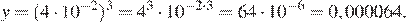
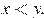
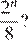
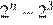 2)
2) 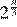 3)
3) 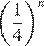 4)
4) 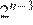
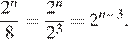
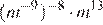 в виде степени с основанием
в виде степени с основанием