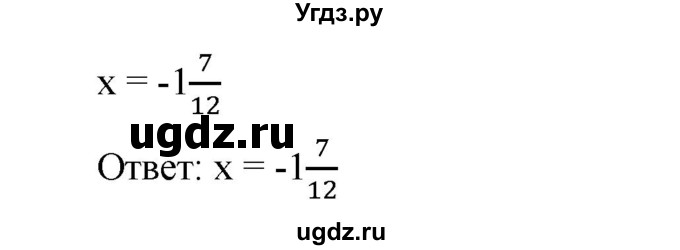
Задание 3. Ответы
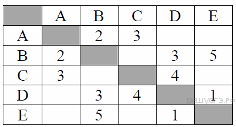
1. Задание 3 № 524. Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых приведена в таблице:
Определите длину кратчайшего пути между пунктами А и F (при условии, что передвигаться можно только по построенным дорогам).
1) 6 2) 8 3) 10 4) 4
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты C, D.
Из пункта B можно попасть в пункты C, F.
Из пункта C можно попасть в пункт F.
Из пункта D можно попасть в пункты E, F.
Из пункта E можно попасть в пункт F.
A—C—F: длина маршрута 8 км.
A—C—B—F: длина маршрута 6 км.
A—D—E—F: длина маршрута 7 км.
A—D—F: длина маршрута 7 км.
Ответ: 1
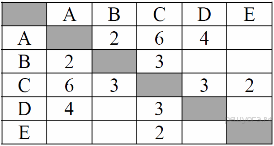
2. Задание 3 № 183. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 5 2) 6 3) 7 4) 8
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C.
Из пункта B можно попасть в пункты D, E.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункт E.
A—B—E: длина маршрута 7 км.
A—B—D—E: длина маршрута 6 км.
A—C—D—E: длина маршрута 8 км.
Ответ: 2
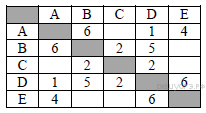
3. Задание 3 № 203. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 6 2) 7 3) 8 4) 9
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C, D.
Из пункта B можно попасть в пункт C.
Из пункта C можно попасть в пункты D, E.
A—B—C—E: длина маршрута 7 км.
A—С—E: длина маршрута 8 км.
A—D—C—E: длина маршрута 9 км.
Ответ: 2
4. Задание 3 № 3. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
| A | B | C | D | E | |
| A | 1 | ||||
| B | 1 | 2 | 2 | 7 | |
| C | 2 | 3 | |||
| D | 2 | 4 | |||
| E | 7 | 3 | 4 |
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 5 2) 6 3) 7 4) 8
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункт B.
Из пункта B можно попасть в пункты C, D, E.
Из пункта C можно попасть в пункт E.
Из пункта D можно попасть в пункт E.
A—B: длина маршрута 1 км.
A—B—C—E: длина маршрута 6 км.
A—B—D—E: длина маршрута 7 км.
A—B—E: длина маршрута 8 км.
Ответ: 2
5. Задание 3 № 1256. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами B и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 7 2) 8 3) 9 4) 10
Пояснение.
Проанализируем некоторые возможные маршруты.
Маршрут B — D — E, длина 11 км.
Маршрут B — C — D — E, длина 10 км.
Маршрут B — С — D — A — E, длина 9 км.
Любые другие маршруты будут длиннее маршрута B — С — D — A — E. Таким образом, кратчайшее расстояние между пунктами B и E составляет 9 км.
Ответ: 3
6. Задание 3 № 223. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 6 2) 7 3) 8 4) 9
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, D.
Из пункта B можно попасть в пункты C, D.
Из пункта C можно попасть в пункты D, E.
A—B—C—E: длина маршрута 9 км.
A—D—B—C—E: длина маршрута 12 км.
A—D—C—E: длина маршрута 9 км.
A—B—D—C—E: длина маршрута 8 км.
Ответ: 3
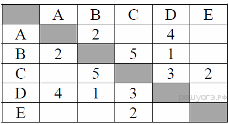
7. Задание 3 № 484. Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых приведена в таблице:
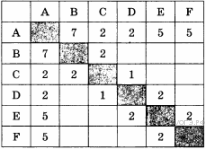
Определите длину кратчайшего пути между пунктами А и F (при условии, что передвигаться можно только по построенным дорогам).
1) 5 2) 6 3) 7 4) 4
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C, D, E, F.
Из пункта B можно попасть в пункт C.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункт E.
Из пункта E можно попасть в пункт F.
A—B—C—D—E—F: длина маршрута 14 км.
A—C—D—E—F: длина маршрута 7 км.
A—D—E—F: длина маршрута 6 км.
A—E—F: длина маршрута 7 км.
A—F: длина маршрута 5 км.
Ответ: 1
8. Задание 3 № 942. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в км) приведена в таблице.
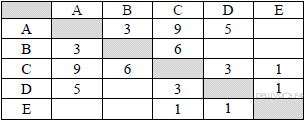
Определите длину кратчайшего пути между пунктами A и C. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 7 2) 8 3) 9 4) 12
Пояснение.
Найдём все варианты маршрутов из A в С и выберем самый короткий.
A—B—C: длина маршрута 9 км.
A—C: длина маршрута 9 км.
A—D—C: длина маршрута 8 км.
A—D—E—C: длина маршрута 7 км.
Ответ: 1
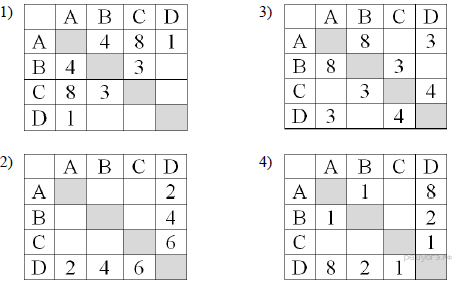
9. Задание 3 № 1034. Машинист электропоезда должен добраться из пункта А в пункт C за 4 часа. Из представленных таблиц выберите такую, согласно которой машинист сможет доехать из пункта А в пункт C за это время. В ячейках таблицы указано время (в часах), которое занимает дорога из одного пункта в другой. Передвигаться можно только по дорогам, указанным в таблицах.
Пояснение.
Найдём кратчайшие маршруты из A в С для каждой таблицы.
Исходя из первой таблицы, кратчайший маршрут из A в С: A—B—C, его можно преодолеть за 7 часов. Кратчайший маршрут из A в С для второй таблицы: A—D—С, занимает 8 часов. Для третьей таблицы кратчайшая дорога: A—D—С, она занимает 7 часов. Для четвёртой таблицы кратчайший маршрут: A—B—D—С, его можно преодолеть за 4 часа.
Ответ: 4
10. Задание 3 № 684. Сельская малокомплектная школа находится в поселке Вершки. Петя Орлов живёт в деревне Дальнее. Определите, какое минимальное расстояние ему надо пройти, чтобы добраться до школы:
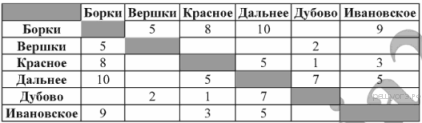
1) 6 2) 8 3) 11 4) 15
Пояснение.
Найдём все варианты маршрутов от деревни Дальнее до поселка Вершки и выберем самый короткий.
Из пункта Дальнее(Да) можно попасть в пункты Борки(Б), Красное(К), Дубово(Ду) и Ивановское(И).
Из пункта Красное(К) можно попасть в пункты Б, Ду, И .
Из пункта Вершки(В) можно попасть в пункты Б, Ду.
Из пункта Б можно попасть в пункт И.
Да—Б—В: длина маршрута 15 км.
Да—Б—К—Ду—В: длина маршрута 21 км.
Да—К—Ду—В: длина маршрута 8 км.
Да—Ду—В: длина маршрута 9 км.
Да—И—Б—В: длина маршрута 19 км.
Да—И—Б—К—Ду—В: длина маршрута 17 км.
Ответ: 2
11. Задание 3 № 841. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
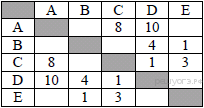
Определите длину кратчайшего пути между пунктами A и B (при условии, что передвигаться можно только по построенным дорогам).
1) 11 2) 12 3) 13 4) 14
Пояснение.
Найдём все варианты маршрутов из A в B и выберем самый короткий.
A—C—D—B: длина маршрута 13 км.
A—C—E—B: длина маршрута 12 км.
A—D—C—E—B: длина маршрута 15 км.
A—D—B: длина маршрута 14 км.
Ответ: 2
12. Задание 3 № 23. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
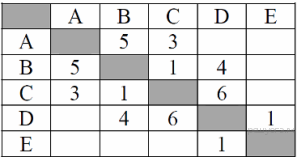
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 7 2) 8 3) 9 4) 10
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, С.
Из пункта B можно попасть в пункты C, D.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункт E.
A—B—C—D—E: длина маршрута 13 км.
A—B—D—E: длина маршрута 10 км.
A—C—D—E: длина маршрута 10 км.
A—C—B—D—E: длина маршрута 9 км.
Ответ: 3
13. Задание 3 № 323. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
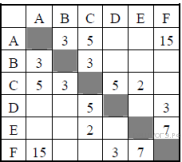
Определите длину кратчайшего пути между пунктами А и F. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 9 2) 11 3) 13 4) 15
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C, F.
Из пункта B можно попасть в пункт C.
Из пункта C можно попасть в пункты D, E.
Из пункта D можно попасть в пункт F.
Из пункта E можно попасть в пункт F.
A—F: длина маршрута 15 км.
A—B—C—E—F: длина маршрута 15 км.
A—B—C—D—F: длина маршрута 14 км.
A—C—E—F: длина маршрута 14 км.
A—C—D—F: длина маршрута 13 км.
Ответ: 3
14. Задание 3 № 83. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
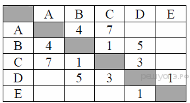
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 8 2) 9 3) 10 4) 11
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, С.
Из пункта B можно попасть в пункты C, D.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункт E.
A—B—C—D—E: длина маршрута 9 км.
A—B—D—E: длина маршрута 10 км.
A—C—D—E: длина маршрута 11 км.
Ответ: 2
15. Задание 3 № 344. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
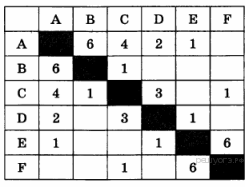
Определите длину кратчайшего пути между пунктами А и F. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 5 2) 6 3) 7 4) 4
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C, D, E .
Из пункта B можно попасть в пункт C.
Из пункта C можно попасть в пункты D, F.
Из пункта D можно попасть в пункт E.
Из пункта E можно попасть в пункт F.
A—E—F: длина маршрута 7 км.
A—B—C—F: длина маршрута 8 км.
A—C—D—E—F: длина маршрута 14 км.
A—D—E—F: длина маршрута 9 км.
A—C—F: длина маршрута 5 км.
Ответ: 1
16. Задание 3 № 404. Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых приведена в таблице:
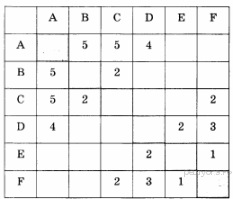
Определите длину кратчайшего пути между пунктами А и F. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 5 2) 6 3) 7 4) 9
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C, D.
Из пункта B можно попасть в пункт C.
Из пункта C можно попасть в пункт F.
Из пункта D можно попасть в пункты E, F.
Из пункта E можно попасть в пункт F.
A—B—C—F: длина маршрута 9 км.
A—C—F: длина маршрута 7 км.
A—D—E—F: длина маршрута 7 км.
A—D—F: длина маршрута 7 км.
Ответ: 3
17. Задание 3 № 243. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
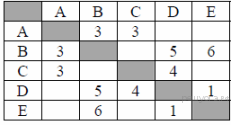
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 6 2) 7 3) 8 4) 9
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C.
Из пункта B можно попасть в пункты D, E.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункт E.
A—B—D—E: длина маршрута 9 км.
A—B—E: длина маршрута 9 км.
A—C—D—E: длина маршрута 8 км.
Ответ: 3
18. Задание 3 № 444. Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых приведена в таблице:

Определите длину кратчайшего пути между пунктами А и F. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 6 2) 7 3) 8 4) 9 Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C, F.
Из пункта B можно попасть в пункты C, D, F.
Из пункта C можно попасть в пункт E.
Из пункта E можно попасть в пункт F.
A—C—E—F: длина маршрута 8 км.
A—F: длина маршрута 7 км.
A—B—C—E—F: длина маршрута 7 км.
A—B—F: длина маршрута 7 км.
Ответ: 2
19. Задание 3 № 143. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
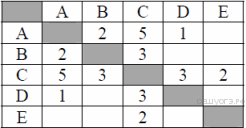
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 4 2) 5 3) 6 4) 7
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C, D.
Из пункта B можно попасть в пункт C.
Из пункта C можно попасть в пункты D, E.
A—B—C—E: длина маршрута 7 км.
A—С—E: длина маршрута 7 км.
A—D—C—E: длина маршрута 6 км.
Ответ: 3
20. Задание 3 № 1117. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
| A | B | C | D | E | |
| A | 2 | 1 | 5 | ||
| B | 2 | 4 | |||
| C | 1 | 4 | 1 | 4 | |
| D | 1 | 2 | |||
| E | 5 | 4 | 2 |
Определите длину кратчайшего пути между пунктами B и E (при условии, что передвигаться можно только по построенным дорогам).
1) 5 2) 6 3) 7 4) 8
Пояснение.
Из пункта B можно добраться в пункт C. Проанализируем некоторые возможные маршруты.
Маршрут B — C — E, длина 8 км.
Маршрут B — С — A — E, длина 10 км.
Маршрут B — A — С — D — E, длина 6 км.
Любые другие маршруты будут длиннее маршрута B — A — С — D — E. Таким образом, кратчайшее расстояние между пунктами B и E составляет 6 км.
Ответ: 2
21. Задание 3 № 364. Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых приведена в таблице:
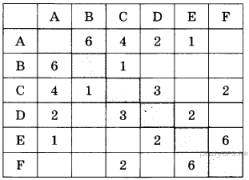
Определите длину кратчайшего пути между пунктами А и F. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 5 2) 6 3) 7 4) 4
Пояснение.
Найдём все варианты маршрутов из A в F и выберем самый короткий.
A-B-C-D-E-F: длина маршрута 18 км.
A-B-C-F: длина маршрута 9 км.
A-C-D-E-F: длина маршрута 15 км.
A-C-F: длина маршрута 6 км.
A-D-C-F: длина маршрута 7 км.
A-D-E-F: длина маршрута 10 км.
A-E-D-C-F: длина маршрута 8 км.
A-E-F: длина маршрута 7 км.
Кратчайший маршрут имеет длину 6 км.
Ответ: 2
22. Задание 3 № 922. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
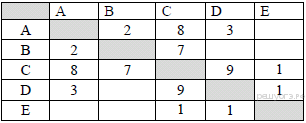
Определите длину кратчайшего пути между пунктами A и C. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 3 2) 5 3) 8 4) 9
Пояснение.
Найдём все варианты маршрутов из A в С и выберем самый короткий.
A—B—C: длина маршрута 9 км.
A—C: длина маршрута 8 км.
A—D—C: длина маршрута 12 км.
A—D—E—C: длина маршрута 5 км.
Ответ: 2
23. Задание 3 № 163. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
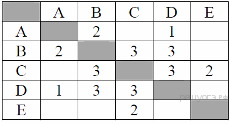
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 6 2) 7 3) 8 4) 9
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, D.
Из пункта B можно попасть в пункты C, D.
Из пункта C можно попасть в пункты D, E.
A—B—C—E: длина маршрута 7 км.
A—D—B—C—E: длина маршрута 9 км.
A—D—C—E: длина маршрута 6 км.
Ответ: 1
24. Задание 3 № 63. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
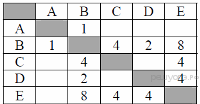
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 5 2) 6 3) 7 4) 9
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункт B.
Из пункта B можно попасть в пункты C, D, E.
Из пункта C можно попасть в пункт E.
Из пункта D можно попасть в пункт E.
A—B—C—E: длина маршрута 9 км.
A—B—E: длина маршрута 9 км.
A—B—D—E: длина маршрута 7 км.
Ответ: 3
25. Задание 3 № 966. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в км) приведена в таблице.
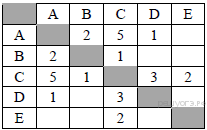
Определите длину кратчайшего пути между пунктами A и Е. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 4 2) 5 3) 6 4) 7
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
A—B—C—E: длина маршрута 5 км.
A—C—E: длина маршрута 7 км.
A—D—C—E: длина маршрута 8 км.
Ответ: 2
26. Задание 3 № 504. Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых приведена в таблице:
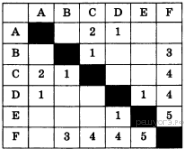
Определите длину кратчайшего пути между пунктами А и F (при условии, что передвигаться можно только по построенным дорогам).
1) 5 2) 7 3) 3 4) 9
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты C, D.
Из пункта B можно попасть в пункты C, F.
Из пункта C можно попасть в пункт F.
Из пункта D можно попасть в пункты E, F.
Из пункта E можно попасть в пункт F.
A—C—F: длина маршрута 6 км.
A—C—B—F: длина маршрута 6 км.
A—D—E—F: длина маршрута 7 км.
A—D—F: длина маршрута 5 км.
Ответ: 1
27. Задание 3 № 584. У Пети Иванова родственники живут в 5 разных городах России. Расстояния между городами внесены в таблицу:
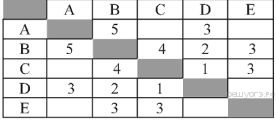
Петя перерисовал её в блокнот в виде графа. Считая, что мальчик не ошибся при копировании, укажите, какой граф у Пети в тетради.
1) 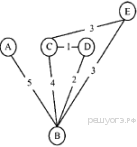 2)
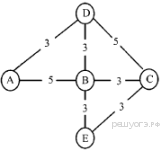
2) 
3) 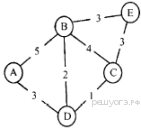 4)
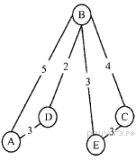
4) 
Пояснение.
Проверим последовательно каждый граф.
1) Не соответствует таблице, поскольку согласно графу не существует прямой дороги из пункта A в пункт D.
2) Не соответствует таблице, поскольку согласно графу расстояние между пунктами D и B равно 3.
3) Граф соответствует таблице.
4) Не соответствует таблице, поскольку согласно графу не существует прямой дороги из пункта D в пункт C.
Ответ: 3
28. Задание 3 № 564. Иван-Царевич спешит выручить Марью-Царевну из плена Кощея. В таблице указана протяжённость дорог между пунктами, через которые он может пройти. Укажите длину самого короткого участка кратчайшего пути от Ивана-Царевича до Марьи Царевны (от точки И до точки М). Передвигаться можно только по дорогам, указанным в таблице:
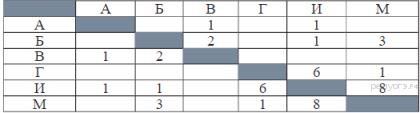
1) 1 2) 2 3) 3 4) 4
Пояснение.
Найдём все варианты маршрутов из И в М и выберем самый короткий.
Из пункта И можно попасть в пункты А, Б, Г, М.
Из пункта Г можно попасть в пункты И, М.
Из пункта В можно попасть в пункты А, Б.
Из пункта Б можно попасть в пункты В, И, М.
И—А—В—Б—М: длина маршрута 7 км.
И—Б—М: длина маршрута 4 км.
И—Г—М: длина маршрута 7 км.
И—М: длина маршрута 8 км.
Самый короткий путь: И—Б—М; Длина маршрута 4 км, самый короткий участок этого пути равен 1.
Ответ: 1
29. Задание 3 № 1097. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
| A | B | C | D | E | |
| A | 1 | 5 | 2 | ||
| B | 1 | 6 | |||
| C | 5 | 1 | 7 | ||
| D | 6 | 1 | |||
| E | 2 | 7 |
Определите длину кратчайшего пути между пунктами A и D (при условии, что передвигаться можно только по построенным дорогам).
1) 5 2) 6 3) 7 4) 8
Пояснение.
Из пункта A можно добраться в пункты B, C и D. Проанализируем некоторые возможные маршруты.
Маршрут A — B — D, длина 7 км.
Маршрут A — С — D, длина 6 км.
Маршрут A — E — С — D явно длиннее маршрута A — С — D.
Любые другие маршруты будут длиннее маршрута A — С — D. Таким образом, кратчайшее расстояние между пунктами A и D составляет 6 км.
Ответ: 2
30. Задание 3 № 43. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
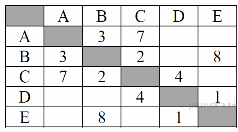
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 9 2) 10 3) 11 4) 12
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, С.
Из пункта B можно попасть в пункты C, E.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункт E.
A—B—C—D—E: длина маршрута 10 км.
A—B—E: длина маршрута 11 км.
A—C—D—E: длина маршрута 12 км.
Ответ: 2
31. Задание 3 № 664. Сельская малокомплектная школа находится в поселке Ивановское. Коля Иванов живёт в деревне Вершки. Определите, какое минимальное расстояние ему надо пройти, чтобы добраться до школы:
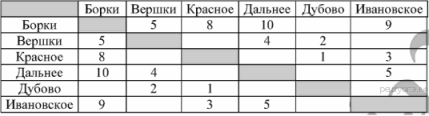
1) 6 2) 9 3) 12 4) 14
Пояснение.
Найдём все варианты маршрутов от деревни Вершки до поселка Ивановское и выберем самый короткий.
Из пункта Вершки(В) можно попасть в пункты Борки(Б), Дальнее(Да) и Дубово(Ду).
Из пункта Б можно попасть в пункты Красное(К), Да, Ивановское(И).
Из пункта К можно попасть в пункты Ду, И.
Из пункта Да можно попасть в пункт И.
В—Б—К—И: длина маршрута 16 км.
В—Б—Да—И: длина маршрута 20 км.
В—Б—И: длина маршрута 14 км.
В—Да—И: длина маршрута 9 км.
В—Ду—К—И: длина маршрута 6 км.
Ответ: 1
32. Задание 3 № 103. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
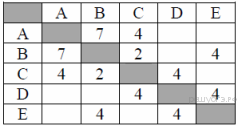
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 9 2) 10 3) 11 4) 12
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, С.
Из пункта B можно попасть в пункты C, E.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункт E.
A—B—C—D—E: длина маршрута 17 км.
A—B—E: длина маршрута 11 км.
A—C—D—E: длина маршрута 12 км.
A—C—B—E: длина маршрута 10 км.
Ответ: 2
33. Задание 3 № 123. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
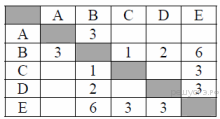
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 9 2) 8 3) 7 4) 6
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункт B.
Из пункта B можно попасть в пункты C, D, E.
Из пункта C можно попасть в пункт E.
Из пункта D можно попасть в пункт E.
A—B—C—E: длина маршрута 7 км.
A—B—D—E: длина маршрута 8 км.
A—B—E: длина маршрута 9 км.
Ответ: 3
34. Задание 3 № 819. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
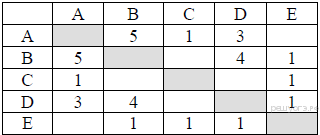
Определите длину кратчайшего пути между пунктами A и B. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 1 2) 5 3) 3 4) 7
Пояснение.
Искать следует маршрут, длина которого не превышает 5 км, поскольку длина A—B составляет 5 км. Рассмотрим маршруты:
A—C—E—B: длина маршрута 3 км,
A—D—B: длина маршрута 7 км,
A—D—E—B: длина маршрута 5 км.
Ответ: 3
35. Задание 3 № 861. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
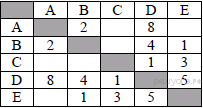
Определите длину кратчайшего пути между пунктами A и C (при условии, что передвигаться можно только по построенным дорогам).
1) 6 2) 7 3) 8 4) 9
Пояснение.
Найдём все варианты маршрутов из A в C и выберем самый короткий.
A—B—D—E—C: длина маршрута 14 км.
A—B—D—C: длина маршрута 7 км.
A—B—E—C: длина маршрута 6 км.
A—D—C: длина маршрута 9 км.
Ответ: 1
36. Задание 3 № 747. Водитель автомобиля должен добраться из пункта А в пункт D за 5 часов. Из представленных таблиц выберите такую, согласно которой водитель сможет доехать из пункта А в пункт D за это время. В ячейках таблицы указано время (в часах), которое занимает дорога из одного пункта в другой. Передвигаться можно только по дорогам, указанным в таблицах.
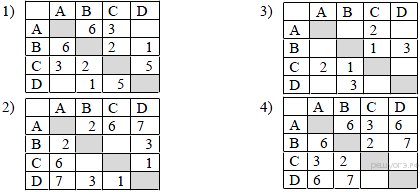
1) 1 2) 2 3) 3 4) 4
Пояснение.
Найдём кратчайшие маршруты из A в D для каждой таблицы.
Исходя из первой таблицы, кратчайший маршрут из A в D: A—C—B—D, его можно преодолеть за 6 часов. Кратчайший маршрут из A в D для второй таблицы: A—B—D, его можно преодолеть за 5 часов. Для третьей таблицы кратчайшая дорога: A—C—B—D, она занимает 6 часов. Для четвёртой таблицы кратчайший маршрут: A—D, его можно преодолеть за 6 часов.
Ответ: 2
37. Задание 3 № 624. Учитель Иван Петрович живёт на станции Антоновка, а работает на станции Дружба. Чтобы успеть с утра на уроки, он должен ехать по самой короткой дороге. Проанализируйте таблицу и укажите длину кратчайшего пути от станции Антоновка до станции Дружба:
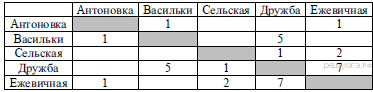
1) 6 2) 2 3) 8 4) 4
Пояснение.
Найдём все варианты маршрутов из Антоновки в Дружбу и выберем самый короткий.
Из пункта Антоновка(А) можно попасть в пункты Васильки(В), Ежевичная(Е).
Из пункта B можно попасть в пункт Дружба(Д).
Из пункта Сельская(С) можно попасть в пункты Д, Е.
Из пункта Д можно попасть в пункт Е.
А—В—Д: длина маршрута 6 км.
А—Е—Д: длина маршрута 8 км.
А—Е—С—Д: длина маршрута 4 км.
Ответ: 4
38. Задание 3 № 283. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
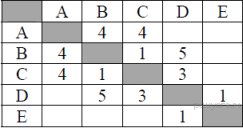
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 7 2) 8 3) 9 4) 10
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C.
Из пункта B можно попасть в пункты C, D.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункт E.
A—B—C—D—E: длина маршрута 9 км.
A—C—D—E: длина маршрута 8 км.
A—B—D—E: длина маршрута 10 км.
Ответ: 2
39. Задание 3 № 799. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
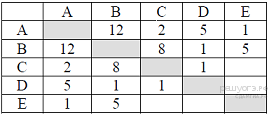
Определите длину кратчайшего пути между пунктами A и B. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 4 2) 6 3) 10 4) 12
Пояснение.
Искать следует маршрут, длина которого не превышает 12 км, поскольку длина A—B составляет 12 км. Рассмотрим маршруты:
A—C—B: длина маршрута 10 км,
A—D—B: длина маршрута 6 км,
A—E—B: длина маршрута 6 км,
A—C—D—B: длина маршрута 4 км.
Ответ: 1
40. Задание 3 № 544. Иван-Царевич спешит выручить Марью-Царевну из плена Кощея. В таблице указана протяжённость дорог между пунктами, через которые он может пройти. Укажите длину самого длинного участка кратчайшего пути от Ивана-Царевича до Марьи Царевны (от точки И до точки М). Передвигаться можно только по дорогам, указанным в таблице:
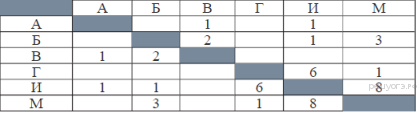
1) 1 2) 2 3) 3 4) 6
Пояснение.
Найдём все варианты маршрутов из И в М и выберем самый короткий.
Из пункта И можно попасть в пункты А, Б, Г, М.
Из пункта Г можно попасть в пункты И, М.
Из пункта В можно попасть в пункты А, Б.
Из пункта Б можно попасть в пункты В, И, М.
И—А—В—Б—М: длина маршрута 7 км.
И—Б—М: длина маршрута 4 км.
И—Г—М: длина маршрута 7 км.
И—М: длина маршрута 8 км.
Самый короткий путь: И—Б—М; Длина маршрута 4 км, самый длинный участок этого пути равен 3.
Ответ: 3
41. Задание 3 № 1137. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
| A | B | C | D | E | |
| A | 5 | 6 | 10 | 5 | |
| B | 5 | 4 | |||
| C | 6 | 2 | 7 | ||
| D | 10 | 4 | 2 | 5 | |
| E | 5 | 7 | 5 |
Определите длину кратчайшего пути между пунктами A и D. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 14 2) 10 3) 9 4) 8
Пояснение.
Из пункта A можно добраться в пункты B, C и D. Проанализируем некоторые возможные маршруты.
Маршрут A — B — D, длина 9 км.
Маршрут A — С — D, длина 8 км.
Маршрут A — D, длина 10 км.
Любые другие маршруты будут длиннее маршрута A — С — D. Таким образом, кратчайшее расстояние между пунктами A и D составляет 8 км.
Ответ: 4
42. Задание 3 № 424. Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых приведена в таблице:
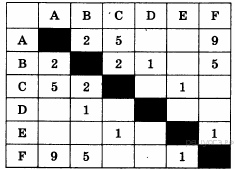
Определите длину кратчайшего пути между пунктами А и F. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 6 2) 7 3) 8 4) 9
Пояснение.
Найдём все варианты маршрутов из A в F и выберем самый короткий.
Из пункта A можно попасть в пункты B, C, F.
Из пункта B можно попасть в пункты C, D, F.
Из пункта C можно попасть в пункт E.
Из пункта E можно попасть в пункт F.
A—C—E—F: длина маршрута 7 км.
A—F: длина маршрута 9 км.
A—B—C—E—F: длина маршрута 6 км.
A—B—F: длина маршрута 7 км.
Ответ: 1
43. Задание 3 № 1074. В таблице приведена стоимость перевозок между пятью железнодорожными станциями, обозначенными буквами A, B, C, D и E. Укажите схему, соответствующую таблице.
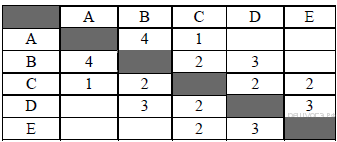
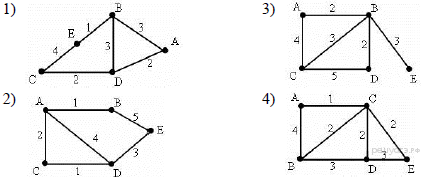

Пояснение.
Из таблицы видно, что из пункта A есть дороги только в пункты B и C. Следовательно, подходят только варианты 3 и 4. Расстояние между пунктами A и C — 1, таким образом, подходит только вариант 4.
Ответ: 4
44. Задание 3 № 704. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых(в километрах) приведена в таблице.
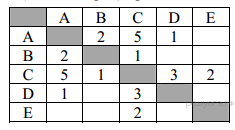
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 4 2) 5 3) 6 4) 7
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C, D.
Из пункта B можно попасть в пункт C.
Из пункта C можно попасть в пункты D, E.
A—B—C—E: длина маршрута 5 км.
A—С—E: длина маршрута 7 км.
A—D—C—E: длина маршрута 6 км.
Ответ: 2
45. Задание 3 № 1054. В таблице приведена стоимость перевозок между пятью железнодорожными станциями, обозначенными буквами A, B, C, D и E. Укажите схему, соответствующую таблице.
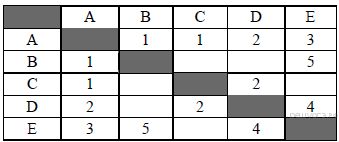
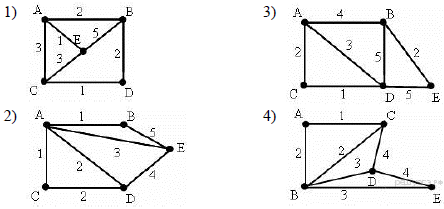

Пояснение.
Из таблицы видно, что из пункта A есть дороги в любой другой пункт. Следовательно, подходит только вариант 2.
Ответ: 2
46. Задание 3 № 1157. Между населёнными пунктами A, B, C, D построены дороги, протяжённость которых (в километрах) приведена в таблице.
| A | B | C | D | |
| A | 2 | 7 | 4 | |
| B | 2 | 5 | 1 | |
| C | 7 | 5 | 2 | |
| D | 4 | 1 | 2 |
Определите длину кратчайшего пути между пунктами A и C. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 4 2) 5 3) 6 4) 7
Пояснение.
Из пункта A можно добраться в пункты B, C и D. Проанализируем некоторые возможные маршруты.
Маршрут A — B — C, длина 7 км.
Маршрут A — D — C, длина 6 км.
Маршрут A — B — D — C, длина 5 км.
Любые другие маршруты будут длиннее маршрута A — B — D — C. Таким образом, кратчайшее расстояние между пунктами A и C составляет 5 км.
Ответ: 2
47. Задание 3 № 604. У Кати Евтушенко родственники живут в 5 разных городах России. Расстояния между городами внесены в таблицу:
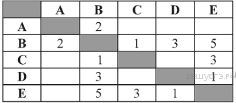
Катя перерисовала её в блокнот в виде графа. Считая, что девочка не ошиблась при копировании, укажите, какой граф у Кати в тетради.
1) 2)
3) 4)
Пояснение.
Проверим последовательно каждый граф.
1) Не соответствует таблице, поскольку согласно графу не существует прямой дороги из пункта C в пункт E.
2) Граф соответствует таблице.
3) Не соответствует таблице, поскольку согласно графу не существует прямой дороги из пункта D в пункт B.
4) Не соответствует таблице, поскольку согласно графу не существует прямой дороги из пункта B в пункт E.
Ответ: 2
48. Задание 3 № 303. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 13 2) 12 3) 11 4) 10
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C.
Из пункта B можно попасть в пункты C, E.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункт E.
A—B—C—D—E: длина маршрута 18 км.
A—B—E: длина маршрута 12 км.
A—C—D—E: длина маршрута 13 км.
А—С—В—Е: длина маршрута 11 км.
Ответ: 3
49. Задание 3 № 902. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами A и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 4 2) 6 3) 8 4) 10
Пояснение.
Найдём все варианты маршрутов из A в D и выберем самый короткий.
A—B—C—E: длина маршрута 6 км.
A—B—D—E: длина маршрута 12 км.
A—D—E: длина маршрута 16 км.
Ответ: 2
50. Задание 3 № 263. Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 4 2) 5 3) 6 4) 7
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C, D.
Из пункта B можно попасть в пункт C.
Из пункта C можно попасть в пункты D, E.
A—B—C—E: длина маршрута 5 км.
A—C—E: длина маршрута 7 км.
A—D—C—E: длина маршрута 6 км.
Ответ: 2
| № | Ответ | № | Ответ | |
| 1 | 26 | |||
| 2 | 27 | |||
| 3 | 28 | |||
| 4 | 29 | |||
| 5 | 30 | |||
| 6 | 31 | |||
| 7 | 32 | |||
| 8 | 33 | |||
| 9 | 34 | |||
| 10 | 35 | |||
| 11 | 36 | |||
| 12 | 37 | |||
| 13 | 38 | |||
| 14 | 39 | |||
| 15 | 40 | |||
| 16 | 41 | |||
| 17 | 42 | |||
| 18 | 43 | |||
| 19 | 44 | |||
| 20 | 45 | |||
| 21 | 46 | |||
| 22 | 47 | |||
| 23 | 48 | |||
| 24 | 49 | |||
| 25 | 50 |
Авторы: Дорофеев Г. В., Шарыгин И. Ф., Суворова С. Б..
Издательство:
Просвещение 2015-2020
Тип: Учебник
Подробный решебник (ГДЗ) по Математике за 5 (пятый) класс — готовый ответ номер — 524. Авторы учебника: Дорофеев, Шарыгин, Суворова. Издательство: Просвещение 2015-2020.
Авторы:
С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин
Издательство:
Просвещение 2016-2019
Тип книги: Учебник
Подробное решение задание № 524 по математике для учащихся 5 класса , авторов Никольский, Потапов, Решетников, Шевкин 2016-2019
-
Готовые домашние задания
-
6 класс -
Математика -
Ткачёва -
524
Показать содержание
- ГДЗ к рабочей тетради по математике за 6 класс Ткачёва М.В. можно найти тут
Решебник/ упражнение номер / 524
ГДЗ
/
Решебники
/
4 класс
/
Информатика
/
Горячев
/
Задание 4.24
ГДЗ(готовые домашние задания), решебник онлайн к учебнику по информатике часть 1, 2 за 4 класс автор Горячев раздел 4 задание(номер) 24 — вариант решения задания 24 раздела 4
Раздел 1:
1
2
3
4
5
8
9
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Контрольная работа, вариант 1
Контрольная работа, вариант 2
Раздел 2:
1
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
Раздел 3:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
Контрольная работа, вариант 1
Контрольная работа, вариант 2
1
2
3
5
6
7
8
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
30
31
33
Контрольная работа, вариант 1
Контрольная работа, вариант 2
© Copyright 2021
Правообладателям
О проекте
resheba-na5@yandex.ru
ИНФОРМАТИКА.
ЛАБОРАТОРНЫЕ РАБОТЫ
СЕМЕСТР
2
Гр.
РТ1101-03 Лектор Мацкевич А.Г.
Номера
задач из задачника: Абрамов.«Задачи по
программированию»
Таб.
1
| № | Модули, | Строки | Текст. файлы | Типиз. файлы | Строки | Графика, окна, |
| 1 | 628а,628б | 251,814в | 501а | 506а,б | 814в | 1 |
| 2 | 628а,628в | 252,820-3 | 502а | 506в,г | 820-3 | 2 |
| 3 | 628а,633 | 253а,б,820-2 | 502б | 506д,е | 820-2 | 3 |
| 4 | 628а,636 | 254,820-1 | 503 | 507а,б | 820-1 | 4 |
| 5 | 628а,642 | 255,819 | 504а | 507в,г | 819 | 5 |
| 6 | 628б,628в | 256,817 | 504б | 507ж | 817 | 6 |
| 7 | 628б,633 | 257а,б,816 | 504в | 508а | 816 | 7 |
| 8 | 628б,636 | 257г,д,815 | 504г | 508б | 815 | 8 |
| 9 | 628б,642 | 258,818 | 518 | 509а | 818 | 9 |
| 10 | 642,628а | 259,814а,б | 519а | 510 | 814 | 10 |
| 11 | 636,628а | 260а,б,813 | 519б | 511а | 813 | 11 |
| 12 | 633,628а | 261,812д,е | 520 | 512 | 812 | 12 |
| 13 | 628в,628а | 262,812в,г | 521 | 513а | 812 | 13 |
| 14 | 628б,628а | 263,811 | 522 | 514а | 811 | 14 |
| 15 | 628б,628в | 264,810 | 523а | 515 | 810 | 15 |
| 16 | 628б,633 | 265,809 | 523б | 516 | 809 | 16 |
| 17 | 628б,636 | 266,808в,г | 524 | 517а,б | 808 | 17 |
| 18 | 628б,642 | 267,808а,б | 525 | 517д,е | 808 | 18 |
| 19 | 628а,628б | 268,807 | 526 | 517ж | 807 | 19 |
| 20 | 628а,628в | 269а,б,806 | 527 | 517в,г | 806 | 20 |
| 21 | 628а,633 | 269в,г,805 | 528 | 514б | 805 | 21 |
| 22 | 628а,636 | 269д,е,804 | 529а | 513б | 804 | 22 |
| 23 | 628а,642 | 270а,б,803 | 530а | 511б | 803 | 23 |
| 24 | 628б,628в | 270в,г,802 | 530б | 509б | 802 | 24 |
| 25 | 628б,633 | 270д,812а,б | 530в | 507д,е | 812 | 25 |
(1)
Модули,
сортировка
Написать подпрограммы,
реализующие методы сортировки из таб.1
. Организовать модуль ( unit
) с этими подпрограммами. Написать
программу для сортировки массива из
50-100 элементов этими методами. Сравнить
методы сортировки по количеству
перестановок и количеству сравнений.
Сделать выводы.
Алгоритмы
сортировки массива.
( Номера соответствуют
задачам из «Задачи по программированию
». С.А. Абрамов. 1988 г.)
№628а. (Сортировка
выбором)
Найти элемент
массива, имеющий наименьшее значение,
переставить его с первым элементом,
затем проделать то же самое, начав со
второго элемента и т.д.
№628б. (Сортировка
обменами, метод пузырька)
Последовательным
просмотром чисел а1,
…, аn
найти наименьшее i
такое, что аi
> ai+1
. Поменять ai
и аi+1
местами, возобновить просмотр с элемента
ai+1
и т.д. Тем самым наибольшее число
передвигается на последнее место.
Следующие просмотры начинать опять с
начала, уменьшая на единицу количество
просматриваемых элементов. Массив будет
упорядочен после просмотра, в котором
участвовали только первый и второй
элементы.
№628в (Сортировка
простыми вставками)
Просматривать
последовательность а1,
…, аn
и каждый новый элемент ai
вставлять на подходящее место в уже
упорядоченную совокупность а1,
…, аi-1.
Это место определяется последовательны
сравнением аi
с упорядоченными элементами а1,
…, аi-1.
№633 (Сортировка
бинарными вставками)
Алгоритм упорядочения
простыми вставками (№628в) можно изменить
следующим образом. Место, на которое
надо вставить аi
в уже упорядоченную совокупность а1,
…, аi-1
определяется алгоритмом деления пополам.
Для этого надо взять первоначально 1 и
i
в качестве границ поиска места элемента.
Далее, до тех пор, пока границы не
совпадут, шаг за шагом сдвигать эти
границы следующим образом: сравнить
ai
с as
, где s
–целая часть среднего арифметического
границ. Если as
< ai
, то заменить прежнюю нижнюю границу
на s+1,
а верхнюю оставить без изменения, иначе
оставить без изменения нижнюю границу,
а верхнюю заменить на s.
Когда границы совпадут, став равными
некоторому числу t,
выполнение алгоритма закончиться с
результатом t.
№636 (Алгоритм фон
Неймана, сортировка слияниями)
Алгоритм фон
Неймана упорядочивания массива a1,
a2,
…,an
по не убыванию основан на многократных
слияниях уже упорядоченных групп
элементов массива. Вначале весь массив
рассматривается как совокупность
упорядоченных групп по одному элементу
в каждом. Слияниям соседних групп
получаем упорядоченные группы, каждая
из которых содержит два элемента ( кроме,
может быть, последней группы, которой
не нашлось парной). Далее упорядоченные
группы укрупняются тем же способом и
т.д. Здесь приходится оперировать не
только с массивом a1,
a2,…,an,
но и с вспомогательным массивом
b1,b2,…,bn.
№642 ( Сортировка
обменами 2)
Последовательным
просмотром чисел a1,a2,…,an
найти наименьшее i
такое, что ai>ai+1.
Поменять ai
и ai+1
местами возобновить просмотр с начала
массива. Когда не удается найти такое
i,
массив будет упорядочен.
(2)
Задание будет уточнено позже.
Соседние файлы в предмете Информатика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
валера8501 / 20 февр. 2015 г., 16:15:31
очередь. Если бы Митя встал посередине очереди, то он стоял бы между Серёжай и Костей, причём Костя стоял бы впереди Мити, а если бы Юра. Но Митя встал впереди своих товарищей. Кто за кем стоит?
2 Задание Пятеро однакласников Аня, Саша, Лена, Вася и Миша стали победителями олимпиад школьников по истроии, математике, информатеки, летературе и географии. Известно, что:
1) Победитель олимпиады по информатике учит Аню и Сашу работе на компьюторе
2) Лена и Вася тоже заинтересовались информатикой
3) Саша всегда побаивался истории
4) Лена, Саша и победитель олимпиады по летературы занимаются плаванием
5)Саша и Лена поздравили победителя олимпиады по математике
6) Аня сожалеет о том, что у нее остаётся мало времени на летературу.
Побидителем какой олимпиады стал каждый из этих ребят?
Поиогите решить спасибо только правильно
6класс
Дорофеев, Шарыгин
Просвещение, 2021
В избранное
Отношения и проценты. 6.3. «Главная» задача на проценты. Номер №524
Номер №523
Номер №525
Номер №523
Номер №525
Смотрите ещё задания из учебника:
518
519
520
521
522
526
527
528
529
530
… смотреть все номера
6 класс
Spotlight Student’s book
Английский язык
Смотреть
6 класс
Кузовлев Activity book — рабочая тетрадь
Английский язык
Смотреть
6 класс
Сонин, Сонина — рабочая тетрадь
Биология
Смотреть
6 класс
Пасечник, Суматохин — рабочая тетрадь
Биология
Смотреть
6 класс
Босова — рабочая тетрадь
Информатика
Смотреть
6 класс
Ладыженская, Баранов, Тростенцова
Русский язык
Смотреть
6 класс
Рыбченкова, Александрова
Русский язык
Смотреть
Задания C4 по информатике
1. Дан список результатов сдачи экзамена учащимися школ некоторого района, с
указанием фамилии и имени учащегося, номера школы и итогового балла.
Напишите эффективную по времени работы и по используемой памяти
программу (укажите используемую версию языка программирования, например,
Borland Pascal 7.0), которая определяет номера школ, имеющих наибольший
средний балл, показанный выпускниками данной школы на экзамене. На вход
программе в первой сроке подается количество учащихся во всех школах района
N. В каждой из последующих N строк находится информация в следующем
формате: <Фамилия> <Имя> <Номер школы> <Балл>
где <Фамилия> – строка, состоящая не более, чем из 20 символов без
пробелов,
<Имя> – строка, состоящая не более, чем из 20 символов без пробелов,
<Номер школы> – число от 1 до 99,
<Балл> — число от 0 до 100.
Порядок следования строк – произвольный.
Пример входных данных:
6
Иванов Сергей 7 70
Сергеев Петр 3 65
Петров Кирилл 7 68
Кириллов Егор 3 75
Егоров Николай 7 71
Николаев Иван 19 70
Программа должна вывести номера школ, имеющих наибольший
средний балл, показанный на экзамене выпускниками этой школы.
Пример вывода для приведенного выше примера ввода:
3
19
При выполнении задания следует учитывать, что значение N может
быть велико (до 10 000).
Содержание верного ответа и указания по оцениванию
(допускаются иные формулировки ответа, не искажающие его
смысла)
Создадим два массива с индексами от 1 до 99, соответствующих номерам школ и
будем хранить в этих массивах количество выпускников из этой школы, сдававших
экзамен и суммарный балл выпускников этой школы. Программа читает все
входные данные один раз. После считывания фамилии, имени, номера школы и
балла считанное значение прибавляется к суммарному баллу для данной школы, а
количество выпускников из этой школы, сдававших экзамен, увеличиваем на 1.
После окончания считывания данных проходим циклом от 1 до 99 по всем школам и
определяем максимальный средний балл по всем школам. Затем во втором цикле
выводим номера школ, средний балл в которых равен максимальному. Ниже
приведены примеры решения задания на языках Паскаль и C++. Допускаются
решения, записанные на других языках программирования. При оценивании
решений на других языках программирования необходимо учитывать особенности
этих языков программирования. Решение на языке Паскаль
var
SchoolSum, SchoolCount: array[1..99] of integer;
i, N, School, Ball, MaxI: integer;
Max: extended;
c: char;
begin
for i:=1 to 99 do
begin
SchoolSum[i] := 0;
SchoolCount[i] := 0
end;
Readln(N);
for i:=1 to N do
begin
repeat
Read(c)
until c=’ ‘;
repeat
Read(c)
until c=’ ‘;
Readln(School, Ball);
SchoolSum[School] := SchoolSum[School] + Ball;
SchoolCount[School] := SchoolCount[School] + 1;
end;
Max:=-1;
for i:=1 to 99 do
if (SchoolCount[i] > 0) and (SchoolSum[i] / SchoolCount[i]
> Max)
then
begin
Max := SchoolSum[i] / SchoolCount[i];
MaxI := i
end;
for i:=1 to 99 do
if (SchoolCount[i]>0) and (SchoolSum[i]*SchoolCount[MaxI]=
SchoolSum[MaxI]*SchoolCount[i])
then
WriteLn(i)
end.
Решение на языке C++
#include<iostream>
#include<string>
using namespace std;
int main()
{
int SchoolSum[100];
int SchoolCount[100];
int i, N, School, Ball, MaxI;
double Max;
string Name;
for (i = 1; i <= 99; ++i)
SchoolSum[i] = SchoolCount[i] = 0;
cin >> N;
for (i = 0; i < N; ++i)
{
cin >> Name >> Name >> School >> Ball;
SchoolSum[School] += Ball;
SchoolCount[School]++;
}
Max=-1;
for(i=1;i<=99;++i)
if (SchoolCount[i]>0 && (double)SchoolSum[i]/SchoolCount
[i]>Max)
{
Max=(double)SchoolSum[i]/SchoolCount[i];
MaxI=i;
}
for(i=1;i<=99;++i)
if (SchoolCount[i]>0 && SchoolSum[i]*SchoolCount[MaxI]=
SchoolSum[MaxI]*SchoolCount[i])
cout << i << endl;
return 0;
}
Указания по оцениванию Балл
Программа работает верно для любых входных данных
произвольного размера и находит ответ, не сохраняя входные данные
в массиве, размер которого соответствует числу N (количество
человек в списке). Программа просматривает входные данные один
раз, сохраняя только информацию о cуммарном балле и количестве
выпускников в каждой школе. Допускается наличие в тексте
программы одной синтаксической ошибки: пропущен или неверно
указан знак пунктуации, неверно написано или пропущено
зарезервированное слово языка программирования, не описана или
неверно описана переменная, применяется операция, недопустимая
для соответствующего типа данных (если одна и та же ошибка
встречается несколько раз, то это считается за одну ошибку).
4
Программа работает верно, но входные данные запоминаются в
массиве, размер которого не меньше N или входные данные
считываются несколько раз. Допускается наличие от одной до трех
синтаксических ошибок. Возможно, в принципиально верно
организованном вводе данных есть одна ошибка. Три балла также
выставляется, если в эффективной программе, удовлетворяющей
критериям выставления 4 баллов, есть одна алгоритмическая ошибка
(например, отсутствует вывод результата при правильном его
нахождении).
3
Программа работает в целом верно, эффективно или нет, но, в
реализации алгоритма содержатся до двух ошибок (неверная
инициализация переменных, в частности значения максимума, выход
за границу массива, перевод символов в числа, используется знак “<”
вместо “<=”, “or” вместо “and” и т.п.). Возможно, некорректно
организовано считывание входных данных. Допускается наличие от
одной до пяти синтаксических ошибок, описанных выше.
2
Программа, возможно, неверно работает при некоторых входных
данных, например, выдает правильный ответ только в том случае,
если школа с максимальным средним баллом только одна. Возможно,
неверно организовано считывание данных и отсутствует вывод
результата. Допускается до 4 различных ошибок в реализации
алгоритма, в том числе описанных в критериях присвоения двух
баллов. Допускается наличие от одной до семи синтаксических
ошибок, описанных выше.
1
Задание не выполнено или выполнено неверно 0
2. Дан список результатов сдачи экзамена учащимися школ некоторого района, с
указанием фамилии и имени учащегося, номера школы и итогового балла.
Напишите эффективную по времени работы и по используемой памяти
программу (укажите используемую версию языка программирования, например,
Borland Pascal 7.0), которая определяет номера школ, имеющих наименьший
средний балл, показанный выпускниками данной школы на экзамене. На вход
программе в первой сроке подается количество учащихся во всех школах района
N. В каждой из последующих N строк находится информация в следующем
формате:
<Фамилия> <Имя> <Номер школы> <Балл>
где <Фамилия> – строка, состоящая не более, чем из 20 символов без
пробелов,
<Имя> – строка, состоящая не более, чем из 20 символов без
пробелов,
<Номер школы> – число от 1 до 99,
<Балл> — число от 0 до 100.
Порядок следования строк – произвольный.
Пример входных данных:
6
Иванов Сергей 7 70
Сергеев Петр 3 68
Петров Кирилл 7 75
Кириллов Егор 3 72
Егоров Николай 7 72
Николаев Иван 19 70
Программа должна вывести номера школ, имеющих наименьший
средний балл, показанный на экзамене выпускниками этой школы.
Пример вывода для приведенного выше примера ввода:
3 19
При выполнении задания следует учитывать, что значение N может
быть велико (до 10 000).
Содержание верного ответа и указания по оцениванию
(допускаются иные формулировки ответа, не искажающие его
смысла)
Создадим два массива с индексами от 1 до 99, соответствующих номерам школ и
будем хранить в этих массивах количество выпускников из этой школы, сдававших
экзамен и суммарный балл выпускников этой школы. Программа читает все
входные данные один раз. После считывания фамилии, имени, номера школы и
балла считанное значение прибавляется к суммарному баллу для данной школы, а
количество выпускников из этой школы, сдававших экзамен, увеличиваем на 1.
После окончания считывания данных проходим циклом от 1 до 99 по всем школам и
определяем минимальный средний балл по всем школам. Затем во втором цикле
выводим номера школ, средний балл в которых равен минимальному. Ниже
приведены примеры решения задания на языках Паскаль и C++. Допускаются
решения, записанные на других языках программирования. При оценивании
решений на других языках программирования необходимо учитывать особенности
этих языков программирования. Решение на языке Паскаль
var
SchoolSum, SchoolCount: array[1..99] of integer;
i, N, School, Ball, MinI: integer;
Min: extended;
c: char;
begin
for i:=1 to 99 do
begin
SchoolSum[i] := 0;
SchoolCount[i] := 0
end;
Readln(N);
for i:=1 to N do
begin
repeat
Read(c)
until c=’ ‘;
repeat
Read(c)
until c=’ ‘;
Readln(School, Ball);
SchoolSum[School] := SchoolSum[School] + Ball;
SchoolCount[School] := SchoolCount[School] + 1;
end;
Min:=101;
for i:=1 to 99 do
if (SchoolCount[i]>0) and (SchoolSum[i] / SchoolCount[i] <
Min)
then
begin
Min := SchoolSum[i] / SchoolCount[i];
MinI := i
end;
for i:=1 to 99 do
if (SchoolCount[i]>0) and (SchoolSum[i]*SchoolCount[MinI]=
SchoolSum[MinI]*SchoolCount[i])
then
WriteLn(i)
end.
Решение на языке C++
#include<iostream>
#include<string>
using namespace std;
int main()
{
int SchoolSum[100];
int SchoolCount[100];
int i, N, School, Ball, MinI;
double Min;
string Name;
for (i = 1; i <= 99; ++i)
SchoolSum[i] = SchoolCount[i] = 0;
cin >> N;
for (i = 0; i < N; ++i)
{
cin >> Name >> Name >> School >> Ball;
SchoolSum[School] += Ball;
SchoolCount[School]++;
}
Min=101;
for(i=1;i<=99;++i)
if (SchoolCount[i]>0 && (double)SchoolSum[i]/SchoolCount
[i]<Min)
{
Min=(double)SchoolSum[i]/SchoolCount[i];
MinI=i;
}
for(i=1;i<=99;++i)
if (SchoolCount[i]>0 && SchoolSum[i]*SchoolCount[MinI]==
SchoolSum[MinI]*SchoolCount[i])
cout << i << endl;
return 0;
}
Указания по оцениванию Балл
Программа работает верно для любых входных данных
произвольного размера и находит ответ, не сохраняя входные данные
в массиве, размер которого соответствует числу N (количество
человек в списке). Программа просматривает входные данные один
раз, сохраняя только информацию о cуммарном балле и количестве
выпускников в каждой школе. Допускается наличие в тексте
программы одной синтаксической ошибки: пропущен или неверно
указан знак пунктуации, неверно написано или пропущено
зарезервированное слово языка программирования, не описана или
неверно описана переменная, применяется операция, недопустимая
для соответствующего типа данных (если одна и та же ошибка
встречается несколько раз, то это считается за одну ошибку).
4
Программа работает верно, но входные данные запоминаются в
массиве, размер которого не меньше N или входные данные
считываются несколько раз. Допускается наличие от одной до трех
синтаксических ошибок. Возможно, в принципиально верно
организованном вводе данных есть одна ошибка. Три балла также
выставляется, если в эффективной программе, удовлетворяющей
критериям выставления 4 баллов, есть одна алгоритмическая ошибка
(например, отсутствует вывод результата при правильном его
нахождении).
3
Программа работает в целом верно, эффективно или нет, но, в
реализации алгоритма содержатся до двух ошибок (неверная
инициализация переменных, в частности значения максимума, выход
за границу массива, перевод символов в числа, используется знак “<”
вместо “<=”, “or” вместо “and” и т.п.). Возможно, некорректно
организовано считывание входных данных. Допускается наличие от
одной до пяти синтаксических ошибок, описанных выше.
2
Программа, возможно, неверно работает при некоторых входных
данных, например, выдает правильный ответ только в том случае,
если школа с максимальным средним баллом только одна. Возможно,
неверно организовано считывание данных и отсутствует вывод
результата. Допускается до 4 различных ошибок в реализации
алгоритма, в том числе описанных в критериях присвоения двух
баллов. Допускается наличие от одной до семи синтаксических
ошибок, описанных выше.
1
Задание не выполнено или выполнено неверно 0
3. Имеется список людей с указанием их фамилии, имени и даты рождения.
Напишите эффективную по времени работы и по используемой памяти
программу (укажите используемую версию языка программирования, например,
Borland Pascal 7.0), которая будет определять самого старшего человека из этого
списка и выводить его фамилию, имя и дату рождения, а если имеется несколько
самых старших людей с одинаковой датой рождения, то определять их
количество. На вход программе в первой строке подается количество людей в
списке N. В каждой из последующих N строк находится информация в следующем
формате: <Фамилия> <Имя> <Дата рождения>
где <Фамилия> – строка, состоящая не более, чем из 20 символов без
пробелов,
<Имя> – строка, состоящая не более, чем из 20 символов без
пробелов,
<Дата рождения> – стока, имеющая вид ДД.ММ.ГГГГ, где ДД –
двузначное число от 01 до 31, ММ – двузначное число от 01 до 12,
ГГГГ – четырехзначное число от 1800 до 2100.
Пример входной строки:
Иванов Сергей 27.03.1993
Программа должна вывести фамилию и имя самого старшего
человека в списке.
Пример выходных данных:
Иванов Сергей
Если таких людей, несколько, то программа должна вывести их
количество. Пример вывода в этом случае: 3
Содержание верного ответа и указания по оцениванию (допускаются иные
формулировки ответа, не искажающие его смысла)
Программа читает все входные данные один раз, не запоминая их в массиве.
Во время чтения данных определяется дата рождения каждого человека,
которая сравнивается с наименьшей из известных дат рождения среди всех
уже просмотренных людей из списка. Также запоминается количество людей,
имеющих наименьшую дату рождения, фамилия и имя человека, имеющего
наименьшую дату рождения.
Баллы начисляются только за программу, которая решает задачу хотя бы для
одного частного случая (например, когда только один человек имеет
наименьшую дату рождения).
Ниже приведены примеры решения задания на языках Паскаль и C++.
Допускаются решения, записанные на других языках программирования. При
оценивании решений на других языках программирования необходимо
учитывать особенности этих языков программирования.
Решение на языке Паскаль
Var
N, i, Day, Month, Year, MinDay, MinMonth, MinYear, MinCount,
Code: integer;
Name, MinName: string;
Begin
MinYear:=9999;
,Считываем количество людей-
ReadLn(N);
for i:=1 to N do
begin
,Считываем данные об одном человеке-
ReadLn(Name);
,Извлекаем из строки значения дня, месяца, года рождения-
val(Copy(Name,Length(Name)-9,2),Day,Code);
val(Copy(Name,Length(Name)-6,2),Month,Code);
val(Copy(Name,Length(Name)-3,4),Year,Code);
,Если дата рождения совпадает с наименьшей известной
датой, то увеличиваем счетчик числа людей, имеющих минимальную
дату рождения}
if (Year=MinYear) and (Month=MinMonth) and (Day=MinDay)
then
MinCount:=MinCount+1;
,Если дата рождения меньше минимально известной, то
сохраняем его дату рождения, как минимальное, счетчик числа
людей, имеющих такую дату рождения, устанавливаем в 1, также
запоминаем имя человека}
if (Year<MinYear) or (Year=MinYear) and (Month<MinMonth)
or (Year=MinYear) and (Month=MinMonth) and (Day<MinDay)
then
begin
MinYear:=Year;
MinMonth:=Month;
MinDay:=Day;
MinCount:=1;
MinName:=Copy(Name,1,length(Name)-11)
end
end;
,Если счетчик числа людей, имеющих минимальную дату рождения
больше 1, то выводим значение счетчика, иначе выводим имя
человека}
if MinCount>1
then
WriteLn(MinCount)
Else
WriteLn(MinName)
end.
Решение на языке C++
#include<iostream>
using namespace std;
int main()
{
int n, i, day, month, year, minday, minmonth, minyear,
mincount;
string name, minname;
cin >> n;
getline(cin, name);
minyear=9999;
for(i=0;i<n;++i)
{
getline(cin, name);
day=(name[name.length()-10]-‘0’)*10 + name[name.length()-
9]-‘0’;
month=(name[name.length()-7]-‘0’)*10 + name[name.length()-
9]-‘6’;
year=(((name[name.length()-4]-‘0’)*10 + name[name.length
()-3]-‘0’) * 10 + name[name.length()-2]-‘0’)*10 + name
[name.length()-1]-‘0’;
if (year==minyear && month==minmonth && day==minday)
++mincount;
if (year<minyear || year==minyear && month<minmonth ||
year==minyear && month==minmonth && day<minday)
{
minyear=year;
minmonth=month;
minday=day;
mincount=1;
name.resize(name.length()-11);
minname=name;
}
}
if(mincount>1)
cout<<mincount<<endl;
else
cout<<minname<<endl;
return 0;
}
Указания по оцениванию Балл
Программа работает верно для любых входных данных
произвольного размера и находит ответ, не сохраняя входные данные
в массиве, размер которого соответствует числу N (количество
человек в списке). Программа просматривает входные данные один
раз, сохраняя только информацию о cуммарном балле и количестве
выпускников в каждой школе. Допускается наличие в тексте
программы одной синтаксической ошибки: пропущен или неверно
указан знак пунктуации, неверно написано или пропущено
зарезервированное слово языка программирования, не описана или
неверно описана переменная, применяется операция, недопустимая
для соответствующего типа данных (если одна и та же ошибка
встречается несколько раз, то это считается за одну ошибку).
4
Программа работает верно, но входные данные запоминаются в
массиве, размер которого не меньше N или входные данные
считываются несколько раз. Допускается наличие от одной до трех
синтаксических ошибок. Возможно, в принципиально верно
организованном вводе данных есть одна ошибка. Три балла также
выставляется, если в эффективной программе, удовлетворяющей
критериям выставления 4 баллов, есть одна алгоритмическая ошибка
(например, отсутствует вывод результата при правильном его
нахождении).
3
Программа работает в целом верно, эффективно или нет, но, в
реализации алгоритма содержатся до двух ошибок (неверная
инициализация переменных, в частности значения максимума, выход
за границу массива, перевод символов в числа, используется знак “<”
вместо “<=”, “or” вместо “and” и т.п.). Возможно, некорректно
организовано считывание входных данных. Допускается наличие от
одной до пяти синтаксических ошибок, описанных выше.
2
Программа, возможно, неверно работает при некоторых входных
данных, например, выдает правильный ответ только в том случае,
если школа с максимальным средним баллом только одна. Возможно,
неверно организовано считывание данных и отсутствует вывод
результата. Допускается до 4 различных ошибок в реализации
алгоритма, в том числе описанных в критериях присвоения двух
баллов. Допускается наличие от одной до семи синтаксических
ошибок, описанных выше.
1
Задание не выполнено или выполнено неверно 0
4. Имеется список результатов голосования избирателей за несколько партий, в
виде списка названий данных партий. На вход программе в первой строке
подается количество избирателей в списке N. В каждой из последующих N строк
записано название партии, за которую проголосовал данный избиратель, в виде
текстовой строки. Длина строки не превосходит 50 символов, название может
содержать буквы, цифры, пробелы и прочие символы.
Пример входных данных:
6
Party one
Party two
Party three
Party three
Party two
Party three
Программа должна вывести список всех партий, встречающихся в
исходном списке, в порядке убывания количества голосов, отданных
за эту партию. При этом название каждой партии должно быть
выведено ровно один раз, вне зависимости от того, сколько голосов
было отдано за данную партию.
Пример выходных данных для приведенного выше примера входных
данных:
Party three
Party two
Party one
При этом следует учитывать, что количество голосов избирателей в
исходном списке может быть велико (свыше 1000), а количество
различных партий в этом списке не превосходит 10.
Содержание верного ответа и указания по оцениванию
(допускаются иные формулировки ответа, не искажающие его смысла)
Программа читает все входные данные один раз, не запоминая все входные данные
в массиве, размер которого равен N, а составляя только список имеющихся
политических партий и количества голосов, отданных за каждую из них. Во время
чтения данных просматривается список ранее сохраненных партий, если данная
партия уже есть в списке, то количество голосов, отданных за эту партию,
увеличивается на 1, иначе партия добавляется в список известных партий. После
окончания ввода производится сортировка массивов партий и количества голосов,
отданных за них в порядке убывания количества голосов, затем выводится список
партий. Баллы начисляются только за программу, которая решает задачу хотя бы
для одного частного случая.
Ниже приведены примеры решения задания на языках Паскаль и C++. Допускаются
решения, записанные на других языках программирования. При оценивании
решений на других языках программирования необходимо учитывать особенности
этих языков программирования.
Решение на языке Паскаль
Var
n, NumParties, i, j, t: integer;
Count:array[1..10] of integer;
s: string;
Names: array[1..10] of string;
Begin
,Общее число партий в списке-
NumParties:=0;
,Считываем количество избирателей-
ReadLn(N);
for i:=1 to N do
begin
,Считываем название партии, за которую проголосовал
избиратель-
ReadLn(S);
,Осуществляем поиск считанного названия в списке всех известных партий-
j:=1;
while (j<=NumParties) and (s<>Names[j])
do
j:=j+1;
,Если партия найдена в списке-
if j<=NumParties
then
,Увеличиваем счетчик числа голосов, отданных за эту
партию}
Count[j]:=Count[j]+1
else
begin
,Иначе добавляем партию в конец списка, увеличиваем
число партий на 1, устанавливаем счетчик голосов, отданных за
новую партию, в 1-
Names[j]:=s;
Count[j]:=1;
NumParties:=NumParties+1
end
end;
,Сортируем массивые Names и Count в порядке убывания
значений массива Count}
for i:=NumParties downto 2 do
© МИОО, 2009 г.
for j:=2 to i do
if Count[j-1]<Count[j]
then
begin
t:=Count[j];
Count[j]:=Count[j-1];
Count[j-1]:=t;
s:=Names[j];
Names[j]:=Names[j-1];
Names[j-1]:=s;
end;
,Выводим содержимое массива Countfor
i:=1 to NumParties do
WriteLn(Names[i])
end.
Решение на языке C++
#include<iostream>
using namespace std;
int main()
{
int n, Count[10], NumParties=0, i, j, t;
string Names[10], s;
cin>>n;
getline(cin,s);
for(i=0;i<n;++i)
{
getline(cin,s);
j=0;
while(j<NumParties && s!=Names[j])
++j;
if(j<NumParties)
++Count[j];
else
{
Names[j]=s;
Count[j]=1;
++NumParties;
}
}
for (i=NumParties-1;i>=1;—i)
for (j=1;j<=i;++j)
if (Count[j-1]<Count[j])
{
t=Count[j];
Count[j]=Count[j-1];
Count[j-1]=t;
s=Names[j];
Names[j]=Names[j-1];
Names[j-1]=s;
}
for(i=0;i<NumParties;++i)
cout<<Names[i]<<endl;
}
Указания по оцениванию Балл
Программа работает верно для любых входных данных произвольного
размера и находит ответ, не сохраняя входные данные в массиве,
размер которого соответствует числу N (количество человек в списке).
Программа просматривает входные данные один раз, сохраняя только
информацию о cуммарном балле и количестве выпускников в каждой
школе. Допускается наличие в тексте программы одной синтаксической
ошибки: пропущен или неверно указан знак пунктуации, неверно
написано или пропущено зарезервированное слово языка
программирования, не описана или неверно описана переменная,
применяется операция, недопустимая для соответствующего типа
данных (если одна и та же ошибка встречается несколько раз, то это
считается за одну ошибку).
4
Программа работает верно, но все входные данные запоминаются в
массиве или входные данные считываются несколько раз.
Допускается наличие от одной до трех синтаксических ошибок. Три
балла также выставляется, если в эффективной программе,
удовлетворяющей критериям выставления 4 баллов, есть одна
ошибка, например, использование неверной границы в алгоритме
сортировке, выход за границы массива, используется знак “<” вместо
“<=” и т.д.
3
Программа работает в целом верно, эффективно или нет, но, в
реализации алгоритма содержатся до двух ошибок (неверная
инициализация переменных, в частности значения минимума, выход
за границу массива, используется знак “<” вместо “<=”, “or” вместо
“and” и т.п.). Возможно, некорректно организовано считывание
входных данных. Допускается наличие от одной до пяти синтаксических
ошибок, описанных выше.
2
Программа, возможно, неверно работает при некоторых входных
данных, например, выдает правильный ответ только в том случае,
если школа с максимальным средним баллом только одна. Возможно,
неверно организовано считывание данных и отсутствует вывод
результата. Допускается до 4 различных ошибок в реализации
алгоритма, в том числе описанных в критериях присвоения двух баллов.
Допускается наличие от одной до семи синтаксических ошибок,
описанных выше.
1
Задание не выполнено или выполнено неверно 0
5. Имеется список результатов голосования избирателей за несколько партий, в
виде списка названий данных партий. При этом некоторые голоса являются
недействительными, в этом случае вместо названия партии записан один символ
«.» (точка). Партия проходит в парламент, если за нее отдано не менее 7% от
общего числа действительных голосов (то есть от количества строк в списке,
которые не равны «.»). На вход программе в первой строке подается количество
избирателей в списке N. В каждой из последующих N строк записано название
партии, за которую проголосовал данный избиратель, в виде текстовой строки
или один символ «.», если данный голос считается недействительным. Длина
строки не превосходит 50 символов, название может содержать буквы, цифры,
пробелы и прочие символы.
Пример входных данных:
Party one
Party two
Party one
Party one
Party two
Party two
.
Party three
Party one
Party one
Party two
Party one
Party two
Party two
Party one
Party two
Программа должна вывести список всех партий, прошедших в парламент, в
произвольном порядке. При этом название каждой партии должно быть выведено
ровно один раз, вне зависимости от того, сколько голосов было отдано за данную
партию.
Пример выходных данных для приведенного выше примера входных данных:
Party one
Party two
При этом следует учитывать, что количество голосов избирателей в исходном
списке может быть велико (свыше 1000), а количество различных партий в
этом списке не превосходит 10.
Содержание верного ответа и указания по оцениванию
(допускаются иные формулировки ответа, не искажающие его смысла)
Программа читает все входные данные один раз, не запоминая все входные данные
в
массиве, размер которого равен N, а составляя только список имеющихся
политических партий и количества голосов, отданных за каждую из них. Во время
чтения данных проверяется, не равна ли считанная строка «.». В этом случае
просматривается список ранее сохраненных партий, если данная партия уже есть в
списке, то количество голосов, отданных за эту партию, увеличивается на 1, иначе
партия добавляется в список известных партий. Также счетчик общего числа
действительных голосов увеличивается на 1. После окончания ввода
просматривается список всех партий и выводятся названия тех из них, за которые
отдано не менее 7% от общего числа голосов. Баллы начисляются только за
программу, которая решает задачу хотя бы для одного частного случая. Ниже
приведены примеры решения задания на языках Паскаль и C++.
Допускаются решения, записанные на других языках программирования. При
оценивании решений на других языках программирования необходимо учитывать
особенности этих языков программирования.
Решение на языке Паскаль
Var
n, NumParties, NumVotes, i, j: integer;
Count:array[1..10] of integer;
s: string;
Names: array[1..10] of string;
Begin
NumParties:=0;
NumVotes:=0;
{Считываем количество избирателей}
ReadLn(N);
for i:=1 to N do
begin
{Считываем название партии, за которую проголосовал избиратель}
ReadLn(S);
if S<>’.’ then
begin
NumVotes:=NumVotes+1;
{Осуществляем поиск названия в списке известных партий}
j:=1;
while (j<=NumParties) and (s<>Names[j])
do
j:=j+1;
{Если партия найдена в списке}
if j<=NumParties
then
{Увеличиваем счетчик числа голосов, отданных за эту партию}
Count[j]:=Count[j]+1
else
begin
{Иначе добавляем партию в конец списка,
увеличиваем число партий на 1,
устанавливаем счетчик голосов,
отданных за новую партию, в 1}
Names[j]:=s;
Count[j]:=1;
NumParties:=NumParties+1
end
end
end;
{Проходим по списку партий и выводим только те,
за которые отдано не менее 7% голосов}
for i:=1 to NumParties do
if Count[i]*100>=NumVotes*7 then
WriteLn(Names[i])
end.
Решение на языке C++
#include<iostream>
using namespace std;
int main()
{
int n, Count[10], NumParties=0, NumVotes=0, i, j;
string Names[10], s;
cin>>n;
getline(cin,s);
for(i=0;i<n;++i)
{
getline(cin,s);
if(s!=».»)
{
NumVotes++;
j=0;
while(j<NumParties && s!=Names[j])
++j;
if(j<NumParties)
++Count[j];
else
{
Names[j]=s;
Count[j]=1;
++NumParties;
}
}
}
for(i=0;i<NumParties;++i)
if(Count[i]*100>=NumVotes*7)
cout<<Names[i]<<endl;
}
Указания по оцениванию Балл
Программа работает верно для любых входных данных
произвольного размера и находит ответ, не сохраняя входные данные
в массиве, размер которого соответствует числу N (количество
человек в списке). Программа просматривает входные данные один
раз, сохраняя только информацию о cуммарном балле и количестве
выпускников в каждой школе. Допускается наличие в тексте
программы одной синтаксической ошибки: пропущен или неверно
указан знак пунктуации, неверно написано или пропущено
зарезервированное слово языка программирования, не описана или
неверно описана переменная, применяется операция, недопустимая
для соответствующего типа данных (если одна и та же ошибка
встречается несколько раз, то это считается за одну ошибку).
4
Программа работает верно, но все входные данные запоминаются в
массиве или входные данные считываются несколько раз.
Допускается наличие от одной до трех синтаксических ошибок. Три
балла также выставляется, если в эффективной программе,
удовлетворяющей критериям выставления 4 баллов, есть одна
ошибка, например, использование неверной границы в алгоритме
сортировке, выход за границы массива, используется знак “<” вместо
“<=” и т.д.
3
Программа работает в целом верно, эффективно или нет, но, в
реализации алгоритма содержатся до двух ошибок (неверная
инициализация переменных, в частности значения минимума, выход
за границу массива, используется знак “<” вместо “<=”, “or” вместо
“and” и т.п.). Возможно, некорректно организовано считывание
входных данных. Допускается наличие от одной до пяти
синтаксических ошибок, описанных выше.
2
Программа, возможно, неверно работает при некоторых входных
данных, например, выдает правильный ответ только в том случае,
если школа с максимальным средним баллом только одна. Возможно,
неверно организовано считывание данных и отсутствует вывод
результата. Допускается до 4 различных ошибок в реализации
алгоритма, в том числе описанных в критериях присвоения двух
баллов. Допускается наличие от одной до семи синтаксических
ошибок, описанных выше.
1
Задание не выполнено или выполнено неверно 0
6. Два игрока играют в следующую игру. На координатной плоскости стоит
фишка.
В начале игры фишка находится в точке с координатами (0,0). Игроки ходят по
очереди. Ход состоит в том, что игрок перемещает фишку из точки с
координатами (x, y) в одну из трех точек: (x + 2, y + 3), (x, y + 2), . Игра
заканчивается, как только расстояние по прямой от фишки до начала координат
станет более 9. Выигрывает игрок, который сделал последний ход. Кто
выигрывает при безошибочной игре – игрок, делающий первый ход, или игрок,
делающий второй ход? Каким должен быть первый ход выигрывающего игрока?
Ответ обоснуйте.
16
Party one
Party two
Party one
Party one
Party two
Party two
.
Party three
Party one
Party one
Party two
Party one
Party two
Party two
Party one
Party two
Программа должна вывести список всех партий, прошедших в парламент, в
произвольном порядке. При этом название каждой партии должно быть
выведено ровно один раз, вне зависимости от того, сколько голосов было
отдано за данную партию.
Пример выходных данных для приведенного выше примера входных данных:
Party one
Party two
При этом следует учитывать, что количество голосов избирателей в исходном
списке может быть велико (свыше 1000), а количество различных партий в
этом списке не превосходит 10.
Содержание верного ответа и указания по оцениванию
(допускаются иные формулировки ответа, не искажающие его смысла)
Программа читает все входные данные один раз, не запоминая все входные данные
в
массиве, размер которого равен N, а составляя только список имеющихся
политических партий и количества голосов, отданных за каждую из них. Во время
чтения данных проверяется, не равна ли считанная строка «.». В этом случае
просматривается список ранее сохраненных партий, если данная партия уже есть в
списке, то количество голосов, отданных за эту партию, увеличивается на 1, иначе
партия добавляется в список известных партий. Также счетчик общего числа
действительных голосов увеличивается на 1. После окончания ввода
просматривается список всех партий и выводятся названия тех из них, за которые
отдано не менее 7% от общего числа голосов.
Баллы начисляются только за программу, которая решает задачу хотя бы для одного
частного случая.
Ниже приведены примеры решения задания на языках Паскаль и C++.
Допускаются решения, записанные на других языках программирования. При
оценивании решений на других языках программирования необходимо учитывать
особенности этих языков программирования.
Решение на языке Паскаль
Var
n, NumParties, NumVotes, i, j: integer;
Count:array[1..10] of integer;
s: string;
Names: array[1..10] of string;
Begin
NumParties:=0;
NumVotes:=0;
,Считываем количество избирателей-
ReadLn(N);
for i:=1 to N do
begin
,Считываем название партии, за которую проголосовал избиратель-
ReadLn(S);
if S<>’.’ then
begin
NumVotes:=NumVotes+1;
,Осуществляем поиск названия в списке известных партий-
j:=1;
while (j<=NumParties) and (s<>Names[j])
do
j:=j+1;
,Если партия найдена в списке-
if j<=NumParties
then
,Увеличиваем счетчик числа голосов, отданных за эту партию-
Count[j]:=Count[j]+1
else
begin
,Иначе добавляем партию в конец списка,
увеличиваем число партий на 1,
устанавливаем счетчик голосов,
отданных за новую партию, в 1-
Names[j]:=s;
Count[j]:=1;
NumParties:=NumParties+1
end
end
end;
,Проходим по списку партий и выводим только те,
за которые отдано не менее 7% голосов-
for i:=1 to NumParties do
if Count[i]*100>=NumVotes*7 then
WriteLn(Names[i])
end.
Решение на языке C++
#include<iostream>
using namespace std;
int main()
{
int n, Count[10], NumParties=0, NumVotes=0, i, j;
string Names[10], s;
cin>>n;
getline(cin,s);
for(i=0;i<n;++i)
{
getline(cin,s);
if(s!=».»)
{
NumVotes++;
j=0;
while(j<NumParties && s!=Names[j])
++j;
if(j<NumParties)
++Count[j];
else
{
Names[j]=s;
Count[j]=1;
++NumParties;
}
}
}
for(i=0;i<NumParties;++i)
if(Count[i]*100>=NumVotes*7)
cout<<Names[i]<<endl;
}
Указания по оцениванию Балл
Программа работает верно для любых входных данных
произвольного размера и находит ответ, не сохраняя входные данные
в массиве, размер которого соответствует числу N (количество
человек в списке). Программа просматривает входные данные один
раз, сохраняя только информацию о cуммарном балле и количестве
выпускников в каждой школе. Допускается наличие в тексте
программы одной синтаксической ошибки: пропущен или неверно
указан знак пунктуации, неверно написано или пропущено
зарезервированное слово языка программирования, не описана или
неверно описана переменная, применяется операция, недопустимая
для соответствующего типа данных (если одна и та же ошибка
встречается несколько раз, то это считается за одну ошибку).
4
Программа работает верно, но все входные данные запоминаются в
массиве или входные данные считываются несколько раз.
Допускается наличие от одной до трех синтаксических ошибок. Три
балла также выставляется, если в эффективной программе,
удовлетворяющей критериям выставления 4 баллов, есть одна
ошибка, например, использование неверной границы в алгоритме
сортировке, выход за границы массива, используется знак “<” вместо
“<=” и т.д.
3
Программа работает в целом верно, эффективно или нет, но, в
реализации алгоритма содержатся до двух ошибок (неверная
инициализация переменных, в частности значения минимума, выход
за границу массива, используется знак “<” вместо “<=”, “or” вместо
“and” и т.п.). Возможно, некорректно организовано считывание
входных данных. Допускается наличие от одной до пяти
синтаксических ошибок, описанных выше.
2
Программа, возможно, неверно работает при некоторых входных
данных, например, выдает правильный ответ только в том случае,
если школа с максимальным средним баллом только одна. Возможно,
неверно организовано считывание данных и отсутствует вывод
результата. Допускается до 4 различных ошибок в реализации
алгоритма, в том числе описанных в критериях присвоения двух
баллов. Допускается наличие от одной до семи синтаксических
ошибок, описанных выше.
1
Задание не выполнено или выполнено неверно 0
7. Статья 83 закона «О выборах депутатов Государственной Думы Федерального
Собрания Российской Федерации» определяет следующий алгоритм
пропорционального распределения депутатских мандатов.
Сначала подсчитывается сумма голосов избирателей, поданных за каждую
партию и подсчитывается сумма голосов, поданных за все партии. Эта сумма
делится на 450 – количество распределяемых мандатов, получается величина,
называемая «первое избирательное частное». Далее каждая партия получает
столько мандатов в парламенте, чему равна целая часть от деления числа голосов
за данную партию на первое избирательное частное.
Если после этого сумма количества мандатов, отданных партиям, меньше 450, то
оставшиеся до 450 мандаты передаются по одному партиям, в порядке убывания
дробной части частного от деления числа голосов за данную партию на первое
избирательное частное. Если же для двух партий эти дробные части равны, то
преимущество отдается той партии, которая получила большее число голосов.
Напишите программу (укажите используемую версию языка программирования,
например, Borland Pascal 7.0), которая по количеству голосов, отданных за
каждую партию, будет определять количество мандатов, полученных этой
партией в парламенте.
На вход программе подается количество партий N, участвовавших в выборах,
N≤20. Далее идет N строчек, каждая строчка содержит название партии (строка
длиной не более 50 символов, возможно, содержащая пробелы), затем, через
пробел, количество голосов, полученных данной партией – число, не
превосходящее .
Пример входных данных:
3
Party One 100000
Party Two 200000
Party Three 400000
Программа должна вывести названия всех партий и количество голосов в
парламенте, полученных данной партией. Названия необходимо выводить в том
же порядке, в котором они шли во входных данных. Пример выходных данных
для данного примера входных данных:
Party One 64
Party Two 129
Party Three 257
Содержание верного ответа и указания по оцениванию
(допускаются иные формулировки ответа, не искажающие его смысла)
Создадим массивы, для хранения следующих данных о партиях:
1. Название партии Names – строкового типа
2. Количество голосов, полученных партиями Votes – целочисленного типа
3. Количество мандатов в парламенте, полученных партией Mandates –
целочисленного типа
4. Дробная часть от деления количества голосов на первое избирательное частное
FracPart – вещественного типа (этот массив необходим для второй части
распределения
голосов).
Программа считывает данные один раз, запоминая названия партии в массиве
Names, а
количество голосов, отданных за партию – в массиве Votes. Одновременно в
переменную
SumVotes считается общее число голосов.
Затем в цикле по всем партиям (индексная переменная i обозначает номер партии)
каждая партия получает количество мандатов, равное целой части от деления
Votes[i]
на (SumVotes/450). Данное число мандатов записывается в элемент массива
Mandates
[i], в массив FracPart[i] записывается дробная часть от указанного частного.
Одновременно в SumMandates записывается общее число распределенных между
партиями мандатов.
В следующем цикле пока величина SumMandates меньше 450, распределяется по
одному
дополнительному мандату между партиями. Для этого определяется партия, для
которой
наибольшая величиа FracPart, а если величины FracPart – одинаковые, то партия,
для
которой больше величина Votes. Номер этой партии записывается в переменную i.
Затем
значение Mandates[i] и SumMandates увеличивается на 1, а значение FracPart[i]
устанавливается в 0, чтобы эта партия выбывала из процедуры вторичного
распределения голосов.
Решение на языке Паскаль:
Const
NumMandates=450; ,Число место в парламенте-
Var
N, SumVotes, SumMandates, i, j: longint;
errcore: integer;
Names: array[1..20] of string; {Названия партий}
Votes: array[1..20] of longint; ,Число голосов, отданных за партию-
Mandates: array[1..20] of longint; {Число мест в парламенте}
FracPart: array*1..20+ of real; ,Дробная часть при определении числа
мест-
Begin
ReadLn(N); ,Считали число партий-
SumVotes:=0; ,Общее число голосов избирателей-
for i:=1 to N do
begin
ReadLn(Names*i+); ,Считали название партии и число голосов-
j:=length(Names[i]);
while Names[i][j]<>’ ‘ do j:=j-1; {Нашли последний пробел в
строке}
val(Copy(Names[i],j+1,10),Votes[i],errcode); {Выделили из строки
число голосов-
Names[i]:=Copy(Names[i],1,j-1); ,Выделили из строки название
партии-
SumVotes:=SumVotes+Votes*i+; ,Увеличили общее число голосов-
end;
SumMandates:=0; {Общее число мандатов}
for i:=1 to N do
begin
FracPart[i]:=Votes[i]/(SumVotes/NumMandates);
Mandates*i+:=trunc(FracPart*i+); ,Столько мандатов получила данная
партия}
SumMandates:=SumMandates+Mandates[i]; {Увеличиваем общее число
мандатов}
FracPart[i]:=frac(FracPart[i])
end;
while SumMandates < NumMandates do {Раздаем дополнительные мандаты}
begin__
i:=1;
for j:=2 to N do ,Выбираем партию с наибольшим значением FracPartif
(FracPart[j]>FracPart[i]) or (FracPart[j]=FracPart[i]) and
(Votes[j]>Votes[i])
then i:=j;
Mandates*i+:=Mandates*i++1; ,Выдаем ей дополнительный мандат-
SumMandates:=SumMandates+1; ,Увеличиваем общее число мандатов-
FracPart[i]:=0;
end;
for i:=1 to N do ,Выводим результаты распределения мандатов-
WriteLn(Names[i],’ ‘,Mandates[i])
end.
Решение на языке C++:
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int main()
{
const int NumMandates=450;
int N, SumVotes, SumMandates, i, j;
string Names[20];
int Votes[20];
int Mandates[20];
double FracPart[20];
cin>>N;
getline(cin,Names[0]);
SumVotes=0;
for(i=0;i<N;i++)
{
getline(cin,Names[i]);
j=Names[i].length()-1;
while(Names[i][j]!=’ ‘) j—;
sscanf(Names[i].c_str()+j,»%d»,&Votes[i]);
Names[i].resize(j-1);
SumVotes+=Votes[i];
}
SumMandates=0;
for(i=0;i<N;i++)
{
FracPart[i]=Votes[i]/((double)SumVotes/NumMandates);
Mandates[i]=trunc(FracPart[i]);
SumMandates=SumMandates+Mandates[i];
FracPart[i]-=trunc(FracPart[i]);
}
while (SumMandates < NumMandates)
{
i=0;
for(j=1;j<N;j++)
if (FracPart[j]>FracPart[i] || FracPart[j]==FracPart[i] &&
Votes[j]>Votes[i])
i=j;
Mandates[i]++;
SumMandates++;
FracPart[i]=0;
}
for(i=0;i<N;i++)
cout<<Names[i]<<» «<<Mandates[i]<<endl;
}
Указания по оцениванию Балл
Программа работает верно для любых входных данных
произвольного размера и находит ответ, не сохраняя входные данные
в массиве, размер которого соответствует числу N (количество
человек в списке). Программа просматривает входные данные один
раз, сохраняя только информацию о cуммарном балле и количестве
выпускников в каждой школе. Допускается наличие в тексте
программы одной синтаксической ошибки: пропущен или неверно
указан знак пунктуации, неверно написано или пропущено
зарезервированное слово языка программирования, не описана или
неверно описана переменная, применяется операция, недопустимая
для соответствующего типа данных (если одна и та же ошибка
встречается несколько раз, то это считается за одну ошибку).
4
Программа работает верно во всех случаях, но содержит одну ошибку
(например, не рассмотрена возможность равенства голосов при
вторичном распределении мандатов, или программа не выводит
результат, при верном его нахождении). Допускается наличие от одной
до трех синтаксических ошибок: Возможно, в принципиально верно
организованном вводе данных есть одна ошибка.
3
Программа работает в целом верно, но в реализации алгоритма
содержатся до двух ошибок (неверная инициализация переменных, в
частности значения максимума, выход за границу массива, перевод
символов в числа, используется знак “<” вместо “<=”, “or” вместо “and” и
т.п.). Помимо этого, возможно, некорректно организовано считывание
входных данных. Допускается наличие от одной до пяти синтаксических
ошибок, описанных выше.
2
Программа, возможно, неверно работает при некоторых входных
данных.
Возможно, неверно реализован (или полностью отсутствует) механизм
вторичного распределения мандатов). Допускается до 4 различных
ошибок в реализации алгоритма, в том числе описанных в критериях
присвоения двух баллов. Допускается наличие от одной до семи
синтаксических ошибок, описанных выше.
1
Задание не выполнено или выполнено неверно 0
309. Общая эффективность автоматизированного решения экономических задач находится в прямой зависимости от (укажите все правильные):
+а) снижения затрат на обработку информации (прямая эффективность)
б) снижения затрат промышленных предприятий на производство
в) инвентаризации товарных запасов
г) индекса физического объема основных фондов
+д) достигнутого повышения уровня информационного обслуживания (косвенная эффективность)
310. В снижении трудовых и стоимостных затрат на обработку экономической информации выражается __________ эффективность
ОТВЕТ: прямая
311. Качественные изменения, происходящие в результате применения средств вычислительной техники, характеризует ___________ эффективность
ОТВЕТ: косвенная
312. Для расчета ожидаемой косвенной эффективности рекомендуется применять:
а) тендерную документацию
б) страховую ответственность
в) систему клиринговых палат
+г) способ экспертных оценок
д) сделки офсетные
313. В результате сравнения затрат на обработку информации нескольких вариантов проектных решений определяются показатели _________ экономической эффективности
ОТВЕТ: прямой
314. Абсолютным показателем экономической эффективности разрабатываемого проекта является , где (укажите все правильные):
+а) — величина снижения затрат на обработку информации
+б) — стоимость обработки информации при базовом варианте
в) — капитальнее вложения законченные
+г) — стоимость обработки информации при проектируемом варианте
д) — качество продукции при базовом варианте
315. Относительным показателем экономической эффективности проекта является или , где (укажите все правильные):
+а) — коэффициент эффективности затрат
+б) — величина снижения затрат на обработку информации
в) — коэффициент выбытия основных фондов
г) — коэффициент трудового участия
+д) — стоимость обработки информации при базовом варианте
316. Относительным показателем экономической эффективности проекта является , где (укажите все правильные):
а) — коэффициент миграции населения
+б) — индекс изменения затрат
в) — коэффициент трудового участия
+г) — стоимость обработки информации при базовом варианте
+д) — стоимость обработки информации при проектируемом варианте
317. Внедрение проекта предполагает дополнительные капитальные затраты , где (укажите все правильные):
+а) — капитальные затраты проектируемой системы обработки информации
+б) — коэффициент неравномерности нагрузки на предприятиях связи
в) — затраты существующей системы обработки информации
г) — критерий Бартлетта
+д) — дополнительные капитальные затраты
318. Эффективность капитальных затрат определяется , где (укажите все правильные):
+а) — срок окупаемости дополнительных капитальных затрат
б) — критерий Вилкоксона
+в) — дополнительные капитальные затраты
г) — лактационный период
+д) — величина снижения затрат на обработку информации
319. Долю окупаемости дополнительных капитальных затрат за год определяют , где (укажите все правильные):
а) — лимитная цена
+б) — коэффициент экономической эффективности капитальных затрат
+в) — величина снижения затрат на обработку информации
+г) — дополнительные капитальные затраты
+д) — срок окупаемости дополнительных капитальных затрат
320. Абсолютным показателем снижения трудовых затрат является разность , где (укажите все правильные):
+а) — годовая трудоемкость проектируемого варианта системы обработки информации
б) — лактационный период
в) — лимитная цена
+г) — годовая трудоемкость существующего варианта системы обработки информации
д) — коэффициент неравномерности нагрузки на предприятиях связи
321. Относительными показателями снижения трудовых затрат являются или , где (укажите все правильные):
+а) — коэффициент снижения трудовых затрат
+б) — разность между годовыми трудовыми затратами базового и проектируемого вариантов решений
в) — коэффициент выбытия основных производственных фондов
+г) — годовая трудоемкость существующего варианта системы обработки информации
д) — коэффициент неравномерности нагрузки на предприятиях связи
322. Индекс изменения трудовых затрат рассчитывается , где (укажите все правильные):
+а) — индекс изменения трудовых затрат
+б) — годовая трудоемкость проектируемого варианта системы обработки информации
в) — лимитная цена
+г) — годовая трудоемкость существующего варианта системы обработки информации
д) — коэффициент неравномерности нагрузки на предприятиях связи
323. Значение абсолютного снижения трудовых затрат , где (укажите все правильные):
+а) — коэффициент, учитывающий возможность полного высвобождения работников
+б) — разность между годовыми трудовыми затратами базового и проектируемого вариантов проектных решений
в) — коэффициент выбытия основных производственных фондов
+г) — годовой фонд времени одного работника, занятого в сфере обработки экономической информации
д) — коэффициент неравномерности нагрузки на предприятиях связи
324. Для выделения несмежных листов рабочей книги Excel, используются клавиши:
а) Alt
б) Shift
+в) Ctrl
г) Alt+Shift
д) Ctrl+Shift
325. Для выделения смежных листов рабочей книги Excel, используются клавиши:
а) Alt
+б) Shift
в) Ctrl
г) Alt+Shift
д) Ctrl+Shift
326. Минимальный элемент электронной таблицы Excel …
ОТВЕТ: ячейка
ОТВЕТ: клетка
327. При копировании в табличном процессоре MS Excel формулы =А3+$В$3 из ячейки С3 в ячейку D4 формула примет вид:
а) =А4+$В$4
+б) =В4+$С$4
в) =В4+$В$3
г) =А3+$В$4
д) =А4+$В$3
328. Адрес в электронной таблице указывает координату:
а) клетки в блоке клеток
б) данных в строке
+в) клетки в электронной таблице
г) данных в столбце
329. Данные в электронной таблице могут быть (укажите все правильные):
+а) текстом
+б) числом
в) оператором
+г) формулой
д) рисунком
330. Для настройки стандартных установок новой рабочей книги Excel, необходимо дать команду:
а) сервис, настройка
б) сервис, надстройки
+в) сервис, параметры
г) сервис, параметры автозамены
д) сервис, исправления
331. В электронных таблицах $А$5 – это:
а) относительная адресная ссылка
б) частичная абсолютная адресная ссылка
+в) абсолютная адресная ссылка
г) формула
д) функция
332. В MS Excel значение в ячейке С3 при копировании формулы =А1*В1 из ячейки С1 в ячейку С3 равно:
ОТВЕТ: 20
333. Операция выполняемая в Excel в отсутствии скобок в первую очередь …
а) «+»
+б) «^»
в) «*»
г) «/»
д) «-»
334. Выделенный блок ячеек в электронной таблице имеет диапазон:
+а) C3:E7
б) C3:E3
в) C3:C7
г) A1:E7
д) E3:E7
335. Текстом ячейке MS Excel является:
а) = В1+3
б) -13,06
+в) А1+А2
г) 5Е-6
д) =А$1/3
336. Табличный процессор предназначен для:
+а) обеспечения работы с таблицами данных
б) управления большими информационными массивами
в) создания и редактирования текстов
г) разработки графических приложений
д) автоматизации задач бухгалтерского учета
337. Правильная запись формулы в табличном процессоре Excel:
+а) =КОРЕНЬ(A1+B1)+(A1-С1)/B1^2+A1/5
б) =КОРЕНЬ(СУММ(A1:B1))+(A1-С1)/B1^2+A1^1/5
в) =КОРЕНЬ(A1+B1)+A1-C1/B1^2+A1/5
г) =КОРЕНЬ(A1+B1+A1-C1)/B1^2+A1/5
д) КОРЕНЬ(A1+B1)+(A1-C1)/B1^2+A1/5
338. В электронной таблице выделен блок ячеек, его диапазон:
+а) B2:C10
б) B2:B10
в) A1:C10
г) B2:C2
д) C2:C10
339. Логические функции табличных процессоров используются для:
+а) построения логических выражений
б) определения размера ежемесячных выплат для погашения кредита
в) исчисления логарифмов, тригонометрических функций
г) вычисления среднего значения, стандартного отклонения
д) вычисления длины строки, преобразования значений букв в строчные
340. Команды редактирования в электронной таблице выполняют функции:
+а) перемещения, вставки, удаления, копирования, замены
б) сохранения файлов, загрузки файлов
в) выравнивания данных в ячейках, назначения шрифтов, толщины линий
г) сортировки, фильтрации, консолидации
341. Создание формулы в электронной таблице Excel начинается с ввода знака _______.
ОТВЕТ: равно
ОТВЕТ: =
342. В электронных таблицах выражение -4Е+05 относится к следующему типу данных:
а) формула
б) текст
+в) число
г) дата
д) функция
343. В MS Excel ячейка, над содержимым которой производятся какие-то действия и выделенная рамкой, является ____________.
ОТВЕТ: активный
344. В электронной таблице выделен блок ячеек, его диапазон:
+а) A1:D4
б) A1:A4
в) A1:D1
г) D1:D4
д) A4:D4
345. В электронных таблицах выделена группа ячеек В2:С4. Сколько ячеек входит в эту группу?
ОТВЕТ: 6
346. В MS Excel результатом вычислений в ячейке С1 будет:
ОТВЕТ: 15
347. Дан фрагмент электронной таблицы, содержащий числа и формулы. В ячейке E5 после выполнения расчетов по формуле будет:
ОТВЕТ: 27
348. В MS Excel результатом вычислений в ячейке С1 будет:
ОТВЕТ: 15
349. Правильный вариант записи формулы в табличном процессоре Excel:
+а) =SIN(A1-1)^2/(A1-1)+B3^2
б) SIN((A1-1)^2)/(A1-1)+B3^2
в) =SIN(A1-1)^2/A1-1+B3^2
г) =SIN(A1-1)^2/(A1-1+B3^2)
д) =SIN^2(A1-1) /(A1-1)+B3^2
350. В электронных таблицах $А5 – это:
а) относительная адресная ссылка
+б) частичная абсолютная адресная ссылка
в) абсолютная адресная ссылка
г) формула
д) функция
351. В MS Excel результатом вычислений в ячейке С1 будет:
ОТВЕТ: 75
352. В электронных таблицах А5 – это:
+а) относительная адресная ссылка
б) частичная абсолютная адресная ссылка
в) абсолютная адресная ссылка
г) формула
д) функция
353. Какое значение будет в ячейке С3 MS Excel при копировании формулы =А1*$В$1 из ячейки С1 в ячейку С3:
ОТВЕТ: 30
354. Для переноса и копирования данных в электронной таблице используется:
+а) буфер промежуточного хранения
б) временный файл
в) системный файл
г) новый лист
д) новая книга
355. К какому типу данных в электронных таблицах относится выражение: $А$4*В5
ОТВЕТ: текст
ОТВЕТ: текстовый
356. После ввода формулы в ячейку электронной таблицы отображается:
а) введенная формула
+б) результат вычислений по этой формуле
в) формула с результатом вычислений
г) ничего не отображается
д) знак равенства
357. При копировании в табличном процессоре MS Excel формулы =$А$3+В3 из ячейки С3 в ячейку D2 формула примет вид:
а) =$А$3+С3
+б) =$А$3+С2
в) =$А$3+В2
г) =$А$2+В2
д) =$А$3+А2
358. Дан фрагмент электронной таблицы, содержащий числа и формулы. В ячейке H9 после выполнения расчетов по формуле будет:
ОТВЕТ: 1
359. В электронных таблицах указывает на использование абсолютной адресной ссылки знак:
а) !
+б) $
в) ?
г) %
д) =
360. Пользователь совершил ряд действий, после которых окно электронной таблицы приобрело вид:. После того, как пользователь нажал клавишу “ENTER” (щёлкнул кнопкой мышки), выполнилась операция…
а) появился дополнительный столбец ячеек
б) в выбранной строке добавилось количество ячеек
в) добавился еще один лист в документе
+г) появилась дополнительная строка ячеек
д) вместо 3-й строки появилась новая строка с пустыми ячейками
361. Обозначение ячейки $А1 является:
а) абсолютным адресом
б) относительным адресом
+в) смешанным адресом
г) текстом
д) формулой
362. В электронных таблицах нельзя удалить:
а) столбец
б) строку
+в) имя ячейки
г) содержимое ячейки
д) лист
363. Блок ячеек электронной таблицы задается:
а) номерами строк первой и последней ячейки
б) именами столбцов первой и последней ячейки
+в) указанием ссылок на первую и последнюю ячейку
г) указанием ссылок на первую ячейку А1 и последнюю ячейку
364. Дан фрагмент электронной таблицы, содержащий числа и формулы. В ячейке D7 после выполнения расчетов по формуле будет:
ОТВЕТ: 5
365. Пункты меню «Формат», «Ячейка» в MS Excel позволяют:
а) перейти на новый лист книги документа
+б) задать форматы чисел, изменить шрифт, задать тип выравнивания
в) изменить масштаб электронной таблицы
г) создать новую книгу электронной таблицы
д) сохранить книгу электронной таблицы
366. Какое значение будет в ячейке С3 при копировании формулы =$А$1*$В$1 из ячейки С1 в ячейку С3:
ОТВЕТ: 3
367. При копировании в табличном процессоре MS Excel формулы =А3+$В$3 из ячейки С3 в ячейку D2 формула примет вид:
а) =В3+$В$3
б) =А2+$В$2
+в) =В2+$В$3
г) =В2+$С$2
д) =А3+$В$2
368. В электронной таблице выделена группа ячеек А1:С2. Сколько ячеек входит в эту группу?
ОТВЕТ: 6
369. Диапазон ячеек в MS Excel – это:
а) строка электронной таблицы
б) группа смежных ячеек в строке
+в) группа смежных ячеек
г) группа смежных ячеек в столбце
д) столбец электронной таблицы
370. Пользователь совершил ряд действий, после которых окно электронной таблицы приобрело вид:. После того, как пользователь нажал клавишу “ENTER” (щёлкнул кнопкой мышки), выполнилась операция…
а) в первом столбце прибавилось количество ячеек
б) появилась дополнительная строка ячеек
+в) появился дополнительный столбец ячеек
г) в выбранном столбце прибавилось количество ячеек
д) вместо столбца С появился новый столбец с пустыми ячейками
371. Чтобы в MS Excel при копировании формулы из одной ячейки в другую адрес ячейки в формуле изменялся автоматически, нужно:
+а) чтобы ячейка имела относительный адрес
б) чтобы ячейка имела абсолютный адрес
в) выполнить команду Формат, Ячейки
г) выполнить команду Правка, Копировать
д) выполнить команду Данные, Сортировка
372. Правильный вариант записи формулы в табличном процессоре Excel:
+а) =COS(B1-A1)^3/(B1-A1)+C1^2
б) =COS^3(B1-A1)/(B1-A1)+C1^2
в) =COS(B1-A1)^3/B1-A1+C1^2
г) =COS(B1-A1^3)/(B1-A1+C1^2)
д) (COS(B1-A1)^3)/(B1-A1)+C1^2
373. Ячейка электронной таблицы определяется:
а) именами столбцов
+б) областью пересечения строк и столбцов
в) номерами строк
г) именами листов
д) именами книг
374. Статистические функции табличных процессоров используются для:
а) построения логических выражений
б) определения размера ежемесячных выплат для погашения кредита
+в) вычисления среднего значения, стандартного отклонения
г) исчисления логарифмов, тригонометрических функций
д) вычисления длины строки, преобразования значений букв в строчные
375. Формулы в электронной таблице обеспечивают:
а) формирование программы с уникальным именем, для которой задаются значения аргументов и функций
б) выполнение математических операций. Не содержат алфавитных и специальных символов
+в) выполнение арифметических, логических и других действий, производимых с данными из других ячеек
г) формирование диаграмм и графиков, таблиц, рисунков
376. В электронной таблице выделена группа ячеек А1:В3. Количество ячеек входящих в эту группу:
ОТВЕТ: 6
377. На рис. представлено окно табличного процессора MS Excel с окном табличного документа. На активном листе данного документа содержимым ячейки A95 является…
+а) текст “сумма”
б) формула “сумма”
в) текст “среднее
г) формула “среднее”
д) число 10
378. Абсолютный адрес в электронных таблицах Excel – это:
а) расстояние от клетки, содержащей формулу, до клетки, на которую в ней имеется ссылка
б) диапазон клеток, содержащих макрос
+в) адрес, в котором не изменяются номера строк и столбцов
г) полный адрес, указывающий номера строки и столбца клетки
379. В электронных таблицах выражение =$А$4*В5 относится к следующему типу данных:
+а) формула
б) текст
в) число
г) дата
д) функция
380. Логические формулы в MS Excel:
а) используют знаки арифметических действий
+б) содержат операторы сравнения, определяют истинность, логичность выражения
в) содержат результат вычисления – число
г) содержат порядок выполнения действий, принятый в математике
381. Команды форматирования в электронной таблице выполняют функции:
а) перемещения, вставки, удаления, копирования, замены
б) сохранения файлов, загрузки файлов
+в) выравнивания данных в ячейках, назначения шрифтов, толщины линий
г) сортировки, фильтрации, консолидации
382. Что из ниже перечисленного является текстом в ячейке Excel?
а) =D1+G1
б) 14,06
+в) F1+F2
г) 1,4Е06
д) =СУММ(А1:А5)
383. Числовые данные в электронной таблице обеспечивают:
а) формирование программы с уникальным именем, где пользователь задает значения аргументов и функций
+б) выполнение математических операций. Не содержат алфавитных и специальных символов
в) выполнение арифметических, логических и других действий, производимых с данными из других ячеек
г) логических действий, производимых с данными из других ячеек
384. Какое значение будет в ячейке С3 при копировании формулы =$А$1*В1 из ячейки С1 в ячейку С3:
ОТВЕТ: 2
385. Для выделения в электронной таблице Excel несколько блоков ячеек, используют на клавиатуре клавишу:
а) Caps Lock
+б) Ctrl
в) «Пробел»
г) Shift и Ctrl
д) Shift
386. Диапазон ячеек электронной таблицы – это:
а) множество ячеек, образующих область произвольной формы
б) множество заполненных ячеек электронной таблицы
в) множество пустых ячеек электронной таблицы
+г) множество ячеек, образующих область прямоугольной формы
д) множество ячеек, образующих область квадратной формы
387. Ячейка электронной таблицы называется текущей, если:
а) она видна на экране
б) в ней находится информация
в) она является пустой
г) она содержит формулу
+д) в ней находится курсор
388. Диапазон A5:D8 включает _______ ячеек электронной таблицы
ОТВЕТ: 16
389. В электронной таблице записано арифметическое выражение: 2 / 3 ^ 2 — (13 — 6) / 2 / 4. Математическую запись, соответствующая этому выражению:
а)
б)
в)
+г)
д)
390. Арифметическое выражение может быть записано в электронных таблицах в виде:
а) (4^5+3/6*7)/2/14*23/8
б) 4^(5+3)/6*7/2/14*23/8
в) 4^(5+3)/6*7/2*8/14*23
г) 4^(5+3)/6*7/2*8/14/23
+д) 4^((5+3)/6)*7/2*8/14/23
391. Числовая константа 300000 может быть записана в электронной таблице в виде:
а) 3,0Е+6
б) 30,0Е+5
+в) 3,0Е+5
г) 0,3Е+5
д) 0,3Е+7
392. Числовая константа12,3Е+4 может быть записана в электронной таблице в виде:
а) 1230
б) 123
+в) 123000
г) 12,3000
д) 0,00123
393. Дан фрагмент электронной таблицы: . Определить, какое из утверждений истинно для этого фрагмента таблицы.
а) В ячейку D4 введена формула: =(A1+B2+C3)/3
б) В ячейку D1 введена формула: =МАКС(A1:C1)
в) В ячейку B4 введена формула: =СУММ(B1:B3)*5
+г) В ячейку C4 введена формула: =МИН(A2;A3;C2)
д) В ячейку D2 введена формула: =СУММ(A2:C2)
394. Дан фрагмент электронной таблицы в режиме отображения формул. Чему равны значения в ячейках В2 и В3 (после выхода из режима отображения формул), если в них скопировано содержимое ячейки В1?
+а) 21 и 21
б) 1 и 1
в) 21 и 22
г) 22 и 23
д) 1 и 2
395. Чему равно значение, вычисленное по формуле: =ИЛИ(A1<10;A1>15), если в ячейке A1 электронной таблицы находится число 27?
+а) ИСТИНА
б) 15
в) 10
г) ЛОЖЬ
д) 27
396. Чему равно значение, вычисленное по формуле: =И(A1>15;A1<20), если в ячейке A1 электронной таблицы находится число 27?
а) ИСТИНА
б) 15
в) 10
+г) ЛОЖЬ
д) 27
397. В ячейку с адресом B1 занесена формула: =ЕСЛИ(A1>22;»НОЧЬ»;»ДЕНЬ»). Чему равно значение в ячейке B1 электронной таблицы, если в ячейке A1 находится число 13?
а) НОЧЬ
б) 22
в) ИСТИНА
г) ЛОЖЬ
+д) ДЕНЬ
398. Учащиеся проходят тестирование. Если сумма баллов больше 16, но меньше 19, то ученик получает оценку 4. Какое условие, проверяет, получит ли тестируемый оценку 4. Сумма баллов хранится в ячейке электронной таблицы с адресом C10.
а) ИЛИ(C10>16;C10<19)
+б) И(C10>16;C10<19)
в) ИЛИ(C10<16;C10>19)
г) И(C10<16;C10>19)
д) ИЛИ(C10=15;C10=19)
399. В ячейку с адресом C1 электронной таблицы занесена формула: =ЕСЛИ(A1<5;1;ЕСЛИ(A1>5;0;-1)). Чему равно значение в ячейке C1, если значение в ячейке A1 равно 15?
ОТВЕТ: 0
400. В ячейку с адресом C1 электронной таблицы занесена формула: =ЕСЛИ(И(A1>10;A1<15);1;0). Чему может быть равно значение в ячейке A1, если значение в ячейке C1 равно 1?
а) 10
б) 15
в) 16
г) 5
+д) 13
401.
а) =ЕСЛИ(B5<=3;A5;ЕСЛИ(B5>6;A5/2;A5/6))
б) =ЕСЛИ(B5<=3;A5;ЕСЛИ(И(B5>3;B5<6);A5/3;A5/2))
в) = ЕСЛИ(B5<=3;A5;ЕСЛИ(B5<6;A5/2;A5/3))
г) =ЕСЛИ(B5<=3;A5;ЕСЛИ(ИЛИ(B5>6;B5<3);A5/2;A5/3))
+д) = ЕСЛИ(B5<=3;A5;ЕСЛИ(B5<6;A5/2;A5/6))
402. Дан фрагмент электронной таблицы в режиме отображения формул. Чему равны значения в ячейках В2 и В3 (после выхода из режима отображения формул), если в них скопировано содержимое ячейки В1?
+а) 30 и 40
б) 40 и 50
в) 20 и 20
г) 40 и 60
д) 10 и 10
403. Дан фрагмент электронной таблицы, содержащий числа и формулы. Чему будет равно значение в ячейке В3 после выполнения расчетов по формулам?
а) 2,4
+б) 2,2
в) 4,2
г) 4
д) 4,4
404. Правильная форма записи арифметического выражения в электронных таблицах:
а) 2^(2*3,15)+7-26/(14*23-45)
б) 2^(2*3,15+7)-26/(14*23-45)
+в) (2^(2*3,15+7)-26)/(14*23-45)
г) 2^(2*3,15+7)-26/14*23-45
д) (2^(2*3,15+7)-26)/14*23-45
405.
а) количество минут
б) норма, абонентская плата
в) абонентская плата, плата сверх нормы
г) количество минут, оплата, норма
+д) норма, абонентская плата, плата сверх нормы
406. Покупатели магазина пользуются скидками в 10%, если покупка состоит более чем из пяти наименований товаров или стоимость покупки превышает 100 рублей. В ячейки электронной таблицы B2 и C2 занесены соответственно количество товаров и стоимость покупки для одного покупателя. Какая формула будет вычислять стоимость покупки с учётом скидки.
а) =ЕСЛИ(И(B2>5;C2>100);C2-0,1*C2;C2)
б) =ЕСЛИ(ИЛИ(B2>5;C2>100);C2+0,1*C2;C2)
в) =ЕСЛИ(ИЛИ(B2>5;C2>100);0,1*C2;C2)
г) =ЕСЛИ(ИЛИ(B2>5;C2>100);(C2-10*C2)/100;C2)
+д) =ЕСЛИ(ИЛИ(B2>5;C2>100);C2-0,1*C2;C2)
407. Дано исходное состояние таблицы:. В ячейку C2 занесена формула: =ЕСЛИ(C1=0;СУММ(A1:A3);ЕСЛИ(C1=1;СУММ(B1:B3);»Данных нет»)). Какое значение находится в ячейке C2, если ячейка C1 пустая?
а) «Данных нет»
+б) 60
в) 45
г) 40
д) сообщение об ошибке
408. В ячейку B1 электронной таблицы занесена формула: =0,314Е+1*2*A1. Чему равно значение в ячейке B1, если ячейка A1 содержит число 6?
а) 9,14
б) 12,314
+в) 37,68
г) 3,768
д) сообщение об ошибке
409. Арифметическое выражение может быть записано в ячейке электронной таблицы в виде:
а) =30*(3,14^3-5/6*2,71)/5*(3,14^(3+23)/56-6*2,71)
б) =30*(3,14^3-5/6*2,71)/(5*(3,14^3+23/56-6*2,71))
в) =30*(3,14^3-5/(6*2,71))/5*(3,14^(3+23)/56-6*2,71)
г) =30*(3,14^3-5/6/2,71)/5*(3,14^(3+23)/56-6*2,71)
+д) =30*(3,14^3-5/6/2,71)/5/(3,14^((3+23)/56)-6*2,71)
410. Дано исходное состояние таблицы в режиме отображения формул: . Что появится в ячейках A2, B2 и C2 в режиме отображения значений?
а) 1; 1; 1
+б) 25; 12,5; 1
в) 2,5; 12,5; 1
г) 1; 12,5; 1
д) 25; 1; 1
411. В MS Exsel при копировании содержимого ячейки A2 в ячейки B2 и A3 в них были занесены формулы $A1+C1 и $A2+B2 соответственно. Что было записано в ячейке A2?
а) $A$1+B1
+б) $A1+B1
в) $A1+C1
г) $A$1+C1
д) A1+B1
412. Дан фрагмент электронной таблицы: . Определить диапазон(ы) ячеек, по значениям которых была построена диаграмма.
а) A1:C1 и A3:C3
+б) A3:C3
в) A1:C1
г) C1:C3
д) A1:C3
Перейти к контенту

Решение ГИА в форме ОГЭ по информатике 4 задание из демоверсии 2021 года. Задание на умение анализировать простейшие модели объектов
Давайте познакомимся с условием поставленной задачи.
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.

Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт С. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Ответ: 8.
Давайте проведем визуализацию данной таблицы.

Мы представили входную информацию в более наглядном виде. Из табличной структуры получили структуру в виде графов. Из полученного рисунка видно, что анализ будет проходить гораздо лучше. Мы должны найти кратчайший путь между пунктом А и Е проходящий через пункт С. Для этого просто переберем все данные маршруты.

Ответ: 8.
Изменения структуры и содержания КИМ 2021 отсутствуют.
Добрый день! Сегодня посмотрим, как «бороться» с 4 заданием из ОГЭ по информатике 2023.
Четвёртное задание из ОГЭ по информатике достаточно простое, хотя и может показаться кому-то скучным.
Рассмотрим простой пример из тренировочных заданий для 4 задания.
Задача (Стандартная)
Между населёнными пунктами A, B, C, D построены дороги, протяжённость которых (в километрах) приведена в таблице.
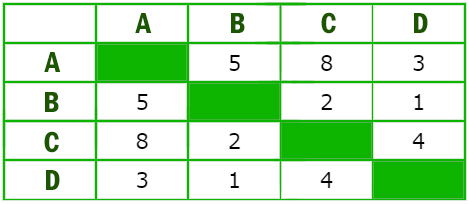
Определите длину кратчайшего пути между пунктами A и C. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Решение:
Расставим точки, которые символизируют города, примерно по кругу.
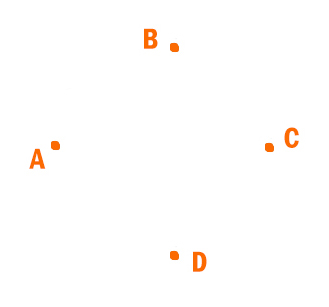
Проведём дороги между городами так, как указано в таблице. Если на пересечении городов стоит число, значит, мы проводим линию между этими точками.
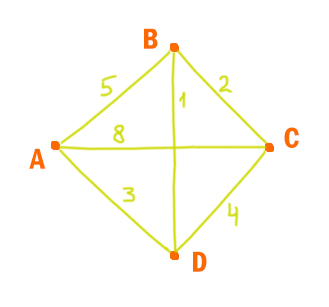
Поставим числа над каждой дорогой, характеризующие длины каждого отрезка.
Теперь найдём самый короткий путь из A в C.
Можно сразу попасть из A в C по прямой дороге за 8. Если пойдём через пункт D, то придём в город C за 7. Через город B так же можно прийти за 7 километров.
Но мы видим, что длина дороги из D в B равна 1. Попытаемся эту дорогу использовать при составлении маршрута. Получим путь: A-D-B-C. Получается 3+1+2=6. Это и есть искомый кратчайший путь.
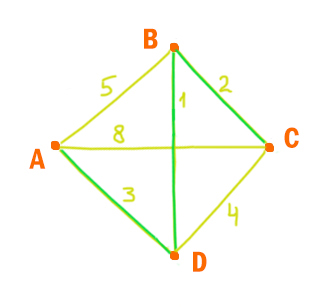
Ответ: 6
Задача (C обязательным узлом)
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых
(в километрах) приведена в таблице.
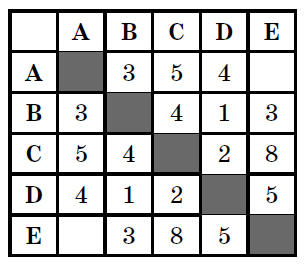
Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт С.
Передвигаться можно только по дорогам, протяжённость которых указана в таблице, два раза
посещать один пункт нельзя.
Решение:
Расставим точки по кругу. Точка С — это обязательный пункт.
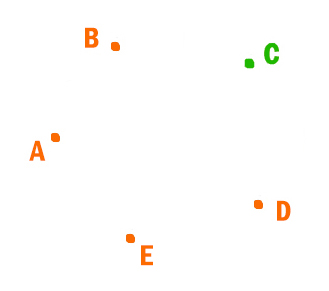
Проведём линии между городами так, как указано в задаче. Поставим числа над каждой дорогой, чтобы было понятно, к какой дороге конкретное число принадлежит.
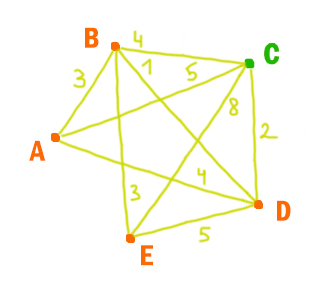
Теперь можно начать искать кратчайший путь от A до E, проходящего через C.
Найдём кратчайший путь до точки С. Это и есть путь A-C. Он равен 5.
От С до E можно добраться разными путями:
C-E = 8
C-D-E = 2 + 5 = 7
C-B-E = 4 + 3 = 7
Видим длину BD = 1. Попытаемся использовать эту дорогу!
C-D-B-E = 2 + 1 + 3 = 6
Это и есть самый короткий путь.
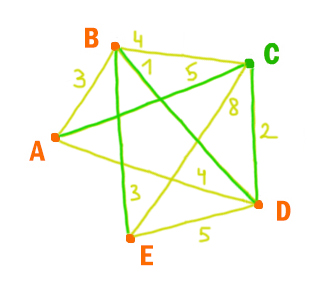
В ответе напишем путь: A-C-D-B-E = 5 + 6 = 11.
Ответ: 11
Задача (Закрепление)
Между населёнными пунктами А, B, С, D, E, F построены дороги, протяжённости которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
.jpg?8)
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
Решение:
Расставим точки А, B, С, D, E, F по кругу.
.jpg?8)
Теперь в соответствии с таблицей соединим эти города, указав числа возле линий. Стараемся сделать рисунок, как можно более понятным, применяем разные цвета.
.jpg?8)
Получилась наглядная карта городов. Оценив все пути от пункта A до пункта F, определяем, что самый короткий путь будет 4 + 3 + 4 + 3 = 14.
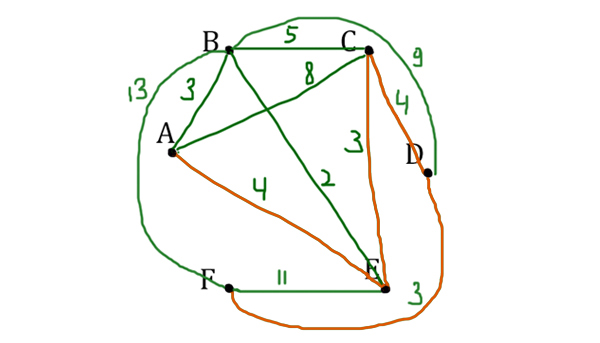
Ответ: 14.
ОГЭ 4.9 Определите длину кратчайшего пути между пунктами A и F
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых (в километрах) приведена в таблице. Определите длину кратчайшего пути между пунктами A и F. Передвигаться можно только по дорогам, протяжённость которых указана в таблице. СтатГрад Вариант ИН2190501 17 марта 2022 – задание №4 Решение: 2+1+1+1+2 = 7 Ответ: 7
Читать далее
ОГЭ 4.8 Между населёнными пунктами A, B, C, D, E построены дороги
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых приведена в таблице. Определите длину кратчайшего пути между пунктами A и E, проходящего через пункт D. Передвигаться можно только по дорогам, указанным в таблице. СтатГрад Вариант ИН2190501 25 апреля 2022 – задание №4
Читать далее
ОГЭ 4.7. Определите длину кратчайшего пути между пунктами A и D
Определите длину кратчайшего пути между пунктами A и D. Передвигаться можно только по дорогам, протяжённость которых указана в таблице. Между населёнными пунктами A , B , C , D , E построены дороги, протяжённость которых приведена в таблице.
Читать далее
ОГЭ 4.6. Определите длину кратчайшего пути между пунктами B и D.
ОГЭ 4. Определите длину кратчайшего пути между пунктами B и D. Досрочный открытый вариант №1 ЕГЭ по информатике 2020. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице. Определите длину кратчайшего пути между пунктами B и D. Передвигаться можно только по дорогам, протяжённость которых указана в таблице. …
Читать далее
ОГЭ 4.5. Определите длину кратчайшего пути между пунктами A и D, проходящего через пункт C.
Определите длину кратчайшего пути между пунктами A и D, проходящего через пункт C. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице (см. рисунок). Определите длину кратчайшего пути между пунктами A и D, проходящего через пункт C. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Читать далее
ОГЭ 4.4. Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт D.
Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт D. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице (см. рисунок). Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт D. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Читать далее
ОГЭ 4.3. Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт E
Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт E. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице (см. рисунок). Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Читать далее
ОГЭ 4.2. Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт D
Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт D. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице (см. рисунок). Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт D. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Читать далее
ОГЭ 4.1. Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт B
Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт B Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице (см. рисунок). Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт B. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Читать далее