1. Задание 1 № 406563
Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета.
Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответе нужно записать
число 51118).
| Мобильный интернет | 2,5 Гб | 3 Гб | 3,25 Гб | 1 Гб |
| Номер месяца |
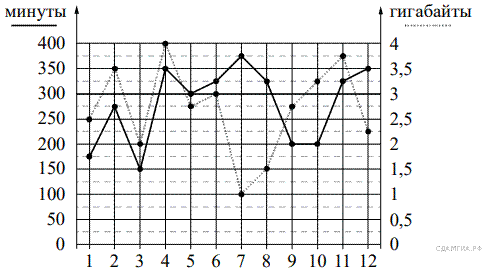
На рисунке точками показано количество минут исходящих вызовов и трафик мобильного интернета в гигабайтах, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2019 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.
В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляла 350 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:
• пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
• пакет интернета, включающий 3 гигабайта мобильного интернета;
• пакет СМС, включающий 120 СМС в месяц;
• безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и СМС сверх пакета тарифа указана в таблице.
| Исходящие вызовы | 3 руб./мин. |
| Мобильный интернет (пакет) | 90 руб. за 0,5 Гб |
| СМС | 2 руб./шт. |
Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 110 СМС.
Решение.
Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года.
Из рисунка видно, что 2,5 Гб было потрачено в первый месяц, 3 Гб — потрачено в шестой, 3,25 Гб — в десятый, 1 Гб — в седьмой.
Ответ: 16107.
2. Задание 2 № 406675
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику израсходованных минут и гигабайтов.
| ПЕРИОДЫ | ХАРАКТЕРИСТИКИ | |
| А) январь−февраль Б) февраль−март В) август–сентябрь Г) ноябрь–декабрь | 1) Расход минут увеличился, а расход гигабайтов уменьшился. 2) Расход гигабайтов увеличился, а расход минут уменьшился. 3) Расход минут увеличился, и расход гигабайтов увеличился. 4) Расход минут уменьшился, и расход гигабайтов уменьшился. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Решение.
Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года, а сплошной линей — количество минут исходящих вызовов.
За период январь−февраль расход минут увеличился, и расход гигабайтов увеличился.
За период февраль−март расход минут уменьшился, и расход гигабайтов уменьшился.
За период август–сентябрь расход гигабайтов увеличился, а расход минут уменьшился.
За период ноябрь–декабрь расход минут увеличился, а расход гигабайтов уменьшился.
Таким образом, получается соответствие: А — 3, Б — 4, В — 2, Г — 1.
Ответ: 3421.
3. Задание 3 № 406564
Сколько рублей потратил абонент на услуги связи в июне?
Решение.
По рисунку видно, что за июнь абонент потратил 3 Гб интернета, 325 минут исходящих вызовов, и в условии сказано, что за год отправил 110 СМС.
Количество потраченного интернета и СМС не превысило это количество в пакете тарифа, а исходящих вызовов сверх пакета было потрачено минут.
Вычислим стоимость услуг связи, потраченных абонентом в июне:
рублей.
Ответ: 425.
4. Задание 4 № 406565
Какое наименьшее количество минут исходящих вызовов за месяц было в 2019 году?
Решение.
Сплошной линей на графике показано количество минут исходящих вызовов, израсходованных за каждый месяц года.
Из рисунка видно, что в третьем месяце было потрачено 150 минут, что является наименьшим количеством за 2019 год.
Ответ: 150.
5. Задание 5 № 367694
Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
| Место | Цена земли (млн руб.) | Цена строительства (млн руб.) | Длина коммуникаций (м) | Стоимость аренды за 1 м2 (руб./месяц) |
| Центр | 64,4 | |||
| Окраина | 11,2 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
На плане (см. рисунок) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.
Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м2. А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.
Решение.
Стоимость постройки ТРК в центре города равна
рублей.
Стоимость постройки ТРК на окраине города равна
рублей.
Разница в стоимости составляет
рублей.
Разница в стоимости аренды составляет
рублей.
Значит, более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций через 34,5 месяцев. Округляя, получаем ответ — 35 месяцев.
Ответ: 35.
6. Задание 6 № 203743
Запишите в ответе номера выражений, значения которых положительны.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
Решение.
Найдём значения выражений:
Таким образом, искомое выражение указано под номером 3.
7. Задание 7 № 314800
На координатной прямой отмечены числа а и b. Какое из следующих утверждений неверно?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Решение.
Заметим, что и , и проверим все варианты ответа:
1) , значит, — верно.
2) — верно.
3) — верно, поскольку , а
4) — неверно.
Неверным является утверждение 4.
Примечание.
Нетрудно заметить, что справедливо неравенство:
8. Задание 8 № 341704
Найдите значение выражения при a = 7,7.
Решение.
Упростим выражение:
Подставим в полученное выражение значение
Ответ: 0,66.
9. Задание 9 № 338610
Решите уравнение
Решение.
Последовательно получаем:
Ответ: −6.
10. Задание 10 № 325541
Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся.
Решение.
Вероятность того, что стрелок промахнётся равна 1 − 0,8 = 0,2. Вероятность того, что стрелок первые два раза попал по мишеням равна 0,82 = 0,64. Откуда, вероятность события, при котором стрелок сначала два раза попадает в мишени, а третий раз промахивается равна 0,64 · 0,2 = 0,128.
Ответ: 0,128.
11. Задание 11 № 193089
Найдите значение по графику функции , изображенному на рисунке.
Решение.
Абсцисса вершины параболы равна −1, поэтому откуда Парабола пересекает ось ординат в точке с ординатой 3, поэтому Тем самым, уравнение параболы принимает вид Поскольку парабола проходит через точку (−1; 2), имеем:
Верный ответ указан под номером 2.
Ответ: 2.
12. Задание 12 № 338396
Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.
Решение.
Найдем расстояние, на котором находится наблюдатель от места удара молнии:
Ответ: 3.
13. Задание 13 № 311312
Решите неравенство .
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Решение.
Решим данное неравенство:
. Произведение двух сомножителей будет больше нуля, если его сомножители имеют одинаковый знак.
В данном случае это выполняется при следующих значениях :
1) ;
2) ;
Решением неравенства будет являться объединение этих промежутков: , что соответствует первому варианту ответа.
Ответ: 1
14. Задание 14 № 394426
Давление воздуха под колоколом равно 625 мм ртутного столба. Каждую минуту насос откачивает из-под колокола 20% находящегося там воздуха. Определите давление (в мм рт. ст.) через 5 минут после начала работы насоса.
Решение.
Через минуту давление воздуха (в мм рт. ст.) под колоколом станет через две минуты — …, через 5 минут давление станет или
мм рт. ст.
Ответ: 204,8.
15. Задание 15 № 348371
Высота BH ромба ABCD делит его сторону AD на отрезки AH = 44 и HD = 11. Найдите площадь ромба.
Решение.
Заметим, что сторона ромба AB = AD = AH + HD = 44 + 11 = 55.
Из прямоугольного треугольника ABH найдем BH по теореме Пифагора:
Площадь ромба можно найти как произведение основания на высоту:
Ответ: 1815.
16. Задание 16 № 339975
Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Решение.
Радиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника по теореме Пифагора найдём
Найдём
Ответ: 10.
17. Задание 17 № 324017
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Решение.
Проведём построение и введём обозначения, как показано на рисунке. Учитывая, что и получаем Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники и , они прямоугольные, следовательно, треугольники и равны, откуда то есть высота Найдём площадь ромба как произведение стороны на высоту:
Ответ: 18.
18. Задание 18 № 311485
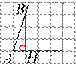
На квадратной сетке изображён угол . Найдите .
Решение.
Опустим перпендикуляр BH. Треугольник ABH — прямоугольный. Таким образом,
Ответ: 3.
19. Задание 19 № 341676
Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
1) «Треугольника со сторонами 1, 2, 4 не существует» — верно, большая сторона треугольника должна быть меньше суммы двух других.
2) «Смежные углы равны» — неверно, смежные углы и связаны соотношением: .
3) «Все диаметры окружности равны между собой» — верно.
Ответ: 13.
20. Задание 20 № 311591
Решите уравнение:
Решение.
Перенесем все члены влево и применим формулу разности квадратов:
Другой способ. Раскроем скобки, пользуясь формулой квадрата разности:
Ответ: 1.
21. Задание 21 № 314507
Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.
Решение.
Пусть скорость пешехода — x км/ч, , тогда скорость велосипедиста равна (x + 11) км/ч.
Составим таблицу по данным задачи:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| Пешеход | |||
| Велосипедист |
Так как по пути велосипедист сделал остановку на ч., составим уравнение:
Корень −22 не подходит нам по условию задачи. Скорость пешехода равна 5 км/ч.
Ответ: 5 км/ч.
22. Задание 22 № 353274
Постройте график функции . Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Решение.
График данной функции — это график параболы отрицательная часть которого отражена относительно оси Этот график изображён на рисунке:
Прямая, параллельная оси абсцисс задаётся формулой где — постоянная. Из графика видно, что прямая может иметь с графиком функции не более четырёх общих точек.
Ответ: 4.
23. Задание 23 № 333321
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56 .
Решение.
Углы и равны как накрест лежащие, углы и равны как вертикальные, следовательно, треугольники и подобны по двум углам.
Значит, Следовательно,
Откуда
Ответ: 40.
24. Задание 24 № 349626
Окружности с центрами в точках и не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.
Решение.
Проведём построения и введём обозначения, как показано на рисунке. Пусть Рассмотрим треугольники и они прямоугольные, углы и равны как вертикальные, следовательно, треугольники подобны, откуда Отношение радиусов равно отношению диаметров.
25. Задание 25 № 311708
В прямоугольном треугольнике ABC с прямым углом B, проведена биссектриса угла A. Известно, что она пересекает серединный перпендикуляр, проведённый к стороне BC в точке K. Найдите угол BCK, если известно, что угол ACB равен 40°.
Решение.
Так как биссектриса острого угла A прямоугольного треугольника ABC не может быть перпендикулярна BC, то биссектриса угла A и серединный перпендикуляр к BC имеют ровно одну общую точку.
Пусть N — середина BC. Рассмотрим окружность, описанную около треугольника ABC. Пусть серединный перпендикуляр к BC пересекает меньшую дугу BC в точке L (см. рисунок), тогда точка L является серединой этой дуги, ⌣BL = ⌣LC. Но тогда как вписанные углы, опирающиеся на равные дуги, а отсюда AL — биссектриса . Но это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой . Заметим, что как вписанные углы, опирающиеся на равные дуги.
Пусть . Четырехугольник ACLB — вписанный, поэтому , то есть , откуда Так как точки K и L совпадают,
Ответ: 25°.
Он-местоимение,выраженное подлежащим
никогда-обстоятельство
не-частица,входящая в роль сказуемого
давал-глагол,выраженный сказуемым
себя-местоимение
в-предлог
обиду-существительное,выраженное дополнением
Скорее всего — да………..
Артист кино великолепно сыграл главную роль в фильме.
Мне с тобой не по пути.
Моей маме поможет не кто иной,как папа
тебе злость не к лицу
Для электрической
системы, представленной на схеме
12 (выключатели
В1и
В2 включен во
всех режимах),
выполнить расчет и анализ переходного
процесса для трех режимов.
1. Режим
– трехфазного
КЗ
В заданной точке
,
которая определена параметром
на воздушной линии
Л1 (выключатель В3
включен), для
рассчитать:
-
– действующие
значения периодической слагаемой тока
короткого замыкания; -
–
ударный ток и
мощность КЗ; -
действующие значения
периодической слагаемой тока генератора
Г8,
посылаемого в место КЗ для трех моментов
времени (результаты представить на
напряжении ступени КЗ 230 кВ):
а)
– для
;
б)
– для
с.;
в)
– для
(ток становившегося режима КЗ), принимая
![]()
;
-
–
остаточное напряжение
на шинах генератора Г8 (узел)
в установившемся режиме КЗ.
2. Режим
– несимметричного
КЗ
В заданной точке
схемы,
которая определена параметром
(выключатель В3
включен), рассчитать:
-
– действующее
значение периодической слагаемой тока
КЗ поврежденной фазы (между цепями Л1
имеется взаимная индуктивность нулевой
последовательности); -
и
,
– симметричные
составляющие напряжения и остаточные
напряжения неповрежденных фаз; -
построить векторные
диаграммыи
;
-
– ток фазы
неповрежденной
цепи Л1; -
симметричные
составляющие напряжениядля узлов:
,
«
»,
«
»,
С1; по
полученным результатам построить эпюры
симметричных составляющих напряжений;
для наглядности
результата напряжения указанных узлов
представить в именованных единицах,
приведенных к ступени КЗ (230 кВ).
3. Режим
– продольной
несимметрии
Для режима (
),
соответствующего отключению ранее
поврежденной фазы выключателем В3,
рассчитать:
-
– ток неповрежденной
фазына участке
;
-
– ток фазы
неповрежденной
цепи Л1
(участок);
-
– падение напряжения
в месте разрыва фазы;
-
симметричные
составляющие напряжения,
,
для узлов: Г8,
,
,
;
по полученным
результатам построить эпюры симметричных
составляющих напряжений; для
наглядности результата напряжения
указанных узлов представить в именованных
единицах, приведенных к ступени 230 кВ; -
,
,– фазные напряжения
на клеммевыключателя В3;
-
– фазное напряжение
отключенной фазына клемме
;
К моменту
отключения фазы
выключателя фаза
эквивалентного вектора ЭДС
генераторов
Г5, Г6, Г7, Г8 ЭСТ1 (![]()
)
опережала фазу
вектора ЭДС
системы С1 (![]()
)
на
.
Задание № 20
Для электрической
системы, представленной на схеме
20, выполнить
расчет и анализ переходного процесса
для трех режимов.
1. Режим
– трехфазного
КЗ
В заданной точке
схемы
для
рассчитать:
-
– действующие
значения периодической слагаемой тока
короткого замыкания; -
–
ударный ток и
мощность КЗ; -
–
остаточное напряжение
на шинах генератора Г10
(узел);
-
– действующие
значения периодической слагаемой тока
генератора Г10
дляс;
-
– действующие
значения тока двухфазного короткого
замыкания.
2. Режим
– несимметричного
КЗ
В заданной точке
схемы,
которая определена параметром
на Л3,
рассчитать:
-
– действующее
значение периодической слагаемой тока
КЗ поврежденных фаз; -
и
– симметричные
составляющие напряжения и остаточное
напряжение неповрежденной фазы; -
построить векторные
диаграммыи
;
3. Режим
– продольной
несимметрии
Для режима (
),
соответствующего отключению ранее
поврежденных фаз, рассчитать:
-
– ток неповрежденной
фазына участке
;
-
– падение напряжения
в месте разрыва фазы -
– ток фазы
не поврежденной
цепи Л3.
К моменту
отключения поврежденных фаз угол
расхождения векторов ЭДС двух
эквивалентных источников схемы,
расположенных по обе стороны места
разрыва, составляет
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Свойства числа 341676
| Множители | 2 * 2 * 3 * 3 * 9491 | |
| Делители | 1, 2, 3, 4, 6, 9, 12, 18, 36, 9491, 18982, 28473, 37964, 56946, 85419, 113892, 170838, 341676 | |
| Количество делителей | 18 | |
| Сумма делителей | 863772 | |
| Предыдущее целое | 341675 | |
| Следующее целое | 341677 | |
| Простое число? | NO | |
| Предыдущее простое | 341659 | |
| Следующее простое | 341681 | |
| 341676th простое число | 4895327 | |
| Является числом Фибоначчи? | NO | |
| Число Белла? | NO | |
| Число Каталана? | NO | |
| Факториал? | NO | |
| Регулярное число? | NO | |
| Совершенное число? | NO | |
| Полигональное число (s < 11)? | NO | |
| Двоичное | 1010011011010101100 | |
| Восьмеричная | 1233254 | |
| Двенадцатеричный | 145890 | |
| Шестнадцатиричная | 536ac | |
| Квадрат | 116742488976 | |
| Квадратный корень | 584.53058089376 | |
| Натуральный логарифм | 12.741618198587 | |
| Десятичный логарифм | 5.5336144741642 | |
| Синус | 0.45770459452592 | |
| Косинус | -0.88910432692112 | |
| Тангенс | -0.51479289962619 |
Математические настройки для вашего сайта
Выберите язык:
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
中文
日本語
한국어
Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.
© 2022
numberempire.com
Все права защищены
А=0.2 в
в-0.2 в=0.8 в
0,8=80%
Ответ:80 %
Контакты
По любым вопросам обращайтесь на e-mail: reshimvsecom@yandex.ru
Огэ математика 341676
Задание 19 № 341676
Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
Если утверждений несколько, запишите их номера в порядке возрастания.
1) «Треугольника со сторонами 1, 2, 4 не существует» — Верно, большая сторона треугольника должна быть меньше суммы двух других.
2) «Смежные углы равны» — Неверно, смежные углы и связаны соотношением: .
Задание 19 № 341676
1 Треугольника со сторонами 1, 2, 4 не существует.
Oge. sdamgia. ru
13.09.2018 9:20:52
2018-09-13 09:20:52
Источники:
Https://oge. sdamgia. ru/problem? id=341676
OГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Огэ математика 341676
Огэ математика 341676
Огэ математика 341676
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Прием работ окончен
Какое из следующих утверждений верно?
1) Внешний угол треугольника равен сумме его внутренних углов.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
1 Внешний угол треугольника равен сумме его внутренних углов.
Math-oge. sdamgia. ru
16.09.2017 16:46:45
2017-09-16 16:46:45
Источники:
Https://math-oge. sdamgia. ru/test? id=24935080
РЕШУ ГВЭ, математика 9: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Огэ математика 341676
Огэ математика 341676
Огэ математика 341676
Задание 8 № 341676
Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
Если утверждений несколько, запишите их номера в порядке возрастания.
1) «Треугольника со сторонами 1, 2, 4 не существует» — Верно, большая сторона треугольника должна быть меньше суммы двух других.
2) «Смежные углы равны» — Неверно, смежные углы и связаны соотношением: .
Задание 8 № 341676
3 Все диаметры окружности равны между собой.
Math9-gve. sdamgia. ru
24.11.2019 13:15:25
2019-11-24 13:15:25
Источники:
Https://math9-gve. sdamgia. ru/problem? id=341676

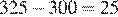 минут.
минут.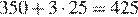 рублей.
рублей.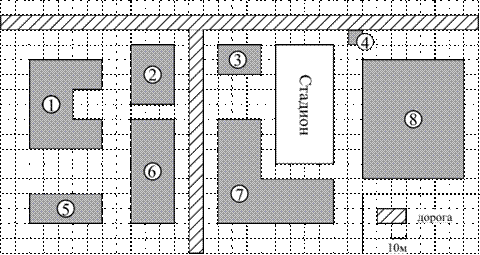
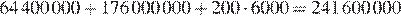 рублей.
рублей.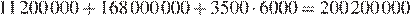 рублей.
рублей.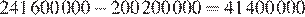 рублей.
рублей.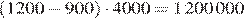 рублей.
рублей.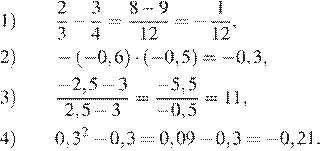

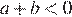
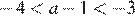
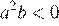
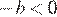
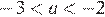 и
и 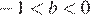 , и проверим все варианты ответа:
, и проверим все варианты ответа: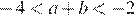 , значит,
, значит, 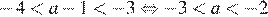 — верно.
— верно.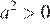 , а
, а 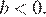
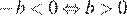 — неверно.
— неверно.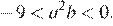
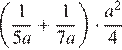 при a = 7,7.
при a = 7,7.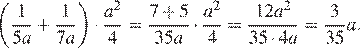
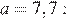
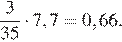
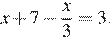
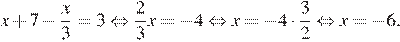
 по графику функции
по графику функции 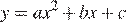 , изображенному на рисунке.
, изображенному на рисунке.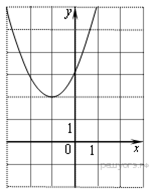
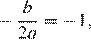 откуда
откуда 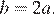 Парабола пересекает ось ординат в точке с ординатой 3, поэтому
Парабола пересекает ось ординат в точке с ординатой 3, поэтому 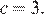 Тем самым, уравнение параболы принимает вид
Тем самым, уравнение параболы принимает вид 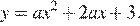 Поскольку парабола проходит через точку (−1; 2), имеем:
Поскольку парабола проходит через точку (−1; 2), имеем: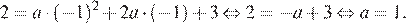
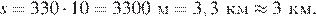
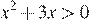 .
.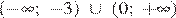
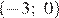
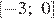
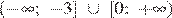
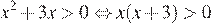 . Произведение двух сомножителей будет больше нуля, если его сомножители имеют одинаковый знак.
. Произведение двух сомножителей будет больше нуля, если его сомножители имеют одинаковый знак. :
: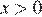 ;
;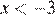 ;
;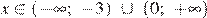 , что соответствует первому варианту ответа.
, что соответствует первому варианту ответа.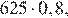 через две минуты —
через две минуты — 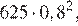 …, через 5 минут давление станет
…, через 5 минут давление станет 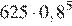 или
или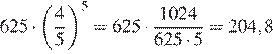 мм рт. ст.
мм рт. ст.
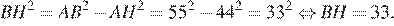
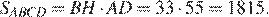

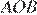 по теореме Пифагора найдём
по теореме Пифагора найдём 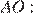
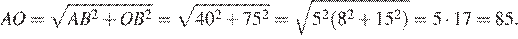
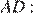
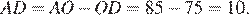
 Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба. Проведём построение и введём обозначения, как показано на рисунке. Учитывая, что
Проведём построение и введём обозначения, как показано на рисунке. Учитывая, что 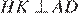 и
и 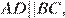 получаем
получаем 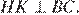 Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники
Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники 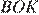 и
и 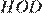 , они прямоугольные,
, они прямоугольные, 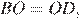
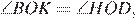 следовательно, треугольники
следовательно, треугольники 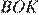 и
и  то есть высота
то есть высота 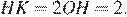 Найдём площадь ромба как произведение стороны на высоту:
Найдём площадь ромба как произведение стороны на высоту: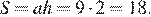

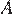 . Найдите
. Найдите 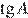 .
.
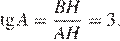
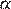 и
и 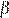 связаны соотношением:
связаны соотношением: 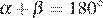 .
.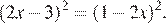
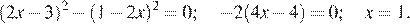
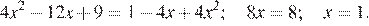
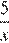
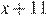
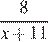
 ч., составим уравнение:
ч., составим уравнение: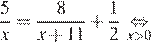
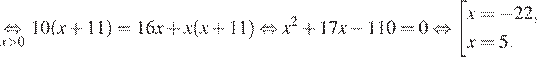
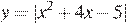 . Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?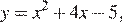 отрицательная часть которого отражена относительно оси
отрицательная часть которого отражена относительно оси 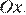 Этот график изображён на рисунке:
Этот график изображён на рисунке: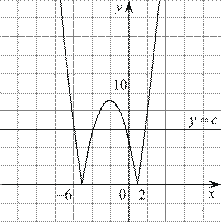
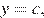 где
где  — постоянная. Из графика видно, что прямая
— постоянная. Из графика видно, что прямая  может иметь с графиком функции не более четырёх общих точек.
может иметь с графиком функции не более четырёх общих точек. Углы
Углы 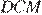 и
и 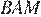 равны как накрест лежащие, углы
равны как накрест лежащие, углы 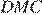 и
и 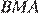 равны как вертикальные, следовательно, треугольники
равны как вертикальные, следовательно, треугольники 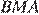 подобны по двум углам.
подобны по двум углам.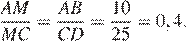 Следовательно,
Следовательно,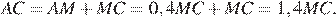
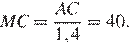
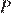 и
и 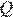 не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.
не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.
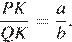 Рассмотрим треугольники
Рассмотрим треугольники 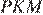 и
и 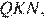 они прямоугольные, углы
они прямоугольные, углы 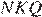 равны как вертикальные, следовательно, треугольники подобны, откуда
равны как вертикальные, следовательно, треугольники подобны, откуда 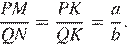 Отношение радиусов равно отношению диаметров.
Отношение радиусов равно отношению диаметров.
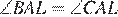 как вписанные углы, опирающиеся на равные дуги, а отсюда AL — биссектриса
как вписанные углы, опирающиеся на равные дуги, а отсюда AL — биссектриса 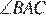 . Но это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой
. Но это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой 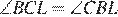 как вписанные углы, опирающиеся на равные дуги.
как вписанные углы, опирающиеся на равные дуги.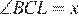 . Четырехугольник ACLB — вписанный, поэтому
. Четырехугольник ACLB — вписанный, поэтому 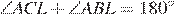 , то есть
, то есть 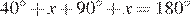 , откуда
, откуда 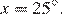 Так как точки K и L совпадают,
Так как точки K и L совпадают,